Ad l)

Równanie charakterystyczne:

Jeżeli S₁,S₂,S_n są pierwiastkami tego równania to rozwiązanie ogólne równania jednorodnego ma postać:

C_1...C_n - stałe całkowania wynikające z warunków początkowych

Gdybyśmy wszystkie pierwiastki rozmieścili na płaszczyźnie liczb zespolonych , zwanej płaszczyzną pierwiastków, to okazałoby się , że wszystkie pierwiastki które nas interesują czyli układu stabilnego leżą z lewej strony osi liczb urojonych lub w lewej półpłaszczyźnie płaszczyzny pierwiastków. Na podstawie tego możemy sformułować kryterium stabilności:

Układ regulacji automatycznej jest stabilny Jeżeli wszystkie pierwiastki równania charakterystycznego leżą w lewej półpłaszczyźnie płaszczyzny pierwiastków- stabilność asymptotyczna, jeżeli istnieje jeden pierwiastek zerowy układ jest stabilny nieasymptotycznie.

Ad 2)

O własnościach regulatora czyli także o jego stabilności decyduje doprowadzenie uchybu ustalonego E_s do wartości zerowej. Osiąga się to poprzez wprowadzenie wymaganego poziomu astatyzmu, czyli liczbę biegunów transmitancji Go(s),

Transmitancja układu zamkniętego regulacji

Ocena stabilności układu zamkniętego może być dokonana na podstawie układu otwartego, ponieważ jak widzimy, mianowniki wyrażeń określających transmitancję układu zamkniętego zawierają wyrażenie

l+G₀(s)

Które można traktować jako równanie charakterystyczne

l+G₀(s)=0

i znaleźć wartości s, które spełniają to równanie. Jak wiemy układ będzie stabilny jeżelipierwiastki te będą w lewej półpłaszczyźnie zmiennej zespolonej s. Istnieją również wskaźniki Jakości regulacji. Jednym z nich jest częstotliwość graniczna modułu Lm charakterystyki amplitudowej.

Oznacza ona częstotliwość ω_m dla której' ^

L_mo(ω_m)=0

lub

|G₀(jω_m)|=1

Gdzie Go(j(ω_m) transmitancja toru otwartego układu regulacji

Ad 3)

Jeżeli układ posiada l wejście wówczas macierz wejść „B" ma postać kolumnową o wymiarach nxl, natomiast macierz wyjść „C" postać wierszową l x n.

Wówczas macierz stanu zgodnie ze wzorem równania stanu

X(t) = A • X(t) + B • U(t) Gdzie A - macierz

stanu wygląda następująca:

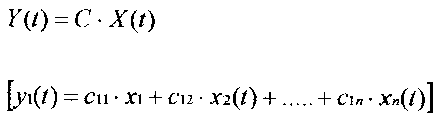
Równanie wyjścia:

Widzimy więc że macierz stanu będzie miała wielkość nxn

n - liniowo niezależne wielkości fizyczne lub abstrakcyjne i oznaczamy je odpowiednio:

x₁(t), x₂(t), ...,x_n(t),

---