Zestaw 1

1. Czy zbiór rozwiązań równania
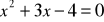
   oraz zbiór A=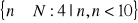
   są równoliczne?

2. Czy istnieje podział zbioru liczb naturalnych od 1 do 8 na dwa podzbiory takie, że żaden z nich nie zawiera rozwiązania równania x+y=z, gdzie
   ? Spróbuj odpowiedzieć na to samo pytanie, ale w odniesieniu do liczb od 1 do9.

3. Rzucono trzema dobrze wyważonymi monetami, których każda ma inny kolor. Obliczyć prawdopodobieństwo, że otrzymano co najmniej dwa orły. Ile byłoby wyników w przypadku rzutu trzema identycznymi monetami równocześnie?

4. Przeliczyć rozmieszczenia trzech przedmiotów w trzech pudełkach. Rozważyć wszystkie trzy przypadki dotyczące rozróżnialności.

5. Ile jest grafów na zbiorze wierzchołków
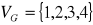
   , które mają dokładnie

1. cztery krawędzie,

2. pięć krawędzi?

6. Na ile różnych sposobów można rozpłaszczyć ośmiościan foremny?

7. Korzystając ze znalezionego na ćwiczeniach równania rekurencyjnego, obliczyć wszystkie wartości funkcji F(n,k) dla
   

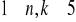
8. Znaleźć równanie rekurencyjne dla ciągu
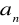
   oznaczającego liczbę uporządkowań zbioru {1,2,3,…n}.

9. Znaleźć funkcję tworzącą dla liczby wyborów r (r=0,1,,…,9) kul spośród trzech kul zielonych, trzech kul białych i trzech niebieskich.

10. Uzasadnij, że w każdym mieście liczącym co najmniej 2,5 miliona mieszkańców znajdziemy co najmniej pięć osób o tej samej liczbie włosów na głowie, jeżeli przyjmiemy, że rośnie ich na ludzkiej głowie co najwyżej 600 000.