Dominika Stoma GR. 3.5 Data wykonania pomiarów

15.11.1999r.

Ćwiczenie 3.2

Pomiar oporu układu za pomocą mostku Wheatstone'a.

1.WPROWADZENIE;

Jednym z najpopularniejszych układów służących do pomiaru oporu przewodników jest mostek Wheatstone'a. Przedstawiony na rysunku poniżej; składający się z:galwanometru, opornika dekadowego, opornika zabezpieczającego, źródła prądu oraz wyłącznika zwykłego i telegraficznego.

W górnej gałęzi mostka włączony jest opór badany R_x i opór wzorcowy R₃=200Ω. Gałąź dolną stanowią drut oporowy o przekroju porzecznym S i długości 1m. Do punktu A i B dołączone jest źródło prądu stałego. Dolną gałąź stanowi drut oporowy o przekroju poprzecznym `'s'' i długości 1m. Wyróżnia się 2 obwody (oczka). Dla których zgodnie z drugim prawem Kirchhoffa możemy zapisać następujące równania;

Stąd możemy zapisać;

Zaś napięcie między punktami C i P jest równe U=U₁-U₂. Więc z powyższych zależności otrzymujemy;

U=J₁*R_X-J₂*R₁

Gdy R₁*R₃=R_X*R₂ to mamy do czynienia z warunkiem równowagi lub zerowania się mostka. Wskaźnikiem zerowania jest galwanometr podłączony w punkcie C i D o wskazaniu J_g=0.

Jeżeli przyjmiemy oznaczenia:

a-długość odcinka AC

l-długość drutu oporowego o oporze właściwym ρ

to możemy zapisać

Podstawiając te wartości do warunków równowagi i przekształcając otrzymane równanie dochodzimy do postaci;

(*)

co pozwoli na wykonanie tego ćwiczenia, a następnie na obliczenie błędu pomiaru.

2. WYNIKI DOŚWIADCZENIA;

Wartości pomiaru umieszczamy w tabeli załączonej poniżej; a następnie przeprowadzamy przykładowe obliczenie dla wartości średniej pomiaru

l.p.	a [cm]	Δa [cm]	R3 [Ω]	RX [Ω]
1	49,8	0,5	200	198,4064
2	50	0,7	200	200
3	49,8	0,4	200	198,4064
4	49,7	0,6	200	197,6143
5	49,7	0,5	200	197,6143
6	50	0,3	200	200
7	49,6	0,7	200	196,8254
8	49,9	0,2	200	199,2016
9	49,7	0,8	200	197,6143
10	49,9	0,2	200	199,2016
11	50	0,3	200	200
Wartości średnie	49,82727	0,472727	200	198,6258

Przykładowe obliczenia dla wartości średniej pomiarów;

2.ANALIZA BŁĘDU;

Zostanie przeprowadzona metodą różniczkowania wzoru (*). Stąd błąd maksymalny może być wyrażony za pomocą wzoru;

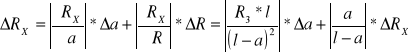
gdzie;

---co stanowi maksymalną wartość `a' przy której galwanometr nie reaguje.

Podstawiając wartości liczbowe do powyższych zależności otrzymamy wartość liczbową błędu maksymalnego, który wynosi;

=6.356009+13.712656=20.068665Ω

Mając wartość błędu maksymalnego możemy teraz obliczyć błąd procentowy;

4.WNIOSKI;

Otrzymany opór obliczany jest za pomocą mostka. Mimo, że metoda jest jedną z najczęściej stosowanych i jedną z dokładniejszych metod używana przy pomiarach laboratoryjnych obarczona jest jak każdy pomiar błędem.

Pomiary przeprowadzone były z dość dużą dokładnością względną. Są jednak obarczone dużym błędem. Dyskusja wykazała błąd pomiaru rzędu 10.104%, Co należy uznać za znaczny, przy wartości samego błędu maksymalnego oporu zmierzonego na poziomie R_X=20.068665Ω.

Wartość tak dużego błędu może być tłumaczona niewielką liczbą pomiarów.

Dlatego przy wykonaniu tego ćwiczenia należy zwrócić baczną uwagę na możliwość zwiększenia dokładności pomiarów. Zastosowanie bardziej dokładnych przybliżeń, oraz zwiększenie liczby pomiarów także doprowadzi do zwiększenia dokładności i jakości wyników.

1

1

R₂

R₃ R₃

R₁

R_s

R_x

G

---