TEMAT: Pomiar pracy wyjścia termoelektronów |
|||
IMIĘ I NAZWISKO: Jacek Szulc |
|||
WYDZIAŁ: Elektryczny |
SEMESTR: IV |
ROK: 1995/96 |
|
ZESPÓŁ: 12 |
DATA WYKONANIA: 1996.03.26 |
||
OCENA: |
PODPIS: |
||
1. PODSTAWY TEORETYCZNE
Prąd nasycenia In odpowiada całkowitemu strumieniowi elektronów emitowanych z katody, jest więc iloczynem gęstości jn prądu emisyjnego i czynnej powierzchni ![]()
katody:
In = jn S
Przy pewnym określonym napięciu anodowym wysokość bariery potencjału staje się równa zeru; odpowiada to napięciu, przy którym wszystkie wyemitowane przez katodę elektrony dotrą do anody. Otrzymamy wtedy prąd nasycenia. Gęstość prądu nasycenia zależy od temperatury katody i wyraża się wzorem Richardsona:
jn = B T2 exp (-A/kT)
gdzie:
B - stała
T - temperatura katody w kelwinach
A - praca wyjścia elektronu z katody
k - stała Boltzmanna
Po uwzględnieniu prawa Richardsona otrzymamy:
In = S B T2 exp (-A/kT)
W oparciu o prawo Richardsona można wyznaczyć pracę wyjścia elektronu. Zakładając, że znamy dwie wartości prądu nasycenia termoemisji I1 i I2 oraz odpowiadające tym prądom temperatury T1 i T2 możemy napisać:
I1 = S B1 T12 exp (-A/kT) ,
I2 = S B1 T22 exp (-A/kT) .
Dzielimy te równania stronami i logarytmujemy:
ln (I1/I2) = 2 ln (T1/T2) - (A/k) (1/T1 - 1/T2)
skąd
Do pomiaru pracy wyjścia wykorzystuje się diodę lampową z katodą wolframową ponieważ charakterystyka prądowo-napięciowa tej lampy wykazuje wyraźne nasycenie prądu anodowego. Aby z wyrażenia wyznaczyć pracę wyjścia elektronu należy znać dwie wartości natężenia prądu nasycenia I1oraz I2 przy tym samym napięciu anodowym oraz temperaturach żarzenia katody równych T1 i T2. W związku z tym należy sporządzić dwie charakterystyki prądowo-napięciowe lampy przy danych temperaturach żarzenia katody.
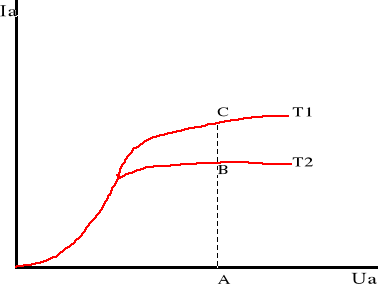
Jak widać z rysunku każdej temprtaturze katody odpowiada inne natężenie prądu nasycenia. Im wyższa jest temperatura katody, tym większe jest natężenie prądu nasycenia. Z uzyskanych charakterystyk wyznacza się wartość prądu nasycenia odpowiadające różnym temperaturą katody, ale tej samej wartości napięcia anodowego (na rysunku wartości natężenia prądów odpowiadają odcinkom ![]()
, ![]()
). Temperaturę żarzenia katody można znaleźć wykorzystując zależność oporu katody od temperatury:
RT = R0 (1+ aDT)
gdzie
![]()
opór w temperaturze T
![]()
- opór w temperaturze ![]()
![]()
temperaturowy współczynnik oporu (dla wolframu ![]()
![]()
)
skąd
![]()
przy czym ![]()
.
Opór ![]()
z dostateczną dokładnością można wyznaczyć z prawa Ohma:
![]()
gdzie ![]()
prąd żarzenia
![]()
napięcie żarzenia
TABELKA
|
IŻ = 2.91 A |
IŻ = 2.7 A |
IŻ = |
IŻ = |
||||
LP |
UŻ = 18 V |
UŻ = 16 V |
UŻ = |
UŻ = |
||||
|
Ua [V] |
Ia [A] |
Ua [V] |
Ia [A] |
Ua [V] |
Ia [A] |
Ua [V] |
Ia [A] |
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
NUMER POMIARU |
|
|
|
|
|
1 |
4,6 |
0,618 |
2294,89 |
0,013 |
47,10 |
2 |
1,79 |
0,592 |
2200,69 |
0,012 |
43,47 |
3 |
1,02 |
0,577 |
2146,34 |
0,012 |
43,47 |
4 |
2,91 |
0,600 |
2229,68 |
0,014 |
50,72 |
NUMER POMIARU |
|
|
|
3,972 |
2,56 |
|
3,920 |
1,789 |
|
2,706 |
2,91 |
|
3,863 |
3,69 |
|
6,700 |
14,88 |
|
13,078 |
3,186 |
|
6,84 |
5,80 |
a) Wartość prądu nasycenia ![]()
odczytane zostały dla wartości napięcia anodowego ![]()
;
b) Obliczeni rezystancji katody w twmperaturze T dla kolejnych prądów żarzenia zostały obliczone ze wzoru ![]()
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Ze wzoru ![]()
gdzie ![]()
, obliczamy kolejno temperaturę katody.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Obliczenia pracy wyjścia termoelektronu 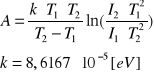
dla każdej
pary prądu nasycenia kolejno obliczamy
![]()
![]()
![]()
![]()
![]()
![]()
Analiza błędów
![]()
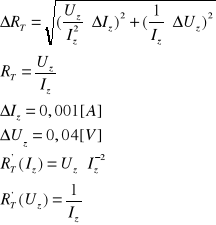
![]()
![]()
![]()
![]()
b) ![]()
błędy temperatury katody
![]()
Jedynie ![]()
jest obarczone błędem
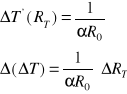
1. ![]()
2. ![]()
3. ![]()
4. ![]()
c) Błąd pracy wyjścia
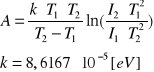
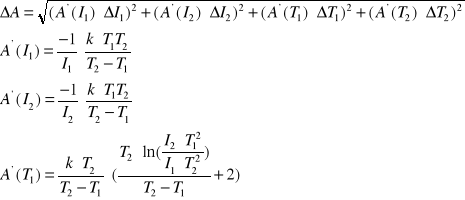
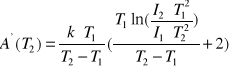
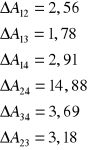
![]()
Wyszukiwarka
Podobne podstrony:
wyznaczanie staej planka oraz pracy wyjcia, Wyznaczanie sta?ej Planka oraz pracy wyj?cia
320 pomiar pracy wyjścia termoelektronów
download Zarządzanie Produkcja Archiwum w 09 pomiar pracy [ www potrzebujegotowki pl ]
Fizyka Laborka temat 1 Pomiar przyśpieszenia ziemskiego metodą?ssela
Inf praktyczne na temat pisania pracy magisterskiej[1], kosmetologia magisterka, wszystko i nic
Temat 2 Pomiar?wek (2)
Wpływ temp na przewo-dnictwo elektryczne, f2, Temat: Pomiar czujnikiem indykcyjnym.
pan wołodyjowski, 14, Po wyj˙ciu z zamku Ketling potrzebuj˙c zebra˙ my˙li i otrz˙sn˙˙ si˙ ze zdumien
Laborki -- Augustyniak, CW7, Temat: Pomiar czujnikiem indykcyjnym.
119, 119jkn, TEMAT: Pomiar napięcia powierzchniowego cieczy metodą
Podstawy wej%c5%9bcia i wyj%c5%9bcia w C
Współczynnik samo-indukcji i pojemności, Fiz-5art, BŁĘDY POMIAROWE
1)Badanie Swobodnego Spadku, SPADEK, Temat: Pomiar d˙ugo˙ci fali ˙wietlnej przy pomocy siatki dyfrak
PRACOWNIA TECHNICZNA Pomiary otworów i wałków, otowry i wałki, Temat : Pomiary otworów i wałków
więcej podobnych podstron