3. Obliczenia:

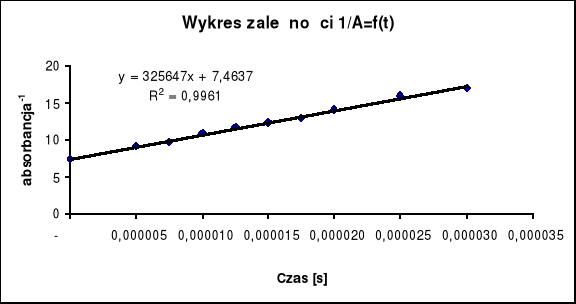
1. Na otrzymanym wykresie obieram 10 punktów pomiarowych odpowiadających wartością U które zamieściłem w tabeli 1, przyjmując czas t_o = 0 w punkcie skoku. Wyliczam absorbancję na podstawie wzoru:

2. Wyznaczam A_o z wykresu zalezności 1/A = f (t), gdzie odpowiada ona wartości stałej b w równaniu prostej y = ax + b. Ao wynosi w moim przypadku A_o=0,13398

Tabela 1:

Czas T [s]	U [V]	(Uo- U)/Uo	A	1/A
-	0,068	1,3696	0,1366	7,3216
0,000005	0,056	1,2857	0,1091	9,1622
0,000008	0,053	1,2663	0,1025	9,7516
0,000010	0,048	1,2353	0,0918	10,8968
0,000013	0,045	1,2174	0,0854	11,7055
0,000015	0,043	1,2057	0,0813	12,3070
0,000018	0,041	1,1943	0,0771	12,9671
0,000020	0,038	1,1776	0,0710	14,0871
0,000025	0,034	1,1560	0,0629	15,8871
0,000030	0,032	1,1455	0,0590	16,9555

3. Obliczam dawkę zaabsorbowanego promieniowania dla roztworu nasyconego tlenem:

gdzie:

N_A - Liczba Avogadro;

ρ - gęstość ładunku dozymetrycznego

G(OH) - wydajność reakcyjna anionorodników (SCN)^-₂

Ao - wartość absorbancji po zakończeniu impulsu

 = 7,35^.10³ [1/(M^.cm)]

[Gy]

4. Wyznaczam wartość stałej szybkości reakcji k_r korzystając z równania kinetyki II rzędu uwzględniając prawo Lamberta-Beera:

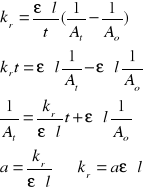
=325647^.7,35^.10^3.1 = 2,39.10⁹ [(1/s)*(dm³/mol)]

5. Obliczam stosunek wskazań dozymetru fizycznego do wyznaczonej dawki w pojedyńczym impulsie:

D_W- dawka wyznaczona na podstawie wykresu;

D_F - dawka dozymetru fizycznego;

4. Wnioski:

W tym ćwiczeniu otrzymałem następujące wartości:

A_o = 0,13398

D = 62,56 [Gy]

k_r = 2,39^.10⁹ [(1/s)*(dm³/mol)]

Stała szybkości reakcji jest bardzo duża co świadczy o dużej szybkości reakcji, a co z kolei wymaga stosowania układów impulsowych do pomiarów