Egzamin 2010-02-15

D1. (B1) Uzyskaj równanie funkcji odwrotnej do funkcji, której wykres nazywamy standardową krzywą łańcuchową.

D2. (U3) Wyznacz szereg T i wielomian w Maclaurina stopnia 3 dla funkcji y = f(x), gdzie f(x) = ln(1 + x), i sporządź, na jednym rysunku, wykresy tej funkcji i tego wielomianu.

D3. Oblicz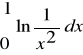
.

D4. (s) Sprawdź, czy są do siebie podobne macierze A :=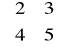 
i B :=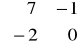 
.

D5. Uzyskaj rozwiązanie y = y(x) równania y'' + y = 0 takie, że y(0) = 1.

-------------------------------------------------------------------------------------------------------------

E1. (Z4) Z materiału o ciężarze właściwym ρ wykonana została płaska płytka o pomijalnej grubości, szerokości 7 cm i długości 30 cm. Oblicz jej moment bezwładności względem dłuższego boku.

D2. Przedstaw zagadnienie oziębiania newtonowskiego i jego rozwiązanie.

E3. Podaj dwa różne określenia hiperboli i jej równania.

E4. (≈A5,s) Oblicz kąt α, jaki tworzą ze sobą proste U i V, gdzie U : x = t, y =   2t, z = t;

V : x = 3, y = 3+t, z = t.

E5. (s) Napisz tabelkę Cayleya na mnożenie pierwiastków 4-tego stopnia z 1 i pokaż, że zbiór tych pierwiastków wraz z mnożeniem stanowi grupę.

-------------------------------------------------------------------------------------------------------------

F1. (U6) Wyznacz rozwiązanie y = y(x) równania y''- y = 0 takie, że y(0) = 1.

F2. (B5,s) Wyznacz punkt Q, w którym płaszczyznę Oxy przebija prosta przechodząca przez punkt P = (4, 5, 6) i prostopadła do płaszczyzny x - y + z - 1 = 0.

F3. (s) Rozwiąż ural A⋅x = b, gdy A := 
, b := 
.

F4. Oblicz powierzchnię, jaką ograniczają półprosta θ = π i łuk o równaniu θ² - r² = 1, gdy r, θ są współrzędnymi biegunowymi ( r ≥ 0, -π < θ ≤ π).

F5.   (s) Wyznacz wartości i wektory własne macierzy obrotu płaskiego o 30°. Otrzymany wynik zinterpretuj w terminach kierunków własnych/głównych obrotu. .

--------------------------------------------------------------------------------------------------------