!.Akcjonomaty prawdopodobieństwa - a) prawd. zdarzenia A jest to stosunek liczby M zdarzeń sprzyjających zajściu zdarzenia A do liczby N wszystkich możliwych zdarzeń

P(a) = M / N ;

b) przestrzeń zdarzeń element. E jest to zbiór którego elementy oznaczone są e z odpowiednimi wskazaniami jeżeli zbiór E jest skończony i liczy n elementów to: ei należy do E , i =1,2,3...n

c) wartość prawdopodobieństwa jest to wartość nieujemna w przedziale 0 < Pa<1 P(a) = 0 zdarzenie niemożliwe , a gdy P(a)= 1 to jest pewne

d) suma prawdopodobieństw- jeżeli zdarzenie A zakłada rozkłada się na dwa zdarzenia A1 A2 przy czym A1 sprzyja m1 zdarzeń , a zdarzenie A 2 sprzyja m2 zdarzeń to całkowite prawdopodobieństwo to suma ich składowych P(a) = P(A1)+ P(A2) P(U)=P(A) )[P] + P(A)[q] = 1 P= 1-q

e) zdarzenie niezależne - dwa zdarzenia są niezależne jeżeli jest spełniony warunek P(A) = P(A/B) - to jest zgodne gdy kulki wracają do puli

2. zmienna losowa- to zmienna która w wyniku doświadczenie przybiera 1 i tylko 1 wartość ze zbioru wszystkich wartości jakie zmienna może przyjąć X,Y,U,W , realizacja doświadczeń x,y,u,w,

• skokowa zmienna losowa (dyskretna)- to zmienna losowa która posiada skończony lub przeliczalny zbiór wartości

• ciągła zmienna losowa to zmienna losowa która może przybrać dowolne wartości liczbowe z pewnego przedziału liczbowego

• zmienna losowa X- to funkcja X=X (e) która określana jest na zbiorze zdarzeń elementarnych E taką że dla każdej liczby rzeczywistej x zbiór A zdarzeń elementarnych e należy E dla których X(e) < x P(A)=P( -∞ <X< x) - nazywamy rozkładem prawdop. zmiennej losowej X

• rozkład zmiennej losowej X nazywamy prawdopod. tego że zmienna losowa X przybierze wartość xi gdzie i =1,2,3... P(X = xi) = pi prawdopodob. Tego że zmienna losowa X przybierze wartość < x jest funkcja osymbolu F(x) - dystrybuanta

• rozkładem ciągłej zmiennej losowej X nazywamy prawdopodob., tego że zmienna X przybierze wartość (a do b) P(a<X<b) =
  f(x) dx gdzie f(x) jest to fu8nkcja gęstości ; prawdopodob. Tego że zmienna losowa X przybierze wartość (a do b) jest całką funkcji gęstości zmiennej losowej X

• dustrybuanta X to funkcja F(x) = P (X <x) w ramach 0 <F(x)<1

• gęstość prawdopodob. f(x) jest to wartość pochodnej z dystrybuanty f(x) = F' (x) w punkcie x F(x) =
  f(x) dx

• zmienna losowa X jest zmienną ciągłą w danym przedziale jeżeli w tym przedziale występuje funkcja gęstości

• wartość przeciętna (oczekiwana) MATEM X to liczba określana wzorem E(x) =
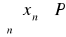
  (X = x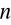
  ) dla skokowej losowej E(x)=
  xf (x) dx
  dla ciągłej

Wariancja => D
(X) =
Pn m=E(X)

- odchylenie średniej zmiennej losowej
X określa się wzorem