Metody i algorytmy sterowania cyfrowego laboratorium
Wykonał:	Temat:	Ocena:
Michał Góra Nr i. 170799	Projektowanie korektorów cyfrowych (odpornych oraz nieodpornych).

1. Cel ćwiczenia:

Celem ćwiczenia było zapoznanie się z właściwościami korektorów oraz zaprojektowanie korektora odpornego i nieodpornego. Służył nam do tego specjalnie przygotowany program w Matlabie (KOR.M).

2. Kolejne kroki przy tworzeniu korektora (dla nr gr.= 3):

Zadana transmitancja:

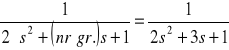
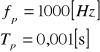
• Dyskretyzacja obiektu:

Podaj współczynniki licznika A(s) f-cji Go(s); liczs=1

Podaj współczynniki mianownika B(s) f-cji Go(s);mians=[2 3 1]

Twoja funkcja przejścia:

1

------------------

2 s^2 + 3 s + 1

Okres próbkowania Tp=0.001

Opóźnienie w jednostkach czasu op=0

Dyskretna funkcja przejścia Go(z):

2.4988e-007 z + 2.4975e-007

------------------------------------

z^2 - 1.9985 z + 0.9985

• Projektowanie korektora/regulatora dowolnego:

Podaj licznik H(z) układu zamkniętego K(z); likz=1

Podaj mianownik T(z) układu zamkniętego K(z) (bez opóźnienia obiektu); mikz =[1 0 0]

Funkcja przejścia korektora G_k(z):

z^2 - 1.9985 z + 0.9985

---------------------------------------------------------------------------------

2.4988e-007 z^3 + 2.4975e-007 z^2 - 2.4988e-007 z - 2.4975e-007

• Efekt działania zaprojektowanego korektora:

• Projektowanie korektora odpornego nieastatycznego:

ng= 1

nt= 3

Podaj zadane przeregulowanie; Dy[%]=20

Podaj zadany czas ustalania 2%; tr[j.cz.]=1

btz= 0.3216 + 0.2714i 0.3216 - 0.2714i 0.7994

Korektor G_k(z):

1502636.5514 z - 1288271.8773

----------------------------------------

z + 0.18049

Transmitancja układu zamkniętego z korektorem G_z(z):

0.37547 z^2 + 0.053377 z - 0.32175

------------------------------------------------

z^3 - 1.4425 z^2 + 0.69117 z - 0.14153

• Efekt działania zaprojektowanego korektora:

3. Wnioski:

Dzięki wykorzystaniu programu KOR.M oraz funkcji Matlaka w nim zawartych mogliśmy zaprojektować korektor o zadanych przez nas warunkach. W przypadku korektora nieodpornego podawaliśmy transmitancję układu zamkniętego, a program samodzielnie dobierał taki korektor, aby ten warunek był spełniony. Jak widać na załączonych rysunkach program poradził sobie z tym zadaniem bardzo dobrze, co świadczy o tym, że w układach cyfrowych możemy dowolnie kształtować odpowiedź układu dzięki zastosowaniu odpowiedniego korektora. W przypadku projektowania korektora odpornego efekt był podobny jednakże zamiast podawać transmitancji układu zamkniętego wyznaczaliśmy ją z biegunów zaznaczanych na płaszczyźnie z.

---