Wahadłem fizycznym jest bryła drgająca wokół osi poziomej, ulokowanej powyżej środka ciężkości. Na bryłę wychyloną z położenia równowagi o kąt ϕ działa moment siły

M = mgx = mgbsinϕ.

We wzorze tym b jest odległością osi obrotu od środka ciężkości. Równanie ruchu bryły zapiszemy w postaci:

Iε = -mgbsinϕ,

gdzie I - moment bezwładności bryły względem osi obrotu, a ε - przyspieszenie kątowe. Jeżeli kąt wychylenia rośnie, to przyspieszenie kątowe maleje (stąd znak minus we wzorze). Dla małych kątów sinus można zastąpić wartością kąta w mierze łukowej i wówczas otrzymamy równanie różniczkowe drgań harmonicznych:

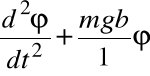
z okresu drgań:

*

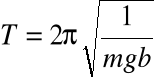
Porównując ten wzór ze wzorem na okres drgań wahadła matematycznego wprowadza się pojęcie długości zredukowanej wahadła fizycznego:

Wzór (*) nie pozwala jednak na bezpośrednie wyznaczenie przyspieszenia ziemskiego ze względu na kłopotliwy sposób określania zarówno momentu bezwładności, jak i odległości b.

Problemów tych unikamy stosując tak zwane wahadło rewersyjne, którego zasada opiera się na własności zwanej dwuosiowością wahadła fizycznego.

Przyjmijmy, że istnieją dwie różne osie O₁ i O₂, dla których okresy drgań wahadła fizycznego są równe:

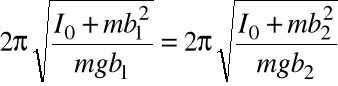
Równość okresów zrealizujemy wtedy, gdy:

(b₂ - b₁)(I₀ - mb₁b₂) = 0

skąd otrzymamy dwa warunki:

1. b₁ = b₂

2. I₀/m = b₁b₂.

Nas interesuje sytuacja druga, zgodnie, z którą otrzymamy:

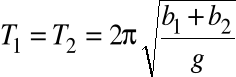
Oznaczając odległość między osiami I₀ = b₁ + b₂ otrzymujemy ostatecznie:

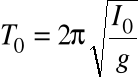
Warunek ten jest tylko jednym z możliwych. Równość okresów zachodzi dla wszystkich osi będących tworzącymi walców o promieniach b₁ i b₂ oraz osi przechodzących przez środek ciężkości.

Zasada pomiaru

Wahadło rewersyjne złożone jest z pręta z nacięciami, co 10 mm i dwóch ciężarków . Jeden z ciężarków jest zamocowany jako nieruchomo, drugi może być przesuwany wzdłuż osi wahadła. Zmiana położenia ciężarka powoduje zmianę usytuowania środka ciężkości oraz zmianę momentu bezwładności I₀. Pociąga to za sobą zmianę okresu drgań. Dla drugiego zawieszenia sytuacja jest analogiczna. Zasada wyznaczania przyśpieszenia ziemskiego sprowadza się do znalezienia takiego położenia ruchomego ciężarka, które odpowiada jednakowym okresom drgań dla obydwu zawieszeń wahadła rewersyjnego. Procedura dochodzenia do stanu odwracalności wahadła realizowana jest w etapach:

1. zmiana odległości x, co 3 cm i pomiar okresu drgań dla obu zawieszeń,

2. sporządzenie wykresu i przybliżone oszacowanie położenia odwracalnego na podstawie przecięcia parabol,

Przyśpieszenie ziemskie obliczamy wg wzoru

,

gdzie

l₀ jest odległością między zawieszeniami.

Przebieg ćwiczenia

1.Mierzymy odległość między ostrzami wahadła.

2.Zawieszamy wahadło na ostrzu zamocowanym na końcu pręta ( ostrze A)

3.Wprawiamy wahadło w ruch i mierzymy czas 10 okresów. ( Kąt wychylenia nie powinien być większy od
)

4.Zawieszamy wahadło na drugim ostrzu i ponownie mierzymy czas 10 okresów.

5.Wykonujemy czynności opisane wyżej dla położeń ciężarka zmienianego, co 3 cm.

6.Rysujemy wykresy zależności okresu wahań od odległości ciężarka od ostrza A (dla obydwu sposobów zawieszenia). Z wykresu określamy położenie ciężarka, przy którym okresy drgań są jednakowe dla obu zawieszeń.

7.Obliczamy przyśpieszenie ziemskie wg wzoru.

8.Przeprowadzamy rachunek błędów.

Tabela wyników

Położenie w [cm]	Ostrze A		Ostrze B
		Czas t [s]	Okres	Czas t [s]	Okres
6	12,996	10	12,982	10
9	12,819	10	12,690	10
12	12,681	10	12,343	10
15	12,599	10	12,020	10
18	12,562	10	11,737	10
21	12,566	10	11,504	10
24	12,609	10	11,368	10
27	12,684	10	11,393	10
30	12,781	10	11,668	10
33	12,908	10	12,432	10
36	13,046	10	13,052	10

Sporządzamy wykres zależności okresu wahań od odległości ciężarka od ostrza A T = f(y).

(Wykres dołączony na papierze milimetrowym)

Punkty przecięcia krzywych przyjmujemy jako y₁ = 6 [cm] i y₂ = 36 [cm].

Ponieważ w zakres ćwiczenia nie wchodziło precyzyjne wyznaczenie okresu w warunkach odwracalności (pomiar 100 okresów), okres wahań obliczymy jako średnią arytmetyczną okresów wahań dla położeń y₁ i y₂.

Dla 10 okresów:

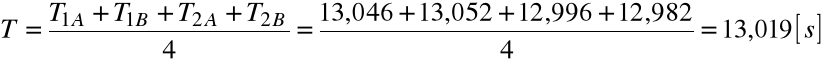
Dla 1 okresu:

T₀ = 1,3019[s]

Tak, więc do obliczeń przyjmujemy T₀ = 1,3019[s]

Odległość między ostrzami I₀ = 0,415[m]

Obliczamy przyspieszenie wg. wzoru:

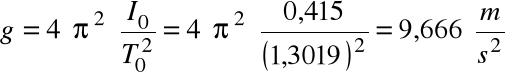
Obliczenia błędów:

Dokładność przyrządu mierzącego okres wynosi 0.02 [%] (wg. skryptu).

Jednakże ze względu na uszkodzenie ostatniej cyfry wskaźnika miernika czasu faktyczną dokładność odczytu przyjęliśmy na 0.01 [s]

T₀ = (1,30 ± 0,01)[ s]

Pomiaru odległości między ostrzami dokonano przy pomocy suwmiarki.

Błąd pomiaru, ze względu na niedoskonałość systemu zawieszenia wahadła przyjęto na 0,001[m].

I₀ = (0,415 ± 0,001)[m]

Błąd obliczenia stałej grawitacji obliczamy przy pomocy metody logarytmicznej.

,

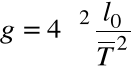
ln g = ln l₀ - 2 ln

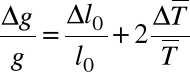
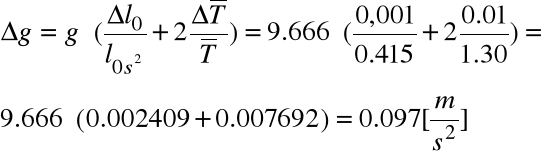
Δg = 0,097[m/s²]

Ostateczny wynik:

g = (9,666 ± 0,097)[m/s²]

Wnioski:

Ćwiczenie wykazało, że nawet w prostym ćwiczeniu laboratoryjnym można wyznaczyć stałą grawitacji z całkiem dobrym przybliżeniem.

Na dokładność wyznaczenia przyśpieszenia ziemskiego wykonanego przez nas dużą rolę odgrywa dokładność czynności manualnych tzn. takich jak precyzyjne wprawienie w ruch wahadła (kąt, płaszczyzna), dokładne wyznaczenie położenia ruchomego ciężarka (położenie było zmieniane, co 3 [cm]).

---