ANALIZA DYNAMIKI

Analiza dynamiki to badanie zmian poziomu badanej cechy statystycznej (zmiennej) w czasie na podstawie szeregów czasowych (dynamicznych). Statystyczna analiza empiryczna szeregów czasowych powinna prowadzić do odpowiedzi na dwa zasadnicze pytania:

1. jaka jest dynamika badanego zjawiska (badanej zmiennej),

2. jakie czynniki wywołują zmienność badanego zjawiska (zagadnieniom tym poświęcony jest przedmiot ekonometria).

Szereg czasowy - ciąg wartości y_t badanej zmiennej obserwowanej w kolejnych jednostkach czasu t = 1,2,…,n.

Ze względu na charakter zmiennej czasowej t wyróżnia się dwa rodzaje szeregów czasowych:

- szereg czasowy okresów (strumieni) - jednostkami czasu są przedziały czasowe - okresy (np. wielkość wydatków inwestycyjnych poniesionych w ciągu roku, liczba urodzeń w ciągu roku),

- szereg czasowy momentów (stanów) - poziom zmiennej y mierzony w ściśle określonych momentach, (np. stan zapasów na dzień 31 grudnia, liczba ludności w dniu 30 czerwca).

Przeciętny poziom zmiennej y w danym okresie obliczamy w następujący sposób w zależności od rodzaju szeregu czasowego:

- dla szeregu czasowego okresów obliczamy średnią arytmetyczna według wzoru: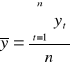
,

- dla szeregu czasowego momentów obliczamy średnią chronologiczną według wzoru:

.

Własności średniej chronologicznej:

1. wyrażona jest w takich samych jednostkach jak badana zmienna,

2. spełnia warunek:
.

Miary dynamiki - miary statystyczne, przy pomocy których opisuje się zmienność badanej zmiennej obserwowane w kolejnych jednostkach czasu t = 1,2,…,n:

- jednopodstawowe miary dynamiki (miary o podstawie stałej) służą do oceny zmian w poziomie badanej zmiennej, jakie nastąpiły w kolejnych badanych okresach/momentach w porównaniu z poziomem tej zmiennej w okresie/momencie przyjętym jako bazowy;

- łańcuchowe miary dynamiki służą do oceny zmian w poziomie badanej zmiennej w danym okresie/momencie t w porównaniu z okresem/momentem poprzednim t - 1.

Wśród miar dynamiki wyróżniamy ponadto:

- miary absolutne - wyrażone w takich jednostkach miary jak badana zmienna (przyrosty bezwzględne),

- miary procentowe - wyrażone w procentach (przyrosty względne, indeksy).

Przyrosty bezwzględne (absolutne) informują o ile jednostek wzrósł (lub zmalał) poziom zjawiska w okresie badanym w porównaniu z jego poziomem w okresie bazowym.

Mogą być obliczane w stosunku do:

- ustalonego okresu k, przyjętego za bazowy - przyrosty jednopodstawowe
,

- okresu poprzedniego w stosunku do badanego - przyrosty łańcuchowe:
.

Przyrosty względne obliczamy jako iloraz przyrostu bezwzględnego i poziomu zjawiska w okresie bazowym. Są wielkościami niemianowanymi, do interpretacji mnożymy przez 100 wyrażając je w procentach. Podobnie jak przyrosty absolutne mogą być wyznaczane jako:

- miary jednopodstawowe: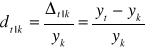
,

- miary łańcuchowe: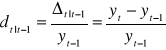
.

Indeksy dynamiki - mierniki określające stosunek wielkości badanego zjawiska w dwóch różnych okresach/momentach. Są wielkościami niemianowanymi. Do interpretacji mnożymy je przez 100 i podajemy w procentach.

Indywidualne indeksy dynamiki - dotyczą zjawisk jednorodnych, opisanych pojedynczym szeregiem czasowym. Wyróżniamy:

- indeksy jednopodstawowe
,

- indeksy łańcuchowe
.

Indeks wyższy od 1 oznacza, że wartość badanej zmiennej w okresie badanym była wyższa niż w okresie bazowym. Do interpretacji procentowej zmiany należy od indeksu odjąć 1 i wynik pomnożyć przez 100:
.

Jeżeli znamy indeksy jednopodstawowe dla okresu bazowego k, to możemy policzyć na ich podstawie indeksy jednopodstawowe dla dowolnego innego okresu bazowego l:

.

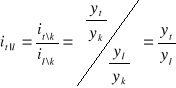
Jeżeli znamy indeksy jednopodstawowe (dla dowolnego okresu bazowego k), to możemy na ich podstawie policzyć indeksy łańcuchowe i na odwrót:

- indeksy łańcuchowe otrzymujemy dzieląc przez siebie kolejne indeksy jednopodstawowe

,

- indeks jednopodstawowy dla dowolnego okresu badanego t i okresu bazowego k otrzymujemy mnożąc przez siebie kolejne indeksy łańcuchowe dla okresów od k+1 do t

,

- w szczególnym przypadku gdy okresem badanym jest ostatni okres (t = n), a okresem bazowym pierwszy (k = 1) indeks jednopodstawowy liczymy jako iloczyn kolejnych indeksów łańcuchowych

.

Między indeksami indywidualnymi i przyrostami względnymi istnieje następujący związek:

,

.

Średnie tempo zmian zjawiska w badanym przedziale czasowym wyznaczamy jako średnią geometryczną indeksów łańcuchowych dla tego przedziału, tzn:

.

Do interpretacji podajemy średnie tempo zmian w procentach:
.

Własności średniej geometrycznej jako miary średniego tempa zmian:

1. jest miarą niemianowaną,

2. spełnia warunek
.

SAN, Finanse i rachunkowość 2012/2013

---