STATYSTYKA OPISOWA

Podstawowe wzory

Szereg rozdzielczo-punktowy:

• Mediana

• Dla szeregu o nieparzystej liczbie jednostek

• Dla szeregu o parzystej liczbie jednostek

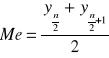
• Dominanta (moda)

Mo=x_i , gdzie f_i= max{f₁,f₂,...f_k}

Szereg przedziałowy:

• Mediana

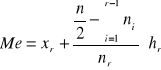
, gdzie

x_r - dolna granica przedziału klasowego zawierającego medianę,

n_r - liczebność przedziału klasowego zawierającego medianę,

h_r - rozpiętość przedziału klasowego zawierającego medianę.

• Kwartyle:

• Q₁

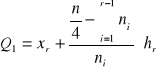
x_r - dolna granica przedziału klasowego zawierającego pierwszy kwartyl

n_r - liczebność przedziału klasowego zawierającego pierwszy kwartyl,

h_r - rozpiętość przedziału klasowego zawierającego pierwszy kwartyl.

• Q₃

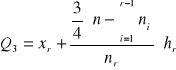
x_r - dolna granica przedziału klasowego zawierającego trzeci kwartyl

n_r - liczebność przedziału klasowego zawierającego trzeci kwartyl,

h_r - rozpiętość przedziału klasowego zawierającego trzeci kwartyl.

• Dominanta (moda)

x_r - dolna granica przedziału klasowego zawierającego dominantę

h_r - rozpiętość przedziału klasowego zawierającego dominantę

n_Dr - liczebność przedziału klasowego zawierającego dominantę

n_Dr-1 - liczebność przedziału klasowego poprzedzającego dominantę

n_Dr+1 - liczebność przedziału klasowego następnego po dominancie

Miary zmienności:

Wariancja:

Dla szeregu rozdzielczo-punktowego :

Dla szeregu przedziałowego:

Odchylenie standardowe:

Odchylenie przeciętne:

Dla szeregu rozdzielczo-punktowego:

Dla szeregu przedziałowego:

Odchylenie ćwiartkowe:

Współczynniki zmienności:

Współczynnik zmienności
jest względną miarą zmienności określającą stosunek odchylenia standardowego do średniej arytmetycznej.

Współczynnik zmienności
jest miarą zmienności określającą stosunek odchylenia przeciętnego do średniej arytmetycznej

Współczynnik zmienności
jest miarą zmienności określającą stosunek odchylenia ćwiartkowego do mediany

Miary asymetrii:

• rozkład symetryczny:
  

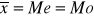
• asymetria prawostronna
  

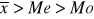
• asymetria lewostronna
  

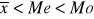
Współczynnik asymetrii:
,

Współczynnik asymetrii:
, gdzie

Współczynnik asymetrii:

---