Zestaw 7:

1. Obliczyć wartość wyznacznika macierzy współczynników podanego równania, podać wartość elementu
macierzy odwrotnej do macierzy współczynników, rozwiązać podany układ równań i sprawdzić rozwiązanie (Excel i Matlab):

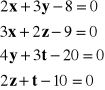
2. Znaleźć miejsca zerowe wielomianu (Excel i Matlab):

3. Znaleźć pierwiastek równania (Excel i Matlab):

4.Utworzyć tabelę wartości funkcji:

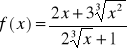
i narysować jej wykres w przedziale [1,2] (dla 51 wartości zmiennej niezależnej ) (Excel i Matlab).

5. Znaleźć całkę:
(Matlab).

6. Obliczyć wartość całki oznaczonej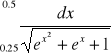
(Matlab).

7. Znaleźć:
jeżeli
(Matlab).

8. Na podstawie podanych pomiarów zmiennych losowych x i y wyznaczyć współczynnik korelacji liniowej r oraz współczynniki a i b równania regresji :

1. liniowej y=ax+b

2. potęgowej y=ax^b

3. wykładniczej y=ae^bx

Proszę wskazać funkcję najlepiej aproksymującą i uzasadnić wybór (Excel i Matlab).

x y

1.2 0.28

2 0.2

3.4 0.11

4.7 0.07

5.1 0.06

6.2 0.04

6.4 0.03

7.8 0.02

8.9 0.01

11 0.01

Obliczyć prognozowaną na podstawie wyznaczonego równania wartość y(7.54).

9. Wyznaczyć punkty przecięcia się krzywych (Matlab):

10. Znaleźć maksimum wyrażenia

przy ograniczeniach:

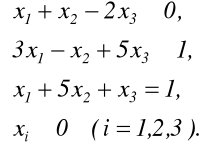
(Matlab, Excel)

11. Na podstawie rzeczywistych pomiarów niecki osiadania wyznaczyć funkcję postaci:
w miarę dokładnie oddającej jej kształt.

gdzie:

x₀ - punkt położenia maksymalnego osiadania

a - wartość maksymalnego osiadania

c - współczynnik potęgowy

x - współrzędna bieżąca

y - wartość osiadania w punkcie x

Przedstawić graficznie pomiary i uzyskaną krzywą.

Tabela pomiarów:

x	obniżenie
40	-1.38
75	-1.67
146	-6.8
207	-2.14
289	-1.93
363	-0.46