6. Informacja merytoryczna

1. Procesy wyciskania

Podczas wyciskania materiał umieszczony w pojemniku lub matrycy i poddany naciskowi stempla (lub tłoczyska - poprzez przekładkę, zwaną także przetłoczką, względnie płytą naciskową) wypływa przez otwór matrycy lub szczelinę pomiędzy stemplem i matrycą, doznając wydłużenia kosztem zmniejszenia przekroju poprzecznego. Stan naprężenia w przeważającej części obszaru uplastycznionego jest trójosiowym nierównomiernym ściskaniem. Możliwe są więc duże odkształcenia plastyczne bez naruszenia spójności materiału (maksymalne współczynniki wydłużenia są rzędu 300, średnie - ok. 50). Jest to główna zaleta procesów wyciskania. Z drugiej strony duże odkształcenia wymagają ogromnych sił. Głównym ograniczeniem wielkości odkształceń możliwych do uzyskania w jednej operacji wyciskania nie jest zjawisko dekohezji materiału (jak w wielu innych procesach), lecz wytrzymałość narzędzi.

Przy dużych odkształceniach stosuje się wyciskanie na gorąco, gdyż podczas wyciskania na zimno siły są tak znaczne, że narzędzia nie wytrzymują obciążeń. Duże odkształcenia mogą być zrealizowane na zimno tylko dla materiałów miękkich (np. czystego aluminium).

Rozróżnia się następujące rodzaje procesów wyciskania:

• współbieżne, gdy zwroty prędkości stempla v_s i materiału v_m wypływającego przez otwór w matrycy są zgodne (rys. VI/2),

• przeciwbieżne, gdy zwroty prędkości stempla v_s i materiału v_m wypływającego przez otwór w matrycy (rys. VI/3 a) lub szczelinę pomiędzy stemplem i matrycą (rys. VI/3 b) są przeciwne,

• z bocznym (poprzecznym, promieniowym) wypływem materiału, gdy matryca lub matryce znajdują się w bocznych ścianach pojemnika (rys. VI/6), względnie materiał wpływa do szczelin matrycy w kierunku poprzecznym (prostopadle do kierunku ruchu stempla),

• złożone, gdy materiał równocześnie wypływa z matrycy zgodnie i przeciwnie do ruchu stempla (rys. VI/7),

• specjalne (wyciskanie hydrostatyczne, z ruchomym pojemnikiem, bez pojemnika i inne, np. wyciskanie osłon kabli, wyciskanie proszków metali - rys. VI/8 - VI/13).

Tzw. wyciskanie z koszulką (rys. VI/14) stosuje się w przy procesie realizowanym na gorąco, aby usunąć zanieczyszczony i utleniony materiał z powierzchni wsadu.

Przekrój poprzeczny wyrobu wyciskanego odpowiada przekrojowi otworu matrycy lub szczeliny pomiędzy stemplem i matrycą. Możliwe jest wyciskanie wyrobów o przekroju zmieniającym się w pewnym zakresie wzdłuż osi w sposób ciągły lub skokowo (rys. VI/4, VI/5).

1. Odkształcenia, siła i naprężenie wyciskania

Stopień odkształcenia określa współczynnik wydłużenia  (stosunek długości materiału po wyciskaniu do długości przed wyciskaniem),, wydłużenie rzeczywiste (logarytmiczne) ₁, lub względny ubytek przekroju z:

(VI.1)

(VI.2)

(VI.3)

gdzie: l₁, F₁ - długość i przekrój wyrobu po wyciskaniu, l₀, F₀ - długość i przekrój wstępniaka. Wartości powyższe określają średnie miary odkształcenia. W rzeczywistości rozkład odkształceń w wyciskanym wyrobie odznacza się niejednorodnością, której stopień jest uzależniony głównie od wartości sił tarcia, kształtu matrycy i ubytku przekroju (rys. VI/15).

Średnie naprężenie wyciskania σ_w określa wzór:

(VI/4)

gdzie P_w jest siłą wyciskania. Smukłością _w wstępniaka walcowego o średnicy d₀ nazywamy stosunek:

(VI.5)

Siłę i naprężenie wyciskania można oszacować w przybliżeniu stosując metodę energetyczną (patrz ćw. I):

(VI.6)

gdzie: ψ - współczynnik wypełnienia wykresu krzywej wzmocnienia:

(VI.7)

σ_pk - naprężenie uplastyczniające materiału dla odkształcenia
= ln  (po wyciskaniu), σ_p(
) - równanie krzywej wzmocnienia, η - współczynnik sprawności:

(VI.8)

przy czym: L_p - praca odkształceń plastycznych, L_t - praca wykonana przeciwko siłom tarcia, L - praca całkowita, potrzebna do realizacji procesu i równa pracy siły wyciskania P na drodze s_k:

(VI.9)

Współczynnik η zależy od sił tarcia działających pomiędzy materiałem wyciskanym i pojemnikiem oraz matrycą, a więc od sposobu smarowania, stopnia odkształcenia, kształtu matrycy i smukłości wstępniaka _w (przy wyciskaniu współbieżnym). Zbyt długie wstępniaki nie dają się wyciskać, gdyż praca tarcia (dyssypowana głównie na ściankach pojemnika) oraz siła potrzebna do wyciskania są zbyt duże.

Jeżeli krzywą wzmocnienia opisuje równanie: σ_p = C
ⁿ, to współczynnik ξ jest stały i wynosi:

(VI.10)

Gdy materiał nie ulega wzmocnieniu (np. podczas wyciskania na gorąco), to ξ = 1 oraz σ_pk = σ_p(T_w), gdzie T_w jest temperaturą wyciskania.

Podane wyżej zależności pozwalają na przybliżone określenie sił i naprężeń podczas wyciskania. Dokładniejsze rozwiązania, pozwalające na wyznaczenie rozkładu nacisków jednostkowych na powierzchniach matrycy i pojemnika, pola prędkości płynięcia i rozkładu odkształceń w materiale z uwzględnieniem rzeczywistych warunków procesu i własności materiału (tarcia, wzmocnienia, wydzielania ciepła, wpływu temperatury itp.) można otrzymać za pomocą metody elementów skończonych (MES).

Schemat zależności siły wyciskania współbieżnego od drogi stempla pokazano na rys. VI/16 (krzywa 1). W fazie I następuje spęczanie wstępniaka w pojemniku i wypełnianie stożka wejściowego matrycy (niestacjonarny etap procesu). Podczas fazy II wypływanie materiału z matrycy ma charakter prawie stacjonarny, a pewiem spadek siły wyciskania jest wywołany obniżeniem całkowitej siły tarcia o pojemnik wskutek zmniejszania się długości wstępniaka, a więc powierzchni, na której działa tarcie. Przy wyciskaniu przeciwbieżnym (krzywa 2 na rys. VI/16) powierzchnia działania tarcia jest prawie stała, więc w fazie II siła wyciskania nie zmienia się. W etapie III, gdy stempel zbliża się do dna pojemnika lub matrycy, następuje szybki wzrost siły wyciskania. Aby nie dopuścić do nadmiernego obciążenia narzędzi, proces należy przerwać przed końcem etapu II.

2. Materiały i wyroby wyciskane

1. Wyciskanie stali na gorąco

Wyciskanie współbieżne na gorąco prętów, rur i kształtowników ze stali węglowych oraz stopowych przeprowadza się w temperaturach 1100 - 1300 [^oC] przy współczynnikach wydłużenia  = 40 - 100. Wstępniak nagrzany do temperatury wyciskania przed załadowaniem do pojemnika jest przetaczany po pochylni posypanej proszkiem szklanym, który topi się i pokrywa cienką warstewką płynnego szkła powierzchnię wstępniaka. Warstewka ta spełnia rolę smaru. Również do pojemnika na powierzchnię czołową matrycy wprowadza się krążek ze szkła. Matrycę i pojemnik wstępnie nagrzewa się do temperatury ok. 300 [^oC]. W czasie wyciskania stosuje się chłodzenie matrycy. Wyciśnięte wyroby poddaje się operacji prostowania. Zwykle w tym celu stosuje się jednoosiowe rozciąganie, tzw. wyprężanie. Podczas prostowania (wyprężania) ulega pokruszeniu zastygnięta warstewka szkła, pozostająca na powierzchni wyciśniętego wyrobu. Ostateczne oczyszczenie powierzchni odbywa się w drodze wytrawiania. Jako obróbkę wykańczającą w celu uzyskania dokładnych wymaiarów i niskiej chropowatości powierzchni wyrobów można stosować ciągnienie na zimno. Przykłady kształtowników wyciskanych na gorąco ze stali pokazano na rys. VI/17. Zwykle długości wyciskanych kształtowników nie przekraczają 15 [m], a ich wymiary poprzeczne - 150 [mm]. Minimalne grubości ścianek profili pustych wynoszą ok. 3,5 [mm], a średnice otworów - 20 [mm] [2,8]. Wyciskanie współbieżne na gorąco znajduje również zastosowanie w produkcji zaworów silników spalinowych [10] i wielu innych części maszyn.

2. Wyciskanie na gorąco stopów aluminium

Kształtowniki ze stopów alumunium wyciska się na gorąco w temperaturze przesycania (380 - 480 [^oC]), gdy materiały te mają strukturę jednofazową i są plastyczne (po wyciskaniu ulegają starzeniu i umacniają się dyspersyjnie). Dobór temperatury nagrzewania wsadu musi uwzględniać zarówno straty ciepła (przepływ ciepła do matrycy i otoczenia), jak również dyssypację energii odkształcenia plastycznego i pracy tarcia. Asortyment wyciskanych wyrobów jest bardzo szeroki i obejmuje pręty i rury o różnorodnych przekrojach poprzecznych, kształtowniki, elementy tzw. stolarki aluminiowej, części grzejników, maszty do żaglówek i szereg innych produktów.

3. Wyciskanie na zimno wyrobów ze stali

Możliwe jest otrzymywanie za pomocą wyciskania współbieżnego, przeciwbieżnego lub złożonego szeregu wyrobów ze stali pod warunkiem, że nie przekroczy się wytrzymałości narzędzi. Nakłada to ograniczenia na stosowane współczynniki wydłużenia. Wyciskaniu poddaje się stale węglowe i stopowe po wyżarzaniu zmiękczającym (R_e < 400 [Mpa], HB < 150). Do typowych wyrobów można zaliczyć trzpienie o stopniowanych przekrojach oraz tuleje i wytłoczki z pogrubinym dnem [7,9,10]. Wiele elementów tego typu wytwarza się na automatach kuźniczych. Technologię wyciskania współbieżnego na zimno stalowych tulei na cylindry ze stali węglowych i stopowych do ulepszania cieplnego (np. siłowników hydraulicznych) opisano w [9] (rys. VI/18). Tuleje te wyciska się, używając jako wstępniaków odcinków rur bez szwu walcowanych na gorąco. Stosuje się współczynniki wydłużenia  ≈ 2,5 (z ≈ 0,6). Powierzchnię wsadu poddaje się fosforanowaniu w celu stworzenia warstwy podsmarnej (patrz ćwicz. nr II). Jako smaru używa się mieszanki stearynianu sodu (mydła szarego) z dwusiarczkiem molibdenu lub grafitem. Typowe średnice zewnętrzne wyciskanych cylindrów wynoszą 80 ÷ 150 [mm], a odpowiednie grubości ścianek - 7 ÷ 15 [mm]; długości są rzędu 1000 [mm].

4. Wyciskanie na zimno czystego aluminium

Ze względu na małą wartość naprężenia uplastyczniającego i dobre własności plastyczne czyste aluminium jest materiałem szczególnie nadającym się do wyciskania przy bardzo dużych współczynnikach wydłużenia. Za pomocą wyciskania przeciwbieżnego i złożonego produkuje się szereg wyrobów aluminiowych, a zwłaszcza naczyń cienkościennych (puszki, pojemniki, pudełka, tuby itp.). Jako wstępniaki do wyciskania przeciwbieżnego stosuje się wyżarzone płytki (krążki) wykrawane z blachy aluminiowej o odpowiedniej grubości.

3. Narzędzia do wyciskania

1. Stemple i matryce

Stemple i matryce do wyciskania należą do najbardziej obciążonych narzędzi spośród stosowanych w procesach obróbki plastycznej. Wynikają stąd wysokie wymagania stawiane materiałom narzędziowym, ich obróbce cieplnej, a także konstrukcji i dokładności wykonania. Matryce do wyciskania mogą być jednolite lub wstępnie sprężone, czyli wzmocnione przez pojedynczy pierścień, lub większą liczbę pierścieni współśrodkowych, pomiędzy którymi istnieją połączenia skurczowe lub wtłaczane. Podstawy projektowania matryc wstępnie sprężonych będą omówione w p. 6.5. Typowe matryce do wyciskania współbieżnego na gorąco pokazano na rys. VI/19. Kolejne rysunki (VI/20, VI/21) przedstawiają matryce i stemple do wyciskania współbieżnego i przeciwbieżnego na zimno. Narzędzia te są mocowane w specjalnych, sztywnych oprawach, przypominających tłoczniki z prowadzeniem słupowym. Oprawy te zapewniają odpowiednie prowadzenie i zamocowanie stempli (rys. VI/22). Stemple podczas pracy powinny być obciążone wyłącznie siłą osiową, gdyż pojawienie się momentu gnącego może spowodować ich pękanie.

2. Matryce mostkowe

Specjalnym typem narzędzi do wyciskania wyrobów o przekrojach wielospójnych są tzw. matryce mostkowe. Odpowiedni schemat procesu pokazano na rys. VI/23, a rodzaje i budowę matryc - na rys. IV/24 - 4/27. Istotą wyciskania w matrycach mostkowych jest podział materiału wyciskanego z pojemnika na oddzielne strugi (dwie lub więcej), które następnie łączą się ze sobą poprzez spajanie na gorąco w tzw. komorach zgrzewania. Możliwe jest wyciskanie wyrobów o skomplikowanych przekrojach wielospójnych bez konieczności stosowania trzpieni i przebijania wstępniaków. Powstają jednak problemy przy usuwaniu odpadu: jeżeli piętka nie zostanie w pojemniku po odcięciu wyrobu i odsunięciu płyty z matrycą, jedyną możliwością jej usunięcia jest przepchnięcie pozostałego materiału przez kolejny wyrób wyciskany; może to okazać się niemożliwe, jeżeli czas załadowania wsadu jest zbyt długi i materiał pozostały w komorach matrycy nadmiernie ostygnie. Jednakową (w przybliżeniu) prędkość wypływania materiału z matrycy na całym obwodzie wyrobu o zróżnicowanej grubości ścianek można osiągnąć przez odpowiednie umieszczenie wykroju matrycy względem osi pojemnika (miejsca o grubszych ściankach bliżej osi pojemnika), lub - gdy nie jest to możliwe - poprzez zastosowanie komór zgrzewania o różnych wysokościach: h₁ > h₂ przy s₁ < s₂ (rys.VI/28).

1. Podstawy projektowania matryc wstępnie sprężonych

Przedstawione w dalszym ciągu podstawy projektowania matryc wstępnie sprężonych są dobrą ilustracją praktycznego wykorzystania znanych z teorii sprężystości związków Lame'go.

1. Zależności i założenia podstawowe

Przyjmiemy, że modelem matrycy jest pojedynczy pierścień, lub pewna liczba "k" pierścieni współśrodkowych, pomiędzy którymi istnieją połączenia skurczowe lub wtłaczane. Jeżeli nie zaznaczono inaczej, stałe sprężyste E (moduł Younga) i  (współczynnik Poissona) są takie same dla wszystkich pierścieni, natomiast różne mogą być naprężenia dopuszczalne K_i. Stan naprężeń i przemieszczeń w otwartym pierścieniu grubościennym o numerze kolejnym "i" obciążonym ciśnieniami: wewnętrznym p_i oraz zewnętrznym p_i+1 (rys. VI/29) opisują znane związki Lame'go:

(VI.11a)

(VI.11b)

(VI.11c)

(VI.12)

gdzie: σ_rr, σ_θθ, σ_zz - składowe tensora naprężenia: promieniowa, obwodowa i osiowa (we współrzędnych walcowych r, θ, z), u_r(r) - promieniowa składowa wektora przemieszczenia. Ponadto wprowadzono oznaczenia:

(VI.13)

gdzie p_w jest ciśnieniem wewnętrznym, obciążającym matrycę. Iloczyn kolejnych współczynników n_i oznaczymy symbolem n_c:

(VI.14)

Do oceny wytężenia pierścieni zastosujemy hipotezy: energii odkształceń postaciowych Hubera - Misesa (H-M) oraz maksymalnych naprężeń stycznych Treski (T). Naprężenia zredukowane wynoszą odpowiednio (przy σ_zz = 0):

(VI.15)

(VI.16)

gdzie σ_I i σ_III oznaczają odpowiednio wartości maksymalnych i minimalnych naprężeń głównych.

2. Matryca w postaci pojedynczego pierścienia

Największe wytężenie panuje dla r = r₁ (rys. VI/29 a). Przyjmując w (VI.11) i = 1, r = r₁ oraz p₂ = 0 otrzymujemy:

(VI.17)

(VI.18)

Naprężenia zredukowane wg (VI.15) lub (VI.16) nie mogą przekraczać naprężenia dopuszczalnego K₁ dla materiału, z którego wykonana jest matryca, a więc:

(VI.19)

zgodnie z hipotezą Hubera - Misesa, lub:

(VI.20)

dla hipotezy Treski. Maksymalne ciśnienie p_{w max}, które może wytrzymać matryca jest funkcją współczynnika n₁ i wynika z (VI.15) lub (VI.16) po podstawieniu σ_H-M = K₁ lub σ_T = K₁. Wyniki obliczeń przedstawiono na rys. VI/30 i w tab. VI/2.

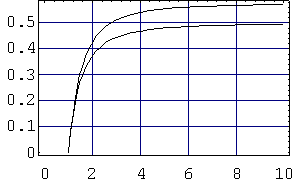
p_{w max}/K₁

TabelaVI/2. Zależność maksymalnego względnego ciśnienia pw max/K1 od dla matrycy w postaci pojedynczego pierścienia
	wg H-M	wg T
2	0,43	0,38
4	0,54	0,47
6	0,56	0,49
8	0,57	0,50
10	0,57	0,50
∞

Przykład 1. Stosując hipotezy T i H-M określić maksymalne ciśnienia p_{w max} dla następujących danych: d₁ = 20 [mm], d₂ = 160 [mm], K₁ = 1200 [MPa]. Wyznaczyć rozkłady naprężeń σ_rr, σ_θθ i σ_T w materiale matrycy przyjmując p_w = p_{w max} obliczone wg hipotezy T.

Wykorzystując dane z tab. VI/2 (lub stosując wzory (VI.19) i (VI.20)) otrzymujemy dla n₁ = d₂²/d₁² = 64: p_{w max} = 0,57*1200 = 684 [MPa] (wg hipotezy Hubera - Misesa) lub: p_{w max} = 0,50*1200 = 600 [MPa] (wg hipotezy Treski). Rozkłady naprężeń wyznaczone z (VI.11) dla i =1, p_w = p_{w max} = 600 [MPa] pokazano na rys. VI/31.

σ_rr , σ_θθ, σ_T [MPa]

r [mm]

3. Matryca wstępnie sprężona

Stan naprężeń w matrycy wstępnie sprężonej 1 (rys. VI/29 b) obciążonej ciśnieniem wewnętrznym p_w i zewnętrznym p₂ opisują związki (VI.11), w których należy podstawić i = 1:

(VI.21)

Największe wytężenie materiału występuje na promieniu r = r₁, gdzie naprężenia wynoszą:

(VI.22)

W zależności od wartości ciśnienia p₂ mogą zaistnieć następujące przypadki.

(i) Naprężenie σ_θθ(r₁) > 0. Ciśnienie p₂ można traktować jako sumę ciśnienia montażowego p_m2 oraz ujemnego naprężenia promieniowego, wynikającego z obciążenia całego narzędzia sprężonego ciśnieniem p_w:

(VI.23)

gdzie σ_rr^'(r₂) wylicza się z (VI.11a), podstawiając r_i = d₁/2, r = d₂/2, n₁ = n_c, p_i = p_w, p_i+1 = 0 i uwzględniając, że
:

(VI.24)

a więc:

(VI.25)

Wstawiając (VI.25) do (VI.22) otrzymujemy dla r = r₁:

(VI.26)

Naprężenie zredukowane wg (VI.16) wynosi:

(VI.27)

(ii) Naprężenie σ_θθ(r₁) = 0. Na średnicy wewnętrznej panuje jednoosiowe ściskanie naprężeniem
, a więc:

(VI.28)

(iii) Naprężenie σ_rr(r₁) < σ_θθ(r₁) < 0. W tym przypadku σ_I = σ_zz = 0, σ_III = σ_rr, a więc związek (VI.16) dla r = r₁ przyjmuje postać:

(VI.29)

Stosując natomiast hipotezę H-M i wykorzystując warunek konieczny istnienia ekstremum funkcji (VI.15):

(VI.30)

otrzymujemy najbardziej korzystną z punktu widzenia wytrzymałości narzędzia wartość naprężenia obwodowego:

(VI.31)

4. Matryca wzmocniona jednym pierścieniem

Jeżeli dla materiału matrycy (np. stali ulepszanej cieplnie) dopuszcza się dodatnie naprężenie obwodowe σ_θθ(r = r₁) > 0, to podstawiając w (VI.11) odpowiednio i = 1, r = r₁ (dla matrycy) oraz i = 2, p₃ = 0, r = r₂ (dla pierścienia wzmacniającego), a następnie stosując hipotezę T w postaci (VI.27) otrzymujemy:

(VI.32)

(VI.33)

Maksymalne wartości ciśnień p_{2 max} i p_{w max} określamy z warunków (VI.32) i (VI.33) po zastąpieniu znaków nierówności znakami równości:

(VI.34a)

(VI.34b)

Optymalna wartość współczynnika n₁ wynika z warunku koniecznego istnienia ekstremum funkcji (VI.34b):

(VI.35)

co daje:

(VI.36)

a więc:

(VI.37)

Wartość ciśnienia montażowego p_m2 oblicza się z (VI.25) po podstawieniu p₂ = p_{2 max} i p_w = p_{w max} z (VI.34):

(VI.38)

Wymagana wartość wcisku W₂₁ pomiędzy pierścieniem wzmacniającym a matrycą wynika z różnicy przemieszczeń na średnicy d₂:

(VI.39)

wywołanych ciśnieniem p_m2, gdzie: u₁₂ i u₂₂ - odpowiednie przemieszczenia: dla matrycy 1 na średnicy d₂ i dla pierścienia wzmacniającego 2 również na średnicy d₂. Przemieszczenia te wylicza się z (VI.12), podstawiając odpowiednio: i = 1, r = d₂/2, p_i = 0, p_i+1 = p_m2 (dla matrycy) oraz i = 2, r = d₂/2, p_i = p_m2, p_i+1 = 0 (dla pierścienia):

(VI.40)

(VI.41)

(VI.42)

Zastosowanie powyższych związków ilustrują wyniki obliczeń (rys. VI/32, tab. VI/3).

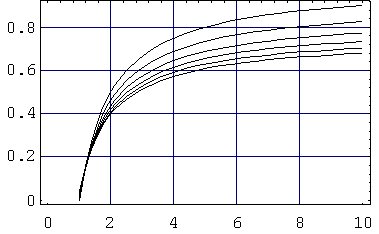
p_{w max}/K₁

Rys. VI/32. Zależność maksymalnego względnego ciśnienia p_{w max}/K₁ od parametru
wg hipotezy T dla różnych wartości ψ (krzywe od górnej do dolnej odpowiadają kolejno wartościom ψ: 1, 1,2, 1,4, 1,6, 1,8 i 2)

Tabela. VI/3. Zależność maksymalnego względnego ciśnienia pw max/K1 od dla matrycy z jednym pierścieniem wzmacniającym wg hipotezy T (przy )
		ψ = 1,0	ψ = 1,2	ψ = 1,4	ψ = 1,6	ψ = 1,8	ψ = 2,0
2	0,500	0,460	0,435	0,417	0,405	0,396
4	0,750	0,688	0,646	0,615	0,591	0,573
6	0,833	0,765	0,716	0,681	0,654	0,632
8	0,875	0,803	0,751	0,714	0,685	0,662
10	0,900	0,825	0,773	0,733	0,703	0,679
∞	1,000	0,917	0,857	0,813	0,778	0,750

Przykład 2. Przyjmując następujące dane: d₁ = 20 [mm], d₃ =160 [mm], K₁ = K₂ =1200 [MPa],  = 0,3, E = 2,1*10⁵ [MPa] obliczyć: optymalną średnicę d₂, dopuszczalne ciśnienie p_{w max}, wartości ciśnienia montażowego (p_m2) i wcisku (W₂₁). Wyznaczyć rozkłady naprężeń promieniowych σ_rr, osiowych σ_θθ oraz zredukowanych σ_T po zmontowaniu i po obciążeniu ciśnieniem p_{w max}.

Wyniki obliczeń zawarto w tab. VI/4 oraz przedstawiono na rys. VI/33, VI/34 i VI/35.

Tab. VI/4. Wyniki obliczeń matrycy i pierścienia wzmacniającego (przykład 2)
Lp	Określana wielkość	Wynik	Wzory
1	d2 [mm]	56,57	VI.37
2	pw max [MPa]	1050	VI.34b
3	pm2 [MPa]	408,333	VI.38
4	W21 [mm]	0,28	VI.42
5	Rozkłady naprężeń σrr, σθθ i σT	Rys. VI/33, VI/34	VI.11, VI.16

Dyskusja. Obciążenie ciśnieniem p_w = p_{w max} = 1050 [MPa] (wg tab. VI/4) matrycy jednolitej lub przy braku ciśnienia montażowego (rys. VI.33 b) wywołuje na promieniu r = d₁/2 = 10 [mm] (powierzchnia otworu matrycy) naprężenia: σ_rr = -1050 [MPa], σ_θθ = 1083,33 [MPa], σ_T = σ_rr - σ_θθ = 2133,33 [MPa], co przekracza dopuszczalne naprężenie K₁ = 1200 [MPa] dla matrycy. Jeżeli matryca będzie wstępnie sprężona ciśnieniem montażowym p_m2 = 408,333 [MPa] (wg tab. VI/4), to otrzymamy rozkłady naprężeń przedstawione na rys. VI/34. Do wywołania takiego ciśnienia p_m2 potrzebna jest różnica średnic W₂₁ = d₂₁ - d₂₂ = 2(u₂₂ - u₁₂) (rys. VI/35). W tym przypadku naprężenia zredukowane na promieniach d₁/2 (w materiale matrycy) i d₂/2 (w materiale pierścienia wzmacniającego) są takie same i wynoszą po 1200 [MPa], co odpowiada warunkom przykładu 2. Współczynnik Poissona jest potrzebny do określenia przemieszczeń u₂₂ i u₁₂ ((VI.40) i (VI.41)), natomiast nie wpływa na ich różnicę W₂₁ (VI.42).

Sposób obliczeń ulega zmianie, gdy matryca (np. wykonana z węglików spiekanych) nie powinna pracować przy dodatnich naprężeniach obwodowych. Warunek wytrzymałościowy dla pierścienia wzmacniającego można przez analogię do (VI.20) zapisać w postaci:

(VI.43)

Naprężenia obwodowe na wewnętrznym promieniu matrycy mają być nie większe od zera:

(VI.44)

Wartość maksymalnego ciśnienia p_w = p_{w max} wyznacza się z (VI.43) i (VI.44) po wprowadzeniu znaków równości:

(VI.45)

Potrzebne ciśnienie montażowe p_m2 oblicza się z (VI.25) po podstawieniu p_w = p_{w max} z (VI.45) i p₂ z (VI.43):

(VI.46)

a wartość wcisku W₂₁ z (VI.42), podstawiając ciśnienie montażowe z VI.46. Przykładowe wyniki obliczeń zawiera tab. VI/5.

σ_rr , σ_θθ , σ_T [MPa]

r [mm]

σ_rr , σ_θθ [MPa]

r [mm]

Rys. VI/33. Rozkłady naprężeń w matrycy i pierścieniu wzmacniającym: a) po zmontowaniu pierścienia (p_w = 0) przy ciśnieniu montażowym p_m2, b) pochodzące od ciśnienia wewnętrznego p_w przy braku ciśnienia montażowego

σ_rr , σ_θθ , σ_T [MPa]

r [mm]

d₁

d₂

d₃

Rys. VI/34. Rozkłady naprężeń w matrycy i pierścieniu wzmacniającym po obciążeniu ciśnieniem wewnętrznym p_w (superpozycja danych z rys. VI/33 a i b); 1 - matryca, 2 - pierścień wzmacniający

Tab. VI/5. Zależność maksymalnego względnego ciśnienia pw max/K1 od dla matrycy z jednym pierścieniem wzmacniającym gdy σ(r = r1) = 0 (przy )
		ψ = 1,0	ψ = 1,2	ψ = 1,4	ψ = 1,6	ψ = 1,8	ψ = 2,0
2	0,333	0,259	0,205	0,165	0,133	0,108
4	0,600	0,493	0,415	0,357	0,311	0,275
6	0,714	0,591	0,503	0,436	0,384	0,341
8	0,778	0,646	0,550	0,479	0,423	0,378
10	0,818	0,680	0,581	0,506	0,448	0,401
∞	1,000	0,833	0,714	0,625	0,556	0,500

Przykład 3. Przyjmując średnice (d₁, d₂, d₃), naprężenia dopuszczalne (K₁, K₂) i stałe sprężyste (, E) jak w przykładzie 2 obliczyć przy warunku: σ_(r = r₁) = 0 dopuszczalne ciśnienie p_{w max}, wartość ciśnienia montażowego (p_m2) i wcisku (W₂₁). Wyznaczyć rozkłady naprężeń promieniowych σ_rr, osiowych σ_θθ oraz zredukowanych σ_T po obciążeniu ciśnieniem p_{w max}.

Wyniki obliczeń zawarto w tab. VI/6 i na rys. VI.36.

Tabela VI/6. Wyniki obliczeń matrycy i pierścienia wzmacniającego (przykład 3)
Lp	Określana wielkość	Wynik	Wzory
1	pw max [MPa]	933,333	VI.45
2	pm2 [MPa]	421,296	VI.46
3	W21 [mm]	0,29	VI.42, VI.46
4	Rozkłady naprężeń σrr, σθθ i σT	Rys. VI/36	VI.11, VI.16

6.5.5. Matryca z dwoma pierścieniami wzmacniającymi

Przy dwóch pierścieniach wzmacniających (i = 3) największe wytężenie matrycy 1 oraz pierścieni 2 i 3 występują odpowiednio na średnicach d₁, d₂ i d₃. Jeżeli przyjmiemy, że na tych średnicach σ_θθ > , to z hipotezy (VI.16) wynika, że:

(VI.47)

σ_rr , σ_θθ , σ_T [MPa]

Rys. VI/36. Rozkłady naprężeń w matrycy i pierścieniu wzmacniającym po obciążeniu ciśnieniem wewnętrznym p_w (przykład 3)

Ciśnienia maksymalne p_{w max} , p_{2 max} i p_{3 max} wynoszą:

(VI.48)

(wykorzystano związek:
)

(VI.49)

(VI.50)

Optymalne wartości współczynników n₁ i n₂ określimy z warunku koniecznego istnienia ekstremum funkcji (VI.48):

(VI.51)

co daje:

(VI.52)

Optymalne średnice d₂ i d₃ wynoszą:

(VI.53)

lub:

(VI.54)

gdzie oznaczono:

(VI.55)

Rozkłady naprężeń w matrycy (1) i pierścieniach wzmacniających (2) i (3) opisują następujące wzory:

- dla matrycy 1:

(VI.56)

(VI.57)

(d₁/2 ≤ r ≤ d₂/2)

- dla pierścienia 2:

(VI.58)

(VI.59)

(d₂/2 ≤ r ≤ d₃/2)

- dla pierścienia 3:

(VI.60)

(VI.61)

(d₃/2 ≤ r ≤ d₄/2)

Wynikają one z (VI.11) i superpozycji stanów naprężeń pochodzących od:

• ciśnienia montażowego p_m3 przy nakładaniu pierścienia 3 na pierścień 2,

• ciśnienia montażowego p_m2 przy nakładaniu zespołu pierścieni 2 i 3 na matrycę 1,

• ciśnienia p_w obciążającego narzędzie sprężone.

Po wstawieniu do (VI.56) - (VI.61) promieni wewnętrznych (gdzie występują największe wytężenia) otrzymujemy:

(VI.62)

Ciśnienia montażowe wyznacza się z zależności:

(VI.63)

(VI.64)

Potrzebne wartości wcisków można wyznaczyć analogicznie jak w p. 6.5.4, modyfikując odpowiednio wzory (VI.40 - VI.42), co daje:

(VI.65)

dla montażu pierścienia 2 w pierścieniu 3, oraz::

(VI.66)

dla montażu pierścienia 1 (matrycy) w zespole pierścieni (2,3).

Przeprowadzając obliczenia wyżej podanym sposobem należy zawsze sprawdzić, czy rzeczywiście naprężenia obwodowe na średnicach d₁, d₂ i d₃ są dodatnie. Zależy to od przyjętych wartości naprężeń dopuszczalnych K₁, K₂ i K₃. W przypadku przeciwnym tok obliczeń musi ulec zmianie (podobnie jak dla matrycy z jednym pierścieniem wzmacniającym - patrz przykład 2).

Przykład 4. Obliczyć wartości: optymalnych średnic (d₂, d₃) ciśnień montażowych (p_m2, p_m3), maksymalnego ciśnienia wewnątrz matrycy (p_{w max}), wcisków (W₃₂, W_(2,3)1) oraz wyznaczyć rozkłady naprężeń obwodowych (σ_), promieniowych (σ_rr) i zredukowanych (σ_T) dla następujących danych: K₁ = 1200 [MPa], K₂ = 1000 [MPa], K₃ = 900 [MPa], E = 2,1*105 [MPa].

Wyniki obliczeń podano w tab. VI/7 i na rys. VI/37.

Tabela VI/7. Wyniki obliczeń matrycy i pierścienia wzmacniającego (przykład 3)
Lp	Określana wielkość	Wynik	Wzory
1	d2 [mm]	43,259	VI.53
2	d3 [mm]	85,416	VI.53
2	pm2 [MPa]	458,976	VI.63
3	pm3 [MPa]	184,535	VI.64
1	pw max [MPa]	1165,26	VI.48
4	W32 [mm]	0,262	VI.65
5	W(2,3)1 [mm]	0,255	VI.66
6	Rozkłady naprężeń σrr, σθθ i σT	Rys. VI/37	VI.56 - VI.61

σ_rr , σ_θθ , σ_T [MPa]

Rys. VI.37. Rozkłady naprężeń obwodowych (σ_), promieniowych (σ_rr) i zredukowanych (σ_T) w matrycy (1) i pierścieniach wzmacniających (2) i (3) (dane jak w przykładzie 4)

1. Uwagi końcowe

Stosowanie pierścieni wzmacniających pozwala na lepsze wykorzystanie własności wytrzymałościowych pierścienia 1 przy ustalonym współczynniku n_c określającym średnicę zewnętrzną narzędzia. Jest to widoczne z przykładów 1, 2 i 4, których wyniki zestawiono w tab. VI/8. Podwyższenie dopuszczalnego ciśnienia wewnątrz matrycy przy tych samych gabarytach narzędzia jest możliwe, nawet gdy pierścienie wzmacniające mają mniejsze wartości napręzeń dopuszczalnych K₂ i K₃.

Tabela VI/8. Stosunek pw max/K1 dla matrycy nie wzmocnionej (1) oraz w przypadku zastosowania jednego (2) i dwóch (3) pierścieni wzmacniających
Lp	nc	K1 [MPa]	K2 [MPa]	K3 [MPa]	pw max [MPa]	pw max/K1	Nr przykładu
1	64	1200	-	-	500	0,500	1
2			1200	1200	-	1050	0,875	2
3			1200	1000	900	1165	0,971	4

Wskazówki praktyczne odnośnie wytrzymałości materiałów stosowanych na pierścienie wzmacniające można znaleźć m. in. w [3,6]. Możliwe jest stosowanie więcej niż 2 pierścieni wzmacniających [7].

6.6. Maszyny do wyciskania

Wyciskanie współbieżne prętów, rur i kształtowników odbywa się na specjalnych prasach poziomych wielokrotnego działania (rys. VI/38). Zapewniają one realizację wszystkich faz procesu wyciskania (rys. VI/39, VI/40). Ponadto do wyciskania współbieżnego i przeciwbieżnego wyrobów o mniejszych długościach mogą być wykorzystywane prasy hydrauliczne oraz prasy kuźnicze korbowe i kolanowe (rys. VI.41).

6. Literatura

1. S. Erbel, K. Kuczyński, Z. Marciniak: Obróbka plastyczna. PWN, Warszawa 1981

2. N. Fromm: Das Warmstrangpressen von Stahl zu Profilen - Möglichkeiten und Grenzen. Schwerter Profil 4, 1962

3. G. Herold, K. Herold, A. Schwager: Massiv - umformung. Veb Verlag Technik, Berlin 1982

4. B. Koszla: Zasady projektowania narzędzi wstępnie sprężonych do wyciskania. Biouletyn informacyjny obróbki plastycznej, t. IX, z. 5, 1973

5. W. Krzyś, M. Życzkowski: Sprężystość i plastyczność. Wybór zadań i przykładów. PWN, Warszawa 1962

6. Lehrbuch der Umformtechnik. Band 2 Massivumforming (red. K. Lange). Springer - Verlag, Berlin, Heidelberg, New York 1974

7. W. Łabędzki: Wyciskanie metali na zimno. Praktyczne zasady. Obróbka plastyczna, t. XVII, z. 2, 1978

8. Obróbka plastyczna metali. Praca zbiorowa pod red. J. Gronostajskiego. Politechnika Wrocławska, Wrocław 1973

9. H. Partyka, J. Myszka, T. Mazak, J. Kranz: Wyciskanie na zimno cylindrów stalowych. Wyd. "Śląsk", Katowice 1970

10. Procesy przeróbki plastycznej metali. Praca zbiorowa pod red. J. Sińczaka. Wyd. Nauk. AKAPIT, Kraków 2003

11. W. P. Romanowski: Poradnik obróbki plastycznej na zimno. WNT, Warszawa 1976

12. J. Wencelis: Zawory tłokowych silników spalinowych. Politechnika Łódzka, filia w Bielsku - Białej, Bielsko - Biała 1997

13. J. Wantuchowski, J. Richert: Matryce mostkowe do wyciskania metali i stopów lekkich. Rudy i metale nieżelazne, 17, 5, 1972

14. Wyciskanie na zimno. Konstrukcja matryc. Obróbka plastyczna metali. Zalecenia. INOP - Z/155 - 03 - 79 (opracował: W. Łabędzki). Instytut Obróbki Plastycznej, Poznań 1979

σ_θθ

σ_T

a)

p_m2

b)

σ_θθ

σ_rr

p_w

σ_rr

σ_θθ

σ_T

Rys. VI/30. Zależność maksymalnego względnego ciśnienia p_{w max}/K₁ od
dla matrycy w postaci pojedynczego pierścienia: górna krzywa - wg hipotezy H-M, dolna - wg hipotezy T

σ_rr

p_w

σ_θθ

1

2

d₃

d₂₂

2

1

d₂₁

Rys. VI/35. Schemat montażu narzędzia wstępnie sprężonego: 1 - matryca, 2 - pierścień wzmacniający

W₂₁ = d₂₁ - d₂₂ = 2(u₂₂ - u₁₂)

u₂₂

d₁

-u₁₂

d₂

σ_T

σ_rr

σ_θθ

p_w

d₁

d₂

Rys. VI/31. Rozkłady naprężeń w materiale matrycy obliczone dla danych z przykładu 1

p_w

r [mm]

d₄

d₃

d₂

d₁

r [mm]

σ_T

σ_θθ

σ_rr

d₃

p_w

d₁

d₂

p_m2

p_m2

σ_T

σ_rr

σ_

1

3

2

---