PKM

EGZAMIN

Pytania + opracowania

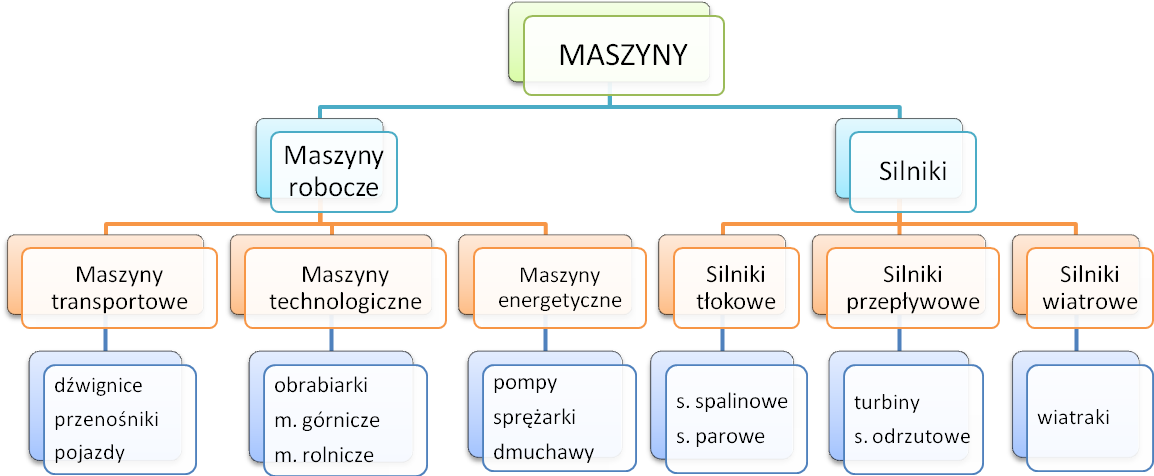
1. Opis maszyn, zasady konstruowania, optymalizacja konstrukcji - kryterium.

Maszyna jest konstrukcją, której co najmniej jedna część jest ruchoma. Maszyna składa się zwykle z zespołów lub części. Zespoły pełnią określone funkcje i również składają się z części. Zespołami są np.: sprzęgła lub hamulce.

Konstruowanie jest szczególnym rodzajem projektowania, dotyczącym maszyn. Projekt maszyny przygotowuje zwykle zespół doświadczonych konstruktorów zgodnie z następującym algorytmem:

• Opracowanie założeń techniczno-ekonomicznych, wskazanie podobnych rozwiązań, określenie potrzeb rynku, oszacowanie kosztów wytwarzania,

• Opracowanie projektu wstępnego, sporządzenie ogólnego rysunku maszyny, wykonanie obliczeń i ocena wytrzymałości konstrukcji,

• Opracowanie projektu szczegółowego, sporządzenie rysunków wykonawczych części oraz rysunku złożeniowego, uzupełnienie obliczeń z uwzględnieniem wytrzymałości konstrukcji,

• Budowa prototypu i wykonanie badań, usunięcie ewentualnych usterek konstrukcji,

• Opracowanie dokumentacji konstrukcyjnej do produkcji seryjnej.

Optymalne projektowanie to wybór takiego wariantu konstrukcji z obszaru rozwiązań dopuszczalnych, których wyróżnione właściwości SA minimalne lub maksymalne. Wyróżnia się optymalizację jednokryterialną, zwaną skalarową, oraz wielokryterialną, zwaną wektorową lub polioptymalizacją.

2. ograniczenia w projektowaniu maszyn - warunki wytrzymałości i stateczności.

Warunek wytrzymałości jest jednym z ograniczeń obowiązujących w projektowaniu maszyn lub ich części. Spełnienie jego jest niezbędne, gdyż wyklucza się w ten sposób zniszczenie konstrukcji przez pęknięcie, w praktyce może to sprawić pewne trudności, które dotyczą:

• Wyznaczenie największej wartości naprężenia σ_max

• Wyznaczenie wartości naprężeń dopuszczalnych σ_dop

Warunek wytrzymałości dla konstrukcji formułowany jest w następująco sposób:

σ_max ≤ σ_dop lub τ_max ≤ τ_dop

gdzie:

σ_max - największe naprężenia normalne lub zastępcze Hubera-Misesa

τ_max - największe naprężenia styczne

σ_dop , τ_dop - naprężenia dopuszczalne

Warunek stateczności jest jednym z ograniczeń obowiązujących w projektowaniu maszyn lub ich części. Jego spełnienie zabezpiecza konstrukcję przed wyboczeniem. Prostymi częściami maszyn narażonymi na wyboczenie są najczęściej ściskane śruby, płyty prostokątne lub walcowe naczynia cienkościenne.

Warunek stateczności dla konstrukcji formułowany jest zwykle następująco:

F_max ≤
lub σ_max ≤

Gdzie:

F_CR , σ_CR - obciążenie, naprężenia krytyczne

C_s - współczynnik bezpieczeństwa na wyboczenie ( 1 < C_s )

Siła Eulera (siła kytyczna) dla ściskanej belki-śruby o długości L, przegubowo podpartej na obu końcach:

gdzie:

E - Moduł sprężystości (Younga)

Jz - moment bezwładności przekroju belki - śruby (πd²/64)

d - średnica rdzenia śruby

3. Wytrzymałość zmęczeniowa, współczynnik asymetrii cyklu.

Wytrzymałość zmęczeniowa (granica zmęczenia) Z_G - to największe naprężenie σmax, przy którym próbka lub część maszyny pod działaniem obciążenia zmiennego sinusoidalnie nie ulega zniszczeniu po osiągnięciu granicznej liczby cykli N_G.

Współczynnik asymetrii cyklu charakteryzuje rodzaj cyklu obciążenia zmiennego i ma wpływ na wartość wytrzymałości zmęczeniowej materiału próbki lub części maszyny. Wartość naprężeń dopuszczalnych σ_dop zależy od rodzaju cyklu.

4. tolerancja wymiarów, odchyłki klasy dokładności, zasada stałego otworu, układ pól tolerancji

Tolerancja wymiaru definiowana jest jako różnica między wymiarami granicznymi. W budowie maszyn tolerancje i pasowania odnosi się do wałków i otworów, należy zauważyć, że wartości odchyłek dolnych mogą być ujemne.

Dla wałka: T_w = dsup - dinf

Dla otworu: To = Dsup - Dinf

gdzie:

d_sup, d_inf , D_sup, D_inf - średnice górne (supremum) i dolne (nifimum)

Odchyłki to różnice między wymiarami granicznymi a nominalnymi - dopuszczalne błędy wymiarów:

• górne es = d_sup - d_nom ES = D_sup - D_nom

• dolne ei = d_inf - d_nom ES = D_inf - D_nom

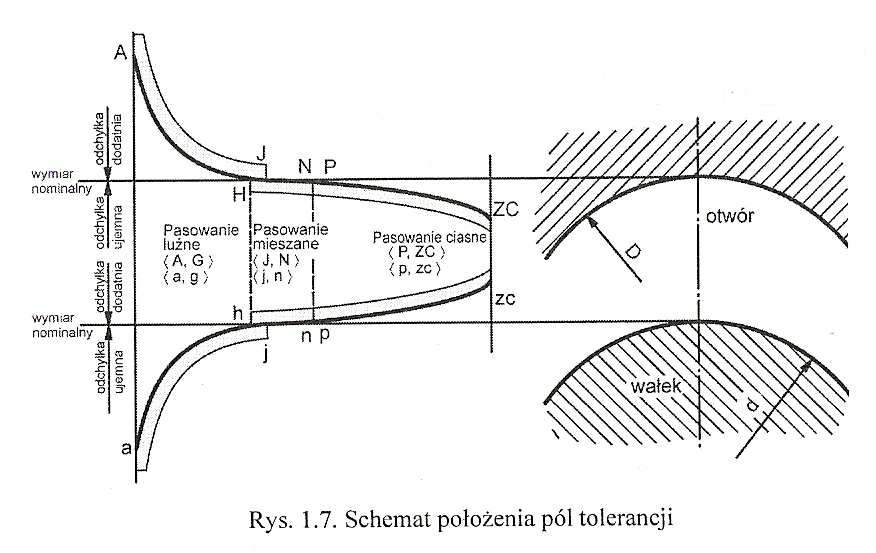
Tolerancje wymiarów są znormalizowane i szczegółowo opisane w obowiązujących normach. Wyróżnia się 20 klas dokładności. Wartości tolerancji są wyznaczone dla pewnych średnic nominalnych i kolejnych klas dokładności. Położenia pól tolerancji (odchyłek podstawowych) w odniesieniu do linii zerowej oznaczone są literami wg normy.

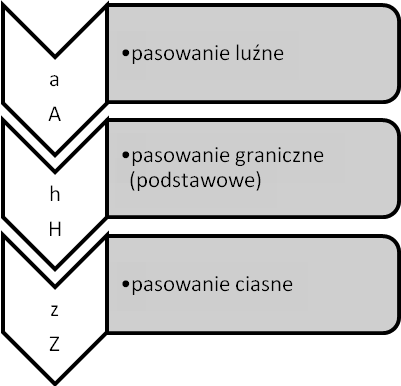
Pasowanie to połączenie dwóch elementów, z których jeden obejmuje drugi. Istnieją dwie możliwości pasowania wałka i otworu wg zasady stałego wałka lub otworu. W budowie maszyn, z uwagi na koszty produkcji, stosowana jest przede wszystkim zasada stałego otworu, która polega na tym, że średnicę otworu wykonuje się jako podstawową, zgodnie z polem tolerancji H, a średnicę wałka wykonuje się z takim polem tolerancji, aby otrzymać założone pasowanie. Pasowania mogą być ciasne, luźne i mieszane.

5. Ogólna charakterystyka podstawowych połączeń - przykłady tych połączeń

Maszyny lub ich zespoły składają się z części, które są ze sobą połączone. Wyróżnia się połączenia rozłączne i nierozłączne.

• W połączeniach nierozłącznych podczas rozłączania części łączone lub łączniki ulegają zniszczeniu, natomiast

• W połączeniach rozłącznych pozostają nieuszkodzone.

6. Połączenie nitowe, warunki wytrzymałościowe dla prostego obciążenia, przykłady połączeń

Połączenie nitowe jest połączeniem nierozłącznym pośrednim. Uzyskuje je się w procesie technologicznym zwanym nitowaniem, który polega na wierceniu otworów w łączonych częściach, np.: blachach, ścięciu krawędzi otworów - usunięciu zadziorów - włożeniu nitu do otworu a następnie wykonaniu zakuwki.

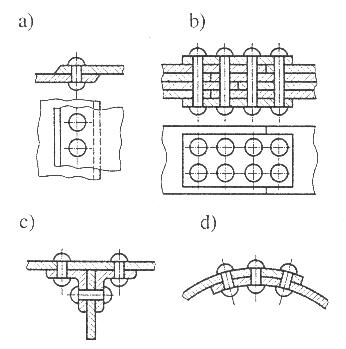
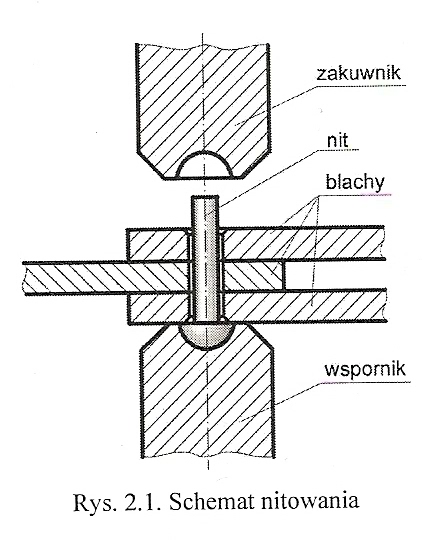
Schemat:

Przykłady połączeń nitowych:

a) zakładkowe b) nakładkowe, c) blachownicy d) zbiornika ciśnieniowego

Istnieje pewna graniczna siła która jest równoważona siłami tarcia między dociskanymi powierzchniami. Istnieją 2 przypadki obciążenia:

- siłą mniejszą od granicznej - nity nie są bezpośrednio obciążone

- siłą większą od granicznej - nity są bezpośrednio obciążone i są narażone na ścinanie

Warunki wytrzymałościowe:

a) wytrzymałość na ścinanie:
lub

gdzie:

F1 - siła obciążająca jeden nit

F - siła

m - liczba poddawanych ścinaniu przekrojów w nicie

A₀ = πd²/4 - pole powierzchni przekroju nita

d - średnica nita, τ_dop=σ_dop/

b) wytrzymałość na nacisk:

gdzie:

n - ilośc nitów w rzędzie

g - grubość blachy

c) wytrzymałość na rozciąganie blachy:
2₂

gdzie:

A₂ - pole przekroju blachy

b - szerokość blachy, podziałka nitów na szerokości

7. Połączenie nitowe wspornika - rozkład sił w łącznikach, warunek wytrzymałości

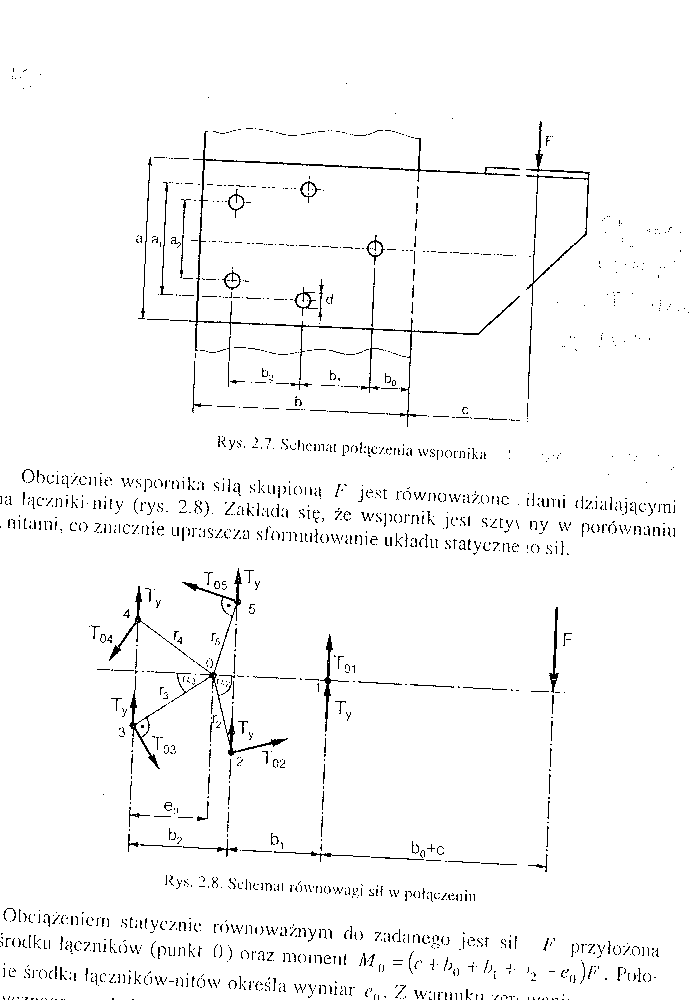
Połączenia nitowe oprócz prostego rozciągania są również pod działaniem złożonych obciążeń. Przykładem jest wspornik obciążony siłą F:

Obciążenie wspornika siłą skupioną F jest równoważone siłami działającymi na łączniki- nity. Zakłada się, że wspornik jest sztywny w porównaniu z nitami, co znacznie upraszcza sformułowanie układu statycznego sił.

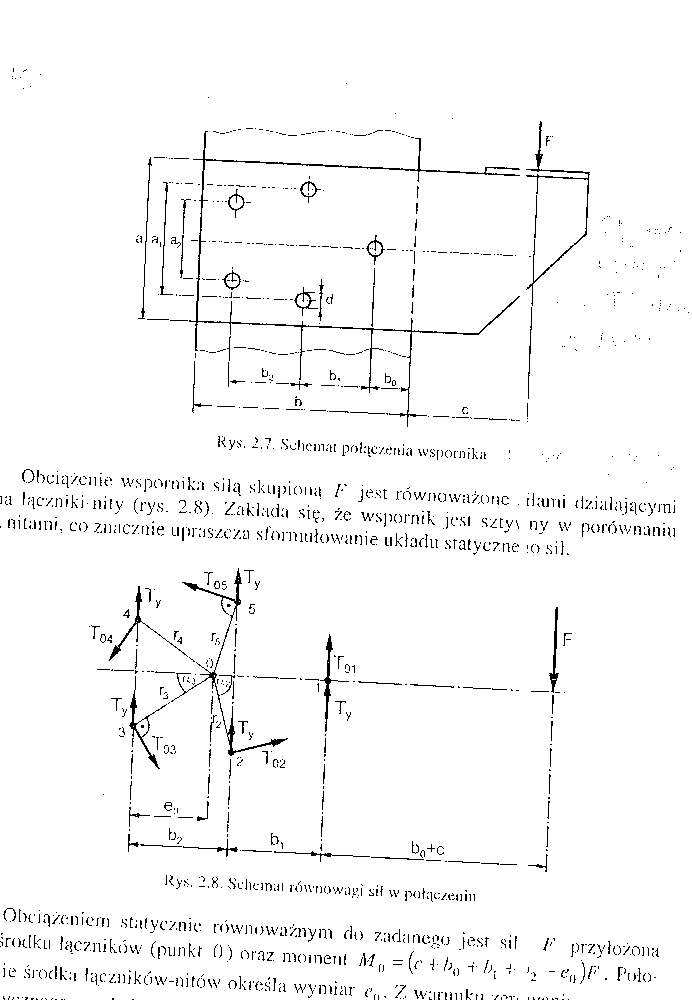
Obciążeniem statycznie równoważnym do zadanego jest siła F przyłożona w środku łączników (punkt 0) oraz moment M­₀= (c + b₀ + b₁ + b₂ - e₀)F. Położenie środka łączników- nitów określa wymiar e₀. Z warunku zerowania momentu statycznego względem osi pionowej do wspornika przechodzącej przez ten punkt po prostych przekształceniach otrzymano:

e₀=
(b₁ + 3b₂)

Siła przyłożona w punkcie 0 rozkłada się równomiernie na wszystkie łączniki- nity, zatem:

T_y=
F Gdzie: n- liczba łączników- nitów,

Moment M­₀ którego wektor jest przyłożony w punkcie 0 i prostopadły do płaszczyzny wspornika, rozkłada się na odpowiednie proste momenty M_i = r_i T_0i zatem:

M₀=
r_iT_oi

Z założenia, że wspornik jest sztywny w porównaniu z łącznikami, wynika, iż proporcja siły T_0i i ramienia r_i jest stała stąd:

T_0i = r_iC₀

Dlatego otrzymano:

C₀ =

Stała C₀ [N/mm] jest wielkością charakterystyczną dla projektowanego wspornika. Promienie r_i jako przeciwprostokątne odpowiednich trójkątów prostokątnych opisuje twierdzenie Pitagorasa.

Dowolny łącznik- nit obciążony jednocześnie dwiema siłami T_y i T_oi, a ich suma (moduł sumy dwóch wektorów)

T­_ti=
gdzie: α- kąt między tymi wektorami- siłami.

Warunek wytrzymałości: dla połączenia wspornika przybiera postać:

gdzie:

T_t,max- max{T_t,1, T_t,2,…, T_t,n}- największa wartość siły działającej na nit

8. Połączenia spajane: spawane, lutowane

Połączenie spawane otrzymuje się w procesie technologicznym zwanym spawaniem, który polega na lokalnym stopieniu łączonych części i wprowadzeniu dodatkowo metalu (spoiwa) w miejscu łączenia, Spoiwami są specjalne elektrody topliwe lub druty spawalnicze. Między łączonymi częściami po ich ostygnięciu powstaje spoina.

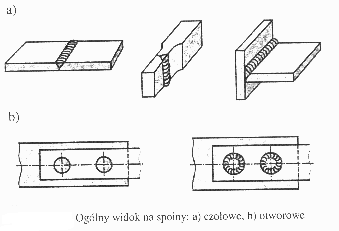
Najczęściej stosuje się spoiny czołowe (doczołowe) i pachwinowe (kątowe) a rzadziej spoiny otworowe lub punktowe.

Warunek wytrzymałości dla spoin pachwinowych formułowany jest następująco:

gdzie:

A = a*Ls - pole pow. Przekroju spoiny

a - najmniejszy wymiar spoiny

Ls - długość spoiny

Połączenie lutowane otrzymuje się w procesie technologicznym zwanym lutowaniem, który polega na łączeniu części za pomocą roztopionego metalu zwanego lutem. Warunkiem uzyskania prawidłowego połączenia jest metaliczna czystość powierzchni łączonych części, dzięki czemu zachodzi zjawisko kohezji i dyfuzji. Wytrzymałość połączenia lutowanego jest większa od wytrzymałości lutu.

Wyróżnia się lutowanie:

• Miękkie, gdy lutem są metale o temp topnienia T < 300°C

• Twarde, gdy lutem są metale o temp topnienia T > 550°C

• Specjalne - jubilerskie, gdy lutem jest metal szlachetny

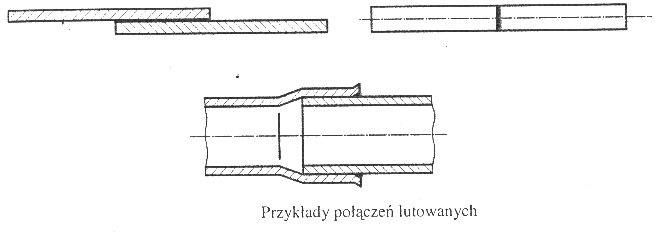
Warunki wytrzymałości dla połączeń lutowanych formułuje się podobnie jak dla spawanych.

9. Połączenia spajane: zgrzewane, klejone - rozkład naprężeń w połączeniu

Połączenie zgrzewane otrzymujemy w procesie technologicznym zwanym zgrzewaniem, który polega na lokalnym dociśnięciu i podgrzaniu łączonych części do temperatury topnienia. Istnieją różne sposoby lokalnego nagrzewania , np.: gazowe, mechaniczne lub elektryczne. W praktyce stosuje się zgrzewanie elektryczne oporowe lub mechaniczne tarciowe. Zgrzewanie elektryczne wykonuje się za pomocą zgrzewarek.

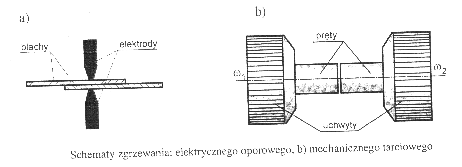
Zgrzewanie mechaniczne tarciowe stosowane jest do łączenia dwóch prętów o przekrojach kołowych wykonywane jest na specjalnej maszynie, wyposażonej w dwa obrotowe uchwyty. Ciepło potrzebne do lokalnego podgrzania końców obu prętów wytwarzane jest przez tarcie powierzchni czołowych. Na początku procesu jeden pręt obraca się z w1 a drugi pozostaje w spoczynku. Po dociśnięciu powstaje tarcie które powoduje wzrost temp. co przyspiesza dyfuzję. Proces kończy się wyrównaniem prędkości obrotowych obu prętów.

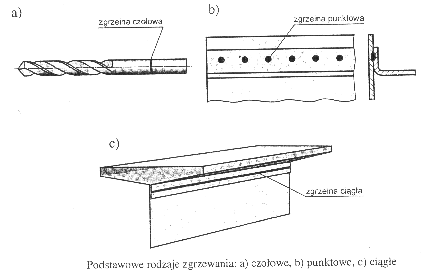
Wyróżnia się następujące rodzaje zgrzewania:

• Czołowe (pręty)

• Punktowe (blachy)

• Liniowe (blachy, rury)

Warunki wytrzymałości dla połączeń zgrzewanych formułuje się podobnie jak dla spawanych lub nitowych.

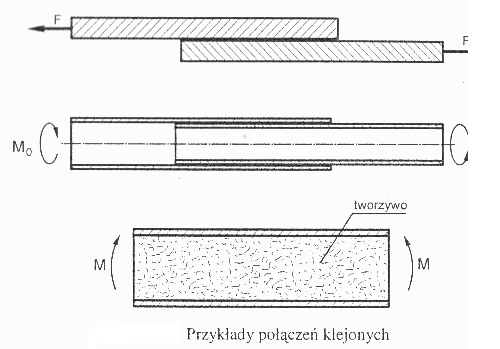
Połączenia klejone otrzymuje się w procesie technologicznym, który polega na łączeniu części za pomocą kleju. Klejenie jest nowoczesna technologią stosowaną w budowie maszyn. Skuteczność klejenia jest ściśle związana ze zjawiskiem adhezji (sił przyczepności) i kohezji (sił spójności międzycząsteczkowej). Kleje konstrukcyjne są tworzywami syntetycznymi, których głównym składnikiem jest żywica. Właściwości połączenia klejonego - spoiny klejowej - zależą od budowy chemicznej podstawowych składników kleju, a także od jakości przygotowanej powierzchni łączonych części.

Warunki wytrzymałości dla połączeń klejonych formułuje się podobnie jak dla spawanych. Przyjmuje się liniową sprężystość spoiny i pomija się właściwości nieliniowe co jest sporym uproszczeniem.

10. Połączenia kształtowe: wpustowe, wypustowe, kołkowe, sworzniowe, klinowe

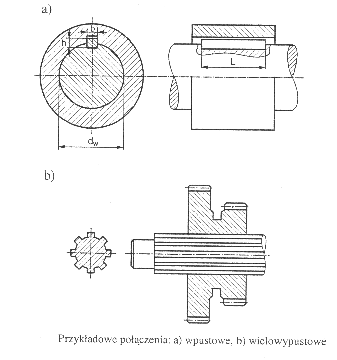
Połączenia wpustowe są połączeniami pośrednimi , w których wpust pełni funkcję łącznika. Połączenia wypustowe są połączeniami bezpośrednimi, w których powierzchnie części łączonych są odpowiednio ukształtowane. Połączenia wielowypustowe są znormalizowane. Przykłady połączeń wpustowych i wielowypustowych:

Warunki wytrzymałości dla połączeń wpustowych formułuje się podobnie jak dla nitowych. W prostym opisie matematycznym przyjmuje się, że zniszczenie wpustu może nastąpić w wyniku jego ścięcia lub ściśnięcia.

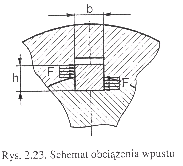
1. Warunek wytrzymałości na ścinanie:

gdzie:

b, L - szerokość i długość wpustu

F - siła obciążająca - F=2M/d

M - moment obrotowy wału

d - średnica wału

h - wysokość wpustu

2. Warunek wytrzymałości na nacisk: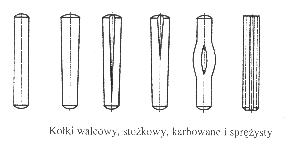

Połączenia kołkowe i sworzniowe są połączeniami pośrednimi, w których sworzeń lub kołek pełni funkcję łącznika. Podstawowe cztery rodzaje kołków stosowane w budowie maszyn:

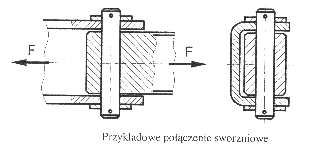
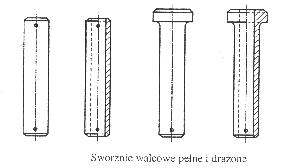
Podstawowe rodzaje sworzni stosowane w budowie maszyn. Sworznie wyposażone są w otwory, w których umieszczone są zawleczki zabezpieczające je przed wypadnięciem.

Warunki wytrzymałości dla połączeń kołkowych i sworzniowych formułuje się podobnie jak dla nitowych.

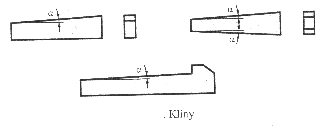
Połączenia klinowe są połączeniami pośrednimi, w których klin pełni funkcję łącznika. Stosowane są kliny jednostronne lub dwustronne.

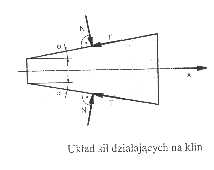
Na powierzchniach bocznych klina działają siły normalne N i siły tarcia T. Klin pozostaje w spoczynku tylko wtedy, gdy składowe sił tarcia w kierunku osi x są większe od składowych sił normalnych w tym kierunku.

Warunek samohamowności dla klina, wyrażony za pomocą sumy rzutów sił na kierunek osi x, ma postać:

N sinα < T cosα

gdzie:

T=μN - siła tarcia

tanα<μ

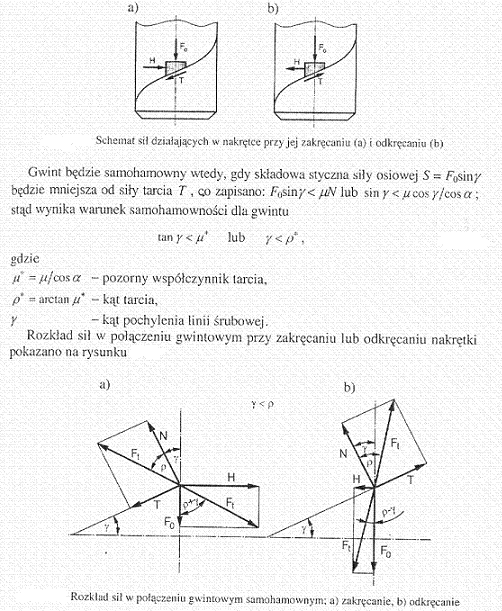
więc warunek samohamowności:

gdzie: μ - współczynnik tarcia

arctan(μ) - kąt tarcia

Wady: zaburzenie osiowosymetrycznego stanu naprężeń, powodują lokalne spiętrzenia nacisków.

11. 
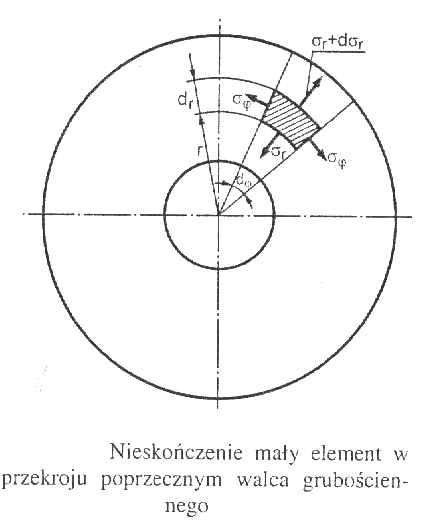
    Połączenia wciskowe - pasowanie ciasne - opis matematyczny - funkcja przemieszczenia

Połączenie wciskowe jest zastosowaniem pasowania ciasnego w praktyce. Początkowa różnica między odpowiednimi wymiarami łączonych części całkowicie zanika na skutek ich odkształceń sprężystych podczas montażu. Ze względu na zastosowaną technologię montażu wyróżnia się połączenia wtłaczane i skurczowe. Pierwsze z nich uzyskuje się przez wtłoczenie jednej części w drugą, a drugie przez podgrzanie lub oziębienie tylko jednej części, a następnie po luźnym ich połączeniu, przez wyrównanie temperatury w obu częściach. Możliwe jest zastosowanie dwóch technologii montażu na raz.

Równanie równowagi sił zapisane dla kierunku dwusiecznej kąta dφ po prostych przekształceniach przybiera postać:

Występują tu dwa nieznane naprężenia:
i obrotowe
, które na podstawie prawa Hooke'a zapisano następująco:

,

Gdzie: E,v - stałe materiałowe (moduł Younga, liczba Poissona)

12. Połączenia wciskowe - opis połączenia tulejki z wałkiem.

Odkształcenia promieniowe i obwodowe:

ε_r=du/dt ε_φ=u/t

co daje wynik:

u=C₁r + C₂*1/r

∆ = δ1 + δ2 δ1 = u₁¹ i δ2 = -u₁²

Więc :
∆ = (C₁¹ - C₁²)r + (C₂¹ - C₂²)*1/r

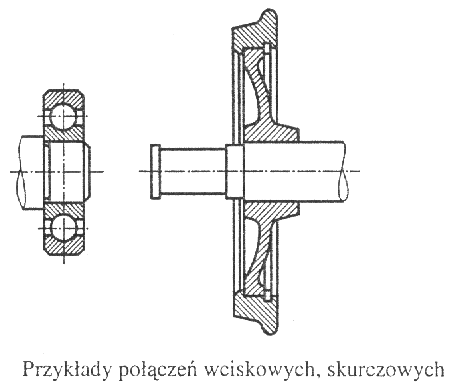
Przykładem połączenia wciskowego jest osadzenie łożyska na czopie wału lub koła na osi zestawu kolejowego. Należy zaznaczyć, że obręcz koła jest również osadzona na kole za pomocą połączenia skurczowego.

13. Połączenia gwintowe - przykłady. Gwint, zarysy gwintu, warunek wytrzymałości.

Połączenia gwintowe są połączeniami rozłącznymi kształtowymi, szeroko stosowanymi w budowie maszyn. Wyróżnia się połączenia pośrednie i bezpośrednie, spoczynkowe i ruchome. W połączeniach pośrednich stosowany jest łącznik - śruba, natomiast w bezpośrednich części łączone wyposażone są w gwint. Najczęściej stosowanymi łącznikami są śruby z nakrętką.

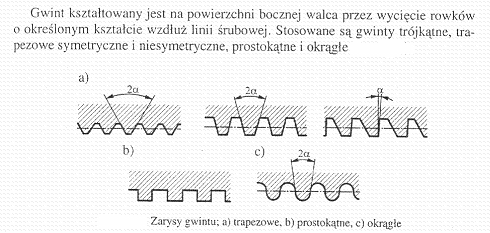
Podstawowym gwintem o zarysie trójkątnym jest gwint metryczny, znormalizowany i stosowany przede wszystkim w połączeniach spoczynkowych. Jego zaletami są duża wytrzymałość i mała wrażliwość na niedokładności wykonania. Gwinty trapezowe są metryczne o zarysie symetrycznym oraz niesymetrycznym. Gwinty prostokątne nie są znormalizowane i stosuje się je rzadko. Korzystniejsze od nich są gwinty trapezowe. Gwinty okrągłe, z uwagi na korzystny kształt karbów, są mało wrażliwe na efekty zmęczeniowe i dlatego znajdują zastosowanie w połączeniach części obciążonych udarowo. Oprócz wymienionych gwintów stosowane są gwinty toczne, w których między śrubę a nakrętkę wprowadzone są kulki, a tarcie ślizgowe zastąpione jest tarciem tocznym.

Kąt pochylenia linii śrubowej: γ = arctan(h/πd) h- skok gwintu, d- średnica walca

Skok gwintu - osiowe przesunięcie nakrętki po jednym obrocie

Podziałka - odległość między sąsiednimi zarysami mierzona wzdłuż osi gwintu (dla gwintów jednorodnych h=p)

Warunki wytrzymałości dla połączeń gwintowych formułuje się podobnie jak dla innych połączeń.

Pojedynczy zwój odkształca się pod wpływem nacisku (obciążania)

14. Śruba jako maszyna prosta - rozkład sił - sprawność mechanizmu przy zakrecaniu.

Śruba jako maszyna prosta jest równią pochyłą. Nakrętka obciążona jest siłą osiową sprężystości śruby F_o, siłą klucza H i siłą tarcia T. W połączeniu spoczynkowym (H=0) siła osiowa F_o dociska gwint nakrętki do gwintu śruby. Na styku tych dwóch powierzchni występuje siła tarcia T = μN , styczna do linii śrubowej, oraz siła nacisku N = F_ocosγ/cosα , normalna do powierzchni bocznej zarysu gwintu.

Sprawność z definicji:

gdzie:

W1= πd*H - praca dostarczona

W2= h*F₀ - praca użyteczna wyprowadzana z maszyny

Sprawność mechanizmu dla zakręcania, po uwzględnieniu siły na kluczu, przybiera postać:

η(zakr) =

Sprawność jest funkcją dwóch zmiennych: kata pochylenia linii śrubowej γ i kąta tarcia ρ*. Wpływ kąta tarcia jest oczywisty; im mniejszy jest ten kąt, tym większa sprawność.

15. Haki - pręty silnie zakrzywione - rozkład naprężeń

Prętem silnie zakrzywionym nazywamy pręt, którego pierwotny promień krzywizny jest dostatecznie mały. Miarą zakrzywienia jest stosunek h/r, gdzie h oznacza wymiar poprzeczny pręta (wysokość), a r początkowy promień krzywizny pręta nieodkształconego. Rozkład odkształceń w obrębie przekroju pręta silnie zakrzywionego odbiega w istotny sposób od rozkładu liniowego przyjmowanego w prętach prostoliniowych i słabo zakrzywionych.

Różnica między prętem silnie a słabo zakrzywionym polega na tym, że promień krzywizny zmniejsza się w pierwszym przypadku, a w drugim promień jest stały.

16. Połączenia kołnierzowe- śrubowe- stan początkowy, eksploatacyjny, szczelność

Połączenie kołnierzowo śrubowe są stosowane w urządzeniach ciśnieniowych. Podstawowymi częściami tych połączeń są kołnierze, śruby i uszczelka. Podstawowym problemem w eksploatacji tych połączeń jest ich szczelność.

Płyn pod ciśnieniem p₀ obciąża połączenie od wewnątrz. Szczelność zapewniona gdy nacisk pu­ _­na powierzchniach bocznych uszczelki przewyższa ciśnienie p_o. Materiał uszczelki ogranicza wartość maksymalnych nacisków. Temperatura, rodzaj płynu i ciśnienie mają decydujący wpływ na wybór uszczelki. Z czasem w uszczelce zanikają odkształcenia sprężyste w ściśniętej uszczelce pod wpływem zjawiska relaksacji oraz połączenie może tracić szczelność przez proces pełzania.

1. stan początkowy (montażowy)

2. stan eksploatacyjny

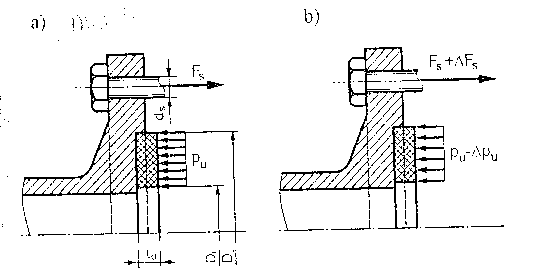
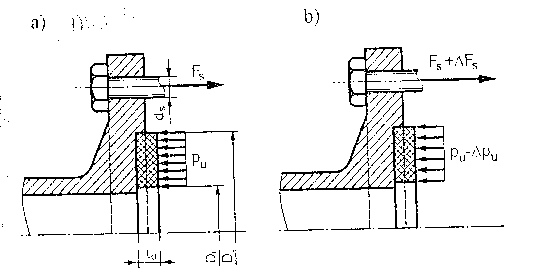
STAN POCZĄTKOWY (p_o=0):

Równanie równowagi sił w stanie początkowym :

n_s F_s= F_u­

n_s- liczba śrub

F_u- A_up_u­ - siła w uszczelce

A­_u = (π/4)(D₂² - D₁²)- powierzchnia boczna uszczelki

Równanie zgodności przemieszczeń:

δ_N= ∆L_s + w_u

δ_N = osiowe przesunięcie nakrętek (dokręcanie)

∆L_s = wydłużenie śrub

w_u = ugięcie uszczelki

STAN EKSPLOATACYJNY (p_o≠0):

Równanie równowagi sił:

n_s ΔF_s + ΔF_u­=
D_u²p₀

Równanie zgodności przemieszczeń:

Δ(ΔL_s) = Δw_u

gdzie:

Δ(ΔL_s) - przyrost wydłużenia śruby

Δw_u - zmniejszenie ugięcia uszczelki

Warunek szczelności połączenia:

C_sp₀
p_u

gdzie:

p_u = (Fu - ΔFu)/Au - nacisk

Cs = współczynnik bezpieczeństwa

17. Sprężyny i drążki skrętne. Klasyfikacja sprężyn, sztywność układu dwóch sprężyn.

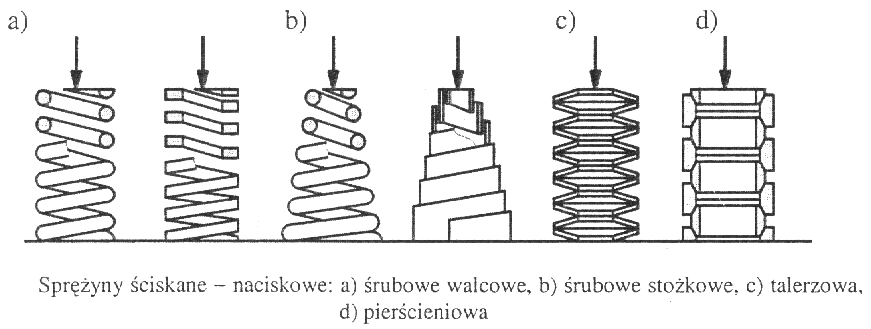
Sprężyny są podstawowymi częściami połączeń podatnych stosowanych w budowie maszyn. Połączenia te pełnią funkcję ograniczników przemieszczeń łączonych części lub zespołów. Części podatne jako łączniki charakteryzuje zdolność do dużych ugięć w zakresie małych odkształceń sprężystych. Tę właściwość można uzyskać przez odpowiednie jego ukształtowanie lub wykonanie z odpowiedniego materiału. Przykładem są stalowe sprężyny, których właściwości użyteczne uzyskano przez odpowiednie ich ukształtowanie.

Sprężyny klasyfikuje się:

• Z uwagi na kształt (śrubowe walcowe lub stożkowe, talerzowe, pierścieniowe, płaskie lub spiralne)

• Z uwagi na obciążenie (rozciągane (naciągowe), ściskane (naciskowe), zginane oraz skręcane)

Sztywność sprężyny definiowana jest następująco:

k =
, gdzie: F - siła - obciążenie

f - ugięcie sprężyny

ugięcie sprężyny f jest odwrotnie proporcjonalne do obciążenia F.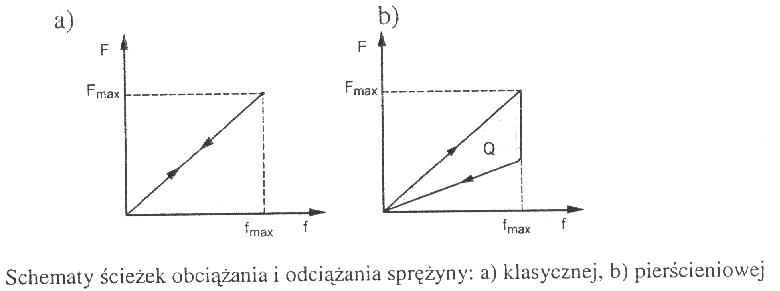
Zależność między siłą i ugięciem dla większości sprężyn jest liniowa. Sprężymy mogą magazynować energię sprężystą U = (Ff)/2 którą można odzyskać. Ścieżki obciążania i odciążania dla klasycznych sprężyn są w praktyce takie same, natomiast dla sprężyny pierścieniowej są różne, na skutek tarcia występującego na dociskanych powierzchniach sąsiednich pierścieni. Energia sprężysta zawarta w tej sprężynie nie może być w całości odzyskana. Jej część zamieniona jest na ciepło Q i oddana do otoczenia.

Sprężyny w połączeniach podatnych są w układach pojedynczym lub wielokrotnym.

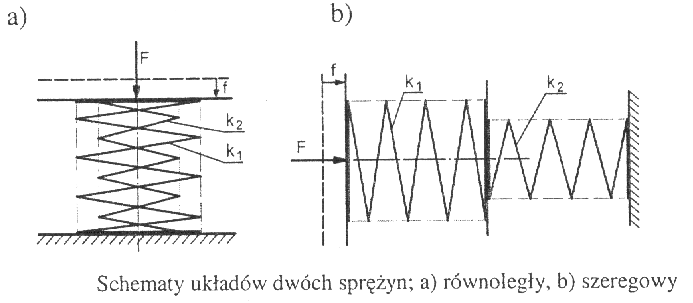
W układzie równoległym | W układzie szeregowym obciążenia

ugięcia sprężyn są takie same, | sprężyn są takie same, natomiast ugięcia są różne:

natomiast obciążenia są różne:

f₁ = f₂ = f , F₁ + F₂ = F , | F₁ = F₂ =F , f₁ +f₂ = f

gdzie siły ściskające sprężyny

pierwszą lub drugą zapisano:

F₁ = k₁f₁ , F₂ = k₂f₂ ;

zatem sztywność zastępcza | Zatem sztywność zastępcza układu dwóch sprężyn:

układu dwóch równoległych sprężyn |

k_zast = k₁ + k₂ 1/k_zast = 1/k₁ + 1/k₂ lub k_zast = k₁k₂/(k₁+k₂)

18. 
    Ugięcie walcowej sprężyny śrubowej- opis matematyczny

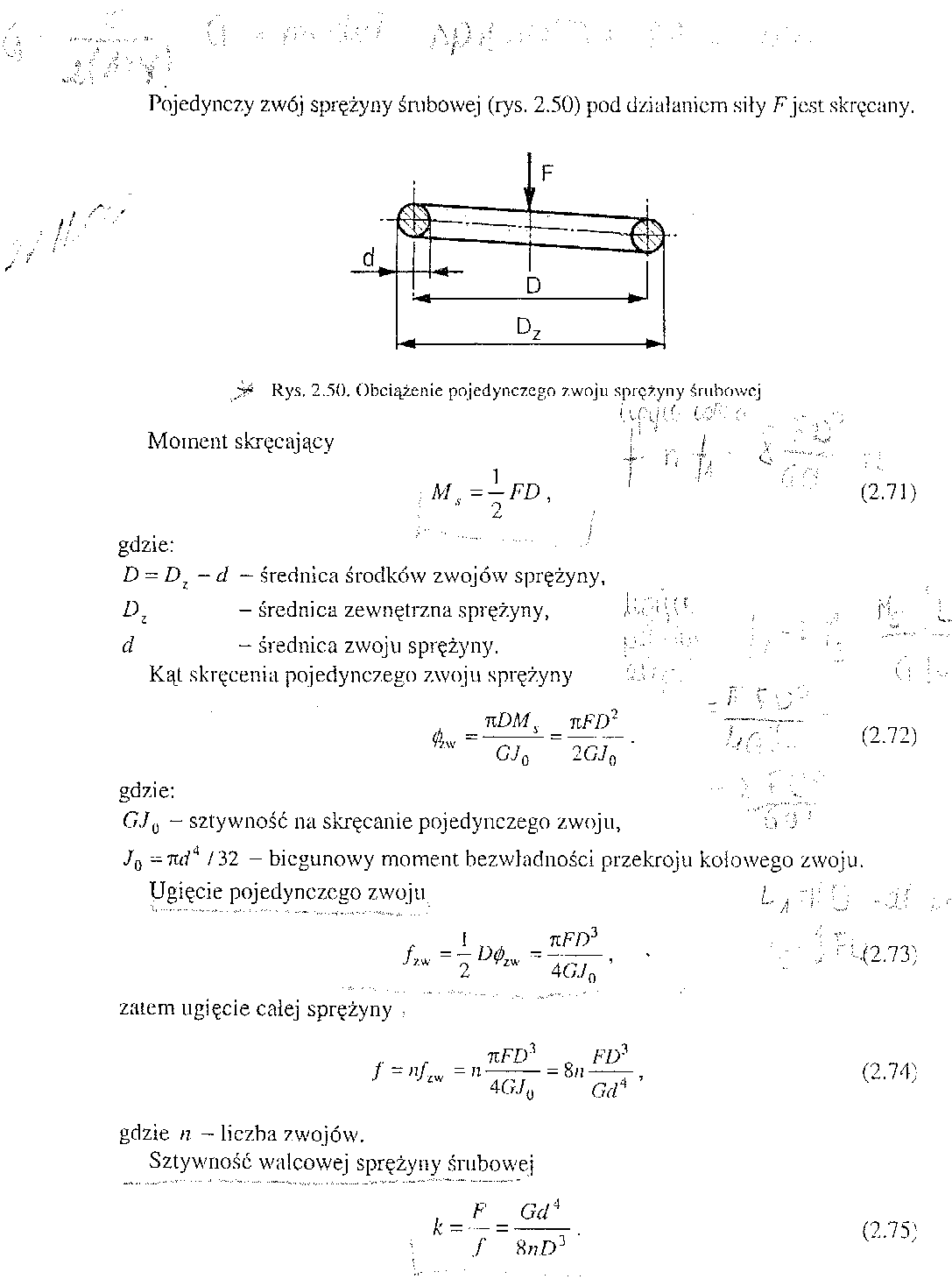
Pojedynczy zwój sprężyny śrubowej pod działaniem siły F jest skręcany

Moment skręcający

M_s =
FD , gdzie: D = D_z - d - średnica środków zwojów sprężyny

D_z - średnica zewnętrzna sprężyny

d - średnica zwoju sprężynyKąt skręcania pojedynczego zwoju sprężyny

Kąt skręcenia pojedynczego zwoju:

φ_zw =
=
, gdzie: G
- sztywność na skręcanie pojedynczego zwoju

=
- biegunowy moment bezwładności przekroju kołowego zwoju

Ugięcie pojedynczego zwoju

f_zw =
Dφ_zw =

zatem ugięcie całej sprężyny

f = nf_zw = π
= 8n
, gdzie : n - liczba zwojów

Sztywność walcowej sprężyny śrubowej k =
=

19. Tłumienie drgań w maszynach. Amortyzatory. Równanie ruchu. Choroby zawodowe

Drgania rozpatrywanego układu mechanicznego zależą od:

• zewnętrznych oddziaływań siłowych {F(t))},

• własności mechanicznych - masowych {m}, sprężystych {k}, i stratnych {c} obiektu

Metody minimalizacji drgań można podzielić na dwie zasadnicze grupy:

• metodę bezpośrednią - polegającą na szeroko rozumianej zmianie wymuszeń w dziedzinie amplitud i częstotliwości - zmiana {F(t)}

• metody pośrednie polegające na zmianie własności dynamicznych układu mechanicznego - zmiana H[{m}, {k}, {c}]; możemy tu dokonać podziału na trzy podstawowe grupy:

• zmiana wartości parametrów dynamicznych układu bez zmiany jego struktury

• wibroizolacja polegająca za wprowadzeniu zmiany struktury układu - przerwanie struktury przez wprowadzenie dodatkowego układu mechanicznego pomiędzy obiekt a podłoże

• eliminacja drgań polegająca na dołączeniu do badanego obiektu dodatkowego układu mechanicznego

Amortyzator - mechanizm, którego zadaniem jest przechwycić i rozproszyć nadmiar energii w układzie mechanicznym. Używany jest w celu zabezpieczenia urządzenia lub operatora przed negatywnym oddziaływaniem drgań i zwiększenia komfortu eksploatacji.

Ze względu na medium tłumiące ruch, amortyzatory można podzielić na:

hydrauliczne, pneumatyczne, hydropneumatyczne, magnetyczne, elektromagnetyczne, cierne, powietrzne, elastomerowe, sprężynowe, gumowe.

Amortyzator posiada 2 części: sprężystą i tarciową.

Charakterystyka części sprężystej:

1. liniowa - jak wykres f=x

2. nieliniowa - jak wykres tanx

Charakterystyka części tarciowej:

1. liniowa - prostokąt

2. nieliniowa - 2 trójkąty (muszka)

Charakterystyka amortyzatora (część sprężysta i tarciowa):

1. liniowa - pochylony dodatnio równoległobok

2. nieliniowa - pochylona dodatnio ósemka

Równanie równowagi:

mx'' + cx' + kx = 0

mx'' - siła

cx' - siła oporu

kx - siła sprężystości

x'' - przyspieszenie

x' - opór ruchu

k=F/f

20. Wały i osie: opis ogólny, zasady obliczeń, moment zastępczy.

Osie i wały są częściami maszyn, na których osadzone są najczęściej koła. Osie mogą być ruchome lub nieruchome. Oś nieruchoma jest trwale połączona z maszyna i nie obraca się, natomiast obracają się koła osadzone na niej za pomocą łożysk. Oś ruchoma obraca się wraz z osadzonymi na niej kołami i połączona jest z maszyną za pomocą łożysk. Osie nie przekazują momentu obrotowego. Działające na nie obciążenia powodują ich zginanie a nie skręcanie. Wały natomiast przekazują moment obrotowy. Osadzone są w łożyskach i obracają się wraz z posadowionymi na nich kołami. Obciążenia powodują jednoczesne ich skręcanie i zginanie. Oś połączona jest trwale z kołami, a na jej czopach za pomocą łożysk podparty jest pojazd. Wał z dwoma kołami osadzony jest na obu końcach w łożyskach.

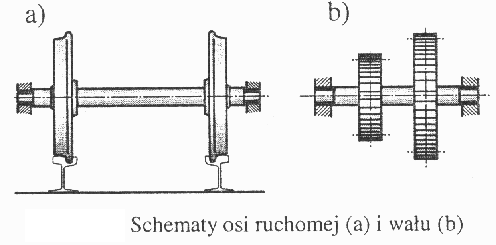
Wał podparty i obciążony siłami działającymi na osadzone na nim koła jest skręcany i zginany. Występuje w nich złożony stan naprężeń o składowych normalnych σ_g i stycznych τ_s. Warunek wytrzymałości, zgodnie z hipotezą Hubera-Misesa, ma postać:

σ_zast
σ_dop ,

gdzie: σ_{zast =}
- naprężenie zastępcze - równoważne

Naprężenia normalne - zginające : σ_g = M_g/W_z ,

i styczne - skręcające dla wału o przekroju kołowym: τ_s = M_s/W_o

gdzie: W_z =
- wskaźnik w wytrzymałości przekroju kołowego na zginanie,

W_o =
- wskaźnik wytrzymałości przekroju kołowego na skręcanie

Naprężenia zastępcze, po uwzględnieniu naprężeń normalnych zapisano:

σ_zast = M_zast/W_z

gdzie M_zast =

Średnica wału, wyznaczona na podstawie warunku wytrzymałości:

Wały kształtuje się przede wszystkim z uwzględnieniem warunku wytrzymałości oraz ograniczenia geometrycznego w postaci :

1
d₂/d₁
1.2

Stopniowanie wału jest ograniczone. Proporcja średnic sąsiadujących części nie powinna być większa niż 20%. Ponadto w miejscach uskoków średnic należy wprowadzić zaokrąglenia w celu złagodzenia efektu spiętrzenia naprężeń.

21. Sztywność statyczna i dynamiczna wału - opis matematyczny.

Warunki wytrzymałości w projektowaniu maszyn są konieczne lecz nie zawsze wystarczające. W normalnych warunkach eksploatacyjnych części maszyn pod wpływem obciążeń odkształcają się sprężyście, zmieniając swój pierwotny kształt, np. wały zginają się i skręcają a osadzone na nich koła przemieszczają się zgodnie z linią ugięcia. Zbyt mała sztywność wału powoduje nadmierne jego ugięcie, które uniemożliwia normalna eksploatację maszyny. Wprowadzono dwa warunki dla sztywności wału: statyczny i dynamiczny.

Warunek statyczny dotyczy ograniczenia maksymalnego ugięcia wału obciążonego osadzonymi kołami. Sztywność wału powinna być taka, aby maksymalne jego ugięcie było mniejsze od dopuszczalnego:

K =

K_dop ,

gdzie: K_dop <0,002 ; 0,00003> - dopuszczalna wartość bezwymiarowego ugięcia

L - rozpiętość wału - odległość między punktami podparć

f - ugięcie wynoszące:

Warunek statyczny wynosi więc:

W podobny sposób wprowadza się ograniczenie na kąt skręcania wału ( φ
φ_dop )

Warunek dynamiczny dotyczy ograniczenia prędkości obrotowej - prędkości kątowej, z uwagi na ich wartość krytyczną ω_KR , przy której ugięcie wału wzrasta nieograniczenie. Wał osadzony na nim jednym kołem o masie m jest klasycznym układem sprężystym z jednym stopniem swobody.

Równanie drgań układu liniowego o jednym stopniu swobody ma postać:

m

gdzie:

m - masa ciała - koła

mÿ - siła bezwładności

ÿ - przyśpieszenie

c - współczynnik liniowego oporu ruchu,

cý - siła oporu - tłumienia,

k - sztywność sprężysta układu,

k_y - siła sprężysta

d²y/dt² = ÿ, dy/dt=ý - oznaczenia pochodnych w czasie t.

Równanie ruchu koła na wale wirującym z prędkością kątową ω z pominięciem oporu ruchu (c=0):

-myω² + ky = 0

gdzie:

- yω² - przyspieszenie dośrodkowe w ruchu kołowym

y - współrzędna, ugięcie które jest w tym przypadku promieniem okręgu po którym przemieszcza się środek masy koła

Stąd prędkość krytyczna wału: ωkr =

gdzie:

k= Q/f = mg/f - sztywność sprężysta wału

g= 9,81 m/s2 - stała

Warunek dynamiczny ma postać: ω ≤ 0,8 ωkr lub 1,2 ωkr ≤ ω

warunek dynamiczny dotyczy ograniczenia prędkości kątowej. Wał nie ulegnie uszkodzeniu, jeżeli jego prędkość będzie co najmniej mniejsza o 20% lub większa o 20% od prędkości krytycznej ω_KR.

22. Krążki wirujące - równanie równowagi - przykłady krążków o stałej i zmiennej grubości

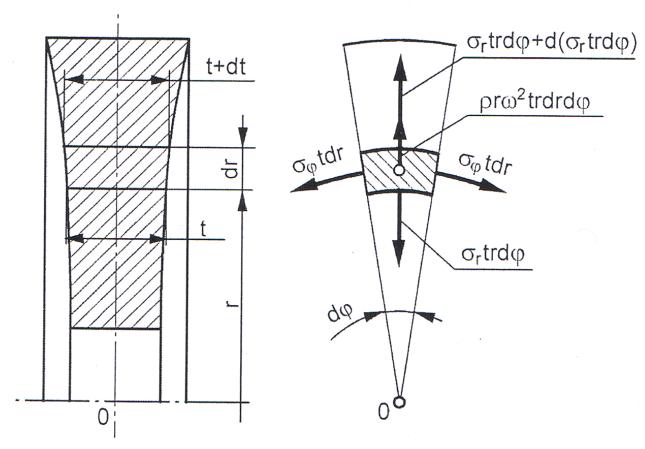
Wyprowadzenie podobne do połączeń wciskowych lecz dodano jeszcze przyspieszenie dośrodkowe.

Krążek o stałej grubości: t(r) = t = const

Krążek o równomiernej wytrzymałości: σr = σφ = σ0 = const

grubość krążka: t=t₀

Równanie równowagi:

23. Łożyska ślizgowe: budowa łożysk, siły tarcia, lepkość smaru, krzywa Stribecka.

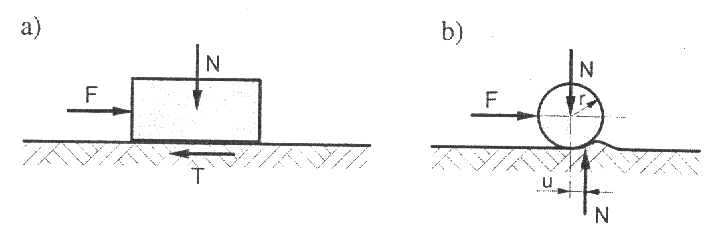
Tarcie jest zjawiskiem związanym z ruchem i występuje w skalach mikro oraz makroskopowej. Tarcie zewnętrzne związane jest z przemieszczeniem względem siebie ciał pozostających w kontakcie. Ciała te mogą przemieszczać się przez poślizg lub toczenie. Wyróżnia się tarcie ślizgowe lub toczne.

Siła tarcia ślizgowego definiowana jest następująco:

T = μN , gdzie: μ - współczynnik tarcia

N - siła nacisku normalna do powierzchni

Wartość współczynnika tarcia wyznaczana jest doświadczalnie i zależy od rodzaju materiałów pozostających w kontakcie, np.: stal/mosiądz, stal/stal, itp.

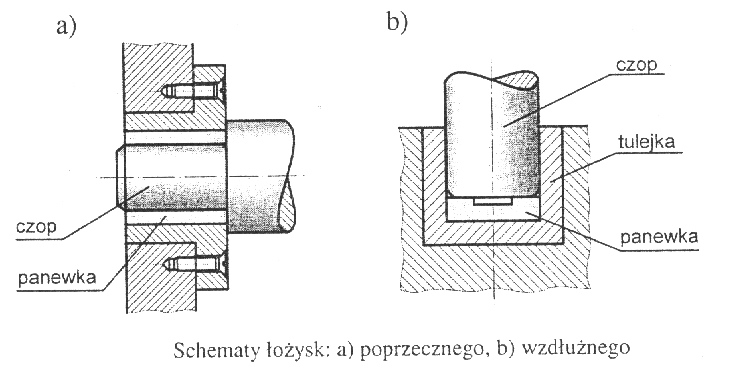
Łożysko ślizgowe zbudowane jest z korpusu, w którym osadzony jest czop wału lub osi. Powierzchnia czopa ma bezpośredni kontakt z powierzchnią panewki. W łożyskach tych występuje tarcie ślizgowe

Podstawową częścią łożyska ślizgowego jest panewka, wykonana z odpowiedniego stopu metali. Właściwości materiału panewki powinny zapewnić minimalne zużycie stalowego czopa wału oraz skutecznie odprowadzać ciepło tarcia do otoczenia.

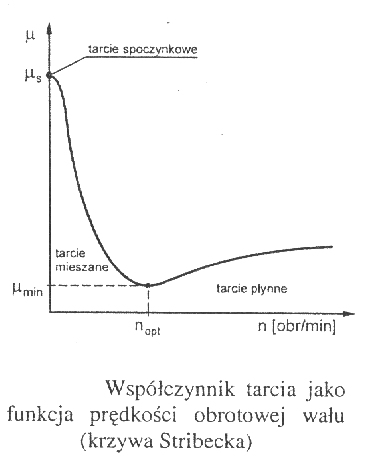
Tarcie ślizgowe między czopem wału i panewką łożyska zachodzi w obecności smaru. W chwili rozruchu maszyny czop wału spoczywa na panewce. Powierzchnie obu części przylegają bezpośrednio do siebie i występuje tarcie suche. Ilość smaru między powierzchniami kontaktu wzrasta ze wzrostem prędkości obrotowej. Tarcie suche zamienia się wtedy w tarcie mieszane, a następnie w tarcie płynne. Szczelina między czopem a panewką wypełnia się smarem. Czop i panewka rozdzielone są warstwą smaru i występuje tarcie płynne. Współczynnik tarcie w łożysku ślizgowym zmienia się wraz ze zmianą prędkości obrotowej wału. Istnieje optymalna prędkość obrotowa n_opt , przy której współczynnik tarcia osiąga wartość najmniejszą. Wzrost współczynnika tarcia dla prędkości większych (n_opt < n ) spowodowany jest lepkością smaru.

24. Warunki wytrzymałości dla czopów wałów posadowionych w łożyskach ślizgowych.

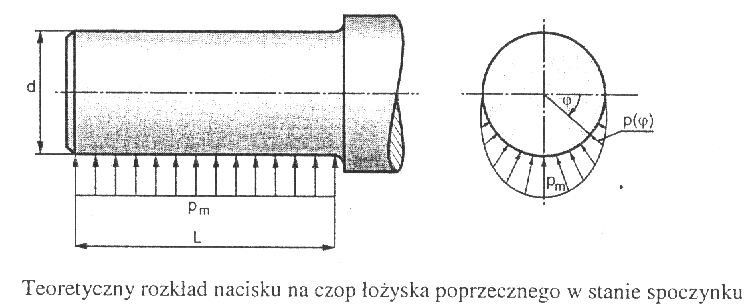
W projektowaniu czopów poprzecznych łożysk ślizgowych przyjmuje się, że rozkład nacisku w stanie spoczynku zmienia się w odpowiedni sposób w kierunku obwodowym, natomiast pozostaje niezmienny na długości czopa.

Zmiana nacisku w kierunku obwodowym można opisać w sposób przybliżony za pomocą następującej funkcji:

p(φ) = p_m sinφ

gdzie: p_m =
- nacisk maksymalny

φ - współrzędna kątowa (0
φ
π)

Obszar rozwiązań dopuszczalnych wyznaczają 3 ograniczenia:

1. warunek wytrzymałości na zginanie

σ_g =
=

σ_dop gdzie: M_g =
- moment zginający

W_z =
- wskaźnik wytrzymałości

2. Warunek wytrzymałości na nacisk

P_m =

P_dop

3. Warunek wytrzymałości na ścinanie

τ_max =
=

τ_dop

gdzie: τ_dop =
- naprężenia dopuszczalne na ścinanie

W wyżej sformułowanych warunkach wytrzymałości uwzględniono obciążenie, wymiary geometryczne oraz naprężenie i nacisk dopuszczalny. Warunki te po prostych przesz kształceniach zapisano w następującej postaci:

C_c1

d ,

, C_c3
d

gdzie: C_c1 =
C_c2 =
C_c3 =

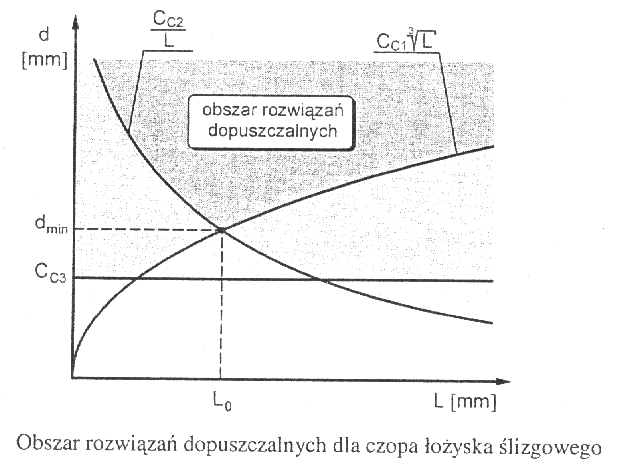
Obszar rozwiązań dopuszczalnych opisany za pomocą tych nierówności przedstawiono na wykresie.

25. Łożyska toczne: tarcie, budowa łożysk, rodzaje łożysk

Tarcie jest zjawiskiem związanym z ruchem i występuje w skalach mikro oraz makroskopowej. Tarcie zewnętrzne związane jest z przemieszczeniem względem siebie ciał pozostających w kontakcie. Ciała te mogą przemieszczać się przez poślizg lub toczenie. Wyróżnia się tarcie ślizgowe lub toczne.

Siła tarcia ślizgowego definiowana jest następująco:

T = μN , gdzie: μ - współczynnik tarcia

N - siła nacisku normalna do powierzchni

Wartość współczynnika tarcia wyznaczana jest doświadczalnie i zależy od rodzaju materiałów pozostających w kontakcie, np.: stal/mosiądz, stal/stal, itp.

Siła tarcia tocznego, wynika z równania równowagi momentów Tr = Nu, definiowana jest następująco:

T = μ₁N , gdzie: μ₁ = u/r - współczynnik tarcia tocznego

N - siła nacisku

u - przesunięcie, którego wielkość zależy od odkształcalności ciał

r - promień części tocznej

Wartość współczynnika tarcia tocznego zależy od rodzaju materiałów pozostających w kontakcie i jest odwrotnie proporcjonalna do promienia części tocznej. Siła tarcia tocznego jest tym mniejsza, im twardsze są części pozostające w kontakcie i im większy jest promień r.

Skutkiem niepożądanym tarcia jest zużywanie się części maszyn, które objawia się zmianą ich pierwotnego kształtu, zmianą wymiarów i właściwości mechanicznych, a także zmniejszeniem ich masy. Skutki tarcia może zmniejszyć smarowanie powierzchni kontaktowych.

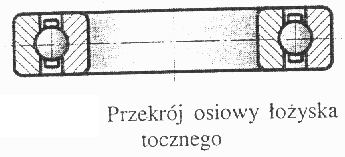
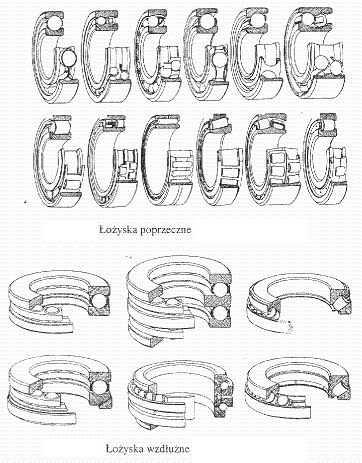
Łożysko toczne zbudowane jest z pierścieni, wewnętrznego i zewnętrznego, części tocznych oraz koszyka. Pierścień wewnętrzny posadowiony jest na czopie, natomiast pierścień zewnętrzny osadzony jest zwykle w korpusie maszyny. w łożyska tocznych występuje tarcie toczne.

Pierścienie wewnętrzny i zewnętrzny wyposażone są w bieżnie, po którym przemieszczają się części toczne. Koszyk spełnia funkcję pomocniczą, zapewnia równomierne rozmieszczenie i oddzielenie części tocznych. Stosowane są następujące podstawowe części toczne:

• kulki - łożyska poprzeczne lub wzdłużne dla małych i średnich obciążeń

• wałeczki walcowe - łożyska poprzeczne lub wzdłużne dla dużych obciążeń

• igiełki (wałeczki walcowe o małych średnicach) - łożyska poprzeczne lub wzdłużne dla dużych obciążeń

• wałeczki stożkowe - łożyska poprzeczne i wzdłużne dla małych i średnich obciążeń

• baryłki (beczułki) - łożyska poprzeczne lub wzdłużne dla dużych obciążeń.

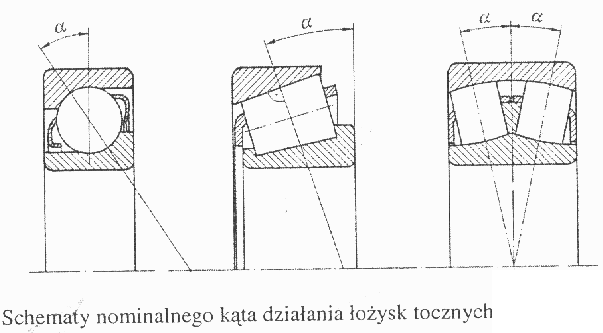
W łożyskach tocznych wyróżnia się nominalny kąt działania α, który w przekroju poprzecznym łożyska jest zawarty między prosta prostopadłą do osi łożyska i prostą łączącą punkty styku bieżni.

Na podstawie nominalnego kąta działania α wyróżnia się łożyska:

• poprzeczne, gdy 0
  α
  
  

• wzdłużne, gdy
  α
  

26. Nośność ruchowa łożysk tocznych - opis, wzór empiryczny

Nośność ruchowa C projektowanego łożyska powinna byś większa od wymaganej (C_min<C). W projektowaniu łożysk tocznych korzysta się z następującego wyrażenia empirycznego:

L=(
)^q gdzie: L [10⁶ obrotów] - trwałość łożyska

C [N] - nośność ruchowa (dynamiczna)

F [N] - obciążenie zastępcze

q =3 - łożyska kulkowe

q=
- łożyska wałeczkowe

w obliczeniach trwałość łożyska wyrażona jest w godzinach jego pracy, zatem wyrażenie L=(
)^q przybiera postać L_h =
L =
(
^q

gdzie: n [obr/min] - prędkość obrotowa łożyska

Wymagana nośność ruchowa łożyska C_min wyrażona za pomocą trwałości L_h [h] oraz zadanego obciążenia zastępczego F ma postać

C_min =
F

Nośność ruchowa C projektowanego łożyska powinna być większa od wymaganej (Cmin < C)

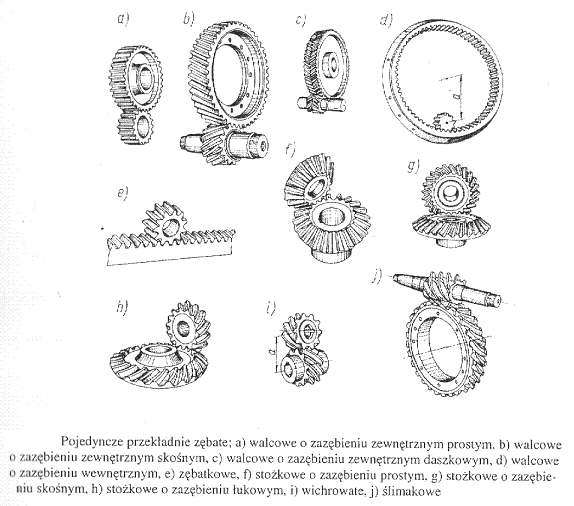
27. Przekładnie zębate, opis ogólny: przełożenie, zarys ewolwenty zęba - opis krzywej.

Przekładnie mechaniczne są głównymi zespołami, które przekazują moment obrotowy od silnika do maszyny roboczej. Podstawowym zadaniem przekładni jest zamiana jest zmiana prędkości obrotowej ( ω₁ => ω₂ ), kierunku obrotów oraz momentu obrotowego ( M₁ => M₂ ). W budowie maszyn najczęściej stosowane są przekładnie zębate.

Przełożenie jest wielkością charakterystyczną dla przekładni. Wyróżnia się następujące przełożenia:

• geometryczne

j_g =
=
, gdzie: d1 , d2 - średnice podziałowe kół

z1 , z2 - liczba zębów kół, koło czynne (napędzające) oznaczone jest numerem 1, zaś koło bierne (napędzane) numerem 2

• kinematyczne

, gdzie:
- prędkość kątowa

- prędkość obrotowa ( i= 1,2 )

• dynamiczne

,

gdzie: M₁ , M₂ - moment obrotowy kół czynnego (1), biernego (2)

η_z - sprawność zazębienia (0.98
0.99)

Przekładnie dzieli się w zależności od wartości przełożenia, na:

• Reduktory - przekładnie zwalniające ( j_k < 1 )

• Multiplikatory - przekładnie przyspieszające ( 1 < j_k )

Prędkość obwodowa punktów leżących na średnicach podziałowych kół przekładni:

v_i = 0,5 * di ωi

Prędkość obrotowa dwóch kół w miejscu ich kontaktu jest jednakowa ( v1 = v2 ), zatem

d₁ω₁ = d₂ω₂

skąd wynika zgodność przełożeń kinematycznego i geometrycznego j_k = j_g

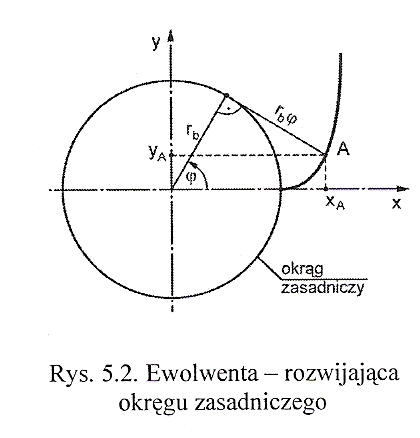
Moment obrotowy przekazywany jest z koła czynnego na bierne za pomocą zębów, które są równomiernie rozmieszczone na obwodzie każdego z kół. Sposób przekazania momentu jest powiązany z kształtem zarysu zębów. Kształt ten powinien zapewnić stałe przełożenie i dużą sprawność. Warunki te spełnia zarys ewolwentowy, gdyż koła z zębami o tym kształcie toczą się względem siebie bez poślizgu. Ewolwenta to krzywa płaska, którą wyznacza koniec nierozciągliwej nici odwijanej z końca walca kołowego. Krzywą tę wyznacza też koniec odcinka, który obtacza się bez poślizgu po powierzchni walca kołowego.

Współrzędne krzywej ewolwentowej: x= (cosφ + φsin φ)Rb

y= (sin φ - φcos φ)Rb

28. Siły w zazębieniu ewolwentowym. Naciski miejscowe.

Przekładnie walcowe z kołami o zarysie ewolwentowym są najczęściej stosowane w budowie maszyn. Zęby dwóch kół obtaczają się względem siebie bez poślizgu, dzięki czemu sprawność takiego zazębienia jest bardzo wysoka (0,98 ≤ η ≤ 0,99 ). Ponadto koła z zębami o zarysie ewolwentycznym są mało wrażliwe na zmianę odległości między ich osiami, co jest dużą zaletą.

W zazębieniu dwóch kół występują siły, które mogą spowodować zniszczenie zębów przez zginanie lub naciski lokalne. Wadą zarysu ewolwentowego jest lokalne spiętrzenie nacisków w postaci naprężeń kontaktowych. Stosuje się też inne zarysy o mniejszych naprężeniach kontaktowych lecz ich wadą jest wrażliwość na zmianę odległości między osiami

29. Opis działania - schematy przekładni walcowej, stożkowej i ślimakowej

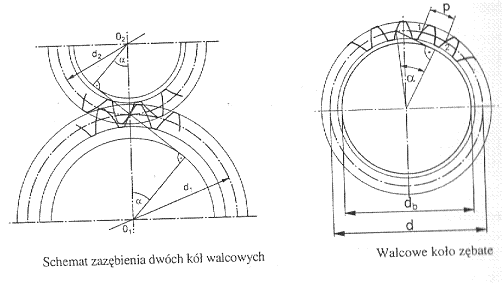
Podstawowymi parametrami geometrycznymi są: z - liczba zębów, m - moduł, α - kąt nominalny zarysu, b - szerokość koła, β - kąt pochylenia linii zęba (dla zębów skośnych)

Podziałka to długość luku okręgu podziałowego zawartego między dwoma punktami sąsiednich zębów. Obwód koła to πd = zp stąd średnica podziałowa d=z*p/π = zm.

Moduł m=p/π to wartość znormalizowana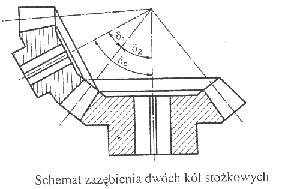

Przekładnie stożkowe są podobne w działaniu do walcowych przekładni zębatych. Osie kół w przekładniach walcowych są równoległe względem siebie, natomiast w przekładniach stożkowych przecinają się pod pewnym kątem. W szczególnym przypadku, gdy kąt jest prosty, przekładnie nazywamy ortogonalną.

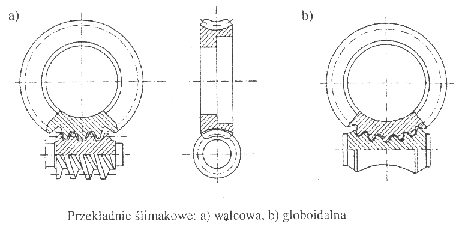
Przekładnie ślimakowe są najstarszymi przekładniami, stosowanymi już w starożytności. Podstawowymi częściami tych przekładni są ślimak i ślimacznica. Ślimak jest kołem mniejszym, z zębami ukształtowanymi w postaci linii śrubowej. Ślimacznica natomiast jest kołem większym, z odpowiednio ukształtowanymi zębami wklęsłymi. Wyróżnia się przekładnie ślimakowe i globoidalne.

Przekładnie globoidalne różnią się od walcowych jedynie kształtem ślimaka. Odpowiednie ukształtowanie ślimaka zapewnia zazębienie większej liczby zębów, a tym samym umożliwia przekazywania większych obciążeń. Przełożenia przekładni ślimakowych są dziesięciokrotnie większe niż przekładni zębatych walcowych lub stożkowych. Moment obrotowy przekazywany jest tylko ze ślimaka na ślimacznicę.

Przekładnie: ślimakowa (u góry), spiroidalna , hipoidalna, stożkowa.

30. Opis działania - schematy przekładni planetarnej i falowej.

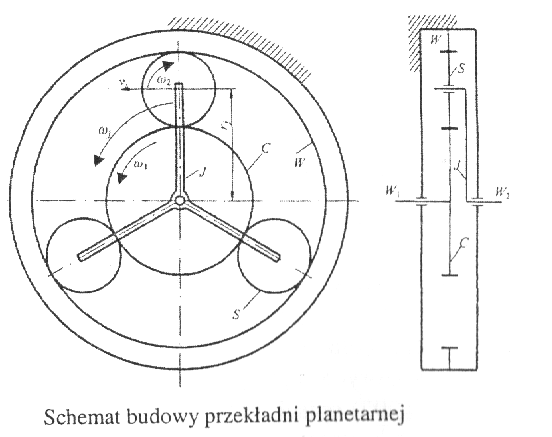
Przekładnie planetarne stanowią odrębną grupę przekładni zębatych. Schemat ich budowy i zasady działania pokazano na rysunku. Koło główne C, napędzane wałkiem czynnym W₁ , zazębione jest trzema obiegowymi kołami mniejszymi S, zwanymi satelitami, które posadowione są na czopach jarzma J.

Koła obiegowe (satelity) S zazębione są również z nieruchomym wieńcem wewnętrznie uzębionym W, który połączony jest z korpusem przekładni.. Moment obrotowy M_o przekazywany jest z wałka czynnego W₁ z udziałem koła głównego C, kół obiegowych (satelitów) S oraz jarzma J na wałek bierny W₂.

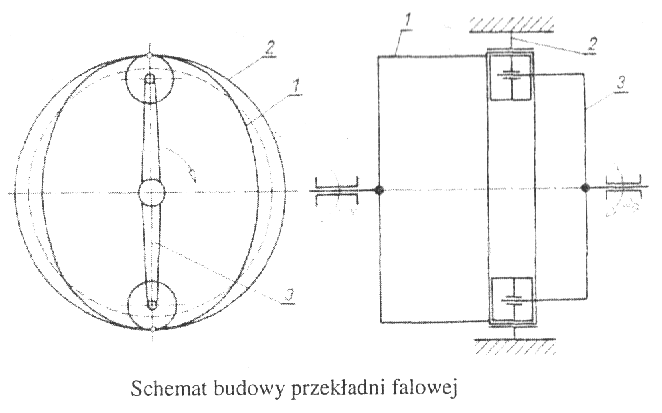
Przekładnie falowe są współczesnymi konstrukcjami, które charakteryzuje duże przełożenie na jednym stopniu i mała masa. Schemat budowy i zasada działania przekładni falowej pokazano na rysunku. Podstawowymi jej częściami, są cienka sprężysta powłoka walcowa z podatnym wieńcem uzębionym zewnętrznie (1), sztywny nieruchomy wieniec z uzębieniem wewnętrznie (2) oraz generator(3) napędzany wałkiem czynnym.

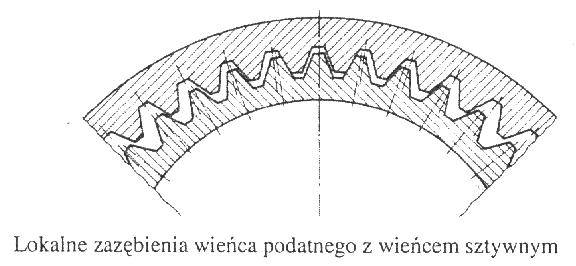
Moment obrotowy Mo przekazywany jest z wałka czynnego, który jest połączony z jarzmem generatora (3), na cienką sprężysta powłokę walcową (1), która połączona jest z wałkiem biernym. Przekazywanie tego momentu odbywa się dzięki lokalnemu zazębieniu podatnego wieńca zębatego osadzonego na powłoce (1) ze sztywnym nieruchomym wieńcem (2).

Przełożenie geometryczne:

gdzie:

z1 - liczba zębów wieńca podatnego

z2 - liczba zębów wieńca sztywnego

Różnica zębów jest niewielka (z2-z1=2) więc na przekładniach falowych uzyskuje się bardzo duże przełożenia (80 <=jg <= 260) na jednym stopniu.

31. Opis działania - schematy przekładni z kołami eliptycznymi i krzywikami.

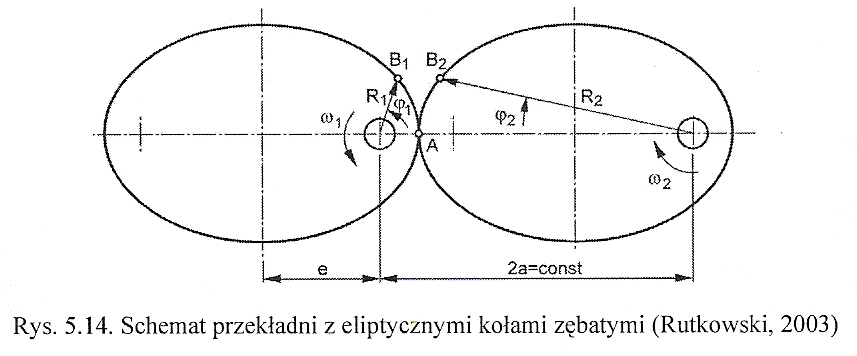
Przekładnie z niekołowymi kołami zębatymi działają jak przekładnie walcowe. Ich cecha charakterystyczną są niekołowe kształty kół zębatych. Klasycznym przykładem jest przekładnia z eliptycznymi kołami zębatymi gdzie odległość między osiami obu kół jest stała.

Osie obrotu tych dwóch jednakowych kół znajdują się w ogniskach elips. Oba koła toczą się względem siebie bez poślizgu, zatem po pewnym obrocie kół punkty B₁ i B₂ będą wspólnym punktem (punktem styku). Przy stałej prędkości kątowej ω₁ koła napędzanego prędkość kątowa ω₂ koła napędzanego jest zmienna. Przebieg tej zmienności jest podobny do wykresu funkcji sinus.

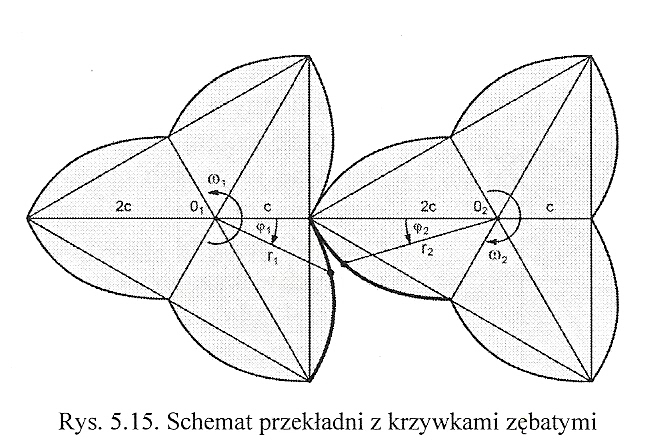
Przekładnie z krzywkowymi kołami zębatymi stosowane są w maszynach o specjalnym przeznaczeniu w których wymagana jest określona zmienność obrotów wału biernego.

Odległość między osiami kół jest stała r1(φ1) + r2(φ2) = 3c

Zatem przełożenie :

Przebieg zmienności przełożenia przedstawia wykres. Przy stałej prędkości kątowej ω1 koła napędzającego prędkość kątowa ω2 koła napędzanego jest zmienna.

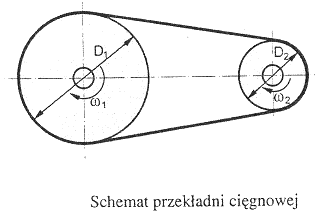
32. Przekładnie cięgnowe, opis działania; pasy płaskie, klinowe, zębate, łańcuchy.

Przekładnie cierne - Przekładnie cierne składa się z 2 kół o powierzchniach gładkich, które dociskane są do siebie z pewną siłą N. Moment obrotowy przekazywany jest z koła czynnego na koło bierne dzięki sile tarcia T, występującą na powierzchniach kontaktu tych kół. Stosowane są przekładnie cierne o stałym lub zmiennym przełożeniu. Przełożeniem można sterować w sposób ciągły (przekładnie wariatory). Przekładnie cierne mają wiele zalet: są cichobieżne, proste w wykonaniu, mają możliwość ciągłej zmiany przełożenia. Wady to duże obciążenie poprzeczne wałów i łożysk, poślizgi przez co przełożenie kinematyczne nie jest stabilne. Materiały na koła cierne muszą charakteryzować się odpornością zmęczeniową, dużym współczynnikiem tarcia ślizgowego, dużym modułem sprężystości, dobrą przewodnością cieplną.

RODZAJE PASÓW STOSOWANYCH W PRZEKŁADNIACH PASOWYCH
RODZAJ PASA	PRZEKRÓJ POPRZECZNY
Płaski	Prostokąt
Klinowy	trapez
Okrągły	Koło
Zębaty

Przekładnia cięgnowa składa się z dwóch kół rozsuniętych i opasanych cięgnem. Wyróżnia się przekładnie cięgnowe pasowe lub łańcuchowe.

Stosuje się pasy: płaskie, klinowe, okrągłe, zębate

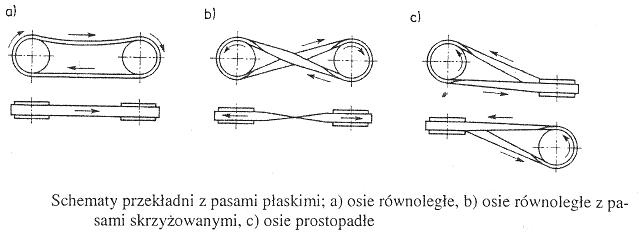
Osie kół czynnego i biernego przekładni z pasami płaskimi są usytuowane względem siebie równolegle lub prostopadle. Pasy płaskie mogą się krzyżować - uzyskuje się również zmianę kierunku obrotów koła biernego względem czynnego.

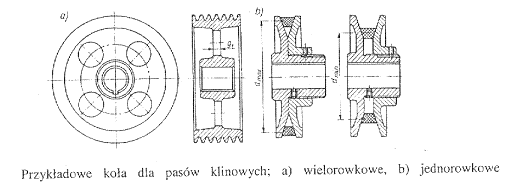
Pasy klinowe lub okrągłe, podobnie jak pasy płaskie, przekazują moment obrotowy z koła czynnego na bierne. Bieżnie kół dla pasów płaskich są lekko wypukłe, dzięki czemu pasy zachowują stabilne położenie w czasie ruchu. Wieńce kół dla pasów klinowych lub kołowych maja odpowiednio ukształtowane rowki. Pasy przylegają do powierzchni bocznych tych rowków i zachodzi sprzężenie cierne, które jest znacznie efektywniejsze niż w przypadku pasów płaskich.

Przekładnie z pasami zębatymi, z uwagi na kształtowe łączenie z kołem, są podobne do przekładni łańcuchowych

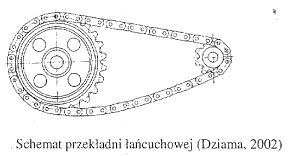
Przekładnie łańcuchowe składają się z dwóch kół zębatych i łańcucha. Łańcuch jest cięgnem giętkim, które nie wykazuje sztywności na zginanie i jest zbudowany jest z ogniw połączonych przegubowo. Przekładnie te z uwagi na brak poślizgów między łańcuchem a kołami zapewniają stałe przełożenie.

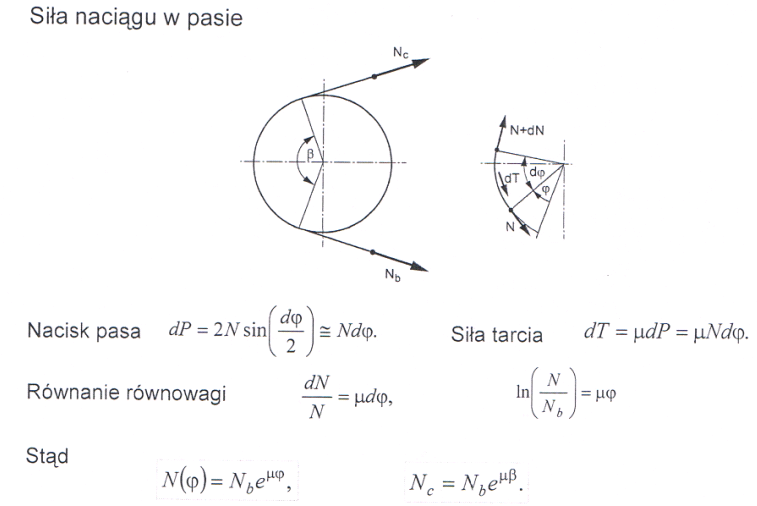
33. Siły naciągu w pasach - opis matematyczny. Moment obrotowy.

Proporcja między siłą naciągu Nc w pasie czynnym i siłą naciągu Nb w pasie biernym jest wyrażona:

Nc/Nb = exp(μβ)

gdzie:

μ - wsp. tarcia między pasem a kołem

β - kąt opasania koła mniejszego

Pas podlega także zginaniu momentem: Mg = EJz/R

EJz - sztywność na zginanie

R - promień

W obszarze opasania pas obciążony jest także siłą odśrodkową która wywołuje siłę rozciągającą:

Nv = Aρv²

gdzie:

A - pole powierzchni przekroju pasa

ρ - gęstość materiału pasa

v - prędkość pasa

Moment obrotowy przekazywany przez koło przekładni z pasem płaskim:

Naciąg wstępny:

Nc= N0 + ∆N Nb= N0 - ∆N N0= 0,5(Nc + Nb) ∆N= 0,5(Nc - Nb)

Stąd:

N0= 0,5Nb (e^μβ+1) ∆N= 0,5Nb (e^μβ-1) ∆N= N0 (e^μβ-1)/( e^μβ+1)

Moment obrotowy:

M0 = (Nc - Nb)R = 2R∆N M0 = N0D(e^μβ-1)/( e^μβ+1)

Naciąg wstępny:

N0= M0/D * (e^μβ+1)/( e^μβ-1)

34. Naprężenia w pasie płaskim

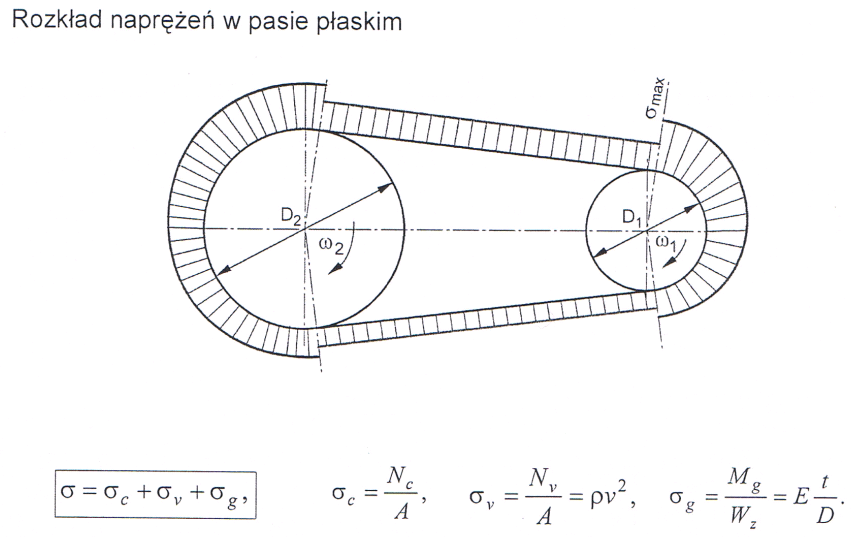
Naprężenia w pasie płaskim są sumą naprężeń rozciągających i zginających.

σ = σ_c + σ_v + σ_g

gdzie:

σ_c = N_c/A - naprężenia rozciągające w pasie czynnym

σ_v = N_v/a = ρv² - naprężenia rozciągające od siły odśrodkowej

σ_g = M_g/W_z = Et/D - naprężenia zginające

A = tb - pole powierzchni prostokątnego przekroju pasa

J_z = bt³/12 - moment bezwładności przekroju pasa

W_z = bt²/6 - wskaźnik wytrzymałości na zginanie przekroju pasa

B,t - szerokość I grubość pasa

Największe naprężenia występują w pasie czynnym na początku jego opasania z kołem mniejszym.

35. 
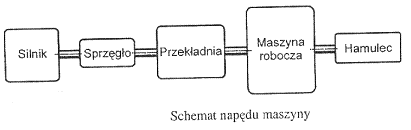
    Schemat napędu maszyny, opis działania jego zespołów

silnik - zamiana pewnego rodzaju energii na pracę mechaniczną,

sprzęgło - zespół układu napędowego maszyny, który łączy dwa wały, przekazuje moment obrotowy z wału czynnego na wał bierny bez zmiany obrotów

przekładnia - główny zespół napędów, który przekazuje moment obrotowy od silnika do maszyny roboczej. Jej zadaniem jest zmiana prędkości obrotowej, kierunku obrotów oraz momentu obrotowego.

36. Budowa i zasada działania sprzęgła. Opis wybranych sprzęgieł.

Sprzęgło jest zespołem układu napędowego maszyny, który łączy dwa wały i przekazuje moment obrotowy z wału czynnego na wał bierny bez zmiany obrotów.

Moment obrotowy przekazywany przez sprzęgło

Mo =
gdzie: P [W] - moc

ω [1/s] - prędkość kątowa

Sprzęgła w układzie napędowym pełnią wiele funkcji; przede wszystkim umożliwiają efektywny montaż maszyn oraz właściwą ich eksploatację.

Wyróżnia się sprzęgła:

1. nierozłączne:

• sztywne - tulejowe, łubkowe, kołnierzowe - stosowane w napędach o równomierny obrotach do stałego łączenia wałów współosiowych

• luźne - kłowe, zębate, łańcuchowe - do łączenia wałów którym nie można zapewnić współosiowości

• podatne - sprężynowe, palcowe, oponowe - do łączenia wałów o nierównomiernych obrotach, oraz gdy nie można zapewnić współosiowości

2. rozłączne:

• włączalne synchronicznie - kłowe, zębate - do łączenia wałów których przełączanie następuje podczas postoju maszyny.

• włączalne asynchronicznie - tarczowe, wielopłytowe, stożkowe - do łączenia wałów których przełączanie następuje podczas pracy maszyny

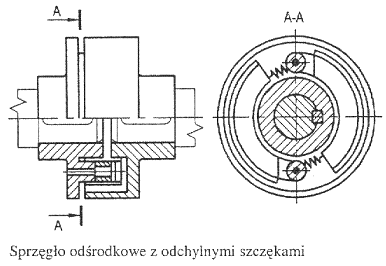
• samoczynne odśrodkowe - gdy zachodzi potrzeba samoczynnego wyłączenia/wyłączenia przy określonej prędkości obrotowej

• bezpieczeństwa - gdy wymagane jest samoczynne odłączenie silnika w przypadku przeciążenia

• zwrotne, jednokierunkowe - gdy wymaga się przekazania obrotów w jednym kierunku

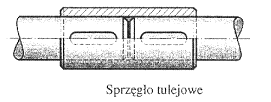
Najprostsze w budowie jest sprzęgło tulejowe, które jest nierozłączne. Tuleja łączy dwa współosiowe wały za pomocą kołków lub wpustów.

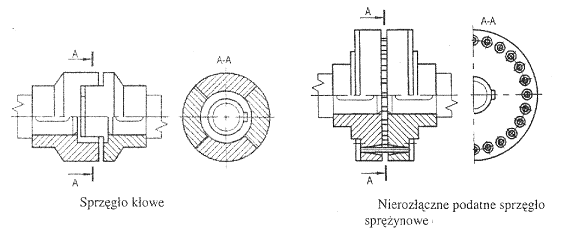
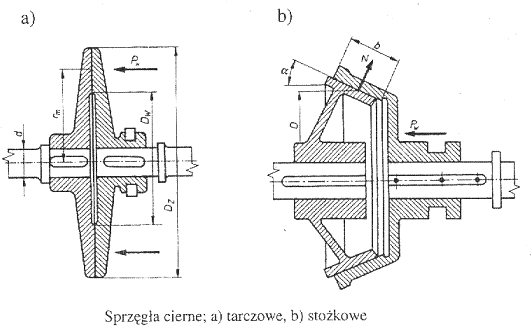
Klasycznym przykładem sprzęgieł rozłącznych jest włączalne asynchronicznie cierne sprzęgło stożkowe lub tarczowe. Dwie odpowiednio ukształtowane tarcze są posadowione na czopach wałów, przy czym jedna z nich posadowiona jest na stałe, a druga przesuwnie. Włączenie sprzęgła polega na dociśnięciu tarcz do siebie i wywołaniu siły tarcia, dzięki której moment obrotowy jest przenoszony z wału czynnego na wał bierny.

Sprzęgła bezpieczeństwa samoczynnie rozłączają wał czynny i bierny w przypadku nadmiernego wzrostu obciążenia. Zapewniają bezpieczną eksploatacje maszyn. Przykładem jest sprzęgło, którego tarcze połączone są kołkami o ograniczonej nośności. Nadmierny wzrost obciążenia spowoduje ścięcie tych kołków i rozłączenie wałów.

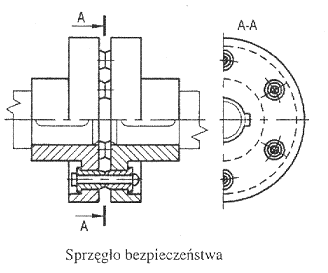
37. Budowa i zasada działania hamulca. Opis wybranych hamulców.

Hamulec jest zespołem układu napędowego maszyny, który pełni funkcję regulatora prędkości. W budowie maszyn stosowane są najczęściej hamulce cierne.

W hamulcach klockowych siła tarcia występuje między kołem a klockiem. Stosowane są hamulce jedno- lub dwuklockowe. Schemat hamulca dwuklockowego pokazano na rysunku.

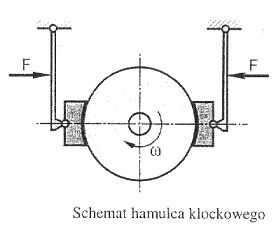
Klocki hamulcowe podczas eksploatacji poddane są działaniu sił normalnych i stycznych, które są zmienne w czasie. Należy zaznaczyć, że występuje tu również obciążenie termiczne, które m a istotny wpływ na proces hamowania. Materiały na klocki hamulcowe powinna charakteryzować duża odporność na zużycie cierne i zniszczenie zmęczeniowe, niski współczynnik rozszerzalności termicznej oraz dobra przewodność cieplna.. Klocki wykonywane są najczęściej z żeliwa stopowego lub sferoidalnego, które spełnia wymienione wymagania.

Szczęki hamulca umieszczone są wewnątrz bębna. Stosowane są warianty z symetrycznym i asymetrycznym rozmieszczeniem szczęk. Włączenie hamulca następuje pod wpływem sił W1 i W2, które dociskają szczęki do powierzchni wewnętrznej bębna. W układzie symetrycznym (W1=W2) naciski N1 i N2 są różne co wynika z równania momentów względem osi przegubów - sworzni. Przy asymetrycznym (W1=W2) naciski szczęk na bęben są takie same: N1=N2

Odmienne w działaniu od klockowych są hamulce tarczowe. Kierunek działania siły między parami ciernymi jest osiowy. Hamulce osiowe wytwarza się w 3 wariantach: jednotarczowe stożkowe, jednotarczowe szczękowe, wielotarczowe płaskie. Ich zalety: brak wrażliwości na kierunek ruchu, zrównoważenie sił dociskających, równomierne zużycie okładzin, wzrost intensywności chłodzenia, mała wrażliwość na odkształcenia termiczne. Tarcza hamulca wraz ze szczękami tworzy parę cierną. Skuteczne odprowadzenie ciepła hamowania zapewnione jest dzięki ukształtowaniu tarczy.

Proces hamowania ma charakter dynamiczny, występują w nim znane z mechaniki zjawiska: drgania, niestateczność, Przedmiotem badań jest problem niestabilności procesu, przez co obniżona jest sprawność hamowania i trwałość części hamulca, oraz zwiększone drgania. Hamulec cierny to urządzenie, które zamienia energię kinetyczną na cieplną (Uk - Q).

38. Ogólny opis zbiorników, zagadnienia wytrzymałości i stateczności.

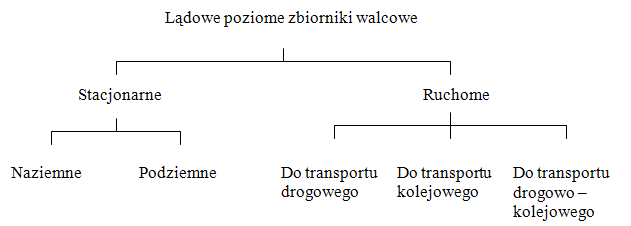
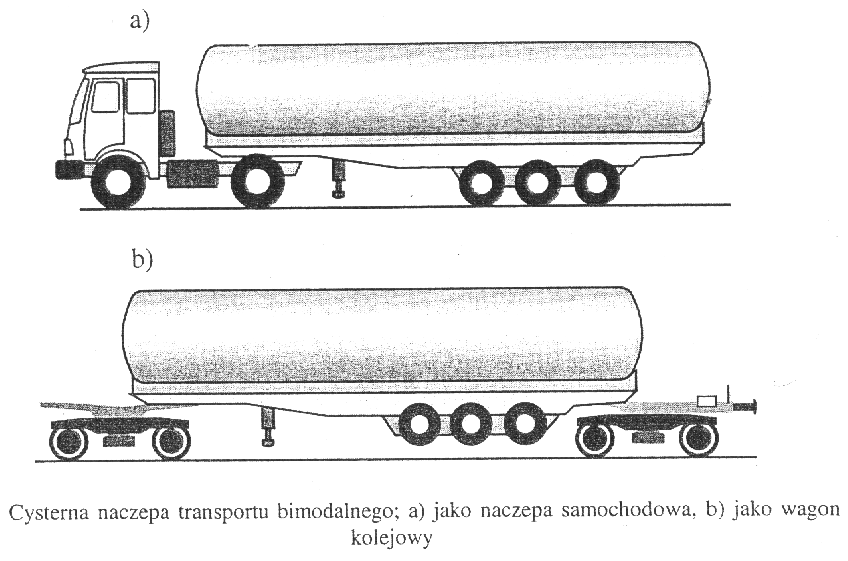
Poziomy zbiornik walcowy jest konstrukcją, której głównymi częściami są powłoka walcowa, dwa dna wypukłe oraz podpory. Wyróżnia się zbiorniki stacjonarne (naziemne i podziemne) i transportowe (samochodowe, kolejowe, samochodowo - kolejowe/ bimodalne).

Zbiornik walcowy z dnami wypukłymi, obciążony równomiernym ciśnieniem wewnętrznym po, narażony jest na zniszczenie jedynie z uwagi na wytrzymałość materiału, z którego jest wykonany.

W powłoce walcowej występuje błonowy stan naprężeń o składowych:

wzdłużnych:

i obwodowych:

W połączeniu powłoki walcowej z dnami występują także: siła poprzeczna Q₀ i moment zginający M₀ które zaburzają błonowy stan naprężeń. Efektem tego jest lokalny wzrost naprężeń w otoczeniu połączenia.

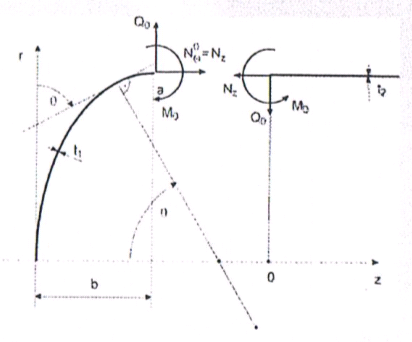
Rys. Siła poprzeczna i moment zginający w połączeniu dna z powłoką walcową.

Współczynnik spiętrzenia naprężeń w połączeniu dna elipsoidalnego z powłoką walcową:

gdzie:

σ_zast - naprężenia zastępcze stanu błonowego

β = b/a - względna głębokość dna elipsoidalnego (dla klasycznych den = 0,5)

W ściankach poziomego zbiornika walcowego, który jest wypełniony cieczą o gęstości ρm, występuje złożony stan naprężenia. Sposób ukształtowania podpór ma istotny wpływ na rozkład naprężeń w zbiorniku. Stosuje się podpory: sztywne siodła podporowe, pierścienie, podatne siodła, wsporniki.

Minimalna grubość ścianki powłoki walcowej tego zbiornika wynosi:

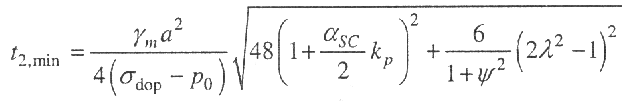
Gdzie:

k_p = p_o/γ_ma, ψ = k_p/100 - bezwymiarowe parametry

a - promień zbiornika

σ_dop - naprężenia dopuszczalne

γ_m = ρ_mg - ciężar właściwy cieczy

p_o - ciśnienie wewnętrzne

λ = L/d - względna długość zbiornika

Efektywna grubość ścianki dna epsoidalnego z uwagi na najmniejsze spiętrzenie naprężeń:

Poziomy zbiornik walcowy wypełniony wodą (w 80%) może ulec zniszczeniu na skutek wyboczenia. Minimalna grubość powłoki walcowej, która zapewnia stan stateczności:

Grubość ścianki nie może być mniejsza niż wartości wyznaczone z warunków wytrzymałości i stateczności

Efektywne podparcia: cienkościenne siodła podatne

Efektywne proporcje zbiornika:

gdzie:

Vo - [m3] pojemność zbiornika

PKM - EGZAMIN - Pytania + opracowania

2008

34

---