Robert Matera 23.10.2002

TRiL gr.II

24.Wyznaczanie ciepła topnienia lodu.

1.Cel.

Celem mojego ćwiczenia jest wyznaczenie ciepła topnienia lodu.

2.Wprowadzenie.

Topnienie jest przemianą fazową polegającą na przejściu ciała stałego w ciecz. Topnienie jest więc związane ze zmianą stanu skupienia substancji. Procesem odwrotnym do topnienia jest krzepnięcie. Topnienie ciał krystalicznych zachodzi zawsze w określonej temperaturze, zwanej temperaturą topnienia i równej temperaturze krzepnięcia. Temperatura topnienia zależy od ciśnienia. Dla większości ciał, które zwiększają swoją objętość podczas topnienia, ze wzrostem ciśnienia wzrasta temperatura topnienia. W przypadku ciał, które zmieniają swoją objętość podczas topnienia (np.lód) zależność ta ma przeciwstawny charakter.

Ogrzewanie kryształu powoduje wzrost prędkości drgań atomów uwięzionych w węzłach sieci, co oznacza wzrost temperatury ciała. Zatem dostarczaniu ciepła towarzyszy wzrost temperatury ogrzewanego ciała i to wprost proporcjonalnie do pobranego ciepła.

Proces topnienia związany jest z pobieraniem ciepła. Celem mojego ćwiczenia jest pomiar ciepła topnienia lodu. Ciepło topnienia jest to ilość ciepła jaką należy dostarczyć jednostce masy ciała stałego, znajdującego się w temperaturze topnienia, aby zmieniło się ono w cieczy o tej samej temperaturze. Jeśli w celu stopienia m kilogramów ciała dostarczono ciepło w ilości Q, to ciepło topnienia l można wyrazić wzorem:

0x01 graphic
(1)

Ponieważ w układzie SI ilość ciepła, jak każdy rodzaj energii, mierzymy w dżulach [J], więc jednostką ciepła topnienia jest J/kg.

Wyznaczanie ciepła topnienia za pomocą kolorymetru.

W celu wyznaczenia ciepła topnienia lodu wprowadzimy określoną ilość lodu, o temperaturze topnienia, do kalorymetru z wodą o temp. Początkowej To, nieco wyższej od temp. Otoczenia. Kolorymetr jest to naczynie o podwójnych, odizolowanych ścianach i małej pojemności cieplnej (pojemność cieplna jest to ilość masy ciała i jego ciepła właściwego). Kolorymetr powinien chronić ciało znajdujące się w nim przed wymianą ciepła z otoczeniem. Lód pobiera ciepło od wody i kolorymetru, co powoduje jego topnienie. Woda powstała z lodu, mająca w chwili początkowej temperaturę topnienia, również pobiera ciepło od kolorymetru i zawartej w nim wody. Procesy przepływu ciepła kończą się w chwili wyrównania się temperatur

--ustala się wówczas pewna temperatura końcowa Tk.

Aby otrzymać równanie, które posłuży do wyznaczenia ciepła topnienia, należy przeprowadzić bilans cieplny, czyli przeprowadzić rozliczenie strat i zysków ciepła. Przypomnijmy sobie wzór na ilość ciepła Q pobranego lub oddanego przez ciało przy zmianie jego temp. o ∆T:

Q=c*m*∆T (2)

gdzie:c-ciepło właściwe (jest to ilość ciepła potrzebna do ogrzania 1kg ciała o jednostkę temp.)

Gdy Q>0, to w przypadku ciepła pobranego przyjmujemy założenie: ∆T=Tk-To, natomiast gdy ciało ciepło oddaje to: ∆T=To-Tk. Ponieważ pomiędzy temp. T (w kelwinach) i t (w Celsjusza) zachodzi związek T==t+273,15, wartość liczbowa przyrostu temp. jest taka sama w jednej i drugiej skali, ∆T=∆t.

Bilans cieplny wymaga aby w układzie izolowanym ciepło pobrane Qp=Q1+Q2 było równe ciepłu oddanemu Qod=Q3+Q4, czyli:

Q1+Q2=Q3+Q4

gdzie:Q1-cieplo pobierane na stopienie m1, Q2-ciepło wody z lodu od temp. topnienia do temp. krzepnięcia, Q3-ciepło pochodzące od wody o masie mw, Q4-ciepło pochodzące od naczynia wewnętrznego kolorymetru.

Wykorzystując wzory (1) i (2), poszczególne ciepła możemy wyrazić następująco:

Q1=ml*l, Q2=ml*cw(tk-tt), Q3=mw*cW*(to-tk), Q4=mk*ck*(to-tk)

gdzie:cw -cieplo właściwe wody, które wynosi 4,19*103 J/kg*K, ck-ciepło właściwe kolorymetru wynosi 896 J/kg*K.

Wzór na ciepło właściwe:

0x01 graphic

W wykonywanym ćwiczeniu badane są zjawiska przechodzenia ciepła, czyli zagadnienia termodynamiczne. Taki przepływ ciepła, wraz z towarzyszącymi mu zmianami energii wewnętrznej ciał biorących udział w doświadczeniu, nazywamy procesem termodynamicznym. Istnieje funkcja, zwana entropią, która ujmuje ilościowo prawdopodobieństwo przejścia układu od jednego stanu do drugiego w tzw. procesach nieodwracalnych. W naszym przypadku jest to mieszanina wody z lodem zamknięta w kolorymetrze, uporządkowanie maleje i entropia wzrasta.

W układzie o stałej temperaturze zmianę entropii ∆S określa się jako stosunek ciepła ∆Q dostarczonego do układu do temp. bezwzględnej T (w kelwinach)

0x01 graphic
[J/K]

W moim doświadczeniu trzy ciała stanowią układ zamknięty. W układzie tym zmieniają one swoje stany termodynamiczne więc obliczamy pełną zmianę entropii układu przez zsumowanie zmian entropii poszczególnych składników:

∆S=∆S1+∆S2+∆S3

gdzie:∆S1-jest zmianą entropii lodu w procesie topnienia, ∆S2-zmianą entropii wody ze stopionego lodu, ∆S3-zmianą entropii kalorymetru wraz z tą ilością wody, która była w kalorymetrze przed wrzuceniem lodu.

Dla lodu T jest stała i wyznacza ją temp. topnienia Tt=273,15 K, natomiast ilość ciepła pobranego do stopienia wynosi ∆Q=Q1=ml*l, a wtedy ∆S1 równa się:

0x01 graphic

Dla wody z lodu temperatura ulega zmianie od Tt do Tk i elementarny przyrost ciepła wynosi dQ2=ml*cw*dT, a ∆S2 równe jest:

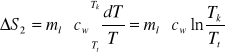
0x01 graphic

W trzecim przypadku, dQ3=(mwcw+mkck)dT oraz ∆S3:

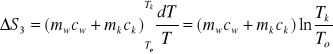
0x01 graphic

tutaj To to temp. początkowa układu.

3.Wykonanie ćwiczenia:

4.Obliczenia:

mw=m1-mk

Pomiar I

mw=0,42502-0,08285=0,34217kg

Pomiar II

mw=0,52515-0,08285=0,4423kg

Pomiar III

mw=0,38092-0,08285=0,29807kg

mL=m2-m1

Pomiar I

mL=0,44045-0,42502=0,01543kg

Pomiar II

mL=0,53251-0,52515=0,0736kg

Pomiar III

mL=0,38636-0,38092=0,0544kg

0x01 graphic

gdzie:ck i cw- ciepło właściwe wody i kalorymetru dla ck=896J/kg*K, dla cw=4,19*103J/kg*K, to=temp. początkowa, tk=temp. końcowa, mL=masa lodu, tt=temp. topnienia równa 273oC, mw=masa wody, mk=masa samego naczynia kalorymetru.

Pomiar I

l=(7304,9454-1013,52748)/0,01484=423949,9946 J/kg

Pomiar II

l=(9084,4425-1365,90648)/0,02312=333846,7128J/kg

Pomiar III

l=(11248,38656-1396,527)/0,033=298539,8352J/kg

lśr=(423949,9946+333846,7128+298539,8352)/3=352112,1809J/kg

Pomiar 1

∆S1=0x01 graphic
 gdzie:∆Q-ciepło dostarczane do układu, T-temp.

l-ciepło topnienia lodu.

∆S1=(0,01484*423949,9946)/273=23,045J/K

∆S2=mLcwln0x01 graphic
 gdzie:Tt-temp. topnienia, Tk-temp. końcowa

mL-masa lodu, cw-ciepło właściwe

∆S2=0,01484*4190*ln(289,3/273)=3,606J/K

∆S3=(mwcw+mkck)ln0x01 graphic
gdzie:To-temp początkowa

∆S3=890,847*ln(289,3/297,5)=-24,899J/K

∆S=∆S1+∆S2+∆S3=1,752 [J/K]

Pomiar 2

∆S1=(0,02312*333846,7128)/273=28,273J/K

∆S2=0,02312*4190*ln(287,1/273)=4,878J/K

∆S3=1009,3825*ln(287,1/296,1)=-31,156J/K

∆S=∆S1+∆S2+∆S3=1,995[J/K]

Pomiar 3

∆S1=(0,033*298539,8352)/273=36,087J/K

∆S2=0,033*4190*ln(283,3/273)=5,121J/K

∆S3=878,7802*ln(283,1/295,9)=-38,861J/K

∆S=∆S1+∆S2+∆S3=2,347[J/K]

WNIOSKI:

Ćwiczenie to pozwoliło mi na wyznaczenie ciepła topnienia lodu. W momencie wrzucenia lodu do kalorymetru lód pobiera ciepło od wody i ulega rozpuszczeniu. Temperatura spada do momentu rozpuszczenia całkowitego lodu, gdy lód ulegnie całkowitemu rozpuszczeniu temperatura zatrzymuje się, po czym znowu rośnie. Temperatura najniższa to temperatura końcowa. Przy obliczeniach i wykonaniu pomiarów pojawia się błąd który wynosi . Który mógł być spowodowany niedokładnym odczytaniem temperatury (początkowej, końcowej) jak i również nie dokładną wagą kalorymetru (która była spowodowana nie do końca suchym kalorymetrem z czego wynikają aż trzy różne wyniki masy kalorymetru.