Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 1/24

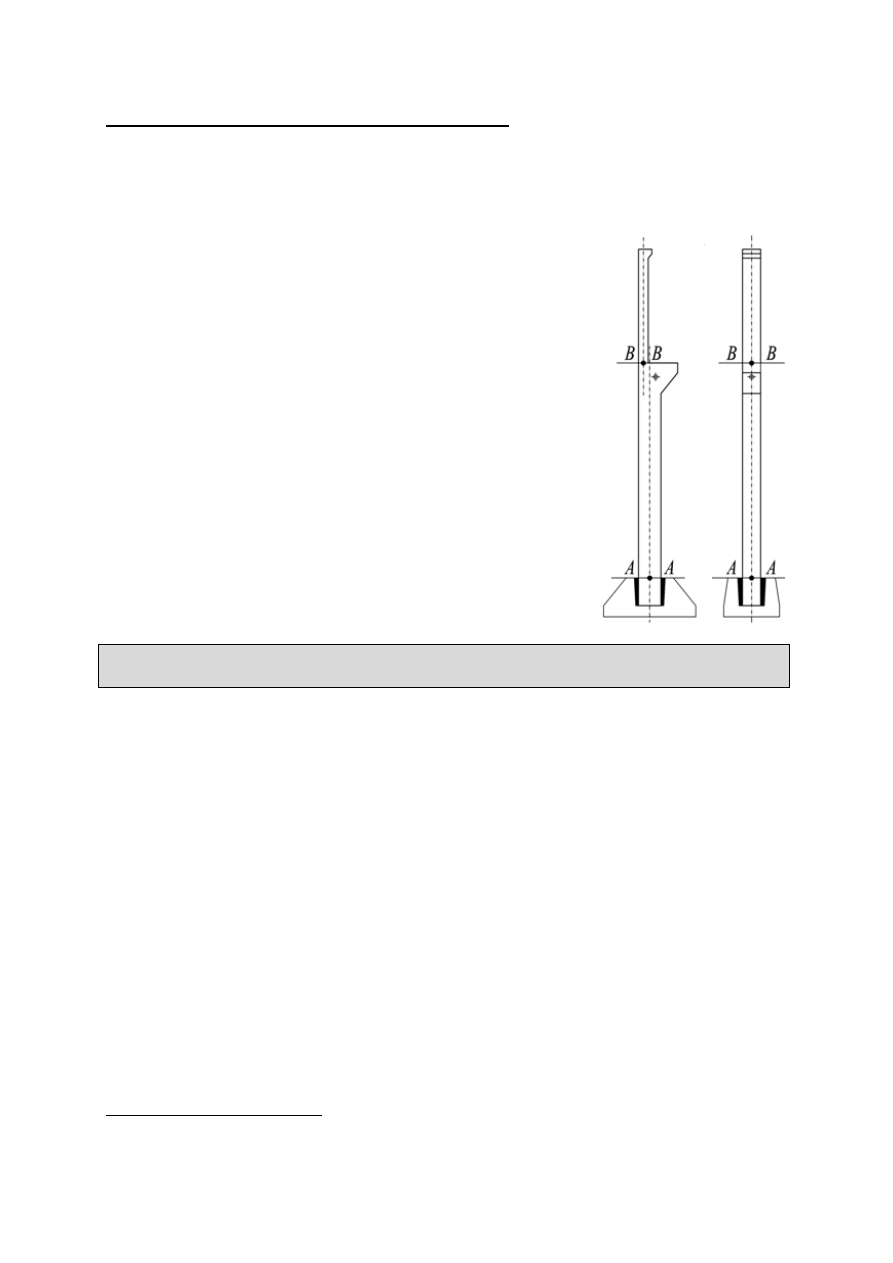
Obliczenia wytrzymałościowe słupa dwugałęziowego

Obliczenia przekroju w miejscu utwierdzenia
(przekrój „A-A”)

Przekrój „A-A” jest wymiarowany w obu płaszczyznach na
następujące wartości sił wewnętrznych:
- w Płaszczyźnie Układu:
a)

M

x(max)

N

odp

(moment maksymalny, siła odpowiadająca)

b)

M

x(min)

N

odp

c)

M

x(odp)

N

max

d)

M

x(odp)

N

min

- w Płaszczyźnie Prostopadłej,
a)

M

y(max)

N

odp

(moment maksymalny, siła odpowiadająca)

b)

M

y(min)

N

odp

c)

M

y(odp)

N

max

d)

M

y(odp)

N

min

Obliczenie górnej gałęzi (przekrój „B-B”)

Przekrój „B-B” należy zwymiarować w obu płaszczyznach:
- w Płaszczyźnie Układu,
- w Płaszczyźnie Prostopadłej,
na układy sił wewnętrznych wyszczególnione wyżej – w p. 1.

PN-EN 1992-1-1:2008
5.8 Analiza efektów drugiego rzędu pod obciążeniem siłą podłużną

Definicje

Obciążenie wyboczeniowe: obciążenie, przy którym występuje wyboczenie; w elementach
wydzielonych jest ono synonimem siły krytycznej według Eulera.

Długość efektywna: długość stosowana w celu uwzględnienia kształtu krzywej ugięcia
(powstającego przy wyboczeniu); może być ona również nazywana długością wyboczeniową.
Innymi słowy; jest to długość słupa podpartego przegubowo na obu końcach, obciążonego
stałą siłą podłużną, mającego taki sam przekrój poprzeczny i obciążenie wyboczeniowe jak
rozpatrywany element.

Efekty drugiego rzędu: dodatkowe efekty oddziaływań (na ogół momenty zginające lub
mimośrody) spowodowane odkształceniami konstrukcji.

Długość efektywna l

0

Długość efektywna l

0

elementów ściskanych nie spełniających warunków słupa

podstawowego

1

, a więc np. takich w których następuje (istotna) zmiana wartości siły osiowej

lub przekroju poprzecznego wzdłuż pręta, jest wyznaczana ze wzoru:

1

Słup podstawowy – pręt pryzmatyczny (o stałym przekroju na długości) z materiału liniowo-sprężystego,

podparty na końcach przegubowo i przegubowo-przesuwnie, obciążony przyłożoną na końcach siłą ściskającą.

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 2/24

B

N

EI

l

/

0

π

=

(5.17)

w którym:

EI – jest reprezentatywną sztywnością giętną,
N

B

– jest obciążeniem wyboczeniowym wyznaczonym dla sztywności EI (wartość i w

wyrażeniu (5.14) powinna również odpowiadać tej sztywności EI)

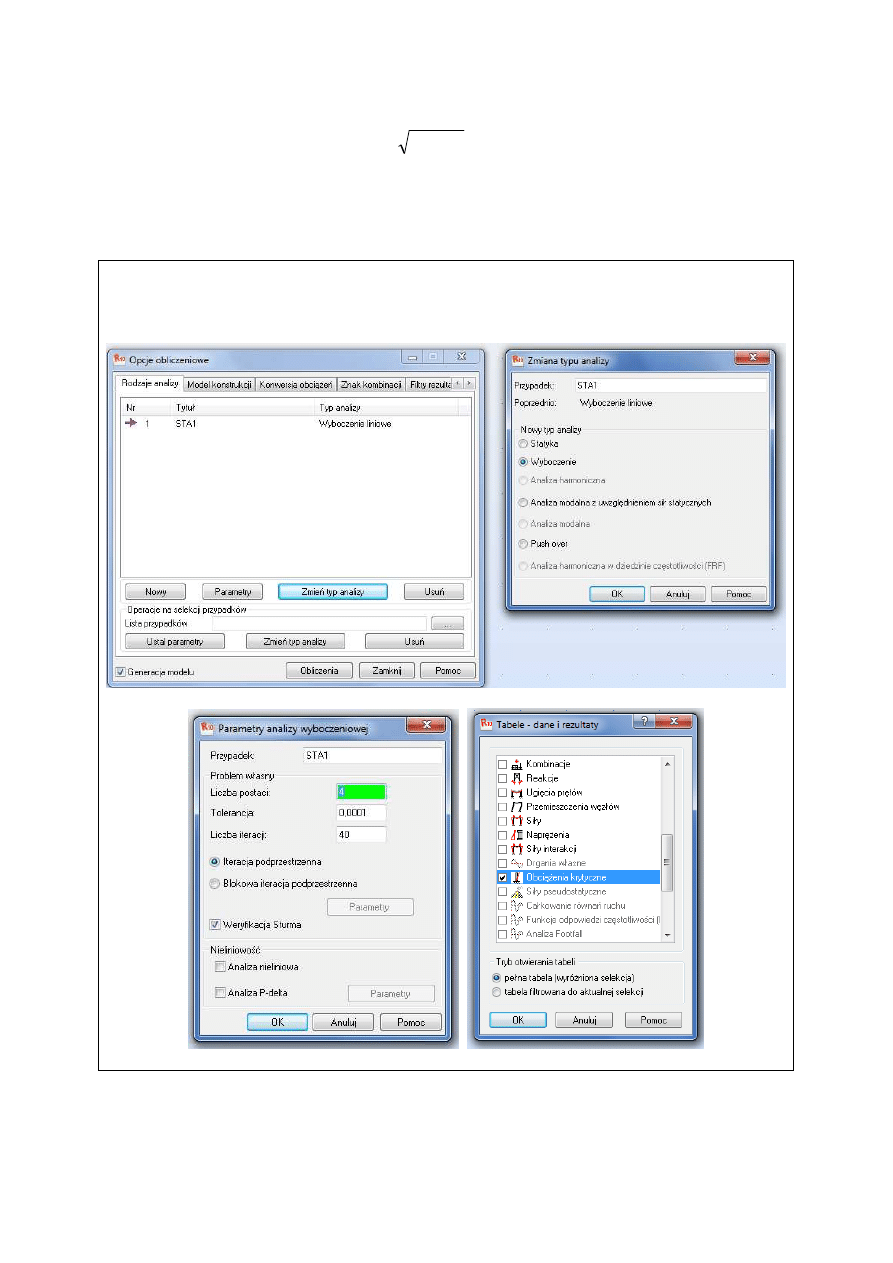
Wartość siły wyboczeniowej N

B

wyznaczyć należy metodami numerycznymi,

np. w programie Autodesk® Robot™ Structural Analysis Professional, wybierając opcję
analizy wyboczeniowej. Wyznaczyć należy obciążenie krytyczne.

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 3/24

Smukłość

λ

Smukłość określa się wzorem:

i

l

0

=

λ

(5.14)

w którym:

l

0

– jest długością efektywną (5.17),

i – jest promieniem bezwładności niezarysowanego przekroju żelbetowego.

Kryterium smukłości elementów wydzielonych

Jeżeli smukłość

λ

(5.14) nie przekracza wartości

λ

lim

, to efekty drugiego rzędu można

pomijać (słup krępy).

Uwaga: Wartość

λ

lim

do stosowania w kraju może być podana w Załączniku krajowym.

Wartości zalecane wynikają ze wzoru

n

C

B

A

20

lim

=

λ

(5.13N)

w którym:

ef

A

φ

2

,

0

1

1

+

=

(jeżeli wartość

ϕ

ef

nie jest znana, to można przyjąć A = 0,7),

ω

2

1

+

=

B

(jeżeli wartość

ω

nie jest znana, to można przyjąć B = 1,1),

C = 1,7 - r

m

(jeżeli wartość r

m

nie jest znana, to można przyjąć C = 0,7),

ϕ

ef

efektywny współczynnik pełzania, patrz 5.8.4,

cd

c

yd

s

f

A

f

A

=

ω

intensywność zbrojenia,

A

s

pole przekroju całego zbrojenia podłużnego,

cd

c

Ed

f

A

N

n

=

względna siła normalna,

02

01

M

M

r

m

=

stosunek momentów,

M

01

, M

02

momenty pierwszego rzędu na końcach elementu, tak ponumerowane,

ż

ebyM

02



≥

M

01

.

Jeżeli momenty na końcach M

01

i M

02

powodują rozciąganie po tej samej stronie elementu, to

zmiennej r

m

należy nadać wartość dodatnią (tj. C

≤

1,7), a w innych przypadkach ujemną (tj.

C > 1,7).

Rozpatrując:

- elementy usztywniane, w których momenty pierwszego rzędu powstają tylko lub

przede wszystkim na skutek imperfekcji lub obciążenia poprzecznego,

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 4/24

- ogólnie, elementy nieusztywnione

należy przyjmować r

m

= 1,0 (tzn. C = 1,7).

W przypadkach dwukierunkowego zginania kryterium smukłości można sprawdzać
oddzielnie dla każdego kierunku. W zależności od wyniku tego sprawdzenia efekty drugiego
rzędu:

(a) mogą być pominięte w obu kierunkach,

(b) powinny być uwzględnione w jednym kierunku (słup smukły),

(c) powinny być uwzględnione w obu kierunkach (słup smukły).

Pełzanie

(1)

Uwzględniając wpływ pełzania, w analizie drugiego rzędu należy brać pod uwagę

zarówno ogólne warunki pełzania (patrz 3.1.4), jak i czas trwania różnych obciążeń
uwzględnianych w rozpatrywanej kombinacji obciążeń.

(2)

Wpływ długotrwałego działania obciążeń można uwzględnić sposobem przybliżonym

za pomocą efektywnego współczynnika pełzania

ϕ

ef

, który (stosowany łącznie z obciążeniem

obliczeniowym) daje odkształcenie pełzania (krzywiznę) odpowiadające obciążeniu quasi-
stałemu

.

Efektywny współczynnik pełzania oblicza się ze wzoru

Ed

Eqp

ef

M

M

t

0

0

0

)

,

(

∞

=

ϕ

ϕ

(5.19)

w którym:

ϕ

(

∞

,t

0

) jest końcowym współczynnikiem pełzania według 3.1.4,

M

0Eqp

jest momentem zginającym pierwszego rzędu wywołanym prawie stałą
kombinacją obciążeń (SLS),

M

0Ed

jest momentem zginającym pierwszego rzędu wywołanym obliczeniową
kombinacją obciążeń (ULS).

Uwaga: Współczynnik

ϕ

ef

można obliczać także na podstawie całkowitych momentów

zginających M

Eqp

i M

Ed

, ale wymaga to iteracji i sprawdzenia stateczności pod

obciążeniem quasi-stałym przy

ϕ

ef

=

ϕ

(

∞

,t

0

).

(3)

Jeśli w elemencie lub w konstrukcji M

0Eqp

/M

0Ed

nie jest wartością stałą,

to we wzorze

(5.19) można zastosować ten stosunek obliczony dla przekroju z maksymalnym momentem
lub reprezentatywną wartość średnią tego stosunku.

(4)

Wpływ pełzania można pominąć, tj. można założyć

ϕ

ef

= 0, gdy spełnione są trzy

poniższe warunki:

-

ϕ

(

∞

,t

0

)

≤

2

-

λ

≤

75

- M

0Ed

/N

Ed

≥

h.

M

0Ed

oznacza tutaj moment pierwszego rzędu, a h wysokość przekroju poprzecznego

odpowiednią dla rozpatrywanego kierunku.

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 5/24

Uwaga: Jeżeli warunki pomijania efektów drugiego rzędu 5.8.2(6) lub 5.8.3.3 są
spełnione, ale są blisko granicy określonej przez te warunki, to łączne pomijanie
efektów drugiego rzędu i pełzania może okazać się niebezpieczne, o ile intensywność
zbrojenia ( (

ω

, patrz 5.8.3.1(1)) nie wynosi co najmniej 0,25.

Sztywność nominalna

Do określania nominalnej sztywności smukłych elementów ściskanych o dowolnym
przekroju można stosować wzór

EI = K

c

E

cd

I

c

+ K

s

E

s

I

s

(5.21)

w którym:

E

cd

jest obliczeniową wartością modułu sprężystości betonu, patrz 5.8.6(3),

I

c

jest momentem bezwładności przekroju betonu,

E

s

jest obliczeniową wartością modułu sprężystości zbrojenia, 5.8.6(3),

I

s

jest momentem bezwładności pola przekroju zbrojenia względem środka
ciężkości powierzchni betonu,

K

c

jest współczynnikiem zależnym od wpływów zarysowania, pełzania itd., patrz
5.8.7.2 (2) lub (3),

K

s

jest współczynnikiem zależnym od udziału zbrojenia, patrz 5.8.7.2 (2) lub (3).

Jeżeli

ρ

≥

0,002, to w wyrażeniu (5.21) można stosować następujące współczynniki:

K

s

= 1,0

ef

c

k

k

K

ϕ

+

=

1

2

1

(22)

W powyższych wzorach:

ρ

jest stopniem zbrojenia, A

s

/A

c

,

A

s

jest całkowitą powierzchnią przekroju zbrojenia,

A

c

jest powierzchnią przekroju betonu,

ϕ

ef

jest efektywnym współczynnikiem pełzania, patrz 5.8.4,

k

1

jest współczynnikiem zależnym od klasy wytrzymałości betonu wg wzoru
(5.23),

k

2

jest współczynnikiem zależnym od siły podłużnej i smukłości wg wzoru (5.24).

20

1

ck

f

k

=

(MPa)

(5.23)

170

2

λ

n

k

=

, lecz nie więcej niż 0,20

(5.24)

n

jest względną siłą podłużną N

Ed

/(A

c

f

cd

) ,

λ

jest smukłością, patrz 5.8.3.

Jeśli smukłość

λ

nie jest określona, to można przyjąć

k

2

= 0,30 n, lecz nie więcej niż 0,20.

(5.25)

Jeżeli

ρ

≥

0,01, to jako uproszczenie, można we wzorze (5.21) zastosować następujące

współczynniki:

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 6/24

K

s

= 0

ef

c

K

ϕ

5

,

0

1

3

,

0

+

=

(5.26)

Uwaga: Powyższe uproszczenie może być odpowiednie jako wstępny krok, po którym
następuje dokładniejsze obliczenie zgodne z (2).

Współczynnik powiększenia momentu

Całkowity moment obliczeniowy, zawierający moment drugiego rzędu, można przedstawić
jako powiększony moment zginający wynikający z analizy pierwszego rzędu, stosując wzór:

























−

+

=

1

1

0

Ed

B

Ed

Ed

N

N

M

M

β

(5.28)

w którym:

M

0Ed

jest momentem pierwszego rzędu, patrz także 5.8.8.2(2),

β

jest współczynnikiem zależnym od rozkładu momentów pierwszego i drugiego
rzędu,

N

Ed

jest obliczeniową wartością siły podłużnej,

N

B

jest siłą krytyczną ze względu na wyboczenie, obliczoną przy założeniu, że

sztywność jest równa nominalnej.

Racjonalnym uproszczeniem jest zwykle przyjęcie

β

= 1.

Wyrażenie (5.28) można wtedy przedstawić w postaci

B

Ed

Ed

Ed

N

N

M

M

−

=

1

0

(5.30)

Siła krytyczna ze względu na wyboczenie (wzór Eulera):

2

0

2

l

EI

N

B

π

=

Zginanie ukośne

Jako pierwsze przybliżenie można przyjąć obliczanie oddzielne dla każdego kierunku
głównego z pominięciem zginania ukośnego. Imperfekcje należy brać pod uwagę tylko na
kierunku, na którym mają one wpływ najbardziej niekorzystny.

Dalsze sprawdzanie nie jest konieczne, gdy

2

≤

z

y

λ

λ

i

2

≤

y

z

λ

λ

(5.38a)

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 7/24

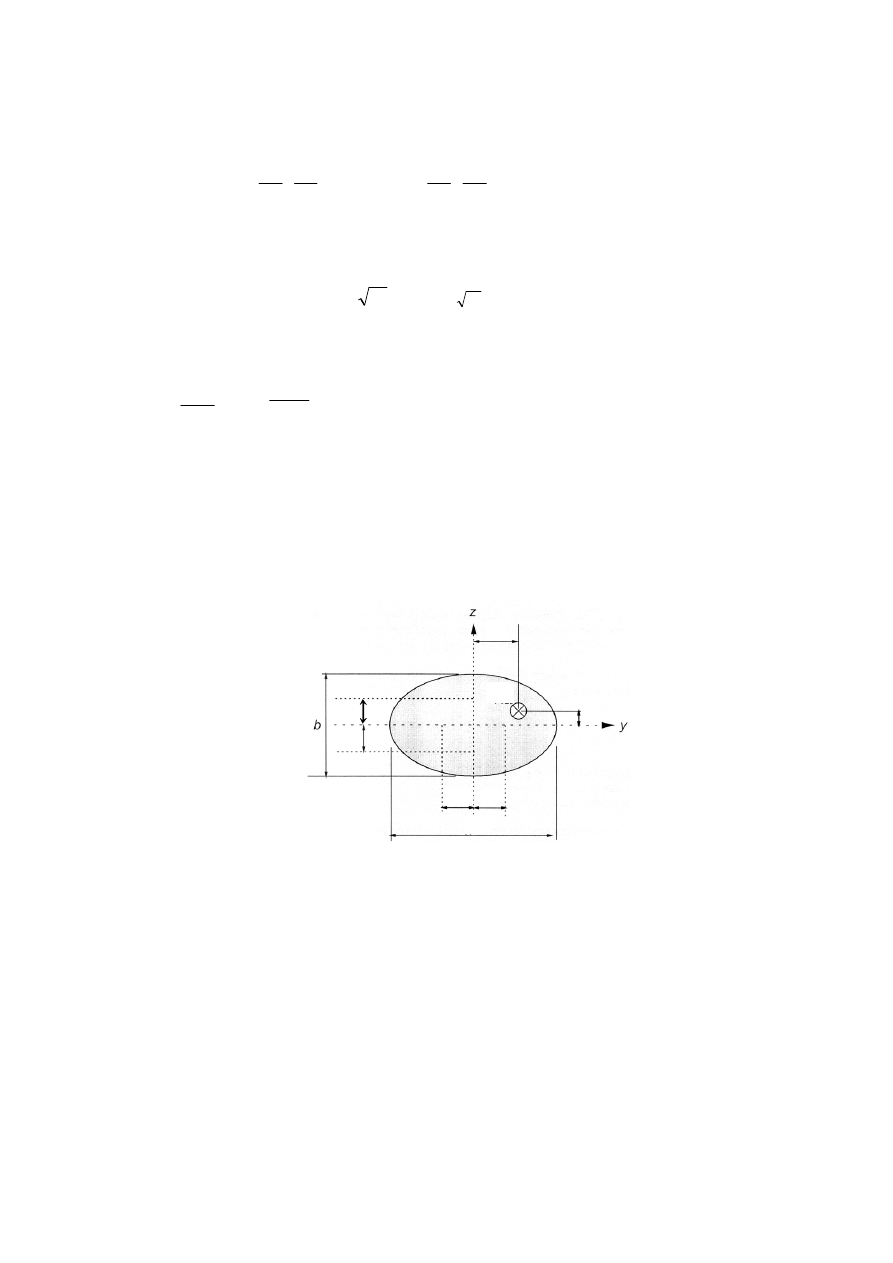
oraz gdy względne mimośrody e

y

/h

eq

i e

z

/b

eq

(patrz Rysunek 5.8) spełniają jeden z

następujących warunków

2

,

0

:

≤

eq

z

eq

y

b

e

h

e

lub

2

,

0

:

≤

eq

y

eq

z

h

e

b

e

(5.38b)

w których:

b, h oznaczają szerokość i wysokość przekroju,

b

eq

, h

eq

oznaczają wymiary zastępczego przekroju prostokątnego obliczane ze wzorów

12

y

eq

i

b

=

i

12

z

eq

i

h

=

λ

y

,

λ

z

są smukłościami l

0

/i odpowiednio względem osi y i z,

i

y

, i

z

są promieniami bezwładności, odpowiednio względem osi y i z,

Ed

Edy

z

N

M

e

=

,

Ed

Edz

y

N

M

e

=

oznaczają mimośrody, odpowiednio względem osi z i y,

M

Edy

jest momentem obliczeniowym względem osi y (łącznie z momentem

drugiego rzędu),

M

Edz

jest momentem obliczeniowym względem osi z (łącznie z momentem
drugiego rzędu),

N

Ed

jest wartością obliczeniową siły podłużnej przy odpowiedniej kombinacji

obciążeń.

e

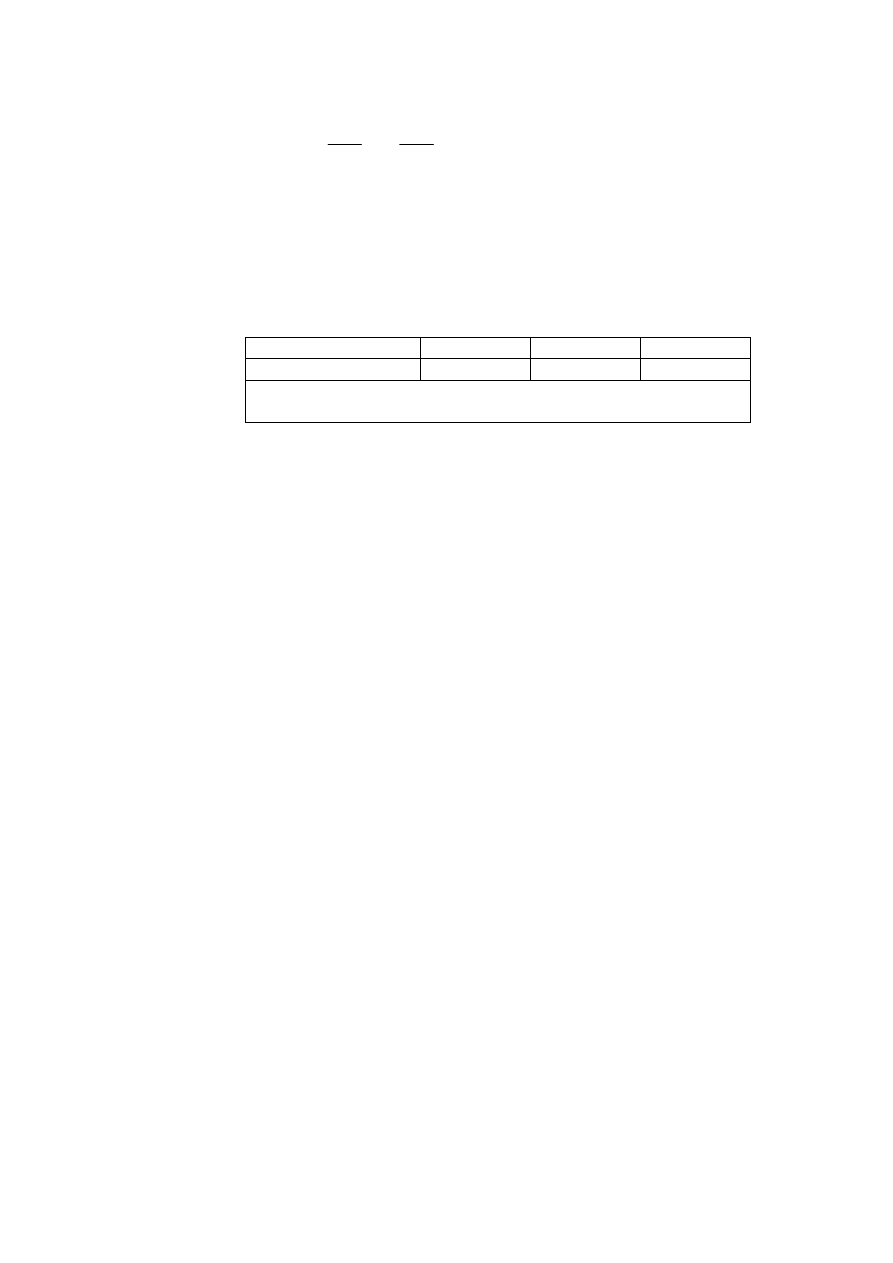
y

e

z

i

y

N

Ed

h

i

z

i

z

i

y

Rysunek 5.8: Mimośrody e

y

i e

z

– oznaczenia

Jeżeli warunki (5.38) nie są spełnione, to należy uwzględnić zginanie ukośne, włączając
efekty drugiego rzędu w każdym kierunku (jeżeli nie mogą być one pominięte zgodnie z
5.8.2(6) lub 5.8.3). Jeżeli nie stosuje się ścisłej metody obliczania ze względu na ukośne
zginanie, to można zastosować kryterium uproszczone

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 8/24

0

,

1

≤















+













a

Rdy

Edy

a

Rdz

Edz

M

M

M

M

(5.39)

w którym:

M

Edz

, M

Eyz

oznaczają momenty obliczeniowe względem odpowiednich osi (z

włączeniem momentów drugiego rzędu),

M

Rdz

, M

Rdy

oznaczają momenty graniczne względem odpowiednich osi,

a

jest wykładnikiem potęgi.
Dla kołowych i eliptycznych przekrojów poprzecznych a = 2
Dla prostokątnych przekrojów poprzecznych:

N

Ed

oznacza wartość obliczeniową siły podłużnej,

N

Rd

= A

c

f

cd

+ A

s

f

yd

oznacza nośność obliczeniową przekroju przy obciążeniu

osiowym.

A

c

oznacza całkowite pole przekroju betonu,

A

s

oznacza pole przekroju zbrojenia podłużnego.

N

Ed

/N

Rd

0,1

0,7

1,0

a

1,0

1,5

2,0

Do wyznaczania wartości pośrednich można stosować interpolację
liniową

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 9/24

Dla porównania: PN-B-03264:2002, str. 138, załącznik C

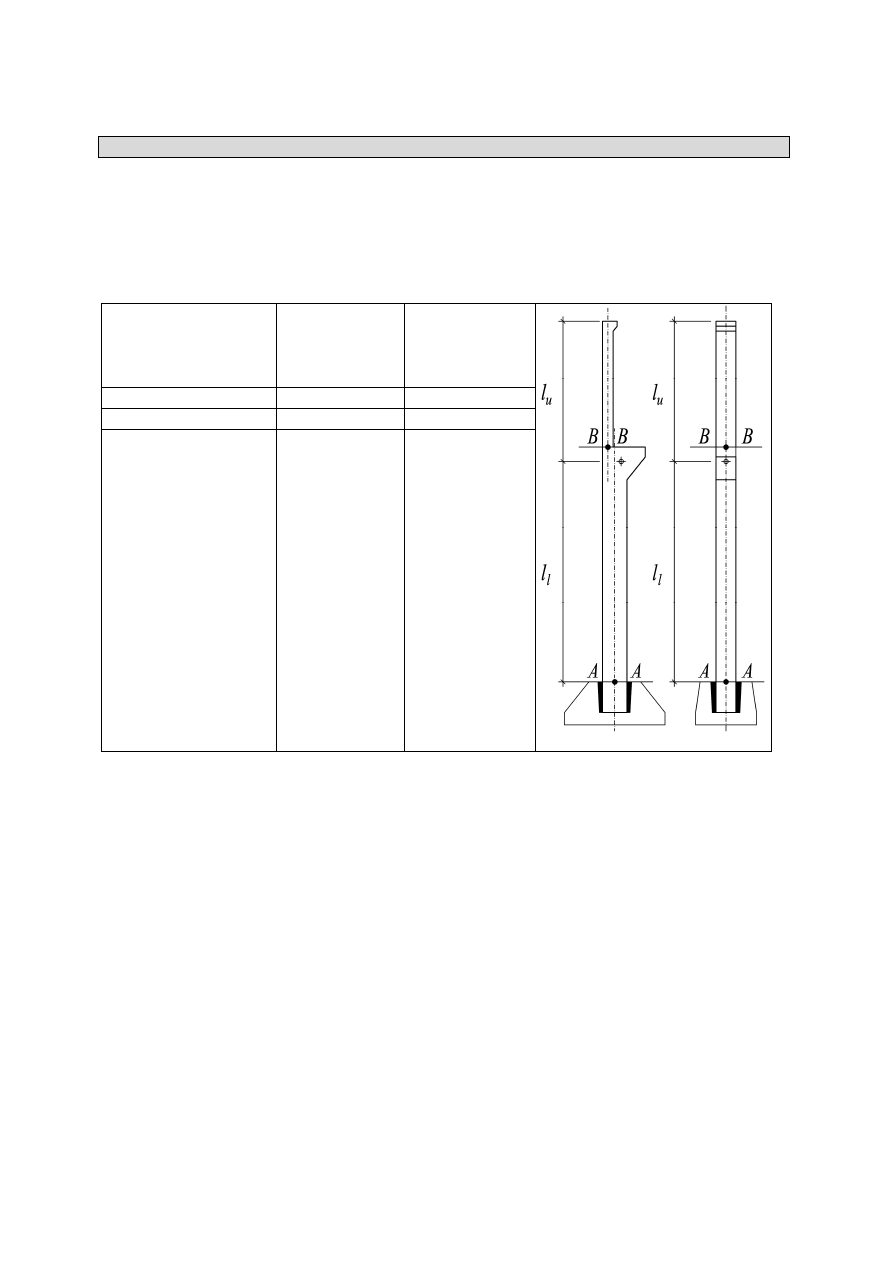
Długości obliczeniowe l

0

zgodnie z Tablicą C.1

Punkt 2. Słupy w jednokondygnacyjnych budynkach halowych, utwierdzone w stopach
fundamentowych i połączone z konstrukcją dachu w sposób przegubowy.

c) budynki z suwnicami

Element

Długość

obliczeniowa l

0

w Płaszczyźnie

Układu

Długość

obliczeniowa l

0

w Płaszczyźnie

Prostopadłej

1

2

3

- dolny odcinek słupa

l

0

= 1,6 l

l

l

0

= 1,2 l

l

- górny odcinek słupa

l

0

= 2,5 l

u

l

0

= 2,0 l

u

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 10/24

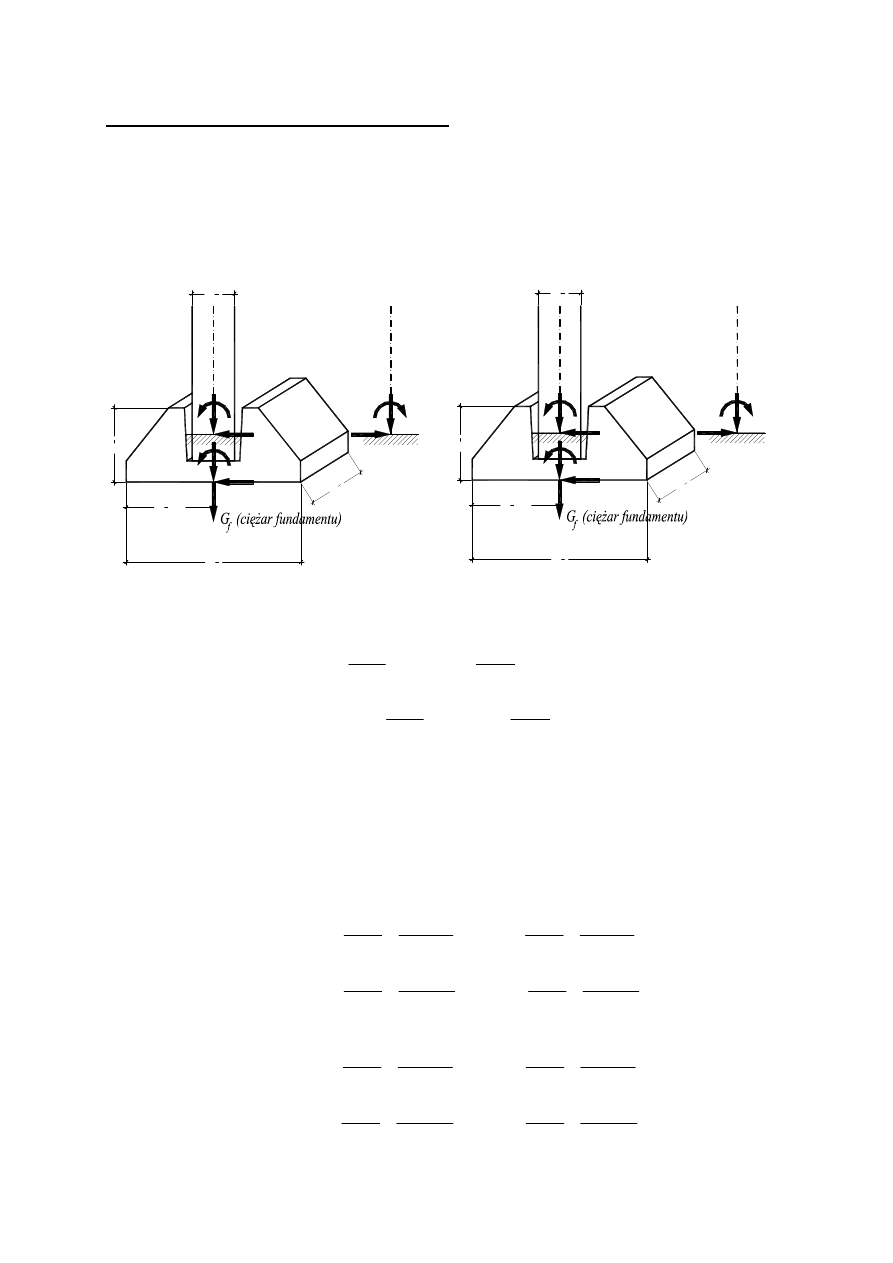
Obliczenie stopy fundamentowej kielichowej

Wartości sił wewnętrznych u podstawy słupa należy sprowadzić do podstawy

fundamentu, uwzględniając ciężar własny fundamentu. W wartościach momentów

f

M

1

i

f

M

2

należy uwzględnić momenty zginające wywoływane w podstawie fundamentu

przez siły poprzeczne

1

Q

oraz

2

Q

.

Wymiarowanie stopy fundamentowej należy wykonać:

a) w Płaszczyźnie Układu,

b) w Płaszczyźnie Prostopadłej.

a

f

b

f

/2

h

f

h

s

b

f

1x

Q

1xf

M

1f

N

2x

M

2x

Q

2

N

1x

Q

M

1

N

1x

1y

N

1

M

Q

1y

N

2

Q

2y

M

2y

N

1f

M

1yf

Q

1y

a

f

b

s

h

f

a

f

/2

b

f

Stopa fundamentowa pracuje jako element mimośrodowo obciążony w płaszczyźnie

ukośnej.

W obu płaszczyznach należy określić wartości mimośrodów statycznych, jako:

- Płaszczyźnie Układu:

f

xf

xf

N

M

e

1

1

1

=

oraz

f

xf

xf

N

M

e

2

2

2

=

,

- Płaszczyźnie Prostopadłej:

f

yf

yf

N

M

e

1

1

1

=

oraz

f

yf

yf

N

M

e

2

2

2

=

.

Wymiary stopy fundamentowej wyznacza się wstępnie, korzystając z zależności:
- w kierunku poprzecznym:

xf

f

e

b

1

6

>

i

xf

f

e

b

2

6

>

,

- w kierunku podłużnym:

yf

f

e

a

1

6

>

i

yf

f

e

a

2

6

>

,

Wartości naprężeń krawędziowych pod fundamentem sprawdza się korzystając ze

wzorów:

- w kierunki poprzecznym:

2

1

1

1

max

,

6

f

f

xf

f

f

f

x

b

a

M

a

b

N

⋅

+

=

σ

,

2

1

1

1

min

,

6

f

f

xf

f

f

f

x

b

a

M

a

b

N

⋅

−

=

σ

2

2

2

2

max

,

6

f

f

xf

f

f

f

x

b

a

M

a

b

N

⋅

+

=

σ

,

2

2

2

2

min

,

6

f

f

xf

f

f

f

x

b

a

M

a

b

N

⋅

−

=

σ

- w kierunku podłużnym:

2

1

1

1

max

,

6

f

f

yf

f

f

f

y

a

b

M

a

b

N

⋅

+

=

σ

,

2

1

1

1

min

,

6

f

f

yf

f

f

f

y

a

b

M

a

b

N

⋅

−

=

σ

2

2

2

2

max

,

6

f

f

yf

f

f

f

y

a

b

M

a

b

N

⋅

+

=

σ

,

2

2

2

2

min

,

6

f

f

yf

f

f

f

y

a

b

M

a

b

N

⋅

−

=

σ

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 11/24

Wymiary fundamentu są dobrane prawidłowo w stosunku do nośności gruntu, jeżeli są

spełnione następujące warunki:

fn

q

<

max

σ

, gdzie:

fn

q

- nośność gruntu (według obliczeń geotechnicznych)

0

min

>

σ

- nie dopuszcza się wystąpienia odrywania pod stopą fundamentową

Wysokość stopy oblicza się jako:

(

)

s

f

f

h

b

h

−

=

4

,

0

(ewentualnie:

(

)

s

f

f

b

a

h

−

=

4

,

0

).

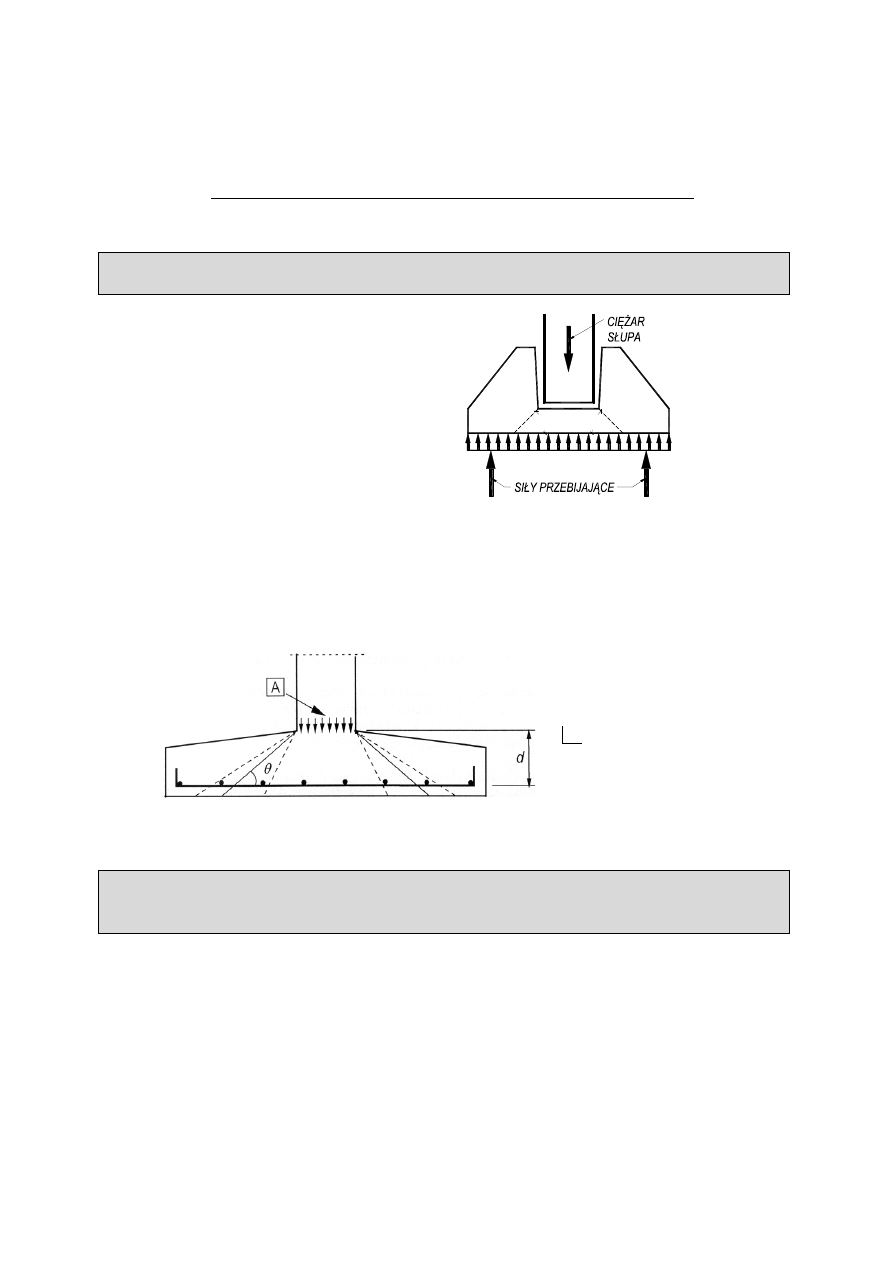
PN-EN 1992-1-1:2008
6.4.2 Rozkład obciążenia i podstawowy obwód kontrolny

Siłę

przebijającą

V

Ed

w

płytach

fundamentowych

można

zmniejszyć

uwzględniając korzystne działanie reakcji
podłoża gruntowego.

45°

45°

Przekrojem kontrolnym jest przekrój mający wysokość użyteczną

d, rozciągający się wzdłuż

obwodu kontrolnego. W płytach o stałej grubości przekrój kontrolny jest prostopadły do
ś

rodkowej powierzchni płyty. W płytach i fundamentach o zmiennej grubości, innych niż

fundamenty schodkowe, za wysokość użyteczną można przyjąć wysokość na obwodzie pola
obciążenia, jak na Rysunku 6.16.

A - pole obci

ąż

enia

θ

≥

arctan (1/2)

Rysunek 6.16: Wysokość przekroju kontrolnego w stopie fundamentowej o zmiennej wysokości

PN-EN 1992-1-1:2008
6.4.4 Nośność na ścinanie przy przebiciu płyt i stóp fundamentowych bez zbrojenia na
ś

cinanie

(2)

Nośność fundamentów słupów na przebicie (przez ścinanie) należy sprawdzać na

obwodach kontrolnych leżących w granicach 2

d od skraju słupa.

W przypadku obciążenia działającego osiowo siłę netto wyznacza się ze wzoru

V

Ed,red

= V

Ed

-

∆

V

Ed

(6.48)

w którym:

V

Ed

jest przyłożoną siłą ścinającą,

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 12/24

∆

V

Ed

jest siłą netto skierowaną ku górze, działającą w granicach rozważanego
obwodu kontrolnego, tzn. siłą wywołaną przez działający na fundament
nacisk gruntu pomniejszoną o ciężar własny fundamentu.

Ś

rednie naprężenie styczne w przekroju kontrolnym v

Ed

i naprężenie graniczne v

Rd

oblicza się

ze wzorów:

d

u

V

v

red

Ed

Ed

,

=

(6.49)

(

)

a

d

f

k

C

v

ck

l

c

,

Rd

Rd

2

100

3

1

ρ

=

, lecz nie mniej niż

a

d

v

2

min

(6.50)

w których:

a

oznacza odległość od skraju słupa do rozważanego obwodu kontrolnego,

C

Rd,c

jest określone w 6.4.4(1),

v

min

jest określone w 6.4.4(1),

k jest określone w 6.4.4(1).

Przy obciążeniu mimośrodowym stosuje się wzór















+

=

W

V

u

M

k

d

u

V

v

red

Ed

Ed

red

Ed

Ed

,

,

1

(6.51)

w którym k jest określone w 6.4.3(3) lub 6.4.3 (4), a W podobnie jak W

1

,

lecz dla obwodu u.

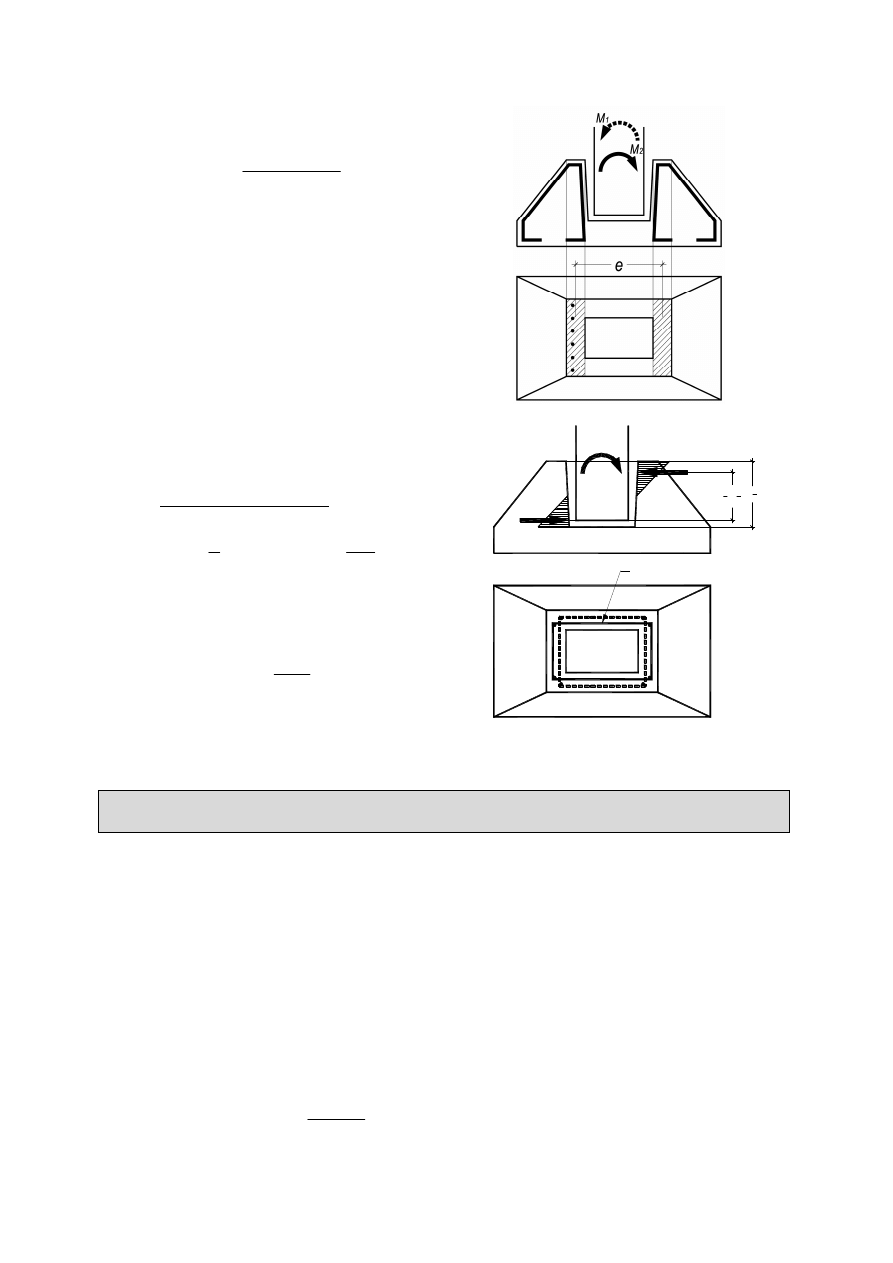
Wymiarowanie zbrojenia kielichowej stopy fundamentowej

Wymiarowanie przeprowadza się w dwóch płaszczyznach:
- w Płaszczyźnie Układu,
- w Płaszczyźnie Prostopadłej,
W kielichowej stopie fundamentowej oblicza się:
a)

zbrojenie poziome (dolne) stopy:

(

)

2

2

max

l

q

g

M

+

=

−

α

α

,

Zbrojenie zwymiarować, przy przyjęciu:

d = h

f

– a

1

l

d

a

1

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 13/24

b)

zbrojenie pionowe kielicha stopy:

(

)

yd

s

f

e

M

M

A

⋅

=

2

1

,

max

c)

zbrojenie poziome kielicha stopy –
zbrojenie w postaci zamkniętych
ramek obwodowych,
skoncentrowanych zwłaszcza w
górnej części kielicha:

k

M

k

M

h

M

H

M

h

H

2

3

3

2

=

→

=

⋅

Q

H

H

M

+

=

,

gdzie: Q -siła poprzeczna (z obliczeń
statycznych)

yd

s

f

H

A

2

=

wymiarowane zbrojenie

h

k

2
3

h

k

H

M

M

H

M

Ogólne zasady zbrojenia słupów

PN-EN 1992-1-1:2008
9.5 Słupy

Zbrojenie podłużne

(1)

Pręty podłużne powinny mieć średnicę nie mniejszą niż

φ

min

..

Uwaga: Wartości

φ

min

do stosowania w kraju mogą być podane w Załączniku krajowym

(

φ

min

= 6 mm). Wartością zalecaną jest 8 mm.

(2)

Minimalne pole przekroju całego zbrojenia podłużnego nie powinno być mniejsze niż

A

s,min

.

Uwaga: Wartości A

s,min

do stosowania w kraju mogą być podane w Załączniku krajowym.

Wartość zalecaną określa wzór

yd

Ed

s

f

N

A

10

,

0

min

,

=

, lecz nie mniej niż 0,002

A

c

(9.12N)

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 14/24

w którym:

f

yd

jest obliczeniową granicą plastyczności zbrojenia,

N

Ed

jest obliczeniową ściskającą siłą podłużną.

(3)

Pole przekroju zbrojenia podłużnego nie powinno być większe niż A

s,max

.

Uwaga: Wartość A

s,max

do stosowania w kraju może być podana w Załączniku krajowym.

Wartością zalecaną poza obszarami połączeń na zakład jest 0,04A

c

(jeśli można wykazać, że

nie wpłynie to negatywnie na zagęszczenie betonu i że w ULS wytrzymałość betonu będzie w
pełni osiągnięta, to granicę tę można przekroczyć). W obszarach, w których występują
zakłady, granicę tę można zwiększyć do 0,08A

c

.

(4)

W słupach o przekrojach wielokątnych należy w każdym narożu umieścić co najmniej

jeden pręt. Liczba prętów podłużnych w słupie o przekroju kołowym nie powinna być
mniejsza od czterech.

Zbrojenie poprzeczne

(1)

Ś

rednica zbrojenia poprzecznego (strzemion, pętli lub uzwojenia) nie powinna być

mniejsza od 6 mm i od jednej czwartej maksymalnej średnicy prętów podłużnych, a średnica
drutów zbrojenia poprzecznego z siatek spajanych nie powinna być mniejsza niż 5 mm.

(2)

Zbrojenie poprzeczne powinno być odpowiednio zakotwione.

(3)

Rozstaw zbrojenia poprzecznego wzdłuż słupa nie powinien przekraczać s

cl,tmax

.

Uwaga: Wartość s

cl,tmax

do stosowania w kraju może być podana w Załączniku krajowym.

Wartością zalecaną jest najmniejsza z trzech następujących odległości:

- 20 minimalnych średnic zbrojenia podłużnego,
- mniejszy wymiar słupa,
- 400 mm.

(4)

Maksymalny odstęp wymagany w (3) należy zmniejszyć do poziomu 0,6s

cl,tmax

:

(I) na odcinkach równych większemu wymiarowi przekroju poprzecznego słupa

powyżej i poniżej połączonej ze słupem belki lub płyty;

(II) w pobliżu połączeń na zakład, gdy maksymalna średnica prętów podłużnych jest

większa niż 14 mm, na długości zakładu należy umieścić co najmniej
trzy równomiernie rozmieszczone pręty poprzeczne.

(5) Jeżeli zmienia się kierunek prętów podłużnych (np. przy zmianie rozmiaru słupa), to
rozstaw zbrojenia poprzecznego należy obliczyć, biorąc pod uwagę siły poziome pojawiające
się w miejscu załamania. Jeżeli kąt zmiany kierunku nie przekracza 1/12, to wpływ załamania
można pominąć.

(6)

Każdy pręt podłużny (lub wiązka prętów) umieszczony w narożu powinien być

trzymany przez zbrojenie poprzeczne. śaden pręt w strefie ściskanej nie powinien być
umieszczony w odległości większej niż 150 mm od pręta trzymanego.

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 15/24

Obliczenia wsporników krótkich
Kształtowanie

Wysokość h w miejscu połączenia ze słupem lub ścianą należy określać ze względu na
ś

cinanie.

PN-EN 1992-1-1:2008
6.2.2 Elementy nie wymagające obliczania zbrojenia na ścinanie

(1)

Wartość obliczeniową nośności na ścinanie V

Rd,c

określają wzory (6.2a) i (6.2.b):

(

)

d

b

k

f

k

C

V

w

cp

ck

l

c

Rd

c

Rd









+

=

σ

ρ

1

3

1

,

,

100

(6.2.a)

lecz nie mniej niż

(

)

d

b

k

v

V

w

cp

c

Rd

σ

1

min

,

+

=

(6.2.b)

W powyższych wzorach:

f

ck

jest wytrzymałością charakterystyczną wyrażoną w MPa,

d

k

200

1

+

=

, lecz nie więcej niż 2,0,

d

jest wysokością użyteczną wyrażoną w mm,

d

b

A

w

sl

l

=

ρ

, lecz nie więcej niż 0,02

A

sl

jest polem przekroju zbrojenia rozciąganego, które sięga na odległość
nie mniejszą niż (l

bd

+ d) poza rozważany przekrój (Rysunek 6.3),

b

w

jest najmniejszą szerokością strefy rozciąganej przekroju (mm),

c

Ed

cp

A

N

=

σ

, lecz nie więcej niż 0,2f

cd

(MPa),

N

Ed

jest siłą podłużną (w N) wywołaną przez obciążenie lub sprężenie (przy

ś

ciskaniu N

Ed

> 0). Wpływ odkształceń wymuszonych na N

Ed

można

pominąć.

A

c

jest polem przekroju betonu (mm

2

),

V

Rd,c

jest siłą według wzorów (6.2) (wyrażoną w N).

Uwaga: Wartości C

Rd,c

, v

min

i k

1

do stosowania w kraju mogą być podane w Załączniku

krajowym. Wartościami zalecanymi są C

Rd,c

= 0,18/

γ

C

, k

1

= 0,15, v

min

według wzoru

(6.3N)

2

1

2

3

min

035

,

0

ck

f

k

v

=

…..

(6) Jeżeli na odcinku 0,5d

≤

a

v

≤

2d od krawędzi podpory (albo od osi podpory, gdy stosuje

się podatne łożyska) obciążenie jest przyłożone do górnej powierzchni elementu, to udział
tego obciążenia w sile poprzecznej V

Ed

można pomnożyć przez

β

= a

v

/(2d). To zmniejszenie

siły poprzecznej można stosować przy sprawdzaniu V

Rd,c

według wzoru (6.2a). Zmniejszenie

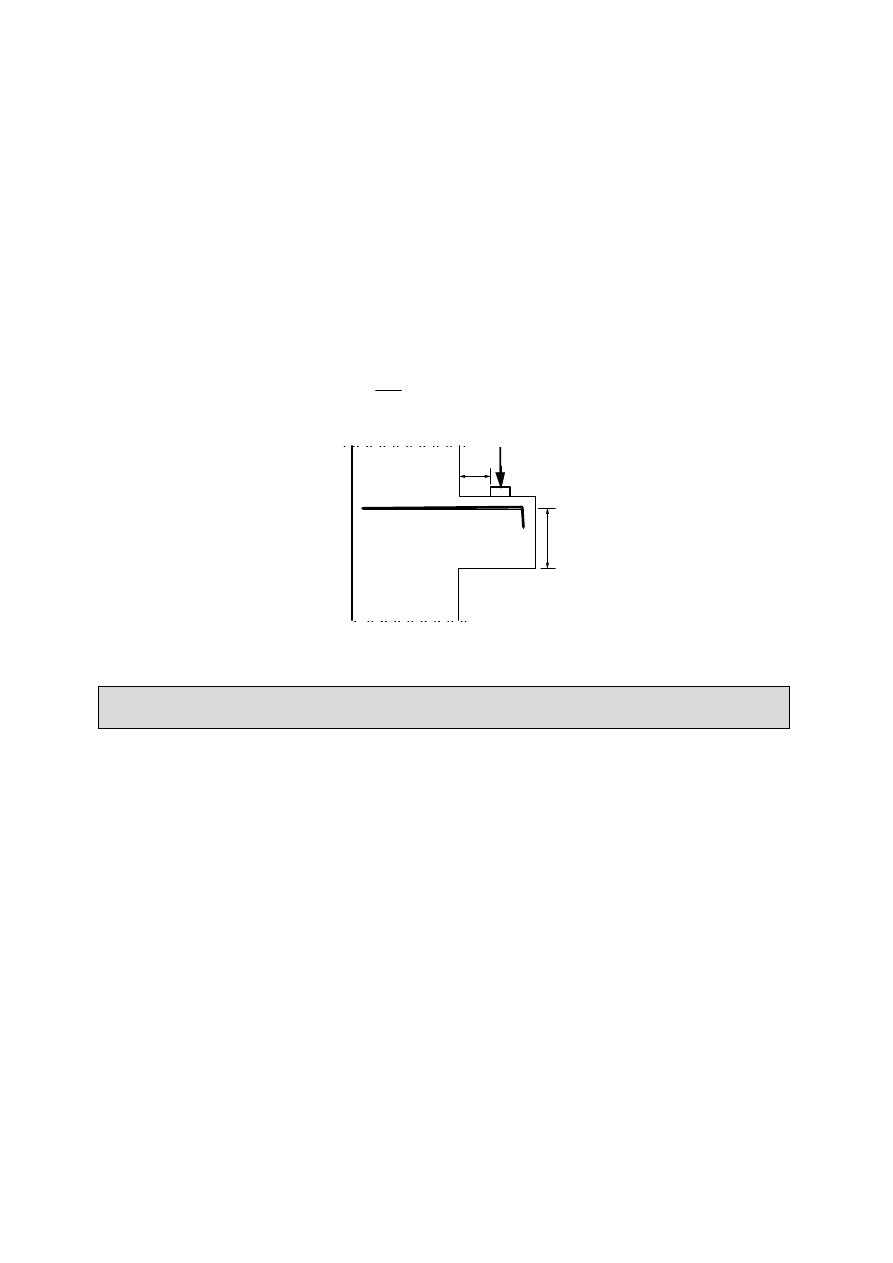
Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 16/24

można stosować tylko wtedy, gdy zbrojenie podłużne jest w pełni zakotwione na podporze.
Jeżeli a

v

≤

0,5d, to powinno się przyjąć a

v

= 0,5d.

Siła poprzeczna V

Ed

, bez zmniejszenia za pomocą współczynnika

β

, powinna jednakże

zawsze spełniać warunek

V

Ed

≤

0,5 b

w

d

v f

cd

(6.5)

w którym:

ν

jest współczynnikiem redukcji wytrzymałości betonu zarysowanego przy

ś

cinaniu.

Uwaga: Wartość v do stosowania w kraju może być określona w Załączniku krajowym.
Wartość zalecana wynika ze wzoru













−

=

250

1

6

,

0

ck

f

ν

(f

ck

w MPa)

(6.6N)

a

v

d

a

v

d

Rysunek 6.4: Obciążenia w pobliżu podpór (krótki wspornik)

PN-EN 1992-1-1:2008
J.3 Krótkie wsporniki

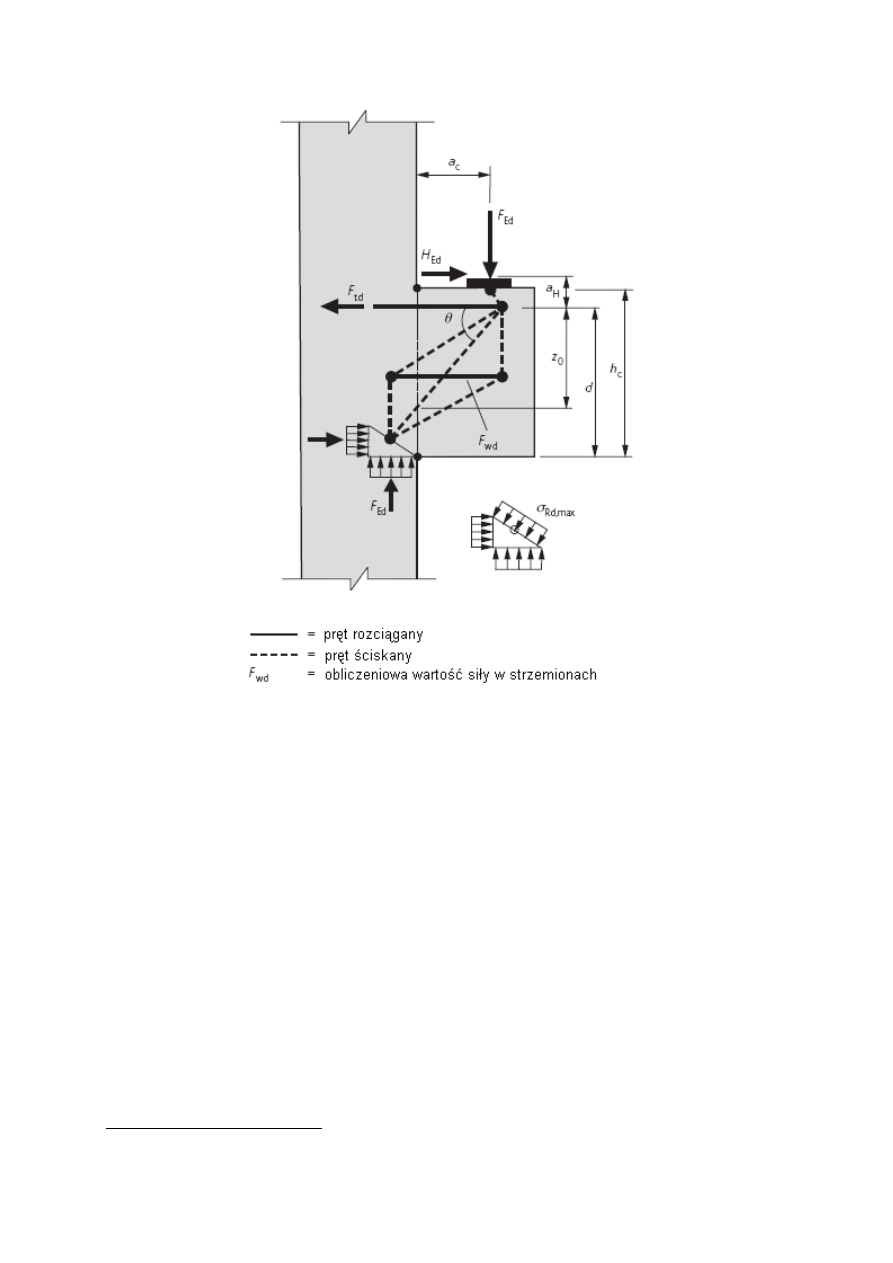
(1)

Krótkie wsporniki (a

c

< z

0

) można obliczać na podstawie modelu ST opisanego w 6.5

(patrz Rysunek J.5). Nachylenie pręta-S powinno spełniać warunek 1,0

≤

tan

θ

≤

2,5.

(2)

Jeżeli a

c

< 0,5h

c

, to jako dodatek do głównego zbrojenia rozciąganego (Rysunek J.6(a))

należy zastosować zamknięte strzemiona poziome lub nachylone o przekroju A

s,lnk

≥

k

1

A

s.main

.

Uwaga: Wartość k

1

do stosowania w kraju może być podana w Załączniku krajowym.

Zalecaną wartością jest 0,25.

(3)

Jeżeli a

c

> 0,5h

c

i F

Ed

> V

Rd,c

, (patrz 6.2.2), to jako dodatek do głównego zbrojenia

rozciąganego (Rysunek J.6(b)) należy zastosować zamknięte strzemiona pionowe o
przekroju A

s,Ink

≥

k

2

F

Ed

/f

yd

.

Uwaga: Wartość k

2

do stosowania w kraju może być podana w Załączniku krajowym.

Zalecaną wartością jest 0,5.

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 17/24

Rysunek J.5: Krótki wspornik - model ST

2

(4)

Główne zbrojenia rozciągane powinno być zakotwione na obydwu końcach. Należy

je zakotwić po dalszej (od wspornika) stronie elementu podpierającego, a długość
zakotwienia należy odmierzać od zbrojenia pionowego umieszczonego przy bliższej
wspornikowi powierzchni bocznej elementu podpierającego (słupa). Zbrojenie należy
zakotwić we wsporniku odmierzając długość zakotwienia od wewnętrznej krawędzi płyty
przekazującej obciążenie.

2

Model kratownicowy krótkiego wspornika

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 18/24

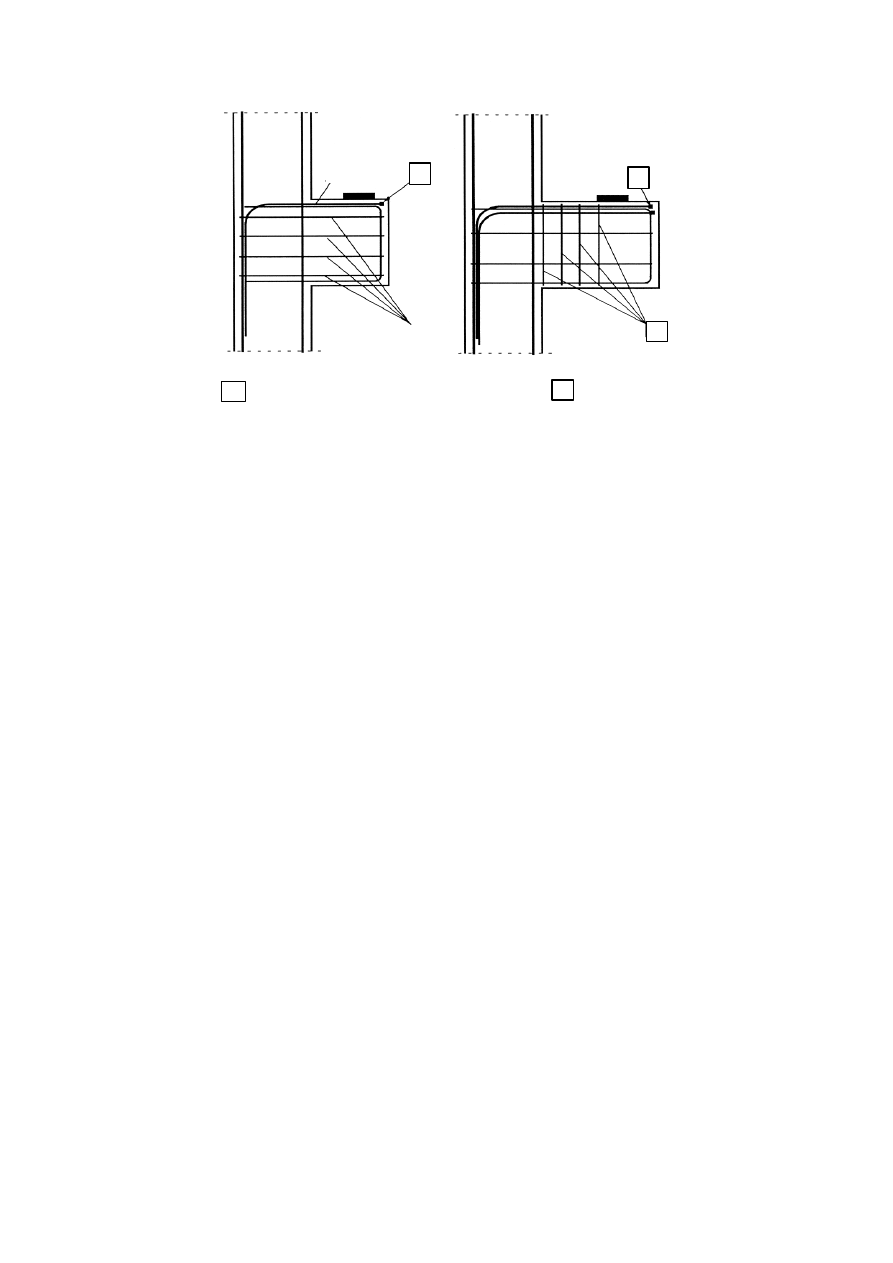
A

s,main

A

s,lnk

≥

k

1

A

s,main

A

A

B

- zakotwienia mechaniczne lub p

ę

tle

A

- strzemiona

B

(a) Zbrojenie przy a

c

≤

0,5h

c

(b) zbrojenie przy a

c

> 0,5h

c

Rysunek J.6: Konstrukcja zbrojenia krótkich wsporników

(5) Jeżeli stawia się szczególne wymagania dotyczące ograniczenia rys, to skuteczne mogą
być ukośne strzemiona.

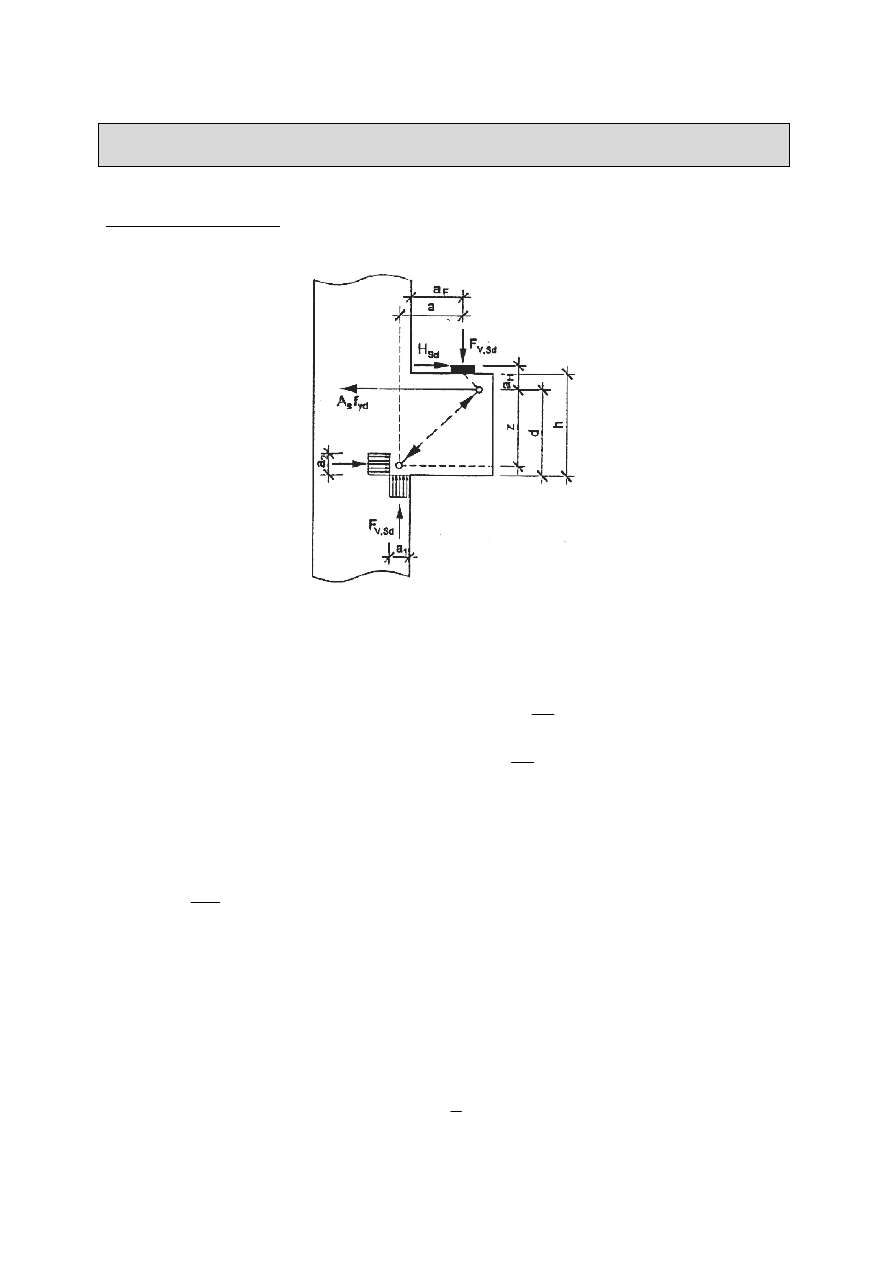
Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 19/24

Dla porównania: PN-B-03264:2002
9.4 Wsporniki krótkie


1. Zasady kształtowania

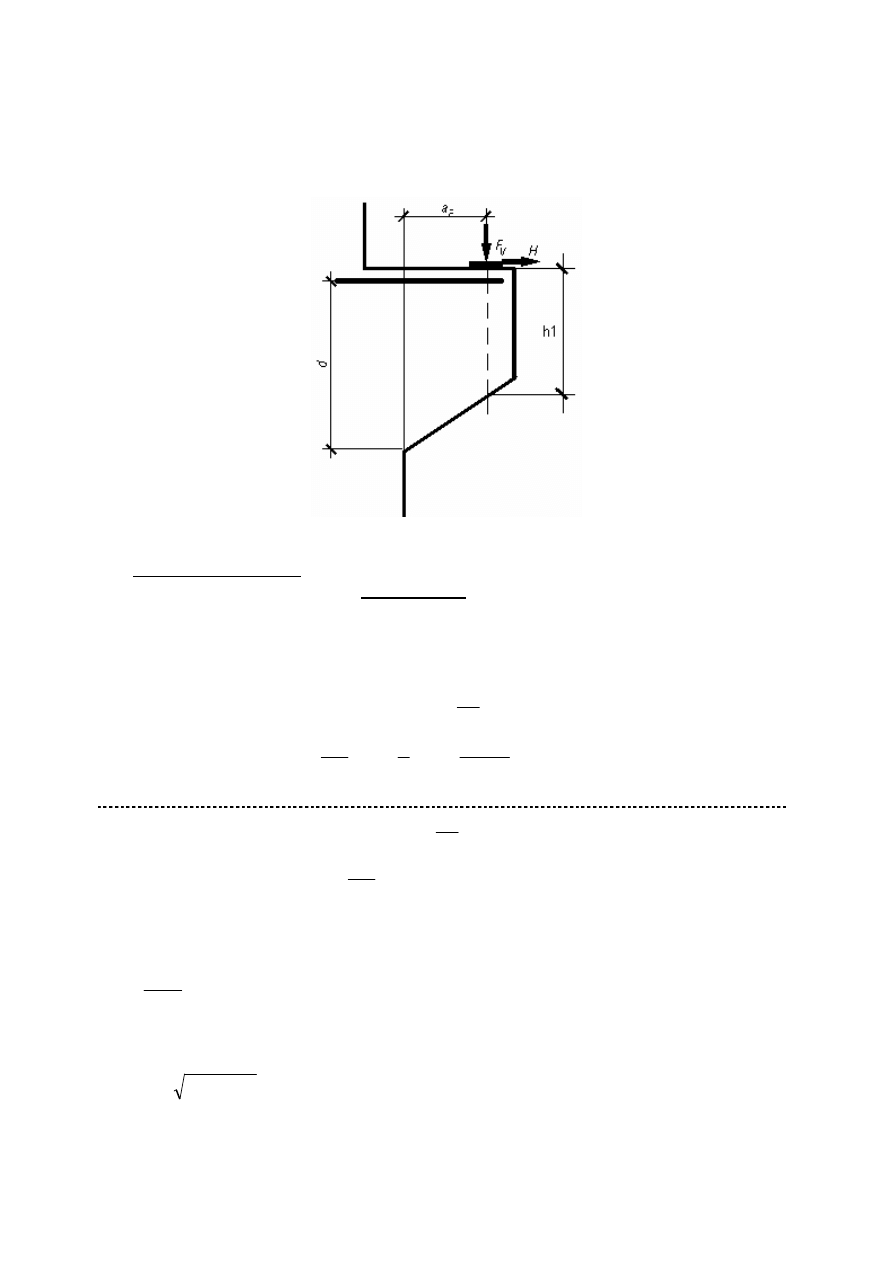
W ćwiczeniu projektowym obciążenie jest przyłożone na górnej krawędzi wspornika, a

więc we wsporniku występuje rozkład sił pokazany na rysunku nr 71, PN-B-03264:2002.

Rys. Obliczeniowy schemat wspornika

Prawidłowo wykształtowany wspornik powinien spełniać następujące warunki:

-

szerokość (wymiar b) równa szerokości słupa lub mniejsza

-

wysokość zapewniająca w przekroju 1-1 nieprzekroczenie warunku ścinania

bd

f

F

F

cd

Rd

V

Sd

V

ν

5

,

0

,

,

=

≤

, jeżeli

0

,

1

3

,

0

≤

<

h

a

F

(215)

bd

f

F

F

cd

Rd

V

Sd

V

ν

4

,

0

,

,

=

≤

, jeżeli

3

,

0

≤

h

a

F

(216)

gdzie:

Sd

V

F

,

- siła pionowa obliczeniowa; dla belek podsuwnicowych obliczeniowa reakcja

belki, wyznaczona z uwzględnieniem współczynnika dynamicznego według
PN-86/B-02005,













−

=

250

1

6

,

0

ck

f

ν

,

b

- szerokość wspornika w przekroju przysłupowym,

d

- wysokość użyteczna wspornika w przekroju przysłupowym,

cd

f

– obliczeniowa wytrzymałość betonu na ściskanie przy

85

,

0

=

cc

α

,

F

a

- odległość od osi siły obciążającej do lica słupa,

h

- całkowita wysokość wspornika.

-

wysokość wspornika w osi przyłożenia obciążenia nie mniejsza od połowy wysokości
przekroju podporowego:

d

h

2

1

1

≥

-

kąt nachylenia dolnej krawędzi wspornika do poziomu nie większy od 45

0

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 20/24

°

≤

45

β

-

wartość

F

a

dla wspornika trapezowego w słupie dwugałęziowym, przy gałęzi dolnej

szerszej od gałęzi górnej, należy przyjmować według rysunku

-

2. Obliczanie zbrojenia
a)

Przypadek siły przyłożonej na wsporniku (przy obciążeniu górnej krawędzi siłą
pionową F

V,Sd

i poziomą H

Sd

- jak w ćwiczeniu projektowym) – patrz rys. 71 według

PN-B-03264.

-

zbrojenie główne:

jeżeli:

0

,

1

3

,

0

≤

<

h

a

F













+

+

≥

z

z

a

H

z

a

F

f

A

H

Sd

Sd

V

yd

s

,

1

(wzór 218)

jeżeli:

3

,

0

≤

h

a

F

(

)

Sd

Sd

V

yd

s

H

F

f

A

+

≥

,

5

,

0

1

(wzór 220)

s

A - przekrój zbrojenia głównego,

yd

f

- obliczeniowa granica plastyczności stali zbrojenia głównego,

b

f

F

a

cd

Sd

V

,

1

=

, przy czym

cd

f

– obliczeniowa wytrzymałość betonu na ściskanie

przy

85

,

0

=

cc

α

,

1

5

,

0 a

a

a

F

+

=

,

a

a

d

d

a

1

2

2

2

−

−

=

,

2

5

,

0 a

d

z

−

=

,

Sd

V

F

,

- siła pionowa obliczeniowa; dla belek podsuwnicowych obliczeniowa reakcja

Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 21/24

belki, wyznaczona z uwzględnieniem współczynnika dynamicznego według
PN-86/B-02005,

Sd

H

- obliczeniowa siła pozioma, wyznaczona według PN-86/B-02005, z zachowaniem

warunku:

Sd

V

Sd

F

H

,

2

,

0

≥

,

H

a

- według rysunku nr 71, PN-B-03264:2002.

-

strzemiona pionowe, jeżeli

6

,

0

>

h

a

F

,

Gdy zachodzi:

(

)

bd

a

d

f

k

V

F

F

ck

s

ct

Rd

Sd

V

























=

>

5

,

2

100

12

,

0

3

1

,

,

ρ

(225)

gdzie:

2

2

,

0

1

≤

+

=

d

k

przy czym d - wysokość użyteczna w [m],

bd

A

s

s

=

ρ

- stopień zbrojenia głównego na odcinku

F

a

,

wtedy sumaryczne pole przekroju poprzecznego strzemion pionowych należy określać ze
wzoru:

ywd

Sd

V

v

sw

f

F

A

,

,

7

,

0

≥

(228)

gdzie:

ywd

f

- obliczeniowa granica plastyczności zbrojenia poprzecznego.

Gdy zachodzi:

(

)

bd

a

d

f

k

V

F

F

ck

s

ct

Rd

Sd

V

























=

≤

5

,

2

100

12

,

0

3

1

,

,

ρ

wtedy sumaryczne pole przekroju poprzecznego strzemion pionowych należy określać ze
wzoru:

Sd

V

ywd

v

sw

F

f

z

a

A

,

,

3

1

2

−

≥

(229)

-

strzemiona poziome o przekroju całkowitym

s

h

sw

A

A

3

,

0

,

≥

a ponadto:

jeżeli

6

,

0

3

,

0

≤

<

h

a

F

:

s

h

sw

A

A

5

,

0

,

≥

(230)

jeżeli

3

,

0

≤

h

a

F

:

ywd

Sd

V

h

sw

f

F

A

,

,

5

,

0

≥

(231)

Zbrojenie minimalne wspornika krótkiego

bd

A

A

sw

s

004

,

0

≥

+

b)

Przypadek siły przyłożonej

poniżej górnej krawędzi wspornika – dla rozkładu sił

jak na rysunku:

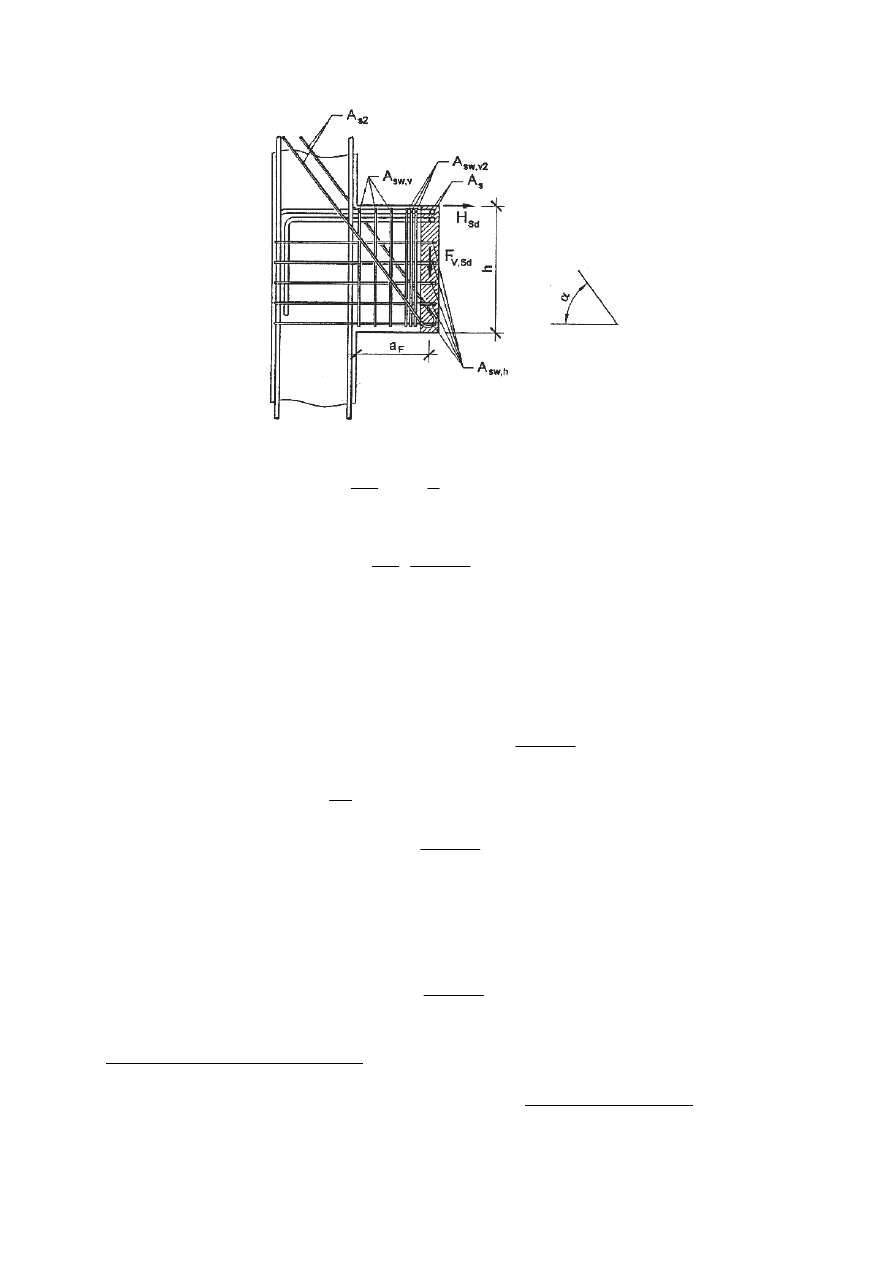
Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 22/24

Rys. Zbrojenie wspornika obciążonego na wysokości

-

zbrojenie główne:













+

≥

Sd

Sd

V

yd

s

H

z

a

F

f

A

,

1

(wzór 232)

-

zbrojenie ukośne (podwieszające):













≥

α

sin

5

,

0

1

,

2

Sd

V

yd

s

F

f

A

(wzór 233)

gdzie:

α

- kąt nachylenia prętów ukośnych do poziomu.

Pręty ukośne należy w sposób pewny zakotwić przy dolnej krawędzi wspornika i w słupie.
Kąt nachylenia zbrojenia ukośnego do poziomu nie może być mniejszy niż 30

o

i nie większy

niż 60

o

. Osie prętów zbrojenia poziomego i ukośnego powinny przecinać się w przekroju

podporowym wspornika.

-

strzemiona poziome o przekroju całkowitym

ywd

Sd

V

h

sw

f

F

A

,

,

5

,

0

≥

,

-

strzemiona pionowe, jeżeli

6

,

0

>

h

a

F

,

ywd

Sd

V

v

sw

f

F

A

,

,

3

,

0

≥

(235)

gdzie:

ywd

f

- obliczeniowa granica plastyczności zbrojenia poprzecznego.

-

dodatkowe strzemiona pionowe podwieszające, w sąsiedztwie belki obciążającej wspornik
o sumarycznym przekroju:

ywd

Sd

V

v

sw

f

F

A

,

2

,

5

,

0

≥

(236)

3. Zasady rozmieszczania zbrojenia

Ś

rednica prętów zbrojenia głównego powinna być

nie większa niż 25mm.

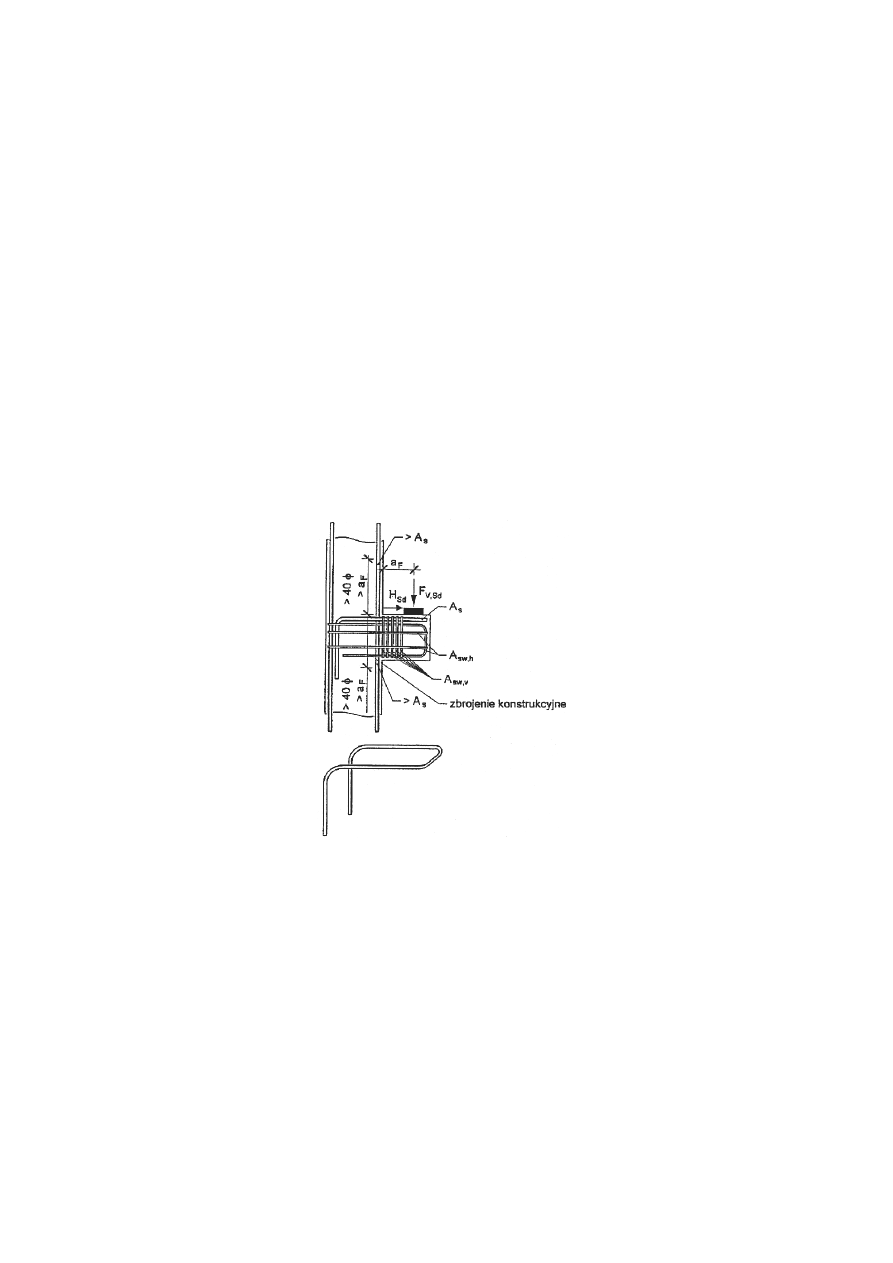
Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 23/24

Kotwienie prętów zgodnie z ogólnymi zasadami, przy czym dla prawidłowego

zakotwienia zaleca się wykonanie zbrojenia głównego w postaci pętli przy zachowaniu
ś

rednic zagięcia prętów według punktu 8.1.1.3 (PN-B-03264:2002).

Odległość krawędzi elementu przekazującego obciążenie (np. krawędź podkładki z

blachy pod belką podsuwnicową) od początku łuku pętli

≥

φ

(średnica prętów zbrojenia

głównego).

Zbrojenie montażowe należy stosować wzdłuż krawędzi górnej, czołowej i dolnej

(ukośnej) wspornika.

Strzemiona poziome należy rozmieścić równomiernie na wysokości wspornika, w

odstępach nie większych niż:













≤

h

mm

s

25

,

0

150

Pionowe zbrojenie słupa usytuowane przy przekroju podporowym wspornika

powinno mieć przekrój

≥

s

A . Ewentualne dodatkowe pręty zbrojenia słupa należy kotwić

poniżej i powyżej osi zbrojenia poziomego wspornika na długości













≥

F

a

φ

40

Graficznie powyższe zalecenia zostały zobrazowane na Rysunkach 72 i 73, na

Stronach 124 i 125; PN-B-03264:2002.

Rys. Zbrojenie wspornika o stosunku a

F

/h > 0,6

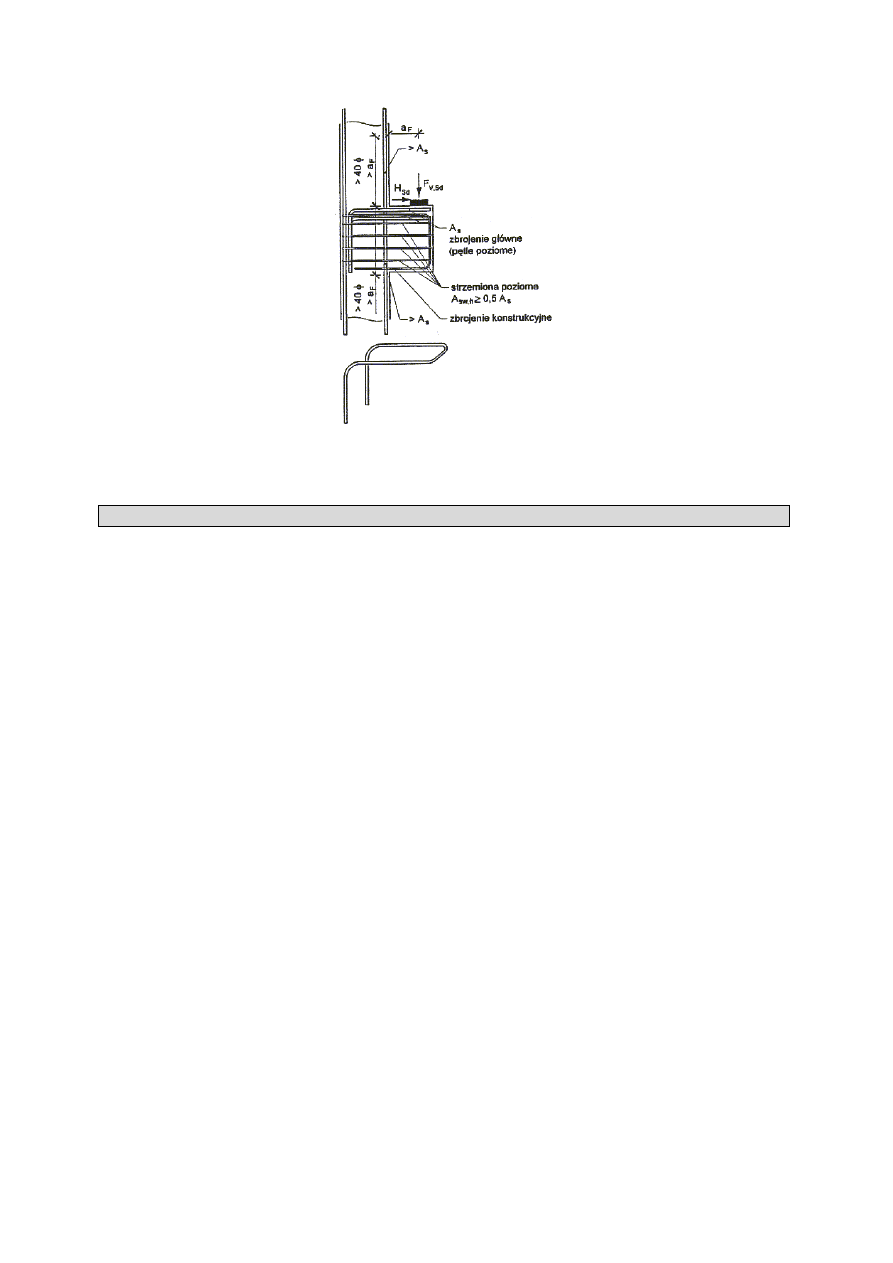
Wymiarowanie wybranych elementów prefabrykowanej hali żelbetowej

KBI sem.V (wer. 2010/2011)

strona 24/24

Rys. Zbrojenie wspornika o stosunku a

F

/h ≤ 0,6

Literatura:

[1] PN-EN 1992-1-1:2008. Eurokod 2: Projektowanie konstrukcji z betonu. Część 1-1:
Reguły ogólne i reguły dla budynków. PKN, wrzesień 2008.
[2] PN-EN 1992-1-2:2008. Eurokod 2: Projektowanie konstrukcji z betonu. Część 1-2:
Reguły ogólne – Projektowanie z uwagi na warunki pożarowe. PKN, maj 2008.
[3] PN-B-03264:2002. Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i
projektowanie.
[4] Ajdukiewicz A.: Eurokod 2. Podręczny skrót dla projektantów konstrukcji żelbetowych.
Stowarzyszenie Producentów Cementu, Kraków 2009.
[5] Podstawy projektowania konstrukcji żelbetowych i sprężonych według Eurokodu 2 (Praca
zbiorowa pod redakcją M. Knauffa). Sekcja Konstrukcji Betonowych KILiW PAN.
Dolnośląskie Wydawnictwo Edukacyjne, Wrocław 2006.
[6] Starosolski W.: Konstrukcje żelbetowe. Tomy 1-3. Wyd. X. Wydawnictwo Naukowe
PWN, Warszawa 2007.