www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
P
RÓBNY
E
GZAMIN
M
ATURALNY
Z
M
ATEMATYKI
POZIOM PODSTAWOWY
7
MARCA
2008
C
ZAS PRACY
: 120
MINUT
Z
ADANIE
1
(6
PKT
.)
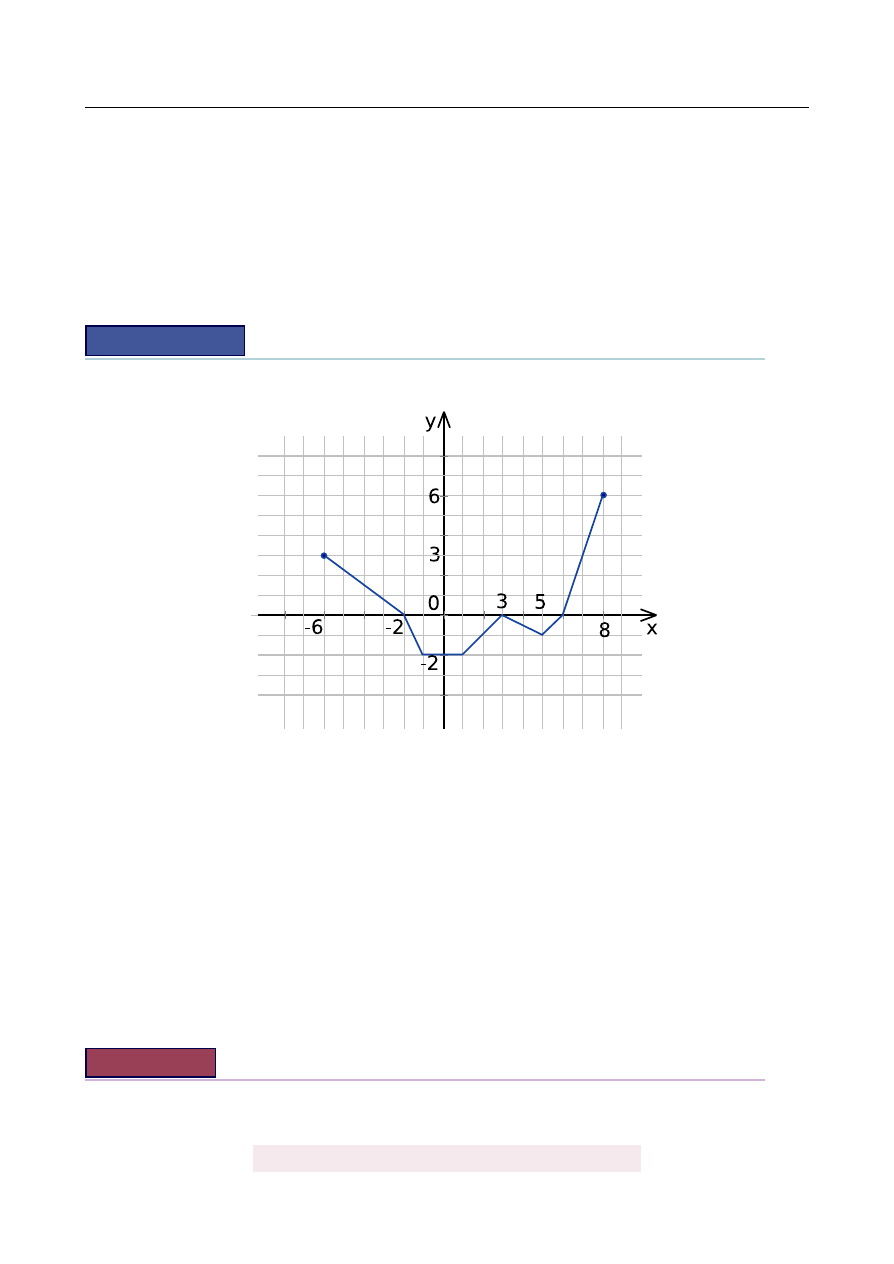
Na rysunku jest przedstawiony wykres funkcji f .
a) Podaj dziedzin˛e funkcji f .
b) Podaj wszystkie miejsca zerowe funkcji f .
c) Odczytaj warto´s´c funkcji f dla argumentu x
=
5.
d) Podaj zbiór warto´sci funkcji f .
e) Podaj maksymalny przedział o długo´sci 3, w którym funkcja f jest rosn ˛
aca.
f) Zapisz w postaci sumy przedziałów zbiór wszystkich argumentów, dla których funk-
cja f przyjmuje warto´sci ujemne.
R
OZWI ˛
AZANIE
a) Dziedzina:
h−
6, 8
i
.
Materiał pobrany z serwisu
1
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
b) Miejsca zerowe:
−
2, 3, 6.
c) f
(
5
) = −
1.
d) Zbiór warto´sci:
h−
2, 6
i
.
e) Przedział
h
5, 8
i
.
f) Zbiór
(−
2, 3
) ∪ (
3, 6
)
.
Z
ADANIE
2
(5
PKT
.)
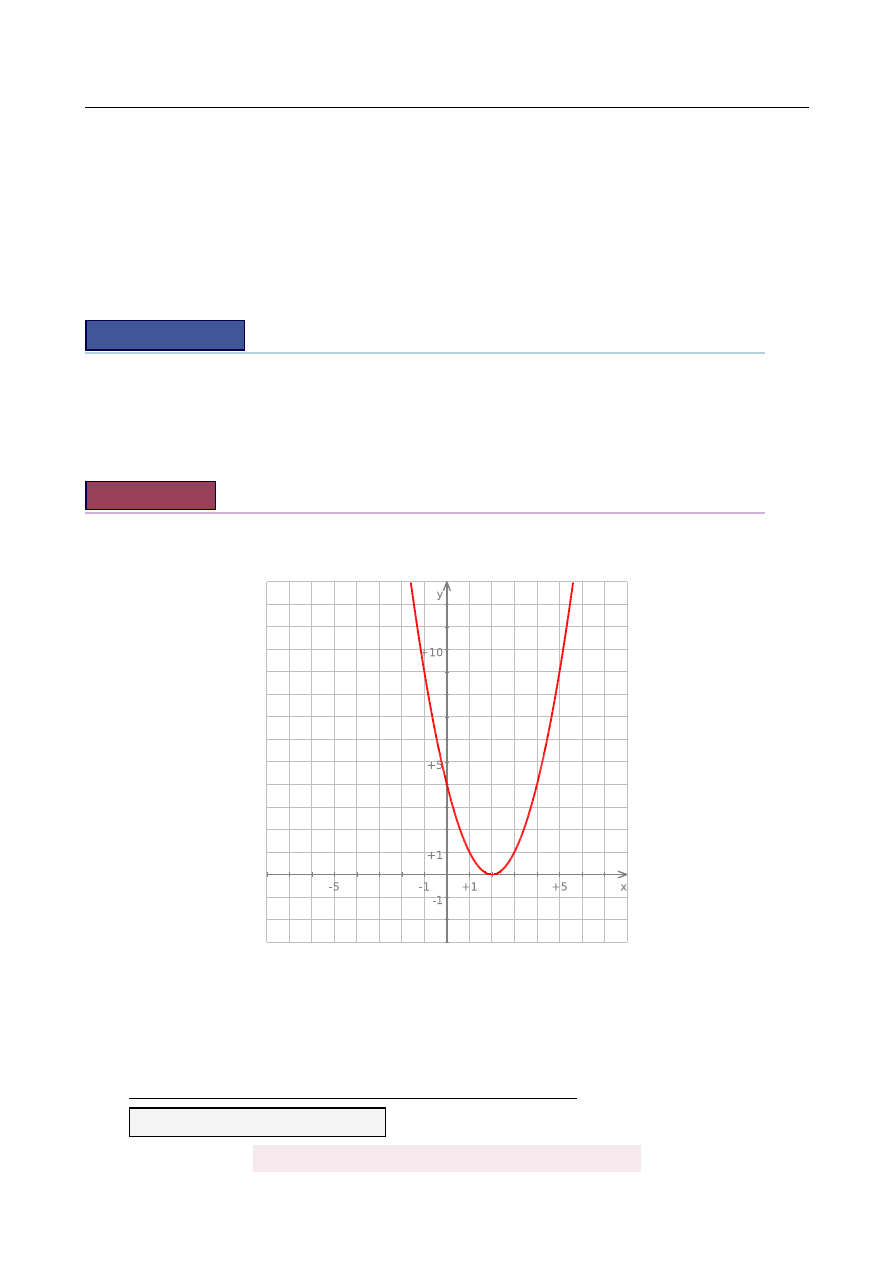
Funkcja kwadratowa f jest okre´slona wzorem f
(
x
) = (
2
−
x
)
2
.
a) Wyznacz najmniejsz ˛
a i najwi˛eksz ˛
a warto´s´c funkcji f w przedziale
h
0, 5
i
.
b) Rozwi ˛
a ˙z nierówno´s´c f
(
x
) − (
2
−
x
) >
0.
R
OZWI ˛
AZANIE
Poniewa ˙z f
(
x
) = (
2
−
x
)
2
= (
x
−
2
)
2
, to wykresem tej funkcji jest parabola z ramionami
skierowanymi do góry, styczna do osi Ox w punkcie 2.
a) Poniewa ˙z wierzchołek paraboli jest w danym przedziale, to wła´snie w nim jest naj-
mniejsza warto´s´c f
(
2
) =
0.
Ze wzgl˛edu na kształt wykresu, najwi˛eksza warto´s´c jest w jednym z ko ´nców przedzia-
łu. Łatwo sprawdzi´c, ˙ze f
(
5
) =
9
>
f
(
0
) =
4.
Odpowied´z: f
min
=
0, f
max
=
9
Materiał pobrany z serwisu
2

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
b) Przekształ´cmy podan ˛
a nierówno´s´c
(
2
−
x
)
2
− (
2
−
x
) >
0
(
2
−
x
)((
2
−
x
) −
1
) >
0
(
2
−
x
)(
1
−
x
) >
0
(−
1
)(
x
−
2
)(−
1
)(
x
−
1
) >
0
(
x
−
2
)(
x
−
1
) >
0.
Nierówno´s´c, któr ˛
a otrzymali´smy to najwyklejsza nierówno´s´c kwadratowa, jej rozwi ˛
a-
zaniem jest zbiór
(−
∞, 1
i ∪ h
2,
∞
)
(oba czynniki maj ˛
a by´c nieujemne lub oba niedodat-
nie).
Odpowied´z:
(−
∞, 1
i ∪ h
2,
∞
)
Z
ADANIE
3
(4
PKT
.)
Suma dwóch liczb jest równa
√
7, a ich ró ˙znica
√
3 . Oblicz iloczyn tych liczb.
R
OZWI ˛
AZANIE
I sposób
Mamy układ równa ´n
(
x
+
y
=
√
7
x
−
y
=
√
3.
Dodaj ˛
ac do pierwszego równania drugie ( ˙zeby skróci´c y), dostajemy 2x
=
√
7
+
√
3, czyli
x
=
√
7
+
√
3
2
.
Podobnie, jak odejmiemy od pierwszego równania drugie ( ˙zeby skróci´c x), dostajemy
x
=
√
7
−
√
3
2
.
Obliczamy st ˛
ad
xy
=
√
7
+
√
3
2
·
√
7
−
√
3
2
=
=
1
4
(
√
7
+
√
3
)(
√
7
−
√
3
) =
1
4
((
√
7
)
2
− (
√
3
)
2
) =
1
4
(
7
−
3
) =
1.
II sposób
Mo ˙zna te ˙z to zadanie zrobi´c szybciej, korzystaj ˛
ac ze sztuczki:
(
x
+
y
)
2
− (
x
−
y
)
2
=
4xy.
Mamy st ˛
ad
4xy
= (
√
7
)
2
− (
√
3
)
2
=
4.
Czyli jak poprzednio xy
=
1.
Odpowied´z: 1
Materiał pobrany z serwisu
3
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
4
(4
PKT
.)
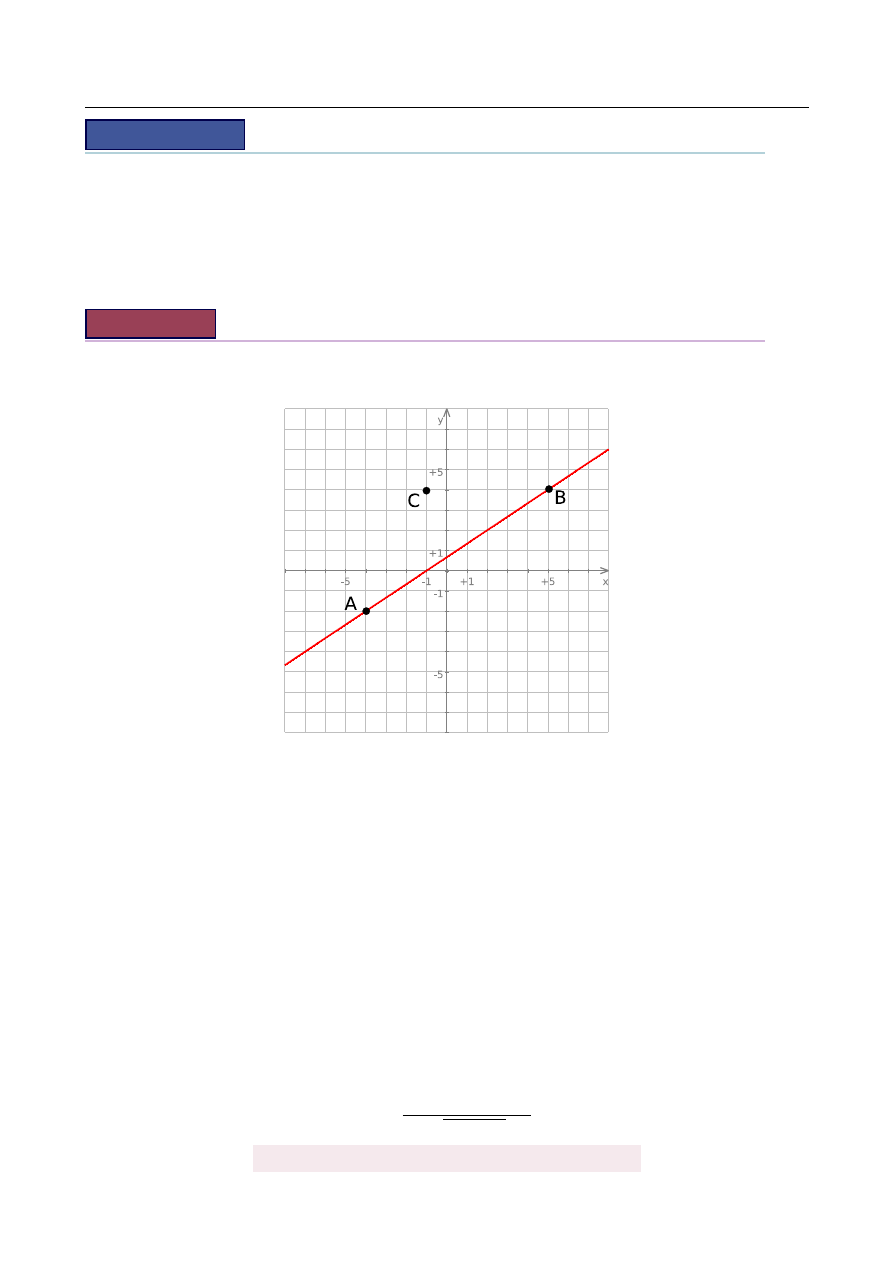
W układzie współrz˛ednych s ˛
a dane punkty A
= (−
4,
−
2
)
, B
= (
5, 4
)
.
a) Oblicz odległo´s´c punktu C
= (−
1, 4
)
od prostej przechodz ˛
acej przez punkty A i B.
b) Uzasadnij, ˙ze je´sli m
6=
0, to punkty A, B oraz punkt D
= (−
1, m
)
s ˛
a wierzchołkami
trójk ˛
ata.
R
OZWI ˛
AZANIE
a) Zacznijmy od rysunku. Aby móc skorzysta´c ze wzoru na odległo´s´c punktu od prostej
musimy mie´c równanie prostej AB. Korzystamy ze wzoru na równanie prostej przez
dwa punkty A
= (
x
A
, y
A
)
i B
= (
x
B
, y
B
)
:
(
y
−
y
A
)(
x
B
−
x
A
) − (
y
B
−
y
A
)(
x
−
x
A
) =
0.
W naszej sytuacji:
(
y
− (−
2
))(
5
− (−
4
)) − (
4
− (−
2
))(
x
− (−
4
))) =
0
(
y
+
2
)
9
−
6
(
x
+
4
) =
0
9y
−
6x
−
6
=
0
3y
−
2x
−
2
=
0
2x
−
3y
+
2
=
0.
Teraz korzystamy ze wzoru na odległo´s´c punktu P
= (
x
0
, y
0
)
od prostej Ax
+
By
+
C
=
0:
|
Ax
0
+
By
0
+
C
|
√
A
2
+
B
2
.
Materiał pobrany z serwisu
4
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
W naszej sytuacji mamy:
|
2
· (−
1
) −
3
·
4
+
2
|
√
9
+
4
=
| −
2
−
12
+
2
|
√
13
=
=
12
√
13
=
12
√
13
13
.
Odpowied´z:
12
√
13
13
b) Co to znaczy, ˙ze 3 punkty s ˛
a wierzchołkami trójk ˛
ata? – to znaczy, ˙ze nie le ˙z ˛
a na jed-
nej prostej. Musimy zatem sprawdzi´c, ˙ze punkt D
= (−
1, m
)
nie le ˙zy na prostej AB.
Poniewa ˙z wyliczyli´smy ju ˙z równanie tej prostej, nie ma z tym problemu (wstawiamy
współrz˛edne tego punktu do równania prostej i patrzymy, ˙ze nie wyjdzie 0):
2
· (−
1
) −
3m
+
2
=
3m
6=
0.
Z
ADANIE
5
(6
PKT
.)
Dany jest wielomian Q
(
x
) =
2x
3
−
3x
2
−
3x
+
d.
a) Liczba 1 jest pierwiastkiem tego wielomianu. Oblicz d.
b) Dla d
=
2 przedstaw wielomian Q w postaci iloczynu wielomianów stopnia pierwsze-
go.
R
OZWI ˛
AZANIE
a) Poniewa ˙z 1 jest pierwiastkiem, to
0
=
Q
(
1
) =
2
−
3
−
3
+
d
= −
4
+
d.
St ˛
ad d
=
4.
Odpowied´z: d
=
4
b) ˙Zeby znale´z´c pierwiastki całkowite (lepiej zacz ˛
a´c od nich zanim spróbujemy z wymier-
nymi), wstawiamy do wielomianu dzielniki wyrazu wolnego, czyli liczby -1,1,-2,2 tak
długo a ˙z dla jakiej´s wyjdzie 0 – wychodzi ju ˙z dla -1 . Jak ju ˙z mamy pierwiastek, to dzie-
limy wielomian przez
(
x
+
1
)
. Robimy to tak jak umiemy, schemat Hornera, dzielenie
Materiał pobrany z serwisu
5
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
wielomianów lub grupowanie odpowiednich czynników. My zrobimy to t ˛
a ostatni ˛
a
metod ˛
a:
2x
3
−
3x
2
−
3x
+
2
=
=
2
(
x
3
+
x
2
) −
2x
2
−
3x
2
−
3x
+
2
=
=
2x
2
(
x
+
1
) −
5x
2
−
3x
+
2
=
=
2x
2
(
x
+
1
) −
5
(
x
2
+
x
) +
5x
−
3x
+
2
=
=
2x
2
(
x
+
1
) −
5x
(
x
+
1
) +
2x
+
2
=
=
2x
2
(
x
+
1
) −
5x
(
x
+
1
) +
2
(
x
+
1
) =
= (
x
+
1
)(
2x
2
−
5x
+
2
)
.
Pozostało teraz rozło ˙zy´c 2x
2
−
5x
+
2. Robimy to standardowo,
∆
=
25
−
16
=
9
=
3
2
.
St ˛
ad
x
1
=
5
−
3
4
=
1
2
x
1
=
5
+
3
4
=
2.
Mamy zatem szukany rozkład
2x
3
−
3x
2
−
3x
+
2
=
2
(
x
+
1
)
x
−
1
2
(
x
−
2
)
.
Odpowied´z: 2
(
x
+
1
)
x
−
1
2
(
x
−
2
)
Z
ADANIE
6
(4
PKT
.)
Rozwi ˛
a ˙z nierówno´s´c
2
32
−
32
2
2
16
+
32
x
>
2
10
−
2
21
. Podaj najmniejsz ˛
a liczb˛e całkowit ˛
a spełniaj ˛
ac ˛
a t˛e
nierówno´s´c.
R
OZWI ˛
AZANIE
Przekształ´cmy podan ˛
a nierówno´s´c
2
32
−
2
10
2
16
+
2
5
x
>
2
10
(
1
−
2
11
)
2
10
(
2
22
−
1
)
2
5
(
2
11
+
1
)
x
>
2
10
(
1
−
2
11
)
/
·
2
5
(
2
11
+
1
)
2
10
(
2
22
−
1
)
x
>
2
5
(
1
−
2
11
)(
2
11
+
1
)
(
2
22
−
1
)
x
>
2
5
(
1
−
2
11
)(
1
+
2
11
)
(
2
22
−
1
)
x
>
2
5
(
1
2
− (
2
11
)
2
)
(
2
22
−
1
)
x
>
2
5
(
1
−
2
22
)
/ :
(
2
22
−
1
)
x
> −
2
5
x
> −
32.
Materiał pobrany z serwisu
6
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Mamy st ˛
ad zbiór rozwi ˛
aza ´n
(−
32,
+
∞
)
. Najmniejsze całkowite rozwi ˛
azanie to oczywi´scie
x
= −
31.
Odpowied´z:
(−
32,
+
∞
)
, -31
Z
ADANIE
7
(4
PKT
.)
Uzasadnij, ˙ze nie istnieje trójk ˛
at prostok ˛
atny, w którym przeciwprostok ˛
atna ma długo´s´c 24,
a k ˛
aty ostre α i β s ˛
a takie, ˙ze cos α
=
3
4
i tg β
=
4
3
.
R
OZWI ˛
AZANIE
Najwa ˙zniejsze przy rozwi ˛
azywaniu tego zadania jest ustalenie dlaczego taki trójk ˛
at miałby
nie istnie´c?
Podane informacje s ˛
a dwóch typów. Funkcje trygonometryczne k ˛
atów zale ˙z ˛
a tylko od
k ˛
atów, a wi˛ec od kształtu trójk ˛
ata, a nie od jego wielko´sci. Innymi słowy, miary k ˛
atów (czy
ich funkcje trygonometryczne) nie maj ˛
a nic do rzeczy z długo´sciami boków (maj ˛
a za to z
ilorazami tych długo´sci). Zatem informacja, ˙ze przeciwprostok ˛
atna ma długo´s´c 24 jest zu-
pełnie bezu ˙zyteczna; je ˙zeli by te warunki z k ˛
atami były ok, to istniałby trójk ˛
at o dowolnej
przeciwprostok ˛
atnej. A jak nie s ˛
a, to niezale ˙znie od przeciwprostok ˛
atnej, takiego trójk ˛
ata
nie ma.
Kolejne pytanie, to dlaczego warunki z k ˛
atami maj ˛
a uniemo ˙zliwia´c istnienie trójk ˛
ata?
Odpowied´z jest bardzo prosta, poniewa ˙z trójk ˛
at ma by´c prostok ˛
atny, to β
=
90
◦
−
α
i tg β
jest jednoznacznie wyznaczony przez cos α (bo sin α mo ˙zemy wyliczy´c z jedynki trygono-
metrycznej). Je ˙zeli trójk ˛
ata ma nie by´c, to widocznie dla podanych liczb si˛e to nie zgadza.
Dobrze, skoro wiemy co mamy zrobi´c, to robimy – wyliczymy tg β z cos α.
sin
2
α
=
1
−
cos
2
α
=
1
−
9
16
=
7
16
.
Poniewa ˙z α jest k ˛
atem ostrym, mamy st ˛
ad sin α
=
√
7
4
. Mo ˙zemy teraz wyliczy´c tg β:
tg β
=
tg
(
90
◦
−
α
) =
ctg α
=
cos α
sin α
=
3
4
√
7
4
=
3
√
7
6=
4
3
.
Skoro si˛e nie zgadza, to trójk ˛
ata nie ma.
Z
ADANIE
8
(6
PKT
.)
Ci ˛
ag arytmetyczny
(
a
n
)
jest okre´slony wzorem a
n
=
1
4
(
3n
+
1
)
dla n
>
1.
a) Sprawd´z, którym wyrazem ci ˛
agu
(
a
n
)
jest liczba 37
3
4
.
b) W´sród pi˛e´cdziesi˛eciu pocz ˛
atkowych wyrazów ci ˛
agu a
n
s ˛
a wyrazy b˛ed ˛
ace liczbami cał-
kowitymi. Oblicz sum˛e wszystkich tych wyrazów.
Materiał pobrany z serwisu
7

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
R
OZWI ˛
AZANIE
a) Musimy rozwi ˛
aza´c równanie
1
4
(
3n
+
1
) =
37
3
4
/
·
4
3n
+
1
=
151
3n
=
150
n
=
50.
Odpowied´z: n
=
50
b) ˙Zeby zobaczy´c o co chodzi, najlepiej wypisa´c kilka pocz ˛
atkowych wyrazów ci ˛
agu:
a
1
=
1
4
·
4, a
2
=
1
4
·
7, a
3
=
1
4
·
10, a
4
=
1
4
·
13, a
5
=
1
4
·
16, a
6
=
1
4
·
19, . . .
Jak si˛e wypisze jeszcze troch˛e to jest jasne, ˙ze wyrazy całkowite, to a
1
, a
5
, a
9
, a
13
, . . ., czyli te
dla których n
=
4k
+
1 (nie b˛edziemy tego robi´c, ale gdyby kto´s chciał uzasadni´c t˛e nasz ˛
a
obserwacj˛e, to trzeba sprawdzi´c, ˙ze dla liczb postaci n
=
4k, n
=
4k
+
2 i n
=
4k
+
3, a
n
nie
wychodzi całkowite – sprawdzenie tego jest do´s´c proste). Musimy zatem obliczy´c sum˛e
S
=
a
1
+
a
5
+
a
9
+
a
13
+ · · · +
a
49
=
=
1
+
4
+
7
+
10
+ · · · +
37.
Poniewa ˙z jest to suma wyrazów ci ˛
agu arytmetycznego (o ró ˙znicy 3), to
S
=
1
+
37
2
·
13
=
247.
Sk ˛
ad wzi˛eli´smy ilo´s´c wyrazów? Jak mówili´smy, indeksy wyrazów s ˛
a postaci 4k
+
1 oraz
pierwszy (czyli a
1
) jest dla k
=
0, a ostatni (a
49
) dla k
=
12. Jest ich zatem 13.
Odpowied´z: S
=
247
Z
ADANIE
9
(4
PKT
.)
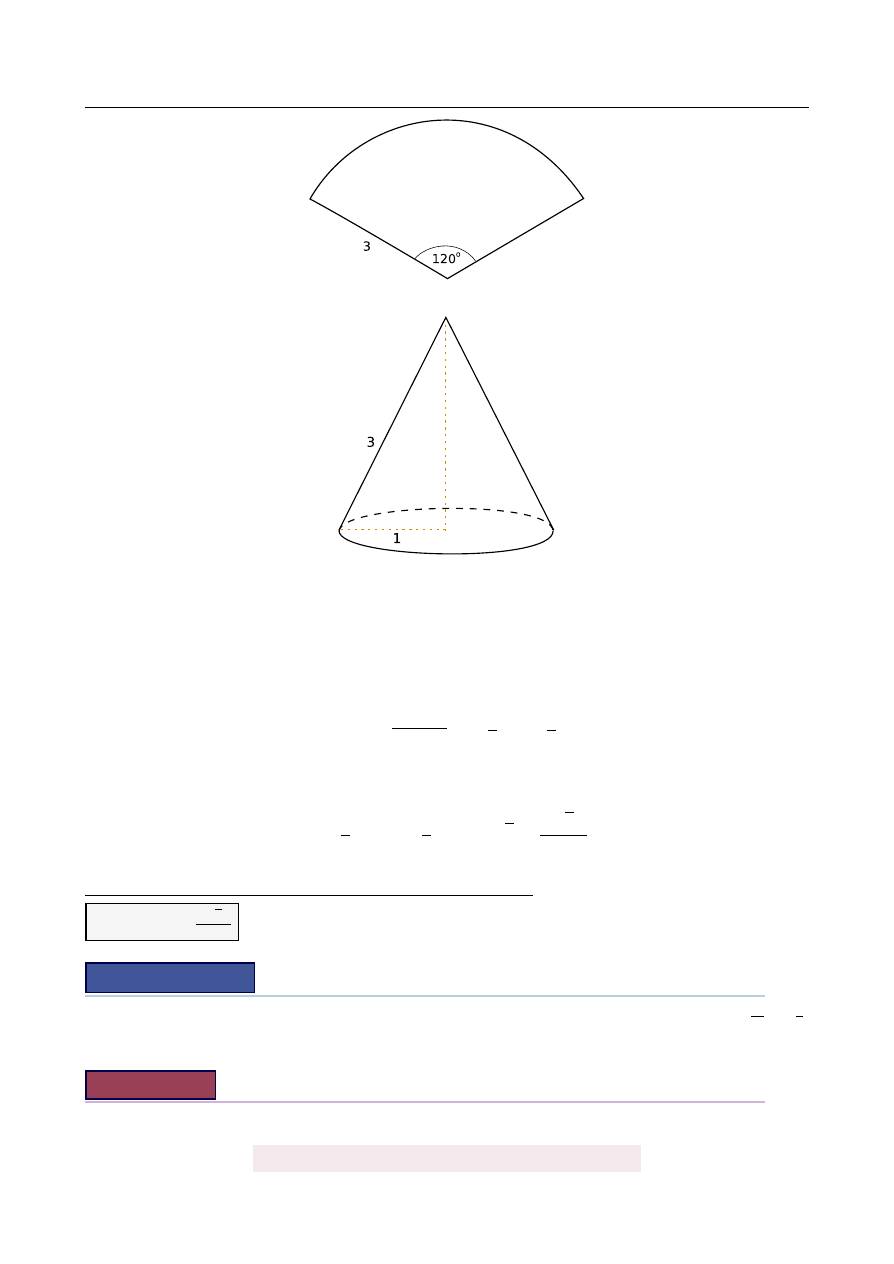
Powierzchnia boczna sto ˙zka po rozwini˛eciu na płaszczyzn˛e jest wycinkiem koła o promie-
niu 3 i k ˛
acie ´srodkowym 120
◦
(zobacz rysunek). Oblicz obj˛eto´s´c tego sto ˙zka.
R
OZWI ˛
AZANIE
Aby obliczy´c obj˛eto´s´c sto ˙zka, potrzebujemy promie ´n podstawy r i wysoko´s´c H. Zauwa ˙zmy,
˙ze długo´s´c łuku podanego wycinka kołowego, to dokładnie długo´s´c okr˛egu w podstawie
sto ˙zka. Pozwoli nam to wyliczy´c promie ´n podstawy:
- długo´s´c łuku odcinka kołowego:
1
3
·
2π
·
3
=
2π,
Materiał pobrany z serwisu
8
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
- długo´s´c okr˛egu w podstawie: 2πr.
Mamy zatem 2πr
=
2π, czyli r
=
1 (równie dobrze mogli´smy wyliczy´c r, korzystaj ˛
ac ze
wzoru na pole powierzchni bocznej sto ˙zka).
Pozostało wyliczy´c H. Robimy to z twierdzenia Pitagorasa (rysunek):
H
=
p
3
2
−
1
2
=
√
8
=
2
√
2.
Korzystamy teraz ze wzoru na obj˛eto´s´c:
V
=
1
3
πr
2
H
=
1
3
π
·
1
·
2
√
2
=
2
√
2π
3
.
Odpowied´z:
2
√
2π
3
Z
ADANIE
10
(4
PKT
.)
W równoległoboku o obwodzie równym 144, wysoko´sci h
1
i h
2
spełniaj ˛
a warunek
h
1
h
2
=
3
5
.
Oblicz długo´sci boków tego równoległoboku.
R
OZWI ˛
AZANIE
Materiał pobrany z serwisu
9

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Zacznijmy od schematycznego rysunku i oznaczmy podstawy na które s ˛
a opuszczone wy-
soko´sci h
1
i h
2
przez a i b odpowiednio. Ze wzoru na pole równoległoboku:
P
=
ah
1
=
bh
2
ah
1
=
bh
2
/ : h
2
a
h
1
h
2
=
b
a
·
3
5
=
b.
Oczywi´scie skorzystali´smy z zało ˙zenia
h
1
h
2
=
3
5
. Wiemy jeszcze, ˙ze 2a
+
2b
=
144. Otrzymu-
jemy st ˛
ad:
2a
+
2
·
a
·
3
5
=
144
a
2
+
2
·
3
5
=
144
16
5
a
=
144
a
=
45.
Ponadto b
=
3
5
a
=
27.
Odpowied´z: 27 i 45
Z
ADANIE
11
(3
PKT
.)
Dane s ˛
a zbiory liczb całkowitych:
{
1, 2, 3, 4, 5
}
i
{
1, 2, 3, 4, 5, 6, 7
}
. Z ka ˙zdego z tych zbiorów
wybieramy losowo po jednej liczbie. Oblicz prawdopodobie ´nstwo, ˙ze suma wylosowanych
liczb b˛edzie podzielna przez 5.
R
OZWI ˛
AZANIE
Wszystkich mo ˙zliwo´sci wylosowania pierwszej liczby jest 5 a drugiej 7, czyli razem 5
·
7
=
35. Łatwo policzy´c, ˙ze zdarze ´n sprzyjaj ˛
acych jest 7:
(
1, 4
)
,
(
2, 3
)
,
(
3, 2
)
,
(
3, 7
)
,
(
4, 1
)
,
(
4, 6
)
,
(
5, 5
)
.
Materiał pobrany z serwisu
10

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Szukane prawdopodobie ´nstwo wynosi zatem
7
35
=
1
5
.
Odpowied´z:
1
5
Materiał pobrany z serwisu
11
Wyszukiwarka
Podobne podstrony:
Zestaw 2 PP rozwiązania
Zestaw 1 PP rozwiązania
Zestaw 2 PP rozwiązania
zestaw 07 rozwiazania
Zestaw1 PR rozwiazania id 58873 Nieznany
2013 02 CEN PP rozwiązania
zestaw 05 rozwiazania
zestaw 06 rozwiazania
zestaw 10 rozwiązania
a6 jezyk polski pp rozwiazania Nieznany (2)
Zestaw 2 PR rozwiązania
2013 05 PP rozwiązania
MJA 1 PP rozwiazania id 303661 Nieznany
zestaw 08 rozwiazania
zestaw 04 rozwiazania
zestaw 03 rozwiazania
2013 05 ED PP rozwiązania
Chemia Ćwiczenia zestawy rozwiązane, Zestaw nr 7 rozwiazany, Zestaw 7
więcej podobnych podstron