Warszawa 08.01.2008r

Łukasz Kucharski
Dominik Czajka

Prowadzący:
Dr inż. Krzysztof Szczypiorski

Projekt z sieci lokalnych

Analiza Aloha i Slotted Aloha

Spis treści

1.Wstęp....................................................................................................................................... 2

1.1 Historia powstania Alohy................................................................................................. 2
1.2 Zasada działania ............................................................................................................... 2
1.3 Aloha a przedmiot LAN................................................................................................... 3

2.Analiza Alohy ......................................................................................................................... 3

2.1 Analiza wydajnościowa Alohy......................................................................................... 3
2.2 Analiza wydajnościowa slotted Alohy............................................................................. 5
2.3 Szczegółowa analiza wydajnościowa slotted Alohy........................................................ 6

2.3.1 Analiza wydajnościowa przy założeniu skończonej liczby stacji............................. 6
2.3.2 Analiza wydajnościowa Alohy z liniowym algorytmem retransmisji ...................... 8

2.4 Opóźnienia ....................................................................................................................... 9

3. Stabilność protokołów Aloha ............................................................................................... 11

3.1 Niestabilność Alohy ....................................................................................................... 11
3.2 Analiza stabilności ......................................................................................................... 12

4. Dynamiczne sterowanie ....................................................................................................... 15
5. Podsumowanie ..................................................................................................................... 16
6. Bibliografia........................................................................................................................... 17

1.Wstęp

1.1 Historia powstania Alohy

Sieć ALOHAnet została opracowana na Uniwersytecie Hawajskim w
roku 1970 przez zespół pod kierownictwem Normana Abramsona, którego na
Hawaje przyciągnęła miłość do surfingu. Chcieli oni za pomocą tanich
radioodbiorników zrealizować sieć komputerową łączącą Uniwersytet z
odległymi Kampusami. Ostatecznie sieć została oparta na systemie transmisji
satelitarnej. Sieć ta, w stronę od użytkowników do huba, została zrealizowana
na protokole Aloha, później na ulepszonej wersji, S-Aloha ( Aloha
szczelinowa ).

1.2 Zasada działania

ALOHAnet jest swego rodzaju siecią o topologii szyny, użytkownicy używają do

transmisji wspólnego medium – fali elektromagnetycznej o tym samym zakresie
częstotliwości. W takim układzie skuteczna transmisja jest możliwa tylko gdy w tym samym
czasie nadaje tylko jedna stacja. W przeciwnym przypadku następuje kolizja i potrzebna jest
retransmisja. Dane ze stacji użytkownika były wysyłane do centralnego komputera – hub-a,
który następnie rozsyłał otrzymane pakiety do wszystkich użytkowników sieci w kanale o
innej częstotliwości.
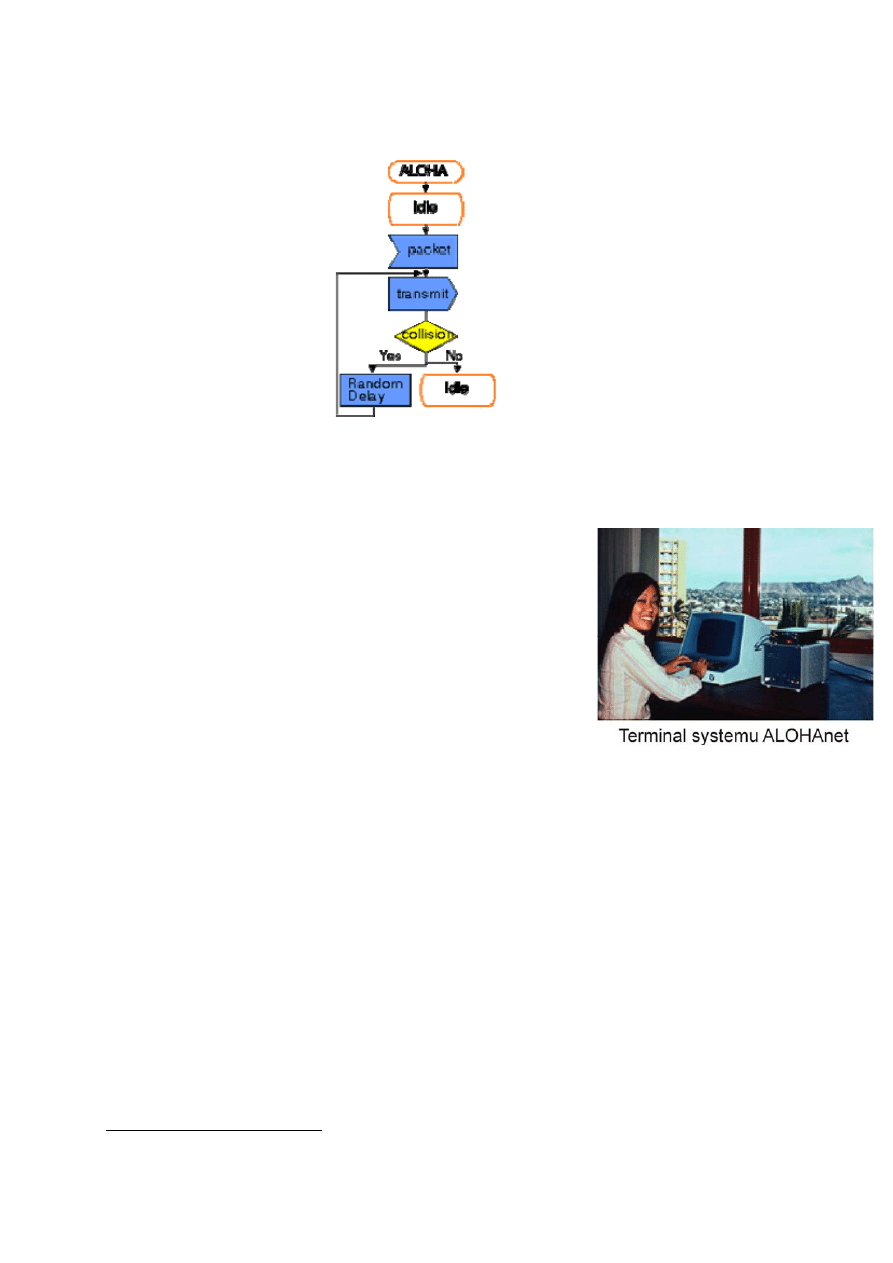
Protokół Aloha, na którym oparto sieć, jest przykładem protokołu o dostępie losowym,
jest protokołem MAC (MediumAccessControl) i należy do warstwy drugiej modelu OSI. Jest
on stosunkowo prosty, obowiązują w nim dwie zasady: jeżeli mamy dane gotowe do wysłania
to po prostu je wysyłamy, jeżeli następuje kolizja to dane retransmitujemy. Protokół nie
posiada ani synchronizacji( w przypadku pure Alohy), ani metody sprawdzania, czy kanał jest
wolny i można wysłać pakiet. W związku z tym jest duże ryzyko wystąpienia kolizji. Pakiety
które uległy kolizji są retransmitowane po czasie określonym przez algorytm retransmisji.
Warto zwrócić uwagę, że ponieważ dane odebrane przez hub są rozgłaszane(wysyłane do
wszystkich), w systemie ALOHAnet nie było potrzeby używania potwierdzeń odebrania
danych(ACK). Stacja stwierdzała, że pakiet został poprawnie odebrany wówczas gdy został

3

on przez nią odebrany. Jednakże, w samym protokole możliwe jest używanie ACK w
przypadku innej realizacji kanału zwrotnego.

1.3 Aloha a przedmiot LAN

Choć protokół Aloha został wymyślony prawie 40lat temu

1

i już od dawna nie opiera się na

nim systemów transmisji danych, to nie można pominąć go przy omawianiu sieci transmisji
danych, gdyż był on pierwszą próbą zapewnienia swobodnej komunikacji pomiędzy wieloma
stacjami roboczymi. Można uznać ją za pierwszą sieć we
współczesnym tego słowa znaczeniu. Sieć ta jako pierwsza
została podpięta do ARPAnetu. Podczas analizy tego protokoły
porusza wiele podstawowych problemów, które dotyczą także
innych protokołów transmisji danych.
Protokół Aloha, znajduje jednak zastosowanie i dziś, jako
składowa innych systemów. Np. w systemie GSM, jako protokół
obsługujący kanał sygnalizacyjny RACCH oraz w protokole
HIPERLAN/2 gdzie dostęp do kanałów RCH odbywa się przy
pomocy protokołu S-ALOHA.

2.Analiza Alohy

2.1 Analiza wydajnościowa Alohy

Załóżmy że dwie stacje robocze chcą wysłać pakiet. Możliwe są wtedy dwie sytuacje:

• pakiety nie nachodzą na siebie – wówczas oba pakiety zostaną pomyślnie przesłane

• pakiety zachodzą na siebie – obie informacje ulegają uszkodzeniu i konieczna jest ich

retransmisja.

1

Stan na 27.12.2007r.

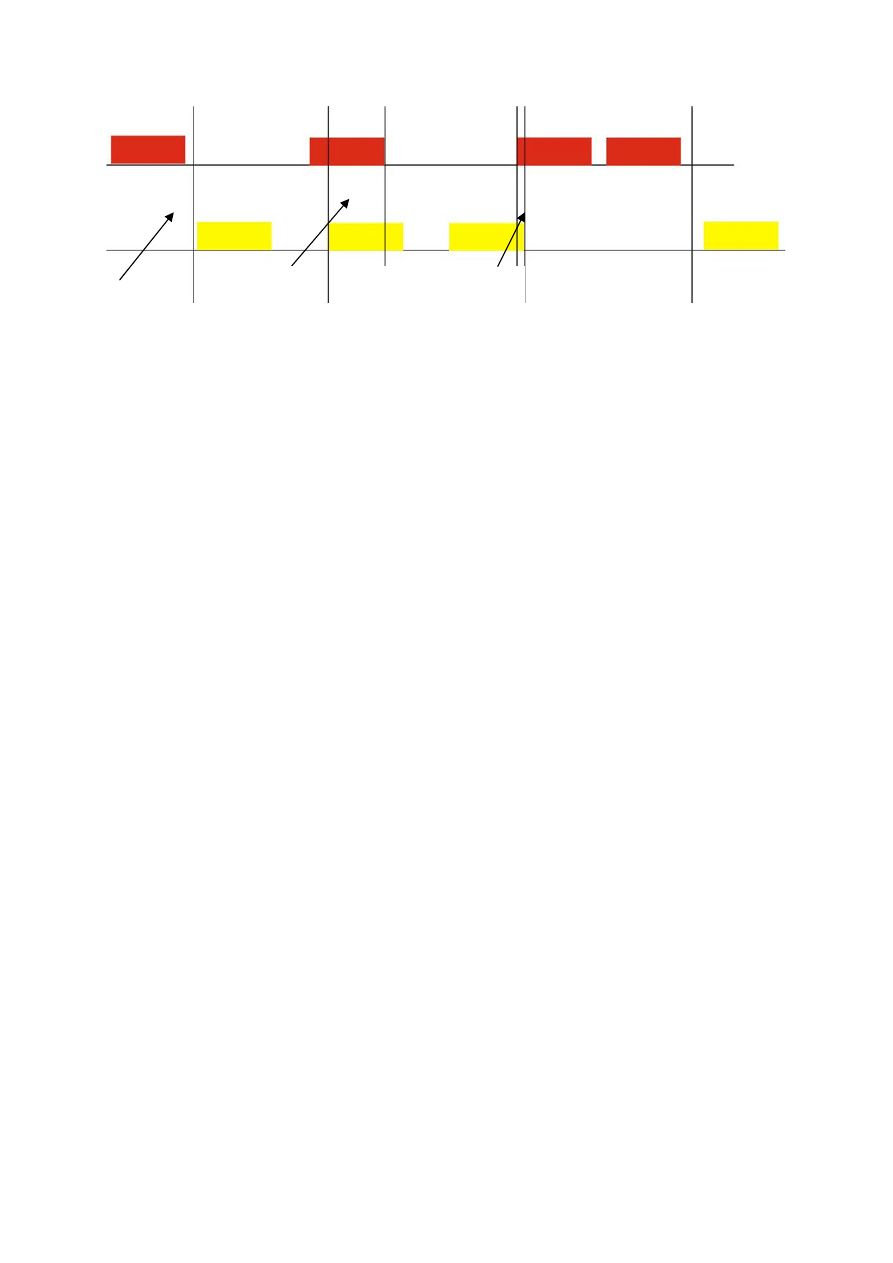
4

Oznaczmy

jako

λ zagregowany ruch ze wszystkich stacji, a jako r ruch pakietów

retransmitowanych. Wówczas poprzez g oznaczymy całkowity ruch w systemie, jako sumę λ
i r. Ponadto zakładamy, że nowe pakiety generowane są zgodnie z rozkładem Poissona, a czas
retransmisji pakietów jest znacznie dłuższy niż czas ich trwania. Wówczas ruch ramek
retransmitowanych ma również rozkład Poissonowski, niezależny od rozkładu ruchu nowych
ramek. Ponadto, aby założenie co do Poissonowskiego rozkładu napływu pakietów było
słuszne należy założyć że liczba użytkowników jest nieskończona( w praktyce okazuje się że
liczba ta nie musi być nieskończona a jedynie bardzo duża).
Poprzez T oznaczmy długość pakietu (gdzie T=L/R, gdzie L długość pakietu a R pojemność
kanału), wówczas wszystkie pakiety transmitowane w czasie pomiędzy t - T a t + T kolidują z
pakietem wysłanym w czasie t. Obliczmy prawdopodobieństwo, że w tym czasie zostanie
wysłane n pakietów:

P(X=n) = (2T

·g)

n

e

-2T ·g

/n!

Aby zagwarantować, że pakiet zostanie przesłany prawidłowo w czasie 2T nie może być
wysyłany żaden inny pakiet. Prawdopodobieństwo udanej transmisji wynosi:

P

succ

= P(X=0) = (2T

·g)

0

e

-2T ·g

/0! = e

-2T ·g

Wydajnością (przepustowością) systemu nazwiemy czas w którym w kanale pakiety są
transmitowane prawidłowo:

S = g·T· P

succ

= gT e

-2T ·g

Zdefiniujmy średni znormalizowany całkowity ruch oferowany w kanale, G, jako G = gT,
wówczas otrzymamy zależność przepustowości od ruchu oferowanego ruchu wejściowego:

S = G e

-2G

Obliczając pochodną i przyrównując do zera, otrzymujemy, że maksymalna przepustowość
Alohy, S wynosi 1/2e = 0.18 dla ruchu oferowanego G równego 0,5. Jeżeli G jest mniejsze
niż 0,5 to większość stacji jest w stanie Idle ( nie wysyłają pakietów ), natomiast gdy G
wzrośnie powyżej 0,5 to w systemie pojawi się więcej kolizji. W obu tych przypadkach
przepustowość maleje.

Pakiety zachodzą
tylko kawałkiem

pakiety nie
zachodzą na siebie

Pakiety
zachodzą na
siebie

5

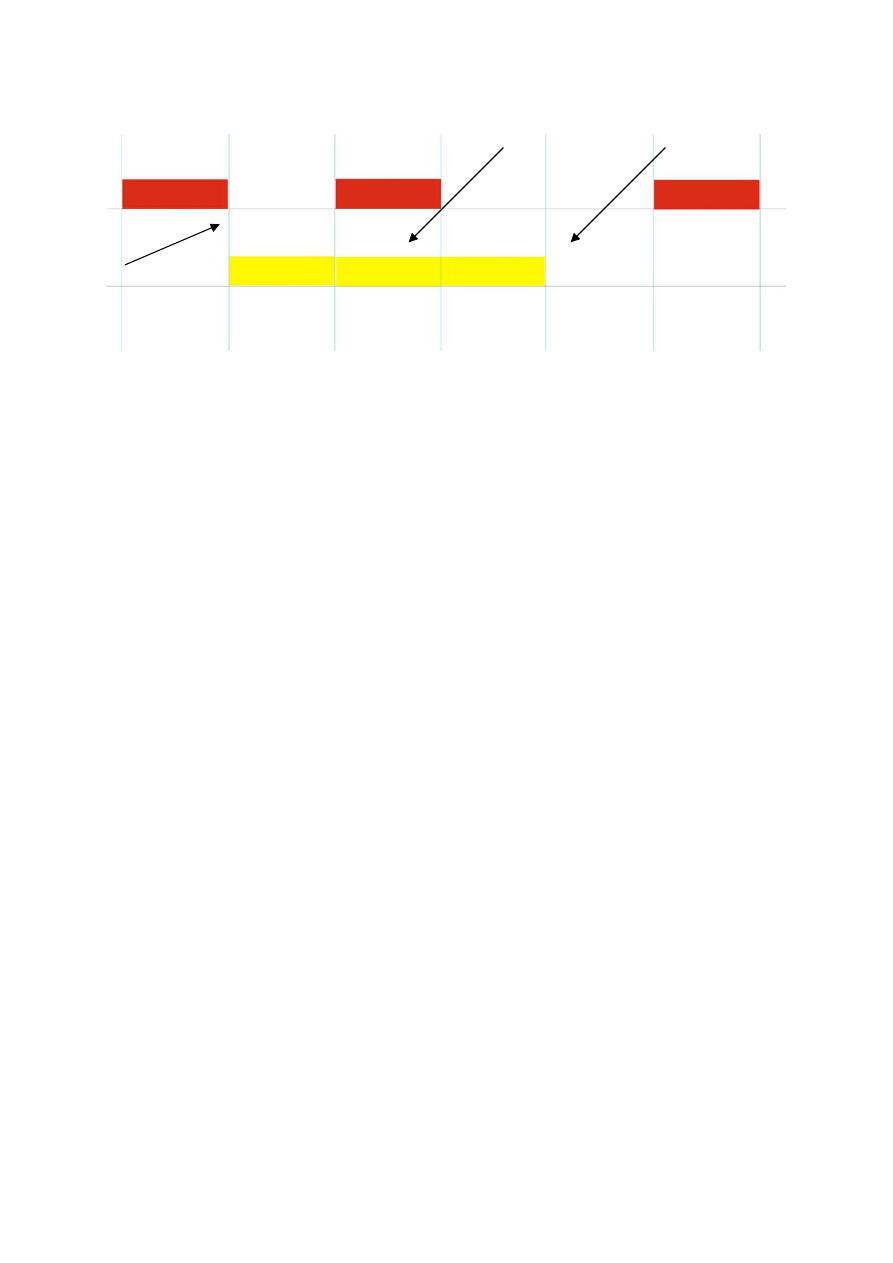
2.2 Analiza wydajnościowa slotted Alohy

Próbą ulepszenia systemu Aloha jest system S-Aloha ( slotted Aloha ). Zastosowano w
nim podzielenie czasu na dyskretne interwały nazwane slotami ( szczelinami ). Długość
szczeliny jest równa czasowi trwania pakietu. Pakiety można wysyłać tylko na początku
każdej szczeliny. Dzięki temu kolizja następuje jedynie pomiędzy ramkami całkowicie
nachodzącymi na sobie. Ogranicza to czas w którym może nastąpić kolizja do wartości T.
Zwiększa się także prawdopodobieństwo udanej transmisji pakietu:

P

succ

= P(X=0) = (T

·g)

0

e

-T ·g

/0! = e

-T ·g

W wyniku czego rośnie przepustowość kanału:

S = G e

-G

Dzięki wprowadzeniu szczelin maksymalna przepustowość wzrasta dwukrotnie i wynosi 1/e
= 0,36 przy oferowanym ruchu wejściowym G równym 1.

brak kolizji

kolizja

retransmisja po kolizji

6

L

144 b

R

16 kbs

M

60
40

λ/r

4 pps

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1

λ

pps

0,1 0,125893 0,158489 0,199526 0,251189 0,316228 0,398107 0,501187 0,630957 0,794328

1 1,258925 1,584893 1,995262 2,511886 3,162278 3,981072 5,011872 6,309573 7,943282

10 12,58925 15,84893 19,95262 25,11886 31,62278 39,81072 50,11872 63,09573 79,43282

100 125,8925 158,4893 199,5262

g

0,1

7,5 9,441941 11,8867 14,96447 18,83915 23,71708 29,85804 37,58904 47,3218 59,57462

75 94,41941 118,867 149,6447 188,3915 237,1708 298,5804 375,8904 473,218 595,7462

750 944,1941 1188,67 1496,447 1883,915 2371,708 2985,804 3758,904 4732,18 5957,462

7500 9441,941 11886,7 14964,47

T

0,009

G

0

0,068

0,085

0,107

0,135

0,170

0,213

0,269

0,338

0,426

0,536

0,675

0,850

1,070

1,347

1,696

2,135

2,687

3,383

4,259

5,362

6,750

8,498 10,698 13,468 16,955 21,345 26,872 33,830 42,590 53,617 67,500 84,977 106,980 134,680

-1,170696 -1,070696 -0,970696 -0,870696 -0,770696 -0,670696 -0,570696 -0,470696 -0,370696 -0,270696 -0,170696 -0,070696 0,029304 0,129304 0,229304 0,329304 0,429304 0,529304 0,629304 0,729304 0,829304 0,929304 1,029304 1,129304 1,229304 1,329304 1,429304 1,529304 1,629304 1,729304 1,829304 1,929304 2,029304 2,129304

S

0

S

_Aloha

1

0,058976 0,071696 0,086374 0,102878 0,12079 0,139284 0,156998 0,171972 0,181708 0,183481 0,174987 0,15531 0,125917 0,091093 0,057094 0,029872 0,012451 0,003898 0,000851 0,000118 9,25E-06 3,53E-07 5,46E-09 2,7E-11 3,18E-14 6,15E-18 1,23E-22 1,4E-28 4,33E-36 1,44E-45 1,58E-57 1,31E-72 1,28E-91 1,4E-115

S

_S-Aloha

1

0,063094 0,078055 0,096126 0,11771 0,143109 0,172426 0,205399 0,241202 0,278189 0,313652 0,343681 0,363288 0,367024 0,350264 0,311134 0,252514 0,182918 0,114836 0,060209 0,025162 0,007903 0,001733 0,000242 1,91E-05 7,34E-07 1,15E-08 5,74E-11 6,87E-14 1,36E-17 2,78E-22 3,27E-28 1,06E-35 3,7E-45 4,35E-57

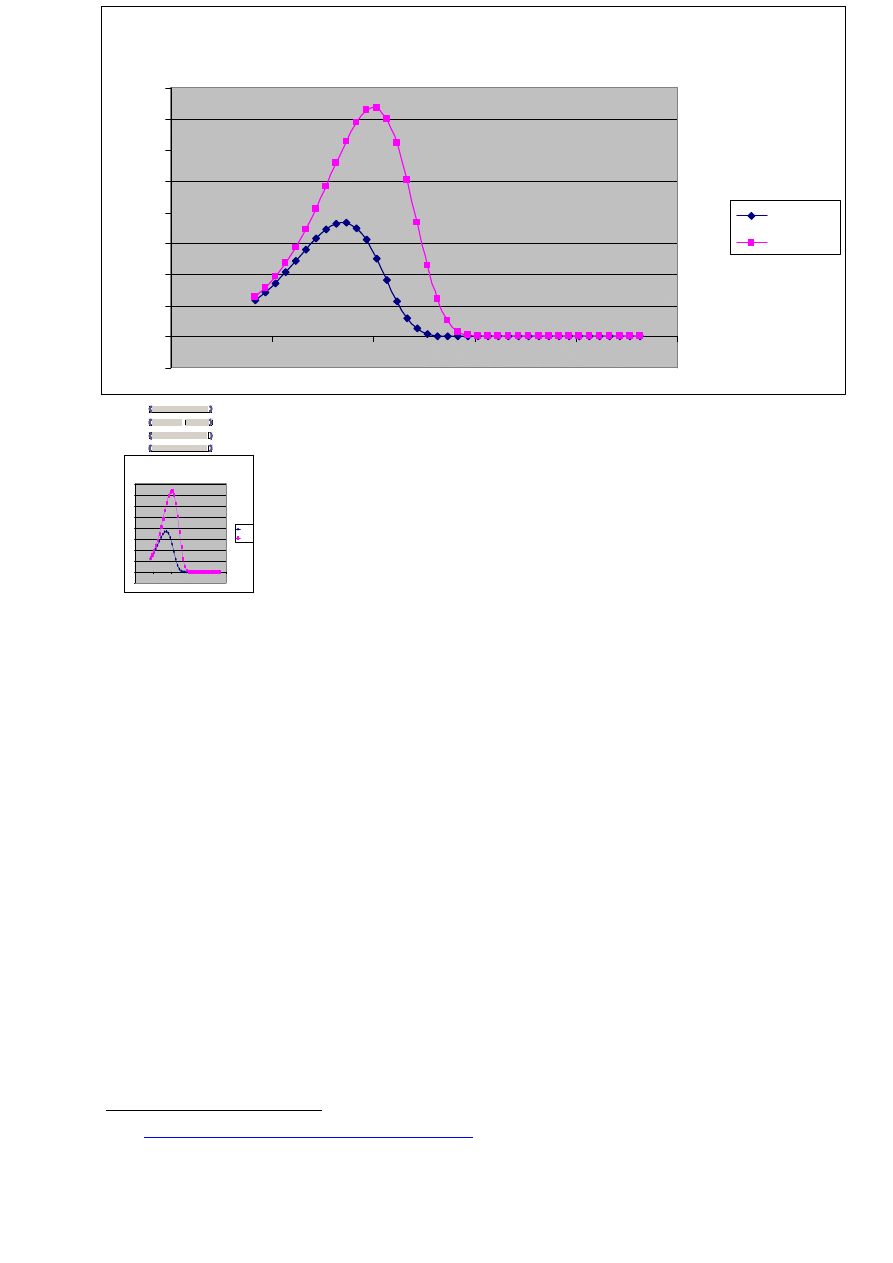
Wykorzystanie łącza w funkcji ruchu oferowanego

-0,05

0

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,010

0,100

1,000

10,000

100,000 1000,000

Aloha
S-Aloha

kilknięcie dwa razy po

powyższy rysunek pozwoli na zmiane wartości danych wejściowych wykresu (suwakami).

2.3 Szczegółowa analiza wydajnościowa slotted Alohy

2.3.1 Analiza wydajnościowa przy założeniu skończonej liczby stacji

Powyższe rozważania były słuszne dla pewnych założeń, dla systemu slotted Aloha można
przeprowadzić bardziej szczegółową analizę, bez założenia o nieskończonej liczbie
użytkowników. Każda ze stacji w sieci może być w jednym z dwóch stanów: thinking i
backlogged. Stacja w stanie thinking nie wysyła w danej chwili pakietu, jednak z
prawdopodobieństwem

σ może wygenerować pakiet, który będzie próbowała wysłać w

najbliższej wolnej szczelinie i wróci do stanu thinking. W stan backlogged, stacja przełączy
się w chwili gdy nowo nadany pakiet ulegnie kolizji i pozostanie w tym stanie, dopóki pakiet
ten nie zostanie pomyślnie zretransmitowany. Czas retransmisji takiego pakietu określa
algorytm retransmisyjny. Stacja w stanie backlogged nie może generować nowych pakietów,
a prawdopodobieństwo nadania retransmitowanego pakietu jest równe v dla każdej z
kolejnych szczelin. Po udanej retransmisji stacja wraca do stanu thinking.
Oznaczmy poprzez N(t) zmienną losową reprezentującą liczbę stacji w stanie backlogged na
początku szczeliny czasowej t. Ponieważ N(t+1) zależy jedynie od N(t) możemy użyć
dyskretnego modelu łańcucha Markova

2

do opisania systemu, w którym poprzez stan

łańcucha reprezentujemy liczbę stacji w stanie backlogged w systemie slotted Aloha.
Zdefiniujmy

π

i

jako prawdopodobieństwo, że system jest w stabilnym stanie i, a p

ij

jako

prawdopodobieństwo przejścia ze stanu i do stanu j. Aby wyznaczyć prawdopodobieństwo, że
stan jest stabilny musimy rozwiązać równanie liniowe:

2

http://pl.wikipedia.org/wiki/Proces_Markowa

Wykorzystanie łącza w funkcji ruchu oferowanego

-0,05

0

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,010

0,100

1,000

10,000

100,000

1000,000

Aloha
S-Aloha

7

π = πP

1=

Σ

i

π

i

gdzie

π jest poziomym wektorem o elementach π

i

, a P macierzą prawdopodobieństw

przejścia, którą można przedstawić jako:

p

ij

= 0,

j < i - 1

P

b

(1,i)·P

t

(0,i),

j = i - 1

[1-

P

b

(1,i)] P

t

(0,i) + P

b

(0,i) · P

t

(1,i), j = i

[1-

P

b

(0,i)] P

t

(1,i),

j = i + 1

P

t

(j – i,i),

j > i + 1

gdzie

P

b

(n,i) = (i po n)v

n

(1 –v)

i – n

i P

t

(n,i) = (M-1 po n)

σ

n

(1 -

σ)

M –i –n

, P

b

(n,i) jest

prawdopodobieństwem że n z i stacji w stanie backlogged wyśle swój pakiet w danej
szczelinie, a P

t

(n,i) to prawdopodobieństwo że n stacji w stanie thinking wyśle pakiet w danej

szczelinie, przy i stacjach w stanie backlogged. Po wyznaczeniu P wyliczamy wektor
prawdopodobieństwa stanu stabilnego.
Z

definicji

przepustowość S jest procentem czasu w którym w kanale odbywa się

prawidłowa transmisja pakietów. Uwzględniając, że długość pakietu jest stała i jego czas
transmisji jest równy czasowi trwania szczeliny, przepustowość jest równa
prawdopodobieństwu, że w danej szczelinie transmisja pakietu powiodła się. Aby to się stało
na początku trwania szczeliny może być nadany tylko jeden pakiet, albo ze stacji w stanie
thinking, albo ze stacji w stanie backlogged. Prawdopodobieństwo, że tylko jeden pakiet
został nadany w danej szczelinie przy i stacjach w stanie backlogged oznaczymy jako P

succ

(i),

i wyliczymy z:

P

succ

(i) = P

b

(1,i) P

t

(0,i) + P

b

(0,i)P

t

(1,i) = iv(1 – v)

i-1

(1 –

σ)

M-1

+ (1 – v)

i

(M – i)

σ(1 – σ )

M-i+1

Z czego wyliczamy przepustowość:

S = suma od i=0 do M ( P

succ

(i) ·

π

i

)

W szczególnym przypadku, gdy stacja w stanie backlogged retransmituje swoją ramkę z
takim samym prawdopodobieństwem, co stacja w stanie thinking, czyli v =

σ, otrzymujemy:

P

succ

(i) = M

σ(1-σ)

M-1

Wynik ten sugeruje, że w takim przypadku P

succ

(i) nie jest już zależne od liczby stacji w

stanie backlogged i, gdyż nie ma różnicy pomiędzy stacjami w stanie thinking a backlogged.
W takim wypadku przepustowość S wynosi:
S = suma od i=0 do M ( P

succ

(i) ·

π

i

) = P

succ

(i) · suma (

π

i

) = M

σ(1-σ)

M-1

W dalszym ciągu zakładany, że stacje w obu stanach generują ruch oznaczony jako G i
wyrażany w liczbie przesyłanych pakietów na szczelinę. W takim wypadku G = M

σ, gdyż w

systemie mamy M stacji, a każda z nich generuje pakiet z prawdopodobieństwem

σ w każdej

szczelinie czasowej. Podstawiając G = M

σ do równania na przepustowość otrzymujemy:

S = G[1 – G/M]

M-1

Zwiększając M do nieskończoności otrzymamy S = Ge

-G

, co daje dokładnie taki sam wynik

gdy analizowaliśmy system z założeniem nieskończonej liczby stacji.
Różniczkując równanie po M i przyrównując do zera otrzymujemy maksymalną
przepustowość kanału w systemie Aloha w zależności od liczby użytkowników M:

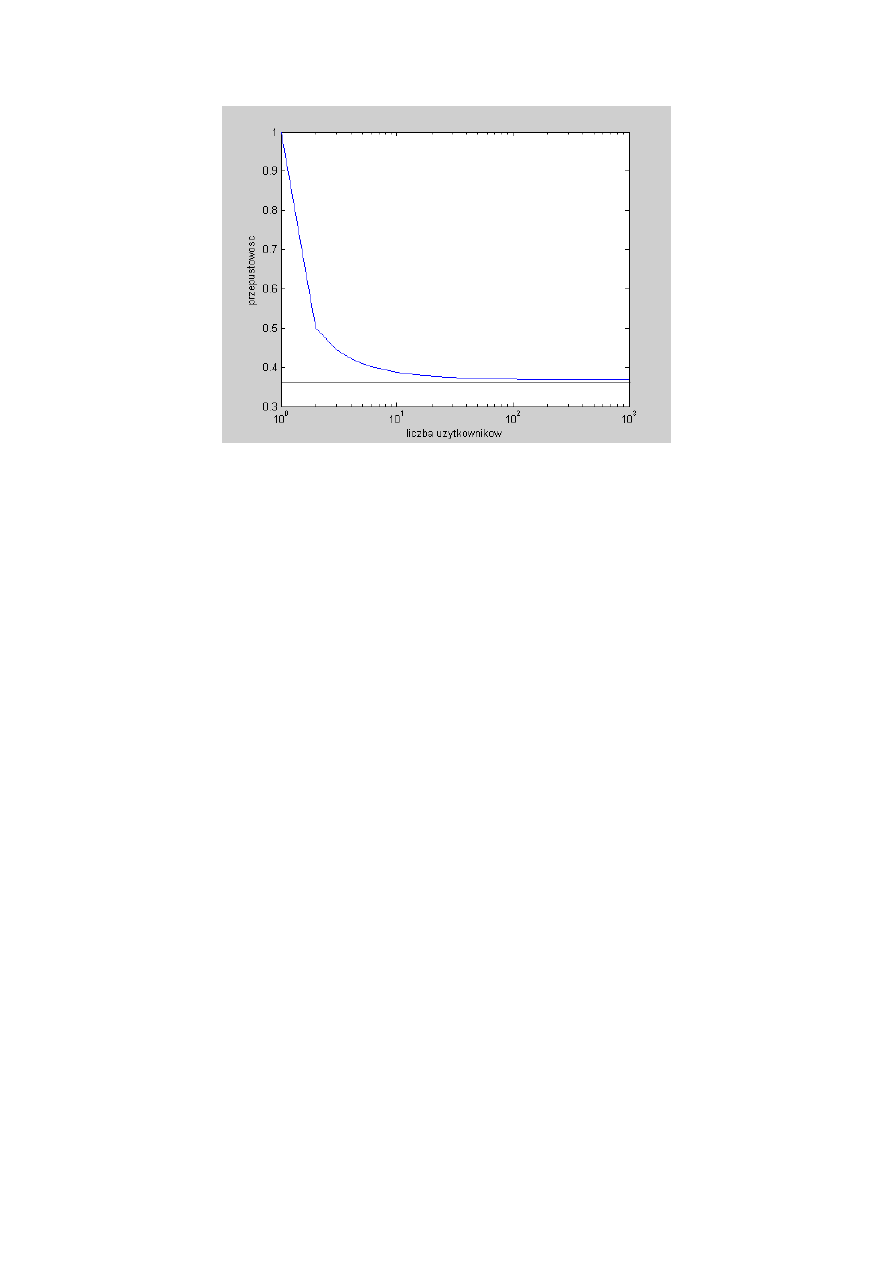
S

max

= [1 – 1/M]

M-1

8

Jeżeli wykreślimy tą zależność, zauważamy, że przy liczbie stacji większej od 15
maksymalna przepustowość ma zbliżoną wartość do wartości wyliczonej przy założeniu
nieskończonej liczby stacji.
Jako ciekawostkę można dodać, że system ALOHAnet w początkowych fazach działania
posiadał 7 użytkowników.

2.3.2 Analiza wydajnościowa Alohy z liniowym algorytmem retransmisji

W poprzednich analizach wydajności Alohy nie rozważaliśmy zastosowania algorytmu
retransmisji. Zakładaliśmy, że natężenie ruchu retransmisyjnego ma rozkład Poissonowski
niezależny od natężenia ruchu nowo wygenerowanych pakietów. Aby usprawiedliwić takie
założenie należy przeanalizować działanie systemu slotted Aloha z liniowym algorytmem
retransmisji.
Model algorytmu opiera się na następujących założeniach:

• czas transmisji pakietu jest równy czasowi trwania jednej szczeliny

• liczba stacji w systemie jest nieskończona, a całkowity proces przychodzenia pakietów

jest procesem Poissonowskim ze średnią wartością G pakietów na slot.

• stacja której ramka uległa kolizji wykryje tą kolizję po r szczelinach po końcu

transmisji.

• każda stacja po wykryciu kolizji jej poprzedniego pakietu zaplanuje jego retransmisję

po k szczelinach, gdzie k jest liczbą całkowitą z przedziału od 0 do K-1. Jeżeli k
będzie równe zeru to retransmisja pakietu odbędzie się od razu po wykryciu błędu
poprzedniej transmisji.

Analiza wydajnościowa wymaga wprowadzenia następujących wartości:

• q

n

– prawdopodobieństwo, że nowo wygenerowany pakiet zostanie przesłany

pomyślnie

• q

t

– prawdopodobieństwo, że retransmitowana ramka zostanie przesłana prawidłowo

• p

i

– prawdopodobieństwo, że retransmitowana ramka zostanie przesłana pomyślnie po

i próbach retransmisji, przy i >= 1

• H - średnia liczba retransmisji potrzebnych do pomyślnego przesłania pakietu, inaczej

wartość oczekiwana p

i

• S – przepustowość systemu

Wartości q

n

i q

t

możemy określić jako:

9

q

t

= [( e

-G/K

– e

-G

)/( 1 – e

-G

)] · [ e

-G/K

+ (G/K)e

-G

]

K-1

·e

-S

q

n

= [ e

-G/K

+ (G/K)e

-G

]

K

·e

-S

Wartość p

i

można wyrazić za pomocą q

n

i q

t

jako:

p

i

= (1 - q

n

)(1 – q

t

)

i-1

q

t

Znając p

i

możemy obliczyć jej wartość oczekiwaną H:

H = E[p

i

] = (1 – q

n

) / q

t

Ostatecznie możemy wyliczyć przepustowość S, zależną od zagregowanego ruchu
oferowanego G i średniej liczby retransmisji H. Średnia liczba transmisji to średnia liczba
retransmisji plus pierwsza próba transmisji pakietu, czyli H + 1. Ponieważ pakiet wymaga
średnio H + 1 prób transmisji aby zostać poprawnie przesłany, to prawdopodobieństwo, P

succ

,

że pakiet zostanie przesłany pomyślnie wynosi 1/(H + 1). Zgodnie z definicją przepustowości
otrzymujemy:

S = G · P

succ

= G · 1/(H + 1) = G · [ q

t

/( 1 – q

n

+ g

t

)]

Biorąc K -> ∞ prawdopodobieństwa q

n

i q

t

dążą do e

-G

i wydajność systemu możemy uprościć

do:

Lim(K -> oo) S= G · [e

-G

/( 1 – e

-G

+ e

-G

)] = G e

-G

Zależność ta jest taka sama jak ta którą otrzymaliśmy w punkcie 2.1, co dowodzi słuszności
założeń jakie przyjęliśmy w tym punkcie.

2.4 Opóźnienia

Na podstawie rozważań przeprowadzonych w punkcie 2.3.1, łatwo można wyprowadzić
zależność na opóźnienia występujące w systemie. Jak, zostało powiedziane w punkcie 2.3.1
średnia liczba transmisji, w systemie slotted Aloha, jaka jest potrzebna do przesłania jednego
pakietu wynosi H+1, gdzie H to średnia liczba retransmisji jednego pakietu. Średnie
opóźnienie (czas od wysłania pakietu do jego odebrania przez odbiorcę) można więc wyrazić
wzorem:

d = H · [ T · r + K / (2 · r) ] + T · r / 2

gdzie:
T-czas trwania szczeliny
H- średnia liczba retransmisji
r- ilość szczelin po których stacja nadawcza wykrywa kolizję, dla Alozy zazwyczaj
przyjmujemy r = 1

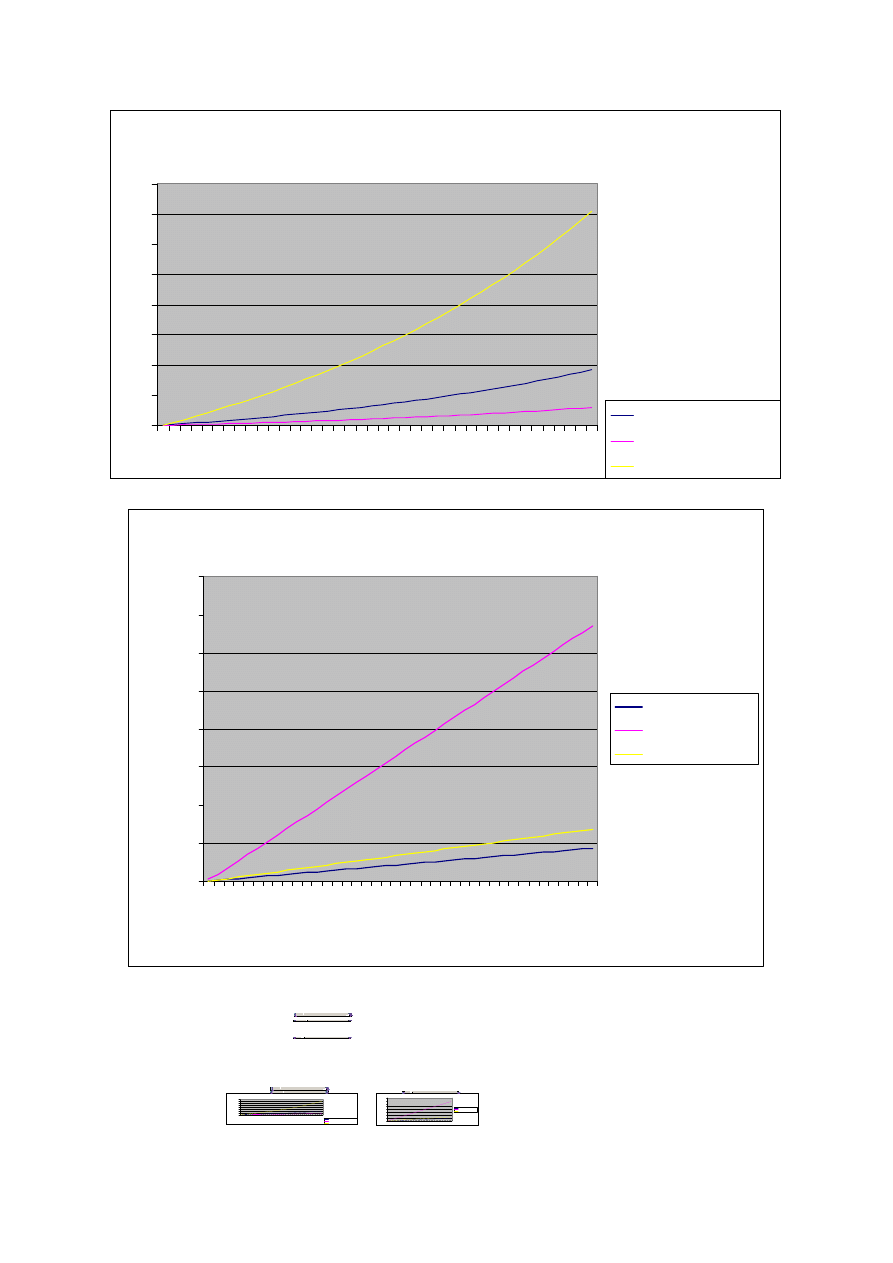
Opóźnienia w systemie (w zależności od parametrów G i K) obrazują wykresy poniżej:

10

L

74 b

R

24 kbps

T

0,003083333 s

g

1

10

20

30

40

50

60

70

80

90

100

110

120

130

140

150

160

170

180

190

200

210

220

230

240

250

260

270

280

290

300

310

320

330

340

350

G

0,003083333

0,030833

0,061667

0,0925

0,123333

0,154167

0,185

0,215833

0,246667

0,2775

0,308333

0,339166667

0,37

0,400833

0,431667

0,4625

0,493333

0,524167

0,555

0,585833

0,616667

0,6475

0,678333

0,709167

0,74

0,770833

0,801667

0,8325

0,863333

0,894167

0,925

0,955833

0,986667

1,0175

1,048333

1,079167

K

10

120

31

qt (G,S)

0,964715097

0,937932

0,909116

0,881255

0,854314

0,828257

0,80305

0,778663

0,755064

0,732223

0,710114

0,688708016

0,66798

0,647907

0,628463

0,609627

0,591378

0,573694

0,556556

0,539945

0,523844

0,508234

0,4931

0,478426

0,464195

0,450394

0,437009

0,424026

0,411432

0,399215

0,387362

0,375863

0,364706

0,35388

0,343376

0,333182

qn (G,S)

0,996921568

0,969652

0,940254

0,911774

0,884183

0,857451

0,83155

0,806452

0,782131

0,758561

0,735717

0,713576183

0,692114

0,671309

0,65114

0,631585

0,612625

0,594241

0,576414

0,559126

0,54236

0,5261

0,510329

0,495032

0,480195

0,465802

0,451841

0,438297

0,425158

0,412412

0,400046

0,388049

0,37641

0,365117

0,35416

0,34353

S(G)

0,003073841

0,029897

0,057979

0,084328

0,109023

0,132141

0,153754

0,173934

0,192746

0,210255

0,226523

0,241610026

0,255572

0,268463

0,280335

0,29124

0,301223

0,310332

0,31861

0,326099

0,33284

0,338871

0,344228

0,348948

0,353064

0,356609

0,359612

0,362105

0,364114

0,365668

0,366792

0,36751

0,367846

0,367824

0,367463

0,366786

H(qt,qn)

0,003191027

0,032356

0,065719

0,100114

0,135568

0,172108

0,209763

0,248565

0,288544

0,329734

0,372169

0,415885702

0,46092

0,507312

0,555101

0,604329

0,655038

0,707275

0,761085

0,816516

0,873619

0,932444

0,993045

1,055478

1,119798

1,186066

1,254342

1,324689

1,397172

1,471859

1,548818

1,628122

1,709845

1,794063

1,880854

1,970302

1

d(G)

0,051012424

0,503164

1,020392

1,553619

2,103258

2,66974

3,253517

3,85506

4,474862

5,113436

5,771314

6,449052369

7,147229

7,866443

8,607317

9,370498

10,15666

10,96649

11,80071

12,66006

13,54533

14,4573

15,39681

16,3647

17,36187

18,38923

19,44771

20,53831

21,66202

22,81989

24,013

25,24246

26,50941

27,81504

29,16058

30,54729

d k =10

0,01750664

0,163423

0,33034

0,502421

0,679798

0,86261

1,051004

1,245131

1,445151

1,651228

1,863536

2,082252493

2,307565

2,539666

2,778758

3,025048

3,278753

3,540097

3,809313

4,086641

4,37233

4,666637

4,96983

5,282185

5,603987

5,93553

6,27712

6,629072

6,991711

7,365374

7,750408

8,147173

8,556038

8,977386

9,411613

9,859126

d k =120

0,193013123

1,943018

3,944896

6,008696

8,136017

10,32853

12,58798

14,91619

17,31507

19,7866

22,33285

24,95596613

27,65819

30,44183

33,30931

36,26312

39,30586

42,44022

45,66899

48,99504

52,42137

55,95106

59,58733

63,33346

67,1929

71,16917

75,26594

79,48697

83,83618

88,31761

92,93541

97,69389

102,5975

107,6508

112,8586

118,2257

qt const

0,964715097

Gconst

0,2

1

0,3

3

Sconst

0,163746151

0,367879

0,222245

K

2

10

20

30

40

50

60

70

80

90

100

110

120

130

140

150

160

170

180

190

200

210

220

230

240

250

260

270

280

290

300

310

320

330

340

350

qt(K) G = 0,2

0,39791319

0,733215

0,775905

0,790165

0,797301

0,801585

0,804441

0,806481

0,808012

0,809203

0,810155

0,810934538

0,811584

0,812134

0,812605

0,813013

0,81337

0,813686

0,813966

0,814217

0,814442

0,814647

0,814832

0,815002

0,815157

0,8153

0,815432

0,815554

0,815667

0,815773

0,815872

0,815964

0,81605

0,816132

0,816208

0,81628

qn(K) G = 0,2

0,826542984

0,820311

0,819522

0,819258

0,819126

0,819047

0,818995

0,818957

0,818929

0,818907

0,818889

0,818874692

0,818863

0,818853

0,818844

0,818836

0,81883

0,818824

0,818819

0,818814

0,81881

0,818806

0,818803

0,8188

0,818797

0,818794

0,818792

0,818789

0,818787

0,818785

0,818784

0,818782

0,81878

0,818779

0,818777

0,818776

H(qt,qn) G = 0,2

0,435916728

0,24507

0,232604

0,228739

0,226857

0,225744

0,225008

0,224485

0,224095

0,223792

0,223551

0,223353796

0,22319

0,223051

0,222933

0,22283

0,22274

0,222661

0,222591

0,222528

0,222471

0,22242

0,222374

0,222331

0,222292

0,222257

0,222224

0,222193

0,222165

0,222139

0,222114

0,222091

0,222069

0,222049

0,22203

0,222012

d(K) G = 0,2

0,438802471

1,22765

2,328297

3,433334

4,539385

5,64583

6,752467

7,859213

8,966027

10,07289

11,17978

12,28668914

13,39362

14,50056

15,60751

16,71448

17,82144

18,92842

20,0354

21,14238

22,24936

23,35635

24,46334

25,57033

26,67733

27,78432

28,89132

29,99832

31,10531

32,21232

33,31932

34,42632

35,53332

36,64032

37,74733

38,85433

qt(K) G =1

0,206576698

0,342197

0,355484

0,359715

0,361793

0,363028

0,363847

0,364429

0,364864

0,365202

0,365472

0,365692067

0,365875

0,366031

0,366163

0,366278

0,366379

0,366467

0,366546

0,366617

0,36668

0,366737

0,366789

0,366837

0,366881

0,366921

0,366958

0,366992

0,367024

0,367053

0,367081

0,367107

0,367131

0,367154

0,367175

0,367195

qn(K) G =1

0,432517009

0,379327

0,373503

0,371606

0,370666

0,370104

0,369731

0,369465

0,369266

0,369112

0,368988

0,368886808

0,368803

0,368731

0,36867

0,368618

0,368571

0,368531

0,368494

0,368462

0,368433

0,368406

0,368382

0,36836

0,36834

0,368322

0,368305

0,368289

0,368274

0,368261

0,368248

0,368236

0,368225

0,368214

0,368205

0,368195

H(qt,qn) G = 1

2,747081337

1,813791

1,762379

1,746923

1,739486

1,735114

1,732237

1,730199

1,728681

1,727505

1,726569

1,725804983

1,72517

1,724634

1,724175

1,723778

1,723431

1,723126

1,722854

1,722612

1,722394

1,722196

1,722017

1,721854

1,721704

1,721566

1,721439

1,721322

1,721212

1,721111

1,721016

1,720927

1,720844

1,720766

1,720693

1,720624

d(K) G = 1

2,757093172

9,076091

17,63077

26,21077

34,79662

43,38474

51,97398

60,56384

69,1541

77,74461

86,33531

94,92613699

103,5171

112,1081

120,6991

129,2902

137,8814

146,4725

155,0637

163,655

172,2462

180,8375

189,4287

198,02

206,6113

215,2026

223,7939

232,3853

240,9766

249,5679

258,1592

266,7506

275,3419

283,9333

292,5246

301,116

qt(K) 0,35995503

0,663962

0,702381

0,715192

0,721599

0,725442

0,728005

0,729835

0,731208

0,732276

0,73313

0,733829192

0,734412

0,734904

0,735327

0,735693

0,736013

0,736296

0,736547

0,736772

0,736974

0,737157

0,737324

0,737476

0,737615

0,737743

0,737861

0,737971

0,738073

0,738167

0,738256

0,738338

0,738416

0,738489

0,738557

0,738622

qn(K) 0,756242808

0,743925

0,742373

0,741855

0,741596

0,74144

0,741336

0,741262

0,741207

0,741164

0,741129

0,741100907

0,741077

0,741057

0,74104

0,741026

0,741013

0,741001

0,740991

0,740982

0,740974

0,740966

0,74096

0,740953

0,740948

0,740943

0,740938

0,740933

0,740929

0,740925

0,740922

0,740919

0,740915

0,740912

0,74091

0,740907

H(qt,qn)

0,677187903

0,385676

0,366792

0,360946

0,3581

0,356417

0,355305

0,354515

0,353925

0,353468

0,353103

0,352805661

0,352558

0,352349

0,352169

0,352014

0,351879

0,351759

0,351653

0,351558

0,351473

0,351395

0,351325

0,351261

0,351203

0,351149

0,351099

0,351053

0,35101

0,35097

0,350933

0,350898

0,350865

0,350835

0,350806

0,350779

d(K) 0,680817565

1,931113

3,67059

5,416838

7,164647

8,913063

10,66178

12,41066

14,15964

15,9087

17,6578

19,40694083

21,15611

22,90529

24,65449

26,4037

28,15293

29,90216

31,6514

33,40064

35,14989

36,89914

38,6484

40,39766

42,14693

43,89619

45,64546

47,39473

49,144

50,89327

52,64255

54,39182

56,1411

57,89038

59,63966

61,38894

G

0,01

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0,45

0,5

0,55

0,6

0,65

0,7

0,75

0,8

0,85

0,9

0,95

1

1,05

1,1

1,15

1,2

1,25

1,3

1,35

1,4

1,45

1,5

1,55

1,6

1,65

1,7

1,75

qn

L

74 b

R

24 kbps

T

0,003083333 s

K

31

G

0,3

Zależność opóżnienia transmisji od ruchu oferowanego

0

20

40

60

80

100

120

140

160

0,

00

30

83

3

0,

09

25

0,

18

5

0,

27

75

0,

37

0,

46

25

0,

55

5

0,

64

75

0,

74

0,

83

25

0,

92

5

1,

01

75

1,

11

1,

20

25

ruch oferowany

o

p

ó

żn

ie

n

ie

przy zmiennym K
przy K = 10
przy K = 120

Zależność opóźnienia od czasu oczekiwania pakietu na retransmisję

0

50

100

150

200

250

300

350

400

2

30

60

90

12

0

15

0

18

0

21

0

24

0

27

0

30

0

33

0

36

0

39

0

o

p

ó

źn

ie

n

ie

dla G = 0,2
dla G = 1
dla wybranego G

Zależność opóżnienia transmisji od ruchu oferowanego

0

20

40

60

80

100

120

140

160

0

0,

09

0,

19

0,

28

0,

37

0,

46

0,

56

0,

65

0,

74

0,

83

0,

93

1,

02

1,

11

1,

2

ruch oferowany

opó

żni

e

n

ie

przy zmiennym K
przy K = 10
przy K = 120

Zależność opóźnienia od czasu oczekiwania pakietu na retransmisję

0

50

100

150

200

250

300

350

400

2

30

60

90 12

0

15

0

18

0

21

0

24

0

27

0

30

0

33

0

36

0

39

0

czas oczekiwania na transmicje K

opó

źni

en

ie

dla G = 0,2
dla G = 1
dla wybranego G

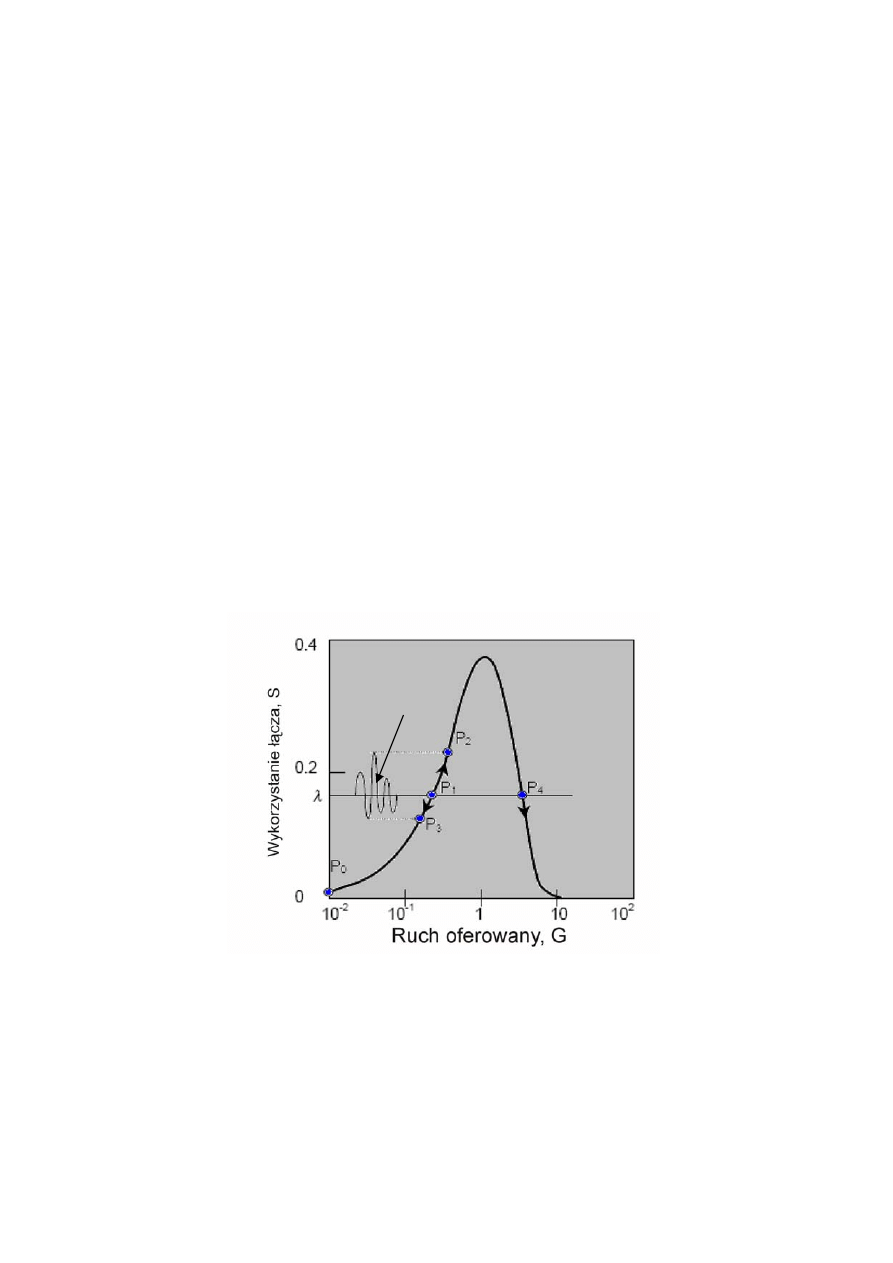
11

kilknięcie dwa razy po powyższy rysunek pozwoli na zmiane wartości danych wejściowych
wykresu (suwakami).
Jak widać wybrany model nie uwzględnia faktu, iż dla bardzo małych K, opóźnienie będzie
rosło z powodu dużej liczby kolizji a zatem i koniecznej liczby retransmisji.
Biorąc pod uwagę że protokół Aloha ma znacznie mniejsze prawdopodobieństwo skutecznej
transmisji należy się spodziewać znacznie większych opóźnienień dla tych samych
parametrów.

3. Stabilność protokołów Aloha

3.1 Niestabilność Alohy

Kolejnym zagadnieniem jakie należy poruszyć przeprowadzając analizę protokołów Aloha i
S-Aloha jest ich stabilność. Przez stabilność rozumiemy taką cechę systemu, że jeżeli system
znajduje się w pewnym stabilnym stanie równowagi, to wytrącony z tego stanu powróci do
niego. W przypadku systemów wykorzystujących protokoły Aloha, będzie to oznaczać tyle
że, jeśli dla pewnych ustalonych parametrów (G, M, K, λ itp.) możemy ustalić pewien
umowny punkt pracy systemu i ponieważ ruch napływający modelowany rozkładem Poissona
podlega pewnym fluktuacjom, to rzeczywisty punkt pracy będzie się stale zmieniał, jednak
dla systemu stabilnego rzeczywisty punkt pracy będzie stale znajdował się (fluktuował) w
otoczeniu pewnego umownego (uśrednionego) punktu pracy.
Z rozważań przeprowadzonych w punkcie 2 i wykresów przepustowości można zauważyć że
protokóły Aloha ani S-Aloha są stabilne tylko dla pewnego przedziału G. Weźmy po uwagę
wykres przepustowości w funkcji ruchu oferowanego

Jeśli punkt pracy systemu znajduje się na lewo o maksimum (P

1

), wtedy zwiększenie ruchu

(np. w wyniku fluktuacji), czyli zwiększenie liczby transmitowanych pakietów (P

2

),

spowoduje wzrost wykorzystania łącza. Rzeczywisty punkt pracy będzie oscylował (P

3

, P

2

)

wokół pewnego umownego punktu pracy. Jeśli natomiast punkt pracy znajdzie się w samym
maksimum lub na lewo od niego(P

4

) jakiekolwiek zwiększenie ruchu oferowanego G

spowoduje wzrost liczby transmitowanych pakietów ale zarazem również spadek
wykorzystania łącza co spowoduje wzrost ilości retransmisji. Punkt pracy będzie przesuwał
się w lewo aż do nieskończoności (w przypadku gdy liczba użytkowników jest nieskończona)

fluktuacje

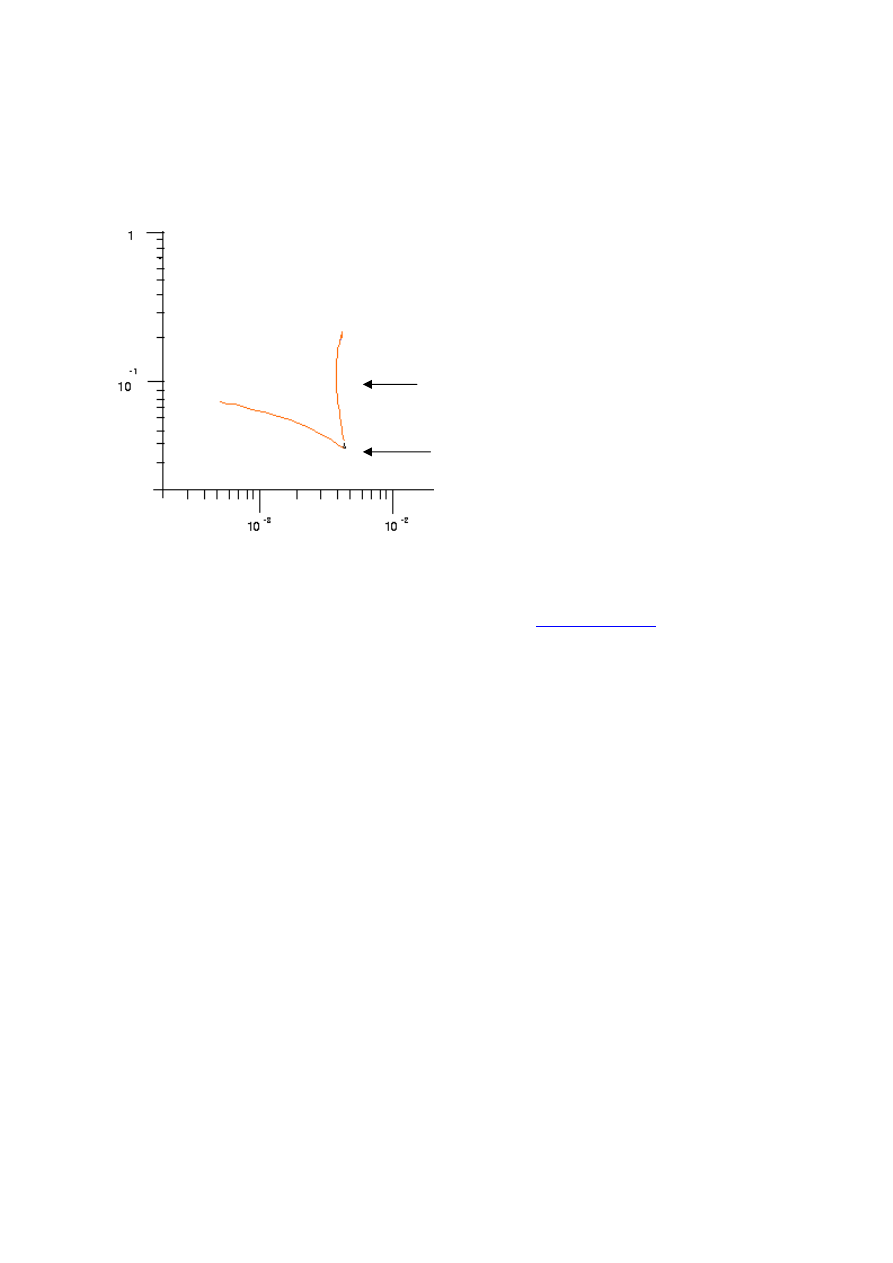
12

lub do pewnej maksymalnej wartości G (przy skończonej liczbie użytkowników). Taka
sytuacja występuje pod nazwą katastrofy. Praktycznie niemożliwa jest wtedy jakakolwiek
skuteczna transmisja. Wyjść z sytuacji katastrofy można poprzez wstrzymanie nowych
transmisji i znaczne wydłużenie czasu K, sam protokół nie przewiduje jednak takich
mechanizmów.

1 Poglądowy rysunek pokazujący zależność pomiędzy parametrami λ i r

Zachęcamy do zapoznanie się z prostym symulatorem działania protokołu Aloha (w
szczególności wychodzenia ze stanu katastrofy) na stronie:

Aloha animation

3.2 Analiza stabilności

Aby rozpocząć dokładniejszą analizę stabilności protokołu S-Aloha wprowadźmy najpierw
wzór na liczbę stacji będącą w stanie backlogged:

n = SH(r+1/2+K/2)

Gdzie:
S przepływność kanału
n liczba stacji w stanie backlogged
H średnia liczba retransmisji potrzebna do przesłania pakietu
K maksymalna liczba slotów po jakiej może nastąpić retransmisja pakietu
r - ilość szczelin po których stacja nadawcza wykrywa kolizję

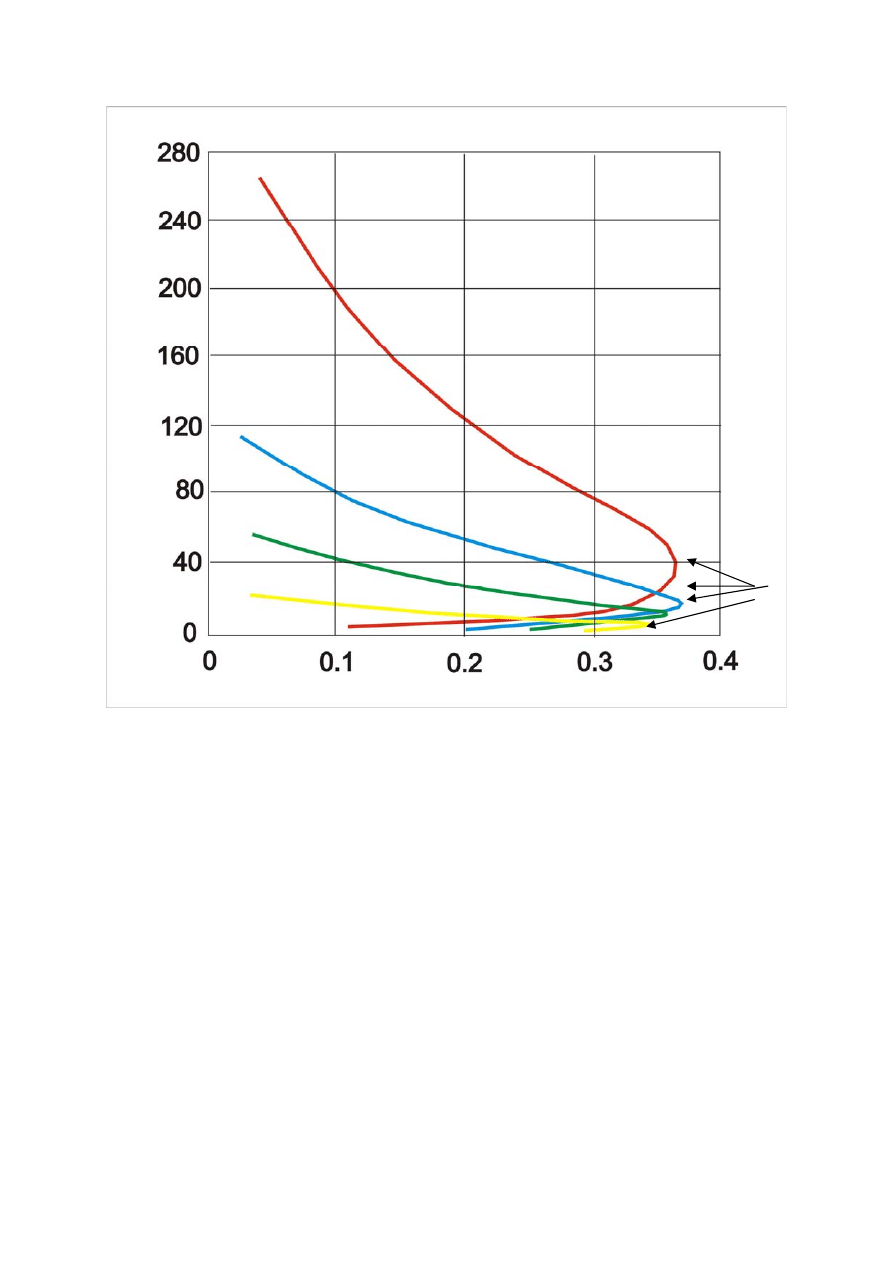
Wykres przedstawiający zależność ilości stacji w stanie backlogged od przepustowości:

Punkt S=S

max

prawdopodobieństwo transmisji

prawdopodobie

ństwo retransmisji

W stanie katastrofy

13

Załóżmy że liczba stacji w systemie wynosi M, średnia liczba stacji w stanie backlogged
wynosi n. Ponieważ stacja może nadawać jednocześnie tylko jedną ramkę liczba stacji które
mogą generować nowe ramki wynosi (M-n). Prawdopodobieństwo dla każdej ze stacji która
może nadać ramkę wynosi σ dla każdej szczeliny, oczekiwana przepustowość kanału wynosi:
S

in

= (M-n)

σ

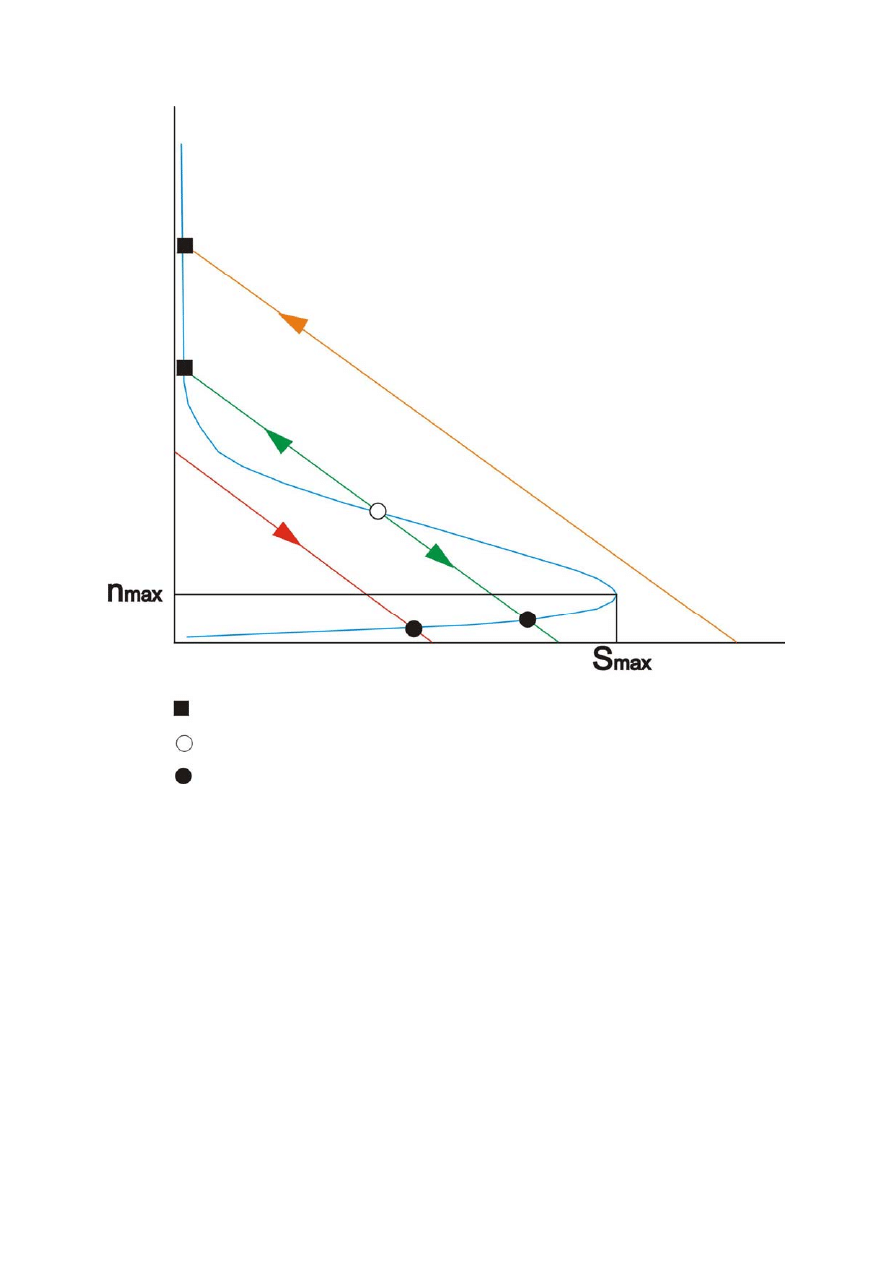
Powyższy wzór wyznacza linie obłożenia kanału. Jeśli nałożymy krzywe obłożenia kanału na
powyższy wykres, na przecięciach wykresów n(S) i S

in

otrzymamy punkty równowagi w

których spodziewane obłożenie kanału jest równe wykorzystaniu kanału.

K=200

K=40

K=20

K=5

Przepustowość, S

Ś

rednia liczba stacji

w stanie backlogged

Punkt S=S

max

14

Jak można zauważyć punkty równowagi leżące pod linią n

max

będą punktami stabilnymi,

ponieważ zwiększenie n, ilości stacji w stanie backlogged, spowoduje wzrost wykorzystania
łącza. Punkty leżące poniżej linii n

max

są stabilnymi punktami równowagi, wzrost liczby n,

stacji w stanie backlogged, powoduje wzrost wykorzystania łącza. Punkty leżące powyżej tej
linii są punktami niestabilnymi, zwiększenie liczby n powoduje zmniejszenie wykorzystania
łącza a zarazem dalsze zwiększanie n. Punkty dla których wykorzystanie łącza jest bliskie
zera nazywamy punktami nasycenia.
Na wykresie naniesiono 3 linie obłożenia łącza. Linia będzie stabilne tylko wtedy gdy posiada
tylko jeden, stabilny punkt równowagi. Najniższa linia jest linią stabilną. Środkowa linia jest
linią niestabilną, gdyż posiada 3 punkty równowagi, stabilny, niestabilny i nasycenia. W
wyniku fluktuacji napływu ruchu, punkt pracy systemu może się przesunąć z punktu
stabilnego do punktu niestabilnego i dalej do punktu nasycenia. Gdy system pracuje po
najwyższej linii, która ma tylko jeden punkt przecięcia i jest to punkt nasycenia kanału, to
mówimy że jest przeciążony, dla żadnej liczby n system nie jest w stanie obsłużyć ruchu
napływającego.

Punkt nasycenia kanału

niestabilny punkt równowagi

stabilny punkt równowagi

Ś

rednia liczba stacji

w stanie backlogged

Przepustowość, S

15

4. Dynamiczne sterowanie

W poprzednim punkcie, wykazaliśmy że protokół slotted Aloha ( a także Aloha) jest
niestabilny. Chcąc uniknąć katastrofy należy stosować odpowiednio duże K w stosunku do
maksymalnej liczby użytkowników tak by sytuacja taka nie miała miejsca, gdyż powoduje
ona, że sieć przestaje działać. Jednakże jak pokazano w punkcie 2.4, ustawienie zbyt dużego
K powoduje wzrost opóźnień oraz spadek wykorzystania kanału. Wykres poniżej jest próbą
pokazania wpływu parametru K na wykorzystanie kanału. Zależność została wyprowadzona
ze wzoru z punktu 2.3.2.

S = G · P

succ

= G · 1/(H + 1) = G · [ q

t

/( 1 – q

n

+ g

t

)]

Uzyskany wynik pokazuje jednak jak daleko niedoskonałe są przyjęte przez nas modele i nie
ma za wiele wspólnego z rzeczywistą zależnością.

W rzeczywistości, z jednej strony czas K powinien być jak najdłuższy by zminimalizować
liczbę kolizji, z drugiej jednak strony czas K powinien być możliwie krótki by zmniejszyć
opóźnienia i zminimalizować ilość szczelin pustych ( w których nic nie zostało nadane).
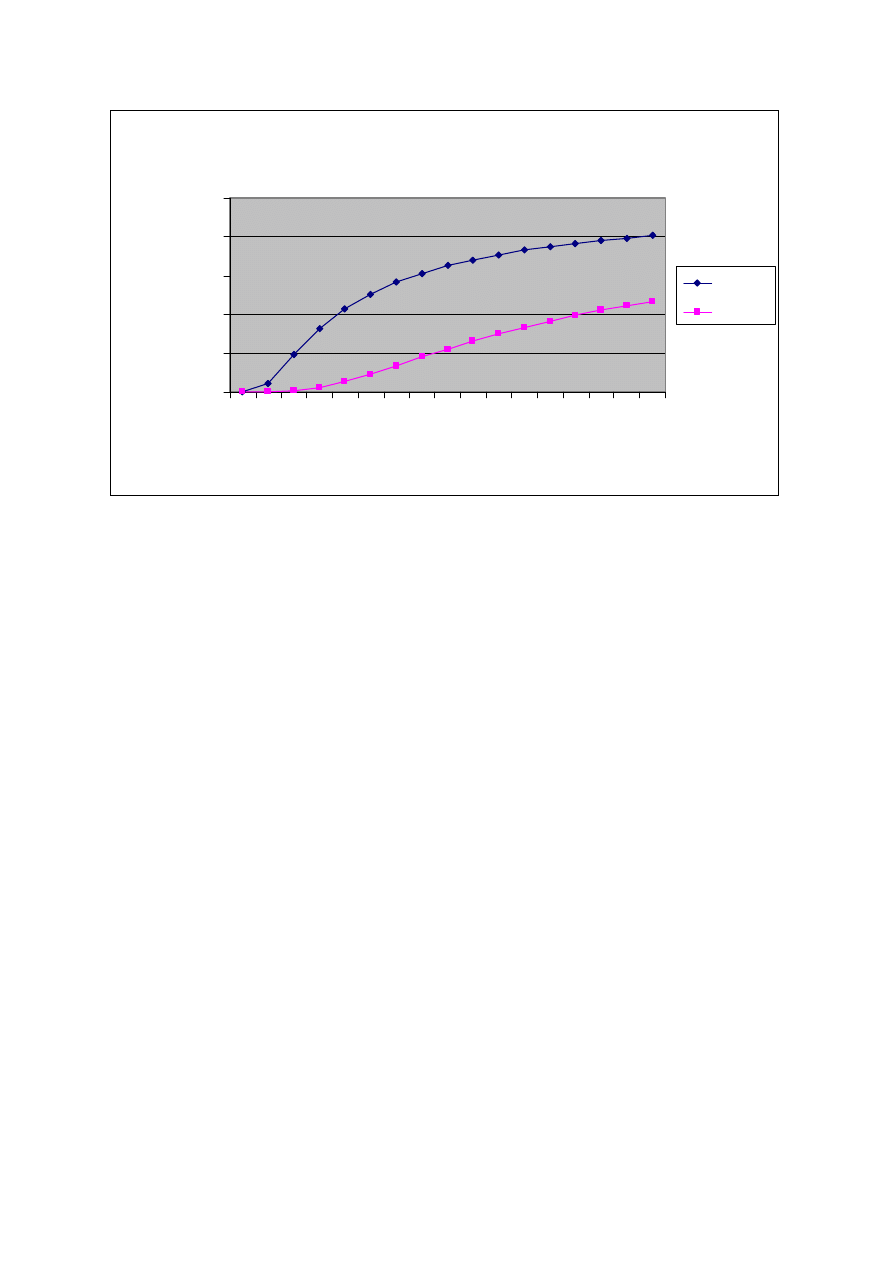
Można więc oczekiwać że wykres wykorzystania kanału w funkcji parametru K, będzie
krzywą która dla pewnego K będzie osiągać maksimum.
Wpływ parametru K na liczbę retransmisji można zilustrować na prostym przykładzie.
Załóżmy że systemie nie jest prowadzona żadna transmisja. W jednej szczelinie czasowej, M
stacji nadaje pakiet, a w przypadku udanego przesłania pakietu nie wysyła żadnych kolejnych
pakietów. W takim przypadku prawdopodobieństwo że w czasie K, choć jedne pakiet zostanie
nadany prawidłowo wynosi

p



k

k−1

M

−1

k

M

16

Jak widać na powyższym przykładzie dla bardzo małych K, bardzo dużo pakietów będzie
retransmitowanych, co będzie powodować spadek wykorzystania łącza.
Zatem, dynamiczne zmienianie, w odpowiedni sposób, parametru K mogło by zapewnić
lepsze niż w przypadku statycznym wykorzystanie łącza oraz zapobiec przejściu systemu w
stan nasycenia w przydatku zmiany liczby użytkowników lub zwiększeniu napływu ruchu.
Zmiana parametru K wymaga jednak aby stacje nadawcze znały parametr n, tak by mogły
dobierać odpowiedni czas retransmisji. Taka zmiana czyni protokół Aloha stabilnym, choć
znacznie go komplikuje.

5. Podsumowanie

Protokołu Aloha i slotted Aloha, cechuje niewielkie wykorzystanie łącza oraz brak stabilność.
Jednak dzięki swojej prostocie nadal znajdują one zastosowanie w dzisiejszym świecie.
Przeprowadzona analiza, pokazała wiele cech i parametrów tych protokołów, nie należy
jednak zapominać, że przyjęte przez nas modele są mocno uproszone i wymagają przyjęcia
szeregu założeń, które nie zawsze są do końca słuszne. Przyjęcie bardziej rozbudowanych
modeli, znacznie trudniejszych w analizie, pozwoliło by na uzyskanie dokładniejszych
wyników i większej liczby parametrów.
W celu uzyskanie dokładniejszych wyników, należało by przeprowadzić symulacje
komputerowe, a nawet badania na istniejących systemach, jednak przeprowadzona tutaj
analiza teoretyczna, ilustruje podstawowe problemy oraz zasady działania całej rodziny
protokołów RandomAcessProtocol.

zależność p(K)

0,000

0,200

0,400

0,600

0,800

1,000

1

9

17

25

33

41

49

57

65

K

p

M=15
M=50

17

6. Bibliografia

1. Wykład z przedmiotu LAN, WEiTI PW.

http://www.tele.pw.edu.pl/lan/

2. Wykład z przedmiotu STS, WEiTI PW.

http://www.tele.pw.edu.pl/sts/

3.

http://www.ee.unimelb.edu.au/multimedia/research/cubin_ChuanHengFoh_thesis.pdf

4.

http://www.wireless.per.nl/reference/chaptr06/aloha/aloha.htm

5.

http://en.wikipedia.org/wiki/ALOHAnet

6.

http://pl.wikipedia.org/wiki/Proces_Markowa

7.

http://www.hicss.hawaii.edu/hicss_31/specpl3.html

8.

http://acsp.ece.cornell.edu/papers/NawareTong03ICC.pdf

9.

http://ocw.mit.edu/NR/rdonlyres/Electrical-Engineering-and-Computer-Science/6-
263JData-Communication-NetworksFall2002/3DED7C41-F650-4FA0-B62F-
604D1B06A1B0/0/Lectures13_14.pdf

10.

http://www.eecs.berkeley.edu/~ananth/1990-1992/Self/FiniteUserALOHA91.pdf

11.

http://www.student.net.pl/materialy/eit_sem9/zttEgzOdp25.pdf

12.

http://www.laynetworks.com/Slotted%20Aloha.html