Sygnał wyjściowy

y(t)

Sygnał wejściowy

u(t)

G(s)

Układ taki może być opisany równaniem różniczkowym

a

n

y

n

ta

n−1

y

n−1

t...a

1

y

'

ta

0

yt=

=b

m

u

m

tb

m−1

u

m−1

ut...b

1

u

'

tb

0

ut

zakładasię przy tym,że m≤n

Opis układów liniowych ciągłych

Dokonującobustronnejtransformacji Laplace' a otrzymujemy

a

n

Yss

n

− y0s

n−1

− y

1

0s

n−2

− y

2

0s

n−3

... y

n−1

0+

a

n−1

Yss

n−1

− y0s

n−2

− y

1

0s

n−3

...y

n−2

0+

.

.

a

0

Y s=

b

m

Uss

m

−u0s

m−1

−u

1

0s

m−2

−u

2

0 s

m−3

'...u

m−1

0+

b

m−1

Uss

m−1

−u0s

m−2

−u

1

0s

m−3

+...+u

m−2

0+

.

.

b

0

Us

Opis układów liniowych ciągłych

jeżeli założymyzerowewarunki początkowe

y0= y

1

0=... y

n−1

0=0

u0=u

1

0=...u

m−1

0=0

wzórupraszcza siędo postaci

a

n

Y s s

n

a

n−1

Y s s

n−1

...a

1

Y s sa

0

Y s=

b

m

Us s

m

b

m−1

Us s

m−1

...b

1

Us sb

0

Us

co po przekształceniudajezależność

Y sa

n

s

n

a

n−1

s

n−1

...a

1

s

1

a

0

=

Usb

m

s

m

b

m−1

s

m−1

...b

1

s

1

b

0



Opis układów liniowych ciągłych

Opis układów liniowych

ciągłych

w efekcie daje t wzór

Ys

Us

=

b

m

s

n

b

m−1

s

m−1

...b

1

s

1

b

0

a

n

s

n

a

n−1

s

n−1

...a

1

s

1

a

0

wielkość Gs =

Y s

Us

nazywamy transmitancją

układui definiujemy jakostosunektransformaty

sygnałuwyjściowegoY sdotransformatysygnału

wejściowegoUs przyzerowychwarunkach początkowych

Opis układów liniowych ciągłych

Opis układów liniowych ciągłych

Wprowadzenie pojęcia transmitancji pozwala na

stosunkowo łatwe obliczanie odpowiedzi układu o znanej

transmitancji na znany sygnał wejściowy. Mamy bowiem:

GS=

Y s

Us

Y s=Gs∗Us

yt=L

−1

[Y s]=L

−1

[Gs∗Us]

Opis układów liniowych ciągłych

Algorytm obliczenia sygnału wyjściowego y(t) dla

znanych transmitancji G(s) i sygnału wejściowego u(t)

ma postać:

1. Obliczamy transformatę Laplace'a sygnału wejściowego

2. Obliczamy transformatę Laplace'a sygnału wyjściowego

3. Obliczamy oryginał sygnału wyjściowego

yt=L

−1

[Y s]=L

−1

[Gs∗Us]

U s= L[ut]

Y s=Gs∗Us

Opis układów liniowych ciągłych

Przykład. Dana jest transmitancja układu G(s)= 5/s

oraz sygnał wejściowy . Obliczyć sygnał y(t)

na wyjściu układu.

1. z definicji lub z tablic znajdujemy transformatę sygnału

wejściowego U(s)

|

ut=3e

−4t

∞

Us=

∫

0

¿

ut∗e

−st

dt=

∫

0

∞

3∗e

−4t

∗e

−st

dt=3

∫

0

∞

e

−4t4s

dt=

=3 −

1

4s

e

−4st

0

∞

 = −

3

4s

0−1=

3

4s

Opis układów liniowych ciągłych

Przykład cd.

2. Obliczamy transformatę sygnału wyjściowego

ze wzoru Y(s)=G(s)*U(s)

3. obliczamy y(t) korzystając z metody residuów:

mamy dwa bieguny pojedyncze oraz

|

Y s=

5

s

∗

3

s4

=

15

s s4

s

1

=0

s

2

=−4

Opis układów liniowych ciągłych

Przykład cd.

res

s=s

n

[Yse

st

]=lim

ss

n

[s−s

n

Yse

st

]

yt=L

−1

[Y s]=

∑

n=1

N

res

s=s

n

[Yse

st

],

res

s=0

[Yse

st

]=lim

s0

[s−0

15

ss4

e

st

] = lim

s0

15

s4

e

st

=

15

4

e

0∗t

=

15

4

res

s=−4

[Yse

st

]=lim

s−4

[s4

15

ss4

e

st

] = lim

s−4

15

s

e

st

=

15

−4

e

−4∗t

yt=

15

4

−

15

−4

e

−4t

=

15

4

1−e

−4t



Opis układów liniowych ciągłych

Ys

Us

=

c

m

s

m

c

m−1

s

m−1

...c

1

s

1

c

0

d

n

s

n

d

n−1

s

n−1

...d

1

s

1

d

0

Ys

Us

=

c

m

d

n

s

m−n



c

m−1

d

n

s

m−1−n

...

c

1

d

n

s

1−n



c

0

d

n

s

−n

1

d

n−1

d

n

s

−1

...

d

1

d

n

s

1−n



d

0

d

n

s

−n

Opis układów liniowych ciągłych

Ys

Us

=

a

m

s

m−n

a

m−1

s

m−1−n

...a

1

s

1−n

a

0

s

−n

1b

m−1

s

−1

...b

1

s

1−n

b

0

s

−n

Gs=

Ys

U s=

Ys

Es×

Es

U s

Opis układów liniowych ciągłych

Es

Us =

1

1b

m−1

s

−1

...b

1

s

1−n

b

0

s

−n

Ys

Es =

a

m

s

m−n

a

m−1

s

m−1−n

...a

1

s

1−n

a

0

s

−n

Opis układów liniowych ciągłych

Es

Us =

1

1b

m−1

s

−1

...b

1

s

1−n

b

0

s

−n

Es[1b

m−1

s

−1

...b

1

s

1−n

b

0

s

−n

]=Us

Es=Us−Es[b

m−1

s

−1

...b

1

s

1−n

b

0

s

−n

]

Opis układów liniowych ciągłych

Ys

Es =

a

m

s

m−n

a

m−1

s

m−1−n

...a

1

s

1−n

a

0

s

−n

Ys = Es[a

m

s

m−n

a

m−1

s

m−1−n

...a

1

s

1−n

a

0

s

−n

]

Opis układów liniowych ciągłych

Ys = Es[a

m

s

m−n

a

m−1

s

m−1−n

...a

1

s

1−n

a

0

s

−n

]

Es=Us−Es[b

m−1

s

−1

...b

1

s

1−n

b

0

s

−n

]

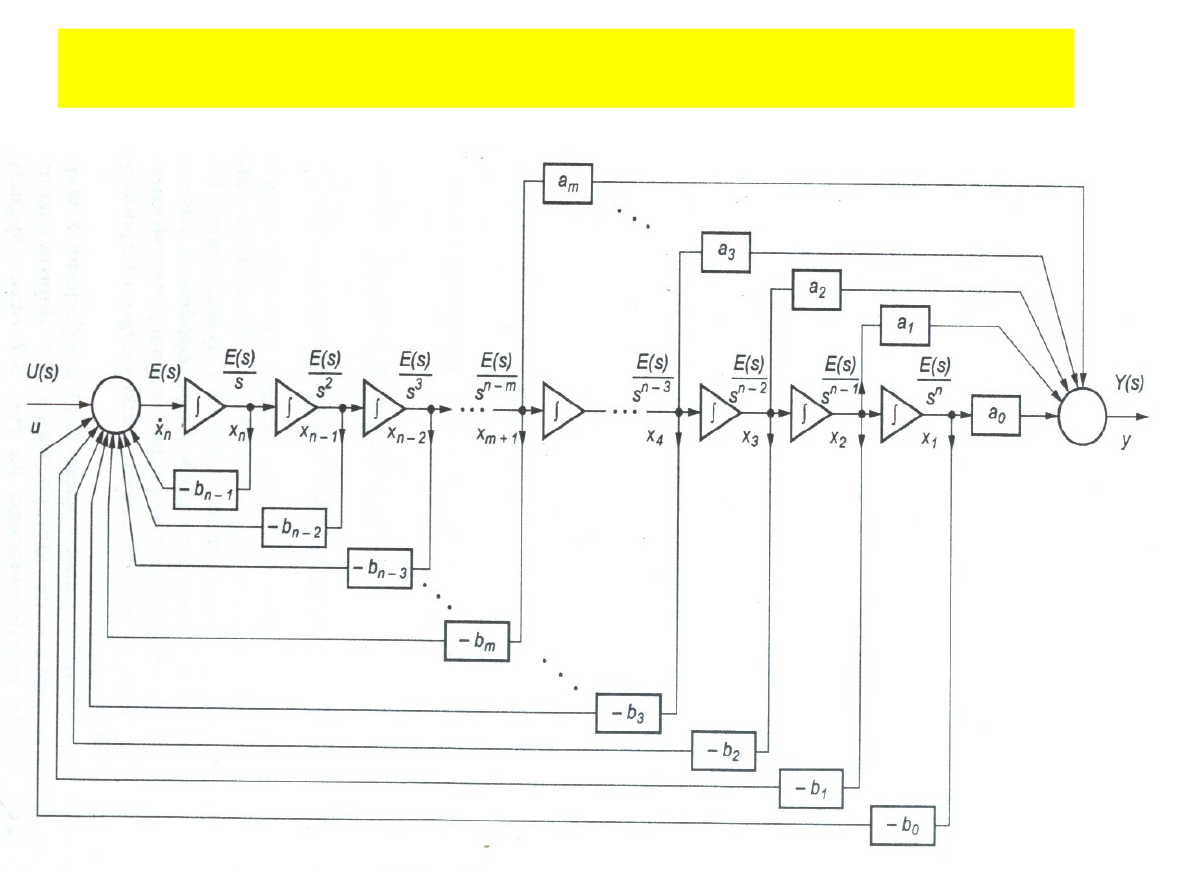
Opis układów liniowych ciągłych

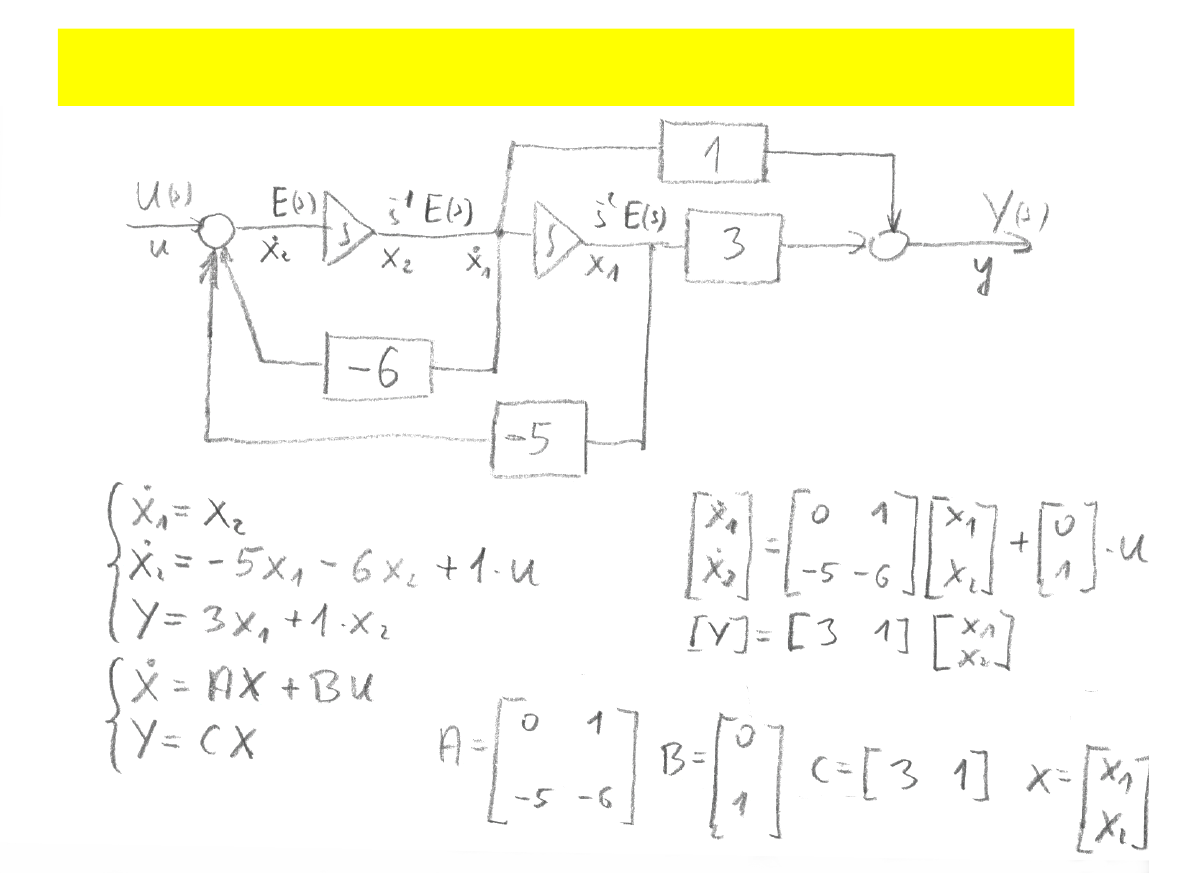
Opis układów liniowych ciągłych

˙x

1

=x

2

˙x

x

=x

3

................

˙x

n−1

=x

n

˙x

n

=−b

0

x

1

−b

1

x

2

−b

2

x

3

−...−b

n−1

u

y=a

0

x

1

a

1

x

2

a

2

x

3

...a

m

x

m−1

Równanie stanu

Równanie wyjścia

Opis układów liniowych ciągłych

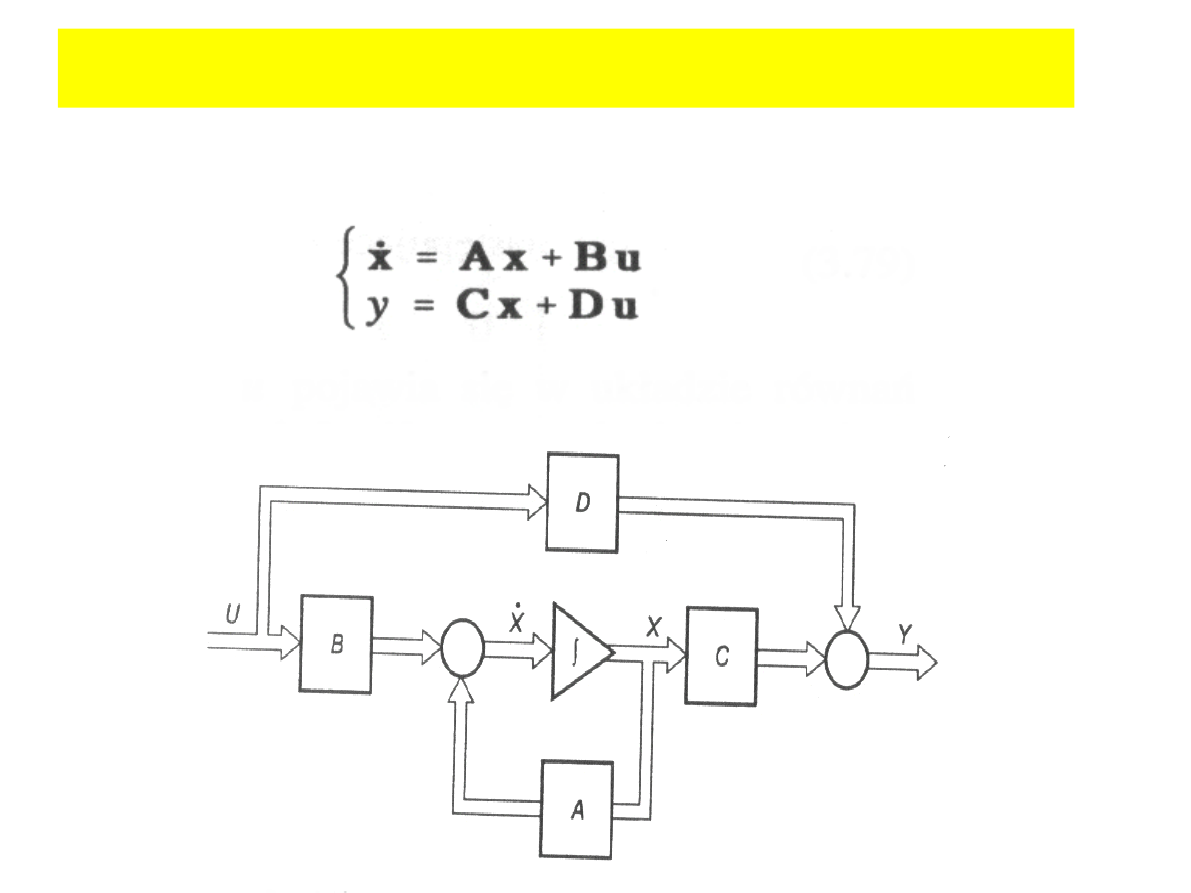
Opis układów liniowych ciągłych

Opis układów liniowych ciągłych

˙xt= AxtBut

yt=C xt

sX s= AX sBU s
sX s− AX s=BU s

[s1− A] X s=BUs

X s=[s1− A]

−1

B

Ys=C[s1− A]

−1

B

Gs=

Ys
Us

=C[s1− A]

−1

B=

C ad [s1− A]

−1

B

det [s1− A]

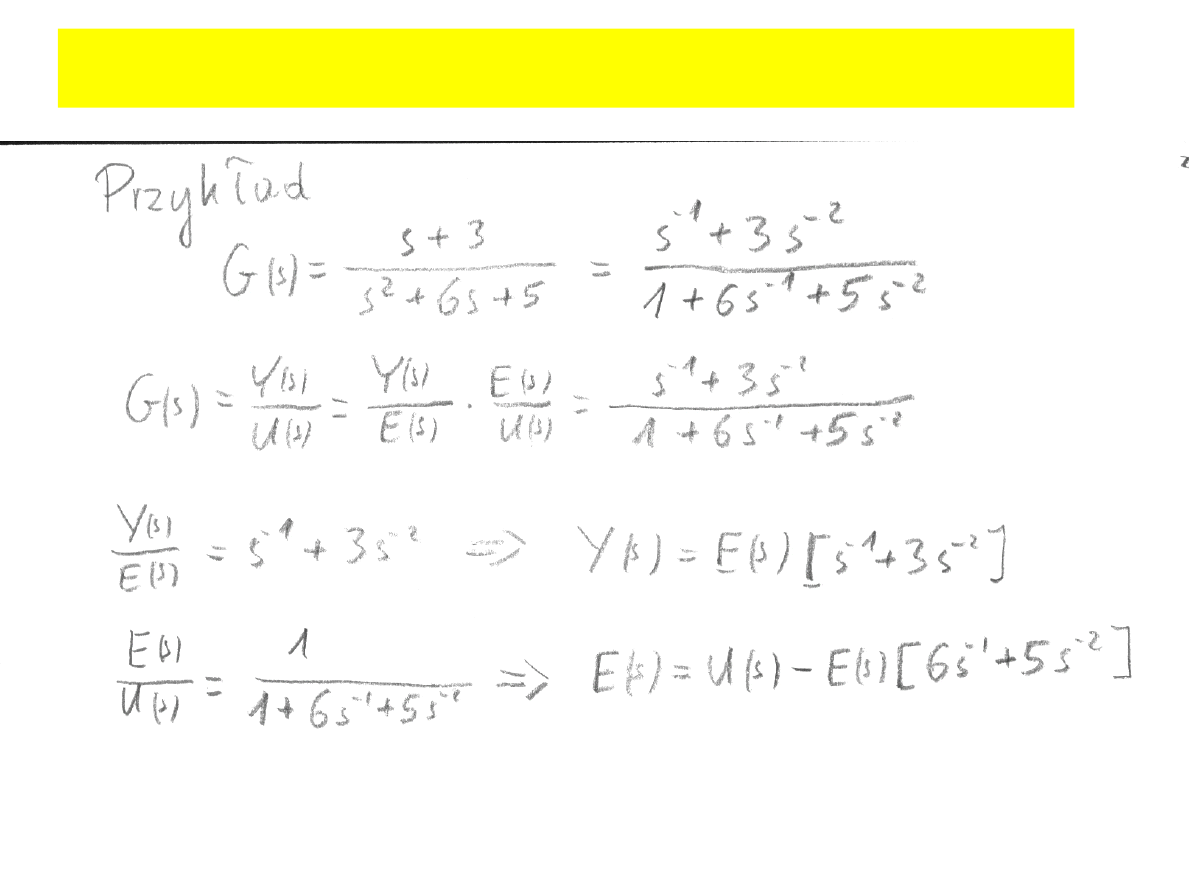
Opis układów liniowych ciągłych

Opis układów liniowych ciągłych