Dynamika

Dynamika



1. Spoczynek a ruch 
jednostajny



2. Idea siły



3. I Zasada Dynamiki



4. II Zasada Dynamiki



5. Definicja siły



6. III Zasada Dynamiki

 

 

1. Spoczynek a ruch 

1. Spoczynek a ruch 

jednostajny

jednostajny



Dawniej sądzono, że aby utrzymać 
ciało w ruchu (także jednostajnym) 
potrzebne jest działanie z zewnątrz



Galileusz (1564 - 1642):

– „Aby zmienić prędkość ciała potrzeba siły, 

aby utrzymać prędkość ciała 

nie 

trzeba 

siły”



Był to efekt ekstrapolacji wyników 
obserwacji (doświadczeń) - usunięcie 
wpływów zewnętrznych (np. tarcia)

 

 

2. Idea siły

2. Idea siły



Coś co powoduje zmiany stanu ruchu 
tj.:

– poruszenie lub zatrzymanie ciała
– przyśpieszenie lub opóźnienie ruchu 

ciała



Ma kierunek i zwrot - jest wektorem 



Siła wypadkowa - suma wektorowa



Powoduje też deformację



F



F

w

 

 

3. I Zasada Dynamiki

3. I Zasada Dynamiki



Ciało pozostaje w spoczynku lub



 w ruchu jednostajnym 

prostoliniowym jeśli nie działa nań 

siła lub siły działające równoważą 

się 

 

 

4. II Zasada Dynamiki

4. II Zasada Dynamiki



Bezwładność ciał - masa



Jeśli                     to gdy 

m  

  to  

a



Newton (1643 - 1727)



F

const

w



.

m

a

m

m

a

a

ma

m a

F

~ ;

;

1

1

2

2

1

1 1

2 2















F

ma

a

F

m

w





;

 

 

II Zasada Dynamiki, c.d.

II Zasada Dynamiki, c.d.



Przyśpieszenie ciała jest 

wprost proporcjonalne do siły 

wypadkowej działającej na to 

ciało i odwrotnie 

proporcjonalne do jego masy

 

 

5. Definicja siły

5. Definicja siły



Definicją siły jest II Zasada 
Dynamiki



[F] = 1N (niuton) = 1kgm/s

2

g

m

G

a

m

F

w













:

np.

;

 

 

6. III Zasada Dynamiki

6. III Zasada Dynamiki



Siły - oddziaływania między ciałami



Zawsze gdy jedno ciało działa na 
drugie samo też doznaje działania siły



Siły te możemy nazwać akcją i reakcją



Każdej akcji towarzyszy reakcja 

równa i przeciwnie skierowana

 

 

Ruch względny

Ruch względny



1. Ruchome układy odniesienia



2. Transformacja Galileusza



3. Względna prędkość układów



4. Względne przyśpieszenie - 
układ 

nieinercjalny



5. Siły pozorne (bezwładności)



6. Przykłady

 

 

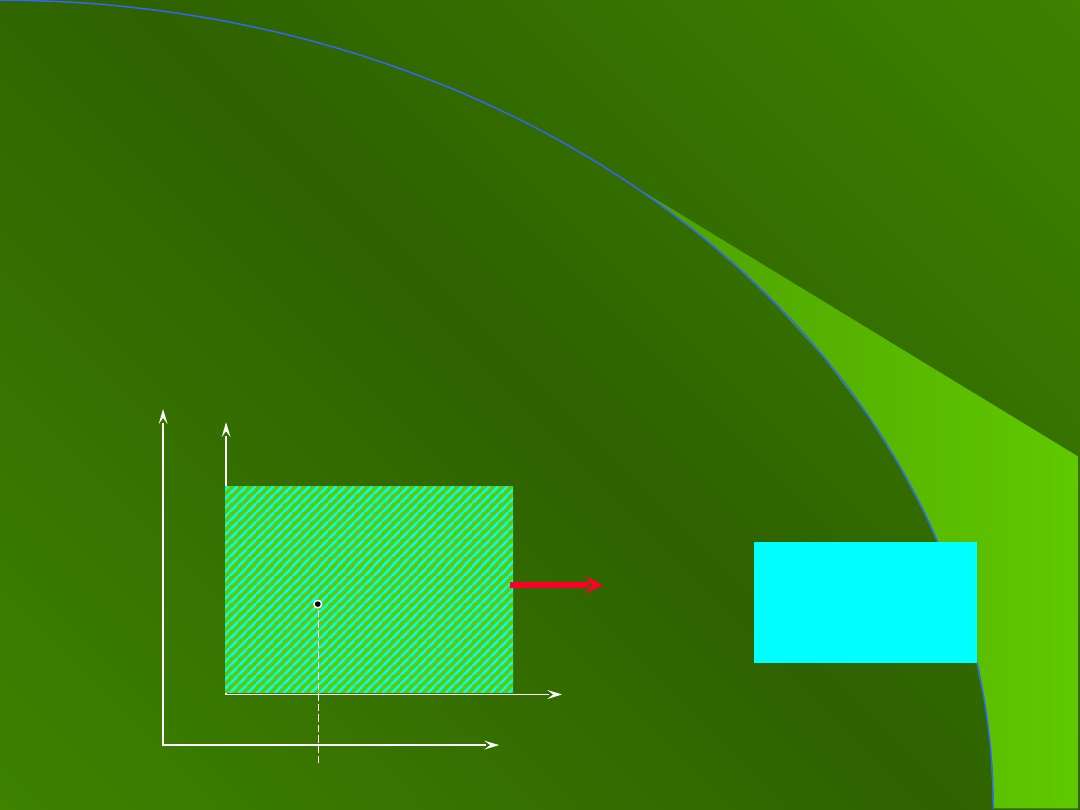
1. Ruchome układy 

1. Ruchome układy 

odniesienia

odniesienia



Nie ma układów nieruchomych 
absolutnie



Zakładamy:

układy „nieruchomy” i 

„ruchomy”

     dla 

y

x

O

u

t t

x

x

 





'

'

0

0

0

0

y’

x’

O’

A=A’

t

1

 

 

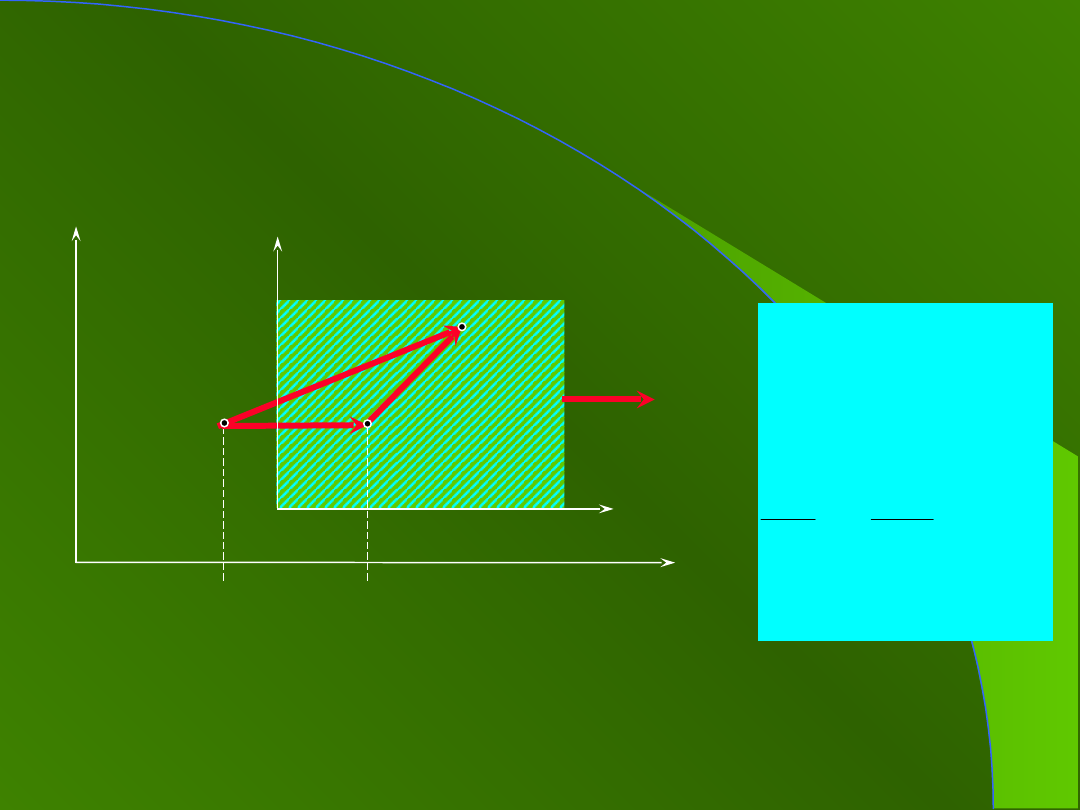
2. Transformacja 

2. Transformacja 

Galileusza

Galileusza

y

x

O

y’

x’

O’

u

A’

B=B’

A

t

2

r

r'



u t











 



 







  

r

r u t

dr dr udt

dr

dt

dr

dt

u

v v u





 





 

'

'

'

'