Nierówność informacyjna

 

 

 

 

 

 

 

 

 

 





 

   





















I

S

I

B

S

x

f

E

E

x

f

x

f

NE

E

I

N

i

1

1

;

ln

''

'

;

;

'

'

2

2

2

1

2

2

2



























































Informacja zawarta w
próbie

Zależność między wariancją estymatora S parametru  a

informacją

Jeżeli obciążenie estymatora (B) jest równe zeru

Weryfikacja hipotez statystycznych

Hipoteza statystyczna – założenie co do

rozkładu cech w populacji.

Test statystyczny – narzędzie weryfikacji tej

hipotezy.

Testy parametryczne: weryfikacja hipotez

parametrycznych, które dotyczą parametrów

rozkładu danej cechy w populacji generalnej.

Testy nieparametryczne: weryfikacja

hipotez nieparametrycznych dotyczących,

np. zgodności rozkładu cech w populacji z

rozkładem teoretycznym, zgodności

rozkładów cech w dwóch różnych

populacjach, losowości próby.

Hipotezy i testy parametryczne

Hipoteza prosta – zakłada wartości

wszystkich parametrów rozkładu.

Hipoteza złożona – wartość co najmniej

jednego parametru jest nieznana (np.
zakładamy tylko postać funkcyjną rozkładu).

Hipoteza zerowa (H

o

) – hipoteza, którą

weryfikujemy.

Hipoteza alternatywna (H

1

) – co najmniej

jeden z parametrów rozkłady jest różny od
tego z hipotezy zerowej.

Błąd pierwszego rodzaju (false
negative) – odrzucenie prawdziwej
hipotezy H

o

.

Błąd drugiego rodzaju (false positive)
–przyjęcie fałszywej hipotezy H

o

.

Błędy popełniane podczas weryfikacji

hipotez statystycznych

Poziom istotności ()
P(|x|x

o

)= (test dwustronny)

P(xx

o

)= (test jednostronny)

Obszar krytyczny (S

c

):

P(xS

c

|H

o

)=

Poziom istotności definiuje
prawdopodobieństwo popełnienia błędu
pierwszwego rodzaju (odrzucenia
prawdziwej hipotezy zerowej).

Moc testu: prawdopodobieństwo
odrzucenia hipotezy zerowej w zależności
od hipotezy alternatywnej.

M(S

c

,)=P(XS

c

|H)=P(XS

c

|)

Test najmocniejszy hipotezy prostej H

o

względem hipotezy alternatywnej H

1

:

P(S

c

,

1

)=1-=max

Test jednostajnie najmocniejszy: test
najmocniejszy względem jakiejkolwiek
hipotezy alternatywnej.

Test F Fishera równości wariancji

Mamy dwie populacje o rozkładzie normalnym (np.
przypadek pomiaru tej samej wielkości różnymi
przyrządami). Pytanie: czy te populacje mają tą samą
wariancję. W tym celu rozważamy iloraz F=s

1

2

/s

2

2

 

 

2

2

2

1

1

2

2

)

2

(

2

1

2

2

1

2

2

2

2

2

2

2

2

2

2

2

2

2

1

2

1

2

1

2

1

1

2

1

2

1

exp

2

2

1

)

1

(

)

1

(

X

X

f

f

F

f

f

fs

s

N

X

fs

s

N

X

f

f













 























































































































 



























































1

1

2

2

2

)

(

1

2

2

2

1

0

2

2

1

1

2

2

1

2

1

2

2

1

2

2

2

1

2

2

2

1

2

1

1

1

F

s

s

P

dF

F

f

f

F

f

f

f

f

f

f

F

s

s

P

F

X

X

P

F

W

F

f

f

f

f

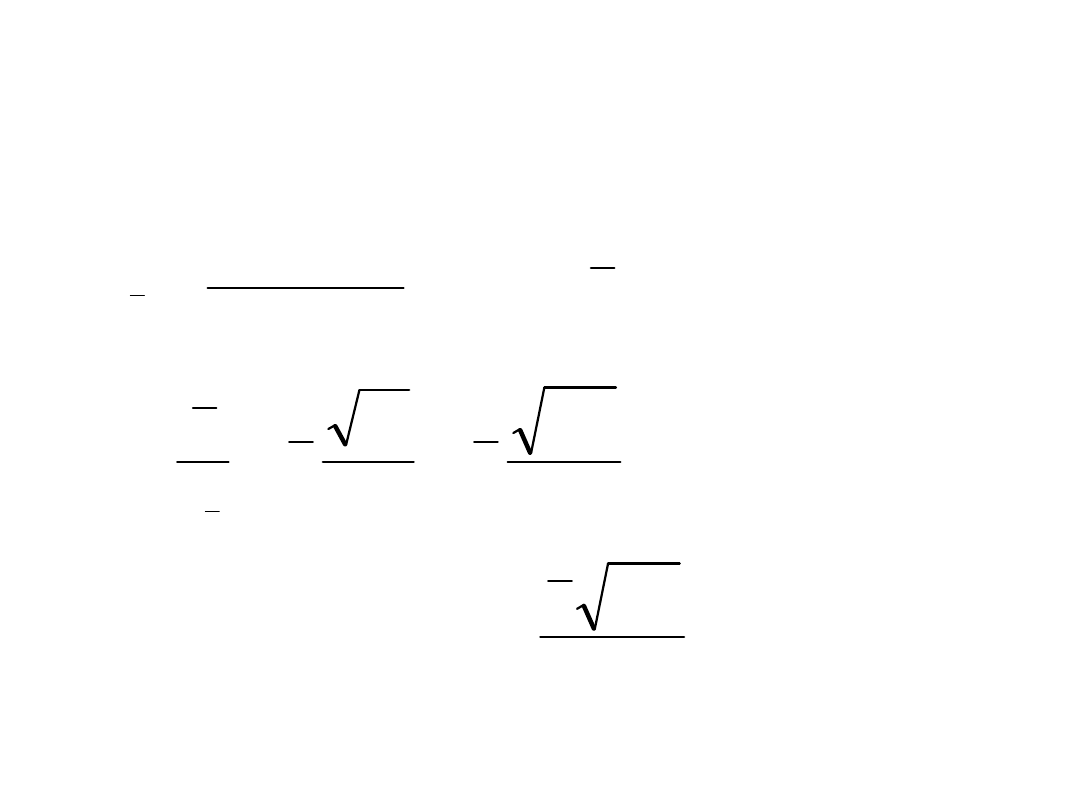
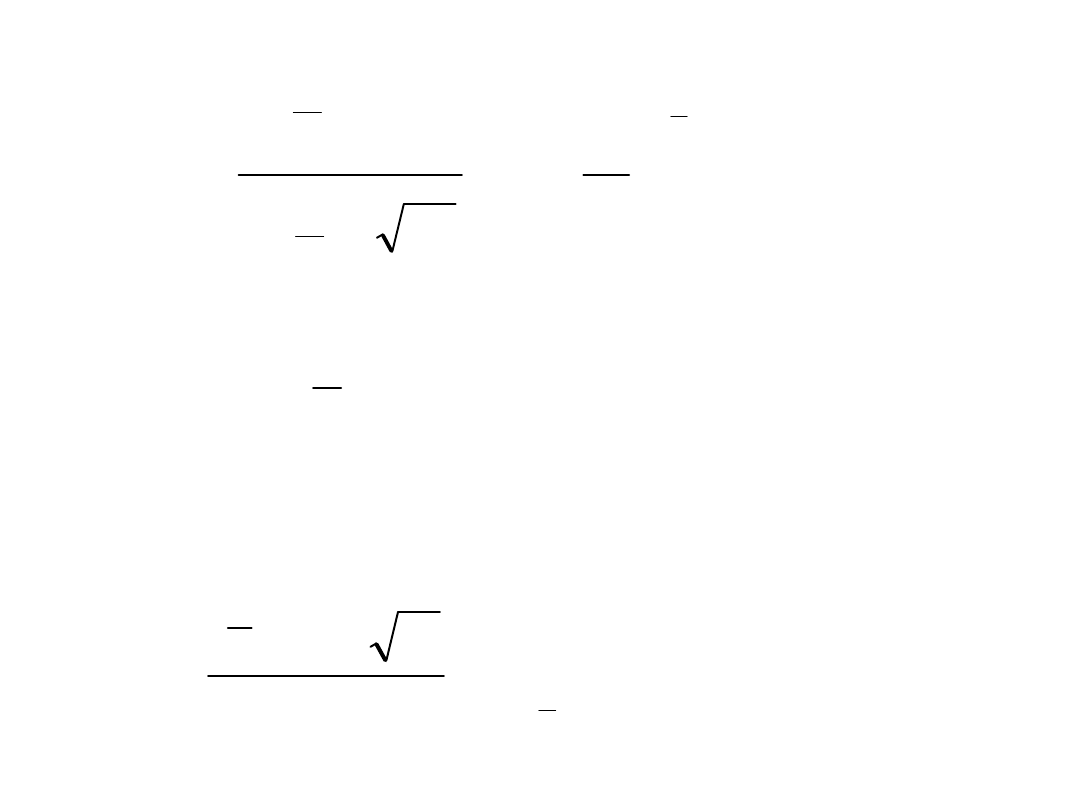
Porównywanie wartości średnich

(test Studenta)











































t

Nf

x

P

t

P

t

F

Nf

x

s

N

x

s

x

t

x

x

N

N

s

x

x

N

j

j

x







)

(

)

(

)

1

(

1

1

2

2

)

1

(

2

1

d

)

(

f

d

f

1

f

f

2

1

)

1

f

(

2

1

)

t

(

F

'

t

0

t

)

1

f

(

2

1

2













































































Weryfikacja hipotezy, że x=

0













2

1

1

x

0

t

s

N

|

x

|

|

t

|

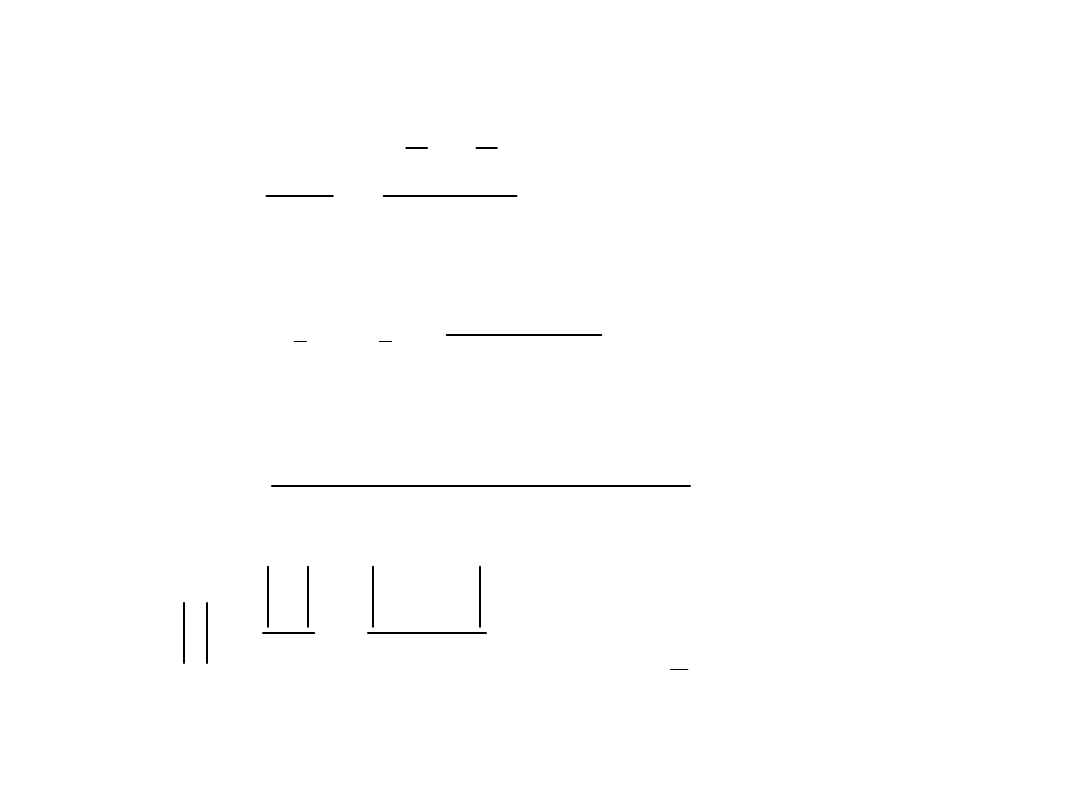
Weryfikacja hipotezy o równości wartości średnich z
dwóch serii pomiarów

)

1

(

)

1

(

)

1

(

)

1

(

|

|

|

|

|

|

2

1

2

2

2

1

2

2

2

1

2

1

2

2

2





































N

N

s

N

s

N

s

s

N

N

N

N

s

s

s

s

y

x

s

t

y

x

y

x

2

2

1

2

1

1

'

























N

N

f

t

t

s

y

x

s

t





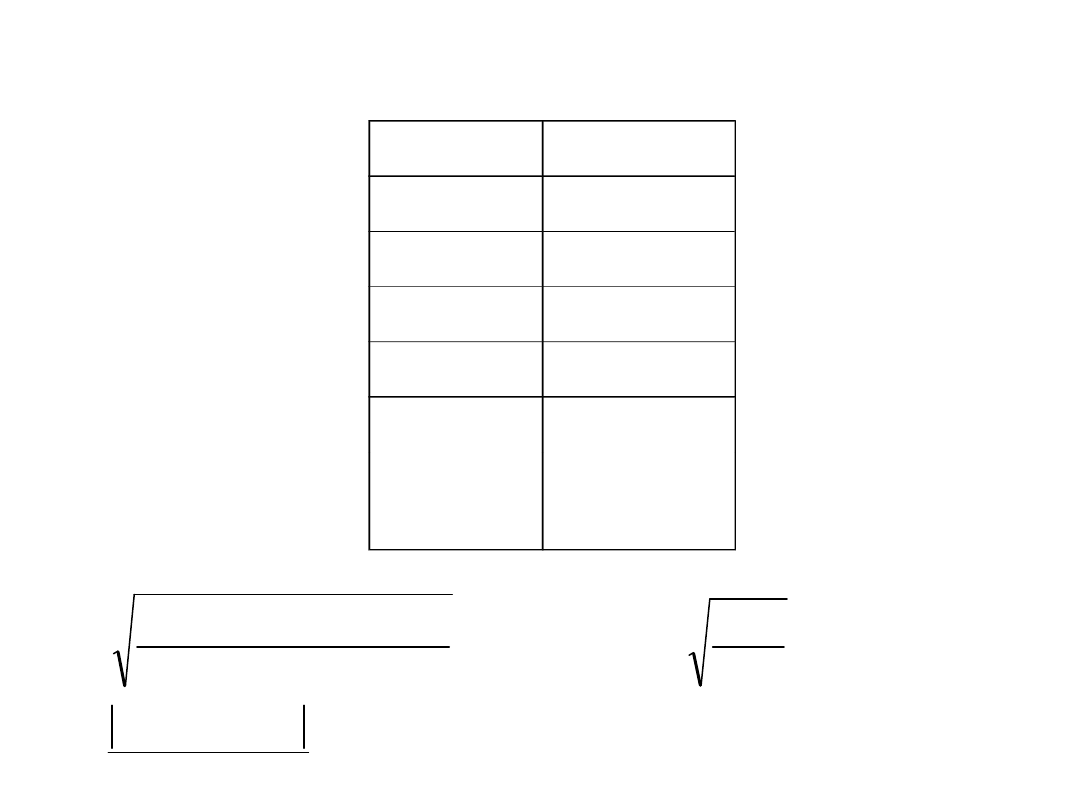
Przykład: porównywanie średnich z dwóch serii

oznaczeń azotu w cynchoninie

Grupa 1 Grupa 1

9,29

9,53

9,38

9,48

9,35

9,61

9,43

9,68

średnia

9,363

9,575

odch.stan
d.

0,058

0,088



 



71

,

3

)

6

,

01

,

0

(

;

6

1

4

1

4

;

02

,

4

0527

.

0

575

,

9

363

,

9

0527

,

0

0745

,

0

4

4

4

4

;

0745

,

0

6

088

,

0

3

058

,

0

3

2

2







































t

f

t

s

s

Test Studenta dla par wiązanych

Oznaczanie zawartości NaOH w dwóch seriach

roztworu po elektrolizie NaCl (mg/dm

3

) przed (x) i za

filtrem (y)

x

y

d=y-x

100,1

96,6

-3,5

115,1

115,6

+0,5

130,0

125,5

-4,5

93,6

94,0

+0,4

108,3

103,3

-5,0

137,2

134,4

-2,8

104,4

100,2

-4,2

97,3

97,3

0





36

,

2

7

,

95

,

0

93

,

2

8

32

,

2

40

,

2

7

1

8

32

,

2

40

,

2





















P

t

f

s

d

d

Wykrywanie błędów grubych: test

Dixona (nieparametryczny)

min

max

2

1

x

x

x

x

Q







x

1

– wynik podejrzany o błąd gruby

x

2

– wynik mu najbliższy

Wynik x

1

możemy odrzucić na poziomie

istotności  jeżeli Q > Q(, n) (n jest liczbą

pomiarów).

Wartości krytyczne testu Dixona

n

1-

0.90

0.95

0.99

3

0.89

0.94

0.99

4

0.68

0.77

0.89

5

0.56

0.64

0.76

6

0.48

0.56

0.70

7

0.43

0.51

0.64

8

0.40

0.48

0.58

Przykład: pomiar zawartości

grafitu w żeliwie

1 2,86

2 2,89

3 2,90

4 2,91

5

2,99





5

,

95

,

0

62

.

0

86

.

2

99

.

2

91

.

2

99

.

2

Q

Q

Q











Testy nieparametryczne

• Testy losowości: badamy, czy próba jest losowa

– test mediany (Stevensa).

• Testy zgodności: badamy, czy rozkład z próby

jest zgodny z założonym

– Test 

2

, test W Shapiro-Wilka, test Kołmogorowa test

Lillieforsa (badanie normalności rozkładu).

• Testy jednorodności: badamy, czy dwie próby

pochodzą z tej samej populacji

– test serii Walda-Wolfowitza, test U Manna-Whitneya,

test Kołmogorowa-Smirnowa (dla prób niezależnych),

– test znaków, test kolejnosci par Wilcoxona (dla prób

zależnych).

Test 

2

dobroci dopasowania































N

i

i

i

i

N

i

i

i

i

i

i

f

g

u

T

f

g

u

1

2

1

2





g

i

: wynik i-tego pomiaru

f

i

: wartość teoretyczna wyniku i-tego pomiaru



i

: odchylenie standardowe i-tego pomiaru.

Wielkości u

i

mają rozkład normalny o zerowej średniej i

jednostkowej wariancji a zatem wielkość T ma rozkład 

2

o N-p

stopniach swobody, gdzie p jest liczbą estymowanych
parametrów funkcji f.

Dopasowanie uznajemy za złe na poziomie istotności  jeżeli

T

2



1

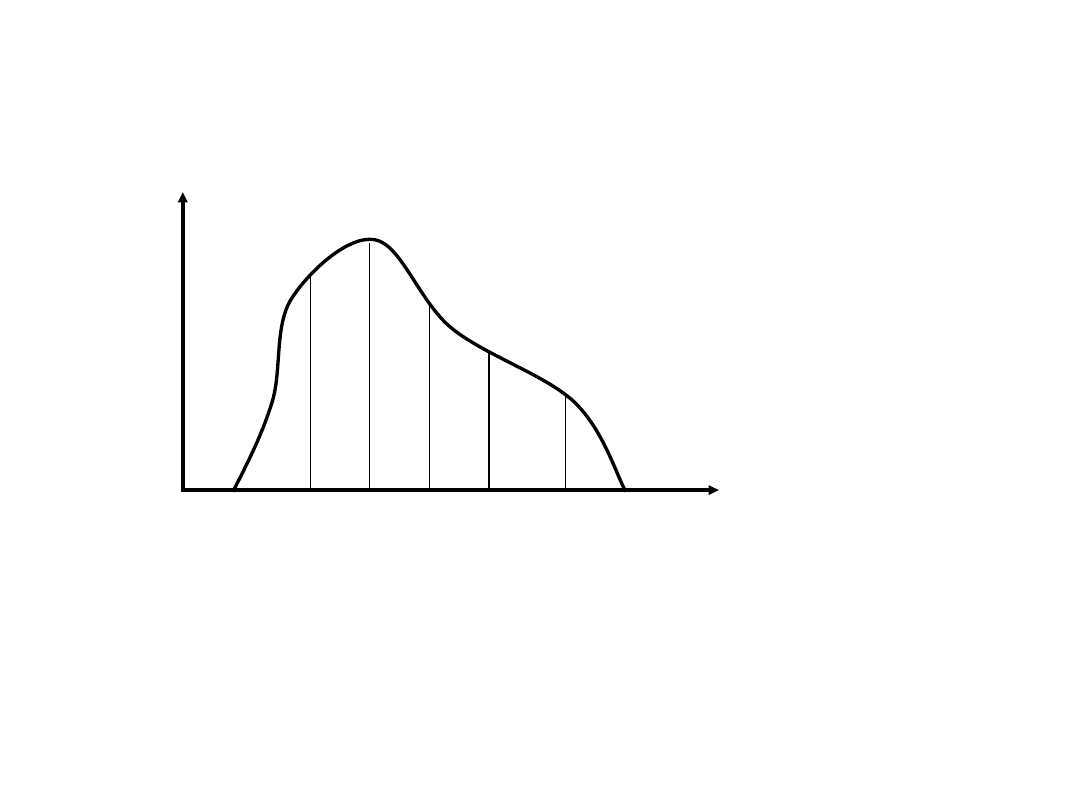
Zastosowanie testu 

2

do weryfikacji

hipotezy o rozkładzie częstości

obserwacji









i

dx

x

f

x

P

p

i

i





)

(

)

(

} }

}

}

x

f(x
)



1





2

… 

k

… 

r

























r

i

i

r

i

i

i

i

r

i

i

i

i

n

n

np

np

n

np

n

1

1

2

1

2

2

2

)

(

)

(



Hipotezę o zgodności rozkładu obserwowanego z
rozkładem założonym odrzucamy na poziomie istotności a
jeżeli 

2







1

dla f stopni swobody.

f=liczba stopni swobody=r-p-1 gdzie p jest liczbą parametrów
rozkładu (najwyżej r-1 stopni swobody).

n

i

: liczba obserwacji wielkości w i-tym przedziale;

n: całkowita liczba obserwacji.

np

i

: wartość oczekiwana liczby obserwacji w i-tym

przedziale

Wartość oczekiwana
wariancji liczby
obserwacji.

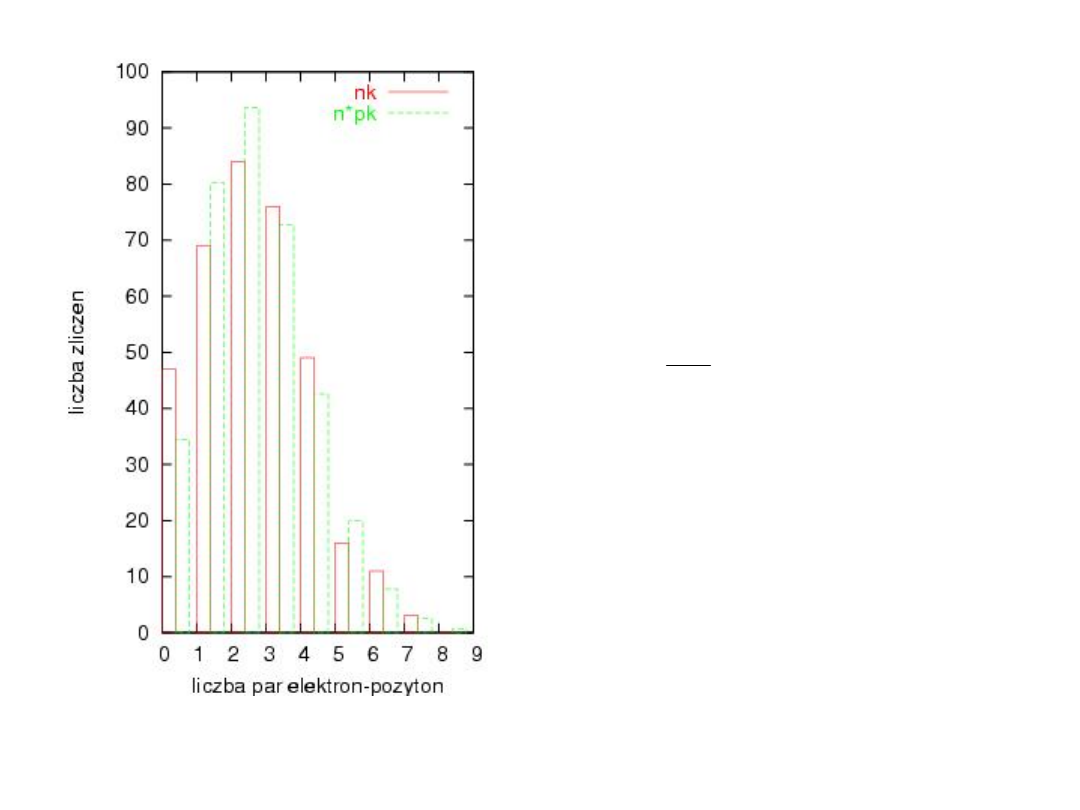
Przykład: porównanie
liczby zliczeń par
elektron-pozyton w
komorze pęcherzykowej
naświetlonej
promieniowaniem  z

rozkładem Poissona.



2

=10.44



2

0.99

=16.81

Nie ma zatem podstaw
do odrzucenia rozkładu
Poissona.









k k

k

k

n

e

k

k

p

!

/

~

!

)

(







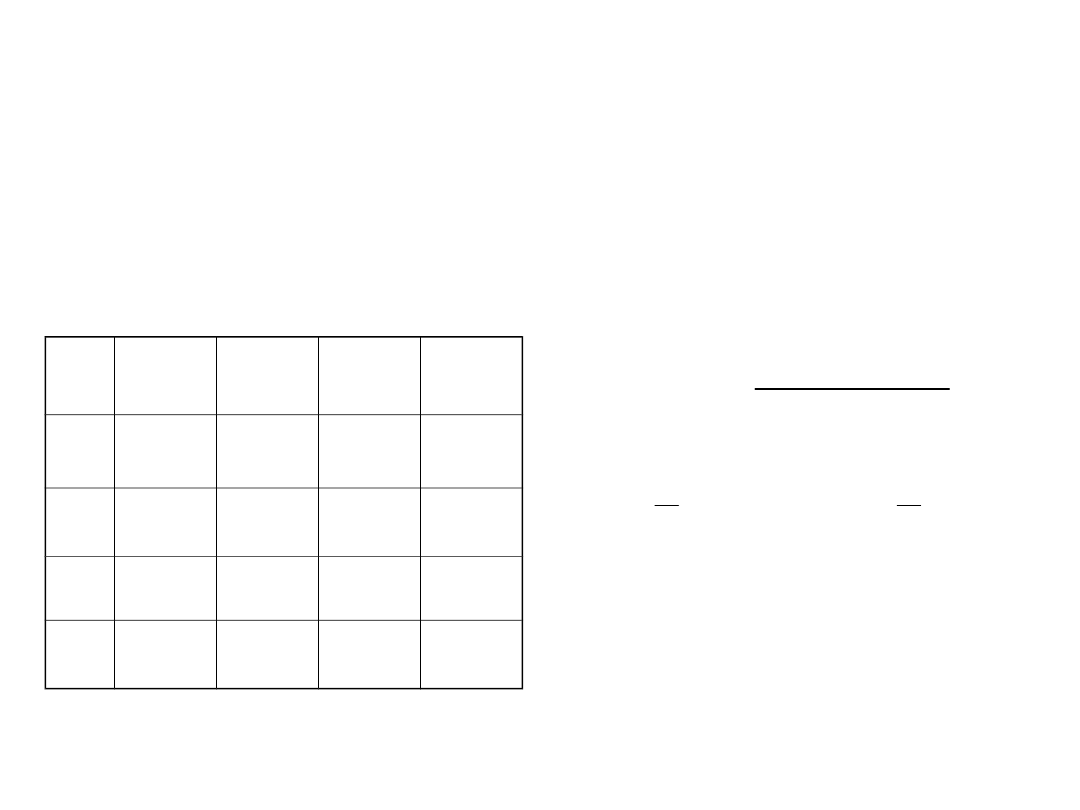
Zastosowanie testu 

2

do analizy tabeli

wkładów

y

1

y

2

…

y

l

x

1

n

11

n

12

…

n

1l

x

2

n

21

n

22

…

n

2l

… …

…

…

…

x

k

n

k1

n

k2

…

n

kl

































k

i

l

j

ij

k

i

ij

j

l

j

ij

i

k

i

l

j

j

i

j

i

ij

n

n

n

n

q

n

n

p

q

p

n

q

p

n

n

1

1

1

1

1

1

2

2

1

~

1

~

~

~

)

~

~

(

x, y: zmienne losowe mogące przyjmować wartości
odpowiednio x

1

, x

2

,…, x

k

oraz y

1

, y

2

,…, y

l

.

Każdej kombinacji zmiennych (x

i

,y

j

)

przyporządkowana jest liczba obserwacji n

ij

.

Jeżeli zmienne są współzależne na poziomie istotności  to 

2







1

dla f=kl-1-(k+l-2)=(k-1)(l-1) stopni swobody.

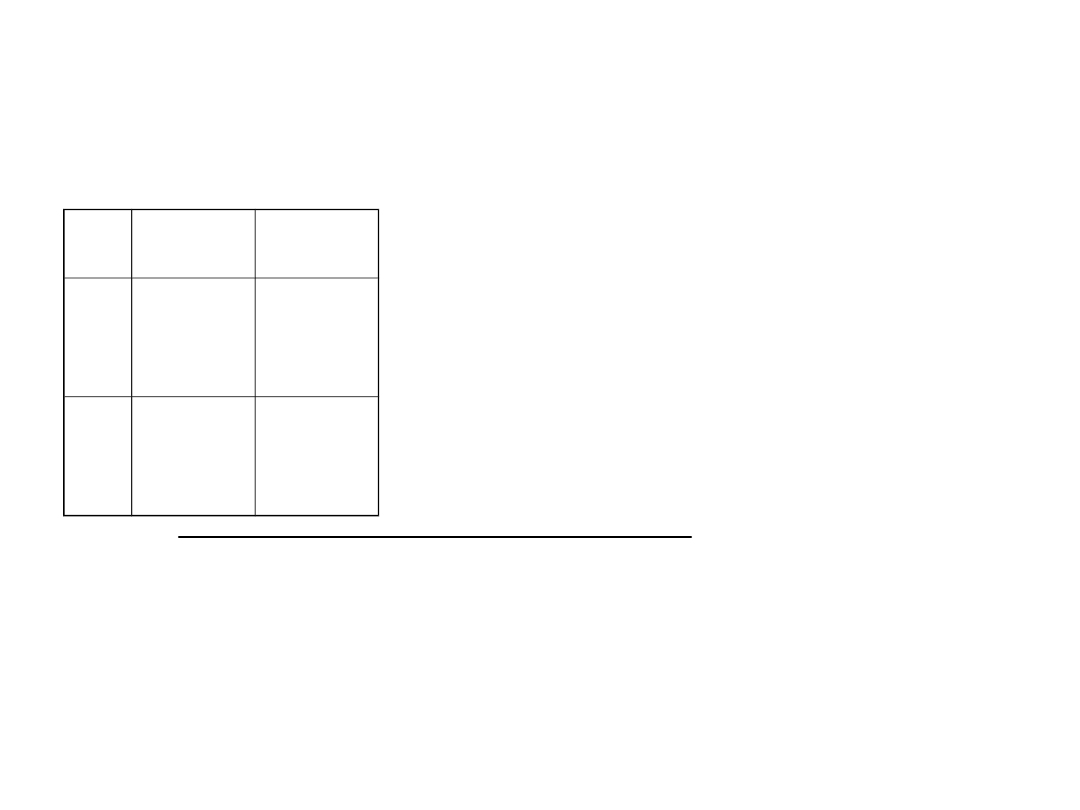
y

1

y

2

x

1

n

11

=

a

n

12

=

b

x

2

n

21

=

c

n

22

=

d

)

)(

)(

)(

(

)

(

2

2

d

b

c

a

d

c

b

a

bc

ad

n















Przykład z medycyny: ocena skuteczności dwóch
metod leczenia danej choroby.

x

1

: pierwsza metoda

leczenia

x

2

: druga metoda leczenia

y

1

: przypadki wyleczone

y

2

: przypadki niewyleczone

f=liczba stopni swobody=(2-1)(2-1)=1

Jeżeli metody leczenia mają różną skuteczność to










Test mediany (badanie losowości

próby)

1.

1.

Wyznaczamy medianę (m).

Wyznaczamy medianę (m).

2.

2.

Danym nieuporządkowanym przyporządkowujemy

Danym nieuporządkowanym przyporządkowujemy

następujące oznaczenia:

następujące oznaczenia:

•

A gdy x<m

A gdy x<m

•

B gdy x>m

B gdy x>m

•

0 gdy x=m

0 gdy x=m

3.

3.

Obliczamy liczbę następujących po sobie serii AAA…

Obliczamy liczbę następujących po sobie serii AAA…

A i BBB…B.

A i BBB…B.

Liczby serii spełniają rozkład normalny z następującą

Liczby serii spełniają rozkład normalny z następującą

wartością średnią i wariancją

wartością średnią i wariancją

 

 









1

1

2

2

1

2

2

2











n

n

n

n

n

n

K

s

n

n

n

K

E

b

a

b

a

b

a

n

a

– liczba pomiarów A; n

b

– liczba pomiarów B; n – liczba

pomiarów

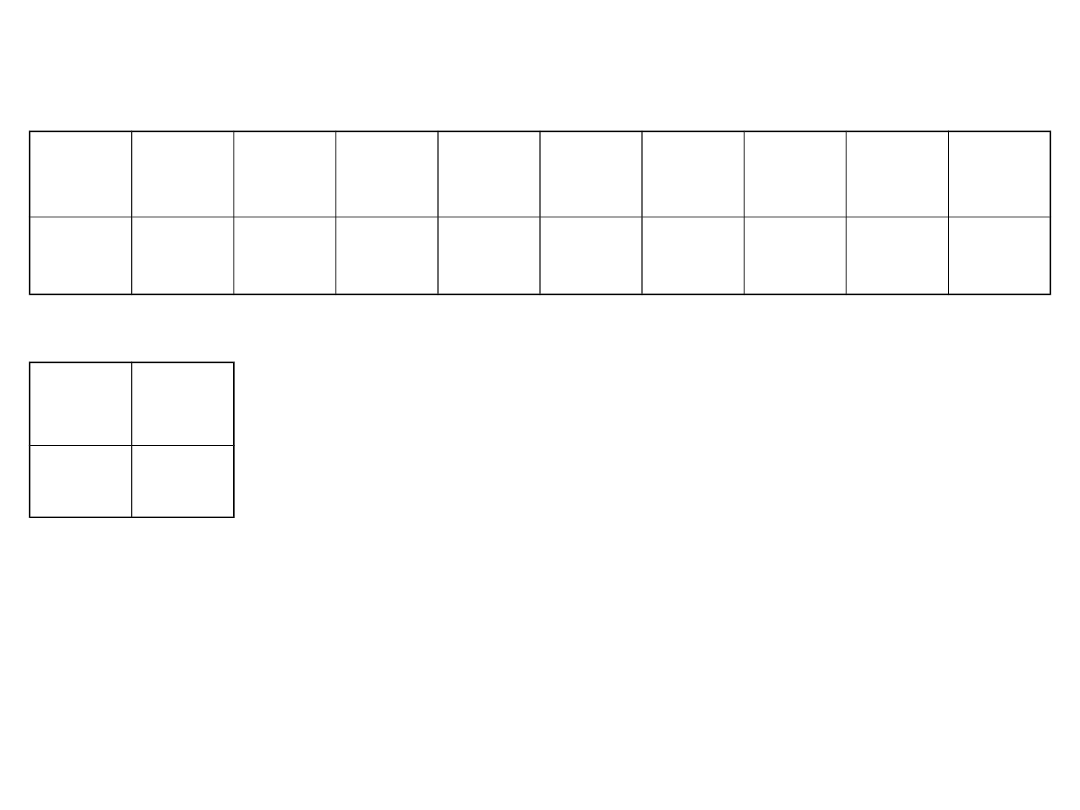
74,5 191,0 55,5

5,15

36,4

35,0

46,0

10,9

7,35

6,65

B

B

B

A

B

A

B

A

A

A

173,

5

26,0

B

A

Mediana m=35,7

n=12, n

a

=6, n

b

=6

Liczba serii k=8

Przykład (seria 12 pomiarów)

E(k)=2*6*6/12+1=7, s

2

(k)=2*6*6*(2*6*6-1)/

[12*12*(12-1)]=3.23

Dla a=5% (ok. 3s odchylenia) przedział ufności rozciąga
się od k=3 do k=10. Próba jest zatem losowa.

Test Wilcoxona (par wiązanych)

• W tabeli ustawiamy w pary odpowiadające

wielkości i obliczamy różnice.

• Sortujemy pary według różnic.
• Każdej parze przyporządkowujemy rangę,

która jest równa numerowi porządkowemu

pary (po sortowaniu), przy czym uśredniamy

rangi, którym odpowiadają te same różnice.

• Osobno sumujemy rangi dodatnie i ujemne.
• Mniejsza z tych sum stanowi statystykę W

Wilcoxona.

• Porównujemy W z wartością krytyczną i

odrzucamy hipotezę o identyczności

wyników w parach jeżeli W>W

tab

.

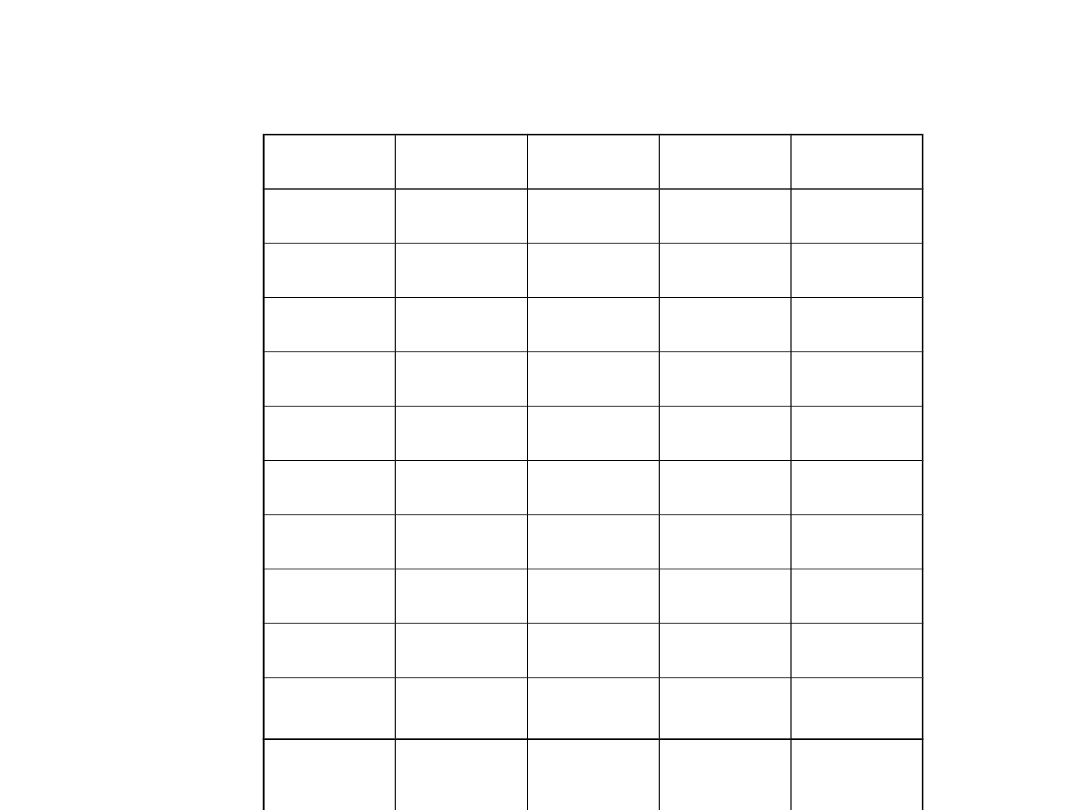
W

J

d

ranga znak

3,2

3,5

0,3

5

+

2,7

3,0

0,3

5

+

3,1

3,8

0,7

10

+

2,9

3,2

0,3

5

+

3,4

3,8

0,4

8,5

+

2,8

3,2

0,4

8,5

+

3,4

3,7

0,3

5

+

3,4

3,6

0,2

1,5

+

3,2

3,4

0,2

1,5

+

3,3

3,6

0,3

6

+

sum

a

31,4

34,8

3,4

55

Przykład: ocena różnic wysokości drzew wiosną

i jesienią

Dla dużych prób liczba znaków „+” spełnia
rozkład normalny z wartością średnią E(W

+

) i

wariancją s

2

(W

+

):

 





 







24

1

2

1

4

1

2















n

n

n

W

s

n

n

W

E