WYKŁAD 7

ATOM WODORU,

JONY WODOROPODOBNE;

PEŁNY OPIS

CZĘŚĆ I

Z protonów i jeden elektron:





























































































E

r

Ze

sin

r

1

sin

sin

r

1

r

r

r

r

1

2

h

2

2

2

2

2

2

2

2

2





  















,

Y

r

R

,

,

r

Podstawiając funkcję postaci:

otrzymamy:



























































































2

2

2

2

2

2

2

Y

sin

1

Y

sin

sin

1

Y

1

r

Ze

E

h

r

2

dr

dR

r

dr

d

R

1

CY

Y

sin

1

Y

sin

sin

1

2

2

2











































CR

R

r

Ze

E

h

r

2

dr

dR

r

dr

d

2

2

2

2



































i w konsekwencji:

C jest wartością własną operatora:

2

2

2

sin

1

sin

sin

1

X

ˆ









































0

R

r

2

C

h

r

Ze

E

h

r

2

dr

dR

r

dr

d

2

2

2

2

2

2







































a z kolei funkcje Y, tworzące funkcje

falowe atomu wodoru, są funkcjami

własnymi operatora X.

Żeby ustalić tożsamość operatora X,

przeanalizujemy drugie równanie:

które przepiszemy w następującej postaci:

ER

R

r

2

h

C

r

Ze

dr

d

r

dr

d

r

1

2

h

2

2

2

2

2

2







































jawnie pokazującej pochodzenie członów

hamiltonianu: energia kinetyczna,

potencjalna i ???.

Dla klasycznej cząstki w polu siły

centralnej, zachowana jest całkowita

energia i moment pędu:

 

const

mr

I

L

const

r

V

2

mv

E

2

2

















Rozkładając prędkość cząstki na

składowe radialną i tangencjalną

otrzymamy:

co ostatecznie można przedstawić w

postaci:

 





 

 

r

V

2

mr

2

mv

r

V

r

v

m

2

1

E

2

2

2

r

2

2

r

















 

r

V

mr

2

L

2

mv

E

2

2

2

r







Porównując otrzymane wyrażenie z

hamiltonianem:

widzimy, że operator X jest operatorem

kwadratu momentu pędu:







































2

2

2

2

2

2

r

2

h

C

r

Ze

dr

d

r

dr

d

r

1

2

h

H

Y

h

C

Y

sin

1

sin

sin

1

h

Y

Lˆ

2

2

2

2

2

2





























































a funkcja Y to funkcja własna tego

operatora; czyli amplituda

prawdopodobieństwa, że cząstka, której

kwadrat momentu pędu wynosi ,

znajdzie się w punkcie określonym kątami

θ i φ.

2

h

C

Rozwiązanie równania:

Y

h

C

Y

sin

1

sin

sin

1

h

Y

Lˆ

2

2

2

2

2

2





























































jest potrzebne.

Możliwość dalszej separacji:

.

   











Y

2

2

2

2

m

d

d

1

sin

C

d

sin

d

d

sin

1













































;

0

m

d

d

2

2

2

















im

e

rozwiązanie

okresowe:

a więc: m = 0, ±1, ±2,

±3….

Interpretacja liczby kwantowej m

y

x

x

y

y

cos

sin

r

x

sin

sin

r

y

y

x

x











































































































cos

r

z

sin

sin

r

y

cos

sin

r

x









































i

h

x

y

y

x

i

h

p

ˆ

r

Lˆ

z

z



 

 

 





















h

m

e

i

h

Lˆ

im

z

rzut momentu

pędu

Równanie na część biegunową będzie

miało postać:





0

m

sin

C

d

sin

d

d

sin

2

2







































 cos

Wprowadzamy nową

zmienną:



















d

d

sin

d

d

d

d

d

d

Ponieważ:





0

sin

m

C

d

sin

d

d

0

m

sin

C

d

sin

d

d

sin

2

2

2

2

2

2

2

















































































Ostatecznie:

Jeśli

przyjmiemy:

otrzymamy tzw równanie różniczkowe

Legendre’a:

 

0

1

m

C

d

1

d

d

2

2

2



















































1

l

l

C





oraz m = 0

 





l

l

2

l

2

2

P

1

l

l

d

dP

2

d

P

d

1



















którego rozwiązania, to tzw. wielomiany

Legendre’a:





 

















0

k

k

k

l

l

a

P

cos

P

Aby znaleźć współczynniki

a

k

wstawiamy:

do równania różniczkowego Legendre’a:

 





l

l

2

l

2

2

P

1

l

l

d

dP

2

d

P

d

1



















i otrzymujemy:

 













0

k

k

k

l

a

P





























































0

k

k

k

0

k

k

k

0

k

k

k

0

k

2

k

k

0

a

1

l

l

k

a

2

1

k

k

a

1

k

k

a

Pomijamy dwa pierwsze wyrazy w

pierwszej sumie i przenumerowujemy ją,

zastępując k przez k+2:

Wszystkie współczynniki przy kolejnych

potęgach muszą być równe 0, zatem:

































































0

k

k

k

0

k

k

k

0

k

k

k

0

k

k

2

k

0

a

1

l

l

k

a

2

1

k

k

a

2

k

1

k

a

















 









k

k

2

k

a

2

k

1

k

1

l

l

1

k

k

a

2

k

1

k

1

l

l

k

2

1

k

k

a





























Nieskończona suma dla ξ równego 1

dałaby nieskończoną wartość. Suma

będzie skończona

dla l naturalnych.

Dodatkowo musimy założyć zerowanie się

jednego z dwóch wyrazów, a

0

lub a

1

.





















































































cos

3

cos

5

cos

P

0

m

1

cos

3

cos

P

0

m

cos

cos

P

0

m

1

cos

P

0

m

3

3

3

2

2

2

1

1

0

0

Można pokazać, że rozwiązaniami

pełnego równania biegunowego:

 

0

1

m

C

d

1

d

d

2

2

2















































dla m różnego od 0, są tzw. stowarzyszone

funkcje Legendre’a:

 

 

 

m

l

m

2

m

2

lm

d

P

d

1

P













z postaci tych funkcji

wynika, że będą one

równe 0 dla:

l

m

Pełne rozwiązanie to tzw. funkcje kuliste

zawierające część azymutalną i

biegunową:

Kilka

pierwszych

funkcji kulistych

(harmonicznych

):

l = 0 (s)

l = 1 (p)
l = 2 (d)

l = 3 (f)



















im

lm

lm

e

cos

P

,

Y





























































i

2

2

2

,

2

i

1

,

2

2

20

i

1

,

1

10

00

e

sin

32

15

Y

e

sin

cos

8

15

Y

1

cos

3

16

5

Y

e

sin

8

3

Y

cos

4

3

Y

4

1

Y

Mamy zatem:



















im

m

,

l

m

,

l

e

cos

P

,

Y





m

,

l

2

2

m

,

l

2

2

m

,

l

2

m

,

l

2

Y

1

l

l

h

Y

sin

1

Y

sin

sin

1

h

Y

Lˆ





























































gdzie:

Zatem l(l+1)ħ

2

to kwadrat momentu

pędu,

a mħ jego rzut na oś z

l

m

l naturalne, m całkowite. Dla

danego l mamy 2l+1 wartości m

(degeneracja)

Funkcje kuliste (harmoniki sferyczne):

funkcje s (l = 0)

brak zależności od kątów θ i φ, stała

wartość









const

e

cos

P

,

Y

0

i

0

,

0

m

,















Y

(0,0)

, funkcja s, l = 0, m = 0

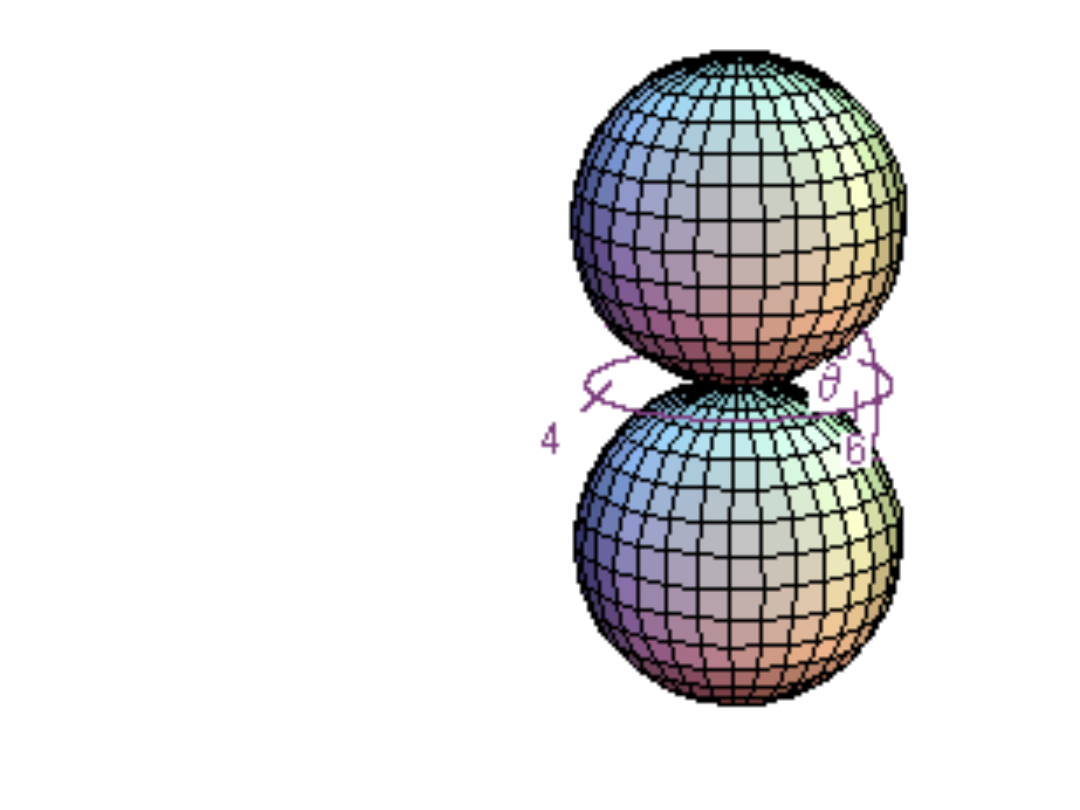
Y

(1,0)

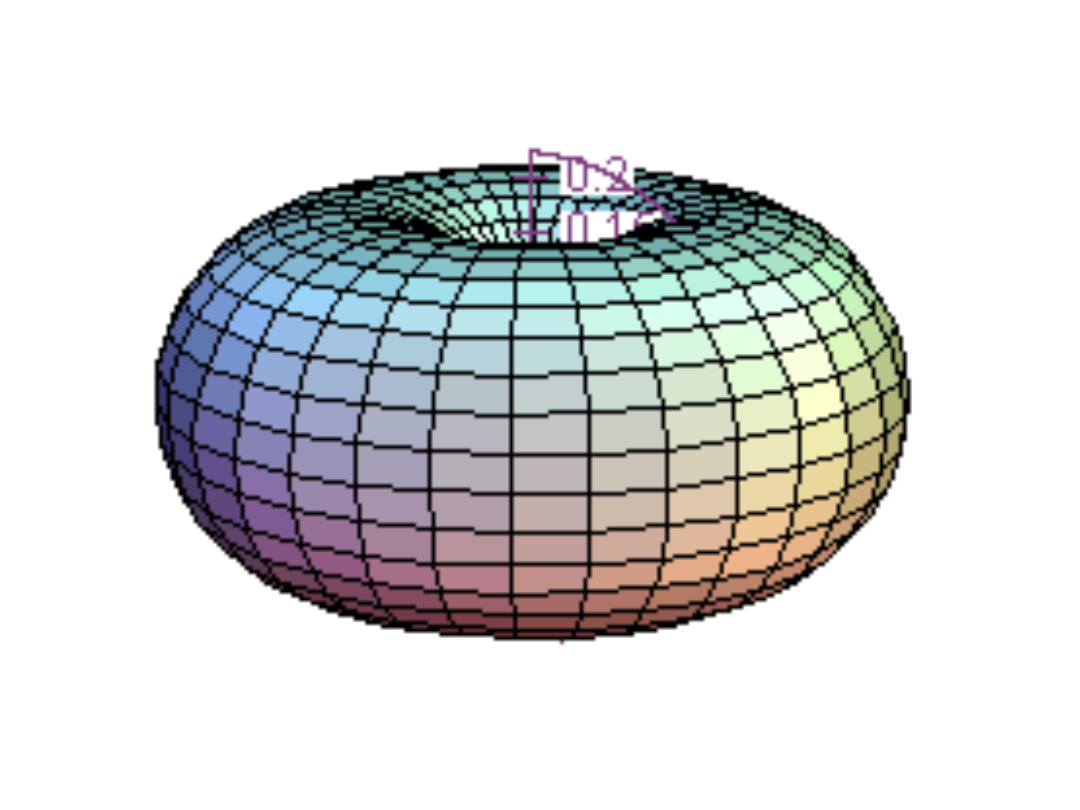
funkcja p,

l = 1, m = 0

~ cosθ

Y

(1,1)

, funkcje p, l = 1, m = ±1, ~sinθ

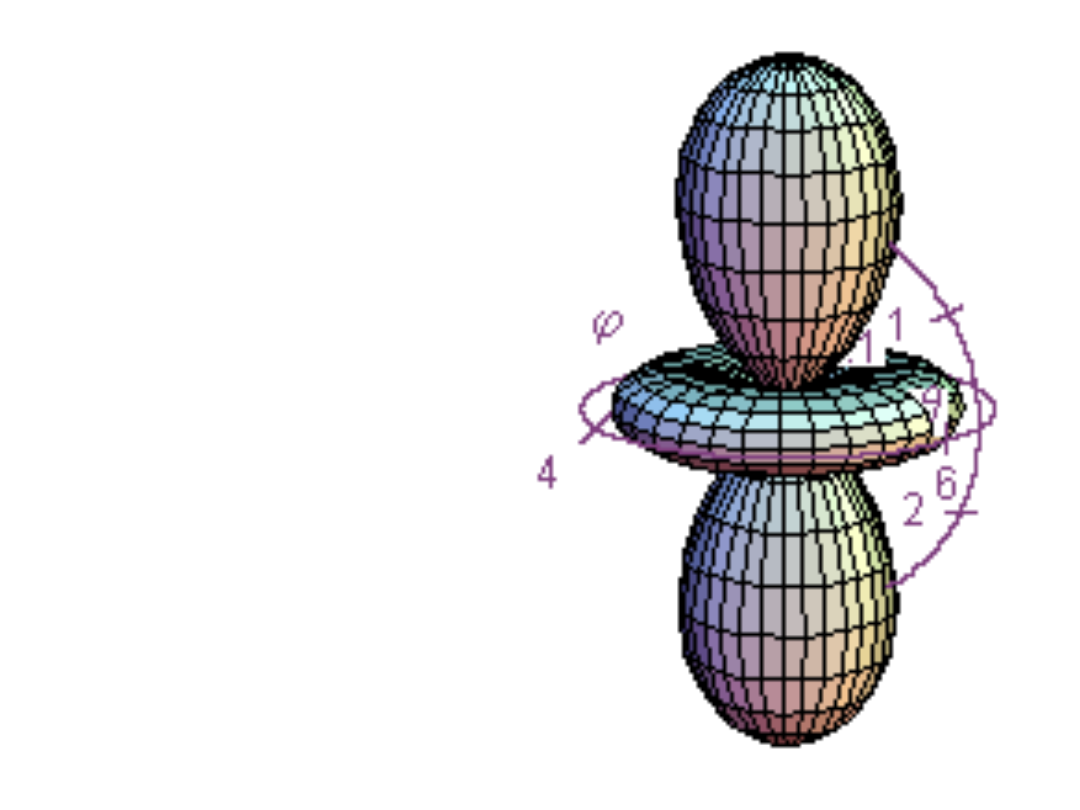
Y

(2,0)

,

funkcja d, l = 2, m

= 0

~(3cos

2

θ-1)

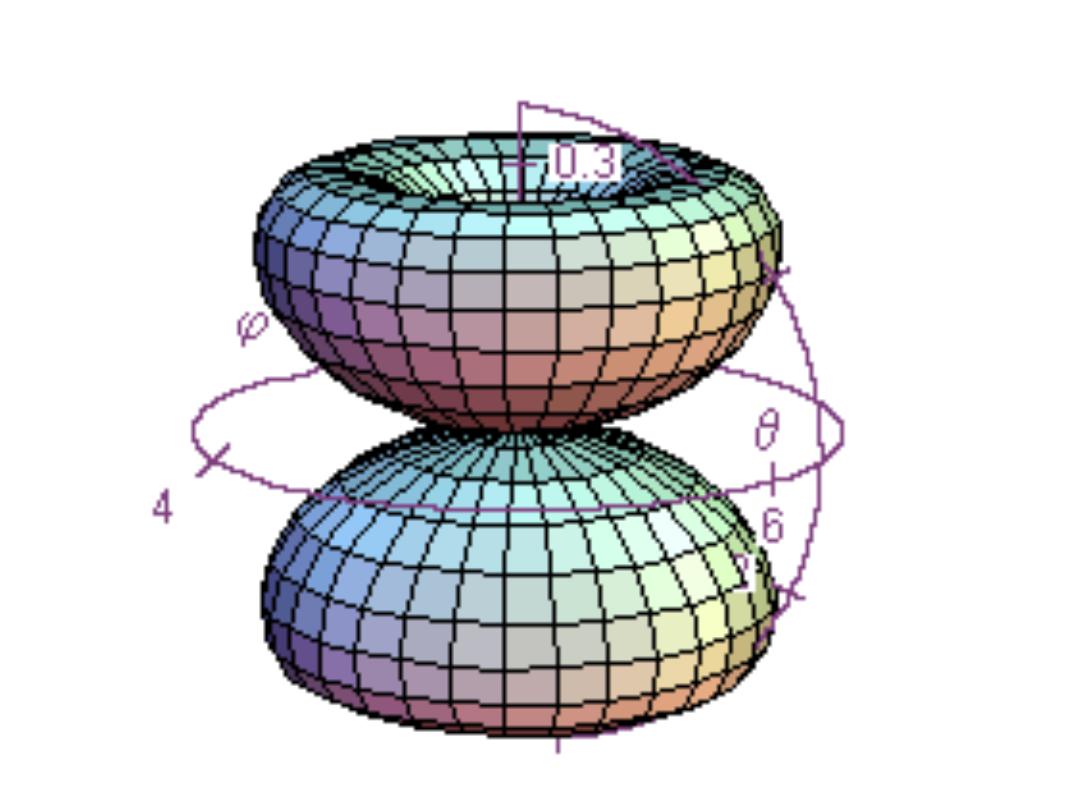
Y

(2,1)

, funkcje d, l = 2, m = ±1,

~cosθsinθ

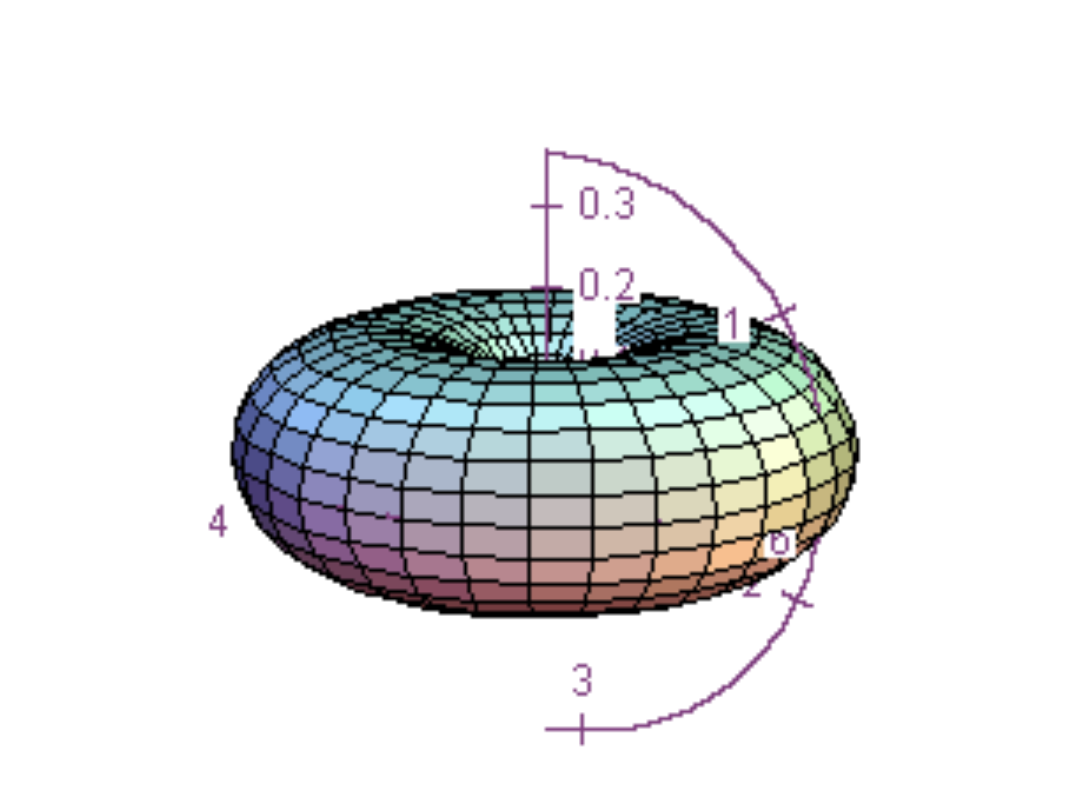
Y

(2,2)

, funkcje d, l = 2, m = ±2,

~sin

2

θ

Y

(3,0)

, funkcje f, l = 3, m = 0,

~cos

3

θ-cosθ

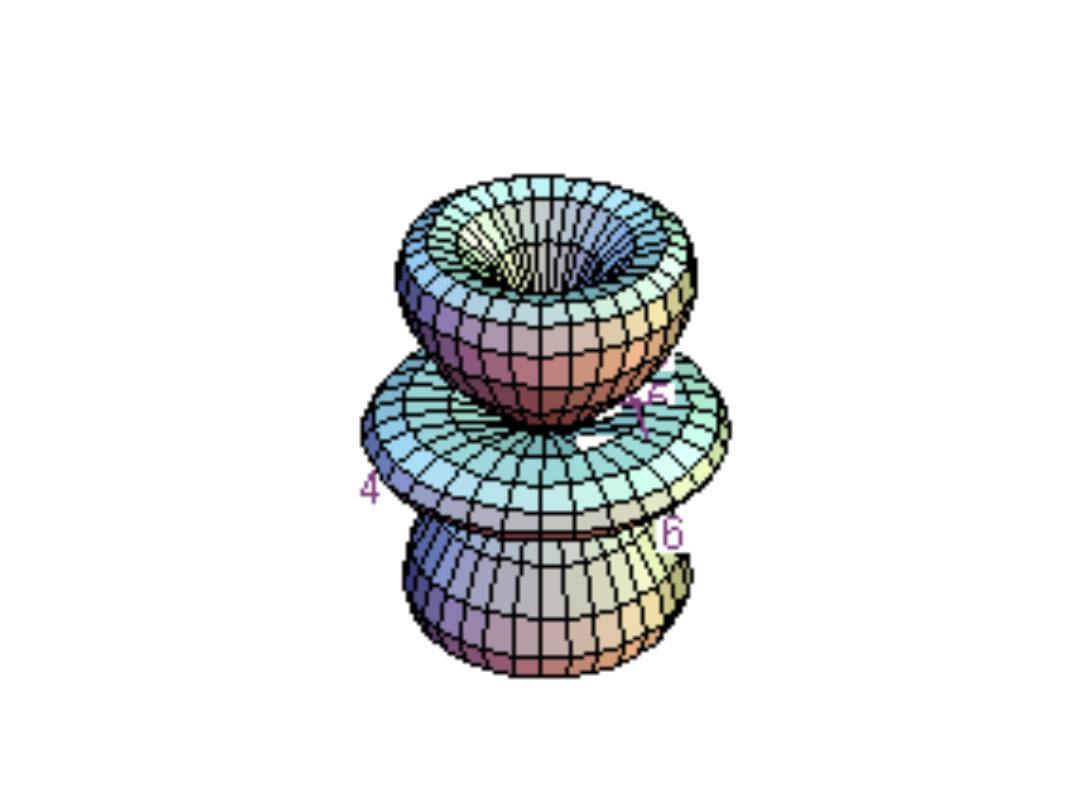
Y

(3,1)

, funkcje f, l = 3, m =

±

1,

~(5cos

2

θ-1)sinθ

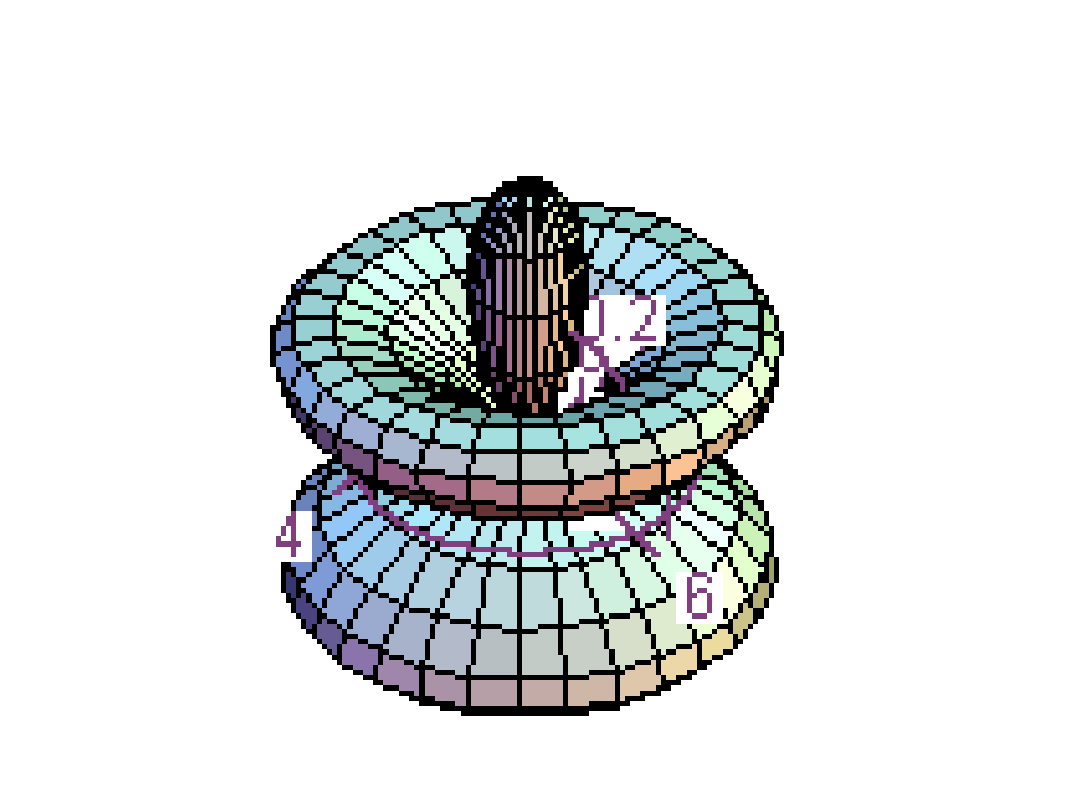
Y

(3,2)

, funkcje f, l = 3, m =

±

2

Y

(3,3)

, funkcje f, l = 3, m =

±

3