METODA SIMPLEX

lkm

Do przewozu środkiem transportowym o

maksymalnej ładowności

16800

i kubaturze

przestrzeni ładunkowej

800

wyznaczone są

trzy produkty:

A, B

i

C.

Masa produktów

wynosi:

280, 120,

i

100

; zaś objętość

odpowiednio

10,

8

oraz

20.

Cena

poszczególnych produktów kształtuje się

następująco:

12, 5

i

10.

Dodatkowo produkty

charakteryzują się zróżnicowanym poziomem

trwałości, który wynosi

2, 5

oraz

10.

Środek

transportowy zapewnia maksymalny poziom

trwałości towarów w granicach

100.

Treść zadania.

.

A(x

1

)

B(x

2

)

C(x

3

)

ograniczen

ia

masa

280

120

100

16800

objętość

10

8

20

800

trwałość

2

5

10

100

cena

12

5

10

MAX

Postać standardowa

układu.

Funkcja celu

12x

1

+ 5x

2

+10x

3

→ MAX

280x

1

+ 120x

2

+100x

3

≤ 16800

10x

1

+ 8x

2

+20x

3

≤ 800

2x

1

+ 5x

2

+10x

3

≤ 100

Warunki nieujemności

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0,

Postać kanoniczna
układu

.

Funkcja celu

12x

1

+ 5x

2

+10x

3

+ 0x

4

+ 0x

5

+ 0x

6

→ MAX

280x

1

+ 120x

2

+100x

3

+ x

4

= 16800

10x

1

+ 8x

2

+20x

3

+ x

5

= 800

2x

1

+ 5x

2

+10x

3

+ x

6

= 100

Warunki nieujemności

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0, x

4

≥ 0, x

5

≥ 0, x

6

≥ 0

Bazowa postać kanoniczna
układu.

Funkcja celu

12x

1

+ 5x

2

+10x

3

+ 0x

4

+ 0x

5

+ 0x

6

→ MAX

280x

1

+ 120x

2

+100x

3

+ 1x

4

+ 0x

5

+ 0x

6

= 16800

10x

1

+ 8x

2

+20x

3

+ 0x

4

+ 1x

5

+ 0x

6

= 800

2x

1

+ 5x

2

+10x

3

+ 0x

4

+ 0x

5

+ 1x

6

= 100

Warunki nieujemności

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0, x

4

≥ 0, x

5

≥ 0, x

6

≥ 0

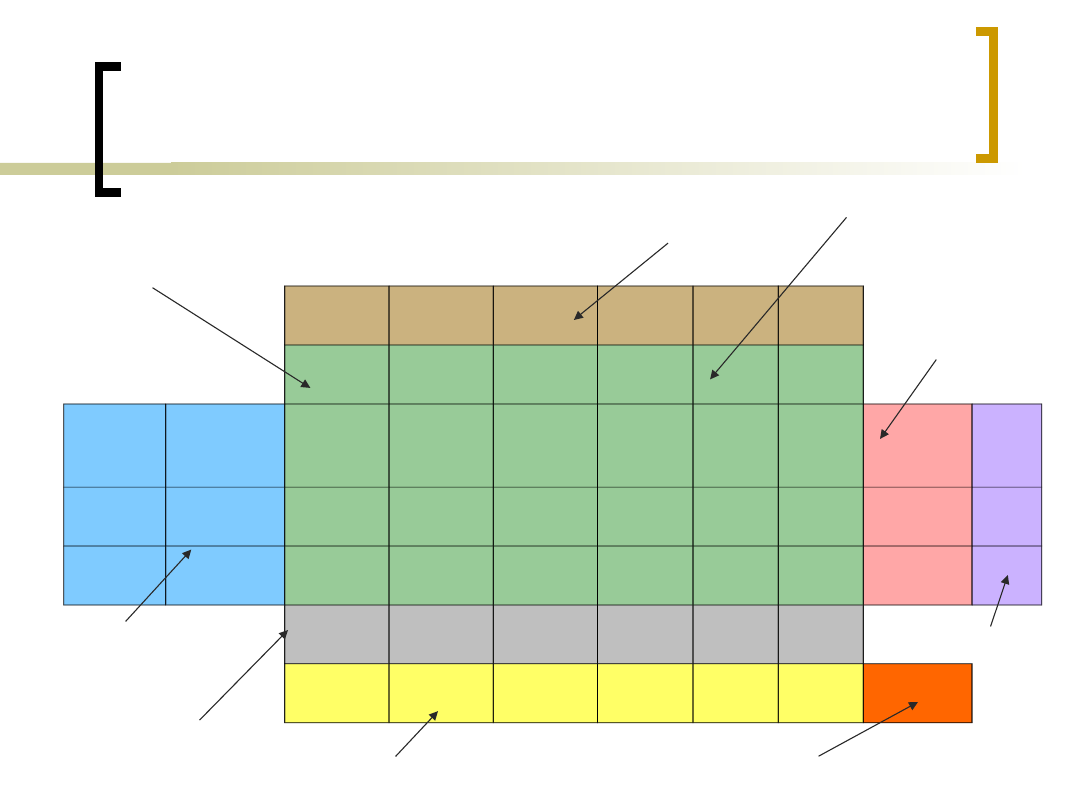
Metoda Simpleks –
tabela.

12

5

10

0

0

0

x1

x2

x3

x4

x5

x6

0

x4

280

120

100

1

0

0

1680

0

 

0

x5

10

8

20

0

1

0

800

0

x6

2

5

10

0

0

1

100

 

 

 

 

 

 

 

 

 

 

 

 

Współczynniki funkcji
celu (ceny)

Współczynniki
przy zmiennych
szukanych

Współczynniki
przy zmiennych
swobodnych

Ograniczenia

Współczynnik
funkcji celu
bieżącego
równania

wartość funkcji celu
bieżącego równania

Wskaźniki
pomocnicze

Wskaźniki
optymalności

Kryteria wyjścia

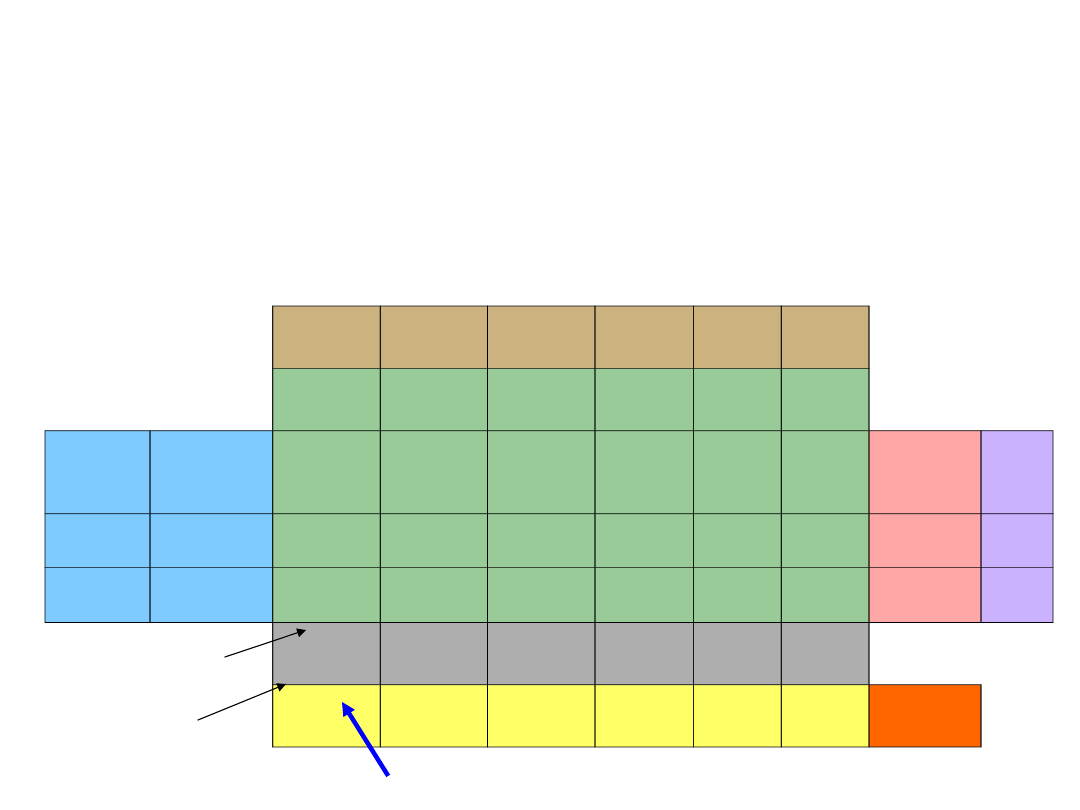
Wskaźniki pomocnicze

wyliczamy jako iloczyn skalarny pierwszej kolumny

współczynnika funkcji celu bieżącego równania oraz kolejnej kolumny
współczynników.

Wskaźnik optymalności

liczymy odejmują od cen współczynniki

pomocnicze. Wskaźniki te pozwalają nam określić czy dane równanie jest
optymalne. Jeżeli wszystkie wskaźniki będą niedodatnie w przypadku
maksymalizacji funkcji celu to nasze rozwiązanie będzie optymalne.

Wartość funkcji

celu dla bieżącego równania (kolor żółty) obliczamy jako

wektor skalarny pierwszej kolumny współczynnika funkcji celu bieżącego
równania

i

kolumny

ograniczeń.

12

5

10

0

0

0

x1

x2

x3

x4

x5

x6

0

x4

280

120

100

1

0

0

1680

0

 

0

x5

10

8

20

0

1

0

800

0

x6

2

5

10

0

0

1

100

 

0

 

0

 

 

0

 

0

0

 

0

12 

5 

10 

0 

 0

0

 

280·0+10·0+3·
0=0

MAX

Kryterium

wejścia

12 – 0 = 8

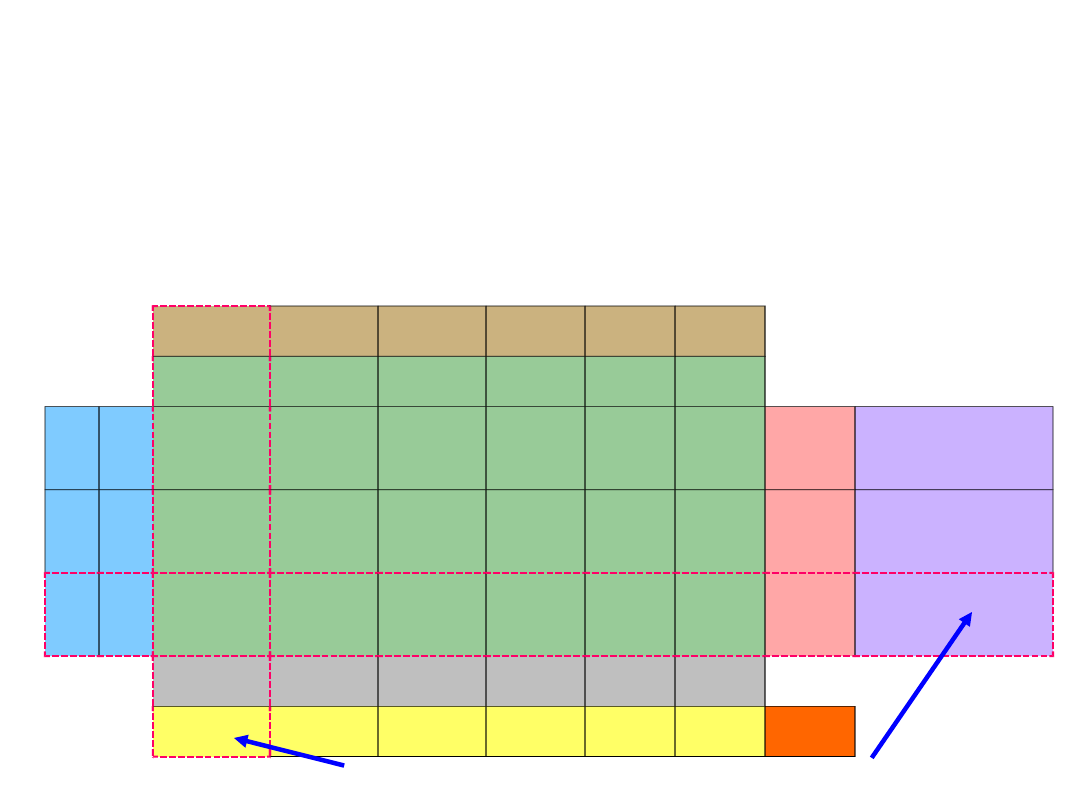
Maksymalizujemy funkcję celu, więc szukamy maksymalnego
wskaźnika

optymalności

i

zaznaczamy

całą

kolumnę.

Wyliczamy kryteria wyjścia, jako iloraz ograniczeń i zaznaczonej
kolumny.

12

5

10

0

0

0

x1

x2

x3

x4

x5

x6

0

x

4 280

120

100

1

0

0

16800

16800/280 

=60

0

x

5 10

8

20

0

1

0

800

800/10

=80

0

x

6

2

5

10

0

0

1

100

100/2

=50

 

0

 

0

 

 

0

 

0

0

 

0

12 

5 

10 

0 

 0

0

 

MAX

Kryterium

wejścia

MIN

Kryterium

wyjścia

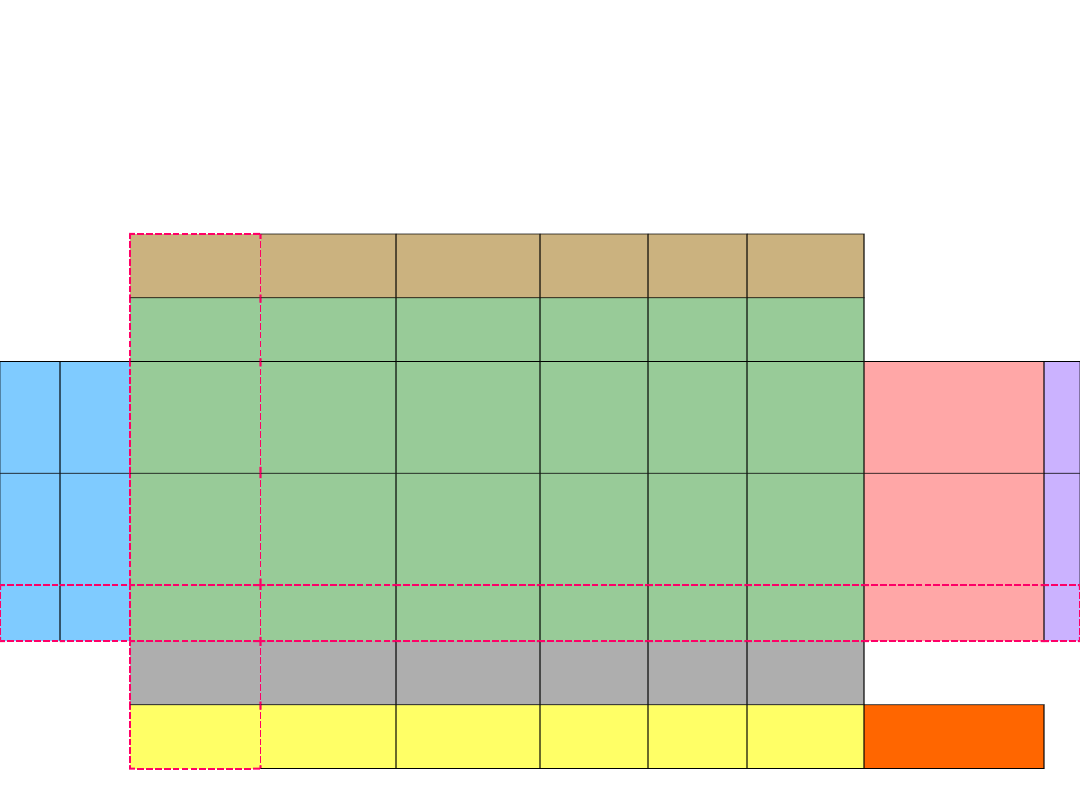
Wymieniamy zmienną bazową – x6 na zmienną

niebazową – x1 oraz zaktualizujemy współczynniki

oraz ograniczenia.

12

5

10

0

0

0

x1

x2

x3

x4

x5

x6

0

x4

280-

1·280

=0

120-

2,5·2

80

= -580

100-5·280

= -1300

1-

0·2

80

=1

0-

0·2

80

=0

0-

0,5·

280

=-140

16800-

50·280

= 2800

 

0

x5

10-1·10

=0

8-2,5·10

=-17

20-5·10

=-30

0-0·10

=0

1-0·10

=1

0-

0,5·

10

=-5

800-50·10

=300

12 x1

2/2 = 1

5/2= 2,5

10/2= 5

0/2= 0

0/2= 0 1/2=0,5

100/2 = 50

 

 

 

 

 

 

 

 

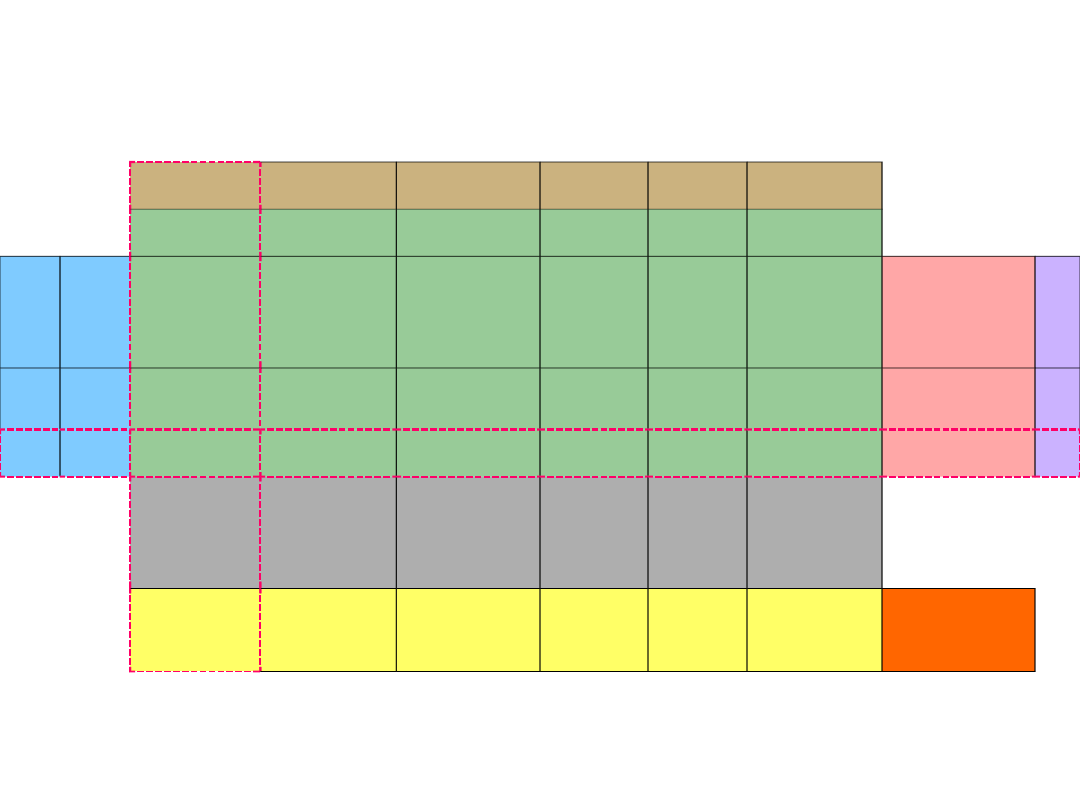
Wyliczamy wskaźniki pomocnicze, wskaźniki

optymalności i wartość funkcji celu.

12

5

10

0

0

0

x1

x2

x3

x4

x5

x6

0

x4

280-

1·280

=0

120-

2,5·28

0

= -580

100-5·280

= -1300

1-

0·2

80

=1

0-

0·2

80

=0

0-0,5·280

=-140

16800-

50·280

= 2800

 

0

x5

10-1·10

=0

8-2,5·10

=-17

20-5·10

=-30

0-0·10

=0

1-0·10

=1

0-0,5·10

=-5

800-50·10

=300

12 x1

2/2 = 1

5/2= 2,5

10/2= 5

0/2= 0

0/2= 0

1/2=0,5

100/2 = 50

 

0·0+0·0

+1·12=1

2

0·-

580+0·-

17+2,5·1

2=30 

0·-

1300+0·-

30+5·12=

60

 

0·1+0·

0+0·12

=0

 

0·0+0·

1+0·1

2=0

0·-

140+0·-

5+0,5·12

=6

12-12

=0

5-30

= -25

10-60

=-50 

0-0

=0

0-0

=0 

0-6

=-6

600 

Otrzymaliśmy rozwiązanie optymalne, gdyż żaden współczynnik nie

jest dodatni.

Rozwiązanie zadania.



x

1

= 50



x

4

= 2 800



x

5

= 300



x2 = 0



x3 = 0



x6 = 0

Maksymalny zysk uzyskany wynosi

600.

Przy założonych ograniczeniach należy wybrać

50

sztuk produktu

A

.