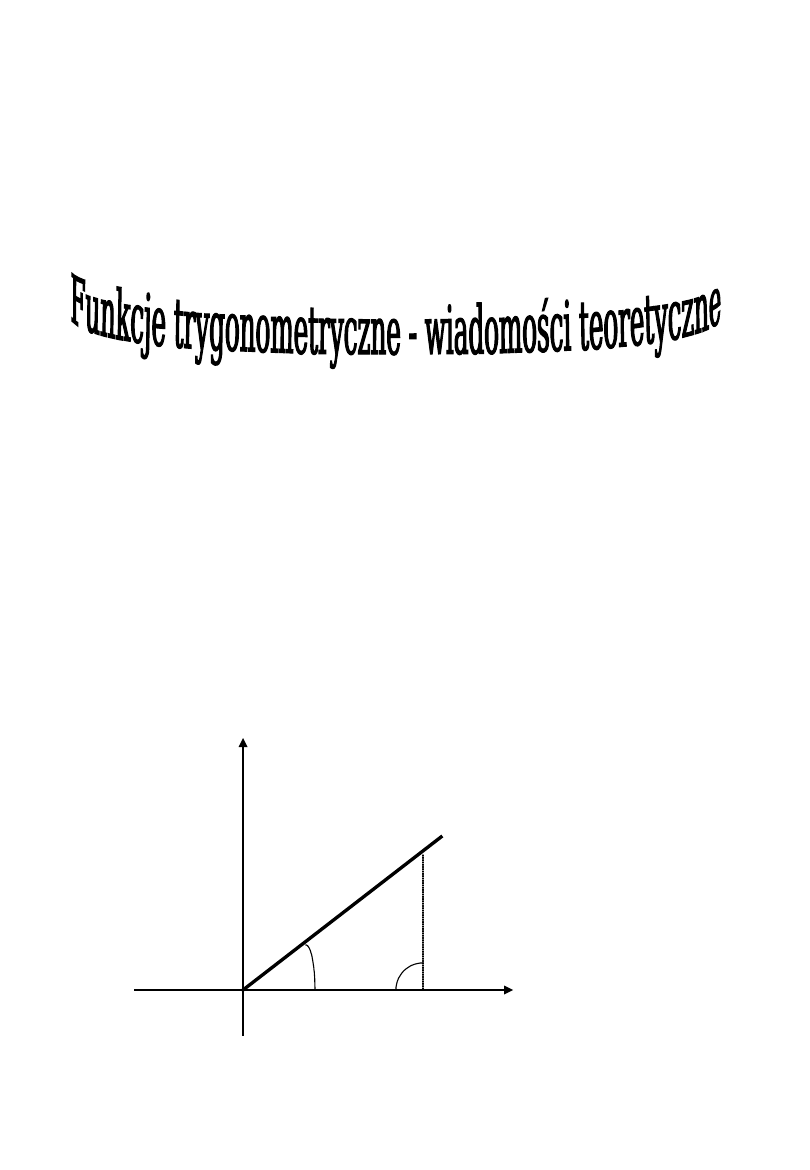
Dobranym układem współrzędnych do kąta α nazywamy taki
układ współrzędnych , że kąt α zawiera się w pierwszej
ćwiartce układu współrzędnych oraz jedno z ramion tego
kąta pokrywa się z dodatnią półosią osi X .

Ramię kąta α pokrywające się z dodatnią półosią osi X
nazywamy pierwszym ramieniem tego kąta , ramię
pozostałe – drugim ramieniem.

α

•

P=(x,
y)

P’=(x,0
)

X

Y

0

r

Bożena Skorłutowska

Nauczyciel matematyki

Gimnazjum nr 5 im. Z. Padlewskiego

w Płocku

ß

α

•

A

B

C

a

b

c

Sinus

α = sin α

Cosinus α = cos α

Tangens α = tg α

Cotangens α = ctg α

Niech

α będzie kątem z dobranym układem współrzędnych ,

P=(x,y) – dowolnym punktem (różnym od punktu 0 ) na
drugim ramieniu tego kąta.

SINUSEM kąta

α

nazywamy liczbę , gdzie r=

jest odległością punktu P od początku układu
współrzędnych.

r

y

2

2

y

x 

COSINUSEM kąta

α

nazywamy liczbę , gdzie r=

jest odległością punktu P od początku układu
współrzędnych.

r

x

2

2

y

x 

TANGENSEM kąta

α

nazywamy liczbę

, tzn. iloraz drugiej

współrzędnej punktu P przez jego pierwszą współrzędną .

COTANGENSEM kąta

α

nazywamy liczbę , tzn. iloraz

pierwszej współrzędnej punktu P przez jego drugą
współrzędną.

y

x

x

y

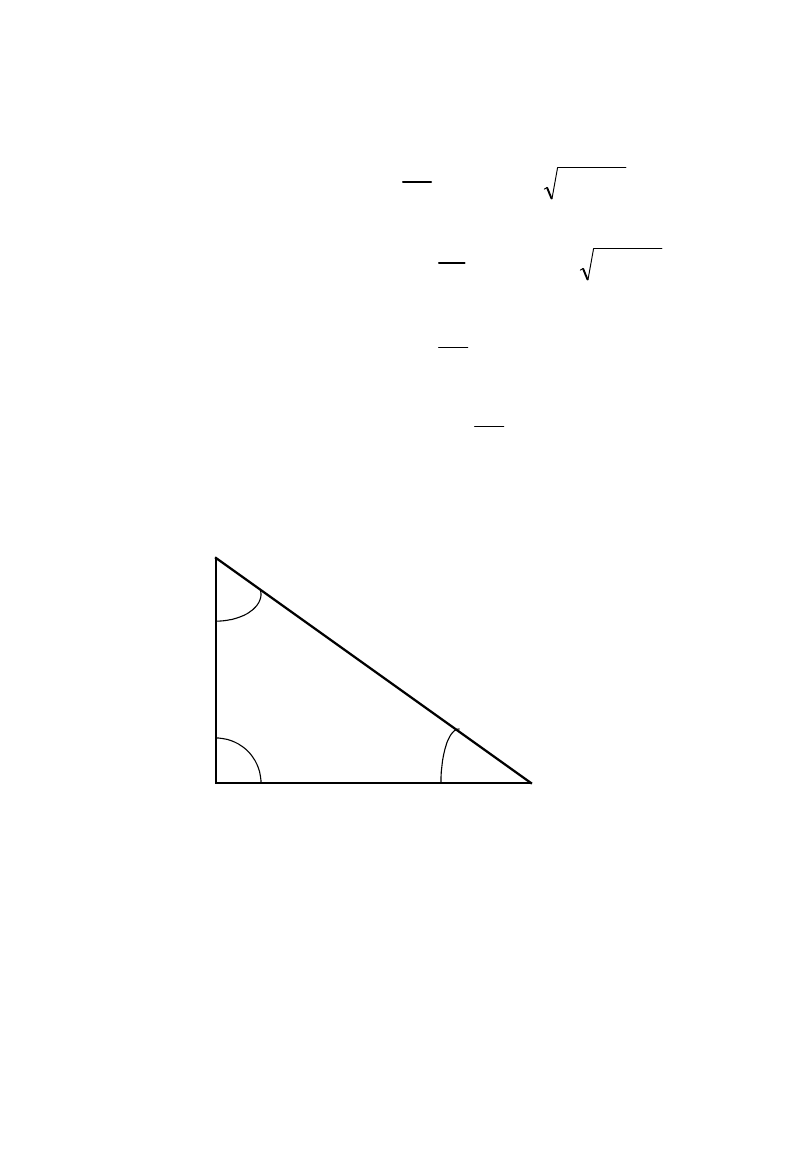
COTANGENSEM kąta

ostrego w trójkącie prostokątnym nazywamy

stosunek długości przyprostokątnej leżącej przy kącie do długości
drugiej przyprostokątnej.

ctg

α =

a

b

ctg

β =

b

a

Nie istnieje tangens kąta o mierze 90

o

.

Nie istnieje cotangens kąta o mierze 0

o

.

sin

α

=

cos (90 -

β)

cos

α =

sin (90 -

β)

tg

α

=

ctg (90 -

β)

ctg

α =

tg (90 -

β)

Jedynka trygonometryczna

sin

2

α + cos

2

α = 1

cos

α =

c

b

cos =

ß

c

a

COSINUSEM kąta

ostrego w trójkącie prostokątnym nazywamy

stosunek długości przyprostokątnej leżącej przy kącie do długości
przeciwprostokątnej.

TANGENSEM kąta

ostrego w trójkącie prostokątnym nazywamy

stosunek długości przyprostokątnej leżącej naprzeciw kąta do
długości drugiej przyprostokątnej.

tg

α =

b

a

ß

tg =

a

b

SINUSEM kąta

ostrego w trójkącie prostokątnym nazywamy

stosunek długości przyprostokątnej leżącej naprzeciw tego kąta do
długości przeciwprostokątnej.

Sin

α =

c

a

Sin =

ß

c

b

Wartości funkcji sinus i cosinus kątów ostrych mogą
być tylko liczbami dodatnimi , mniejszymi od
jedności.

Znajomość wartości funkcji trygonometrycznych kątów
ostrych w trójkącie prostokątnym umożliwia obliczenie
długości boków i miar kątów w tym trójkącie oraz w
innych wielokątach , a także rozwiązywanie zadań o
charakterze praktycznym.

tg α

=





cos

sin

ctg α =





sin

cos

tg α

=



ctg

1

ctg α =



tg

1

tg α • ctg α
= 1

Przy wzroście kąta ostrego od 0

o

do 90

o

wartość funkcji

sinus rośnie od 0 do 1,

cosinus maleje od 1 do 0,

tangens rośnie od 0 do +

cotangens maleje od + do 0
.



