1

SPEKTROSKOPIA ROTACYJNA

2

Promieniowanie

podczerwone

powoduje oscylację molekuł (ciepło)
Zdalne sterowanie sprzętu RTV,
sprzęt termowizyjny, meteorologiczne
obrazowanie satelitarne IR ,
efekt cieplarniany  absorpcja IR

przez cząsteczki gazów w atmosferze
(H

2

O,

CH

4

,

N

x

O

y

,

chlorofluorowęglowodory

Mikrofale powodują
rotację molekuł (ciepła)
(temperatura jest miarą
ruchu
molekularnego!!)
Kuchenka mikrofalowa
 rotacja H2O w wyniku

absorpcji mikrofal
Telefony komórkowe,
sieć bezprzewodowa
Wi-Fi (Wireless Fidelity)
 emisja i odbiór

mikrofal

3

Pogoda nad Europą
(17/02/2004)

Huragan Andrew (16-
28/08/1992)

4

5

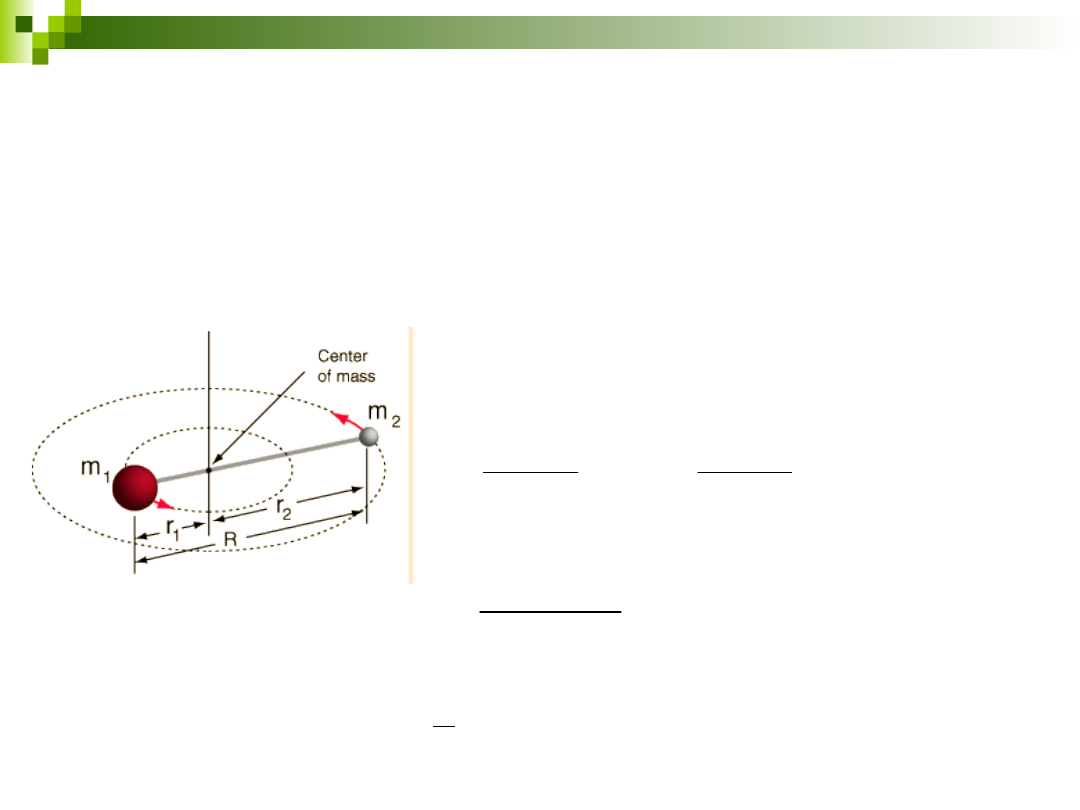
Rotator sztywny

Moment bezwładności dla 2 rotujących mas wokół ich środka ciężkości:

2

2

2

2

1

1

r

m

r

m

I





z zasady środka ciężkości:

2

2

1

1

r

m

r

m 

R

r

r





2

1

R

m

m

m

r

2

1

2

1





R

m

m

m

r

2

1

1

2





2

2

2

1

2

1

R

R

m

m

m

m

I

red











red

- masa zredukowana

Jedynie energia kinetyczna  - prędkość kątowa

2

2

1



I

E

k



E

k

dla rotatora makroskopowego zmienia się w sposób ciągły

6

Mechanika kwantowa przewiduje dla tego ruchu kwantowanie
Rozwiązanie równania Schrödingera  rotator sztywny











E

h

red

2

2

2



)

1

(

2

2





J

J

I

E

J



rotacyjna liczba kwantowa J = 0,1,2,…

Stała rotacyjna

I

h

I

J

B

2

2

2

'

8

2

]

[









Ic

h

s

cm

c

s

J

h

J

B

cm

B

2

1

'

1

_

8

]

[

]

[

]

[

]

[

















I

h

s

J

h

J

B

Hz

B

2

'

8

]

[

]

[

]

[









2

2

2

2

2

2

dz

d

dy

d

dx

d







operator energii kinetycznej

7

Różnica energii pomiędzy poziomami rotacyjnymi

)

1

(

'





J

J

B

E

J

J

-56 B’

7

-42 B’

6

-30 B’

5

-20 B’

4

-12 B’

3

-6 B’

2

-2 B’

1

-0

0

E

n

e

rg

ia

r

o

ta

c

y

jn

a

k

w

a

n

to

w

a

l

ic

zb

a

r

o

ta

c

y

jn

a

J

J = 0 

J = 1 

'

2

)

1

1

(

1

'

1

B

B

E

J











0

)

1

0

(

0

'

0











B

E

J

J = 2 

'

6

)

1

2

(

2

'

2

B

B

E

J











)

1

(

'

2

)

1

(

'

)

1

1

)(

1

(

'

1



























J

B

J

J

B

J

J

B

E

E

E

J

J

 spektroskopia mikrofal (zakres GHz)

J = 0  J = 1 E = 2B’

J = 1  J = 2 E = 4B’

J = 2  J = 3 E = 6B’

ale mierzymy różnice pomiędzy poziomami, stąd

8

Problem 1

Znaleźć wartość energii rotacyjnej dla liczby kwantowej J = 0,1,2 dla

12

C

16

O,

przyjmując

R

CO

= 1,1283 Å. Wartość podać w joulach i cm

-1

.

kg

mol

mol

kg

mol

kg

mol

g

mol

g

m

m

m

m

O

C

O

C

red

26

1

23

1

3

1

3

1

1

10

1385

,

1

10

023

,

6

10

8562

,

6

10

8562

,

6

8562

,

6

995

,

15

0

,

12

995

,

15

0

,

12

























































2

46

2

2

10

26

10

4494

,

1

)

10

1283

,

1

(

10

1385

,

1

m

kg

m

kg

I





















3. Obliczamy wartość stałej rotacyjnej

]

[

10

8365

,

3

10

4494

,

1

8

)

10

626

,

6

(

8

23

2

46

2

2

2

2

34

2

2

J

m

kg

s

J

I

h



























0

0





J

E

4. Obliczamy wartość energii

]

[

10

673

,

7

23

1

J

E

J









]

[

10

301

,

2

22

2

J

E

J









5. Zmieniamy energię wyrażoną w [J] na [cm

-1

] dzieląc przez h·c

0

0





J

E

]

[

863

,

3

1

1







cm

E

J

]

[

590

,

11

1

2







cm

E

J

2

R

I

red





2. Obliczamy moment bezwładności

)

1

(

2

2





J

J

I

E

J



Rozwiązanie:
1. Korzystamy z
wzoru

9

Problem 2

Widmo mikrofalowe rodnika CN wykazuje serię linii oddalonych od
siebie o 3,797 cm

-1

. Znaleźć długość wiązania R

CN

.

1. Z warunków zadania:

1

1

_

898

,

1

797

,

3

2

















cm

B

cm

B

E

2

46

1

8

1

2

34

_

2

10

474

,

1

10

3

8

,

189

8

10

626

,

6

8

m

kg

s

m

m

s

J

Bc

h

I

































2. Obliczamy moment bezwładności

kg

mol

mol

g

m

m

m

m

N

C

N

C

red

26

1

23

1

10

074

,

1

10

023

,

6

1

0

,

14

0

,

12

0

,

14

0

,

12





























3. Obliczamy długość wiązania

nm

m

kg

m

kg

I

R

red

117

,

0

10

17

,

1

10

074

,

1

10

474

,

1

10

26

2

46

























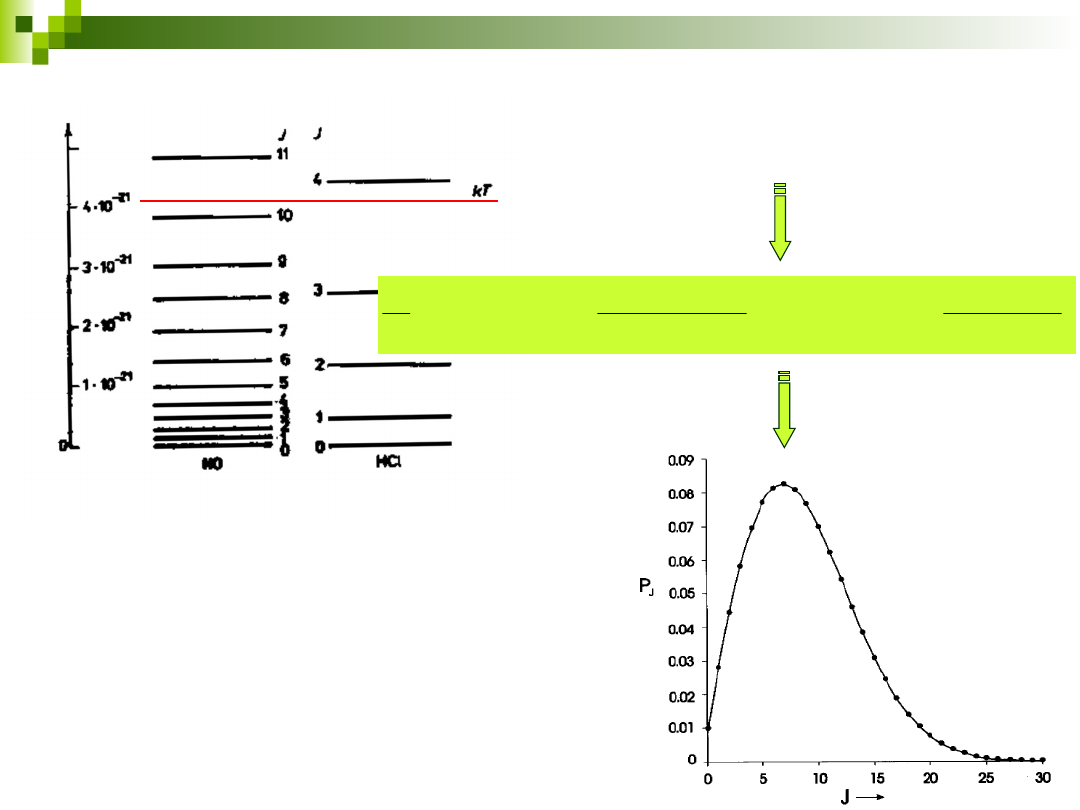
10

E

n

e

rg

ia

J

/c

z

ą

s

te

c

z

k

a

Obsadzenie poziomów

rotacyjnych

Degeneracja każdego poziomu 2J+1

wiele poziomów leży poniżej kT

wzrost J, wzrost czynnika
(2J+1)
dalszy wzrost J, dominacja
czynnika wykładniczego

I

HCl

 I

NO

B

HCl

 B

NO

]

)

1

(

'

exp[

)

1

2

(

)

exp(

)

1

2

(

0

0

kT

J

J

B

J

kT

E

E

E

J

n

n

J

J





















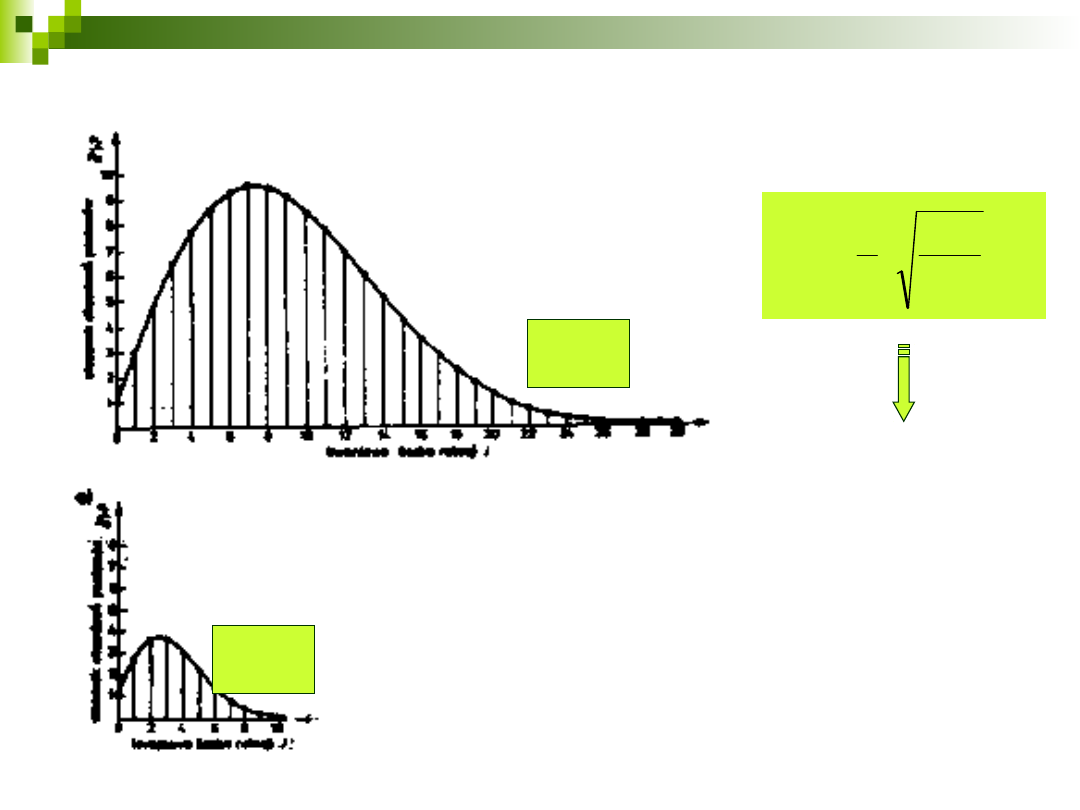
11

NO

T=25

o

C

HCl

T=25

o

C

HCl

T=1000

o

C

J

max

=7

J

max

=3

J

max

=6



















1

2

2

1

_

max

B

hc

kT

J

termometr

(wnętrze pieca hutniczego,

ciała niebieskie,

zorza polarna)

I

HCl

 I

NO

B

HCl

 B

NO

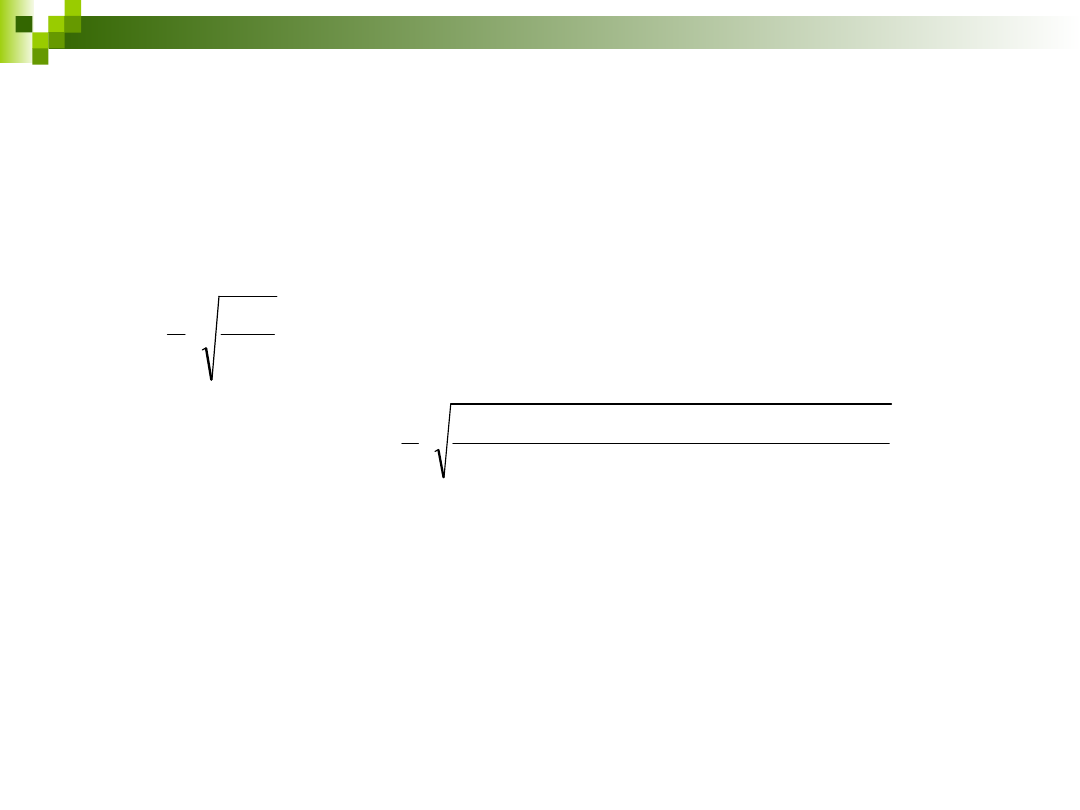
12

Problem 3

Jaka jest wartość liczby kwantowej J, dla której poziom rotacyjny jest
maksymalnie obsadzony dla cząsteczki CN w temperaturze
pokojowej i 1000 K? Przyjąć stałą rotacyjną równą 1,57 cm

-1

.



















1

2

2

1

_

max

B

hc

kT

J

8

62

.

7

1

0

,

3

10

626

,

6

10

57

,

1

298

10

380

,

1

2

2

1

1

34

1

2

1

23

max























































s

m

s

J

m

K

K

J

J

dla temperatury pokojowej:

dla temperatury 1000 K:

J

max

 14

13

Efekt izotopowy w widmach rotacyjnych

red

red

red

red

R

c

h

R

c

h

B

B













*

2

*

2

2

2

_

*

_

8

8





Dla J = 0  1

E = 2B



1

_

8423

,

3





cm

B

1

_

*

6735

,

3





cm

B









































9949

,

15

0

,

12

9949

,

15

0

,

12

9949

,

15

9949

,

15

10

6735

,

3

10

8423

,

3

13

13

2

2

C

C

A

A

Problem 4

Linia J = 0  1 w widmie mikrofalowym

12

C

16

O ma wartość 3,8423 cm

-1

,

natomiast dla

13

C

16

O liczba falowa wynosi 3,6734 cm

-1

. Wiedząc, że względne

masy atomowe wynoszą 12,000 i 15,9949 dla

12

C i

16

O – obliczyć względną

masę atomową

13

C.

0007

,

13

13



C

A

14



Problem 5

Obliczyć długość wiązania CO znając z absorpcyjnego
widma rotacyjnego położenia pasm: 3.84, 7.68 i 11.51 cm

-1

.

przejście J = 0  J = 1

 = 3.84 cm

-

1

B = 1.92 cm

-

1

B =

h

8

2

cI

I =

h

8

2

cB

I = = 1.45·10

-46

(kg·m

2

)

6.62 ·10

-34

(kg·m

2

·s

-1

)

8

2

·

3·10

10

(m·s

-1

)

·1.92 (cm

-1

)

I = m

red

R

2

m

red

= = = 1.14·10

-26

kg

m

C

m

O

(0.012 · 0.016)/N

A

2

m

C

+ m

O

(0.012 + 0.016)/N

A

R

CO

=



= 0.113 nm

I

m

red

15

Rotator niesztywny (zmiana odległości między

jądrami)



działanie siły odśrodkowej na poziomach rotacyjnych J  0

E = 2B (J+1)

rotator sztywny

 = 2B (J+1) – 4D (J+1)

3

D – stała odkształcenia odśrodkowego

(~1MHz dla 2-atomowych cząsteczek

o lekkich atomach; 10

-3

MHz dla wieloatomowych; znaczna dla dużych J)



sprzężenie oscylacyjno-rotacyjne

B

e

– stała rotacji odpowiadająca punktowi równowagi oscylacji



i

– stała sprzężenia oscylacyjno-rotacyjnego (rzędu 10 MHz, czyli 0,1 %wartości

B

e

, czyli ~0,002 Å w długości wiązania)

)

2

1

(

1













e

B

B

16

Oddziaływanie promieniowania z rotującymi 2-

atomowymi molekułami



absorpcja



dopasowanie energetyczne E =

h



trwały moment dipolowy (H

2

, N

2

, O

2

, CO

2

, CCl

4

, CH

4

nie dają absorpcyjnego widma rotacyjnego)



J = +1 oraz +  - lub -  + (symetria stanów

rotacyjnych)



rozpraszanie



anizotropia polaryzowalności



J = 0, +2 oraz +  + lub -  -

17

Dla podania pełnej charakterystyki

poziomów energii rotacji molekuły

konieczna jest znajomość

jej podstawowego stanu

elektronowego

 własności symetrii poziomów

rotacyjnych

18

Symetria stanów
rotacyjnych



całkowita funkcja falowa  po inwersji jąder i elektronów
x

1

, y

1

, z

1

 -x

1

, -y

1

, -z

1



nie zmienia znaku,

stany rotacyjne dodatnie (+)



zmienia znak,

stany rotacyjne ujemne (-)



całkowita funkcja falowa  po zamianie miejscami

identycznych jąder

x

1

, y

1

, z

1

 x

2

, y

2

, z

2



nie zmieniona,

symetryczne stany rotacyjne (s)



zmieniona,

antysymetryczne stany rotacyjne (a)

19

Symetria poziomów energii rotacji molekuły 2-
atomowej heterojądrowej w stanach
elektronowych 

dla 

+

dla 

-

J

-

7

+

6

-

5

+

4

-

3

+

2

-

1

+

0

J

+

7

-

6

+

5

-

4

+

3

-

2

+

1

-

0

■

poziomy o

parzystej J

są

dodatnie

■

poziomy o

nieparzystej J

są

ujemne

■

poziomy o

parzystej J

są

ujemne

■

poziomy o

nieparzystej J

są

dodatnie

20

Dozwolone przejścia i widmo rotacyjne 2-
atomowych cząsteczek heterojądrowych

J=6

J=5

J=4

J=3
J=2
J=1
J=0

J=+1

E=2B(J+1)

J=+2

dla części stokesowskiej

E=2B(2J+3)

absorpcyjne

ramanowskie

A

_



I

RS

_



2B

2B

6B

6B

4B

6B

8B

10B

12B

4B

6B

8B

10B

12B

10B

14B

18B

22B

22B

10B

14B

18B

21

Widmo rotacyjne 2-atomowych cząsteczek
homojądrowych



brak absorpcyjnego widma rotacyjnego, tylko
widma ramanowskie



struktura widma rotacyjnego zależy od spinu
jądrowego: I = 0 lub I ≠ 0

22

Rotacyjne widmo
ramanowskie



identyfikacja



wyznaczanie
parametrów
struktury (B, I, r)



analiza ilościowa



pomiar T

tlen

azot

powietrze

23

Symetria poziomów energii rotacji molekuły 2-
atomowej homojądrowej w stanach
elektronowych 

■

dodatnie poziomy są symetryczne

■

ujemne poziomy są antysymetryczne

■

dodatnie poziomy są antysymetryczne

■

ujemne poziomy są symetryczne

dla parzystego



g

+

lub 

g

-

dla nieparzystego



u

+

lub 

u

-

24

Dozwolone przejścia i widmo rotacyjne 2-atomowych

cząsteczek homojądrowych o spinie jądrowym I=0

dozwolone
są tylko
symetryczne
względem
wymiany
jąder
poziomy
rotacyjne

J=6

J=5
J=4
J=3
J=2

J=1

J=0



u

+

i 

g

-

brak J parzystych

16

O

2

,

3



g

-



u

-

i 

g

+

brak J nieparzystych

I

RS

_



I

RS

_



6B

6B

10B

18B

26B

10B

8B

14B

30B

14B

22B

J=7

J=8

18B

26B

8B

8B

8B

22B

8B

8B

8B

8B

30B

25

Dozwolone przejścia i widmo rotacyjne 2-
atomowych cząsteczek homojądrowych o
spinie jądrowym I0

Dla cząsteczek ze spinem połówkowym (statystyka Fermiego-
Diraca, n.p.:

1

H

2

)

– cząsteczki orto  nieparzyste stany

rotacyjne (J=1,3,5,..)

– cząsteczki para  parzyste stany

rotacyjne (J=0,2,4,..)

Dla cząsteczek ze spinem całkowitym (statystyka Bosego-
Einsteina, n.p.:

14

N

2

)

– cząsteczki orto  parzyste stany

rotacyjne (J=0,2,4,..)

– cząsteczki para  nieparzyste stany

rotacyjne (J=1,3,5,..)

I

I

I

I

I

I

N

N

para

orto

1

)

1

2

(

)

1

)(

1

2

(













1

H

2

, I=1/2, N

orto

/N

para

= 3

 maksima przejść dla J nieparzystych mają

3-krotnie większą intensywność niż

przejścia dla J parzystych

2

H

2

,

14

N

2

, I=1, N

orto

/N

para

= 2

 maksima przejść dla J parzystych mają 2-krotnie

większą intensywność niż przejścia dla J

nieparzystych

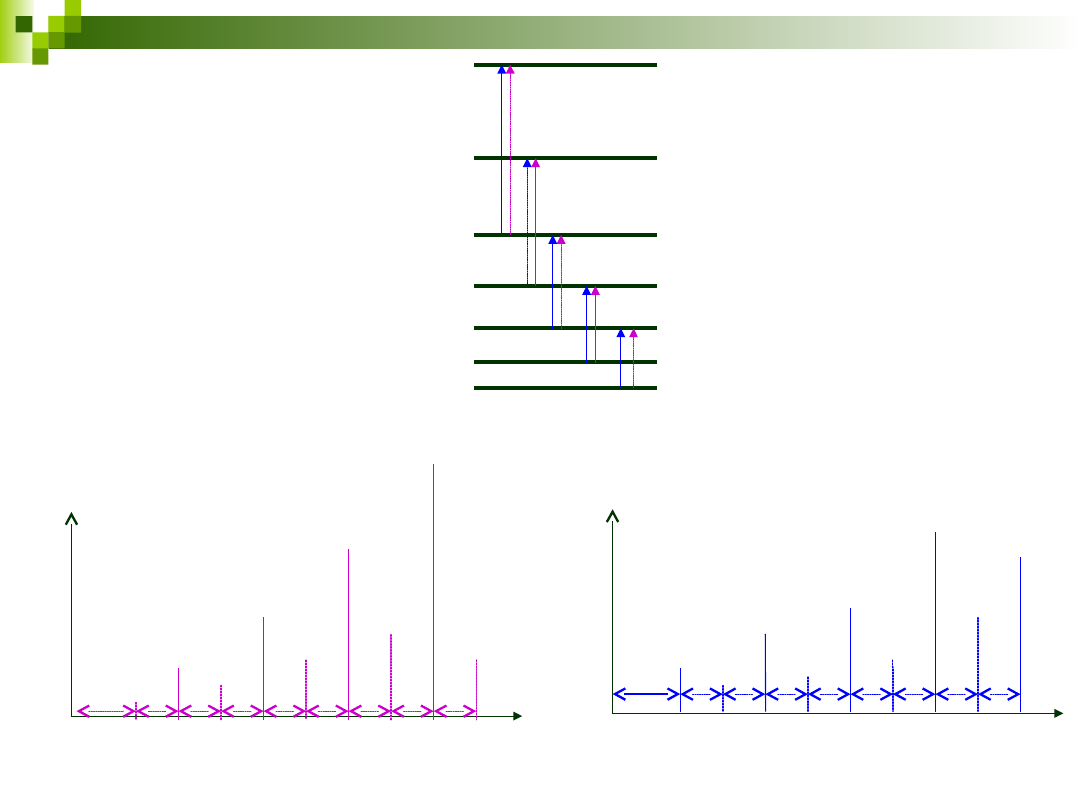
26

J=6

J=5

J=4

J=3

J=2
J=1
J=0

J=+2

dla części stokesowskiej
E=2B(2J+3)

I = 1/2

I = 1

I

RS

_



6B

6B

10B

14B

18B

I

RS

_



6B 4B 4B

4B

22B

4B

maksima przejść dla J
nieparzystych mają 3-
krotnie większą
intensywność niż
przejścia dla J
parzystych

maksima przejść dla J

parzystych mają 2-

krotnie większą

intensywność niż

przejścia dla J

nieparzystych