Programowanie
Programowanie
dynamiczne
dynamiczne
Opracowano na podstawie:
Opracowano na podstawie:
1.
1.
„
„
Badania operacyjne w przykładach i
Badania operacyjne w przykładach i
zadaniach” pod red. Karola Kukuły
zadaniach” pod red. Karola Kukuły
Wyd. Naukowe PWN
Wyd. Naukowe PWN
2.
2.
„
„
Matematyczne techniki zarządzania”
Matematyczne techniki zarządzania”
pod red. Zbigniewa Łuckiego Wyd.
pod red. Zbigniewa Łuckiego Wyd.
AGH
AGH
3.
3.
Badania operacyjne mgr inż. Piotr
Badania operacyjne mgr inż. Piotr
Betlej
Betlej
Programowanie
Programowanie
dynamiczne
dynamiczne
•
jest jedną z technik matematycznych
jest jedną z technik matematycznych
poszukiwania rozwiązań
poszukiwania rozwiązań
optymalnych
optymalnych
•
określa sposób podejścia do
określa sposób podejścia do
rozwiązywania problemu niż jako
rozwiązywania problemu niż jako
pojedynczy uniwersalny algorytm.
pojedynczy uniwersalny algorytm.
rozwiązanie
rozwiązanie
•
polega na podziale zagadnienia pierwotnego na
polega na podziale zagadnienia pierwotnego na
podproblemy lub etapy, a następnie na ich sekwencyjnym
podproblemy lub etapy, a następnie na ich sekwencyjnym
rozwiązywaniu, aż do znalezienia rozwiązania
rozwiązywaniu, aż do znalezienia rozwiązania
optymalnego.
optymalnego.
•
Stosuje się przy tym, niezależnie od algorytmu,
Stosuje się przy tym, niezależnie od algorytmu,
zasadę
zasadę
optymalności Bellmana
optymalności Bellmana
, w myśl której optymalne
, w myśl której optymalne
rozwiązanie zagadnień z zakresu programowania
rozwiązanie zagadnień z zakresu programowania
dynamicznego ma tę własność, że optymalne rozwiązanie
dynamicznego ma tę własność, że optymalne rozwiązanie
dla
dla
k
k
-tego etapu jest jednocześnie rozwiązaniem
-tego etapu jest jednocześnie rozwiązaniem
optymalnym dla etapów k + 1, k + 2, ..., N. Tak więc
optymalnym dla etapów k + 1, k + 2, ..., N. Tak więc
optymalne rozwiązanie dla etapu pierwszego stanowi
optymalne rozwiązanie dla etapu pierwszego stanowi
optymalne rozwiązanie dla całego problemu.
optymalne rozwiązanie dla całego problemu.
•
W związku z powyższą zasadą problem z zakresu
W związku z powyższą zasadą problem z zakresu
programowania dynamicznego rozwiązuje się
programowania dynamicznego rozwiązuje się
rozpoczynając od poszukiwania rozwiązania dla ostatniego
rozpoczynając od poszukiwania rozwiązania dla ostatniego
etapu (N), a następnie cofając się poszukuje się
etapu (N), a następnie cofając się poszukuje się
rozwiązania dla etapu N-1 Uzyskane w ten sposób
rozwiązania dla etapu N-1 Uzyskane w ten sposób
rozwiązanie dla etapów N-1 oraz N jest optymalne bez
rozwiązanie dla etapów N-1 oraz N jest optymalne bez
względu na to, w jaki sposób osiągnięto etap N- 1.
względu na to, w jaki sposób osiągnięto etap N- 1.
Powtarzając w powyższy sposób etap po etapie dochodzimy
Powtarzając w powyższy sposób etap po etapie dochodzimy
do rozwiązania optymalnego dla pierwszego etapu, a więc i
do rozwiązania optymalnego dla pierwszego etapu, a więc i
dla całego problemu.
dla całego problemu.
Zadania programowania
Zadania programowania
dynamicznego
dynamicznego
•
zagadnienie dyliżansu
zagadnienie dyliżansu
,
,
•
zagadnienie finansowania
zagadnienie finansowania
inwestycji
inwestycji
,
,
•
optymalizacja zapasów
optymalizacja zapasów
,
,
•
alokacja zasobów
alokacja zasobów
, czy
, czy
wymiana
wymiana
majątku trwałego
majątku trwałego
.
.
Zagadnienie finansowania
Zagadnienie finansowania
przedsięwzięcia
przedsięwzięcia
inwestycyjnego
inwestycyjnego
•
Zagadnienie finansowania przedsięwzięcia inwestycyjnego
Zagadnienie finansowania przedsięwzięcia inwestycyjnego
można scharakteryzować jako problem alokacji określonego
można scharakteryzować jako problem alokacji określonego
zasobu środków (w tym przypadku wyrażonego w jednostkach
zasobu środków (w tym przypadku wyrażonego w jednostkach
pieniężnych) pomiędzy poszczególne zadania (programy
pieniężnych) pomiędzy poszczególne zadania (programy
inwestycyjne), tak aby osiągnąć maksymalny efekt.
inwestycyjne), tak aby osiągnąć maksymalny efekt.
•
Przyjmuje się przy tym następujące założenia:
Przyjmuje się przy tym następujące założenia:
•
Efekt zastosowania każdego z programów inwestycyjnych nie
Efekt zastosowania każdego z programów inwestycyjnych nie
zależy od tego, czy zostały zastosowane równocześnie inne
zależy od tego, czy zostały zastosowane równocześnie inne
programy inwestycyjne.
programy inwestycyjne.
•
Zwrot nakładów inwestycyjnych jest mierzony w tych samych
Zwrot nakładów inwestycyjnych jest mierzony w tych samych
jednostkach.
jednostkach.
•
Nakłady inwestycyjne są liczbami całkowitymi.
Nakłady inwestycyjne są liczbami całkowitymi.
•
Funkcje określające związki między nakładami inwestycyjnymi
Funkcje określające związki między nakładami inwestycyjnymi
a wysokością zwrotu z nakładów są niemalejące.
a wysokością zwrotu z nakładów są niemalejące.
Przykład zagadnienia
Przykład zagadnienia
alokacji inwestycji
alokacji inwestycji
•
Przedsiębiorca Jan Rogala, posiadający kredyt inwestycyjny w wysokości
Przedsiębiorca Jan Rogala, posiadający kredyt inwestycyjny w wysokości
6 min złotych oraz halę produkcyjną w Rzeszowie, postanowił
6 min złotych oraz halę produkcyjną w Rzeszowie, postanowił
zainstalować nowoczesne linie piekarnicze:
zainstalować nowoczesne linie piekarnicze:
•
francuską (F),
francuską (F),
•
szwedzką (S)
szwedzką (S)
•
oraz polską (P).
oraz polską (P).
•
Dobowe zdolności produkcyjne pieczywa (w tonach) w zależności od
Dobowe zdolności produkcyjne pieczywa (w tonach) w zależności od
wysokości nakładów inwestycyjnych przeznaczonych na zainstalowanie
wysokości nakładów inwestycyjnych przeznaczonych na zainstalowanie
linii produkcyjnej danego typu, przedstawiono w poniższej tabeli:
linii produkcyjnej danego typu, przedstawiono w poniższej tabeli:
Analiza rynku wykazała, że każda z linii produkcyjnych, pozwala uzyskiwać
Analiza rynku wykazała, że każda z linii produkcyjnych, pozwala uzyskiwać
jednakowe zyski w przeliczeniu na 1 t pieczywa.
jednakowe zyski w przeliczeniu na 1 t pieczywa.
Jan Rogala musi więc w tym przypadku podjąć decyzję dotyczącą podziału
Jan Rogala musi więc w tym przypadku podjąć decyzję dotyczącą podziału
kredytu pomiędzy poszczególne programy inwestycyjne, tak aby
kredytu pomiędzy poszczególne programy inwestycyjne, tak aby
piekarnia osiągnęła maksymalną, dobową zdolność produkcyjną.
piekarnia osiągnęła maksymalną, dobową zdolność produkcyjną.
Rozwiązanie
Rozwiązanie
•
Powyższy problem, należący do
Powyższy problem, należący do
kategorii programowania
kategorii programowania
dynamicznego, można rozwiązać za
dynamicznego, można rozwiązać za
pomocą procedury opisanej w kilku
pomocą procedury opisanej w kilku
etapach.
etapach.
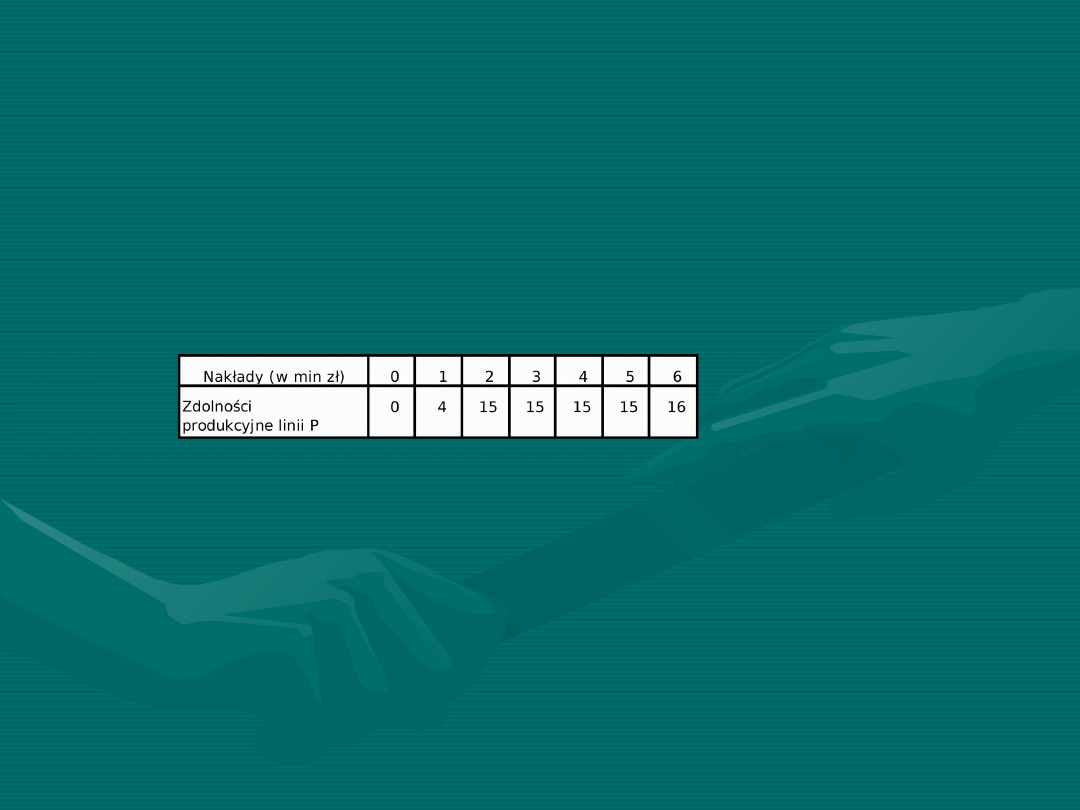
KROK 1.
KROK 1.
•
Załóżmy, że jedynym możliwym rozwiązaniem jest
Załóżmy, że jedynym możliwym rozwiązaniem jest
zakupienie polskiej linii produkcyjnej i zadajmy sobie
zakupienie polskiej linii produkcyjnej i zadajmy sobie
pytanie dotyczące uzyskanej w ten sposób dobowej
pytanie dotyczące uzyskanej w ten sposób dobowej
zdolności produkcyjnej w zależności od zainwestowanej
zdolności produkcyjnej w zależności od zainwestowanej
kwoty.
kwoty.
•
W tym przypadku, jedynym sensownym rozwiązaniem
W tym przypadku, jedynym sensownym rozwiązaniem
jest zainwestowanie 6 min zł w polską linię produkcyjną
jest zainwestowanie 6 min zł w polską linię produkcyjną
w celu osiągnięcia zdolności produkcyjnej 16 t pieczywa
w celu osiągnięcia zdolności produkcyjnej 16 t pieczywa
na dobę. Rezultat ten zapiszemy następująco:
na dobę. Rezultat ten zapiszemy następująco:
P(6) = 16,
P(6) = 16,
co oznacza, że 6 mln zł zainwestowane w polską linię
co oznacza, że 6 mln zł zainwestowane w polską linię
produkcyjną zapewnia produkcję 16 t pieczywa na dobę.
produkcyjną zapewnia produkcję 16 t pieczywa na dobę.
KROK 2.
KROK 2.
•
Załóżmy, że dostępne są dwa typy
Załóżmy, że dostępne są dwa typy
linii produkcyjnych P oraz S i
linii produkcyjnych P oraz S i
zadajmy sobie następujące pytanie:
zadajmy sobie następujące pytanie:
jak należy podzielić kredyt
jak należy podzielić kredyt
inwestycyjny pomiędzy te dwa
inwestycyjny pomiędzy te dwa
programy, aby uzyskać maksymalną
programy, aby uzyskać maksymalną
dobową zdolność produkcyjną?
dobową zdolność produkcyjną?
•
W tym przypadku możliwe jest siedem wariantów
W tym przypadku możliwe jest siedem wariantów
podziału 6 min kredytu, które dają następujące
podziału 6 min kredytu, które dają następujące
dobowe zdolności produkcyjne:
dobowe zdolności produkcyjne:
P(6) + S(0)= 16 + 0= 16,
P(6) + S(0)= 16 + 0= 16,
P(5) + S(l)= 15 + 5 = 20,
P(5) + S(l)= 15 + 5 = 20,
P(4) + S(2)= 15 + 8 = 23,
P(4) + S(2)= 15 + 8 = 23,
P(3) + S(3)= 15 + 11 =26,
P(3) + S(3)= 15 + 11 =26,
P(2) + S(4)= 15 + 14 = 29,
P(2) + S(4)= 15 + 14 = 29,
P(1) + S(5)= 4+17 = 21,
P(1) + S(5)= 4+17 = 21,
P(0) + S(6) = 0+18 = 18.
P(0) + S(6) = 0+18 = 18.
W powyższej sytuacji należy więc zainwestować 2
W powyższej sytuacji należy więc zainwestować 2
mln w polską linię oraz 4 mln w szwedzką linię,
mln w polską linię oraz 4 mln w szwedzką linię,
osiągając w ten sposób 29 t pieczywa na dobę, tzn.
osiągając w ten sposób 29 t pieczywa na dobę, tzn.
P(2) + S(4) = 29.
P(2) + S(4) = 29.
KROK 3.
KROK 3.
•
Spróbujmy obecnie znaleźć optymalny podział
Spróbujmy obecnie znaleźć optymalny podział
kredytu pomiędzy linię P oraz S przy malejącej
kredytu pomiędzy linię P oraz S przy malejącej
kwocie nakładów inwestycyjnych:
kwocie nakładów inwestycyjnych:
a)
a)
5 mln na linie P oraz S
5 mln na linie P oraz S
P(5) + S(O) = 15 + 0 = 15,
P(5) + S(O) = 15 + 0 = 15,
P(4) + S(1) = 15 + 5 = 20,
P(4) + S(1) = 15 + 5 = 20,
P(3) + S(2) = 15 + 8 = 23,
P(3) + S(2) = 15 + 8 = 23,
P(2) + S(3) = 15 + 11 = 26,
P(2) + S(3) = 15 + 11 = 26,
P(1) + S(4) = 4 + 14 = 18,
P(1) + S(4) = 4 + 14 = 18,
P(0) + S(5) = 0 + 17 = 17.
P(0) + S(5) = 0 + 17 = 17.
W przypadku dysponowania kwotą 5 mln zł na
W przypadku dysponowania kwotą 5 mln zł na
linię P oraz S należy zainwestować 2 mln w linię
linię P oraz S należy zainwestować 2 mln w linię
P oraz 3 mln w linię S, osiągając 26 t pieczywa
P oraz 3 mln w linię S, osiągając 26 t pieczywa
dobę. Rezultat zapiszemy w następujący sposób:
dobę. Rezultat zapiszemy w następujący sposób:
P(2) + S(3) = 26.
P(2) + S(3) = 26.
b) 4 mln zł na linie P oraz S
b) 4 mln zł na linie P oraz S
P(4) + S(0) = 15 + 0 = 15,
P(4) + S(0) = 15 + 0 = 15,
P(3) + S(1) = 15 + 5 = 20,
P(3) + S(1) = 15 + 5 = 20,
P(2) + S(2) = 15 + 8 = 23,
P(2) + S(2) = 15 + 8 = 23,
P(1) + S(3) = 4 + 11 = 15,
P(1) + S(3) = 4 + 11 = 15,
P(0) + S(4) = 0 + 14 = 14.
P(0) + S(4) = 0 + 14 = 14.
W przypadku dysponowania kwotą 4 mln zł
W przypadku dysponowania kwotą 4 mln zł
należy zainwestować po 2 mln zł w linię P
należy zainwestować po 2 mln zł w linię P
oraz S:
oraz S:
P(2) + S(2) = 23.
P(2) + S(2) = 23.
c) 3 mln zł na linie P oraz S:
c) 3 mln zł na linie P oraz S:
P(3) + S(0) = 15 + 0 = 15.
P(3) + S(0) = 15 + 0 = 15.
P(2) + S(1)= 15 + 5 = 20,
P(2) + S(1)= 15 + 5 = 20,
P(1) + S(2) = 4 + 8 = 12,
P(1) + S(2) = 4 + 8 = 12,
P(0) + S(3) = 0 + 11 = 11.
P(0) + S(3) = 0 + 11 = 11.
W tym przypadku należy zainwestować
W tym przypadku należy zainwestować
2 mln w linię P oraz 1 mln w linię S:
2 mln w linię P oraz 1 mln w linię S:
P(2) + S(1) = 20.
P(2) + S(1) = 20.
d) 2 mln zł na linie P oraz S
d) 2 mln zł na linie P oraz S
P(2) + S(0) = 15 + 0 = 15,
P(2) + S(0) = 15 + 0 = 15,
P(1) + S(1) = 4 + 5 = 9,
P(1) + S(1) = 4 + 5 = 9,
P(0) + S(2) = 0 + 8 = 8.
P(0) + S(2) = 0 + 8 = 8.
W tym przypadku należy
W tym przypadku należy
zainwestować 2 min zł w linię polską
zainwestować 2 min zł w linię polską
(P):
(P):
P(2) + S(0)= 15.
P(2) + S(0)= 15.
e) 1 mln zł na linie P oraz S
e) 1 mln zł na linie P oraz S
P(1) + S(0) = 4 + 0 = 4,
P(1) + S(0) = 4 + 0 = 4,
P(0) + S(1) = 0 + 5 = 5.
P(0) + S(1) = 0 + 5 = 5.
W tym przypadku należy zainwestować
W tym przypadku należy zainwestować
1 mln zł w linię szwedzką (S):
1 mln zł w linię szwedzką (S):
P(0) + S(1) = 5.
P(0) + S(1) = 5.
A zatem, w kroku 3 określiliśmy
A zatem, w kroku 3 określiliśmy
optymalne kombinacje nakładów na
optymalne kombinacje nakładów na
linie P oraz S.
linie P oraz S.
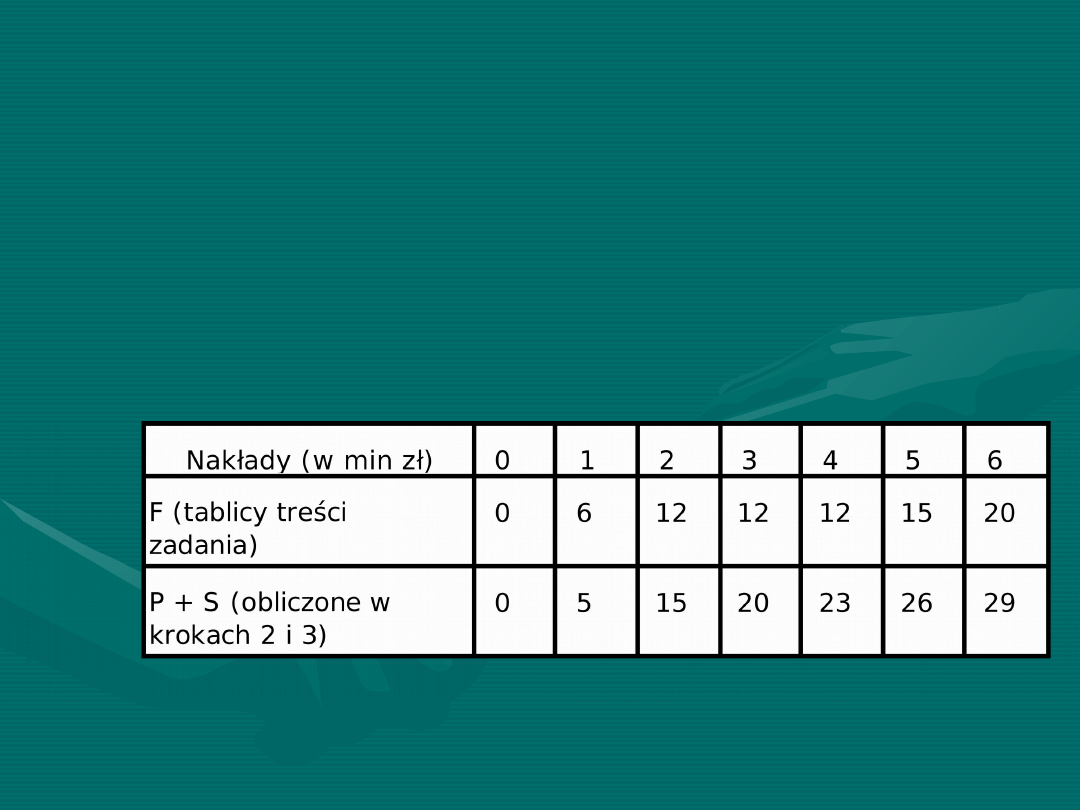
KROK 4.
KROK 4.
Konsekwentnie, w kroku 4 wystarczy rozpatrzyć
Konsekwentnie, w kroku 4 wystarczy rozpatrzyć
wszystkie kombinacje podziału 6 mln zł kredytu
wszystkie kombinacje podziału 6 mln zł kredytu
pomiędzy linię F oraz linie P + S. Zdolności
pomiędzy linię F oraz linie P + S. Zdolności
produkcyjne w zależności od nakładów
produkcyjne w zależności od nakładów
kredytowych przedstawiono w poniższej tabeli:
kredytowych przedstawiono w poniższej tabeli:
Jak łatwo zauważyć możliwych jest siedem wariantów
Jak łatwo zauważyć możliwych jest siedem wariantów
podziału 6 mln kredytu pomiędzy linie F oraz linie
podziału 6 mln kredytu pomiędzy linie F oraz linie
P + S, dających następujące zdolności produkcyjne:
P + S, dających następujące zdolności produkcyjne:
F(6) + (P + S)(0) = 20 + 0 = 20,
F(6) + (P + S)(0) = 20 + 0 = 20,
F(5) + (P + S)(1) = 15+5 = 20,
F(5) + (P + S)(1) = 15+5 = 20,
F(4) + (P + S)(2) = 12 + 15 = 27,
F(4) + (P + S)(2) = 12 + 15 = 27,
F(3) + (P + S)(3) = 12 + 20 = 32,
F(3) + (P + S)(3) = 12 + 20 = 32,
F(2) + (P + S)(4) = 12 + 23 = 35,
F(2) + (P + S)(4) = 12 + 23 = 35,
F(1) + (P + S)(5)= 6 + 26 = 32,
F(1) + (P + S)(5)= 6 + 26 = 32,
F(0) + (P + S)(6) = 0 + 29 = 29.
F(0) + (P + S)(6) = 0 + 29 = 29.
Tak więc maksymalną zdolność produkcyjną
Tak więc maksymalną zdolność produkcyjną
piekarni można uzyskać inwestując 2 min w linię
piekarni można uzyskać inwestując 2 min w linię
francuską (F) oraz 4 mln zł w linię P i S.
francuską (F) oraz 4 mln zł w linię P i S.
Aby uzyskać rozwiązanie ostateczne,
Aby uzyskać rozwiązanie ostateczne,
wystarczy odszukać w kroku 3 optymalny
wystarczy odszukać w kroku 3 optymalny
sposób podziału tych 4 mln zł pomiędzy
sposób podziału tych 4 mln zł pomiędzy
linię P oraz S (krok 3b).
linię P oraz S (krok 3b).
W rezultacie otrzymujemy rozwiązanie: 2
W rezultacie otrzymujemy rozwiązanie: 2
mln zł na linię F, 2 mln zł na linię P oraz 2
mln zł na linię F, 2 mln zł na linię P oraz 2
mln ma linię S, co zapewnia 35 t pieczywa
mln ma linię S, co zapewnia 35 t pieczywa
na dobę.
na dobę.
Zagadnienie dyliżansu
Zagadnienie dyliżansu
•
Nazwa zagadnienia pochodzi od pewnego kupca
Nazwa zagadnienia pochodzi od pewnego kupca
amerykańskiego, który transportował towary ze
amerykańskiego, który transportował towary ze
Wschodniego Wybrzeża USA na Wybrzeże
Wschodniego Wybrzeża USA na Wybrzeże
Zachodnie, używając w tym celu różnych
Zachodnie, używając w tym celu różnych
połączeń realizowanych za pomocą dyliżansu.
połączeń realizowanych za pomocą dyliżansu.
•
Oczywiście chodziło o dobór takich połączeń, aby
Oczywiście chodziło o dobór takich połączeń, aby
transport odbywał się w miarę bezpiecznie, a
transport odbywał się w miarę bezpiecznie, a
miarą bezpieczeństwa na danej linii były stawki
miarą bezpieczeństwa na danej linii były stawki
pobierane przez towarzystwo ubezpieczeniowe.
pobierane przez towarzystwo ubezpieczeniowe.
•
Rozwiązanie problemu wymagało podzielenia
Rozwiązanie problemu wymagało podzielenia
całej trasy na etapy, a w każdym z etapów
całej trasy na etapy, a w każdym z etapów
określenia miast etapowych oraz wszystkich
określenia miast etapowych oraz wszystkich
możliwych połączeń pomiędzy nimi.
możliwych połączeń pomiędzy nimi.
Przykład problemu
Przykład problemu
dyliżansu
dyliżansu
Firma transportowa EuroTrans, ustalając nowe
Firma transportowa EuroTrans, ustalając nowe
trasy przejazdu swych ciężarówek z Polski do
trasy przejazdu swych ciężarówek z Polski do
Hiszpanii, podzieliła całą trasę na pięć etapów.
Hiszpanii, podzieliła całą trasę na pięć etapów.
W każdym z etapów wyznaczono po kilka miast,
W każdym z etapów wyznaczono po kilka miast,
przez które przejeżdżać będą ciężarówki.
przez które przejeżdżać będą ciężarówki.
Problem polega na znalezieniu najkrótszej drogi
Problem polega na znalezieniu najkrótszej drogi
przejazdu pomiędzy Polską a Hiszpanią.
przejazdu pomiędzy Polską a Hiszpanią.
Odległości drogowe pomiędzy miastami (w
Odległości drogowe pomiędzy miastami (w
km) zaznaczono na poniższym rysunku:
km) zaznaczono na poniższym rysunku:
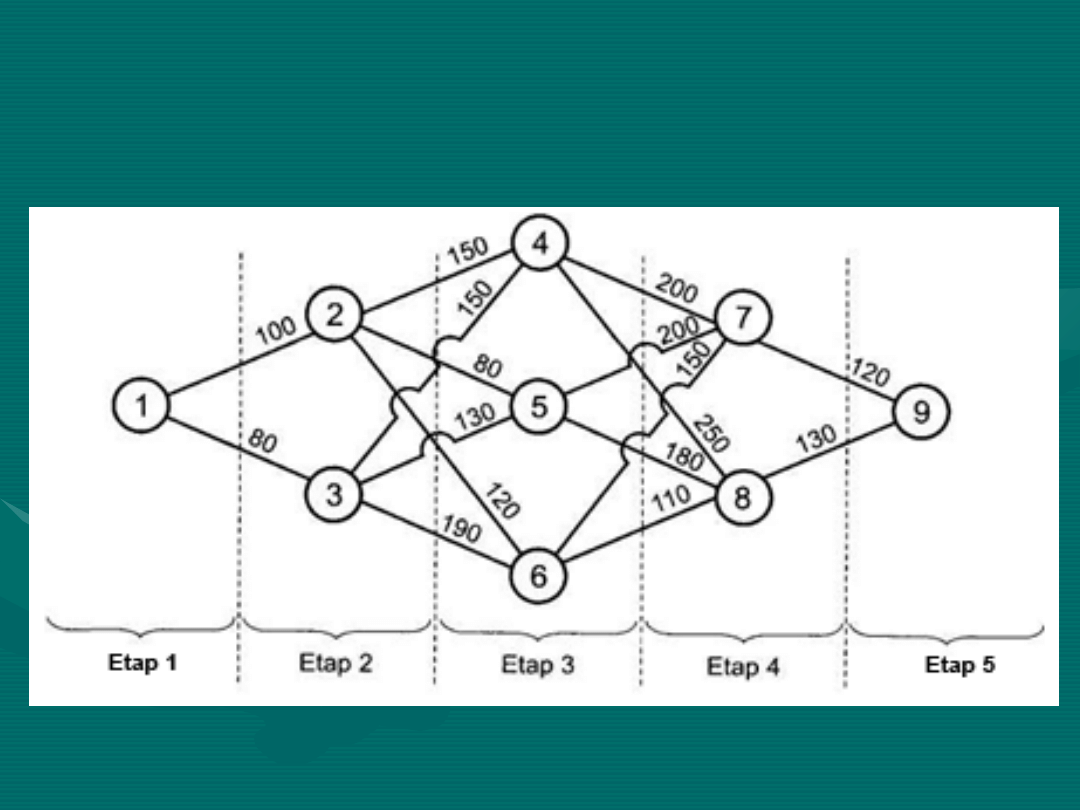
KROK 1.
KROK 1.
Załóżmy, że ciężarówki dotarły do
Załóżmy, że ciężarówki dotarły do
etapu 4.
etapu 4.
W tej sytuacji odległość od celu
W tej sytuacji odległość od celu
wynosi:
wynosi:
d
d
7,9
7,9
= 120 km lub d
= 120 km lub d
8,9
8,9
= 130
= 130
km,
km,
w zależności od tego, w którym z
w zależności od tego, w którym z
miast w etapie 4 zatrzymano się na
miast w etapie 4 zatrzymano się na
postój.
postój.
KROK 2.
KROK 2.
Cofnijmy się o jeden etap.
Cofnijmy się o jeden etap.
Odległość miast od celu w etapie 3 wynosi:
Odległość miast od celu w etapie 3 wynosi:
d
d
4,7
4,7
+ d
+ d
7,9
7,9
= 200 + 120 = 320,
= 200 + 120 = 320,
d
d
4,8
4,8
+ d
+ d
8,9
8,9
= 250 + 130 = 380.
= 250 + 130 = 380.
Tak więc z miasta 4 do 9 należy wybrać drogę o długości
Tak więc z miasta 4 do 9 należy wybrać drogę o długości
d
d
4,7,9
4,7,9
= 320. Podobnie:
= 320. Podobnie:
d
d
5,7
5,7
+ d
+ d
7,9
7,9
= 200 + 120 = 320,
= 200 + 120 = 320,
d
d
5,8
5,8
+ d
+ d
8,9
8,9
= 180 + 130 = 310,
= 180 + 130 = 310,
a więc z miasta 5 do 9 należy wybrać drogę o długości d
a więc z miasta 5 do 9 należy wybrać drogę o długości d
5,8,9
5,8,9
= 310.
= 310.
Następnie:
Następnie:
d
d
6,7
6,7
+ d
+ d
7,9
7,9
= 150 + 120 = 270,
= 150 + 120 = 270,
d
d
6,8
6,8
+ d
+ d
8,9
8,9
= 110 + 130 = 240,
= 110 + 130 = 240,
a więc z miasta 6 do 9 należy wybrać drogę o długości
a więc z miasta 6 do 9 należy wybrać drogę o długości
d
d
6,8,9
6,8,9
=
=
240
240
.
.
KROK 3.
KROK 3.
Powtórzmy całe postępowanie biorąc za punkt wyjścia
Powtórzmy całe postępowanie biorąc za punkt wyjścia
etap 2:
etap 2:
d
d
2,4
2,4
+ d
+ d
4,9
4,9
= 150 + 320 = 470,
= 150 + 320 = 470,
d
d
2,5
2,5
+ d
+ d
5,9
5,9
= 80 + 310 = 390,
= 80 + 310 = 390,
d
d
2,6
2,6
+ d
+ d
6,9
6,9
= 120 + 240 = 360,
= 120 + 240 = 360,
a więc z miasta 2 do 9 należy wybrać drogę:
a więc z miasta 2 do 9 należy wybrać drogę:
2-6-8-9
2-6-8-9
o długości 360 km.
o długości 360 km.
Podobnie
Podobnie
d
d
3,4
3,4
+ d
+ d
4,9
4,9
= 150 + 320 = 470,
= 150 + 320 = 470,
d
d
3,5
3,5
+ d
+ d
4,9
4,9
= 130 + 310 = 440,
= 130 + 310 = 440,
d
d
3,6
3,6
+ d
+ d
4,9
4,9
= 190 + 240 = 430,
= 190 + 240 = 430,
a więc z miasta 3 do 9 należy wybrać drogę:
a więc z miasta 3 do 9 należy wybrać drogę:
3-6-8-9
3-6-8-9
o długości 430 km.
o długości 430 km.
KROK 4.
KROK 4.
Dotarliśmy do punktu startowego, w
Dotarliśmy do punktu startowego, w
którym rozpatrujemy sposób dotarcia do
którym rozpatrujemy sposób dotarcia do
celu z miasta 1 przez miasta 2 lub 3:
celu z miasta 1 przez miasta 2 lub 3:
d
d
1,2
1,2
+ d
+ d
2,9
2,9
= 100 + 360 = 460,
= 100 + 360 = 460,
d
d
1,3
1,3
+ d
+ d
3,9
3,9
= 80 + 430 = 510,
= 80 + 430 = 510,
a więc z miasta 1 do 9 należy wybrać
a więc z miasta 1 do 9 należy wybrać
drogę:
drogę:
1-2-6-8-9
1-2-6-8-9
o długości 460 km.
o długości 460 km.
Document Outline