Elżbieta Szwajczak
WMiFS PRz

Mechanika

MECHANIKA KLASYCZNA

KINEMATYKA

Kinematyka nie uwzględnia materii zawartej

w cząstce materialnej oraz przyczyn ruchu.

Do opisu zachowania się cząstki materialnej

w mechanice klasycznej niezbędna jest
znajomość:
położenia (zmiany położenia) – r(t),
prędkości – υ(t),
przyspieszenia – a(t)

w zależności od czasu t.

POŁOŻENIE CZĄSTKI

można przedstawić w kartezjańskim układzie

współrzędnych (x,y,z) za pomocą wektora r (tj.

wektora wodzącego punktu materialnego):
r = x + y + z

lub r = i x + j y + k z
lub r = ρ |r| = ρ r
gdzie i, j, k są wersorami,
ρ służy do pokazania kierunku wektora r w

przestrzeni - ρ = r / |r| = r / r,
x,y,z są długościami wektorów x,y,z, odpowiednio,

lub współrzędnymi końca wektora wodzącego r.

Przy czym wektor r jest funkcją czasu - r(t).

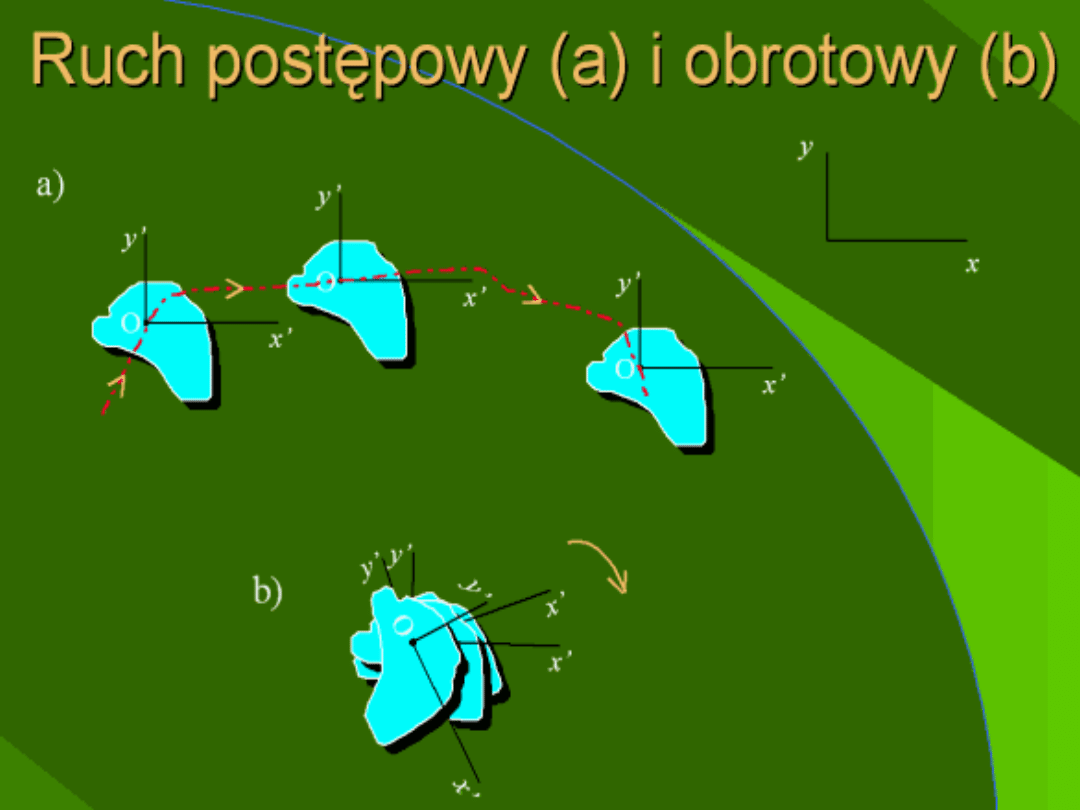
Zmiana położenia. Jeśli ciało fizyczne
znajduje się w chwili t w punkcie A, to w
punkcie B znajdzie się w chwili późniejszej
(t + Δt).

Tor ruchu – krzywa geometryczna, którą
zakreśla punkt materialny podczas swego
ruchu.

Droga – długość łuku, który punkt
materialny zakreśla podczas swego ruchu
w przedziale czasowym
<t

A

, t

B

>.

PRĘDKOŚĆ

Prędkość średnia
 

Prędkość chwilowa

t

t

t

t

t

















r

r

r

υ

śr

)

(

)

(

dt

d

t

t

t

t

t

t

t

r

r

r

r

υ



























lim

lim

0

0

)

(

)

(

Prędkość (chwilowa) jest, z punktu

widzenia fizyki, zmianą położenia ciała w
czasie, zaś z punktu widzenia matematyki
pierwszą pochodną „położenia po czasie”.
Jest to wektor styczny do toru w każdym
punkcie.

Jeśli r = ρ |r| = ρ r to (zgodnie z

definicją pochodnej iloczynu) prędkość
jako wielkość wektorowa zależy zarówno
od zmiany długości wektora wodzącego,
jak również od zmiany jego kierunku

 

-

        

 

- pierwszy wyraz opisuje prędkość liniową ciała tak jak
w ruchu po prostej (gdy zmianie w czasie ulega długość
wektora wodzącego r).

- drugi wyraz opisuje prędkość liniową tak jak w ruchu
po okręgu (gdy zmianie w czasie ulega kierunek wektora
wodzącego r).

-

        

 

-

        

 

dt

d

r

dt

dr

dt

d

dt

d

ρ

ρ

r

ρ

r

υ











Prędkość

)

(

)

(

)

(

t

t

t

r

ω

ρ

υ

υ







Jeśli skorzystać z wzorów Freneta, to
prędkość można przedstawić następująco

:

 

gdzie ω jest wektorem prędkości kątowej

.

PRZYŚPIESZENIE

Przyśpieszenie średnie

t

t

t

t

t

a

















υ

υ

υ

śr

)

(

)

(

2

2

0

lim

dt

d

dt

d

t

t

a

r

υ

υ















Przyspieszenie chwilowe

Przyspieszenie całkowite

Jeśli do definicji przyspieszenia podstawić
wyrażenie na prędkość, a następnie skorzystać z
wyrażenia na wektor wodzący punktu

materialnego,

to okaże się, że:

przyspieszenie całkowite jest sumą
przyspieszenia stycznego,
przyspieszenia normalnego (w ruchu po okręgu

zwanego dośrodkowym)

oraz przyspieszenia Coriolisa,

)

8

.

1

(

a

a

a

a

C

n

s







przyspieszenie styczne

związane jest ze zmianą wartości

prędkości

liniowe(czyli stycznej do toru) i jest

wektorem

stycznym do toru w każdym punkcie

:

dt

d

a





s

r

n

2







a

przyspieszenie normalne



       

występujące w ruchu krzywoliniowym, jest
wektorem skierowanym radialnie (wzdłuż wektora
wodzącego, lecz z przeciwnym zwrotem), czyli
prostopadle do krzywizny toru w danym punkcie. W
ruchu po okręgu jest skierowany wzdłuż promienia
okręgu, do środka okręgu i nazywa się
przyspieszeniem dośrodkowym

.

przyspieszenie Coriolisa

Przyspieszenie Coriolisa

υ'

ω

C



2

a

występuje wtedy, gdy cząstka
poruszająca się z prędkością liniową υ’
znajduje się w wirującym układzie
odniesienia (z prędkością kątową ω).
Występuje zatem przy złożeniu równoczesnych
ruchów: postępowego i obrotowego.

Przykład – podmywanie brzegów rzek płynących
południkowo.

    

KLASYFIKACJA RUCHÓW

Klasyfikacja ruchów ze względu na:
* tor ruchu
* przyspieszenie.

Klasyfikacja została dokonana ze względu

na

przyspieszenie w ruchu postępowym i
obrotowym (bez zapisu wektorowego).

TAB.

prostoliniowy
krzywoliniowy/obrotowy

t

t

s

s

dt

d

dt

ds

const

const

a

y

jednostajn

o

o

t

t

s

s

o





















































0

0

0

.

.

0

0

2

2

)

(

)

(

)

0

,

0

(

)

0

,

0

(

2

2

0

0

0

0

0

t

t

at

t

s

s

dt

t

d

dt

at

ds

t

at

dt

d

dt

a

d

const

o

a

const

a

opózniony)

zony,

(przyspies

zmienny

ie

jednostajn

o

o

o

o

t

o

t

o

s

s

o

o

t

t

o

o

o

















































































































!!

!

cakowanie

dt

d

dt

ds

dt

d

dt

a

d

const

const

a

zmienny



























DYNAMIKA

 

Zasady dynamiki Newtona

W dynamice szukamy związków między
oddziaływaniem ciał a ich ruchem.

Podstawę dynamiki stanowią zasady

dynamiki Newtona.

Oddziaływanie ciał może być bezpośrednie

lub na

odległość (poprzez pole).

Zasady dynamiki obowiązują w inercjalnych

układach

odniesienia.

I zasada dynamiki

Ciało pozostaje w spoczynku (υ=0) lub
porusza się ruchem jednostajnie
prostoliniowym (υ=const) jeżeli na ciało
nie działają żadne siły (F=0) lub działające
siły równoważą się (∑F

i

=0).

Jest to tzw. zasada bezwładności.

0

lub

0

1











υ

υ

F

i

const

to

Jesli

i

II zasada dynamiki

dt

d

to

Jesli

n

i

p

F

F

F

i







1

gdzie p = m υ, jest to pęd równy iloczynowi
masy m i prędkości υ punktu materialnego.

Jeżeli na ciało działają siły niezrównoważone
to zmienia się w czasie pęd ciała; czyli
zmianie może ulegać prędkość ciała, jak
również jego masa.

a

υ

υ

υ

υ

F

m

dt

dm

dt

d

m

dt

dm

dt

m

d











)

(

To prawo można przedstawić inaczej:

t

dt

d









F

p

F

p

lub

przyrost pędu ciała równy jest popędowi

siły wywartemu na to ciało.

Jeżeli masa poruszającego się ciała nie
zmienia się w
czasie (m=const), to druga zasada dynamiki
Newtona
przyjmuje postać:

a

F m



Siła zatem jest wielkością proporcjonalną do
przyspieszenia, które nadaje ciału, przy czym
współczynnikiem proporcjonalności jest masa
ciała.

III zasada dynamiki

Jeżeli ciało A działa na ciało B siłą F, to ciało B
działa na ciało A siła -F, równa co do wartości
bezwzględnej lecz z przeciwnym zwrotem.

BA

AB

F

F





Prawo to uwzględnia rodzaj czy sposób
oddziaływań ciał. Znane jest jako prawo akcji i
reakcji.

Równanie ruchu cząstki

materialnej (

gdy m=const

) 

      

 

w inercjalnym układzie

odniesienia









n

i

gdzie

m

1

i

F

F

F

a



       

 

w nieinercjalnym układzie odniesienia

















3

1

j

gdzie

m

bj

b

n

1

i

i

b

F

F

F

F

F

F

a

Jeśli ruch punktu materialnego rozpatrujemy
w nieinercjalnym układzie odniesienia, to
oprócz sił które występują w układach
inercjalnych (będących wynikiem
wzajemnego oddziaływania ciał), należy
dodatkowo uwzględnić siły bezwładności.
Przy czym siły bezwładności (pozorne,
rzekome) to siły „przekory”, tzn. zwrot siły
bezwładności F

b

jest przeciwny do zwrotu

przyspieszenia układu a

u.

u

b

a

F

m





II zasada dynamiki Newtona

w ruchu obrotowym

(krzywoliniowym)

dt

d

to

Gdy

n

i

K

M

M

M

i







1

gdzie M jest momentem siły, K momentem
pędu:

p

r

K

F

r

M









Jeśli w czasie ruchu nie zmienia się masa
ciała
(bryły sztywnej) ani też rozkład masy czyli
moment bezwładności jest stały (I=const),
to druga
zasada dynamiki przyjmuje postać:

const

I

dla

I



 ε

M

Gdzie moment bezwładności definiuje się
następująco

:

ego

materia

punktu

dla

m

I

ych

materia

punktów

n

ukladu

dla

m

I

sztywnej

bryly

dla

dm

I

n

i

ln

ln

2

1

2

2

r

r

r













Zasady zachowania
Praca – moc, energia
Zasady zachowania
Związki pomiędzy wielkościami charakterystycznymi
w ruchu prostoliniowym i obrotowym bryły sztywnej
dookoła nieruchomej osi