© 2014 Marcin Skotnicki, IIŚ PP

1

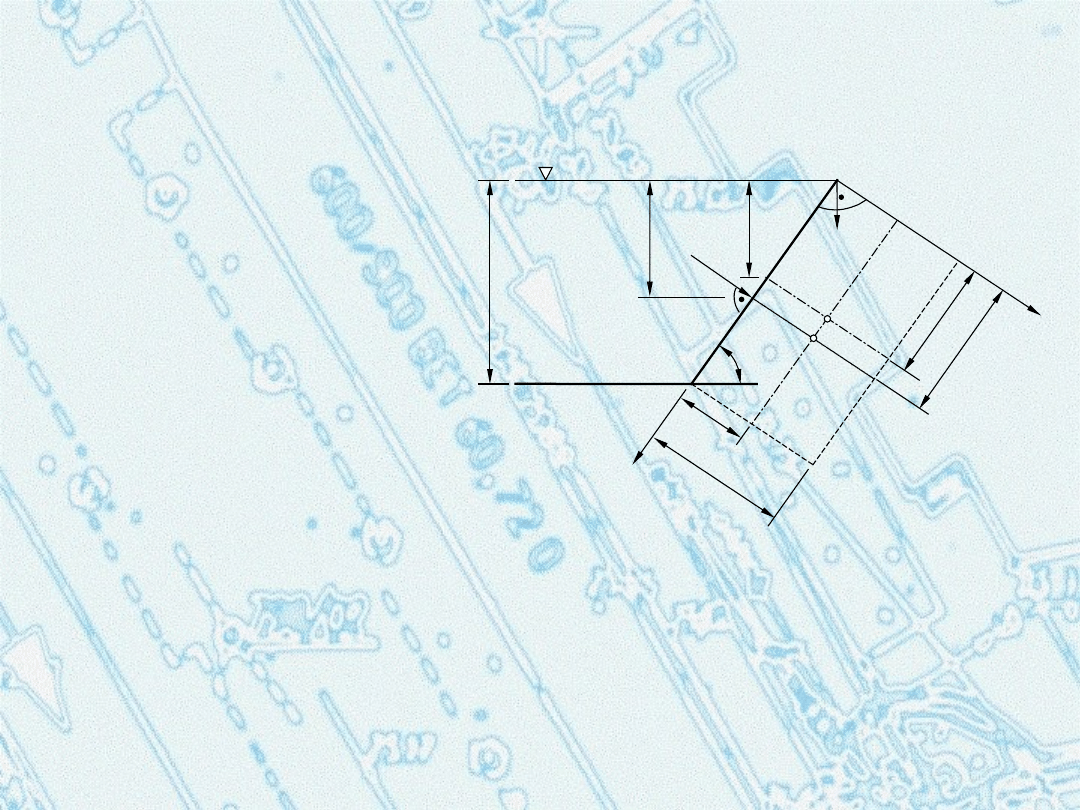
Zadanie 1

Wyznaczyć

wartość

oraz

punkt przyłożenia

siły

parcia działającej na płaską ściankę pokazaną na
rysunku.

Ile wyniesie

wartość

siły parcia i jak zmieni się

przyłożenie parcia

jeżeli ścianka zostanie ustawiona

pionowo ?

h



w



x

y

N

y

S

x

N

=

x

S

y

b

z

S

N

P

z

N

z

S

Do obliczeń przyjąć:
h = 1 m,
b = 1 m

(szerokość ścianki, wymiar prostopadły do płaszczyzny

rysunku)

,



w

= 9 810 N/m

3

,

 = 45

o

.

© 2014 Marcin Skotnicki, IIŚ PP

2

Rozwiązanie:







sin

y

z

S

S

P =   z

S

 A [N/m

3

 m  m

2

= N]

2

h

sin

sin

1

2

h

z

S



















sin

1

2

h

y

S

b

sin

h





]

N

[

b

sin

h

2

h

P













z

S

≠ f()

A = f()

© 2014 Marcin Skotnicki, IIŚ PP

3

kN

6,99

N

987

6

1

45

sin

2

1

810

9

P

o

2











Rozwiązanie:

]

N

[

b

sin

2

h

b

sin

h

2

h

P

2























4





kN

4,91

N

905

4

1

90

sin

2

1

810

9

P

o

2













0



Współrzędne punktu przyłożenia parcia N(x

N

, y

N

, z

N

):

A

y

I

y

y

S

x

S

N

S







A

y

I

x

x

S

y

x

S

N

S

S













sin

y

z

N

N

m

5

,

0

2

b

x

x

S

N







© 2014 Marcin Skotnicki, IIŚ PP

4

Rozwiązanie:













sin

hb

sin

2

h

sin

12

b

h

sin

2

h

y

3

3

N





















sin

h

3

2

sin

6

h

sin

6

h

3

sin

6

h

sin

2

h

y

N









m

94

,

0

45

sin

1

3

2

y

o

N





m

67

,

0

90

sin

1

3

2

y

o

N





sinα

z

y

S

S



© 2014 Marcin Skotnicki, IIŚ PP



Rozwiązanie:

h

3

2

sin

sin

h

3

2

sin

y

z

N

N















m

67

,

0

h

3

2

z

N





© 2014 Marcin Skotnicki, IIŚ PP

6

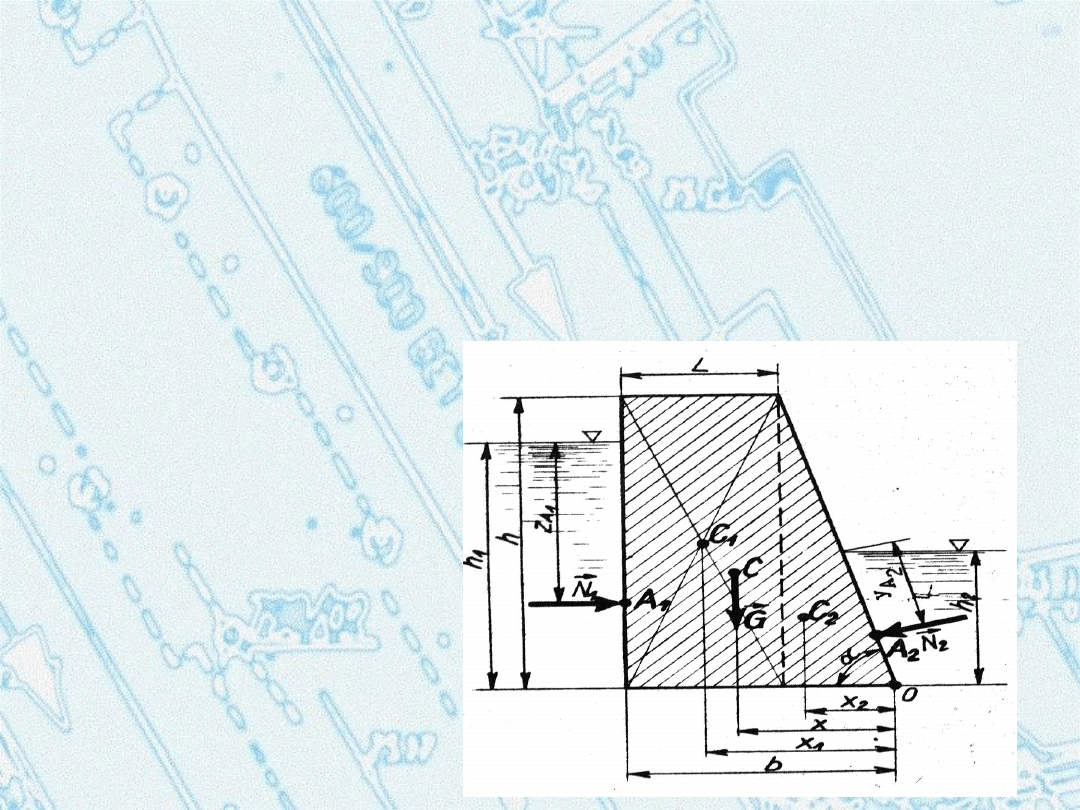
Zadanie 2

Ile powinien wynosić wymiar

liniowy b

przegrody

betonowej
o kształcie pokazanym na rysunku, aby moment
stabilizujący był dwukrotnie większy niż wypadkowy
moment sił przewracających zaporę. Dla uproszczenia
przyjąć,
że przegroda ma możliwość obrotu jedynie dokoła osi
przechodzącej przez jej dolną, prawą krawędź.

Do obliczeń przyjąć:

h

1

= 15 m,

h

2

= 6 m,

L = 3 m,
h = 16,5 m


B

= 23544 N/m

3

.

© 2014 Marcin Skotnicki, IIŚ PP

7

Rozwiązanie:

Moment sił wywracający przegrodę pochodzi od naporu N

1

:





1

A

1

1

w

z

h

N

M





Moment sił stabilizujący przegrodę
(przeciwdziałający momentowi
wywracającemu)
pochodzi od ciężaru przegrody i naporu N

2

:























2

A

2

2

s

y

sin

h

N

x

G

M

Współrzędna środka ciężkości przekroju ściany
(prostokąt
i trójkąt) względem punktu obrotu O wynosi (wg
warunku równowagi momentów):

trapezu

2

troj

1

prost

A

x

A

x

A

x









© 2014 Marcin Skotnicki, IIŚ PP

8

trapezu

2

troj

1

prost

A

x

A

x

A

x









Rozwiązanie:













h

L

b

2

1

L

b

3

2

h

L

b

2

1

2

L

b

hL

x



































 







L

b

3

bL

2

b

2

L

x

2

2











© 2014 Marcin Skotnicki, IIŚ PP



Rozwiązanie:





hB

L

b

2

1

V

G

b

b















Ciężar przegrody G

B – wymiar
prostopadły
do przegrody,
w dalszych
obliczeniach
przyjąć B = 1 m

B

h

2

1

γ

B

h

2

h

N

2

1

w

1

1

w

1







B

h

sin

2

1

B

sin

h

2

h

N

2

2

w

2

2

w

2













Napór N

1

Napór N

2

© 2014 Marcin Skotnicki, IIŚ PP

10

Rozwiązanie:

Współrzędna z

A1

A

z

I

z

y

z

S

x

S

A

A

S

1

1









1

A

h

3

2

z

1



B

h

2

h

12

B

h

2

h

z

1

1

3

1

1

A

1





Współrzędna y

A2

A

y

I

y

y

S

x

S

A

S

2







B

sin

h

sin

1

2

h

12

B

h

sin

1

2

h

y

2

2

3

2

A

2















sin

2

h

y

2

A

2

© 2014 Marcin Skotnicki, IIŚ PP

11





3

1

w

A

1

1

w

h

6

1

γ

z

h

N

M

1







Rozwiązanie:













































2

3

2

w

2

2

b

A

2

2

s

sin

h

6

1

bL

2

b

2

L

h

6

1

y

sin

h

N

x

G

M

2

M

s

= 2M

w





3

1

w

2

3

2

w

2

2

b

h

6

1

γ

2

sin

h

6

1

bL

2

b

2

L

h

6

1

















© 2014 Marcin Skotnicki, IIŚ PP

12

Rozwiązanie:





2

2

h

L

-

b

h

sin







Po przekształceniach:

0

10

84

,

1

b

10

622

b

10

211

10

6

2

6













m

98

,

7

b

m,

9

,

10

b

2

1





