
Matematyczne podstawy opracowania pomiarów
• statystyczne metody analizy danych eksperymentalnych (przedziały
ufności, zagadnienia regresji, wybrane testy statystyczne)
• rachunek błędu
1 godzina wykładu (zaliczenie na podstawie wyniku kolokwium)
1 godzina laboratorium (zajęcia komputerowe grupowane po 3 godziny –
zaliczenie na podstawie wyniku kolokwium)
(dyskietka, tablice dystrybuanty rozkładu normalnego i rozkładu t-Studenta)
Literatura:
1. J. B. Czermiński, A. Iwasiewicz, Z. Paszek, A. Sikorski
Metody statystyczne dla chemików
PWN, Warszawa 1992
2. J. Greń
Statystyka matematyczna
PWN, Warszawa 1987
3. J. Greń
Statystyka matematyczna. Modele i zadania
PWN, Warszawa 1978
4. J. R. Taylor
Wstęp do analizy błędu pomiarowego
PWN, Warszawa 1995
5. W. Klonecki
Statystyka dla inżynierów
PWN, Warszawa 1995
6. W. Ufnalski, K. Mądry
Excel dla chemików i nie tylko
WNT, Warszawa 2000
Ramowy program zajęć
Matematyczne podstawy opracowania pomiarów
WYKŁADY
Ćwiczenia
1. Histogram, średnia, odchylenie stand.
Zapisy
2. Rozkłady ciągłe, rozkład normalny
3. Rozkład t-Studenta, przedziały ufności
4. Testy parametryczne, test chi-kwadrat
5.Korelacja, regresja
6. Błędy, ANOVA, Excel
7. Wielomian, regresja wieloraka
8. Regresja nieliniowa linearyzowalna
9. Regresja nieliniowa
10.Rachunek błędu
11. Rachunek błędu, funkcje
Kolokwium
12. Kolokwium wykładowe
13. Podsumowanie (błędy, wykresy, prezentacja)
14. Oceny
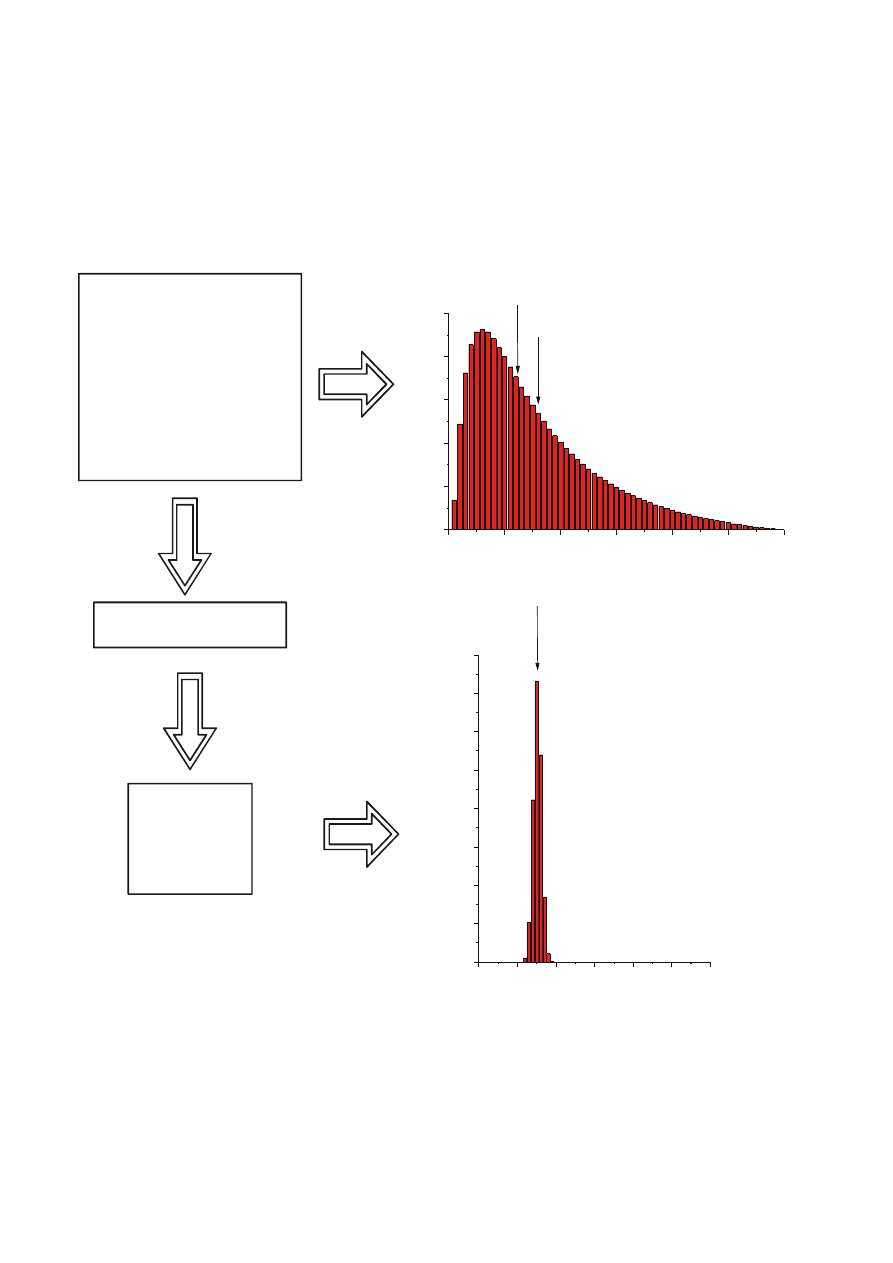
Cały zbiór
(populacja)
Próba
Estymator
0
5
10
15
20
25
30
Średnia
n=100
x
śr.
=7,7
S
2
=0,3
Cz
ęst
ość
wz
gl
ędn
a
Stężenie średnie próby
0
5
10
15
20
25
30
Średnia
mediana
n=17912
μ=7,7
σ
2
=30
Cz
ęst
ość
wz
gl
ędn
a
Stężenie x

12,8
8,2
19,1
22,6
26,1
13,3
9,1
19,2
22,7
26,2
14,5
9,2
19,2
22,7
26,2
15,5
11,1
19,3
22,7
26,3
17,3
11,4
19,4
22,7
26,3
17,5
12,8
19,4
22,7
26,4
17,8
13,1
19,4
22,9
26,4
18,2
13,2
19,7
23
26,5
18,7
13,3
19,8
23
26,5
20,8
13,4
19,8
23,1
26,8
21
13,5
19,9
23,2
27,2
21
13,9
20
23,2
27,2
21,3
14,2
20,1
23,3
27,4
21,8
14,3
20,1
23,3
27,4
22,4
14,4
20,2
23,5
27,5
22,6
14,5
20,2
23,5
27,6
23,6
14,8
20,3
23,6
27,7
24
15,1
20,3
24
28
24,2
15,1
20,4
24,1
28,2
24,5
15,2
20,4
24,2
28,3
25
15,5
20,4
24,2
28,3
25,3
15,6
20,4
24,3
28,3
25,8
15,6
20,5
24,3
28,4
26,1
15,9
20,6
24,3
28,5
26,7
16
20,8
24,3
28,5
26,9
16,4
20,8
24,4
28,7
27,3
16,4
20,8
24,6
28,7
27,3
16,6
20,8
24,6
28,8
27,4
16,7
20,9
24,6
29,2
27,6
16,9
21,1
24,7
29,2
27,7
17,1
21,2
24,7
29,3
27,7
17,2
21,3
24,7
29,3
29,1
17,3
21,4
24,7
29,4
17,4
21,4
24,8
17,4
21,6
24,8
suma 534,3 17,8 21,6 24,9 suma 4021,9
średnia 22,50606 17,8
21,8
25
średnia 21,62312
odch.stand. 4,633974
17,9
21,8
25,1 odch.stand. 4,598443
18
21,9
25,2
18,1
21,9
25,2
18,1
22
25,4
18,3
22
25,5
18,5
22,1
25,5
18,7
22,2
25,6
18,7
22,2
25,6
18,7
22,3
25,8
18,7
22,3
25,8
18,8
22,4
25,8
18,8
22,4
25,9
19
22,4
26
19
22,5
26,1

Średnia
n
x
x
n
i
i
∑
=
=
1
= 21,6 Odchylenie standardowe
1
)
(
2
1
−
−
=
∑
=
n
x
x
S
n
i
i
= 4,6
x
i
x
i
-
x
(x
i
-
x
)
2
x
i
2
8,2 -13,4
179,56
67,24
9,1 -12,5
156,25
82,81
9,2 -12,4
153,76
84,64
11,1 -10,5
110,25
123,21
11,4 -10,2
104,04
129,96
... ... ... ...
21,4 -0,2 0,04 457,96
21,6 0 0 466,56
21,8 0,2 0,04
475,24
... ... ... ...
29,3 7,7 59,29
858,49
29,4 7,8 60,84
864,36
∑
=
n
i
i
x
1
= 4021,9
)
(
1
x
x
n
i
i
−
∑
=
= 0
2
1
)
(
x
x
n
i
i
−
∑
=
=
3911,95
∑
=
n
i
i
x
1
2
= 90878
Uwaga:
2
1
)
(
x
x
n
i
i
−
∑
=
=
∑
=
n
i
i
x
1
2
- n
x
2
= 90877,97 – 186*(21,62311828)
2
= 3911,95
Różne definicje średniej:
średnia arytmetyczna
n
x
x
n
i
i
∑
=
=
1
średnia geometryczna x
geom.
=
n
n
x
x
x
...
2
1
średnia harmoniczna
n
x
x
n
i
i
harm
∑
=
=
1
1
1
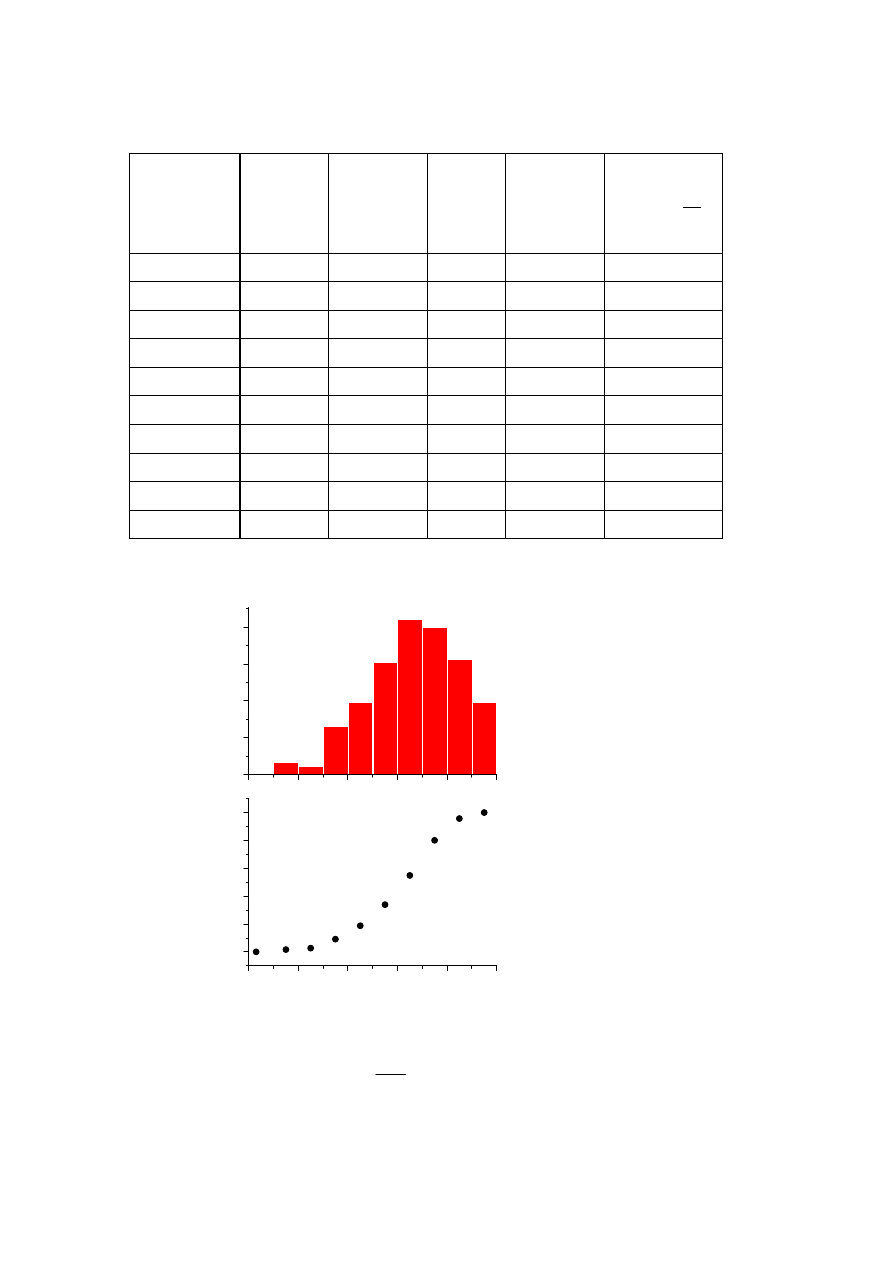
Zakres x
Środek
przedziału
Liczebność
n
k
Częstość
względna
F
k
=n
k
/n
Liczebność
łączna
∑
<
=
L
k
k
L
n
n
Dystrybuanta
n
n
x
F
L
k
=
)
(
od 5 do 7,5
6,25
0
0
0
0
od 7,5 do 10
8,75
3
0,01613
3
0,01613
od 10 do 12,5
11,25
2
0,01075
5
0,02688
od 12,5 do 15
13,75
12
0,06452
17
0,0914
od 15 do 17,5
16,25
18
0,09677
35
0,18817
od 17,5 do 20
18,75
28
0,15054
63
0,33871
od 20 do 22,5
21,25
39
0,20968
102
0,54839
od 22,5 do 25
23,75
37
0,19892
149
0,80108
od 25 do 27,5
26,25
29
0,15591
178
0,95699
od 27,5 do 30
28,75
18
0,09677
186
1
F(x
k
)=P{x
≤ x
k
}; F(x
k
)-F(x
p
)
= P{x
p
< x
≤ x
k
}
k
k
k
F
f
Δ
=
⎟
⎠
⎞
⎜
⎝
⎛
=
Δ
⋅
∑
k
k
k
f
1
5
10
15
20
25
30
0,0
0,2
0,4
0,6
0,8
1,0
D
ystry
buanta
Temperatura
5
10
15
20
25
30
0,00
0,05
0,10
0,15
0,20
Cz
ę
st
o
ść
wzgl
ę
dna
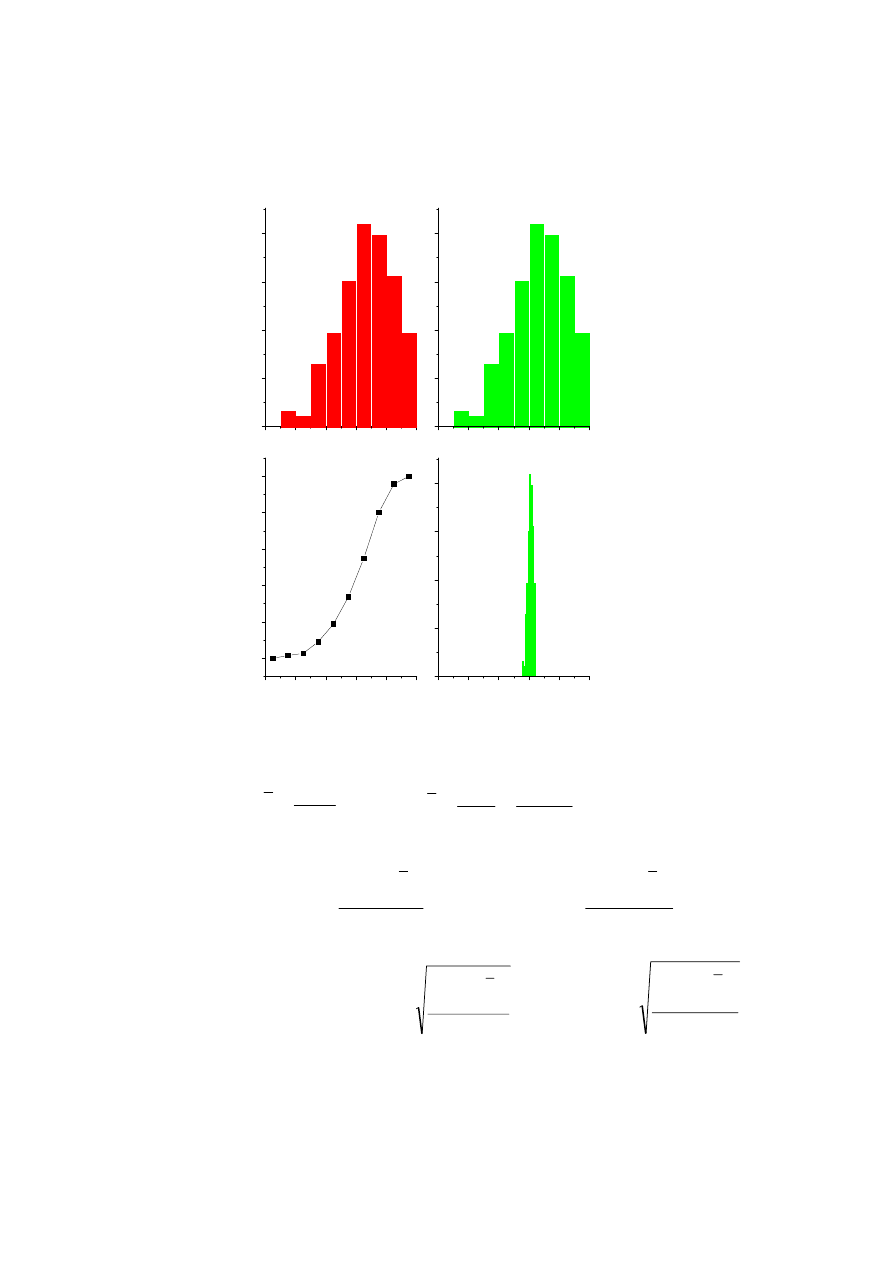
Średnia
n
x
x
n
i
i
∑
=
=
1
Uwaga:
∑
∑
∑
=
=
=
=
=
=
K
k
k
k
K
k
k
k
n
i
i
F
x
n
n
x
n
x
x
1
1
1
Wariancja
n
x
x
n
i
i
2
1
2
)
(
−
=
∑
=
σ
lub
1
)
(
2
1
2
−
−
=
∑
=
n
x
x
S
n
i
i
Odchylenie standardowe
n
x
x
n
i
i
2
1
)
(
−
=
∑
=
σ
lub
1
)
(
2
1
−
−
=
∑
=
n
x
x
S
n
i
i
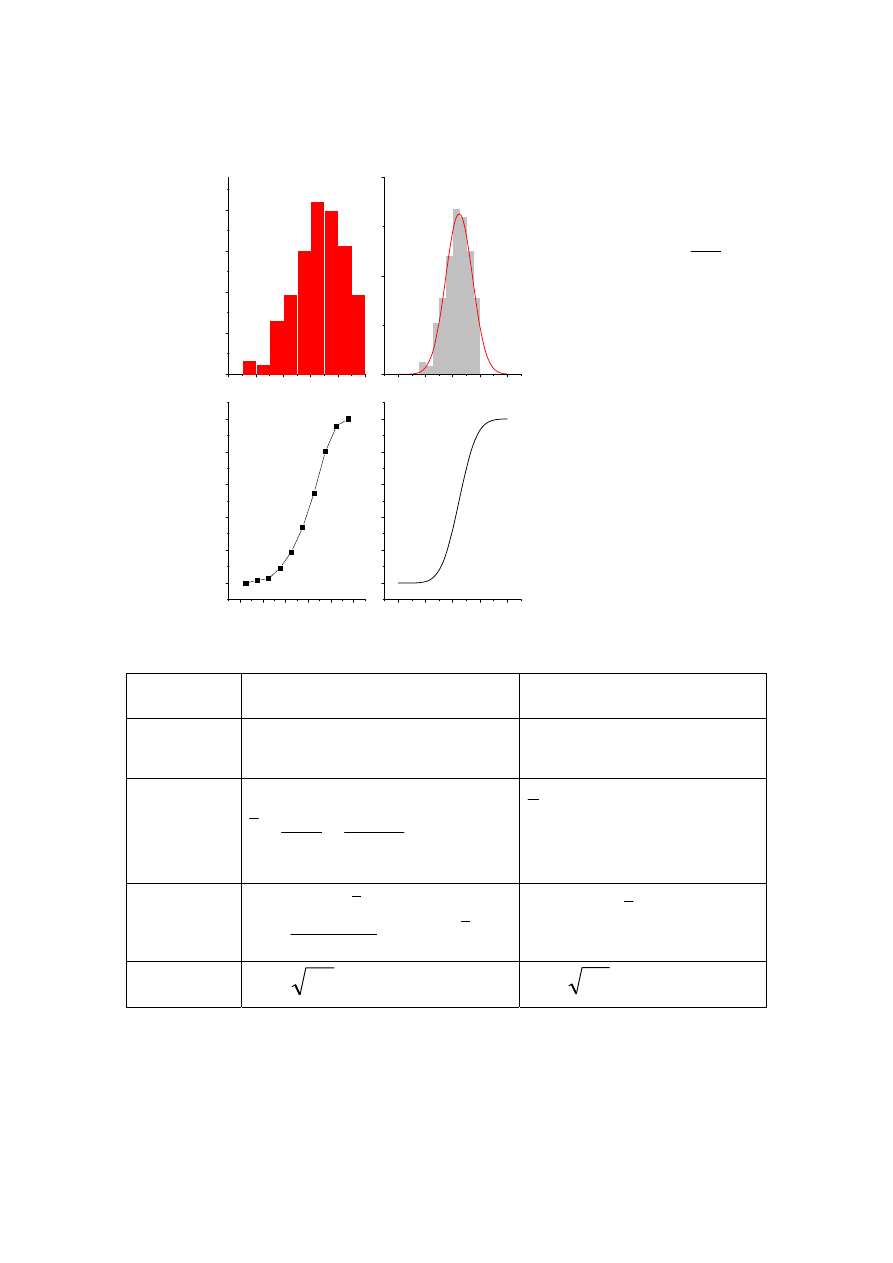
5
10
15
20
25
30
0,00
0,05
0,10
0,15
0,20
Cz
ęsto
ść
wz
gl
ędna
Badana wielkość
18,5
19,0
19,5
20,0
20,5
21,0
0,00
0,05
0,10
0,15
0,20
5
10
15
20
25
30
0,0
0,2
0,4
0,6
0,8
1,0
Dy
st
ry
buan
ta
Badana wielkość
5
10
15
20
25
30
0,00
0,05
0,10
0,15
0,20
5
10
15
20
25
30
0,00
0,05
0,10
0,15
0,20
Cz
ęsto
ść
wz
gl
ędn
a
Badana wielkość
0
10
20
30
40
0,00
0,05
0,10
f
k
5
10
15
20
25
30
0,0
0,2
0,4
0,6
0,8
1,0
D
ys
tr
yb
uan
ta
Badana wielkość
0
10
20
30
40
0,0
0,2
0,4
0,6
0,8
1,0
k
k
k
F
f
Δ
=
⎟
⎠
⎞
⎜
⎝
⎛
=
Δ
⋅
∑
k
k
k
f
1
Rozkłady ciągłe i dyskretne
Wykres Histogram
(F
k
vs. x
k
) Funkcja
gęstości
prawdopodobieństwa f(x)
Dystrybuanta
∑
<
=
L
k
k
k
n
n
x
F
/
)
(
∫
∞
−
⋅
=
y
dx
x
f
y
F
)
(
)
(
Średnia
∑
∑
∑
=
=
=
=
=
=
K
k
k
k
K
k
k
k
n
i
i
F
x
n
n
x
n
x
x
1
1
1
x
d
x
f
x
x
∫
+∞
∞
−
⋅
⋅
=
)
(
Wariancja
k
K
k
k
n
i
i
F
x
x
n
x
x
⋅
−
=
−
=
∑
∑
=
=
2
1
2
1
2
)
(
)
(
σ
∫
+∞
∞
−
⋅
⋅
−
=
dx
x
f
x
x
)
(
)
(
2
2
σ
Odchylenie
standardowe
2
σ
σ
=
2
σ
σ
=
Uwaga:
•
)}
,
(
{
)
(
dx
x
x
x
P
dx
x
f
+
∈
=
⋅
•
}
{
)
(
b
x
a
P
dx
x
f
b
a
<
<
=
⋅
∫
∫
+∞
∞
−
=
⋅
1
)
(
dx
x
f
(
∑
=
=
K
k
k
F
1
1
)
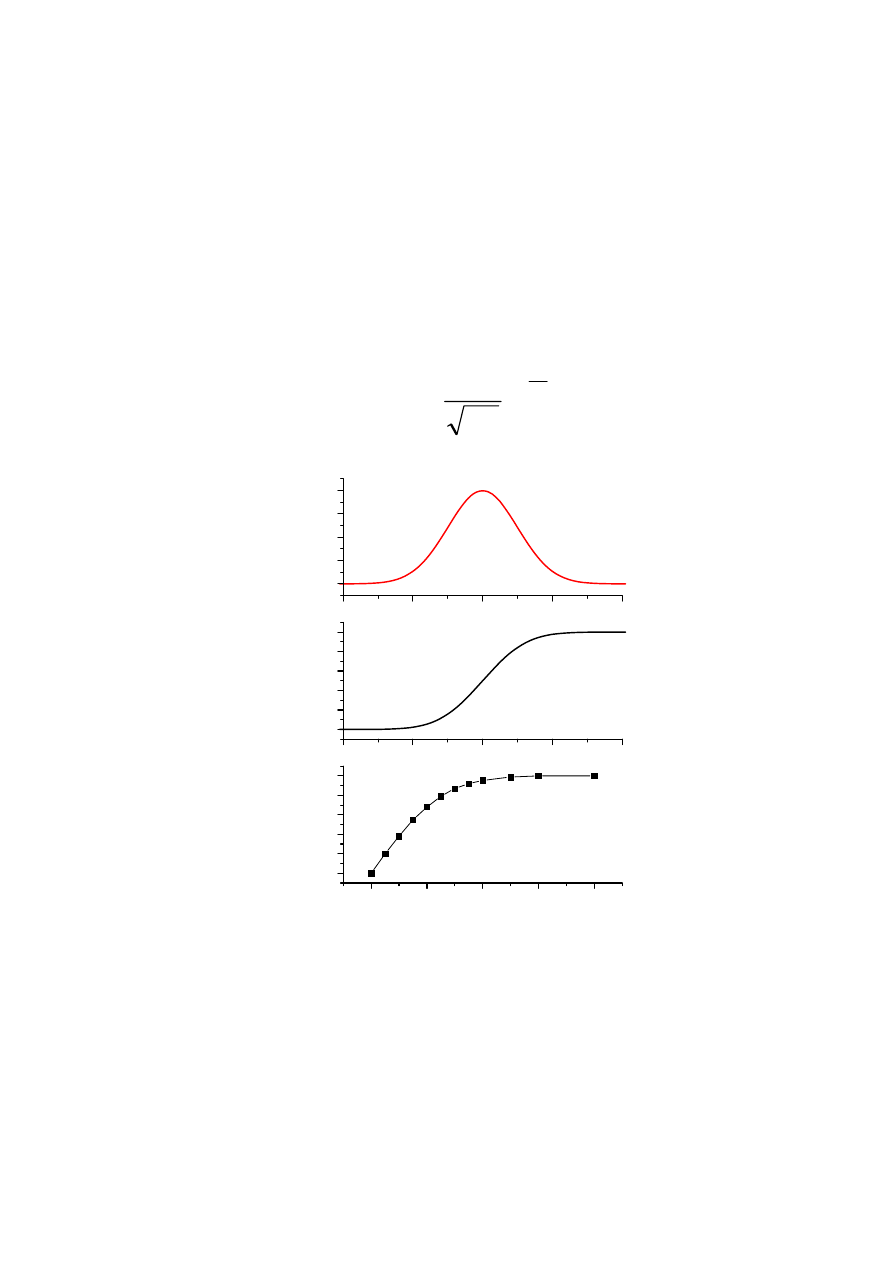
Rozkład normalny N(0,1)
2
1
,
0
2
2
1
)
(
u
e
u
f
−
=
π
0
1
2
3
4
0
20
40
60
80
100
99,7%
95,4%
68%
σ
P
ra
w
do
pod
ob
ie
ńst
w
o
m+/-
σ
-4
-2
0
2
4
0,0
0,2
0,4
0,6
0,8
1,0
F(
x)
-4
-2
0
2
4
0,0
0,1
0,2
0,3
0,4
f(
x)
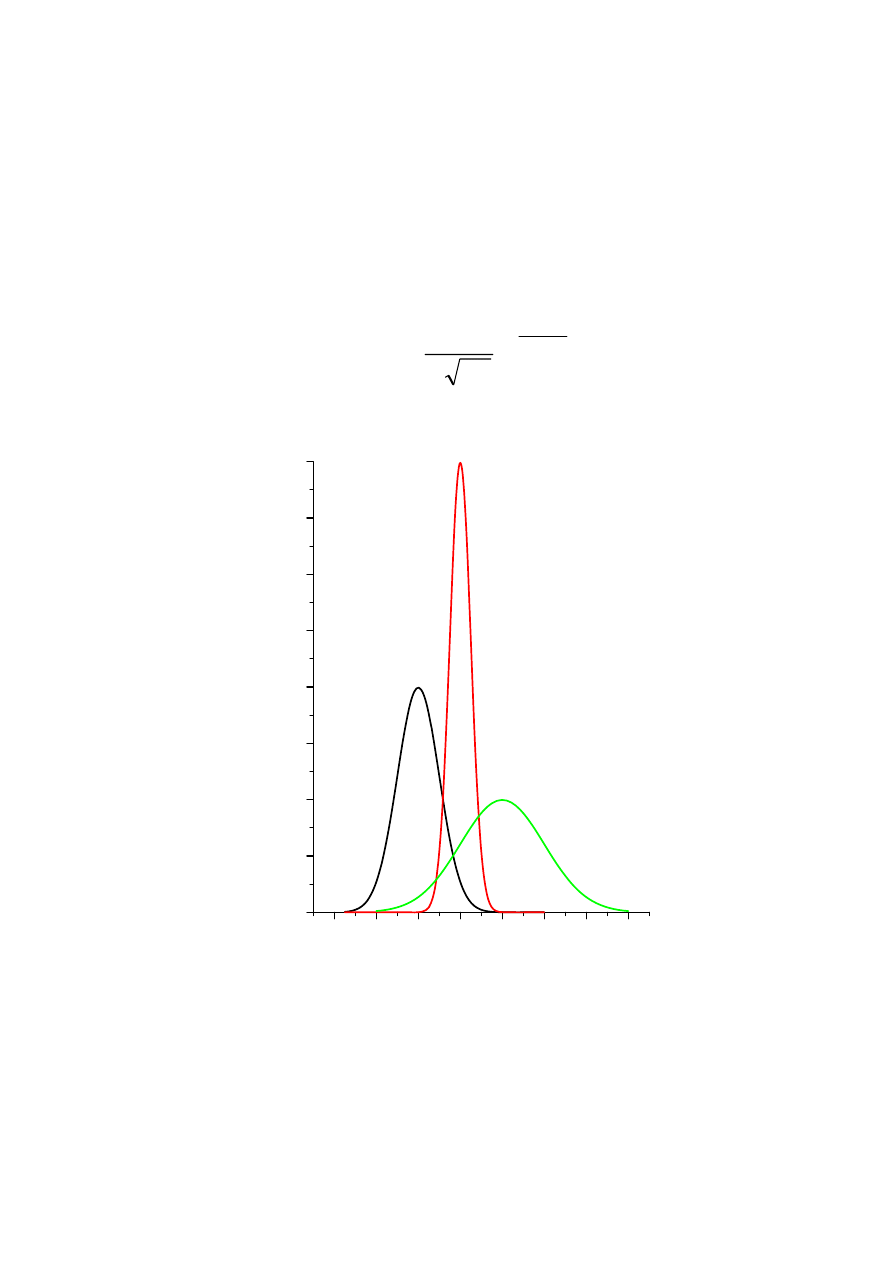
Rozkład normalny N(m,
σ)
2
2
2
)
(
,
2
1
)
(
σ
σ
π
σ
m
x
m
e
x
f
−
−
=
-4
-2
0
2
4
6
8
10
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
N(0,1)
N(2;0,5)
N(4,2)
f(x)
x
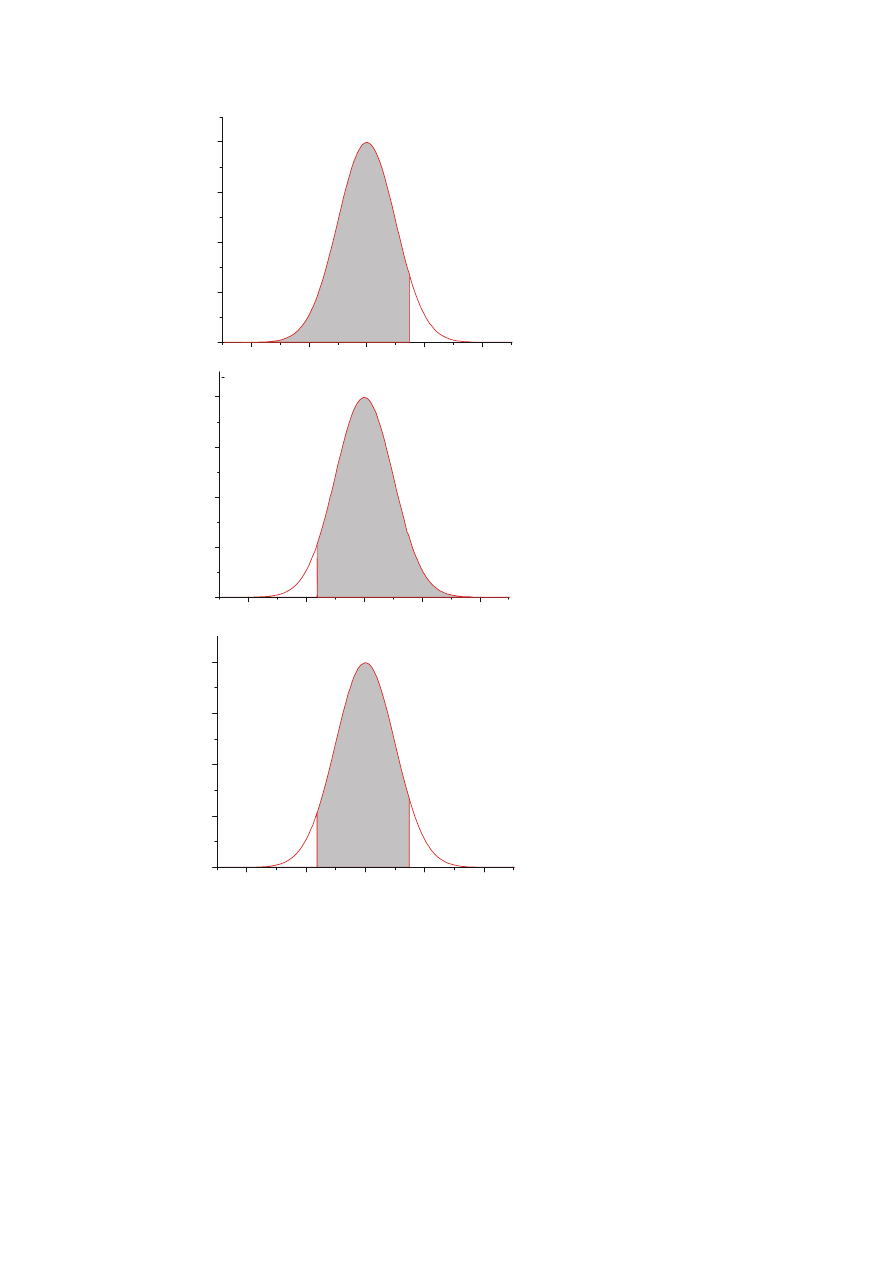
P{x < b} =
⋅
∫
∞
−
b
dx
x
f )
(
=F(b)
P{x > a} =
⋅
−
=
⋅
∫
∞
−
a
∫
∞
a
dx
x
f
dx
x
f
)
(
1
)
(
= 1-F(a)
P{a < x < b} =
∫
⋅
b
a
dx
x
f )
(
= F(b) – F(a)
Uwaga: F(-c)=1 - F(c)
b
a
a
b
0
0
0
f(
x)
f(
x)
f(
x)

-4
-2
0
2
4
6
8
10
0,0
0,1
0,2
0,3
0,4
f(x
)
x
N(4,2)
N(0,1)
Normalizacja x
→u:
σ
m
x
u
−
=
(
σ
dx
du
=
)
)
(
)
(
}
{
)
(
2
1
2
1
)
(
}
{
1
,
0
2
)
(
,
2
2
σ
σ
σ
σ
π
π
σ
σ
σ
σ
σ
σ
σ
m
a
F
m
b
F
m
b
u
m
a
P
du
u
f
e
dx
e
dx
x
f
b
x
a
P
m
b
m
a
m
b
m
a
b
a
m
x
b
a
m
−
−
−
=
−
<
<
−
=
⋅
=
⋅
=
⋅
=
<
<
∫
∫
∫
∫
−
−
−
−
−
−
−
Przykład:
N(4,2)
P{6<x<8} = P{1<u<2} = F(2) – F(1) = 0,97725 - 0,8413 = 0,13595 = 13,6%
2
2
2
)
(
,
2
1
)
(
σ
σ
π
σ
m
x
m
e
x
f
−
−
=
x N(m
x
,
σ
x
) y N(m
y
,
σ
y
)
q=Bx N(B
⋅m
x
, B
⋅σ
x
)
0
10
0,0
0,1
0,2
0,3
0,4
N(4,2)
N(2,1)
x
f(x)
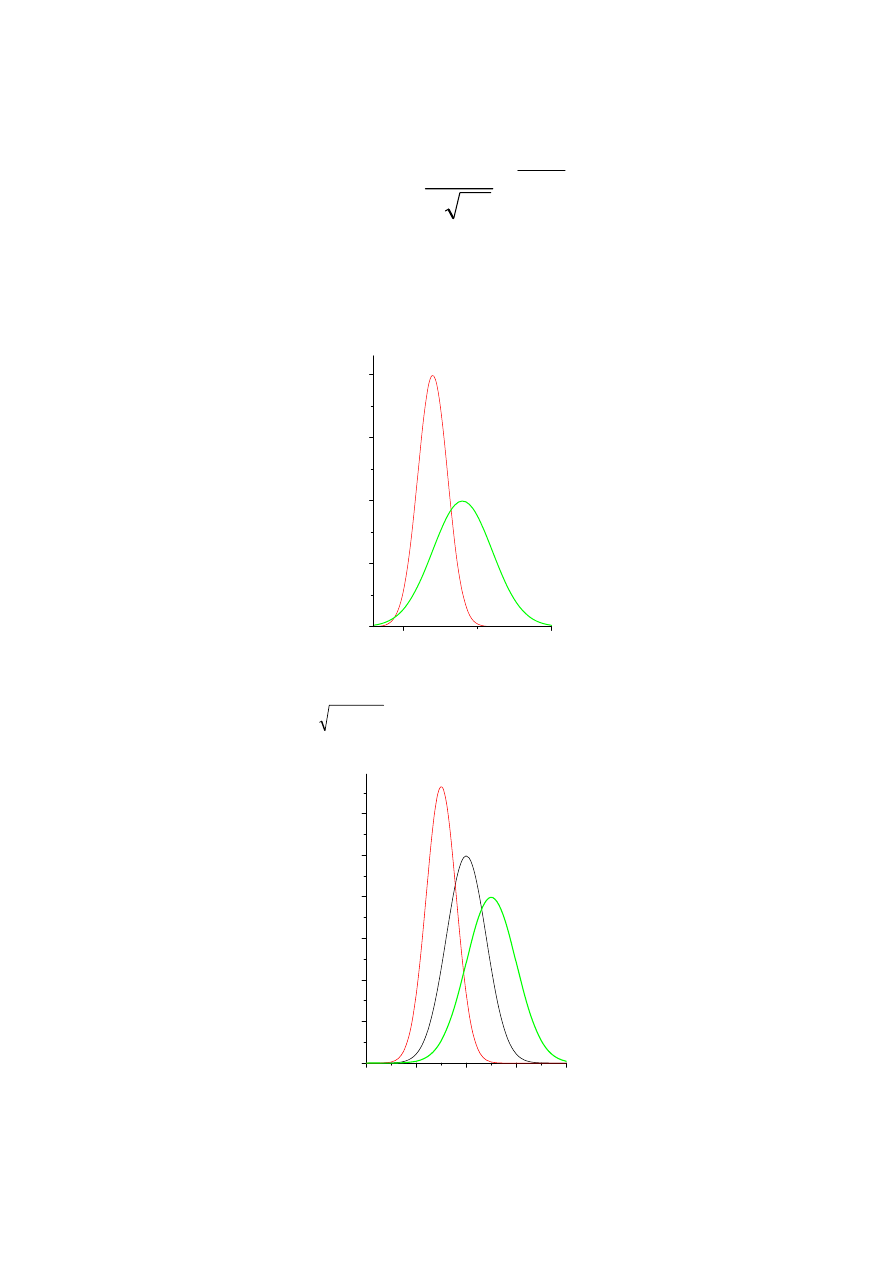
q=x + y N(m
y
+ m
x
,
2
2
y
x
σ
σ
+
)
-10
0
10
20
30
0,00
0,02
0,04
0,06
0,08
0,10
0,12
N(15,5)
N(10,4)
N(5,3)
f(x
)
x
x N(m,
σ) ⇒
x
N(?, ?)
i
i
i
i
x
n
n
x
x
⋅
=
=
∑
∑
1
x N(m,
σ) ⇒
i
x
n
⋅
1
N(
⋅
n
1
m,
⋅
n
1
σ
)
⇒
i
i
x
n
⋅
∑
1
N(
∑
i
n
m
,
∑
i
n
2
)
(
σ
)
n
n
n
n
n
i
σ
σ
σ
σ
=
=
⋅
=
∑
2
2
2
)
(
)
(
m
n
m
n
n
m
i
=
⋅
=
∑
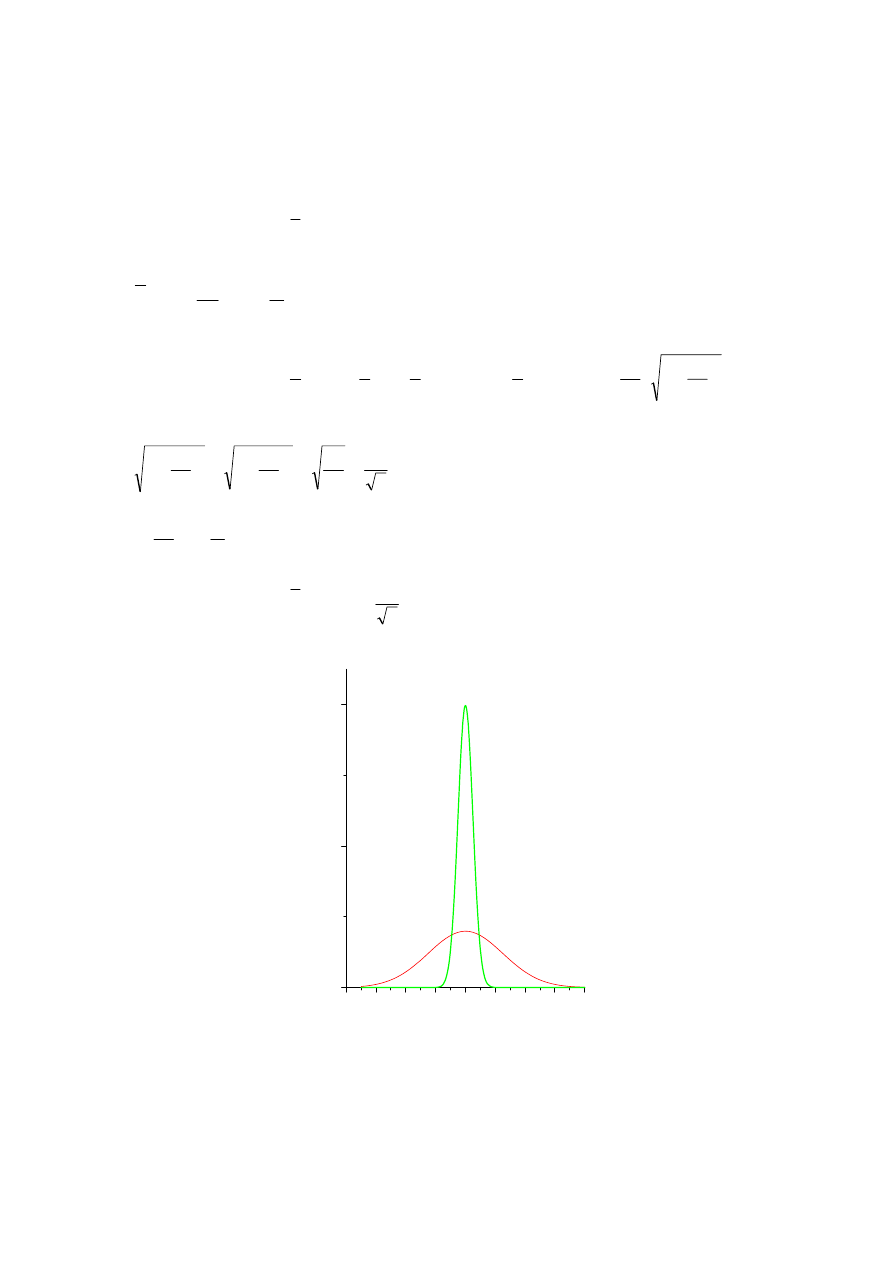
x N(m,
σ) ⇒
x
N(m,
n
σ
)
-12 -8
-4
0
4
8
12
16
20
0,0
0,2
0,4
N(4,1)
N(4,5)
f(x)
x
74,44634
74,4221
125,5295
101,339
134,6627 101,1795
95,31638 108,4944
78,26599 104,0849
66,19135 93,33418
80,44741 112,1937
57,64138 69,32283
91,91905 101,1841
92,69014
101,97
92,59519 116,5623
98,29431 89,17501
89,73585 72,22985
117,3135 62,19394
86,90187 71,14228
67,75205 79,83114
118,0438 103,0403
98,30966 97,53895
113,5028 137,4115
115,1522 158,0141
94,73557 97,73321
40
60
80
100
120
140
160
0,000
0,005
0,010
0,015
0,020
n
i
/f(x
)
x
40
60
80
100
120
140
160
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
n
i
/f(x
)
x
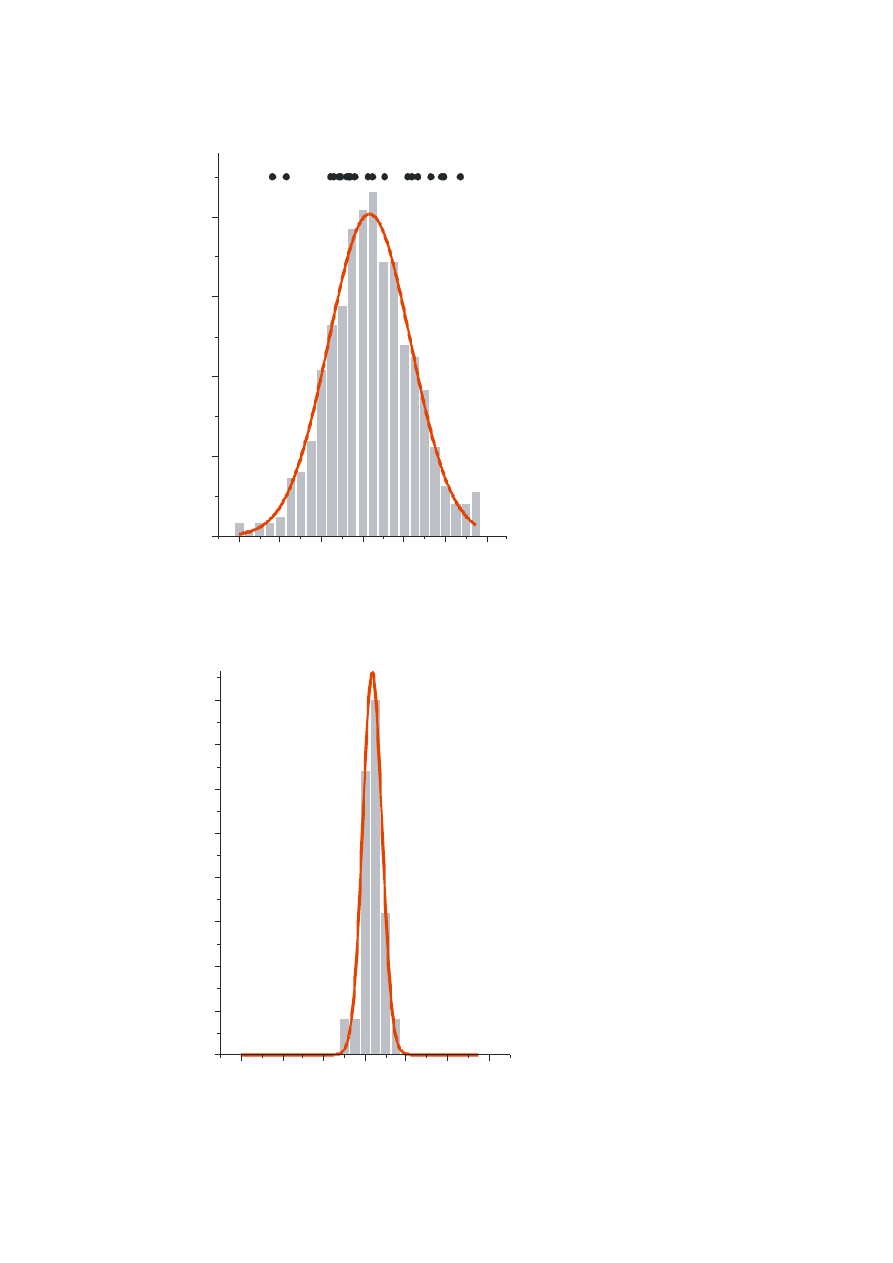
śr.
n=2
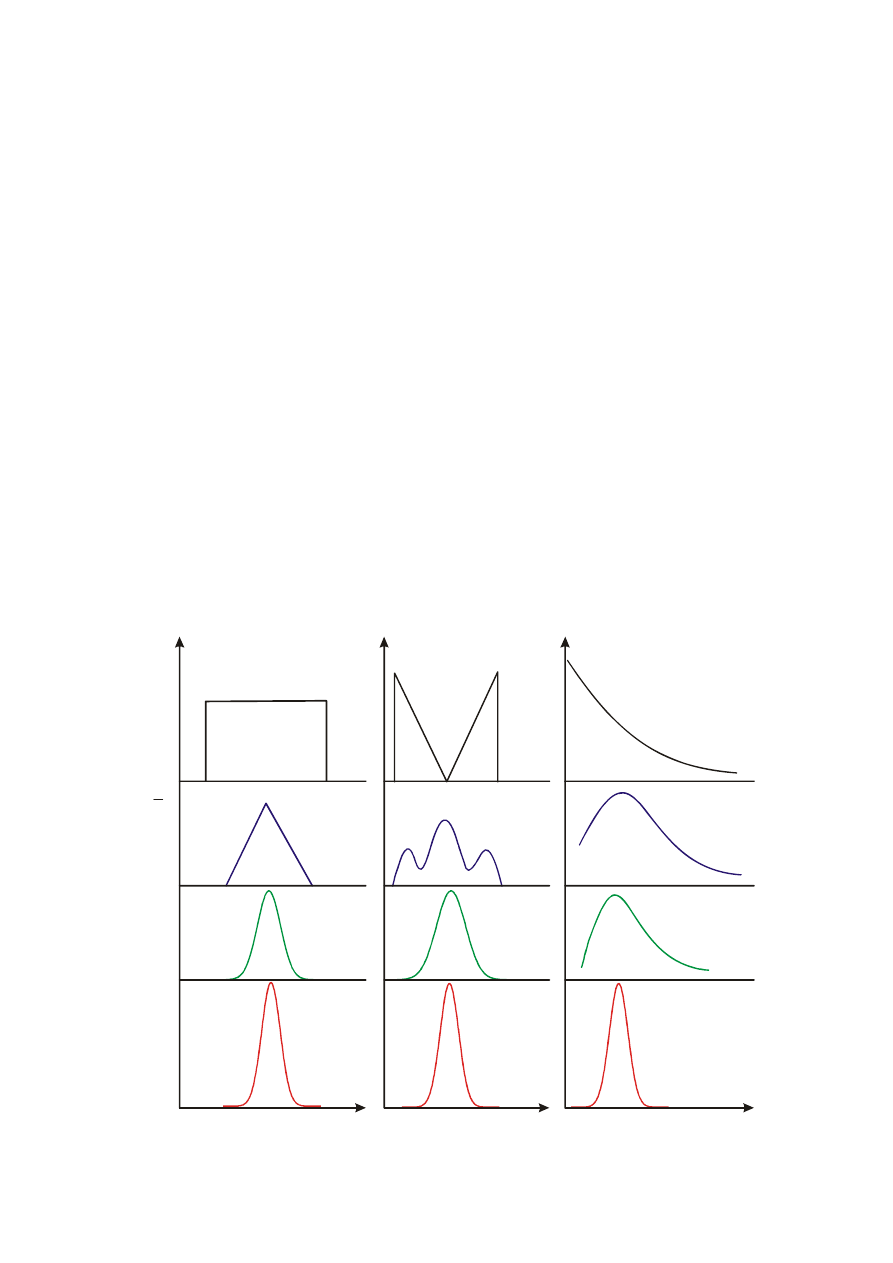
Rozkład średniej dla różnych populacji
TWIERDZENIE
Suma dużej liczby zmiennych losowych niezależnych ma
asymptotyczny (tzn. graniczny) rozkład normalny.
f(x)
f(x)
n=8
n=50
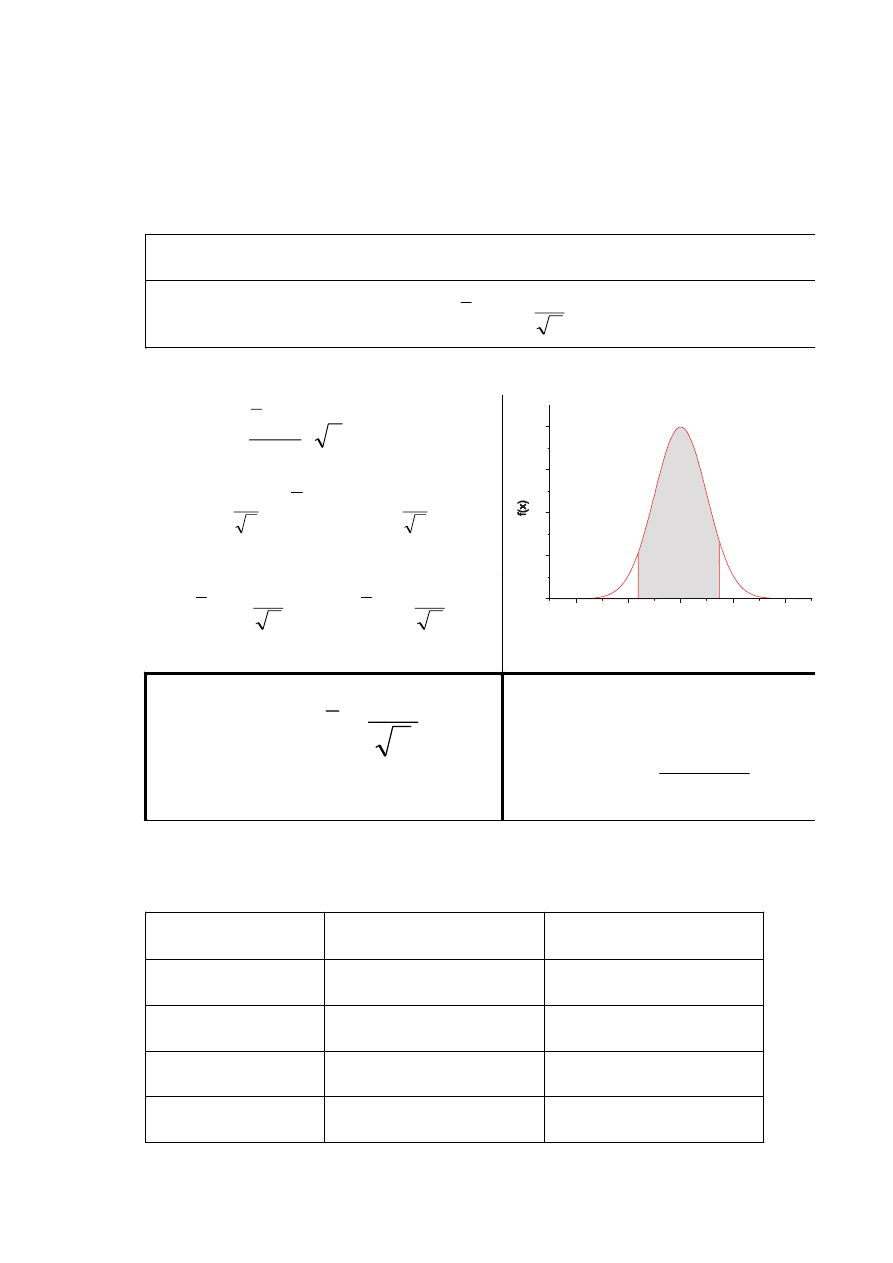
Przedziały ufności
Przedział zawierający z określonym prawdopodobieństwem wynoszącym 1-
α
(poziom ufności) szacowany parametr np. wartość m rozkładu normalnego.
Model I
x N(m,
σ), σ znane lub n>50 ⇒ x
N(m,
n
σ
)
P{-u
α
< u < u
α
} = 1-
α (na ogół 1-α=95%, 99%, 99.9%)
P{-u
α
<
n
m
x
⋅
−
σ
< u
α
} = 1-
α
P{- u
α
n
σ
<
m
x
− < u
α
n
σ
} = 1-
α
P{
x
- u
α
n
σ
< m <
x
+
u
α
n
σ
}=
1-
α
-uα
uα
0
)
(
n
u
x
m
σ
α
±
∈
Precyzja pomiarowa d
2
2
2
d
u
n
σ
α
⋅
>
Znajdowanie u
α
: P{-u
α
< u < u
α
} = 2F(u
α
)-1 = 1-
α
1-
α F(u
α
) u
α
0,9 0,95 1,645
0,95 0,975 1.96
0,99 0,995 2.575
0,999 0,9995
3,29
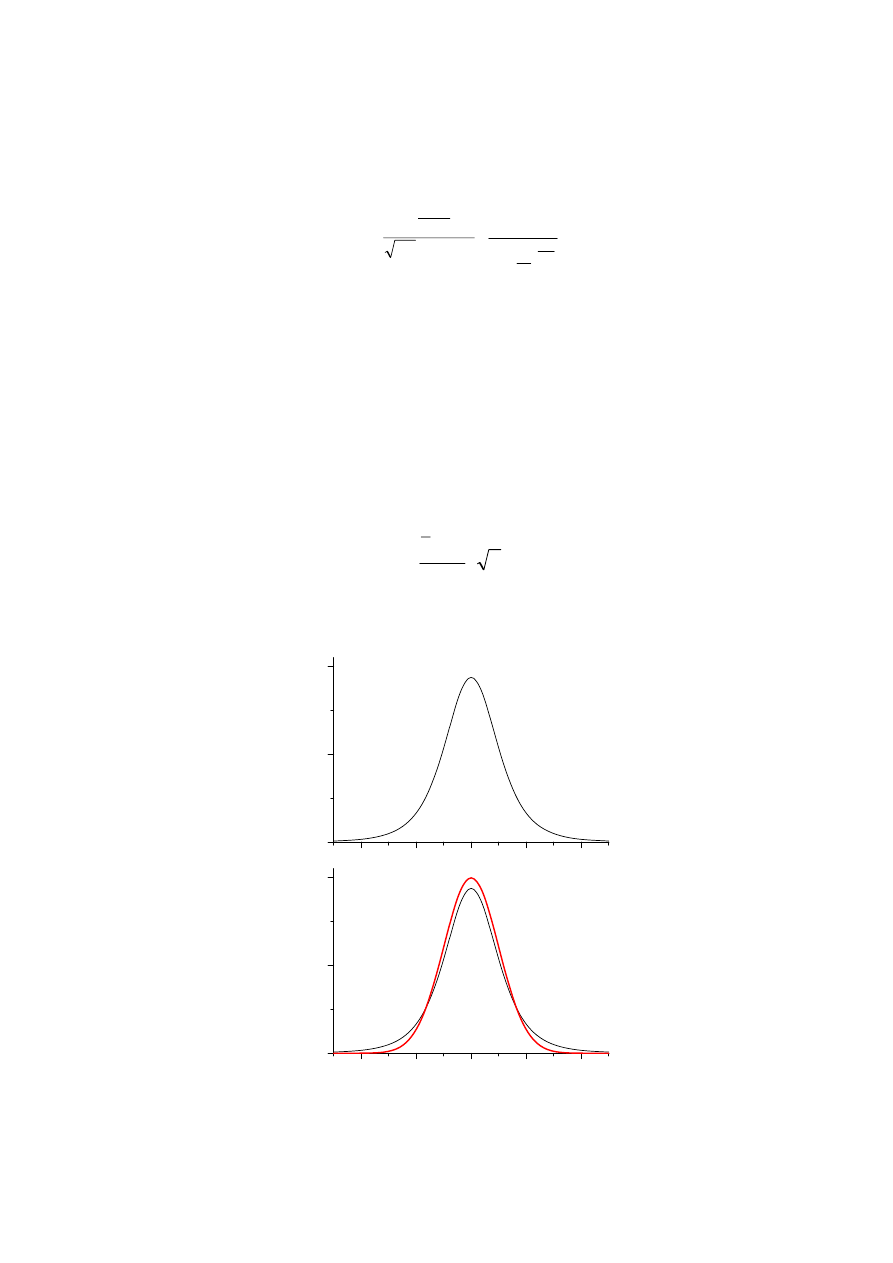
Rozkład t-Studenta
2
1
2
)
1
(
1
)
2
/
(
)
2
1
(
)
(
+
+
•
Γ
⋅
+
Γ
=
k
k
t
k
k
k
t
f
π
gdzie: k=n-1 lb. stopni swobody,
∫
+∞
−
−
⋅
⋅
=
Γ
0
1
)
(
dx
e
x
p
x
p
dla p>0
(
Γ(n+1)=n!)
Dystrybuanta
dt
t
f
y
F
y
⋅
=
∫
∞
−
)
(
)
(
TWIERDZENIE Jeżeli z populacji o rozkładzie normalnym N(m,
σ),
gdzie
σ nie jest znane, losujemy n-elementową próbę prostą to
zmienna losowa
n
S
m
x
t
⋅
−
=
ma rozkład t-Studenta o n-1 stopniach swobody.
-4
-2
0
2
4
0,0
0,2
0,4
N(0,1)
f(
x)
t
-4
-2
0
2
4
0,0
0,2
0,4
f(
t)
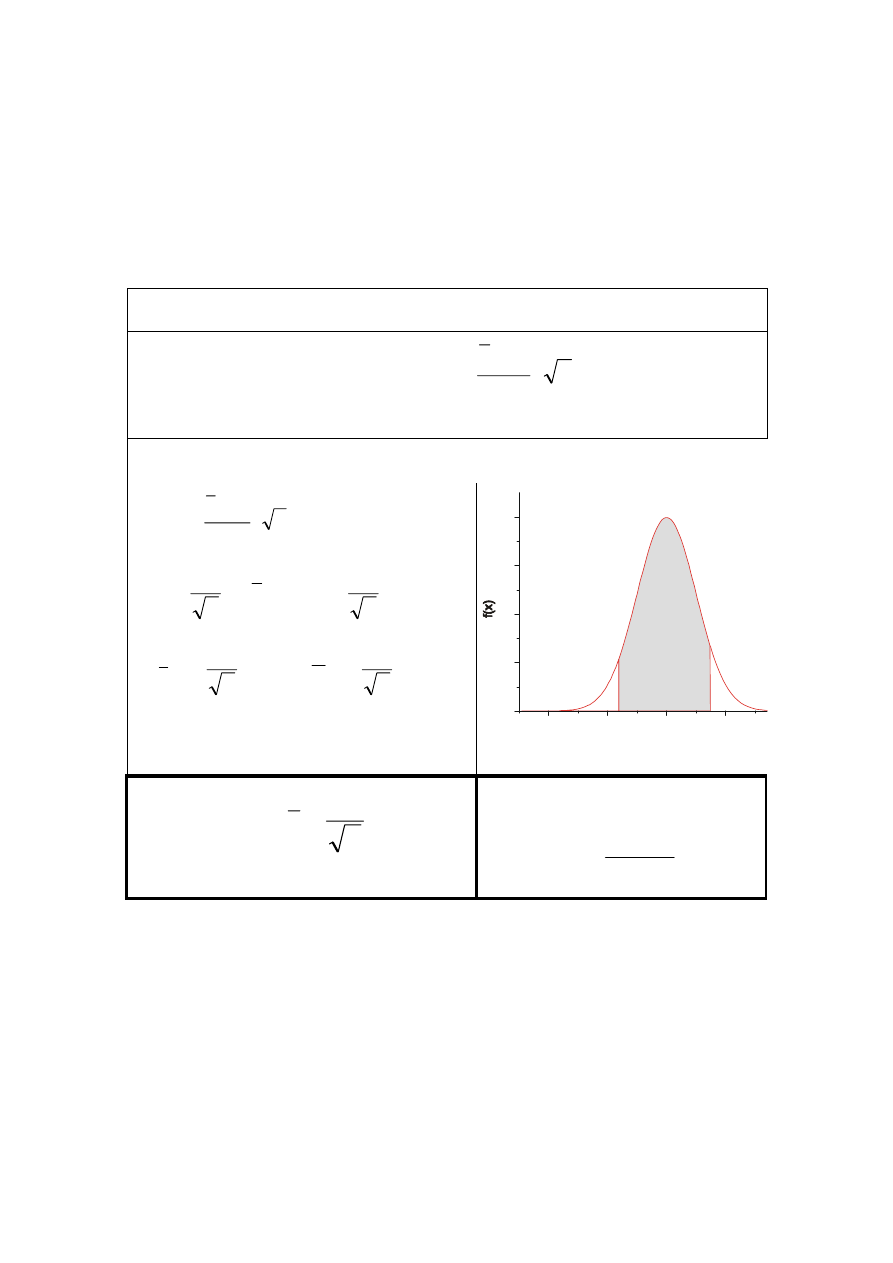
Model II
x N(m,
σ), σ nie jest znane, n<50 ⇒
n
S
m
x
t
⋅
−
=
podlega rozkładowi
t-Studenta o k=n-1 stopniach swobody
P{-t
α
< t < t
α
} = 1-
α
P{-t
α
<
n
S
m
x
⋅
−
< t
α
} = 1-
α
P{- t
α
n
S
<
m
x
−
< t
α
n
S
} = 1-
α
P{
x
- t
α
n
S
< m <
x
+
t
α
n
S
} = 1-
α
-tα
tα
0
)
(
n
S
t
x
m
α
±
∈
Precyzja pomiarowa d
2
2
2
d
S
t
n
⋅
>
α
Znajdowanie t
α
P{
| t |> t
α
} =
α
- tablice wartości t
α
dla różnych k i
α
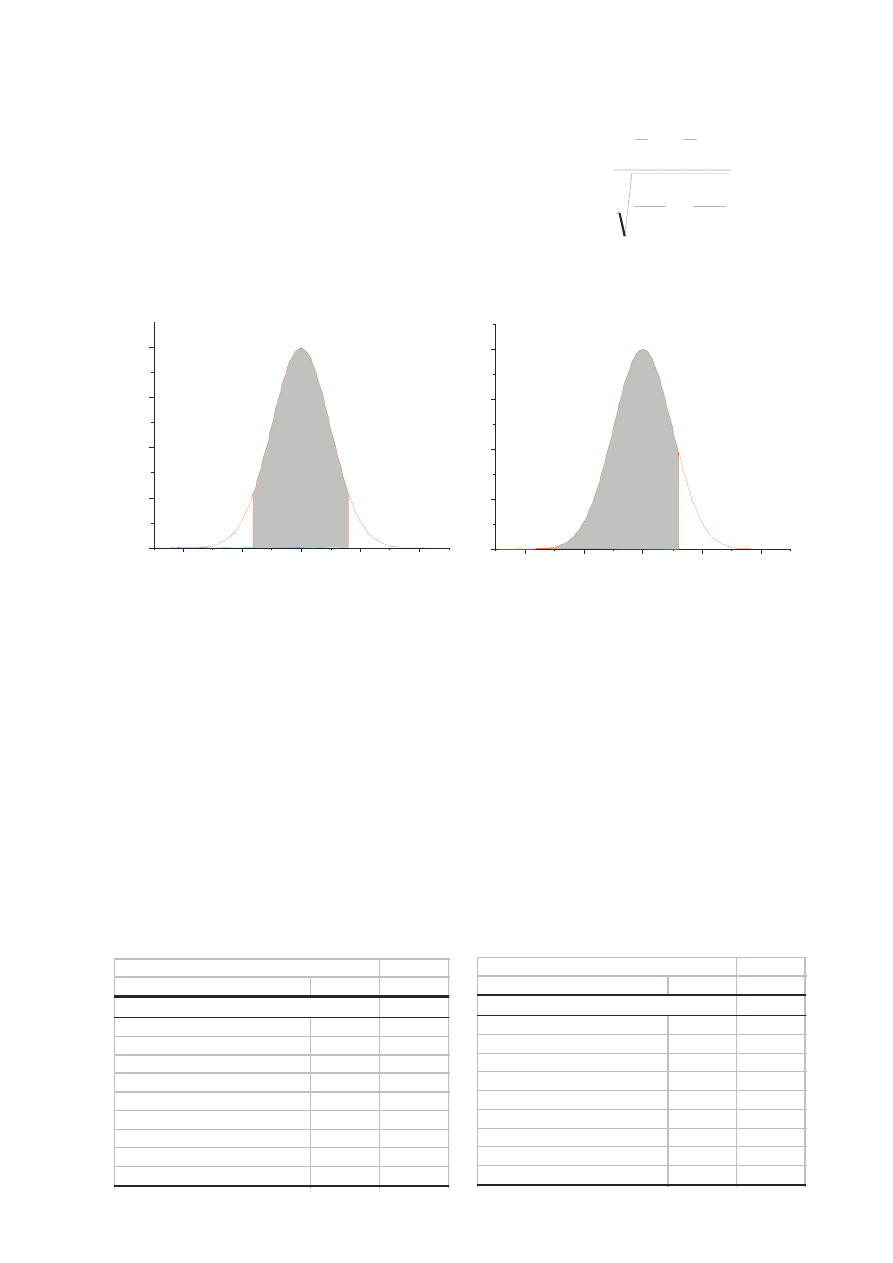
0
ua
-ua
f(x)
0
ua
f(x)
Testy statystyczne: test dla dwóch średnich
Test z: z dwiema próbami dla średnich
- rozkłady normalne
- znane odchylenia standardowe ,
- gdy próby dla n , n >50 (wykorzystujemu S , S )
s s
1
2
1
2
1
2
2
2
2
1
2
1
2
1
n
n
x
x
z
u
σ
σ
+
−
=
=
Poziom ufności 1-a
P{ u >u
F( )]=
| | a}=a 2[1-
a ®
u
u
a
a
·
ą
H0: m1=m H : m m
2
1
1
2
· H0: m1=m H : m > m
2
1
1
2
Wynik testu:
gdy u >
˝ ˝ u hipotezę H0 odrzucamy
gdy u u nie ma podstaw do
odrzucenia hipotezy H0
a
˝ ˝ < a
P{u > u
F( )=
a} =a 1-
a ®
u
u
a
a
Wynik testu:
gdy u > u hipotezę H0 odrzucamy
gdy u < u nie ma podstaw do
odrzucenia hipotezy H0
a
a
Przykład:
roztwór A n1=450, x =12,3 mM, S =3,4
roztwór
1
1
2
B n2=500, x2=11,9 mM, S22=4,4
a=0,05
a=0,001
Test z: z dwiema próbami dla œrednich
Zmienna 1 Zmienna 2
Œrednia
12,31267
11,943
Znana wariancja
3,4
4,4
Obserwacje
450
500
Ró¿nica œrednich wg hipotezy
0
z
2,890531
P(Z<=z) jednostronny
0,001923
Test z jednostronny
1,644853
P(Z<=z) jednostronny
0,003846
Test z dwustronny
1,959961
Test z: z dwiema próbami dla œrednich
Zmienna 1 Zmienna 2
Œrednia
12,31267
11,943
Znana wariancja
3,4
4,4
Obserwacje
450
500
Ró¿nica œrednich wg hipotezy
0
z
2,890531
P(Z<=z) jednostronny
0,001923
Test z jednostronny
3,090245
P(Z<=z) jednostronny
0,003846
Test z dwustronny
3,290479
0
tα
-tα
f(x)
0
tα
f(x)
Testy statystyczne: test dla dwóch średnich
Poziom ufności 1-
α
P{ t >t
r=n1+n -2 t
| | α}=α
, α →
2
α
•
≠
H0: m1=m H : m m
2
1
1
2
• H0: m1=m H : m > m
2
1
1
2
Wynik testu:
gdy t >
⏐ ⏐ t hipotezę H0 odrzucamy
gdy t
t nie ma podstaw do
odrzucenia hipotezy H0
α
⏐ ⏐< α
Wynik testu:
gdy t > tα
α
hipotezę H0 odrzucamy
gdy t < t nie ma podstaw do
odrzucenia hipotezy H0
Przykład:
z katalizatorem n1=8; 17, 11, 22, 18, 19, 13, 14, 16
bez katalizatora
n2=7; 15, 12, 10, 18, 14, 15, 13
)
1
1
(
2
2
1
2
1
2
2
2
2
1
1
2
1
n
n
n
n
S
n
S
n
x
x
t
+
−
+
+
−
=
P{t>t
r=n1+n -2 2 t
α}=α
, α →
2
α
Zmienna 1 Zmienna 2
Œrednia
16,25 13,85714
Wariancja
12,5
6,47619
Obserwacje
8
7
Wariancja sumaryczna
9,71978
Ró¿nica œrednich wg hipotezy
0
df
13
t Stat
1,482986
P(T<=t) jednostronny
0,080956
Test T jednostronny
1,770932
P(T<=t) dwustronny
0,161912
Test t dwustronny
2,160368
Zmienna 1 Zmienna 2
Œrednia
16,25 13,85714
Wariancja
12,5
6,47619
Obserwacje
8
7
Ró¿nica œrednich wg hipotezy
0
df
13
t Stat
1,517122
P(T<=t) jednostronny
0,076586
Test T jednostronny
1,770932
P(T<=t) dwustronny
0,153172
Test t dwustronny
2,160368
Test zgodności
χ
2
(służy określeniu czy badana zmienna podlega określonemu rozkładowi)
Przykład
n=200 Obliczamy średnią
x
= 2,0 i odchylenie standardowe S = 0,5
x
k
n
k
1,0 - 1,4
15
1,4 - 1,8
45
1,8 - 2,2
70
2,2 - 2,6
50
2,6 - 3,0
20
0,0 0,4 0,8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 4,0
0,0
0,2
0,4
0,6
0,8
1,0
x
k
n
k
p
k
n
⋅p
k
(n
k
- n
⋅p
k
)
2
(n
k
- n
⋅p
k
)
2
/n
⋅p
k
1,0 - 1,4
15
0,115
23
64
2,78
1,4 - 1,8
45
0,23
46
1
0,02
1,8 - 2,2
70
0,31
62
64
1,03
2,2 - 2,6
50
0,23
46
16
0,35
2,6 - 3,0
20
0,115
23
9
0,39
χ
2
=4,57
0,0
1,4 1,
2,2 2,6
4,0
0,0
0,2
0,4
0,6
0,8
1,0
x N(2; 0,5)
⇒ u=(x-m)/σ N(0,1)
p
1
=P{x<1,4}=P{u<-1,2}=F(-1,2)=1-F(1,2)
p
2
=P{1,4<x<1,8}=P{-1,2<u<-0,4}=F(-0,4)-F(-1,2)=1-F(0,4)-1+F(1,2)
p
3
=P{1,8<x<2,2}=P{-0,4<u<0,4}=F(0,4)-F(-0,4)=F(0,4)-1+F(0,4)
p
4
=P{2,2<x<2,6}=P{0,4<u<1,2}=F(1,2)-F(0,4)
p
5
=P{x>2,6}=P{u>1,2}=1-F(1,2)
H
0
: badana zmienna podlega testowanemu rozkładowi
H
1
: badana zmienna nie podlega testowanemu rozkładowi
P{
χ
2
≥ χ
2
k,
α
} =
α
gdzie k = r-m-1 (r -lb. przedziałów, m - lb. parametrów wyznaczanych
na podstawie próby) (dla k=5-2-1 i
α=0,05 ⇒ χ
2
k,
α
=5,991)
• Gdy wartość obliczona
k
k
k
k
p
n
p
n
n
⋅
⋅
−
=
∑
2
2
)
(
χ
≥
χ
2
k,
α
to znajduje się ona w obszarze krytycznym i hipotezę H
0
należy
odrzucić.
• Gdy χ
2
<
χ
2
k,
α
nie ma podstaw do odrzucenia hipotezy H
0
χ
2 ,α
k
1-
α
Estymatory (np. średnia arytmetyczna, odchylenie standardowe,
współczynnik korelacji z próby)
1. nieobciążoność
m
m
n
x
E
n
n
x
E
x
E
m
x
E
i
i
=
=
=
=
=
∑
∑
1
)
(
1
)
(
)
(
)
(
∑
∑
=
⇔
=
−
⇔
=
∑
−
⇔
⋅
⋅
⋅
⋅
∑
=
=
⋅⋅
⋅
⋅
=
⋅
⋅
⋅
⋅
⋅
=
−
−
−
−
m
n
x
m
x
m
x
P
dx
dx
e
dx
e
x
P
x
P
x
P
x
P
x
x
x
x
P
i
i
i
n
m
x
m
x
n
n
i
0
)
(
2
2
min
2
)
(
2
1
2
1
}
{
}
{
}
{
}
{
}
...
,
,
{
2
2
2
max
1
2
)
(
1
2
)
(
3
2
1
3
2
1
2
2
2
2
1
σ
σ
π
σ
π
σ
σ
σ
2. zgodność
1
2
}
{
}
{
1
}
{
lim
0
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
<
−
=
<
−
=
<
−
∞
→
>
Λ
σ
ε
σ
ε
σ
ε
ε
ε
n
F
n
n
m
x
P
m
x
P
m
x
P
n
n
n
n
gdy nN to FN1, czyli PN1

q = q(x,y)
xy
y
x
y
x
i
y
x
i
i
i
y
x
i
y
x
i
q
i
y
x
i
y
x
i
i
y
x
i
y
x
i
i
i
y
q
x
q
y
q
x
q
y
x
x
y
q
x
q
n
y
y
y
q
n
x
x
x
q
n
y
x
q
y
y
y
q
x
x
x
q
y
x
q
n
q
q
n
y
x
q
y
y
y
q
x
x
x
q
y
x
q
n
q
n
q
y
y
y
q
x
x
x
q
y
x
q
y
x
q
q
y
x
y
x
y
x
y
x
y
x
y
x
σ
σ
σ
σ
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⋅
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⋅
+
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
⋅
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⋅
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⋅
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⋅
+
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
⋅
+
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⋅
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
−
⋅
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
=
−
=
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
−
⋅
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
=
=
−
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
−
⋅
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
≅
=
∑
∑
∑
∑
∑
∑
∑
,
2
2
2
2
,
2
2
2
2
2
,
,
2
2
,
,
,
,
,
,
,
,
,
,
2
(
)
(
2
)
(
1
)
(
1
)
,
(
)
(
)
(
)
,
(
1
)
(
1
)
,
(
)
(
)
(
)
,
(
1
1
)
(
)
(
)
,
(
)
,
(
Kowariancja:
⎪
⎪
⎩
⎪⎪
⎨
⎧
−
−
⋅
−
−
=
=
∫ ∫
∑∑
∞
+
∞
−
∞
+
∞
−
dxdy
y
f
x
f
m
y
m
x
p
m
y
m
x
y
x
y
x
ij
i
j
y
i
x
i
xy
)
(
)
(
)
)(
(
)
)(
(
)
,
cov(
σ
Współczynnik korelacji :
)
1
1
(
)
,
cov(
≤
≤
−
⋅
=
⋅
=
ρ
σ
σ
σ
σ
σ
ρ
L
y
x
xy
y
x
y
x
ρ = 0 x,y nieskorelowane
ρ ≠ 0 x,y skorelowane
1. x, y niezależne
⇒ nieskorelowane tzn. ρ = 0 (Uwaga: gdy x, y zależne to
mogą być nieskorelowane)
2.
ρ ≠ 0, czyli zmienne losowe są skorelowane to są również zależne
Współczynnik korelacji z próby
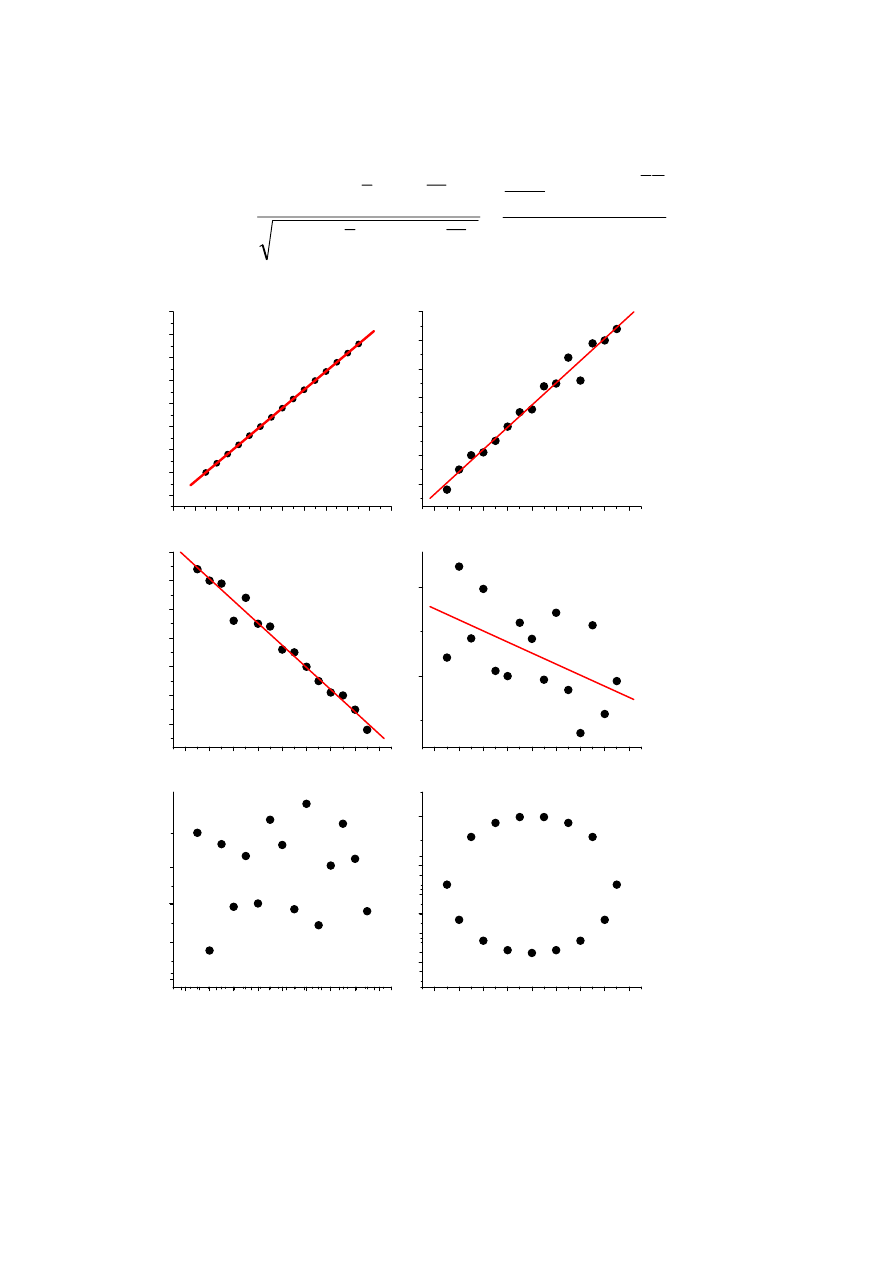
y
x
i
i
i
i
i
i
S
S
y
x
n
y
x
n
y
y
x
x
y
y
x
x
r
⋅
−
−
=
−
−
−
−
=
∑
∑
∑
∑
1
1
)
(
)
(
)
)(
(
2
2
y
x
r=0,988
r=-0,988
r=-0,54
r=0,06
(x-8)
2
+(y-8)
2
=49
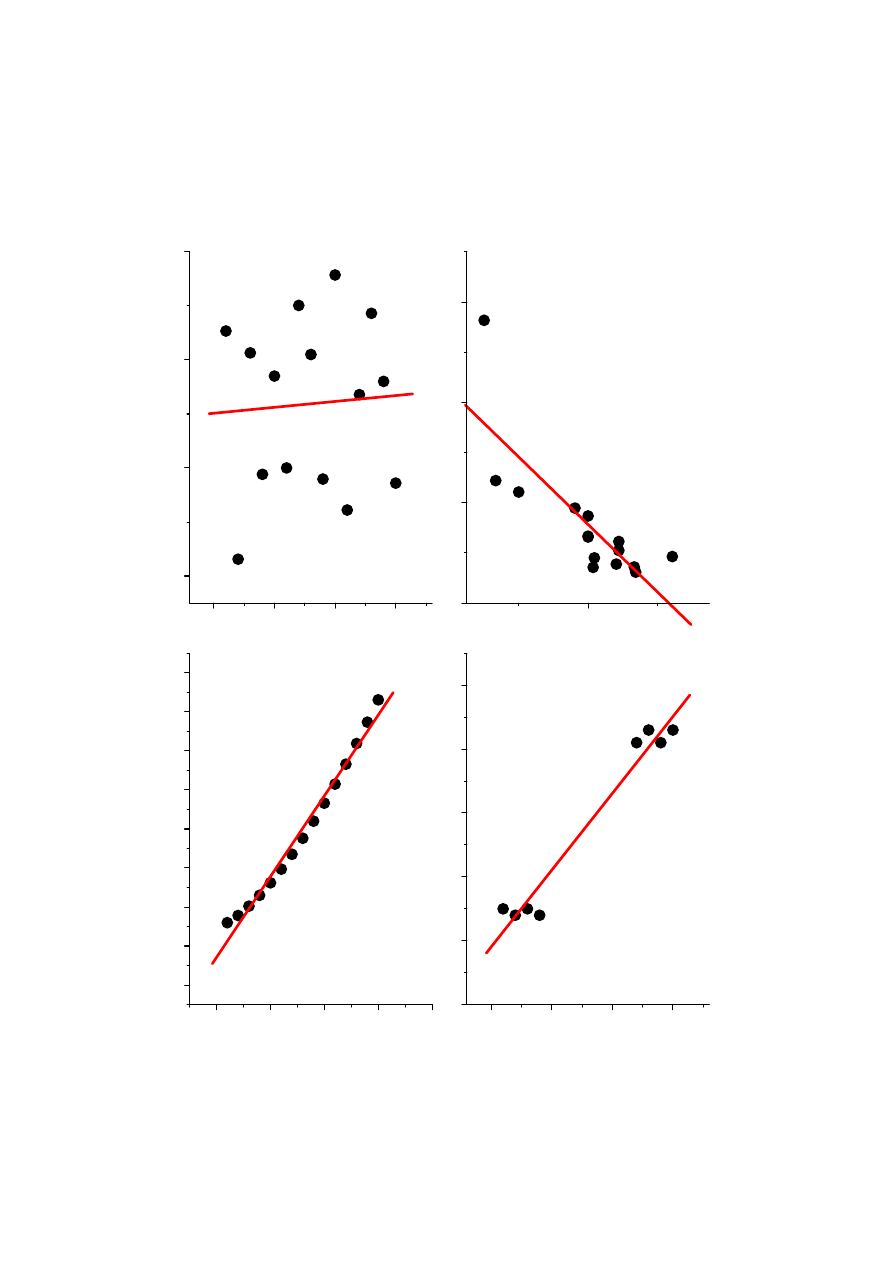
y
r=0,06
x
r=0,80
y/z vs. x/z
r=0,99
y=x
1,5
+5
r=0,98
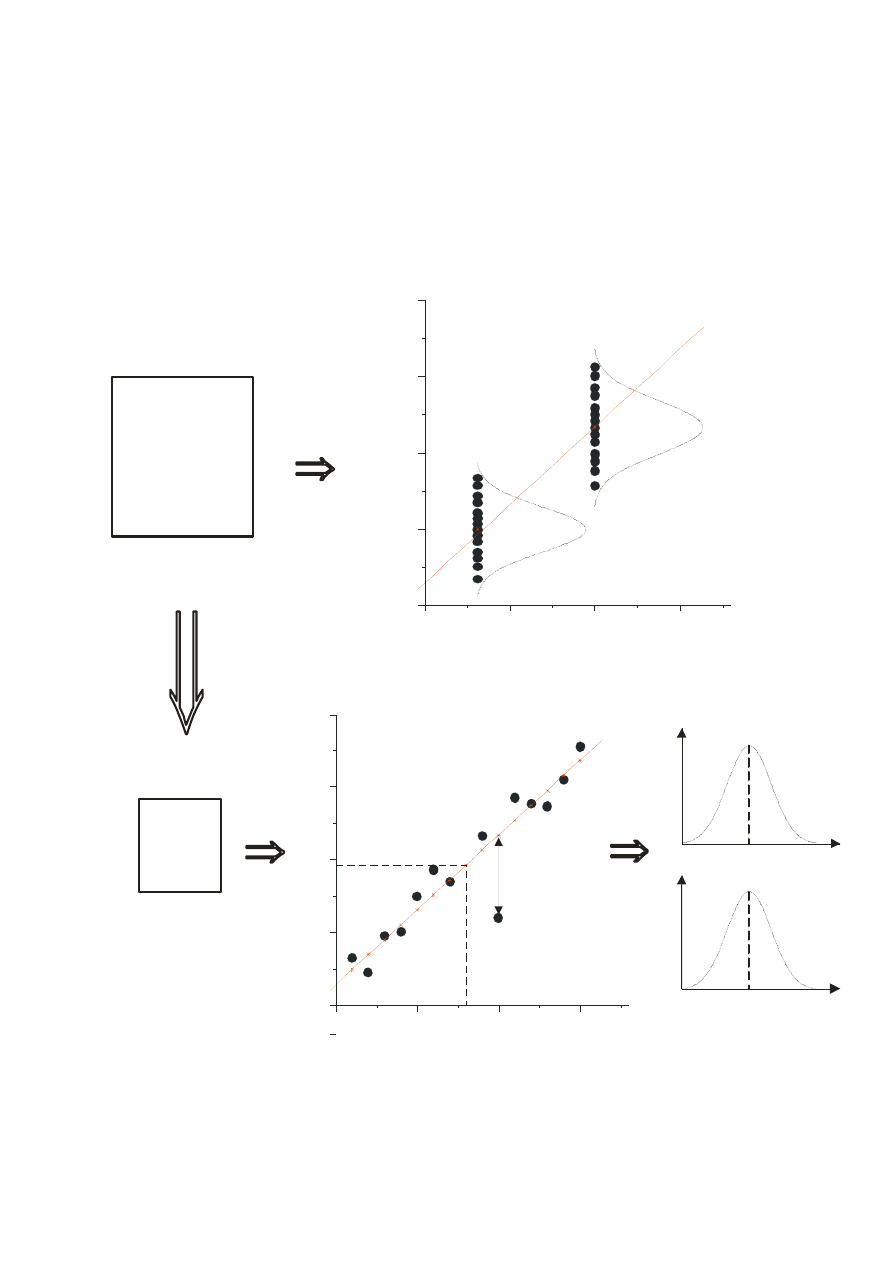
y = + x
b
b
0
1
0
5
10
15
0
10
20
30
y
e =y -y^
i
i i
y = b + b x
0
1
0
5
10
15
0
10
20
30
y
f(b )
0
f(b )
1
b
0
b
1
POPULACJA
PRÓBA
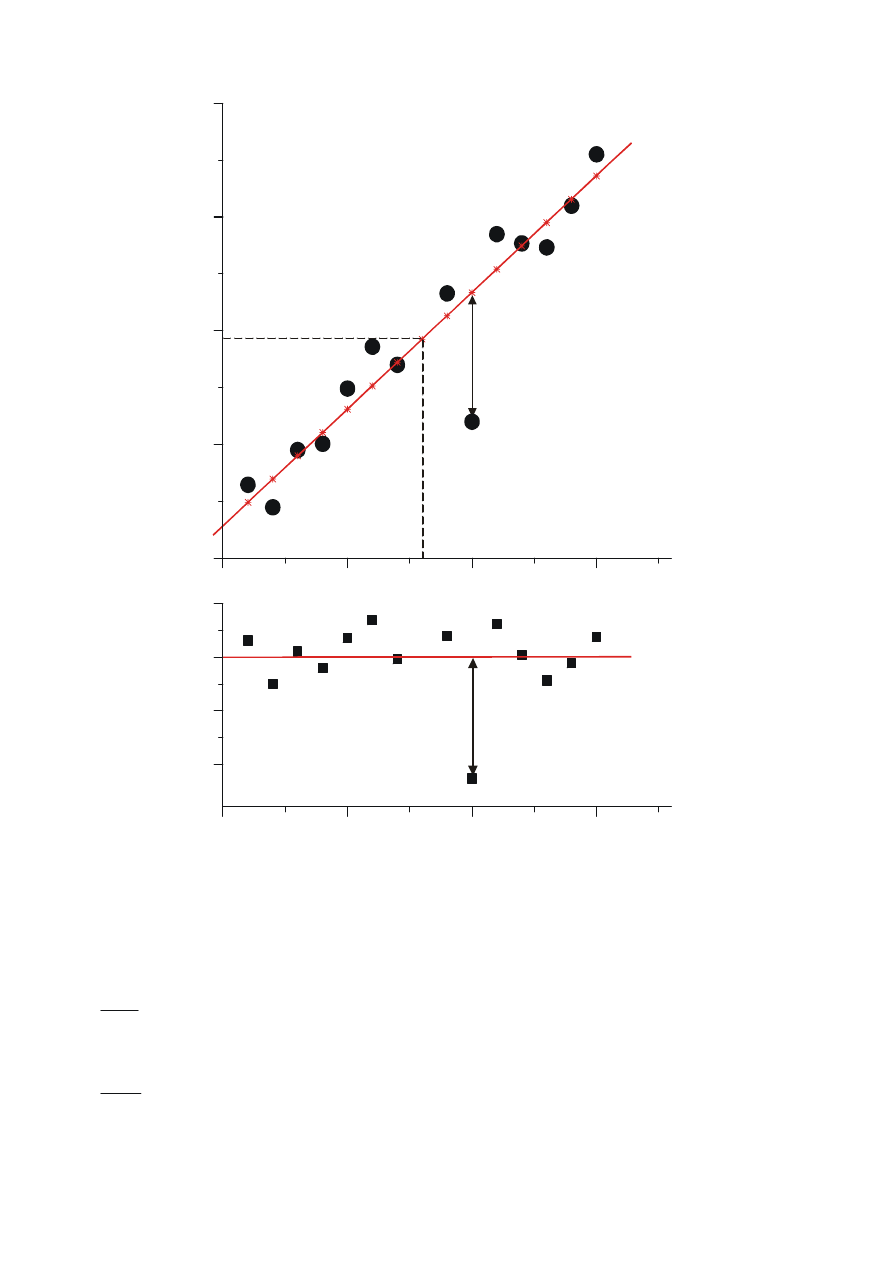
x
e =y -y^
i
i i
e =y -y^
i
i i
y = b + b x
0
1
0
5
10
15
-10
-5
0
5
e
0
5
10
15
0
10
20
30
40
y
(
)
=
−
−
=
−
=
=
∑
∑
∑
=
n
i
i
i
i
i
i
b
x
b
y
y
y
e
Q
⎪⎩
⎪
⎨
⎧
=
⋅
+
=
+
∑
∑
∑
∑
∑
i
i
i
i
i
i
y
b
n
x
b
y
x
x
b
x
b
0
1
0
2
1
2
0
1
1
2
2
⎪
⎪
⎩
⎪⎪
⎨
⎧
=
−
−
−
=
∂
∂
=
−
−
−
=
∂
∂
∑
∑
i
i
i
b
x
b
y
b
Q
x
b
x
b
y
b
Q
0
1
0
0
1
1
0
)
1
)(
(
2
0
)
)(
(
2
.
min
)
(
Gdy jeden z parametrów znany: jedno równanie, jedna niewiadoma
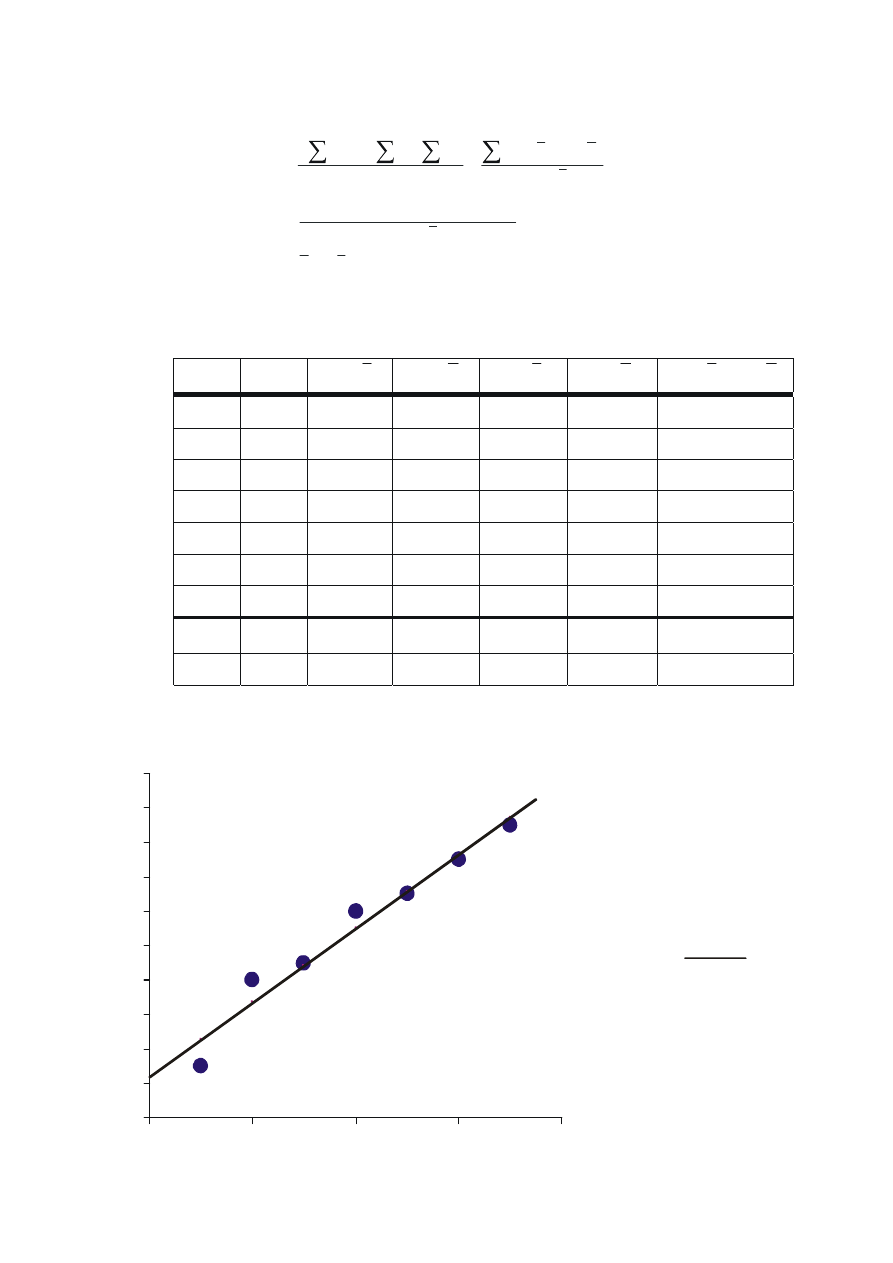
5
9
13
17
21
25
0
2
4
6
8
x
y
x
i
y
i
)
(
x
x
i
−
)
(
y
y
i
−
2
)
(
x
x
i
−
2
)
(
y
y
i
−
)
)(
(
y
y
x
x
i
i
−
−
1
8 -3 -8
9
64
24
2
13
-2 -3
4
9
6
3
14
-1 -2
1
4
2
4
17 0 1
0
1
0
5
18 1 2
1
4
2
6
20 2 4
4
16
8
7
22 3 6
9
36
18
∑
28 112 0
0
28
134
60
średnia 4 16
x
b
y
b
x
x
n
y
x
x
y
x
b
x
x
y
y
x
x
x
x
n
y
x
y
x
n
b
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
1
0
2
2
0
2
2
2
1
)
(
)
)(
(
)
)(
(
)
(
)
)(
(
)
(
)
(
)
(
−
=
−
−
=
−
−
−
=
−
−
=
∑
∑
∑
∑
∑
∑
∑
∑
y=2,14 x+7,43
⋅
b =60/28=2,14
b =16-2,14 4=7,43
r=60/ 28 134=0,98
1
0
⋅
√ ⋅
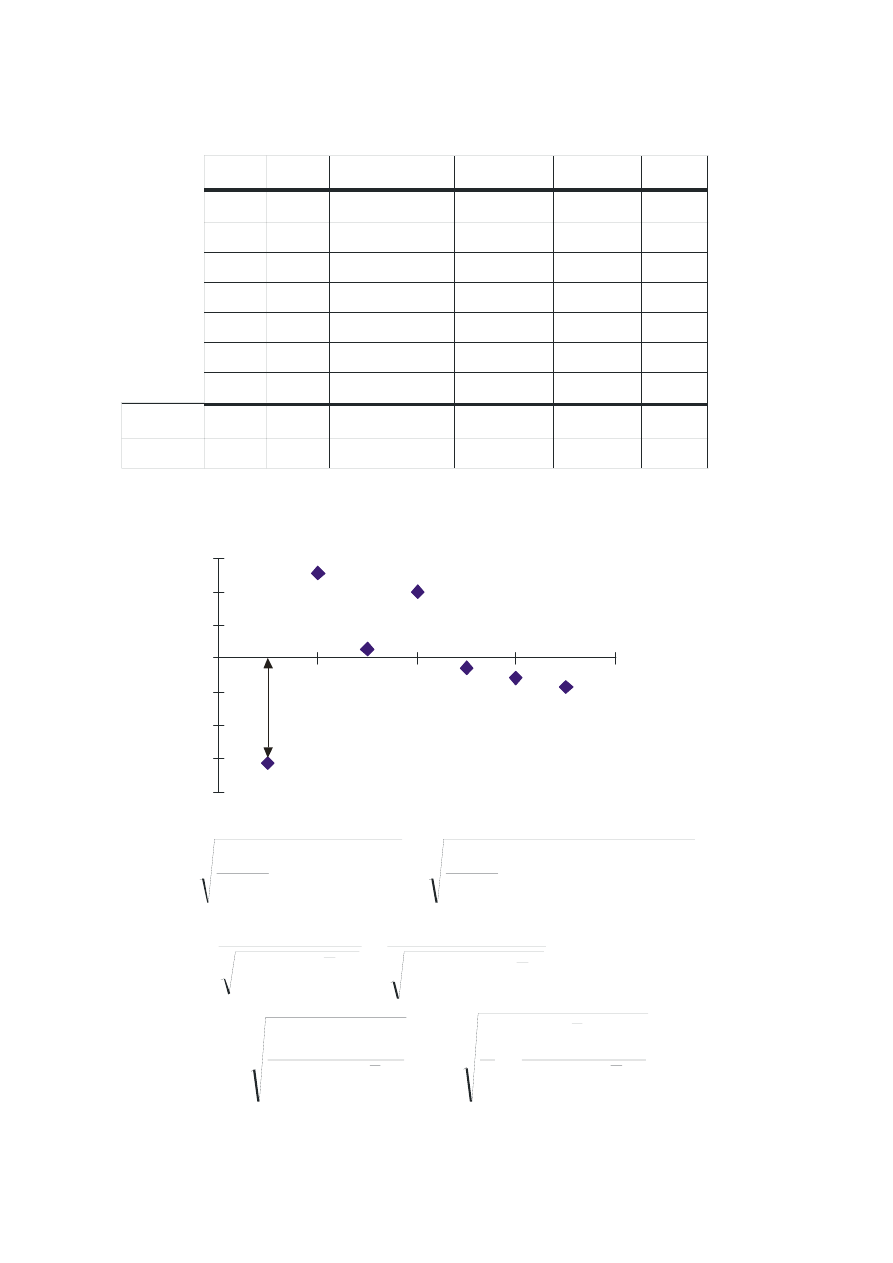
-2
-1,5
-1
-0,5
0
0,5
1
1,5
0
2
4
6
8
X
Sk
ład
ni
ki
r
e
sz
to
w
e
x
i
y
i
0
1
b
x
b
y
i
i
+
×
=
i
i
i
y
y
e
-
=
2
)
(
i
i
y
y -
2
i
x
1
8 9,57 1,57
2,4694
1
2
13 11,71 -1,29
1,6531
4
3
14 13,86 -0,14
0,0204
9
4
17 16 -1 1 16
5
18 18,14 0,14
0,0204
25
6
20 20,29 0,29
0,0816
36
7
22 22,43 0,43
0,1837
49
ĺ
28 112
0 5,4286 140
średnia 4 16
S = 1,04
S = 0,88
b1
S = 0,20
b0
∑
∑
∑
∑
∑
∑
∑
−
+
⋅
=
−
⋅
=
⋅
−
=
−
=
−
−
−
=
−
−
=
2
2
2
2
2
2
2
2
0
1
2
)
(
1
)
(
)
(
)
(
2
1
)
(
2
1
0
1
x
x
x
n
S
x
x
n
x
S
S
x
n
x
S
x
x
S
S
b
x
b
y
n
y
y
n
S
i
i
i
b
i
i
b
i
i
i
)
e =y -y^
i
i
i
Regresja liniowa: EXCEL
x y
0
1
ˆ
b
x
b
y
i
i
+
⋅
=
REGLINW
1 8 9,571429 7,428571
ODCIĘTA
2 13 11,71429 2,142857
NACHYLENIE
3 14 13,85714
7
ILE.LICZB
4 17
16
1,041976
REGBŁSTD.
5 18 18,14286
6 20 20,28571
8,571429 KOWARIANCJA
7 22 22,42857 0,979535 WSP.KORELACJI
2,142857 7,428571429 b
1
b
0
REGLINP
0,196915 0,880630572
S
b1
S
b0
0,959488 1,041976145 r
2
S
118,4211
5 F
df
128,5714 5,428571429 SSR
SSE
EXCEL:
Regresja liniowa
5
7
9
11
13
15
17
19
21
23
25
0
1
2
3
4
5
6
7
8
x
y
ORIGIN:
1
2
3
4
5
6
7
6
8
10
12
14
16
18
20
22
24
B
Data1B
UCL
LCL
UPL
LPL
y
x
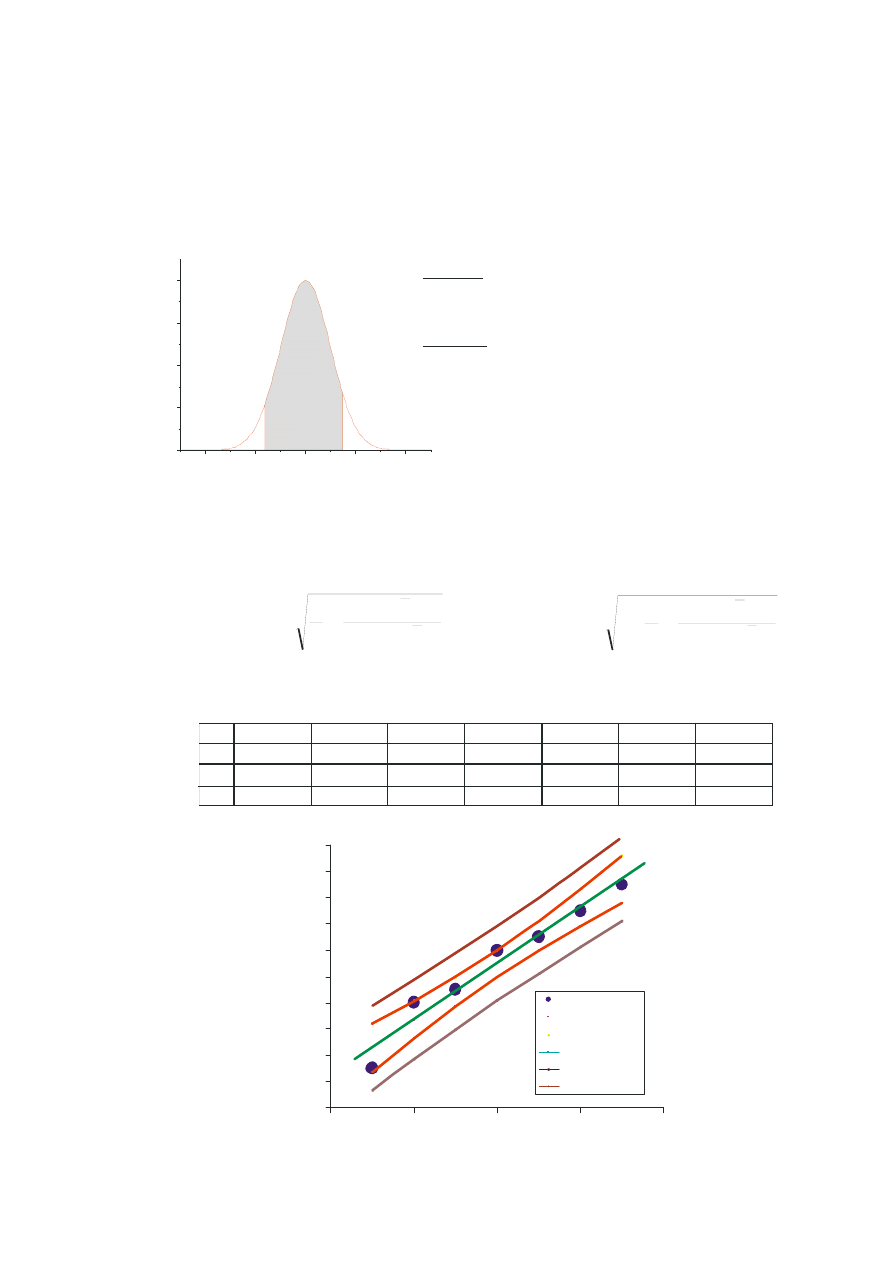
Przedziały ufności w analizie regresji
-ta
ta
0
2
,
1
0
0
0
1
1
1
−
=
−
−
=
−
=
n
k
S
b
t
S
b
t
b
b
α
β
β
P{b - S < < b + S }= 1-
P{b - S < < b + S }= 1-
1
b1 1
1
b1
0
b0 0
0
b0
b
a
b
a
t
t
t
t
a
a
a
a
k=5, 1- =0,95 t =2,57
(5,16; 9,69)
a
Ţ
b Î
a
0
b Î
1
(1,64; 2,65)
Krzywe ufności
α
α
t
ufn
S
y
ufn
G
t
ufn
S
y
ufn
D
x
x
x
x
n
S
ufn
S
i
i
i
y
i
y
i
i
i
y
⋅
+
=
⋅
−
=
−
−
+
⋅
=
∑
.)
(
.)
(
.)
(
.)
(
)
(
)
(
1
.)
(
ˆ
ˆ
2
2
ˆ
)
)
Przedział tolerancji
α
α
t
tol
S
y
tol
G
t
tol
S
y
tol
D
x
x
x
x
n
S
to l
S
i
i
i
y
i
y
i
i
i
y
⋅
+
=
⋅
−
=
−
−
+
+
⋅
=
∑
.)
(
.)
(
.)
(
.)
(
)
(
)
(
1
1
.)
(
ˆ
ˆ
2
2
ˆ
)
)
5
9
13
17
21
25
0
2
4
6
8
x
y
Dane
Krzyw a regres ji
Krzyw a ufnos ci g.
Krzyw a ufnos ci d.
K. Tolerancji d.
K. Tolerancji g.
x
i
y
i
S(ufn.) D(ufn.) G(ufn.) S(tol.) D(tol.) G(tol.)
9,57
0,70999 7,74605 11,3968 1,26087 6,32973 12,8131
11,71
2
1
0,55696 10,2823 13,1462 1,18149 8,67668 14,7519
...
... ... ... ... ... ... ...
^
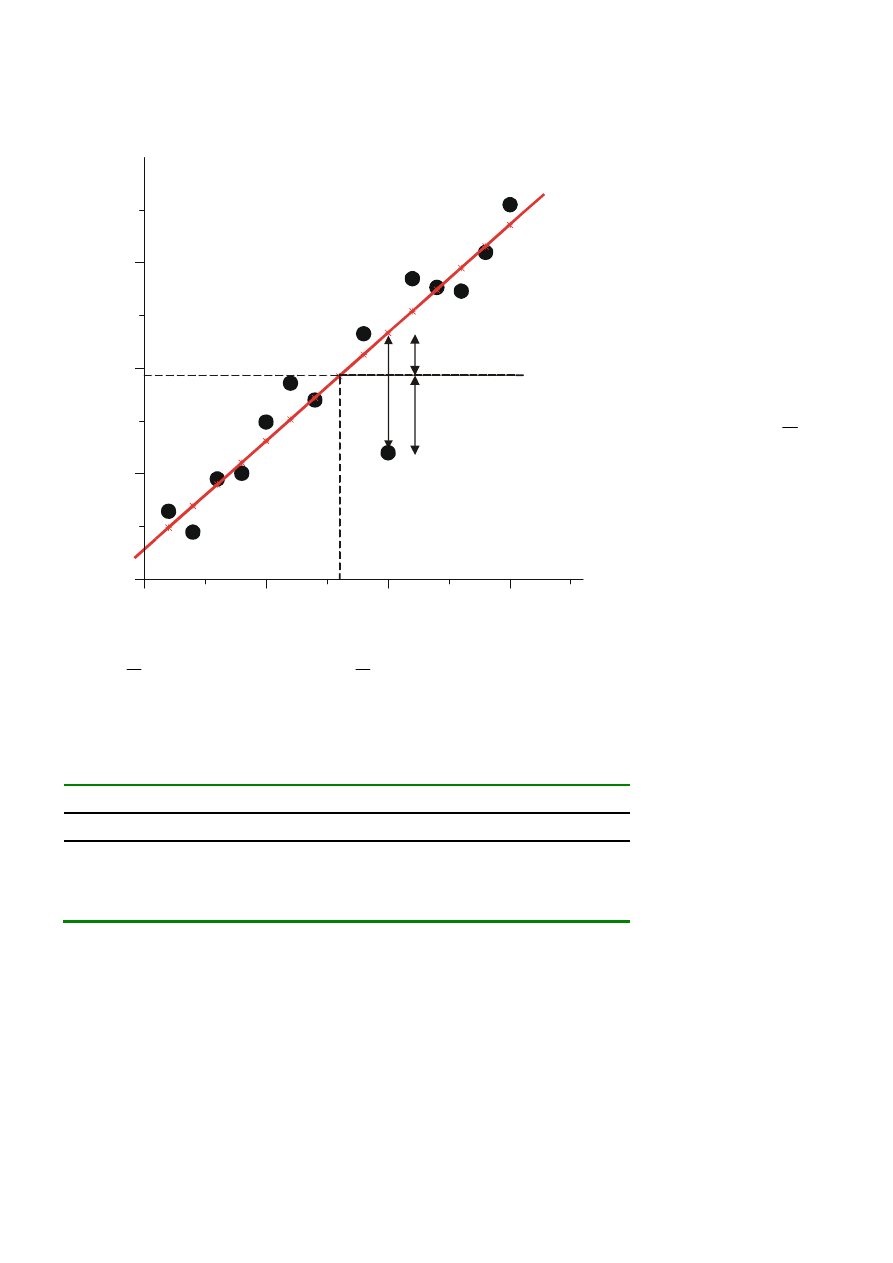
e =y -y^
i
i
i
y -y
i
i
_
y -y
^
i
_
y = b + b x
0
1
0
5
10
15
0
10
20
30
y
∑
−
=
i
i
i
y
y
SSR
2
)
ˆ
(
∑
−
=
i
i
i
y
y
SSE
2
)
ˆ
(
∑
−
=
i
i
i
y
y
SSTO
2
)
(
)
ˆ
(
)
ˆ
(
)
(
i
i
i
i
i
y
y
y
y
y
y
−
+
−
=
−
SSTO=SSE + SSR
(gdy b
0
, b
1
sa dopasowane metodą regresji liniowej)
ANALIZA WARIANCJI
df
SS
MS
Regresja m-1
SSR
MSR=SSR/(m-1)
Resztkowy n-m
SSE
MSE=SSE/(n-m)
Razem n-1
SSTO
df – liczba stopni swobody
m – liczba parametrów regresji (prosta regresja liniowa – b
0
, b
1
)
n – lb. punktów pomiarowych
Cd = r
2
= SSR/SSTO – współczynnik determinacji
(względna miara dopasowania)
1-Cd – współczynnik indeterminacji
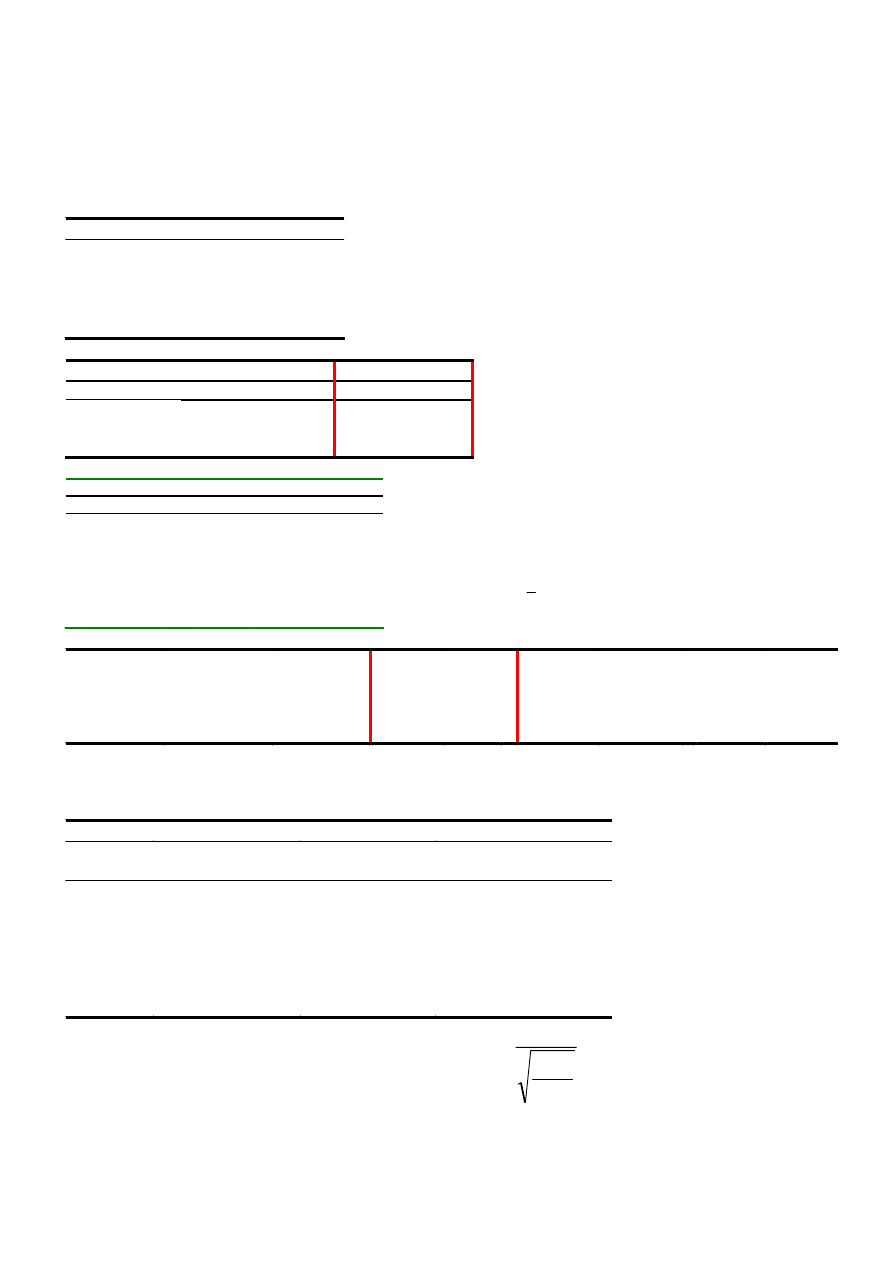
EXCEL: Analiza danych: regresja
ANALIZA WARIANCJI
df
SS
MS
F
Istotność F
Regresja 1
128,5714 128,5714 118,4211 0,000114
Resztkowy 5
5,428571 1,085714
Razem
6
134
ANALIZA WARIANCJI
df
SS
MS
Regresja m-1
SSR
MSR=SSR/(m-1)
∑
−
=
i
i
i
y
y
SSR
2
)
ˆ
(
Resztkowy n-m
SSE MSE=SSE/(n-m)
∑
−
=
i
i
i
y
y
SSE
2
)
ˆ
(
Razem n-1
SSTO
∑
−
=
i
i
i
y
y
SSTO
2
)
(
Współczynniki
Błąd
standardowy t
Stat
Wartość-
p
Dolne
95%
Górne
95%
Dolne
99,0%
Górne
99,0%
Przecięcie 7,428571 0,880631
8,435514 0,000384 5,164842 9,692301
3,877766 10,97938
Zmienna X 1 2,142857
0,196915 10,88214 0,000114 1,636672 2,649042 1,348873 2,936841
b
0
b
1
S
b0
S
b1
b
0
-t
α
⋅S
b0
b
1
-t
α
⋅S
b1
b
0
+t
α
⋅S
b0
b
1
+t
α
⋅S
b1
SKŁADNIKI RESZTOWE - WYJŚCIE
Obserwacja Przewidywane Y
Składniki
resztowe Std.
składniki resztowe
1 9,571429 -1,57143 -1,65207
2 11,71429 1,285714 1,351691
3 13,85714 0,142857 0,150188
4 16
1 1,051315
5 18,14286 -0,14286 -0,15019
6 20,28571 -0,28571 -0,30038
7 22,42857 -0,42857 -0,45056
0
1
ˆ
b
x
b
y
i
i
+
⋅
=
i
i
i
y
y
e
ˆ
−
=
1
*
−
=
n
SSE
e
e
i
i
PODSUMOWANIE - WYJŚCIE
Statystyki regresji
Wielokrotność R
0,979535
r- współczynnik korelacji
R kwadrat
0,959488
r
2
=SSR/SSTO
Dopasowany R kwadrat
0,951386
R
2
dop.
=1-(n-1)/(n-m)*(SSE/SSTO)
Błąd standardowy
1,041976
S
Obserwacje 7
n
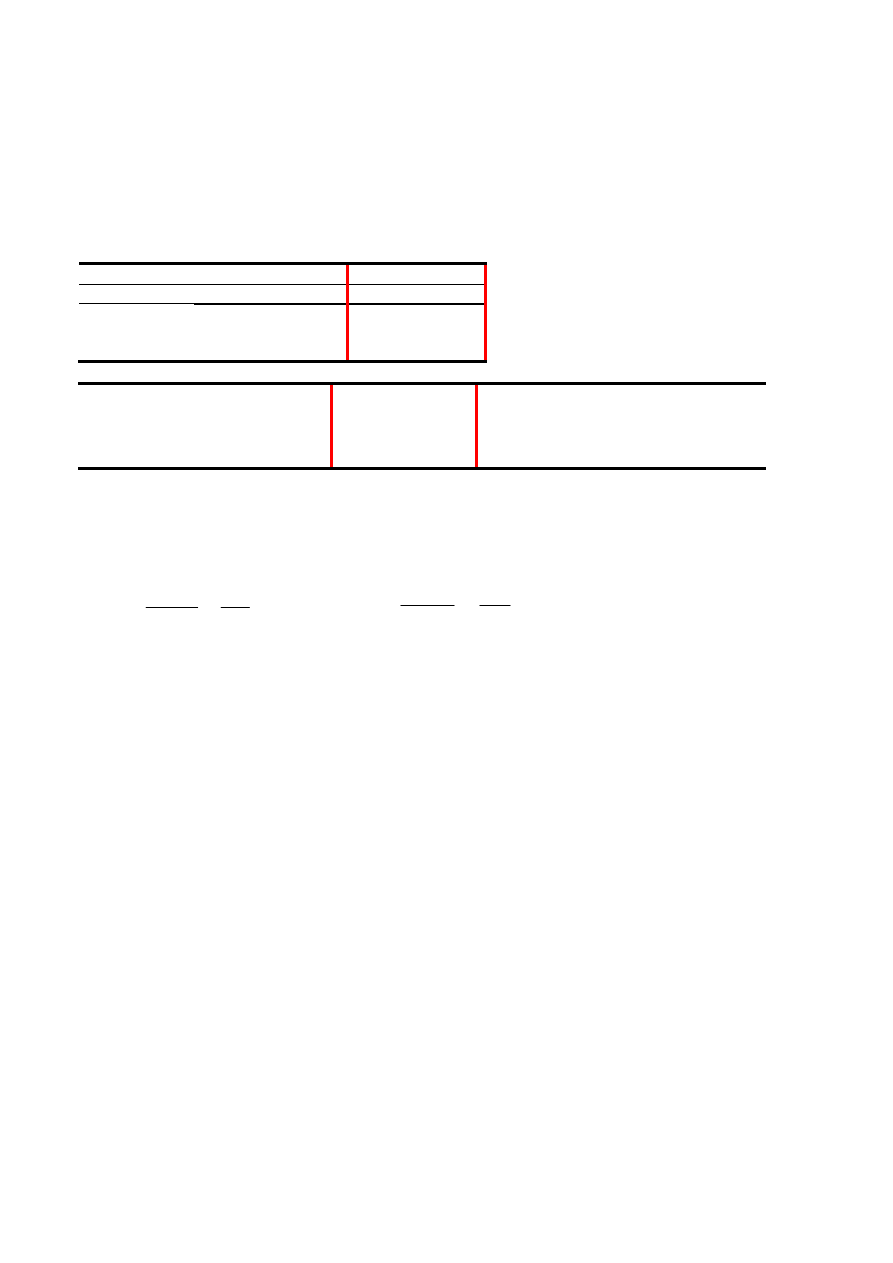
Testy statystyczne w analizie regresji
ANALIZA WARIANCJI
df
SS
MS
F
Istotność F
Regresja 1
128,5714 128,5714 118,4211 0,000114
Resztkowy 5
5,428571 1,085714
Razem
6
134
Współczynniki
Błąd
standardowy t
Stat
Wartość-
p
Dolne
95%
Górne
95%
Dolne
99,0%
Górne
99,0%
cięcie 7,428571 0,880631
8,4355140,000384 5,164842 9,692301 3,877766
10,97938
na X 1 2,142857
0,196915 10,882140,000114 1,636672 2,649042 1,348873 2,936841
• Test t (Służy testowaniu założenia, że β
0
=0, lub
β
1
=0)
0
0
0
0
0
b
b
S
b
S
b
tStat
=
−
=
lub
1
1
1
1
0
b
b
S
b
S
b
tStat
=
−
=
H
0
:
β
0
=0, H
A
:
β
0
≠0 lub H
0
:
β
1
=0, H
A
:
β
1
≠0
Hipotezę H
0
odrzucamy gdy
⏐tStat⏐ > t
n-2, 1-
α
, gdyż uzyskany został wynik mało
prawdopodobny. Wartość-p określa wartość tego prawdopodobieństwa (gdy
mniejsze od wybranego
α to H
0
odrzucamy).
• Test F (Dotyczy istotności tylko współczynnika kierunkowego. Dla
prostej regresji liniowej oba testy są równoważne - t
2
=F)
F=MSR/MSE
H
0
:
β
1
=0, H
A
:
β
1
≠0
Hipotezę H
0
odrzucamy gdy
⏐F⏐ > F
1,n-2, 1-
α
, gdyż uzyskany został wynik mało
prawdopodobny. Istotność F określa to samo co Wartość-p, czyli wartość tego
prawdopodobieństwa (gdy mniejsze od wybranego
α to H
0
odrzucamy).

ORIGIN: Tools: Linear Fit
Linear Regression for Data1_B:
Y = A + B * X
Parameter Value
Error
t-Value
Prob>|t|
A 7,42857A
0,88063
8,43551 3,84132E-4
B
2,14286 0,19691 10,88214 1,1382E-4
-----------------------------------------------------------------
R R-Square(COD) Adj.
R-Square
Root-MSE(SD) N
--------------------------------------------------------------------------------------
0,97953 0,95949 0,95139
1,04198 7
--------------------------------------------------------------------------------------
ANOVA Table:
-------------------------------------------------------------------------------------------------
Degrees of
Sum of
Mean
Item Freedom
Squares
Square
F
Statistic
-------------------------------------------------------------------------------------------------
Model 1
128,57143
128,57143 118,42105
Error 5
5,42857
1,08571
Total 6
134
Prob>F
-----------------
1,1382E-4
-----------------
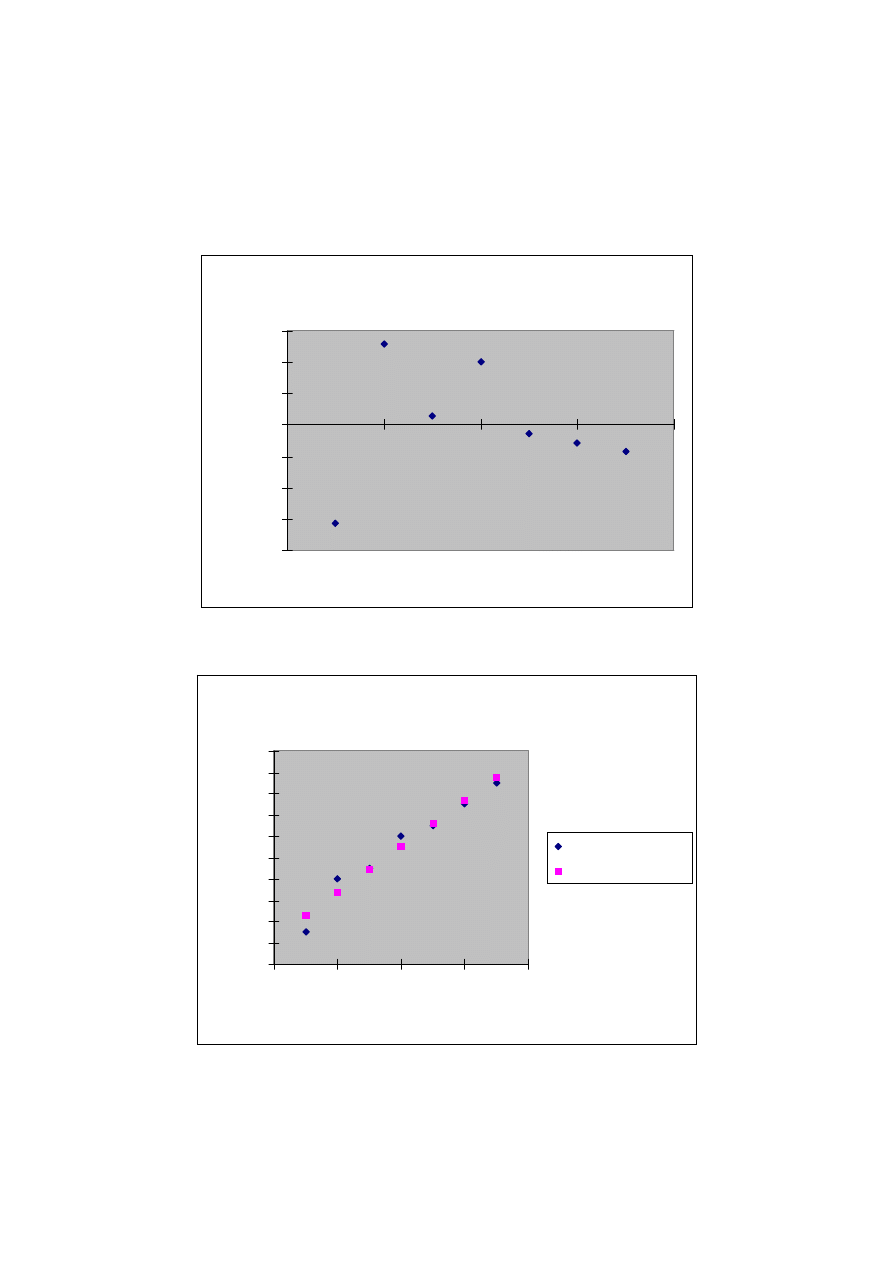
Zmienna X 1 Rozkład reszt
-2
-1,5
-1
-0,5
0
0,5
1
1,5
0
2
4
6
8
Zmienna X 1
Sk
ładniki resztowe
Zmienna X 1 Rozkład linii dopasowanej
5
7
9
11
13
15
17
19
21
23
25
0
2
4
6
8
Zmienna X 1
Y
Y
Przewidywane Y
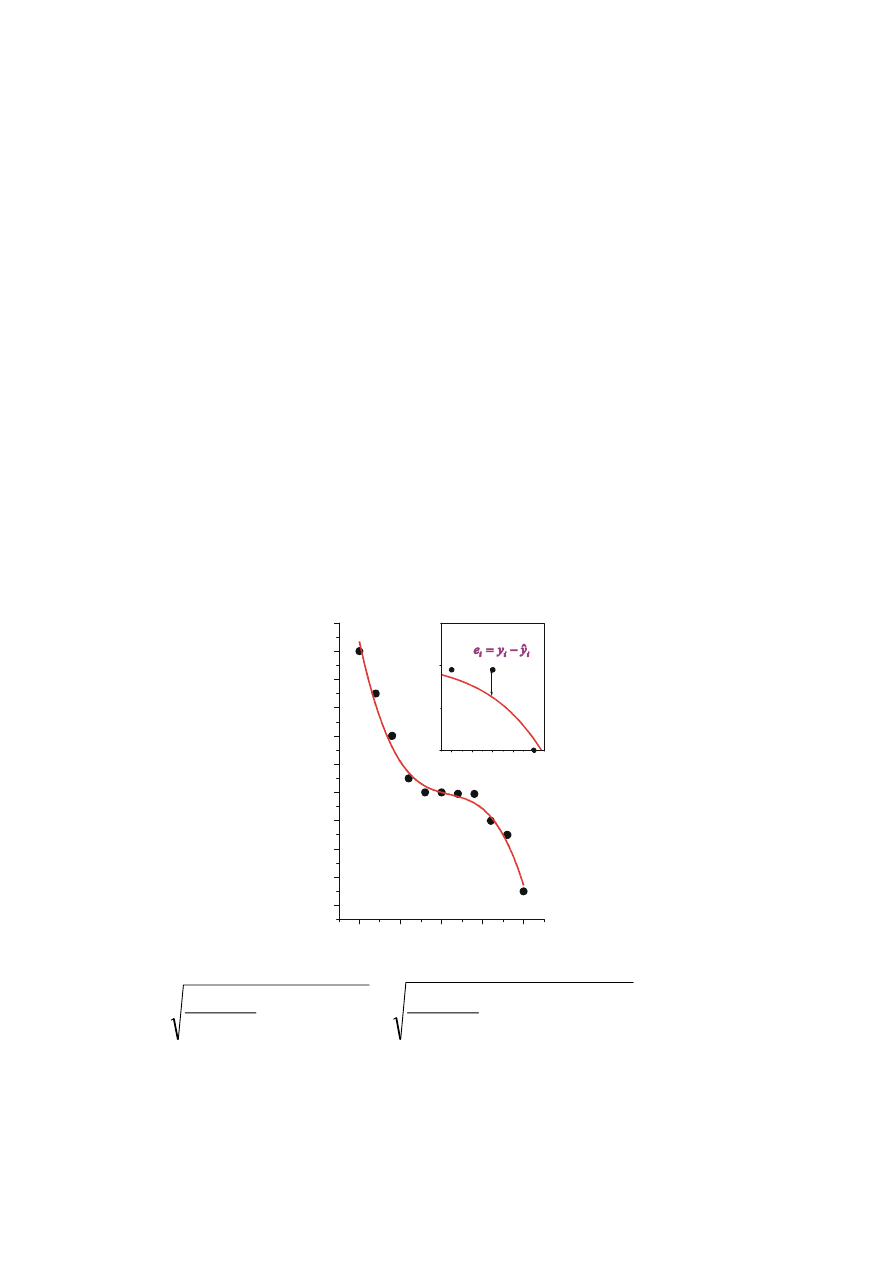
Wielomian k-tego stopnia
y =
β
0
+
β
1
⋅ x + β
2
⋅ x
2
+ ... +
β
k
⋅ x
k
y = b
0
+ b
1
⋅ x + b
2
⋅ x
2
+ ... + b
k
⋅ x
k
=
∑
=
⋅
k
k
k
k
x
b
0
∑
∑
=
=
⋅
−
=
i
k
k
k
k
i
x
b
y
Q
0
2
.
min
)
(
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⋅
⋅
⋅
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
+
+
+
+
k
i
i
i
i
i
i
i
k
k
i
k
i
k
i
k
i
k
i
i
i
i
k
i
i
i
i
k
i
i
i
x
y
x
y
x
y
y
b
b
b
b
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
n
...
...
...
...
...
...
...
...
...
...
...
2
2
1
0
2
2
1
2
4
3
2
1
3
2
2
2
2
)
(
1
1
)
ˆ
(
1
1
∑
∑
∑
⋅
−
−
−
=
−
−
−
=
i
k
k
i
k
i
i
i
i
x
b
y
k
n
y
y
k
n
S
-10
-5
0
5
10
-8
-6
-4
-2
0
2
4
6
8
10
12
y
x
Przykład:
y =A + Bx + Cx
2
⎪
⎪
⎩
⎪⎪
⎨
⎧
⋅
=
+
+
⋅
=
+
+
=
+
+
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⋅
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
2
4
3
2
3
2
2
2
4
3
2
3
2
2
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
x
y
x
C
x
B
x
A
x
y
x
C
x
B
x
A
y
x
C
x
B
n
A
x
y
x
y
y
C
B
A
x
x
x
x
x
x
x
x
n
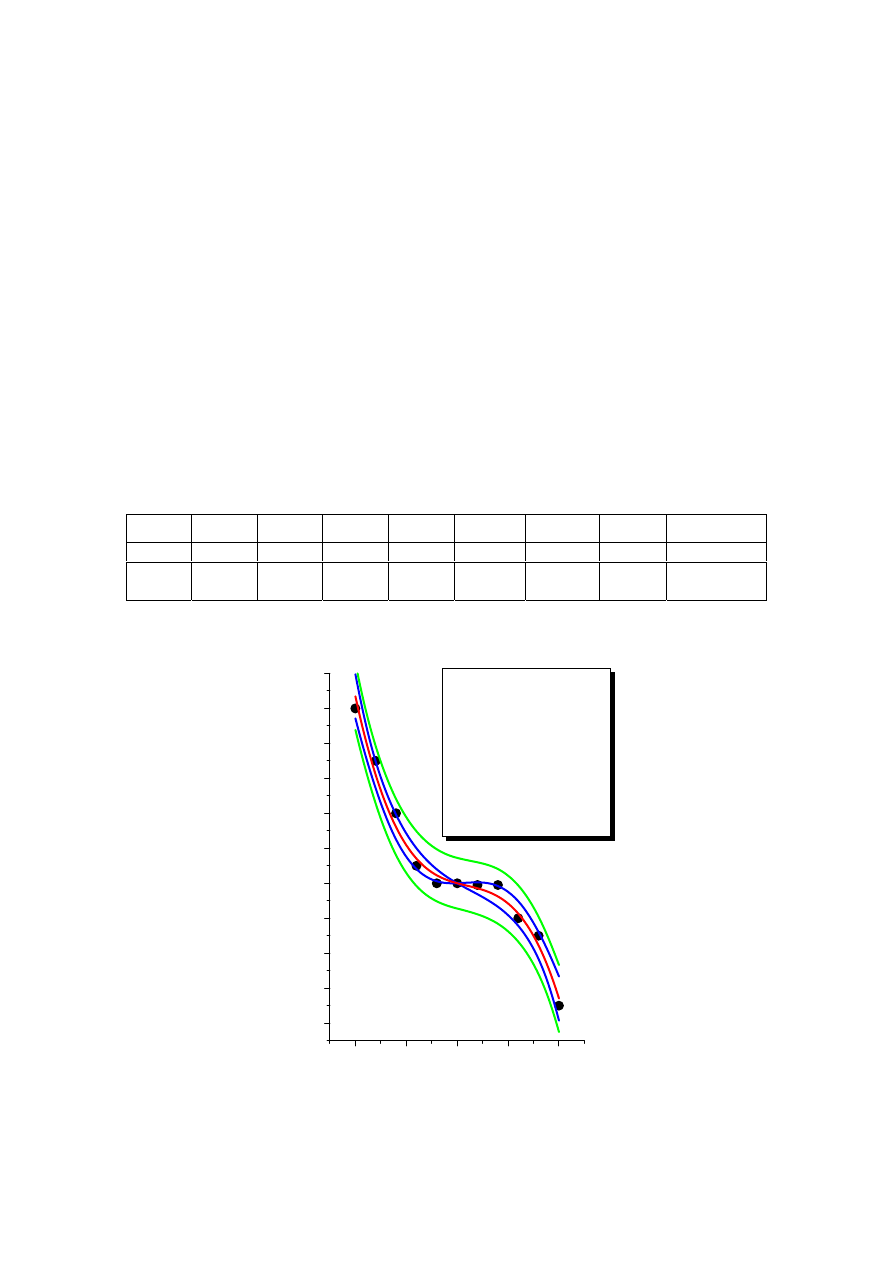
Przykład: Origin:
-10
-5
0
5
10
-8
-6
-4
-2
0
2
4
6
8
10
12
y=A+Bx+Cx
2
+Dx
3
Data: Data1_B
Model: wielom3
Chi^2 = 0.39445
A=0
B=-0.15685±0.07716
C=0.02049±0.00355
D=-0.00707±0.001
y
x
x
i
y
i
x
i
2
x
i
3
x
i
4
y
i
⋅x
i
y
i
⋅x
i
2
i
i
y
y
ˆ
−
2
)
ˆ
(
i
i
y
y
−
... ... ... ... ... ... ... ... ...
∑
i
x
∑
i
y
∑
2
i
x
∑
3
i
x
∑
4
i
x
i
i
x
y
⋅
∑
2
i
i
x
y
⋅
∑
∑
−
i
i
i
y
y
2
)
ˆ
(
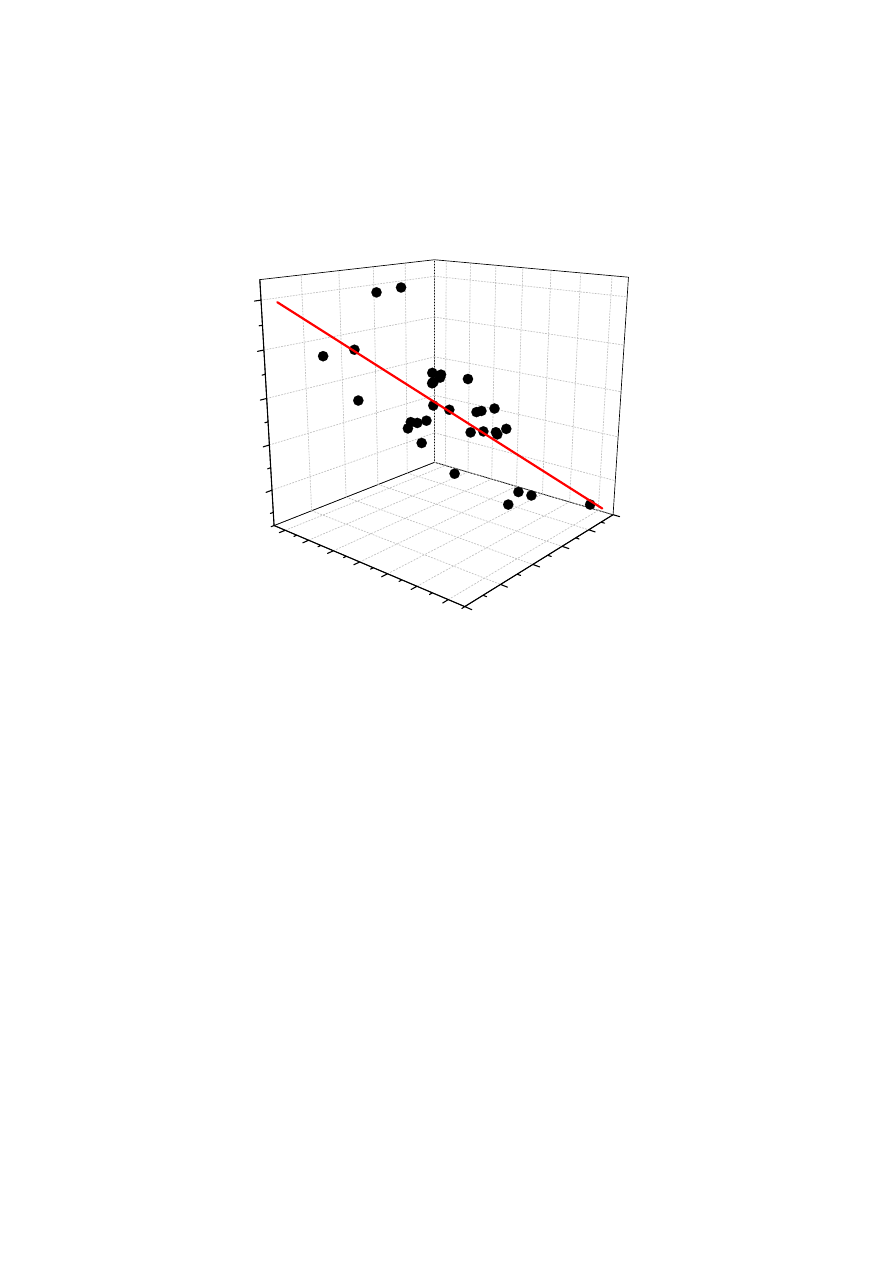
Regresja wieloraka
z =A + Bx + Cy
⎪
⎪
⎩
⎪⎪
⎨
⎧
⋅
=
+
+
⋅
=
+
+
=
+
+
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⋅
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
⋅
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
y
z
y
C
x
y
B
y
A
x
z
x
y
C
x
B
x
A
z
yx
C
x
B
n
A
y
z
x
z
z
C
B
A
y
x
y
y
x
y
x
x
y
x
n
2
2
2
2
8
9
10
11
12
13
14
140
150
160
170
180
190
40
45
50
55
60
Z Axis
Y A
xis
X Axis

Regresja wieloraka
y x1 x2 x3
x4 x5 x6
44,609 44 89,47 11,37 62 178 182
45,313 40 75,07 10,07 62 185 185
54,297 44 85,84 8,65 45 156 168
59,571 42 68,15 8,17 40 166 172
49,874 38 89,02 9,22 55 178 180
44,811 47 77,45 11,63 58 176 176
45,681 40 75,98 11,95 70 176 180
49,091 43 81,19 10,85 64 162 170
39,442 44 81,42 13,08 63 174 176
60,055 38 81,87 8,63 48 170 186
50,541 44 73,03 10,13 45 168 168
37,388 45 87,66 14,03 56 186 192
44,754 45 66,45 11,12 51 176 176
47,273 47 79,15 10,6 47 162 164
51,855 54 83,12 10,33 50 166 170
49,156 49 81,42 8,95 44 180 185
40,836 51 69,63 10,95 57 168 172
46,672 51 77,91 10 48 162 168
46,774 48 91,63 10,25 48 162 164
50,388 49 73,37 10,08 67 168 168
39,407 57 73,37 12,63 58 174 176
46,08 54 79,38 11,17 62 156 165
45,441 52 76,32 9,63 48 164 166
54,625 50 70,87 8,92 48 146 155
45,118 51 67,25 11,08 48 172 172
39,203 54 91,63 12,88 44 168 172
45,79 51 73,71 10,47 59 186 188
50,545 57 59,08 9,93 49 148 155
48,673 49 76,32 9,4 56 186 188
47,92 48 61,24 11,5 52 170 176
47,467 52 82,78 10,5 53 170 172
EXCEL: Analiza danych: Korelacja
y x1 x2 x3 x4 x5
x6
y
1
x1
-0,30
1
x2 -0,16 -0,23 1
x3 -0,86 0,19 0,14 1
x4 -0,40 -0,16 0,04 0,45 1
x5 -0,40 -0,34 0,18 0,31 0,35 1
x6 -0,24
-0,43 0,25 0,23 0,31 0,93 1

EXCEL: Analiza danych: Regresja
Statystyki regresji
Wielokrotność R
0,8726
R kwadrat
0,7614
Dopasowany R kwadrat
0,7444
Błąd standardowy
2,6933
Obserwacje 31
ANALIZA WARIANCJI
df
SS
MS
F
Istotność F
Regresja 2
648,2622 324,1311 44,68146
1,94E-09
Resztkowy 28
203,1194 7,254263
Razem
30
851,3815
Współczynniki Błąd stand.
t Stat
Wartość-
p
Dolne
95%
Górne
95%
A 93,09 8,25
11,29
6E-12 76,19
109,99
B -3,14 0,37
-8,41
3E-09
-3,90
-2,38
C -0,07 0,05
-1,46
0,16
-0,18
0,03
Sprawdźmy, czy jeden bądź więcej współczynników kierunkowych jest istotnie
różny od zera.
• Ho: B=C=0 vs. Ha: przynajmniej jeden jest różny od zera
F
2,28,0.95
= 3,34 < F=38,64
przynajmniej jeden współczynnik jest różny od zera na 5% poziomie istotności.
Odrzucamy hipotezę Ho na rzecz hipotezy alternatywnej.
Ponieważ t
28,0.95
=2.048
⇒ wnioskujemy, że C nie jest istotnie różne od zera
na 5% poziomie istotności.

Model 1 – bierzemy pod uwagę wszystkie zmienne
EXCEL: Analiza danych: Regresja
Statystyki regresji
Wielokrotność R
0,9212
R kwadrat
0,8487
Dopasowany R kwadrat
0,8108
Błąd standardowy
2,3169
Obserwacje 31
ANALIZA
WARIANCJI
df
SS
MS
F
Istotność F
Regresja 6
722,5436 120,4239 22,43263
9,72E-09
Resztkowy 24
128,8379 5,368247
Razem
30
851,3815
Współczynniki. Błąd stand.
t Stat
Wartość-
p
Dolne
95%
Górne
95%
Przecięcie 102,93
12,40 8,30 2E-08 77,33
128,53
x1 -0,23 0,10
-2,27
0,03
-0,43
-0,02
x2 -0,07 0,05
-1,36
0,18
-0,19
0,03
x3 -2,63 0,38
-6,84
5E-07
-3,42
-1,83
x4 -0,02 0,07
-0,33
0,74
-0,16
0,11
x5 -0,37 0,12
-3,09
0,01
-0,62
-0,12
x6 0,30
0,14
2,22
0,04
0,02
0,58
Sprawdźmy, czy jeden bądź więcej parametrów jest istotnie różnych od zera.
• Ho: b1=b2=b3=b4=b5=b6=0 vs. Ha: przynajmniej jeden jest różny od zera
Ponieważ F
6,24,0.95
= 2.51 < F=22.43
⇒ przynajmniej jeden współczynnik jest
różny od zera na 5% poziomie istotności.
Odrzucamy hipotezę Ho na rzecz hipotezy alternatywnej.
• Ponieważ t
24,0.95
=2.064
⇒ Przecięcie, b1, b3, b5, b6 są istotnie różne od zera
na 5% poziomie istotności.

Model 2
Statystyki regresji
Wielokrotność R
0,9148
R kwadrat
0,8368
Dopasowany R kwadrat
0,8117
Błąd standardowy
2,3116
Obserwacje 31
ANALIZA
WARIANCJI
df
SS
MS
F
Istotność F
Regresja 4
712,4515 178,1129 33,33286
6,91E-10
Resztkowy 26 138,93 5,343462
Razem
30
851,3815
Współczynniki Błąd stand. t Stat Wartość-p
Dolne
95%
Górne
95%
Przecięcie 98,15
11,79 8,33 8E-09 73,92
122,37
x1 -0,20 0,10
-2,07
0,048
-0,39
-0,001
x3 -2,77 0,34
-8,13
1E-08
-3,46
-2,07
x5 -0,35 0,12
-2,96
0,01
-0,59
-0,11
x6 0,27 0,13
2,02
0,053
-0,004
0,55
• Dla t
26,0.95
=2.056 wnioskujemy, iż tylko b6 nie jest istotnie różne od
zera na 5% poziomie istotności.

Model 3
Statystyki regresji
Wielokrotność R
0,9006
R kwadrat
0,8110
Dopasowany R kwadrat
0,7901
Błąd standardowy
2,4406
Obserwacje 31
ANALIZA WARIANCJI
df
SS
MS
F
Istotność F
Regresja 3
690,5509 230,1836 38,64286
6,56E-10
Resztkowy 27
160,8307 5,956692
Razem
30
851,3815
Współczynniki Błąd stand.
t Stat
Wartość-
p
Dolne
95%
Górne
95%
Przecięcie 111,72
10,24 10,92 2E-11
90,72
132,72
x1 -0,26 0,10
-2,66
0,01
-0,45
-0,06
x3 -2,83 0,36
-7,89
2E-08
-3,56
-2,09
x5 -0,13 0,05
-2,59
0,02
-0,23
-0,03
Sprawdźmy, czy jeden bądź więcej parametrów jest istotnie różnych od zera.
• Ho: b1=b3=b5=0 vs. Ha: przynajmniej jeden jest różny od zera
F
3,27,0.95
= 2.96 < F=38.64,
przynajmniej jeden współczynnik jest różny od zera na 5% poziomie istotności.
Odrzucamy hipotezę Ho na rzecz hipotezy alternatywnej.
• Ponieważ t
27,0.95
=2.052
⇒ wszystkie wybrane parametry są istotnie różne od zera
na 5% poziomie istotności.

Model 4
Statystyki regresji
Wielokrotność R
0,8842
R kwadrat
0,7817
Dopasowany R kwadrat
0,7575
Błąd standardowy
2,6235
Obserwacje 31
ANALIZA
WARIANCJI
df
SS
MS
F
Istotność F
Regresja 3
665,5506 221,8502 32,23337
4,53E-09
Resztkowy 27
185,8309 6,882626
Razem
30
851,3815
Współczynniki Błąd stand. t Stat
Wartość-
p
Dolne
95%
Górne
95%
Przecięcie 106,00
13,03 8,13 1E-08
79,25
132,74
x1 -0,23 0,11
-2,13
0,04
-0,45
-0,01
x3 -3,01 0,37
-8,03
1E-08
-3,78
-2,24
x6 -0,09 0,06
-1,47
0,15
-0,22
0,03
Ponieważ x5 i x6 są silnie skorelowane sprawdzamy czy ich zamiana nie
doprowadzi do poprawnego modelu.
• Ho: b1=b3=b6=0 vs. Ha: przynajmniej jeden jest różny od zera
F
3,27,0.95
= 2.96 < F=32.23,
przynajmniej jeden współczynnik jest różny od zera na 5% poziomie istotności.
Odrzucamy hipotezę Ho na rzecz hipotezy alternatywnej.
• Ponieważ t
27,0.95
=2.052 wnioskujemy, że b6 nie jest istotnie różny od zera
na 5% poziomie istotności.
Model 5
Statystyki regresji
Wielokrotność R
0,8726
R kwadrat
0,7614
Dopasowany R kwadrat
0,7444
Błąd standardowy
2,6933
Obserwacje 31
ANALIZA WARIANCJI
df
SS
MS
F
Istotność F
Regresja 2
648,2622 324,1311 44,68146
1,94E-09
Resztkowy 28
203,1194 7,254263
Razem
30
851,3815
Współczynniki Błąd stand.
t Stat
Wartość-
p
Dolne
95%
Górne
95%
Przecięcie 93,09
8,25 11,29 6E-12
76,19
109,99
x3 -3,14 0,37
-8,41
3E-09
-3,90
-2,38
x5 -0,07 0,05
-1,46
0,16
-0,18
0,03
• Dla t
28,0.95
=2.048 wnioskujemy, że b5 nie jest istotnie różne od zera na
5% poziomie istotności.
Model 6
Statystyki regresji
Wielokrotność R
0,8622
R kwadrat
0,7434
Dopasowany R kwadrat
0,7345
Błąd standardowy
2,7448
Obserwacje 31
ANALIZA WARIANCJI
df
SS
MS
F
Istotność F
Regresja 1
632,9001
632,9001 84,0076
4,59E-10
Resztkowy 29
218,4814
7,533843
Razem
30
851,3815
Współczynniki Błąd stand.
t Stat
Wartość-
p
Dolne
95%
Górne
95%
Przecięcie 82,42
3,86 21,38 3E-19
74,54
90,31
x3 -3,31 0,36
-9,16
5E-10
-4,05
-2,57
• Dla t
29,0.95
=2.045 wnioskujemy, że b3 jest istotnie różne od zera na 5%
poziomie istotności.
Podsumowanie
Model x1 x2 x3 x4 x5 x6 MSE
R
2
F
1 # x # x # # 5,37 0,85 22,4
2 # # # x 5,34 0,84 33,3
3 # # # 5,96 0,81 38,6
4 # # x 6,88 0,78 32,2
5 # # 7,25 0,76 44,7
6 # 7,53 0,74 84,0
Wybieramy model 3. Wszystkie zmienne są istotnie różne od zera na 5%
poziomie istotności i nie obserwuje się istotnego pogorszenia MSE, R
2
oraz F.
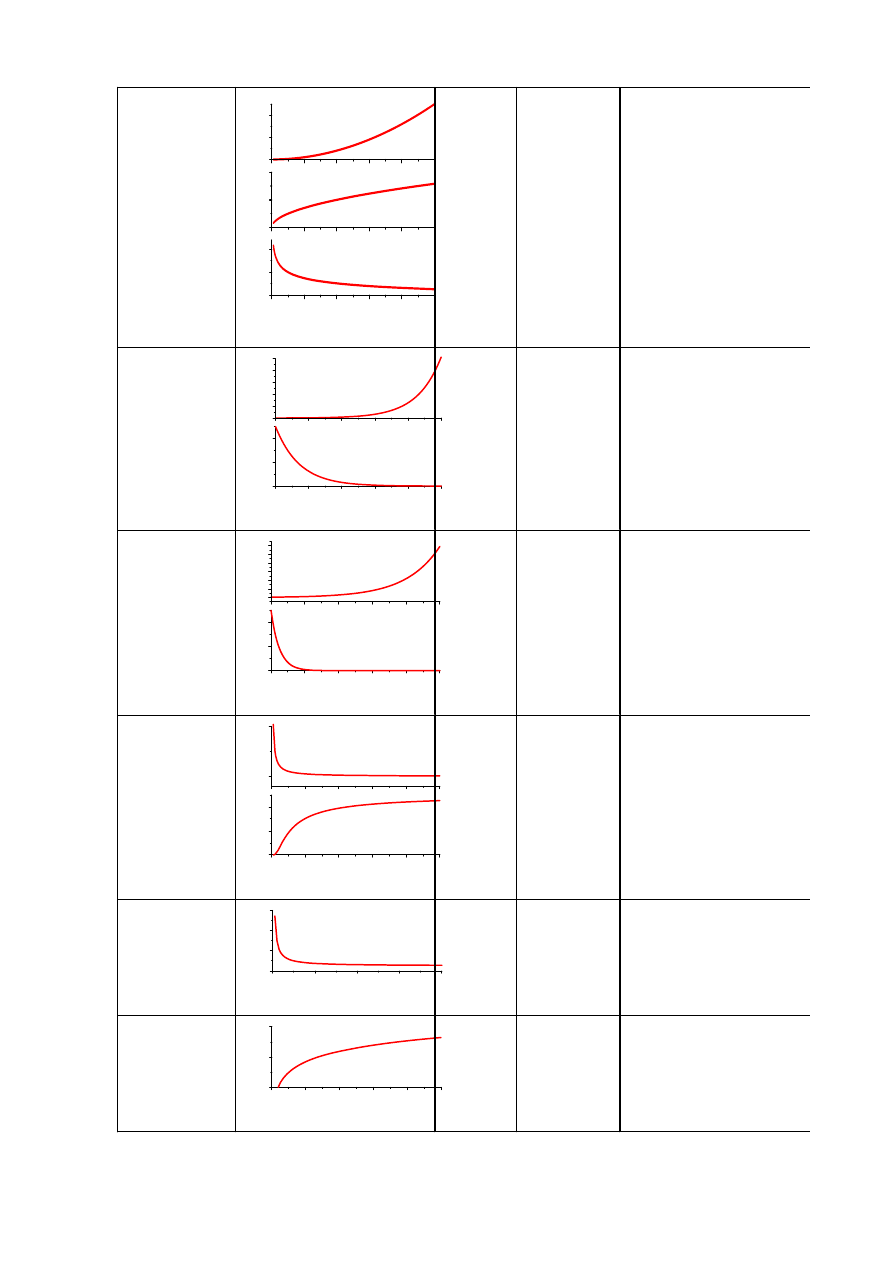
Funkcja
potęgowa
np.
kinetyka
dyspersyjna
k(t)=B
⋅t
1-
α
b<0
x
f(
x)
0<b<1
b>1
y=a·x
b
x*=ln(x)
y*=ln(y)
a*=ln(a)
ln(y)=ln(a) +b·ln(x)
y*=a* + b·x*
Funkcja
wykładnicza
0<b<1
f(x)
x
b>1
y=a
⋅b
x
y*=ln(y)
a*=ln(a)
b*=ln(b)
ln(y)=ln(a)+x·ln(b)
y*=a*+ x·b*
Funkcja
wykładnicza
-
eksponencjalna
np. I=I
0
e
-
μx
Q=Q
0
e
-
λt
b<0
f(
x)
x
b>0
y=a
⋅e
bx
y*=ln(y)
a*=ln(a)
ln(y) = ln(a)+b·x
y*=a* + b·x
Funkcja
wykładnicza
-
eksponencjalna
np. zależność
Arrheniusa
k=Ae
-E/RT
b<0
f(x)
x
b>0
y=a
⋅e
b/x
x*=1/x
y*=ln(y)
a*=ln(a)
ln(y) = ln(a)+b·
1/x
y*=a* + b·x*
Funkcja
hiperboliczna
np. r. Causiusa-
Clapeyrona
lnp
i
=-
ΔH
par
/RT +
const
f(
x)
x
y=b/x+
a
x*=1/x
y=b·x*+a
Funkcja
logarytmiczna
np. stała podziału
lg c
1
=n lg c
2
+ lg
K
f(
x)
x
y=b
⋅logx
+a
x*=logx
y=b·x* + a
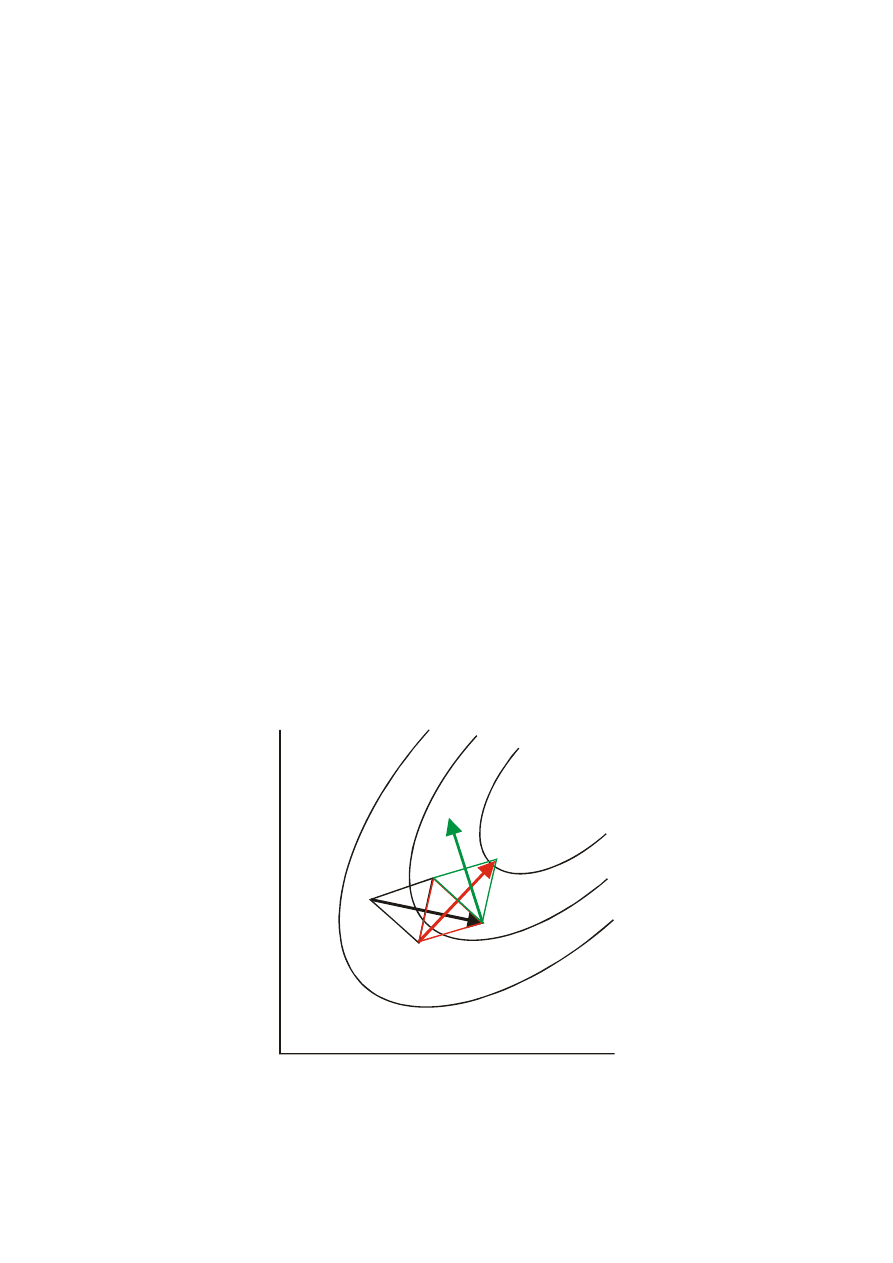
Regresja nieliniowa
• metody gradientowe (wymagana znajomość pochodnych funkcji)
• metody bezpośrednie poszukiwania minimum bez liczenia pochodnych
Metoda Simplex
(metoda bezpośrednia, nie jest wymagana znajomość pochodnych funkcji, służy
znajdywaniu min. lub max.)
.
min
)]
(
ˆ
[
2
2
=
−
=
=
∑
∑
b
i
i
i
i
y
y
e
Q
i
Simplex jest figurą geometryczną, w n wymiarach zbudowaną z
n+1połączonych punktów (w dwóch wymiarach jest to trójkąt, w trzech
czworobok).
Algorytm (przykład dwuwymiarowy):
1. Wybierane są trzy punkty trójkąta i obliczane Q dla każdego punktu
(podawane
są początkowe wartości tylko jednego punktu, pozostałe są znajdywane automatycznie)
.
2. Punkt odpowiadający największej wartości Q jest zastępowany przez punkt
stanowiący jego zwierciadlane odbicie względem pozostałych punktów.
3. Proces jest powtarzany, gdy Q ulega dalszej minimalizacji.
4. Wielkość Simplexu może być redukowana w miarę osiągania minimum.

Metoda Gaussa
Metoda najmniejszych kwadratów w modelu nieliniowym
(model nieliniowy jest nieliniowy w odniesieniu do parametrów - porównaj
wielomian y=b
0
+b
1
x+b
2
x
2
+...+b
k
x
k
i funkcję y=b
0
+b
1
exp(b
2
x):
i
p
p
i
i
i
i
n
n
n
n
n
n
i
i
i
i
y
b
b
b
y
b
b
b
y
b
b
y
y
b
y
y
y
b
y
y
y
b
y
y
y
b
y
y
y
b
y
y
y
b
y
y
y
y
y
e
Q
i
∂
∂
−
+
+
∂
∂
−
+
∂
∂
−
+
≈
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
∂
∂
−
−
−
∂
∂
−
−
∂
∂
−
−
=
∂
∂
−
−
−
∂
∂
−
−
∂
∂
−
−
=
=
−
=
=
∑
∑
ˆ
)
(
...
)
(
ˆ
)
(
)
(
ˆ
)
(
)
(
ˆ
)
(
ˆ
...
ˆ
)]
(
ˆ
[
2
...
ˆ
)]
(
ˆ
[
2
ˆ
)]
(
ˆ
[
2
0
ˆ
)]
(
ˆ
[
2
...
ˆ
)]
(
ˆ
[
2
ˆ
)]
(
ˆ
[
2
0
.
min
)]
(
ˆ
[
)
0
(
1
)
0
(
)
0
(
1
1
0
)
0
(
)
0
(
0
0
)
0
(
1
1
2
2
2
1
1
1
1
0
0
2
2
2
0
1
1
1
2
2
b
b
b
b
b
b
b
b
b
b
b
Algorytm obliczeń
1. Wybór parametrów początkowych b
(0)
2. Obliczenie macierzy Jacobiego
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
)
exp(
)
exp(
1
...
...
...
)
exp(
)
exp(
1
)
exp(
)
exp(
1
.
)
(
ˆ
...
)
(
ˆ
)
(
ˆ
...
...
...
...
)
(
ˆ
...
)
(
ˆ
)
(
ˆ
)
(
ˆ
...
)
(
ˆ
)
(
ˆ
2
1
2
2
2
2
1
2
2
1
2
1
1
1
2
)
0
(
1
)
0
(
0
)
0
(
)
0
(
2
1
)
0
(
2
0
)
0
(
2
)
0
(
1
1
)
0
(
1
0
)
0
(
1
n
n
n
p
n
n
n
p
p
x
b
x
b
x
b
x
b
x
b
x
b
x
b
x
b
x
b
np
b
y
b
y
b
y
b
y
b
y
b
y
b
y
b
y
b
y
b
b
b
b
b
b
b
b
b
3. Rozwiązanie układu równań prowadzącego do nowego zestawu parametrów
b
(k)
4. Obliczenie wartości Q
5. Powrót do pkt. 1 z nowym zestawem parametrów b
(k)
6. Program zostaje zatrzymany, gdy Q nie ulega dalszej minimalizacji.
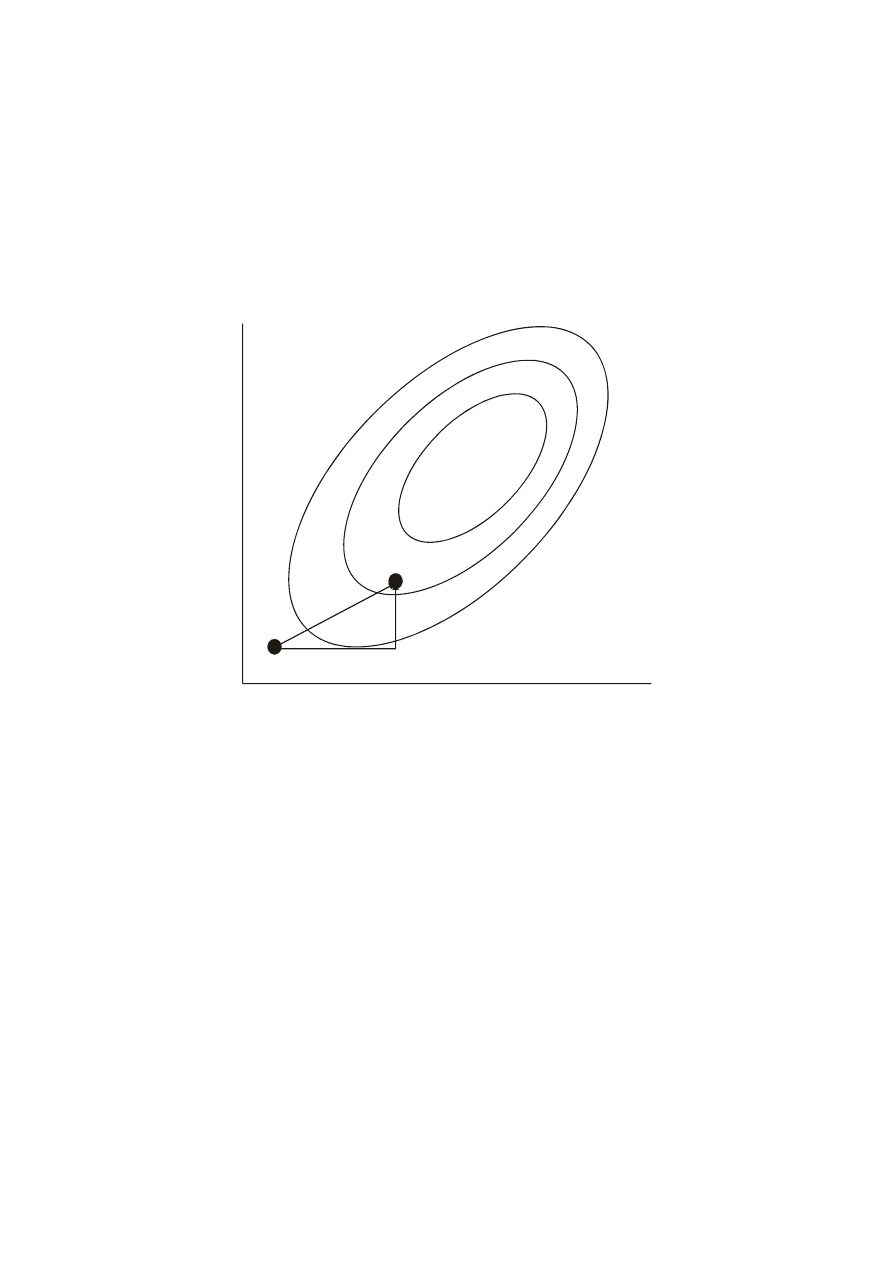
Najbardziej sprawną i ekonomiczną metodą minimalizacji jest obecnie metoda
Levenberga - Marquardta (metoda gradientowa).
x
1
x
2
b
(0)
b
(k)
min.
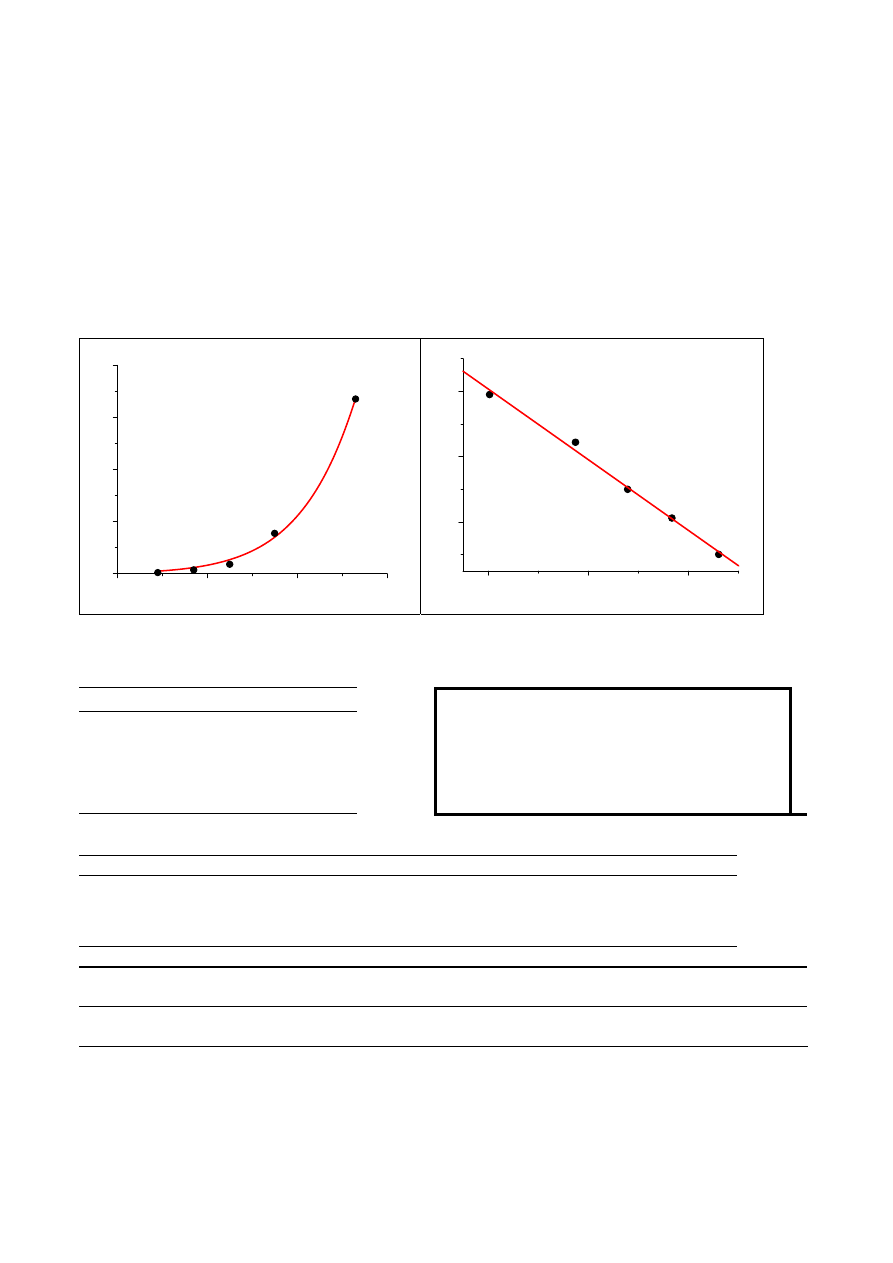
Przykład: regresja nieliniowa linearyzowalna
T k 1/T
ln
k
289 0,0503
0,00346
-2,98975
297 0,1531
0,003367 -1,87666
305 0,368
0,003279 -0,99967
315 1,556
0,003175 0,442118
333 6,71
0,003003 1,903599
280
300
320
340
0
2
4
6
8
k[1/s]
T[K]
0,0030
0,0032
0,0034
-2
0
2
ln k
1/T[1/K]
k = A exp(-E
A
/RT)
⇒ ln k = ln A - (E
A
/R)
⋅(1/T) (y* = b
0
+b
1
⋅x*)
Statystyki regresji
ln k = 34,59 - 10838,7
⋅(1/T)
Wielokrotność R
0,996748
k = 1
⋅10
15
exp(-10838,7/T)
R kwadrat
0,993507
asowany R kwadrat
0,991342
q=f(x)
⇒ Δq=⏐df/dx⏐⋅Δx
ąd standardowy
0,178982
A=1
⋅10
15
±1,7⋅10
15
s
-1
Obserwacje 5
E
A
=21,5
±1 kcal/mol
ANALIZA WARIANCJI
df
SS
MS
F
Istotność F
Regresja 1
14,70427
14,70427 459,0119
0,000223
Resztkowy 3
0,096104
0,032035
Razem 4
14,80038
Współczynniki Błąd stand.
t Stat
Wartość-p Dolne
95%
Górne
95%
Przecięcie 34,5942
1,649504
20,97248 0,000237
29,34474
39,84367
1/T -10838,7
505,8988
-21,4246 0,000223
-12448,7
-9228,66
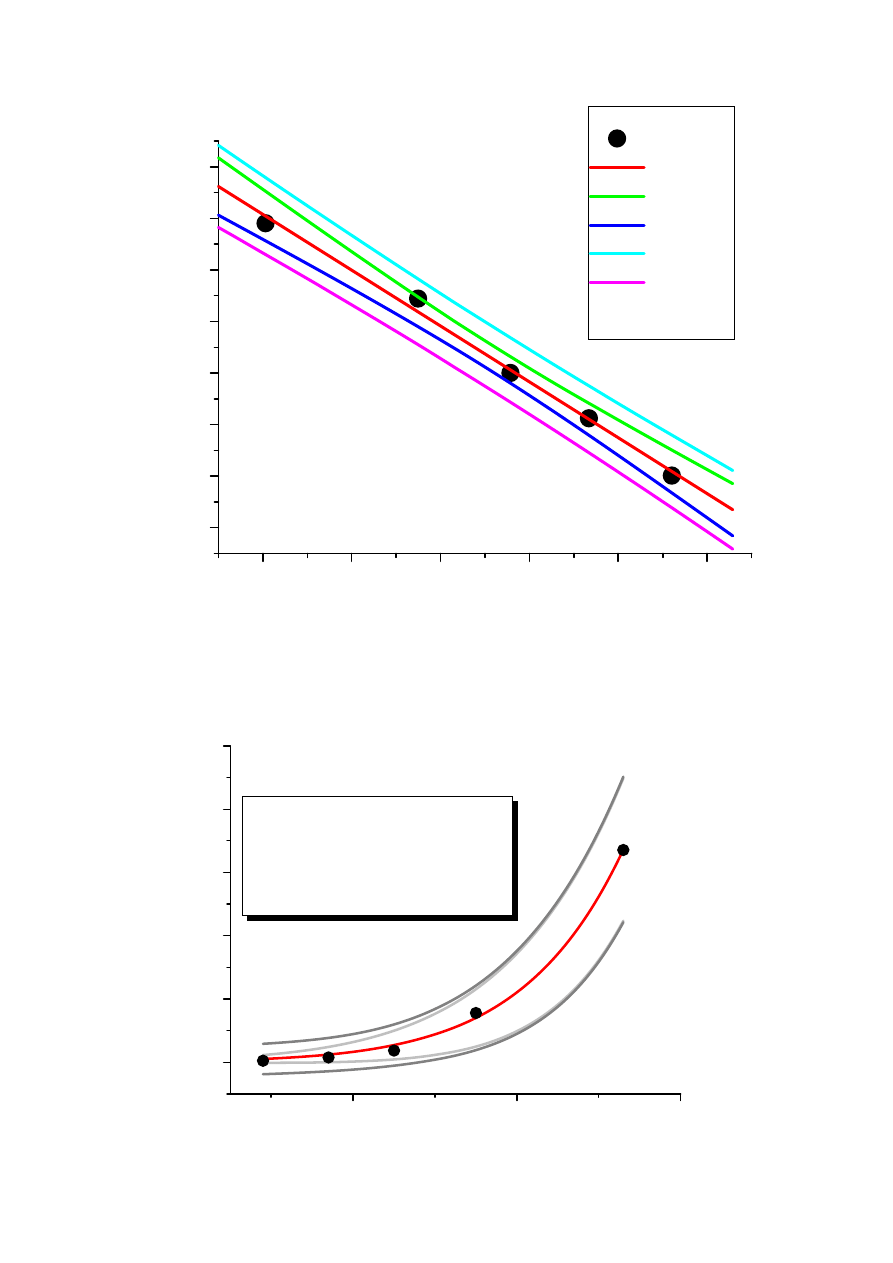
0,0030 0,0031
0,0032
0,0033
0,0034
0,0035
-4
-3
-2
-1
0
1
2
3
D
Data1D
UCL
LCL
UPL
LPL
lnk
1/T[1/K]
300
320
340
0
2
4
6
8
10
Model: y=aexp(b/x)
Chi^2 = 0.02158
a=5.3874E12±8.1147E12
b=-9127.35161±499.96936
k[1/s]
T[K]
k=5,4
⋅10
12
exp(-9127,4/T) vs. k = 1
⋅10
15
exp(-10838,7/T)
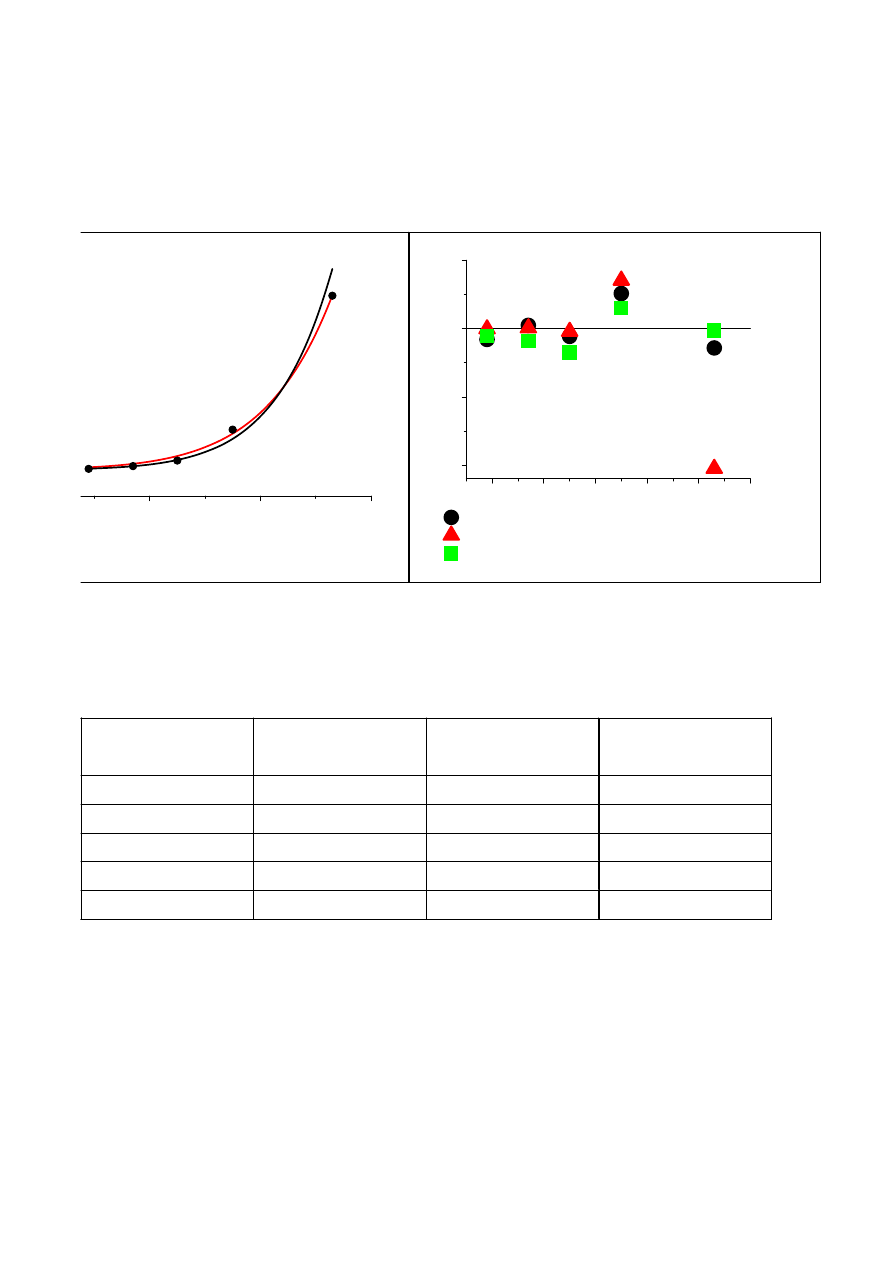
300
320
340
[1/s]
T[K]
290
300
310
320
330
340
-1.0
-0.5
0.0
0.5
regresja liniowa (S=0,18)
po powrocie do początkowych współrzędnych (S=0,63)
regresja nieliniowa (S=0,15)
e
i
=y
i
-y^
i
T[K]
y*
i
= ln y
i
⇒ y
i
= exp(y*
i
)
Δy
i
=
⏐df/dx⏐⋅Δy*
i
= exp(y*
i
)
⋅Δy*
i
y*
i
Δy*
i
(regresja
liniowa)
Δy
i
e
i
(regresja
nieliniowa)
-2,90981 -0,07994 -0,00419 -0,05328
-1,8996 0,02293 0,00347 -0,0894
-0,94239 -0,05728 -0,02171 -0,17499
0,18576 0,25636 0,35184 0,15195
2,04567 -0,14207 -1,02455 -0,01355
Transformacja współrzędnych prowadzi do redukcji wagi wyników o dużej
wartości y.

Rachunek błędu maksymalnego
x
± Δx, y ± Δy ⇒ q = f(x,y); q ± Δq
błąd względny
δx = Δx/⏐x⏐
Suma, różnica
q = x + y
Min. (x -
Δx) + (y - Δy) = (x + y) - (Δx + Δy)
Max. (x +
Δx) + (y + Δy) = (x + y) + (Δx + Δy)
q = x - y
Min. (x -
Δx) - (y + Δy) = (x - y) - (Δx + Δy)
Max. (x +
Δx) - (y - Δy) = (x - y) + (Δx + Δy)
Niepewność sumy i różnicy
q = x + y
Δq = Δx + Δy
q = x - y
Δq = Δx + Δy
Iloczyn, iloraz
x
± Δx = x(1 ± Δx/x) = x(1 ± δx)
y
± Δy = y(1 ± δy)
q = x
⋅ y
Min. x(1 -
δx)⋅y(1 - δy) = x⋅y(1 - δx - δy + δx⋅δy) ≈ x⋅y[1-(δx+δy)]
Max. x(1 +
δx)⋅y(1 + δy) = x⋅y(1 + δx + δy + δx⋅δy) ≈ x⋅y[1+ (δx+δy)]
Ponieważ
δx i δy jako błędy pomiarowe są małe
( na ogół < 0,1) to
δx⋅δy jest pomijalnie małe.
Niepewność iloczynu i ilorazu
q = x
⋅ y
δq = δx + δy
q = x/y
δq = δx + δy

Mnożenie przez stałą
q = B
⋅x(1 ± δx) ⇒ (δq = δB + δx = δx) ⇒
Δq = δq⋅⏐q⏐= δx⋅ ⏐B⋅x⏐= ⏐B⏐⋅Δx
q
± Δq = Bx ± ⏐B⏐⋅Δx
Potęgowanie
q = x
n
= x
⋅x⋅...⋅x ⇒ δq = δx + δx + ... + δx = n⋅δx
Porównanie rachunku błędu maksymalnego z metodami statystycznymi
q = x + y
Δq = Δx + Δy
N(m
x
,
σ
x
) + N(m
y
,
σ
y
) =
N(m
q
,
σ
q
)
m
q
=m
x
+ m
y
;
2
2
y
x
q
σ
σ
σ
+
=
Δx
Δy
2
2
y
x
q
Δ
+
Δ
=
Δ
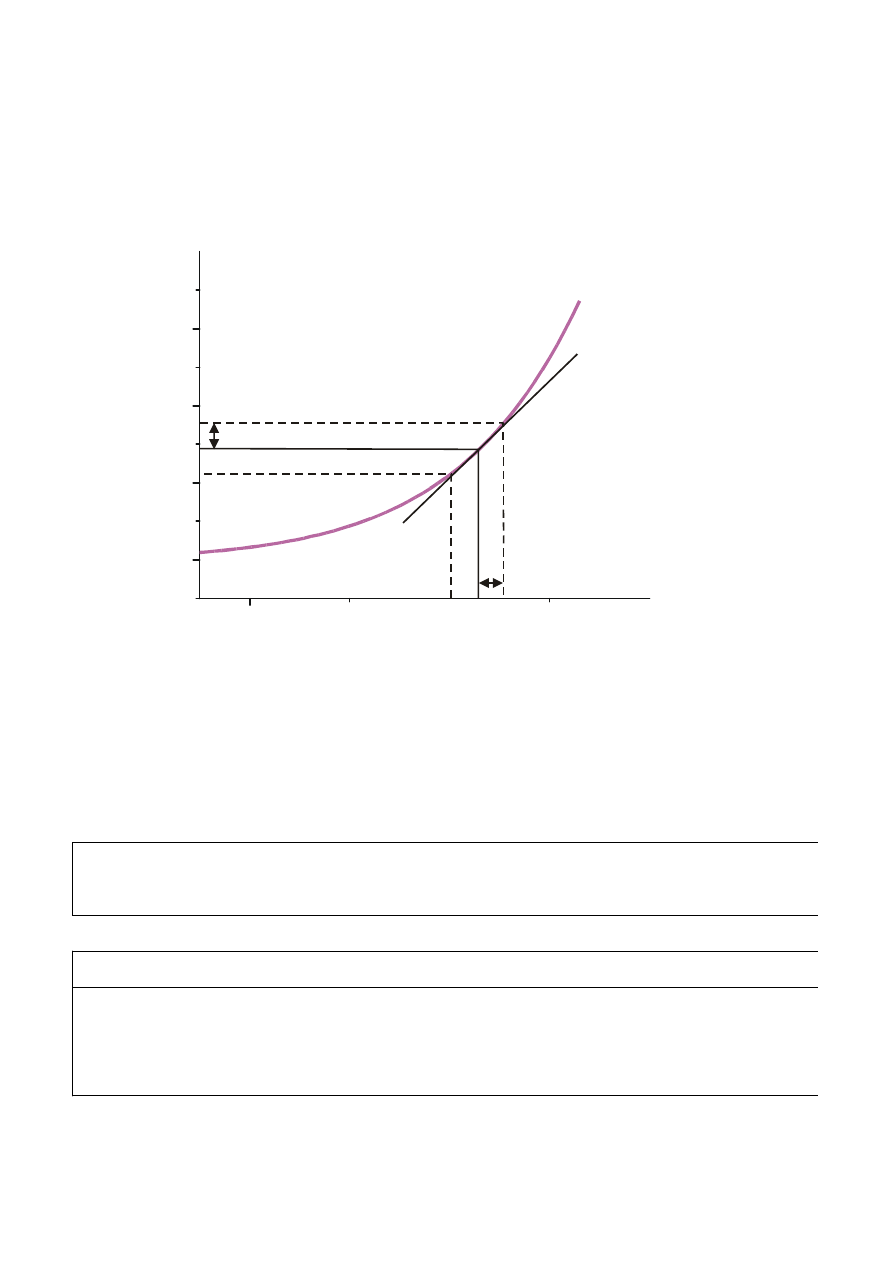
Funkcje jednej zmiennej
q(x)
x
Δx
Δq
q
y=[df(x)/dx] x+C
⋅
q = q(x) = f(x)
Δq = q(x + Δx) - q(x)
Ponieważ dla dostatecznie małego przedziału f(x+u)-f(x) = df/dx
⋅u ⇒
Niepewność wartości funkcji jednej zmiennej
Δq = ⏐dq/dx⏐⋅Δx
Niepewność wartości funkcji wielu zmiennych q(x, y,...z)
Δq = ⏐∂q/∂x⏐⋅Δx + ⏐∂q/∂y⏐⋅Δy + ... + ⏐∂q/∂z⏐⋅Δz

Przykład 1:
Pojemność cieplna kalorymetru: K = i
2
⋅R⋅t/ΔT gdzie:
i - natężenie prądu = 12
± 0,225A
R - opór spirali grzejnej = 57
± 3 Ω
t - czas przepływu prądu = 600
± 2 s
ΔT - przyrost temperatury kalorymetru = 30 ± 1°K
ΔK = ⏐∂K/∂i⏐⋅Δi + ⏐∂K/∂R⏐⋅ΔR + ⏐∂K/∂t⏐⋅Δt + ⏐∂K/∂(ΔT)⏐⋅Δ(ΔT)
ΔK = ⏐2iRt/ΔT⏐⋅Δi + ⏐i
2
t/
ΔT ⏐⋅ΔR + ⏐ i
2
R/
ΔT ⏐⋅Δt +
+
⏐ i2Rt/(ΔT)
2
⏐⋅Δ(ΔT)
Przykład 2
z
x
y
x
q
+
+
=
Policzyć
Δq dla x=20 ± 1, y = 2, z = 0
Δq = ⏐∂q/∂x⏐⋅Δx + ⏐∂q/∂y⏐⋅Δy + ⏐∂q/∂z⏐⋅Δz =
=
2
)
(
1
)
(
)
(
1
z
x
y
x
z
x
+
⋅
+
−
+
⋅
⋅Δx = 2/400⋅1=0,005
=
±
±
1
20
1
22
1,1(1
± (1/22+1/20) =1,1 ± 0,1
Wyszukiwarka
Podobne podstrony:
Matematyka wykład 1
Matematyka Wykład 1 10 14
mat, Politechnika Lubelska, Studia, Studia, Sprawozdania, studia, Matematyka, MATEMATYKA WYKŁADY
Matematyka wykład
Fizyka Matematyczna Wykłady
Analiza matematyczna Wykłady, GRANICE FUNKCJI
matematyka wykłady
Statystyka matematyczna, Wykład 9
Analiza matematyczna Wykłady, CIAGI LICZBOWE
Analiza matematyczna wykład(1)(1)
Analiza matematyczna. Wykłady CAŁKI NIEOZNACZONE
29 04 07r matematyka, wykład
matematyka wykłady z równan różniczkowych
Matematyka 2 wykład
Statystyka matematyczna - wyklad 1, Studia materiały
Analiza matematyczna. Wykłady GRANICE FUNKCJI
tablice-matematyczne, Matematyka wykład
Analiza matematyczna, Analiza matematyczna - wykład, Ściąga z wykładów
Matematyka - Wykład 1, Studia, ZiIP, SEMESTR II, Matematyka
więcej podobnych podstron