1

Ć

wiczenie.54

Sprawdzanie działania interferometru Michelsona.

Wyznaczanie długości fali światła lasera półprzewodnikowego

I. Zagadnienia do samodzielnego opracowania

1.

Fale świetlne, foton.

2.

Zjawisko interferencji, spójność fal świetlnych.

3.

Zasada działania lasera.

4.

Budowa interferometru Michelsona.

II. Wprowadzenie

Ś

wiatło emitowane przez źródła naturalne jak gwiazdy, rozgrzane ciała stałe, oraz

ź

ródła sztuczne z wyjątkiem laserów, stanowi zawsze strumień fotonów poruszających

się niezależnie od siebie. Fazy, częstotliwość, kierunki rozchodzenia się i kierunki
polaryzacji poszczególnych fotonów są przypadkowe i zupełnie niezależne od tych
parametrów charakteryzujących inne fotony. Światło takie nazywa się światłem
niespójnym. Jednakże światło jest falą i jako fala pozwala na obserwację zjawiska
interferencji, chociaż interferencja dwóch niespójnych wiązek światła jest niemożliwa.
Interferować mogą jedynie fale spójne.

Jedynym źródłem światła dającym światło spójne nawet o bardzo dużym

natężeniu jest laser. Aby zrozumieć zasadę działania lasera trzeba poznać podstawowe
zjawiska dotyczące emisji i absorpcji światła przez atomy.

Absorpcja fotonu padającego na atom

W wyniku pochłonięcia energii niesionej przez foton jeden z elektronów w atomie

może przeskoczyć na wyższy poziom energetyczny. Atom przechodzi z niższego stanu
energetycznego

1

E

do wyższego

2

E

. Warunkiem zajścia tego zjawiska jest, aby

energia fotonu była odpowiednio „dopasowana” do układu poziomów energetycznych
atomu tzn.:

1

2

E

E

f

h

−

=

gdzie: h – stała Plancka (

s

J

10

626

,

6

34

⋅

⋅

=

−

h

),

f – częstotliwość fali świetlnej.
Zjawisko to można przedstawić schematycznie w następujący sposób:

atom
w stanie

E

1

atom
w stanie

E >E

2

1

h f

Emisja spontaniczna

Atom wzbudzony po pewnym czasie (od

s

10

~

8

−

do

s

10

3

−

) emituje foton

hf

:

h f

Emisja wymuszona

Jeśli na atom wzbudzony padnie foton spełniający warunek energetyczny

zasygnalizowany w punkcie 1, to może zainicjować emisję fotonu przez atom:

2

h f

h f

h f

Dwa fotony, które poruszają się dalej w wyniku tego zjawiska, posiadają taką

samą fazę, częstotliwość, kierunek propagacji i polaryzację. Fotony takie będą
stanowiły wiązkę światła spójnego. Wiązka światła będzie miała tym większe natężenie
im więcej takich fotonów uda się uzyskać.

Mechanizm działania lasera

W zbiorze atomów będących w równowadze termodynamicznej ilość atomów w

wyższym stanie energetycznym jest zawsze mniejsza od ilości atomów w niższym
stanie energetycznym. Prawidłowość tę wyraża rozkład Boltzmana:

kT

E

E

e

N

N

1

2

1

2

−

−

=

gdzie:

2

N

- ilość atomów wzbudzonych do poziomu energetycznego

2

E

,

1

N

- ilość atomów w stanie energetycznym

1

E

.

Jak łatwo zauważyć jeżeli

1

2

E

E

>

, to

1

2

N

N

<

.

Zbiór

atomów

w

równowadze termodynamicznej

można

przedstawić

schematycznie w poniższy sposób:

zbiór atomów
w równowadze
termodynamicznej

Jeżeli na taki zbiór atomów padnie wiązka światła składająca się z fotonów o

energii:

1

2

E

E

hf

−

=

to

prawdopodobieństwo

zajścia

emisji

wymuszonej

będzie

mniejsze

od

prawdopodobieństwa zajścia absorpcji. Część atomów wzbudzonych może także
wyemitować foton w wyniku emisji spontanicznej.

Wiązka światła została osłabiona.
Istnieje możliwość wytworzenia takiego zbioru atomów, w którym ilość atomów

w wyższym stanie energetycznym jest większa od ilości atomów w niższym stanie.
Proces prowadzący do uzyskania takiej sytuacji nazywa się pompowaniem optycznym.
Istnieje wiele metod pompowania optycznego, a każda z nich jest dopasowana do
rodzaju atomów lub cząsteczek.

Zbiór atomów, w którym większość stanowią atomy w wyższym stanie

energetycznym nazywa się zbiorem antyboltzmanowskim lub układem wykazującym
inwersję obsadzeń. W wyniku omówionych wcześniej procesów zbiór taki powróciłby

3

w krótkim czasie do stanu równowagi termodynamicznej, jednakże odpowiednie
intensywne pompowanie optyczne pozwala utrzymywać stan inwersji obsadzeń przez
długi czas. W zbiorze takim możliwe jest zainicjowanie przebiegającego lawinowo
zjawiska emisji wymuszonej (akcja laserowa). W wyniku tego zjawiska uzyskamy
impuls światła spójnego. Urządzenie, w którym zostało wykorzystane to zjawisko
nazywa się laserem impulsowym. Słowo laser jest skrótem angielskiej nazwy tego
urządzenia. Nazwa ta w dowolnym tłumaczeniu na język polski brzmi: wzmacniacz
ś

wiatła wykorzystujący zjawisko wymuszonej emisji promieniowania.

Jeżeli układ atomów umieścimy pomiędzy dwoma zwierciadłami, z których jedno

będzie częściowo przepuszczalne, zaś pompowanie optyczne będziemy przeprowadzali
w sposób ciągły, to uzyskamy laser o działaniu ciągłym. Część wiązki odbijając się
wielokrotnie od zwierciadeł i przechodząc przez układ atomów będzie stanowiła
czynnik inicjujący akcję laserową.

Ponieważ jak wspomniano wyżej fotony wymuszający i wymuszony są

identyczne,

zatem

ś

wiatło

lasera

będzie

charakteryzować

się

spójnością,

monochromatycznością, a w przypadku stosowania zwierciadeł płaskich wiązka światła
będzie wiązką równoległą.

Lasery są najlepszym źródłem światła do badania i wykorzystania zjawiska

interferencji. Przyrządy służące do badania tego zjawiska nazywają się
interferometrami.

III. Wykonanie ćwiczenia

Ć

wiczenie polega na obserwacji prążków interferencyjnych na ekranie.

Zmieniając położenie jednego ze zwierciadeł w interferometrze możemy zamieniać fazę
jednej z wiązek światła biorących udział w interferencji.

Zmiana centralnego prążka na ekranie z ciemnego poprzez jasny do ciemnego

oznacza, że zwierciadło przesunęło się o połowę długości fali. Zwierciadło jest
poruszane za pomocą układu dźwigniowego. Na końcu dźwigni znajduje się czujnik
przesunięcia mierzący z dokładnością 0.01 mm. Układ dźwigniowy jest skonstruowany
w taki sposób, że wskazanie miernika wynoszące „x” odpowiada przesunięciu
zwierciadła o odcinek „0,05x”.

1.

Wyjustować interferometr:

-

zdjąć oprawkę z soczewką z lasera,

-

wykorzystując jako ekran odległą ścianę doprowadzić do pokrycia się obu
plamek świetlnych, oznacza to, że promienie biegnące w kierunku ekranu
biegną równolegle.

2.

Założyć oprawkę z soczewką na laser.

3.

Ustawić ekran (np. kartka papieru) w odległości ok. 30 - 50 cm od interferometru.

4.

Wyznaczyć ilość kolejnych wygaszeń się prążka centralnego odpowiadających
przesunięciu końca dźwigni (wskazanie miernika), np. o x = 0,30 mm. Pomiar
powtórzyć 50 razy dla tego samego „x”. Pomiary powinny być wykonywane przez
obu ćwiczących.

5.

Długość fali można obliczyć ze wzoru:

ś

r

n

x

05

.

0

2

⋅

=

λ

gdzie

x – przesunięcie końca dzwigni,

ś

r

n

- ilość wygaszeń prążka ciemnego.

4

Tabela pomiarowa

x

n

i

r

ś

n

i

r

ś

i

n

n

−

=

α

λ

∆λ

[mm]

[ - ]

[ - ]

[ - ]

[

µ

m]

[

µ

m]

i

n

- ilość wygaszeń prążka ciemnego,

r

ś

n

,

i

α

zaokrąglić do liczby całkowitej.

6.

Opracować wyniki pod względem statystycznym.
a)

Obliczyć błąd średni kwadratowy.

50

50

1

2

∑

=

=

i

i

m

α

b)

Obliczyć wskaźnik dokładności.

2

1

m

h

=

c)

Pogrupować błędy i obliczyć prawdopodobieństwo wystąpienia danego błędu

)

(

α

f

=ilość przypadków

⁄

50.

α

Ilość przypadków

)

(

α

f

0
1
2
itd.

d)

Otrzymane prawdopodobieństwa

)

(

α

f

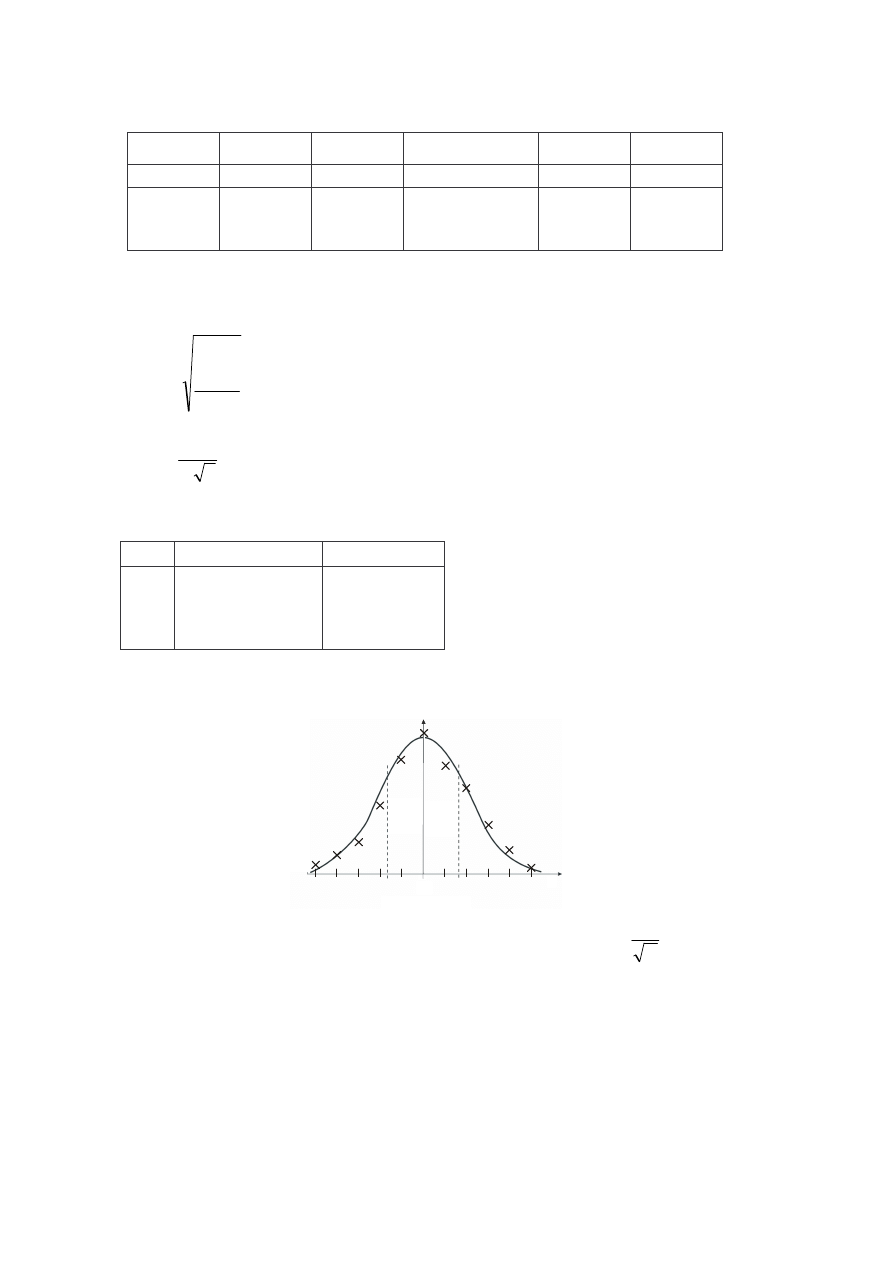
zaznaczyć na wykresie

Przykład

α

α

f( )

-4

-5

-3

-2

-1

1

2

3

4

5

0

e)

Dla poszczególnych

α

obliczyć wartość funkcji Gaussa

2

2

)

(

α

π

α

h

e

h

f

−

=

.

Linią ciągłą narysować na wykresie funkcję Gaussa.

Literatura

M. Leśniak, Fizyka. Laboratorium, wydanie II, Oficyna Wydawnicza PRz, 2002
S. Szczeniowski, Fizyka doświadczalna, PWN, Warszawa 1980