1

WŁAŚCIWOŚCI MECHANICZNE GRUNTÓW.

WŁAŚCIWOŚCI MECHANICZNE GRUNTÓW.

WYTRZYMAŁOŚĆ GRUNTÓW NA ŚCINANIE

WYTRZYMAŁOŚĆ GRUNTÓW NA ŚCINANIE

MECHANIKA GRUNTÓW I FUNDAMENTOWANIE

MECHANIKA GRUNTÓW I FUNDAMENTOWANIE

Budownictwo              semestr 4

Budownictwo              semestr 4

2

Mechanizm utraty wytrzymałości w odniesieniu do gruntów jest inny niż w przy-
padku  ośrodków  stałych  typu  metal  czy  skała,  które  są  zdolne  do  przeniesienia 
znacznych naprężeń ściskających, czy rozciągających. Wytrzymałość gruntów na 
ś

ciskanie w porównaniu z nimi jest nieznaczna, zaś wytrzymałość na rozciąganie 

w gruntach praktycznie nie istnieje. 

Analiza  sytuacji,  w  których  doszło  do  naruszenia  stateczności  posadowienia 
obiektu  lub  np.  wystąpienia  osuwiska  mas  gruntowych  dowodzi,  że  zawsze 
można  w  takich  przypadkach  zaobserwować  przemieszczenie  (poślizg)  pewnej 
części podłoża gruntowego względem pozostałej części. Oznacza to, że wskutek 
oddziaływania  zewnętrznego,  np.  obiektu  budowlanego  (jego  obciążenia), 
nastąpiło na pewnej powierzchni wewnątrz masywu gruntowego osiągnięcie sta-
nu, w którym naprężenie styczne do takiej powierzchni jest równe wytrzymałości 
gruntu  na  ścinanie.  Dominujące  znaczenie  dla  gruntów  posiada  zatem 

wytrzymałość na ścinanie

. 

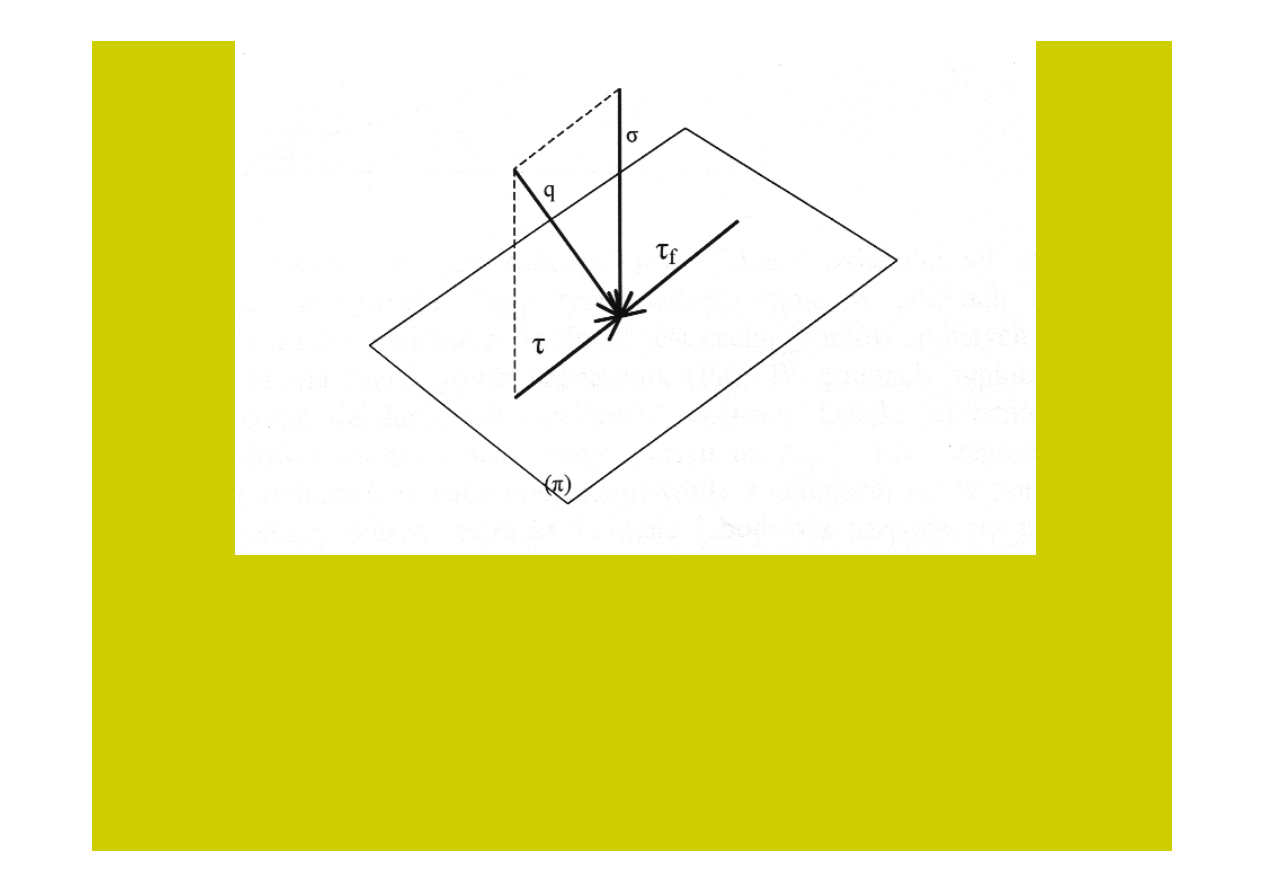
Można  powiedzieć,  że  ścinanie  w  gruncie  polega  na  przesunięciu  (prze-
mieszczeniu)  jednej  części  ośrodka  gruntowego  względem  pozostałej  w  wyniku 
przekroczenia  oporu  gruntu  na  ścinanie  (wytrzymałości  gruntu  na  ścinanie  -

ττττ

f

) 

przez składową styczną (ścinającą) działającego naprężenia -

ττττ

f

ττττ

ττττ ≥

3

Jeżeli 

ττττ

= 

ττττ

f

, to występuje 

stan graniczny ścinania

w gruncie, a gdy 

ττττ

< 

ττττ

f

, to mamy 

do  czynienia  ze 

stanem  równowagi  sprężystej

w  gruncie.  Opór  gruntu 

ττττ

f

działa  w 

tej samej płaszczyźnie  co składowa ścinająca 

ττττ

, lecz ma zwrot przeciwny.

Wytrzymałością  gruntu  na  ścinanie

ττττ

f

nazywa  się  największy  (graniczny)  opór, 

jaki stawia grunt składowym stycznym (ścinającym) naprężenia, w rozpatrywanym 
punkcie ośrodka gruntowego.

Rys. 1

4

Znajomość  wytrzymałości  gruntu  na  ścinanie  jest  nieodzowna  przy  rozpatrywa-
niu zagadnień  związanych  z  bezpiecznym  (czyli  w  zakresie  równowagi 
quasisprężystej)  posadawianiem  obiektów  budowlanych,  formowaniu  zboczy 
gruntowych  (np.  w  nasypach  drogowych  czy  kolejowych)  o  bezpiecznym 
nachyleniu itp. Zagadnienie to zostało sformułowane przez Ch. Coulomba, który –
będąc  inżynierem  wojskowym  zajmującym  się  budową  fortyfikacji  – jako 
pierwszy  podał  wzór  ujmujący  wytrzymałość  gruntu  sypkiego  na  ścinanie  (1773 
r.). Wychodząc z zależności dotyczącej tarcia pomiędzy dwoma ciałami stałymi –
T = N ·

µ

- zapisał ją w odniesieniu do tarcia zachodzącego wewnątrz gruntu:·

Φ

⋅

=

tg

f

σσσσ

ττττ

gdzie:  

σσσσ

- składowa normalna działającego naprężenia, 

Φ

Φ

Φ

Φ

- kąt tarcia wewnętrz-

nego, tg

Φ

Φ

Φ

Φ

– współczynnik tarcia wewnętrznego

.

Równanie to zostało później uogólnione również na grunty spoiste w postaci:

c

tg

f

+

Φ

⋅

= σσσσ

ττττ

gdzie: 

c  – spójność  (kohezja)

, czyli  opór  gruntu  stawiany  siłom  zewnętrznym, 

wywołany  wzajemnym  przyciąganiem  cząstek  gruntu.  Dla 

σσσσ

=  0  mamy 

ττττ

f

=  c,  a 

więc  spójność  jest  to  wytrzymałość  gruntu  na  ścinanie  przy  braku  naprężeń 
normalnych.

5

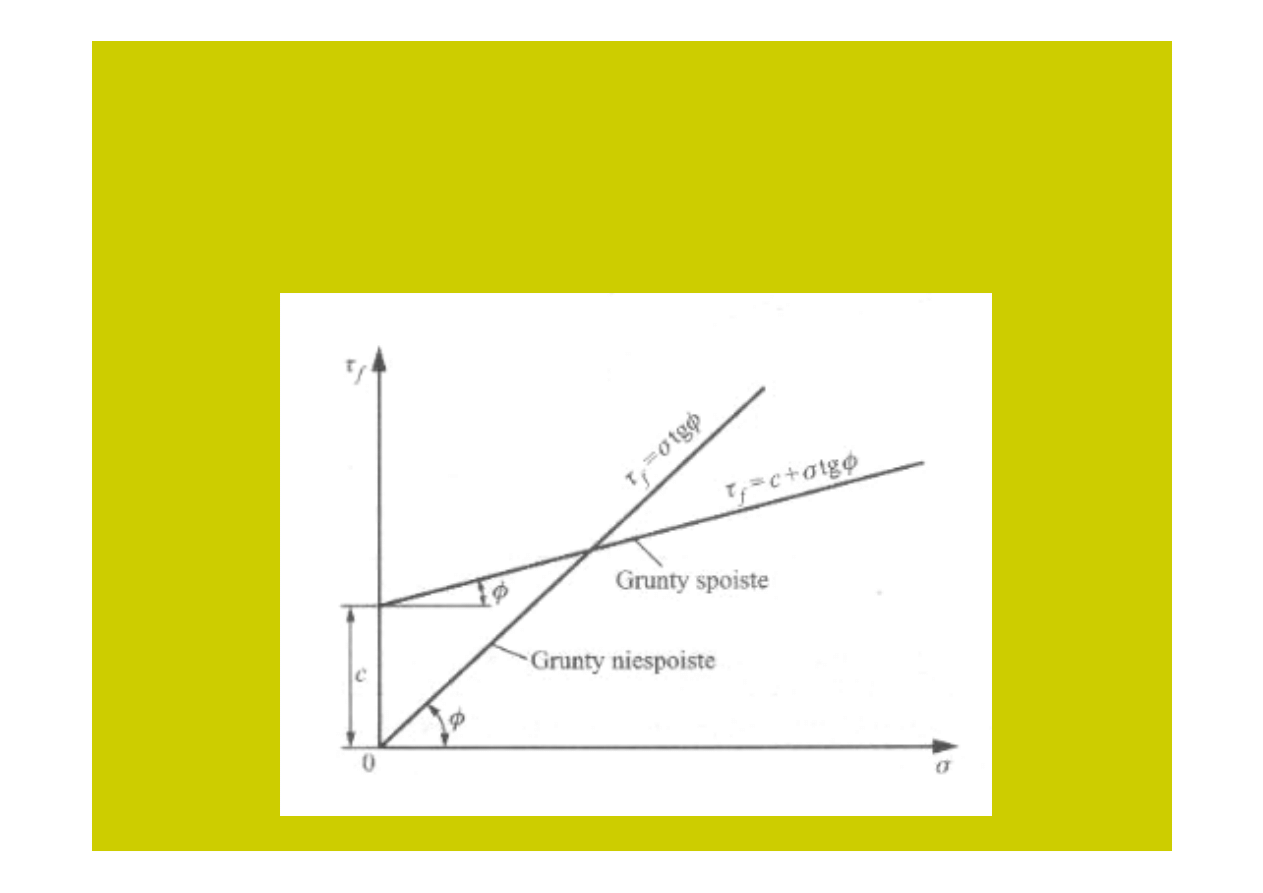
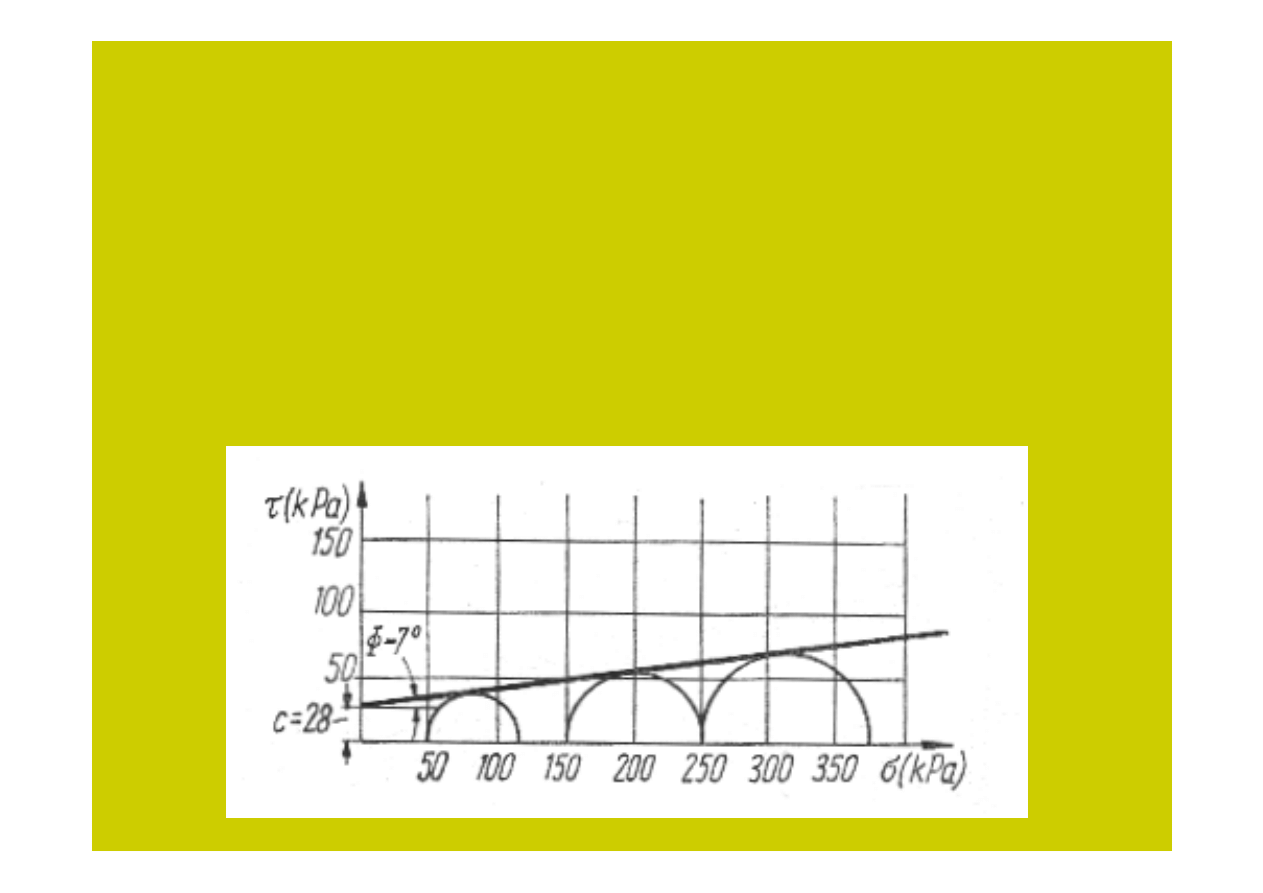
Obrazem  graficznym  równania  Coulomba  jest  linia  prosta  przechodząca  przez 
początek układu współrzędnych 

ττττ

-

σσσσ

dla gruntów sypkich i przecinająca oś

ττττ

na 

rzędnej 

ττττ

= c  w przypadku gruntów spoistych. Prosta Coulomba stanowi zatem 

zbiór  punktów  spełniających  warunek  stanu  granicznego 

ττττ

= 

ττττ

f

.  Nachylenie 

prostej do poziomu wyznacza wartość kąta tarcia wewnętrznego 

Φ

Φ

Φ

Φ

:

Rys. 2

6

Opór ścinania 

ττττ

f

składa się z dwu składowych: oporu tarcia wewnętrznego i oporu 

spójności.  W  przypadku  ścinania  gruntów  o  strukturze  ziarnistej  mamy  do 
czynienia  z  oporem  tarcia  posuwistego  oraz  z  oporem  tarcia  obrotowego  na 
kontaktach  ziaren.  Występuje  tam  również  opór  związany  z  wzajemnym 
zazębianiem  się  ziaren,  a  także  z  ich  wielkością  i  stopniem  obtoczenia.  Opór 
spójności  zależy  w  największej  mierze  od  zawartości  cząstek  frakcji  iłowej  i 
występujących pomiędzy nimi sił molekularnych.

Oba parametry: 

Φ

Φ

Φ

Φ

oraz 

c

charakteryzują więc wytrzymałość gruntów na ścinanie i 

w  związku  z  tym  zachodzi  konieczność oznaczania  ich  wartości.  Są to 
podstawowe  parametry  wytrzymałościowe  gruntów.  W  warunkach  laborato-
ryjnych wykorzystuje się do ich oznaczenia dwa rodzaje przyrządów:

-

aparat bezpośredniego ścinania (skrzynkowy),

- aparat trójosiowego ściskania.

Do  przeprowadzenia  oznaczenia  niezbędna  jest  próbka  o  naturalnej  strukturze  –
NNS.  Ponieważ uzyskanie  takiej  próbki  dla  gruntów  sypkich  jest  utrudnione, 
badanie  wykonuje  się wtedy  na  próbce  o  naruszonej  strukturze,  która  w  samym 
aparacie  jest  zagęszczona  do  stopnia  zagęszczenia  zbliżonego  do  wartości 
naturalnej.

7

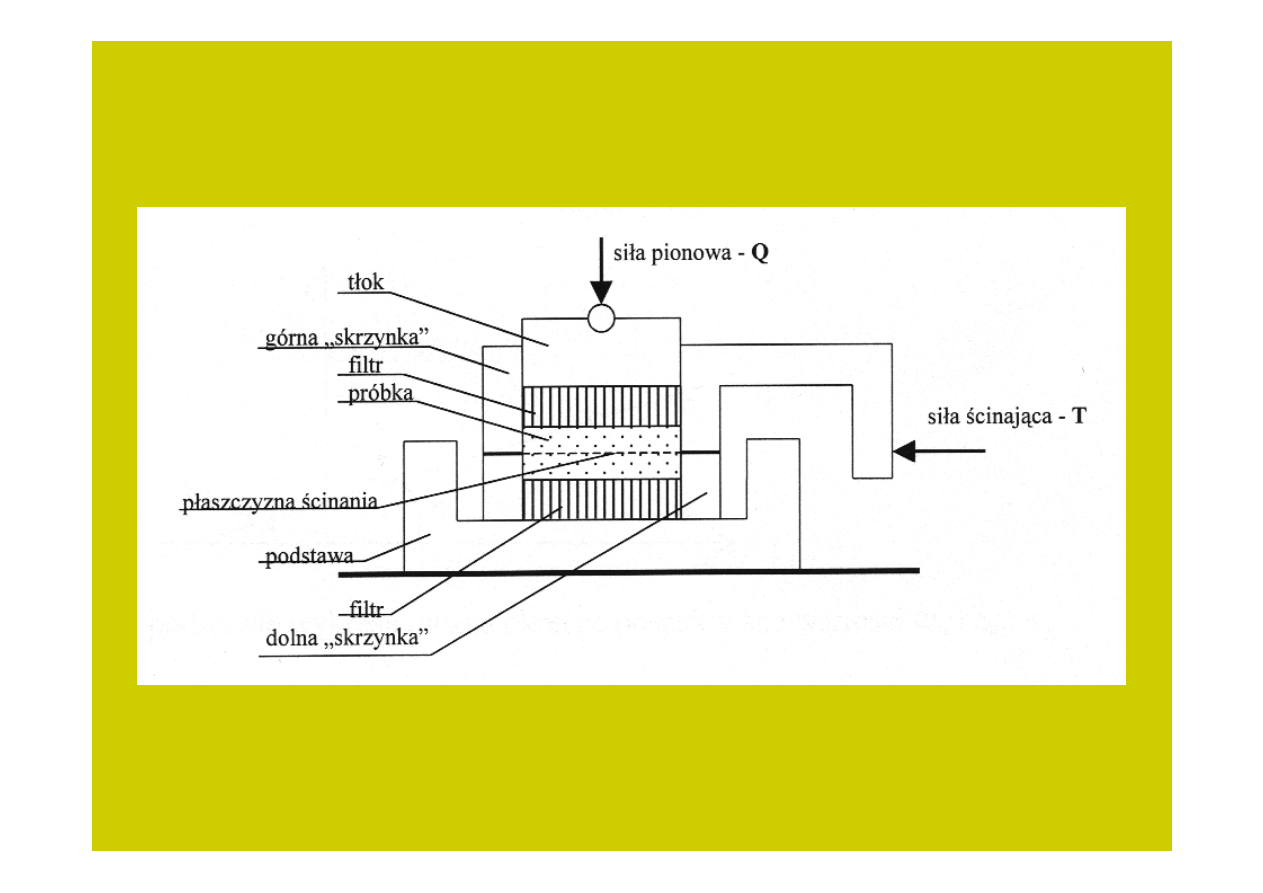
Aparat bezpośredniego ścinania

Rys. 3

8

W 

aparacie  bezpośredniego

ś

cinania próbka  gruntu  znajduje  się  wewnątrz 

dwudzielnej  skrzynki  o  przekroju  kwadratowym.  Wymienne  skrzynki  mają 
długość boku próbki od 6,0 cm do 12,0 cm (im grubsze uziarnienie gruntu – tym 
większa  skrzynka),  zaś  wysokość  próbki  1,5  – 2,5  cm.  Płaszczyzna  podziału 
skrzynki  na  część  górną  – ruchomą  i  dolną  – nieruchomą,  przebiega  w  połowie 
wysokości  próbki.  Górna  i  dolna  powierzchnia  próbki  ma  kontakt  z płytkami 
filtracyjnymi  umożliwiającymi  swobodny  odpływ  wody  z  próbki  pod 
obciążeniem.  Na  próbkę,  za  pośrednictwem  tłoka,  można  przykładać obciążenie 
siłą  pionową,  która  w  trakcie  badania  jest  niezmienna,  zaś  do  górnej  części 
skrzynki przykłada się obciążenie siłą poziomą. Zamocowane czujniki pozwalają 
na  dokonanie  pomiaru  wzajemnego  przemieszczenia  obu  części  skrzynki  jak  i 
zmian  wysokości  próbki  w  trakcie  badania.  Po  umieszczeniu  próbki w  aparacie 
poddaje się ją wstępnej konsolidacji naciskiem siłą pionową, która działa również 
na próbkę podczas ścinania dając naprężenie pionowe -

σσσσ

. Następnie poddaje się 

próbkę  ścinaniu  poprzez  przyłożenie  zwiększającej  się  siły  poziomej.  Moment 
ś

cięcia objawia się ustaniem przyrostu (a nawet lekkim cofnięciem) odczytów na 

czujniku dynamometru do pomiaru siły poziomej. Ustala się największą wartość 
siły w momencie ścięcia  -

T

max

oraz  wzajemne  przesunięcie skrzynek  aparatu -

∆∆∆∆

a

. Na tej podstawie oblicza się pole przekroju ścięcia próbki:

)

a

a

(

a

F

s

∆

−

⋅

=

9

Wartości  naprężeń: 

stycznego

w  chwili  ścięcia  (wytrzymałości  na  ścinanie)  i 

normalnego

oblicza się ze wzorów:

s

i

max

fi

F

T

====

ττττ

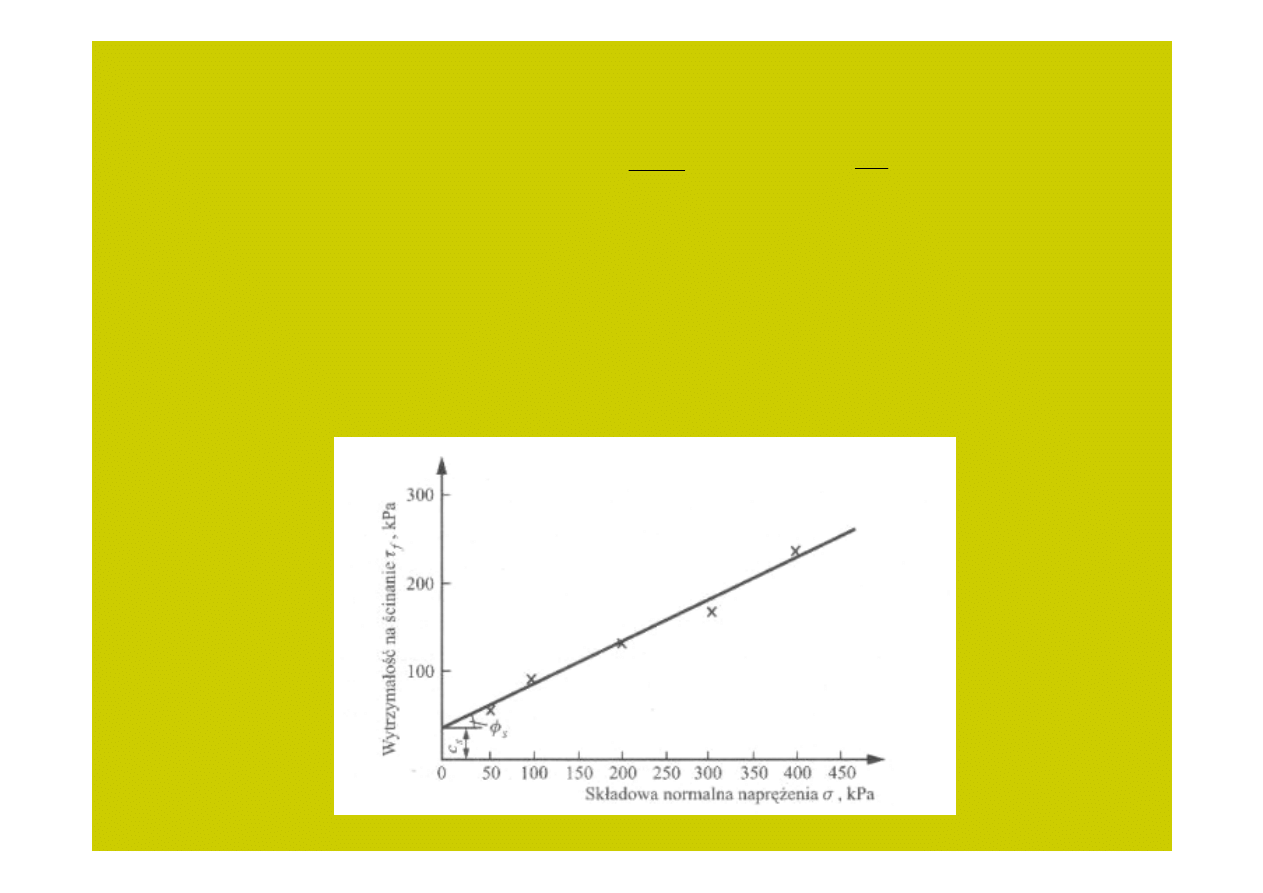
Mając 

σσσσ

i

oraz

ττττ

fi

uzyskuje  się  jeden  punkt  wykresu 

σσσσ

-

ττττ

.  Wykonując kolejne 

próby (N 

≥

5), przy różnych wartościach naprężenia pionowego 

σσσσ

działającego na 

próbki  dysponujemy  zbiorem  punktów,  które  następnie  aproksymujemy  linią
prostą graficznie, lub - dla uzyskania większej dokładności - analitycznie metodą
najmniejszych kwadratów.  Pozwala  to  na  wyznaczenie  kąta  tarcia  wewnętrznego 
oraz spójności.

Rys. 4

s

i

i

F

Q

====

σσσσ

10

Wzory na obliczenie kąta tarcia wewnętrznego i spójności w metodzie najmniej-
szych kwadratów są następujące:

∑

∑

−

∑

∑

∑

∑

−

=

∑

∑

−

∑

∑

∑

−

=

2

2

2

2

2

)

(

)

(

N

)

(

c

)

(

)

(

N

N

ctg

ar

i

i

fi

i

i

fi

i

i

i

fi

i

fi

i

σσσσ

σσσσ

ττττ

σσσσ

σσσσ

ττττ

σσσσ

σσσσ

σσσσ

ττττ

σσσσ

ττττ

σσσσ

Φ

Φ

Φ

Φ

Ś

rednie odchylenia kwadratowe (błędy oznaczenia) kąta tarcia wewnętrznego i 

spójności oblicza się ze wzorów:

2

1

2

2

1

2

2

2

2

2

1

2

2

2

2

2

180











∑

⋅













∑

∑

−

∑

⋅

−

=

⋅













∑

∑

−

∑

⋅

−

=

N

)

(

)

(

)

(

N

N

N

s

cos

)

(

)

(

N

N

N

s

i

i

i

i

c

i

i

i

σσσσ

σσσσ

σσσσ

∆∆∆∆

Φ

Φ

Φ

Φ

σσσσ

σσσσ

∆∆∆∆

ππππ

Φ

Φ

Φ

Φ

o

gdzie: 

σσσσ

i

- naprężenia  normalne  w  poszczególnych  próbkach, 

ττττ

fi

- wytrzymałość  na 

ś

cinanie  poszczególnych  próbek, 

∆∆∆∆

i

- różnice  oznaczonych  i  obliczonych  wartości 

wytrzymałości na ścinanie:

c

tg

i

fi

i

−

−

=

Φ

Φ

Φ

Φ

σσσσ

ττττ

∆∆∆∆

11

Przy  badaniu  w  aparacie  bezpośredniego  ścinania  nie  ma  możliwości  dokonania 
pomiaru bardzo ważnego parametru, jakim jest wartość ciśnienia wody w porach 
gruntu podczas ścinania. Wady tej nie ma 

aparat trójosiowego ściskania

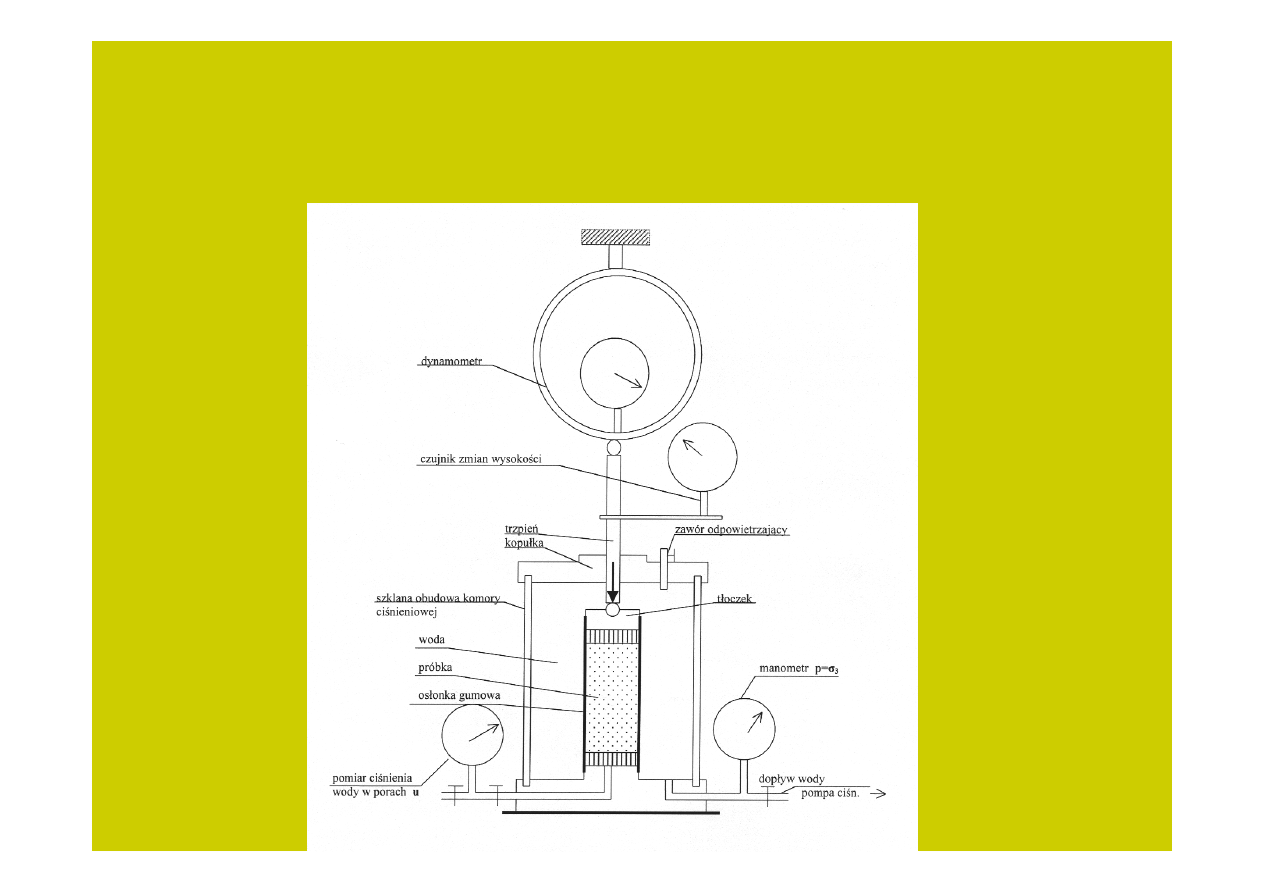
Rys. 5

12

Próbka  gruntu  w  aparacie  trójosiowego  ściskania  ma  kształt  walca o  średnicy 
najczęściej 38 mm i wysokości 76 mm. Jest ona otoczona cienką gumową osłonką i 
znajduje się wewnątrz komory ciśnieniowej, ustawiona na perforowanej podstawie, 
z  góry  przykryta  tłoczkiem  z  perforacją.  Zadaniem  filtrów  dolnego  i  górnego  jest 
odprowadzenie wody z próbki w trakcie badania. Osłonka jest szczelnie połączona 
z  podstawą  i  tłoczkiem  tak,  że  próbka  jest  odizolowana  od  wnętrza  komory.  Do 
wnętrza  komory  doprowadzona  jest  woda  pod  ciśnieniem  -

p

,  które  jest  stałe 

podczas badania. Do górnego  tłoczka przylega trzpień,  za pośrednictwem  którego 
przykładane  jest  na  próbkę  obciążenie  siłą  pionową,  mierzoną  dynamometrem. 
Istnieje również możliwość pomiaru zmian wysokości próbki. Do podstawy próbki 
podłączony  jest  za  pośrednictwem  zaworu  układ  do  pomiaru  ciśnienia  wody  w 
porach gruntu. 

Po  zamocowaniu  próbki  wewnątrz  komory  i  uszczelnieniu  komory  przez 
dokręcenie do podstawy, napełnia się ją wodą pod określonym ciśnieniem. Zgodnie 
z  prawem  Pascala  ciśnienie  to  działa  we  wszystkich  kierunkach  jednakowo, 
obciąża więc powierzchnię boczną próbki i działa też na jej górną powierzchnię –
jest  to  etap 

konsolidacji  izotropowej

(wszechstronnego  ściskania)  próbki.  Po 

zakończeniu  konsolidacji  następuje  ścinanie  próbki  przez  zwiększenie  obciążenia 
pionowego za pośrednictwem trzpienia. Ścięcie objawia się ustaleniem największej 
wartości siły pionowej, odczytywanej na dynamometrze.

13

Ze  względu  na  cylindryczny  kształt  próbki  oraz  sposób  przyłożenia  na  nią 
obciążenia, w próbce panuje 

przestrzenny obrotowo-symetryczny stan naprężenia

. 

Ciśnienie wody,  stanowiące obciążenie próbki,  nie  wywołuje  na jej powierzchni 
naprężeń stycznych, a zatem normalne naprężenia poziome, równe co do wartości 
ciśnieniu wody w komorze aparatu są równocześnie 

naprężeniami głównymi

σσσσ

2

i

σσσσ

3

.  Są  one  sobie  równe.  Naprężenie  pionowe,  wywołane  obciążeniem  zew-

nętrznym,  jako  prostopadłe  do  naprężeń 

σσσσ

2

i

σσσσ

3

jest  również 

naprężeniem 

głównym

σσσσ

1

.  Zatem  stan  naprężenia  w  momencie  ścięcia  można  opisać 

następująco:             

σσσσ

2

=

σσσσ

3

= p

oraz

σσσσ

1

>

σσσσ

2 

= 

σσσσ

3

.

Naprężenie 

σσσσ

1

przy ścięciu jest równe:

σσσσ

1

= 

σσσσ

3

+Q

max

/ A

Ś

cięcie  zostało  zatem  spowodowane  przyrostem 

naprężeń

σσσσ

1

-

σσσσ

3

= Q

mqx

/ A

Ten przyrost nosi  nazwę 

dewiatora naprężenia

.

Rys. 6 - Schemat obciążenia (naprężenia)               
działającego na próbkę przy ścięciu

A - pole przekroju poprzecznego próbki                     
przy ścięciu

14

Do interpretacji wyników badania trójosiowego korzystamy z konstrukcji 

koła 

Mohra

, które w sposób graficzny przedstawia stan naprężenia w próbce gruntu 

w momencie osiągnięcia stanu granicznego - ścięcia próbki:

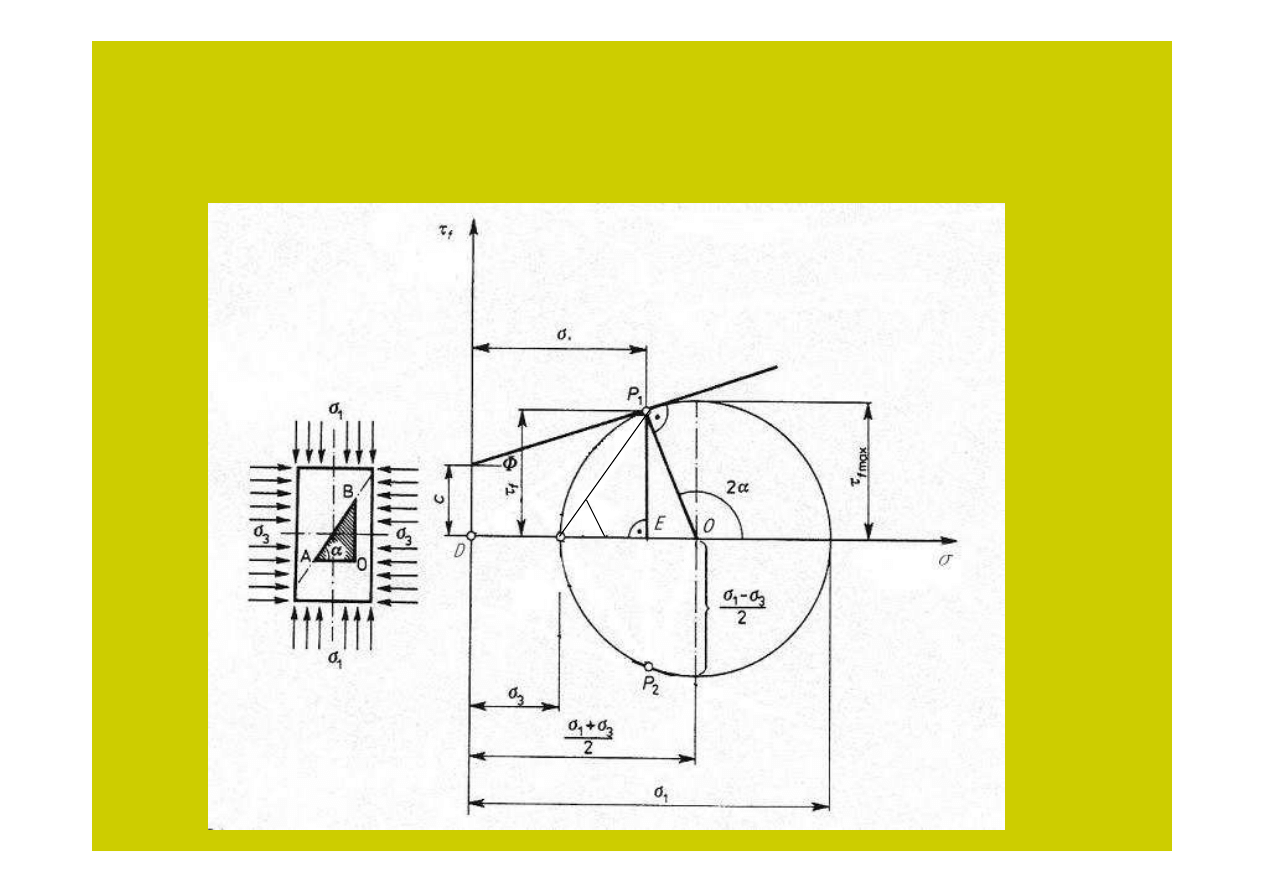
Rys. 7

F

AB || FP

1

α

15

Koło  Mohra  kreśli  się  na  podstawie  znanych  wartości  naprężeń  głównych 

σσσσ

1

i 

σσσσ

3

. Odległość środka  koła Mohra od początku układu współrzędnych wynosi:

Współrzędne punktu

P

1

na  kole Mohra przedstawiają  składowe naprężenia  (

σσσσ

;

ττττ

f

) 

jakie występują na płaszczyźnie ścięcia wewnątrz próbki, nachylonej pod kątem 

αααα

względem  kierunku  działania  mniejszego  z  naprężeń  głównych 

σσσσ

3

:  AB  ||  FP

1

. 

Punkt  P

1

przedstawia  więc  stan  naprężeń  granicznych.  Jak  wynika  z  rysunku  kąt 

EP

1

O jest równy 

Φ

Φ

Φ

Φ

. Wobec tego kąt 

2

αααα

:

2

3

1

σσσσ

σσσσ +

=

=

DO

a

Promień koła Mohra jest równy:

2

3

1

1

σσσσ

σσσσ −

=

=

OP

R

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

αααα

+

=

−

−

=

o

o

o

90

90

180

2

)

(

A zatem płaszczyzna AB jest nachylona do poziomu pod kątem: 

2

45

Φ

Φ

Φ

Φ

αααα

+

=

o

16

Dla  określenia  parametrów  wytrzymałościowych 

Φ

Φ

Φ

Φ

i 

c

niezbędne  jest  ścięcie 

kilku  próbek  tego  samego  gruntu  (N 

≥

5)  przy  różnych  wartościach  ciśnienia 

wody 

p=

σσσσ

3

w  komorze  aparatu.  Uzyskujemy  zatem  odpowiadającą  liczbie 

próbek liczbę kół Mohra. Wspólna styczna (obwiednia) do kół Mohra jest prostą 
daną  równaniem Coulomba,  gdyż  każdy  punkt  styczności  przedstawia  stan 
graniczny naprężeń występujący w danej próbce przy ścięciu. Równanie prostej 
(a  stąd  wartości 

Φ

Φ

Φ

Φ

i 

c

)  wyznacza  się  najczęściej  przez  aproksymację  wyników 

linią  prostą  przy  pomocy  metody  najmniejszych  kwadratów,  korzystając  ze 
wzorów  analogicznych  jak  przy  interpretacji  rezultatów  bezpośredniego 
ś

cinania

Rys. 8

17

Naprężenia efektywne. Efektywne parametry wytrzymałościowe

Omawiając  zjawisko  konsolidacji  zwróciliśmy  uwagę  na  rolę  wody  znajdującej 
się w porach gruntu przy przenoszeniu obciążeń. Wiąże się z tym bardzo ważne 
pojęcie  w  mechanice  gruntów  jakim  jest  pojęcie 

naprężenia  efektywnego

.  Otóż 

naprężenie  efektywne  jest  to  wartość  naprężenia 

normalnego

działającego  na 

szkielet  gruntowy.  Zasadę  naprężeń  efektywnych  w  gruntach  wprowadził  K. 
Terzaghi w postaci następującego wyrażenia

u

'

+

= σσσσ

σσσσ

gdzie: 

σσσσ

- wartość całkowitego naprężenia normalnego w rozpatrywanym punkcie 

ośrodka gruntowego, 

σσσσ

‘

- wartość naprężenia efektywnego,

u

- wartość ciśnienia 

wody w porach gruntu.

Znając  zatem  oprócz  całkowitego  naprężenia  normalnego  w  gruncie, również 
wartość  ciśnienia  wody  w  porach  możemy  wyznaczyć  naprężenie  działające  na 
szkielet  gruntowy.  Woda  jest  czynnikiem  współdziałającym  ze  szkieletem  w 
przenoszeniu  obciążenia  tylko  w  początkowym  okresie  jego  działania.  Później 
następuje częściowy odpływ wody z porów,a w końcowym efekcie całe obciąże-
nie  przejmuje  szkielet.  Dlatego  tak  ważna  jest  znajomość  ciśnienia  wody  w 
porach możliwa do realizacji w aparacie trójosiowego ściskania.

18

Wartość  naprężenia  efektywnego  można  wyznaczyć  z  przekształcenia
powyższego wzoru:

u

'

−

= σσσσ

σσσσ

Jeżeli  podstawimy  teraz  do  wzoru  Coulomba  naprężenie  efektywne 
otrzymamy:

'

c

'

tg

)

u

(

'

c

'

tg

'

f

+

−

=

+

=

Φ

Φ

Φ

Φ

σσσσ

Φ

Φ

Φ

Φ

σσσσ

ττττ

Występujące  w  tym  wzorze  parametry 

Φ

Φ

Φ

Φ

’

i 

c’

noszą  nazwę 

efektywnych 

wartości kąta tarcia wewnętrznego i spójności. 

Jak zauważyliśmy wcześniej, w 

aparacie  trójosiowego  ściskania  istnieje  możliwość  pomiaru  ciśnienia  wody  w 
porach,  a  więc  oznaczenia  efektywnych  wartości 

Φ

Φ

Φ

Φ

’

i 

c’

.  Jak  przebiega 

inter-

pretacja wyników badania dla naprężeń efektywnych?

Współrzędna środka koła 

Mohra oraz jego promień dla naprężeń efektywnych będą równe :

R

)

(

,

)

u

u

(

,

)

'

'

(

,

'

R

u

a

u

)

(

,

)

u

(

,

)

u

u

(

,

)

'

'

(

,

'

a

=

−

⋅

=

=

+

−

−

⋅

=

−

⋅

=

−

=

−

+

⋅

=

−

+

⋅

=

=

−

+

−

⋅

=

+

⋅

=

3

1

3

1

3

1

3

1

3

1

3

1

3

1

5

0

5

0

5

0

5

0

2

5

0

5

0

5

0

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

σσσσ

gdzie a, R - współrzędna koła Mohra i jego promień dla naprężeń całkowitych

19

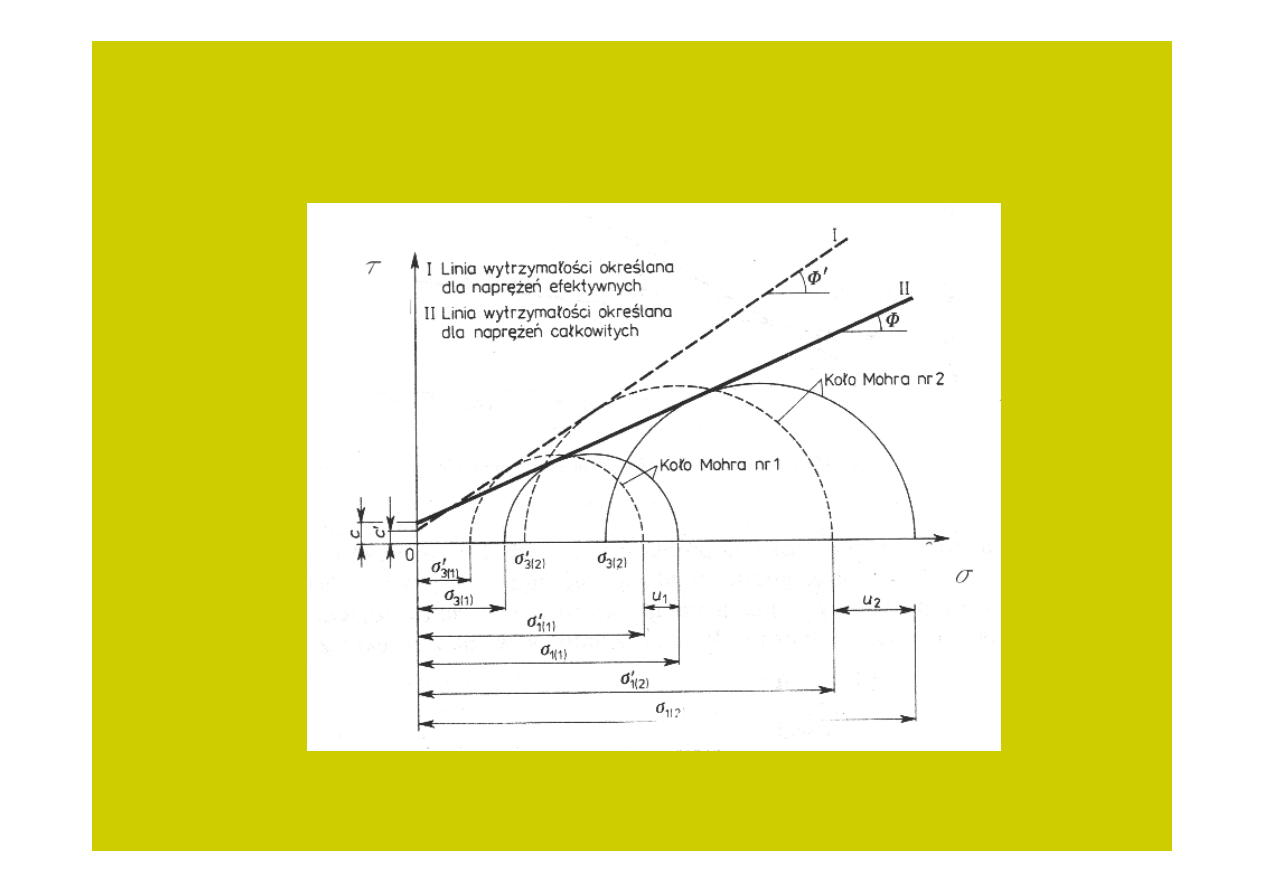
Jak widać z powyższych obliczeń koło Mohra w naprężeniach efektywnych ma 

taki  sam  promień

jak  koło  w  naprężeniach  całkowitych,  zaś  jego  środek  jest 

przesunięty w kierunku początku układu współrzędnych

o wielkość 

u

:

Na wykresie widać, z porównania wartości, że : 

Φ

Φ

Φ

Φ

’ > 

Φ

Φ

Φ

Φ

oraz  

c’ < c

Rys. 9

20

Równanie Coulomba - Mohra

Rozpatrzmy zależności na kole Mohra - rysunek 7:

Φ

Φ

Φ

Φ

σσσσ

σσσσ

σσσσ

σσσσ

Φ

Φ

Φ

Φ

σσσσ

σσσσ

σσσσ

Φ

Φ

Φ

Φ

σσσσ

σσσσ

Φ

Φ

Φ

Φ

ττττ

σσσσ

σσσσ

Φ

Φ

Φ

Φ

sin

sin

R

EO

DO

DE

cos

cos

R

EP

R

OP

O

EP

f

⋅

−

−

+

=

⋅

−

+

=

−

=

=

⋅

−

=

⋅

=

=

−

=

=

=

∀

2

2

2

2

2

3

1

3

1

3

1

3

1

1

3

1

1

1

Podstawmy wypisane powyżej wartości 

ττττ

f

i 

σσσσ

do wzoru Coulomba:

c

tg

f

+

⋅

=

Φ

Φ

Φ

Φ

σσσσ

ττττ

c

cos

sin

sin

cos

+

⋅













⋅

−

−

+

=

⋅

−

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

σσσσ

σσσσ

σσσσ

σσσσ

Φ

Φ

Φ

Φ

σσσσ

σσσσ

2

2

2

3

1

3

1

3

1

21

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

σσσσ

σσσσ

Φ

Φ

Φ

Φ

σσσσ

σσσσ

Φ

Φ

Φ

Φ

σσσσ

σσσσ

cos

c

sin

)

(

sin

)

(

cos

)

(

2

2

3

1

3

1

2

3

1

+

−

−

+

=

−

Po uporządkowaniu otrzymanego wyrażenia mamy:

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

σσσσ

σσσσ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

σσσσ

σσσσ

cos

c

sin

)

(

)

sin

)(cos

(

2

3

1

2

2

3

1

+

+

=

+

−

Czyli ostatecznie:

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

σσσσ

σσσσ

σσσσ

σσσσ

cos

c

sin

)

(

2

3

1

3

1

+

+

=

−

W  tej  postaci  równanie  obowiązuje  oczywiście  dla  gruntów  spoistych.  Dla 
gruntów sypkich (c = 0) będzie:

Φ

Φ

Φ

Φ

σσσσ

σσσσ

σσσσ

σσσσ

sin

)

(

3

1

3

1

+

=

−

Po wymnożeniu obu stron przez 

2 cos

Φ

Φ

Φ

Φ

otrzymamy:

Otrzymane  wyrażenia  noszą  nazwę 

równań  Coulomba-Mohra

,  gdyż  stanowią 

zapis prawa Coulomba z wykorzystaniem koncepcji koła naprężeń Mohra.