
7.
Elementy teorii chaosu deterministycznego
Str 265- 271
7.1 ____________________________________
Istota chaosu deterministycznego.
Chaos w układach zachowawczych i dyssypatywnych
W poprzednich rozdziałach zostały omówione przykłady oscylatorów, których
dynamiczne zachowanie było chaotyczne, tzn. wykazujące niemożliwą do przewidzenia
i zarazem niepowtarzalną nieregularność Zjawiska takie mogą być przejawem
chaosu deterministycznego, czyli zachowania praktycznie nieprzewidywalnego, w którym
jednak można dopatrywać się pewnego złożonego, ukrytego porządku, niezwykle— co
bardzo ważne — wrażliwego na warunki początkowe ewolucji układu. Matematycznym
obrazem chaosu deterministycznego jest takie właśnie zachowanie rozwiązań
(trajektorii) ściśle deterministycznych (czyli nie zawierających żadnych elementów
prawdopodobieństwa)
równań
opisujących
dynamikę
zachowania
układu.
Intensywne prace nad chaosem deterministycznym liczą sobie niewiele ponad
dwadzieścia lat — ale jest to już uznana dyscyplina naukowa [A3.1-A3.17, B7.1-
B7.32]. Pojecie chaosu deterministycznego jest bowiem niezmiernie ważne dla
zrozumienia wielu zjawisk przyrody nieożywionej i ożywionej, które tylko wydają się
całkowicie chaotyczne, a wiec podporządkowane wyłącznie prawom statystycznym.
Ponadto wśród teoretyków chaosu pojawia się pogląd, że prawie wszystkie układy
dynamiczne wykazują zachowanie chaotyczne dla odpowiedniego zespołu parametrów
stanu, a wiec teoria chaosu nie dotyczy zachowań wyjątkowych. Przeciwnie, z takiego
punktu widzenia, to układy wykazujące jedynie regularną dynamik? mogą stanowić
wyjątki. Inna sprawa, że uchwycenie parametrów odpowiadających chaotycznemu
zachowaniu może me być proste i dotyczyć bardzo wąskiego ich zakresu. Przed
przystąpieniem do dalszego opisu chaosu deterministycznego warto dokonać
podziału rozważanych układów na dyssypatywne i zachowawcze (czyli
konserwatywne, zwane są także hamiltonowskimi, ponieważ ich ewolucję opisują
klasyczne równania ruchu Hamiltona . O podziale tym była już mowa w p. 3.3, gdzie
model Lotki-Volterry byt zaklasyfikowany jako konserwatywny, w przeciwieństwie do
pozostałych, typowo dyssypatywnych modeli (np. modelu Lotki, Brukselatora czy
Oregonatora). Nie wdając się tutaj w szczegółowe rozważania, można powiedzieć
jedynie, że praktycznym przejawem zachowawczego charakteru układu jest nieistnienie
jakichkolwiek atraktorów (a więc pojedynczych stabilnych stanów stacjonarnych,
stabilnych cykli granicznych itp.), do których mogłyby zdążać trajektorie w przestrzeni
fazowej. Taka właśnie sytuacja miała miejsce w przypadku modelu Lotki-Volterry,
generującego niegasnące oscylacje, opisywane cyklicznymi, lecz niestabilnymi
trajektoriami. Dyssypatywny charakter układu przejawia się natomiast w istnieniu
różnego typu a traktorów, do których zdążają, trajektorie opisujące .ewolucję układu w
czasie. Istotne jest, że chaos deterministyczny może wystąpić w układach obu typów,
choć musi on być inaczej opisany.
Znanym układem zachowawczym, w którym przejawia, się chaos deterministyczny, jest
układ trzech ciał [A 1.5]. Trajektorie fazowe ich ruchu, opisywanego równaniami
klasycznej dynamiki, wykazują powyżej pewnej krytycznej wartości całkowitej energii
układu przebieg chaotyczny, co opisał H. Poincare. Nieprzewidywalność zachowania
zespołu trzech ciał jest znakomitym dowodem na to, że chaos deterministyczny
może wystąpić już w stosunkowo prostych układach o niewielu stopniach swobody, co
ma istotne znaczenie praktyczne, np. w zagadnieniu stabilności trajektorii planet w
Układzie Słonecznym. Omówiony tutaj układ zachowawczy klasyfikuje się tradycyjnie jako
należący do układów klasycznych — w odróżnieniu od kwantowych. Istnienie chaosu
deterministycznego w układach kwantowych jest obecnie przedmiotem intensywnych
badań, o czym będzie jeszcze mowa. Bardziej istotny jest jednak opis chaosu w układach
dyssypatywnych[ B7.321. Jednym z najprostszych takich układów jest tłumione wahadło
napędzane sinusoidalnie zmienna siłą [A3.l, A3.16]. Powyżej pewnej krytycznej wartości
amplitudy siły wymuszającej ruch wahadła zależność kąta wychylenia wahadła z
położenia równowagi od czasu staje się nieprzewidywalna, choć przecież — w
istocie — nie losowa. Chaotyczny może być także przebieg opisanego w p. 2.1.1 zjawiska
Benarda, polegającego na tworzeniu zespołów regularnych wirów (komórek)
konwekcyjnych w ogrzewanej cieczy. Dla odpowiednio dużej różnicy temperatur
między dolną i górną powierzchnią cieczy może pojawić się chaos, polegający na
zniesieniu owej regularności w obrazie zjawiska Benarda. O uproszczonym opisie tego
zjawiska będzie jeszcze mowa w następnych rozdziałach. Wreszcie, źródłami struktur dys-
sypatywnych są, jak wiadomo z poprzednich rozważań, wszystkie układy, w których
przebiegają chemiczne reakcje oscylacyjne. Przykłady ich chaotycznego przebiegu zostały
opisane w rozdz. 3 (układy modelowe), 4 i 6 (układy rzeczywiste).
7.2
_____________________________________________________________________
Przegląd dróg do chaosu w układach dyssypatywnych
Nie ulega wątpliwości, że zachowanie chaotyczne jest bardzo złożone. Okazuje się jednak,
że można zaproponować stosunkowo niewiele sposobów (scenariuszy) [A3.1, B7.1,
B7.32]
pojawiania się chaosu deterministycznego w układach zachowujących się uprzednio w
sposób uporządkowany (periodyczny). Najważniejsze są następujące
trzy
drogi do
chaosu
1. Scenariusz Ruelle'a-Takensa-Newhouse'a (RTN).
W uporządkowanym zachowaniu układu pojawiają się kolejne bifurkacje Hopfa,
polegające w najprostszym przypadku
(jak
wiadomo np. z p. 3.4) na przejściu od atraktora
punktowego do atraktora cyklicznego-— stabilnego cyklu granicznego. Można wykazać,
że już po trzech takich bifurkacjach istnieje duże prawdopodobieństwo pojawienia się

szczególnego, jakościowo nowego tworu odpowiedzialnego za istnienie chaosu
deterministycznego, tzw. dziwnego atraktora, który dokładniej zostanie omówiony niżej.
2. Scenariusz Feigenbauma. Zmiana wartości parametru kontrolnego powoduje (o czym
wspominano już kilkakrotnie w poprzednich rozdziałach) wystąpienie kolejnych bifurkacji,
polegających na podwajaniu się okresu regularnych oscylacji. Jest to tzw. kaskada
bifurkacji Feigenbauma. Powyżej pewnej krytycznej wartości owego parametru bifurkacje
te narastają lawinowo, prowadząc do chaosu
. Zagadnienia te będą szerzej omawiane w p. 7.6.
3. Scenariusz Pomeau-Manneville'a (PM). Polega on na pojawieniu się intermitencji, tj.
losowo występujących i narastających zakłóceń w zachowaniu periodycznym, co
prowadzi do chaosu.
Dla danego procesu może wystąpić więcej niż jeden scenariusz, np. kaskada Feigenbauma
może doprowadzić do chaosu, którego charakterystyka ukazuje intermitencje w miarę
dalszych zmian parametru kontrolnego. Możliwe są też inne, rzadziej spotykane
scenariusze, jak np. kryzysy, tj. nagłe jakościowe zmiany chaotycznej dynamiki układu
wynikające ze „zderzeń" między dziwnym atraktorem i współistniejącymi z nim
niestabilnymi stanami stacjonarnymi [A3.1]. Dla chemików ważne jest to, iż wszystkie te
scenariusze osiągania chaosu znaleziono w przebiegu rzeczywistych reakcji oscylacyjnych.
7.3
______________________________________________________________________
Odkrycie dziwnych atraktorów. Zjawiska Benarda i atraktor Lorenza
Pojęcie dziwnego atraktora jest jedną z najważniejszych koncepcji związanych z
przejawami chaosu deterministycznego w układach fizykochemicznych, której historia
wiąże się z pochodzącymi z lat 60. naszego wieku próbami
komputerowego prognozowania pogody prowadzonymi przez Edwarda N. Lorenza.
Zasadniczym elementem takiego numerycznego modelu jest opis stanu atmosfery
ziemskiej przez układ równań różniczkowych, opisujących ruchy konwekcyjne powietrzu
pod wpływem różnic temperatur. Najprostszy model takich procesów to tzw. układ
Lorenza, który stanowi uproszczony układ równań Benarda opisujący konwekcje cieczy
miedzy płytkami o różnicy temperatur ΔT, (p. 2.1.1) :
v jest proporcjonalne do szybkości cyrkulującej
między
poziomymi
płytkami
cieczy,
y
charakteryzuje
różnicę
temperatur
między
wznoszącymi się i opadającymi strumieniami
cieczy, z jest proporcjonalne do wielkości od-
chylenia pionowego profilu temperatury od
wartości
równowagowej,
bezwymiarowy
parametr 5 jest tzw. liczba Prandtla
21
,(
określa
stosunek szybkości cząsteczkowego przenoszenia pędu
w cieczy do szybkości przewodzenia w niej energii na
sposób ciepła, tak wiec <5 =
V
/
K
,
gdzie v — lepkość
kinematyczna.
K
— przewodnictwo cieplne cieczy).
r jest
również
bezwymiarowym
parametrem,
proporcjonalnym do tzw. liczby Rayleigha (proporcjonalnej z kolei do różnicy temperatur ΔT,
p. 2.1.1), zaś parametr b zdefiniowany jest relacją 4Π
2
/(Π
2
+k
2)
, gdzie k jest liczbą określającą
stosunek pionowego (h) do poziomego (h/k) rozmiaru komórki konwekcyjnej.
W swojej fundamentalnej pracy Deterministic Nonperiodic Flow, opublikowanej w 1962 r. w
czasopiśmie Journal of Atmospheric Sciences [B7.4], E. N. Lorenz wykazał, że dla pewnych
wartości parametrów (np. δ = 10, b = 8/3 i r = 28) przebieg rozwiązań .x(t), y (t) i z(t) jest
niezwykle czuły na drobną nawet zmianę ich wartości początkowych. Odkrycie tego
zjawiska związane było z istotnymi i nieoczekiwanymi trudnościami obliczeniowymi.
Próbując przewidzieć modelową pogodę, np. z dwutygodniowym wyprzedzeniem,
wprowadzano aktualne wyjściowe dane atmosferyczne (x
0
, y
0
i z
0
) i otrzymywano pewne
wyniki (prognozę pogody). W kilka dni później powtarzano obliczenia, wprowadzając
odpowiadające tym dniom dane początkowe. Oczekiwano zbliżonego wyniku końcowego
symulacji, a tymczasem otrzymywano zupełnie odmienne rezultaty (rys. 7.1) [A3.11]! Co
więcej, wprowadzanie praktycznie tych samych danych początkowych, z różną dokładno-
ścią na dalekich miejscach po przecinku, prowadziło także do zupełnie różnych wyników.
Okazało się, że ta nieprzewidywalność ma swoje przyczyny nie w błędach programu, ale
w uzyskiwanym, ze skończoną dokładnością obliczeń, numerycznym zachowaniu
rozwiązań układu Lorenza, wykazującym zdeterminowany przez te równania chaos, czyli
chaos deterministyczny. Zapewne pojawienie się owego chaosu w układzie Benarda-
Lorenza w pewnym stopniu tłumaczy znany nam dobrze fakt, iż prognozy pogody nie
należą do najlepiej sprawdzających się.
Rys. 7.1
Przykładowy przebieg rozwiązań
układu Lorenza (7.3.1) w czasie dla
dwóch nieznacznie różniących się
wartości początkowych, ilustrujący
zasadę powstawania chaosu
deterministycznego [A3. II); oś
odciętych — czas, oś rzędnych —
zmienna y układu (7.3.1)
Uogólniając dotychczasowe rozważania można stwierdzić, że eksperymentalne
obserwacje chaosu oraz próby modelowania takiego zachowania wykazały, iż istnieje
klasa zjawisk przyrodniczych, których nie można opisać dotychczas istniejącymi modelami
matematycznymi. W szczególności rozszerzeniu musiało ulec dotychczasowe pojęcie
atraktora. Pozostanie przy jego koncepcji —jako stabilnego stanu, czy zespołu stanów,
charakteryzującego się pewnym uporządkowaniem zachowania układu — uniemożliwia
jakiekolwiek przewidywania teoretyczne rozwoju sytuacji w układach, w których może
przejawić się chaos deterministyczny.
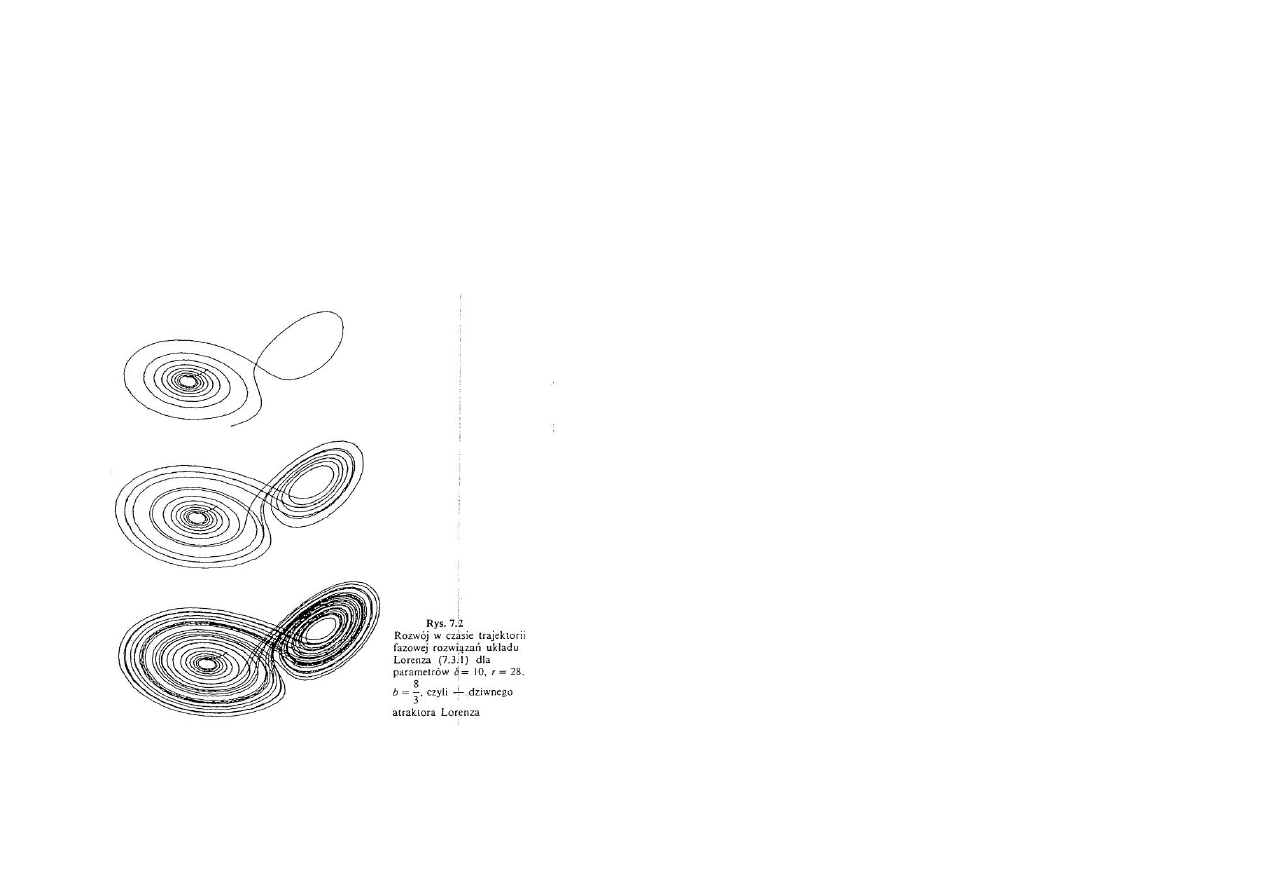
Dziwny atraktor Lorenza
Aby wprowadzić pojęcie dziwnego atraktora, należy rozważyć przebieg rozwiązań
układu Lorenza w postaci trajektorii w przestrzeni fazowej (x, y, z) dla takich wartości
parametrów, które zapewniają ich „chaotyczny" charakter. Taką typową trajektorię
dla trzech etapów ewolucji czasowej w postaci rzutu na płaszczyznę xy ilustruje rys. 7.2.
Pouczające jest obserwowanie rozwoju trajektorii układu Lorenza na bieżąco, w trakcie
symulacji. Lepiej niż powyższe statyczne rysunki uwidacznia to jej następujące
własności: 1) dążenie do ograniczonego obszaru przestrzeni fazowej i pozostawanie w
nim (a - więc tworzenie arraktora); 2) błądzący charakter ruchu po takiej trajektorii, tzn.
zakreślanie pętli w prawo, potem kilku pętli w lewo i znów w prawo, na przykład
dwukrotnie, po czym raz w lewo itd.; 3) wrażliwość trajektorii na nawet minimalne
zmiany warunków początkowych, co w pewnym stopniu
odpowiada opisanym wyżej kłopotom z ustaleniem właściwej prognozy pogody (ta
szczególna wrażliwość nadaje atraktorowi dziwny charakter). Słowem jest to dziwny
atraktor Lorenza. Warto przytoczyć prostą analogię sposobu tworzenia podobnej
trajektorii [B7.3]. Można wyobrazić sobie, iże wyrabiając ciasto dodajemy do niego w
pewnym momencie małą krople roztworu dowolnego barwnika. Wyrabianie ciasta polega
na rozciąganiu i ugniataniu nakładanych na siebie warstw, co powoduje powstawanie
fałd. Razem z rozciąganymi i fałdowanymi partiami ciasta wędrują cząsteczki barwnika,
przy czym — co ważne — drogi poszczególnych jego cząsteczek stopniowo coraz bardziej
się rozchodzą. Barwne pasemka rozchodzą się w całej objętości ciasta. To tak, jakby małe
różnice stanów początkowych cząsteczek ulegały wzmocnieniu do poziomu zjawisk
makro. W toku dalszego ugniatania oddalone cząsteczki mogą znów się do siebie zbliżyć,
a potem znowu rozejść, ale nigdy ich sytuacja nie powtórzy się.
Tak więc ogólnie dziwny atraktor oznacza skomplikowana i czują na warunki
początkowe trajektorię rozwijającą się w przestrzeni fazowej o wymiarze większym
od 2. Podlegające jej zachowanie układu ;ma charakter chaosu deterministycznego. Choć
przebieg rozwiązań układu Lorenza (7.3.1) jest istotnie nieprzewidywalny, to jednak nie
jest on — ściśle rzecz biorąc — losowy, jako że wyjściowy układ równań (7.3.1) nie
zawierał żadnych członów związanych z prawdopodobieństwem (stochastycznych). Jest
to zespół ściśle deterministycznych wyrażeń. Rozwiązanie tego układu równań dla
danego zestawu parametrów to także nie zespół, ale pojedyncza trajektoria fazowa, która
powinna z upływem czasu przejść przez każdy punkt atraktora.
Chaos a fluktuacje
Przedstawiając taki obraz powstawania chaosu deterministycznego, należy skomentować
istotną różnice w chaotycznym zachowaniu modelu matematycznego i realnego układu.
O ile bowiem modelowanie matematyczne pozwala na powtarzalne generowanie
przebiegu takich wrażliwych „chaotycznych" trajektorii, o tyle pojawienie się dziwnego
atraktora w realnym układzie fizykochemicznym może być źródłem dodatkowych
komplikacji. Układy rzeczywiste bowiem nieustannie „szumią", tj. parametry stanu ich
cząstek ulegają ciągłym fluktuacjom, co wobec niezwykłej czułości przebiegu trajektorii
dziwnego atraktora na wybór warunków początkowych może oznaczać niekontrolowane
osiąganie przez układ zupełnie różnych stanów, nawet mimo starań o zachowanie stałych
warunków początkowych (które— notabene – nigdy nie są idealnie powtarzalne). Można
powiedzieć, że dziwne atraktory działają wtedy jako swoiste wzmacniacze
mikroskopowych fluktuacji do poziomu makroskopowego. W rezultacie miedzy
przeszłością a przyszłością układu może przestać istnieć jakikolwiek uchwytny związek
przyczynowo-skutkowy. Wzmocnienie fluktuacji dobrze ilustruje zabawne pytanie
sformułowane przez samego Lorenza: „Czy trzepot skrzydeł motyla w Brazylii wywoła
tornado w Teksasie?" Problem ten znany jest w literaturze przedmiotu jako „efekt
motyla" [A3.11]. Taki obraz wpływu fluktuacji( lub ogólniej losowego szumu) komplikujący
zachowanie układu, podporządkowane dziwnemu atraktorowi, jest zapewne intuicyjnie
zrozumiały. Wydaje się jednak, że nie jest on jedynym możliwym. W p. 7.8 zostanie
omówiony przypadek, w którym - jak przynajmniej sugerują modelowe rozważania - w
pewnych sytuacjach szum może wywierać działanie paradoksalne, tj. porządkujące chaos
(w literaturze anglojęzycznej efekt ten nosi nazwę noise--induced order).

Na zakończenie tego rozdziału warto przypomnieć to, co sygnalizowano we wstępie do
rozważań o chaosie — że nie każde chaotyczne zachowanie wynika z istnienia dziwnego
atraktora. W układach niedyssypatywnych,' takich jak klasyczne (hamiltonowskie) układy
dynamiczne, chaotyczny przebieg trajektorii fazowych nie jest związany z istnieniem i
przyciągającym działaniem takiego obiektu.
Str 290 -298
7.7
_______________________________________
Miary chaosu deterministycznego
Żeby stwierdzić, czy konkretne zachowanie układu jest przejawem chaosu
deterministycznego, należy sformułować możliwie pewne jakościowe i ilościowe kryteria
jego istnienia, odnoszące się zarówno do modeli teoretycznych, jak i do wyników
pomiarów dla różnych układów rzeczywistych. Teoretyczna analiza układów równań
różniczkowych lub zależności iteracyjnych pod kątem badania istnienia dziwnego
atraktora nie jest prosta, ponieważ nie ma jak dotąd twierdzeń gwarantujących jego
istnienie. W związku z tym uznanie trajektorii układu Lorenza lub Rósslera za
dziwny atraktor też nie jest ściśle uzasadnione. Obrazowo mówiąc, przypisuje się im
właściwości atraktorowe, ponieważ nie znaleziono dotychczas żadnej sąsiadującej z nimi
trajektorii, która nie byłaby przez nie ściągana. Tak więc tylko numeryczne rozwiązanie
takiego zagadnienia (czyli tzw eksperyment numeryczny) i jego analiza pozwala na
uznanie konkretnego zachowania za przejaw chaosu deterministycznego. Jak już
wspomniano przy omawianiu chaosu w reakcji Biełousowa-Żabotyńskiego (p. 4.1), można
wskazać dwa najważniejsze problemy w takiej analizie: 1) ustalenie, czy obserwowana
aperiodyczność jest istotnie obrazem chaosu deterministycznego, a więc pewnej
złożonej, ale wewnętrznej, kinetycznej charakterystyki układu, czy odpowiedzią układu
na zewnętrzne, istotnie przypadkowe (losowe), a więc chaotyczne w klasycznym
rozumieniu, zmiany stanu otoczenia, 2) udowodnienie, że ewentualnie zaobserwowany
chaos deterministyczny nie jest w istocie złożonym zachowaniem periodycznym, ale o
bardzo długim okresie. Wniosek o wykryciu chaosu może wtedy wyniknąć ze zbyt
krótkiego czasu pomiaru, krótszego od długości pojedynczego okresu. Można
sformułować dynamiczne i statyczne kryteria kwalifikacji obserwowanych zjawisk jako
przejawów chaosu deterministycznego [A3.1, A3.12, B7.32, B7 15, B7 16]. Są to, odpo-
wiednio: wykładnik Lapunowa, będący ilościową miarą rozbiegania się trajektorii dla
początkowo niewiele różniących się stanów początkowych oraz wymiar Hausdorffa
(a także inne Koncepcje wymiaru), wskazujące na fraktalną naturę dziwnego atraktora.
7.7.1
______________________________________
Wykładnik Lapunowa. Chaos i hiperchaos
Charakterystyczną cechą chaosu deterministycznego (wynikającą z konstrukcji
dziwnych atraktorów) jest, jak wielokrotnie wspominano wyżej, bardzo silne
rozbieganie się trajektorii opisujących ewolucję układu w czasie, nawet dla bardzo
zbliżonych stanów początkowych .układu. Matematycznie można określić tę
rozbieżność jako wykładniczą, tzn. dającą się opisać zależnością proporcjonalną do
członu exp(λ), gdzie wielkość λ decyduje o stopniu rozbiegania się owych
trajektorii. Można powiedzieć, że wielkość λ już oddaje sens wykładnika Lapunowa.
Będzie z nim tożsama, zgodnie z definicją wynikającą z przeprowadzonego poniżej
rozumowania praw dziwnego dla zbioru dyskretnych (nieciągłych) wartości x,
oznaczających wyniki pomiaru pewnej wielkości eksperymentalnej (np. stężenia
wybranej substancji)
9
'.
Należy rozważyć pewną trajektorię zmian wielkości x w czasie i należące do niej dwa
stany początkowe, oznaczone jako x
0
oraz x
0
+ e (e > 0). Niech ewolucja stanu układu
prowadząca do kolejnych wartości x (x
1
, x
2
, ... itd.) odbywa się krok po kroku zgodnie z
zależnością iteracyjną
Jeśli równania (7.7.1) lub (7.7.2) opisują ewolucję układu po trajektorii należącej do
dziwnego atraktora, to różnica ε miedzy początkowymi wartościami x ulegnie
zwiększeniu, co widać na rys. 7.21. A zatem, wykładnicza rozbieżność trajektorii
przejawia się w tym, że po N przekształceniach początkowa różnica e między
wartościami x osiąga następującą wartość [A3.1]:
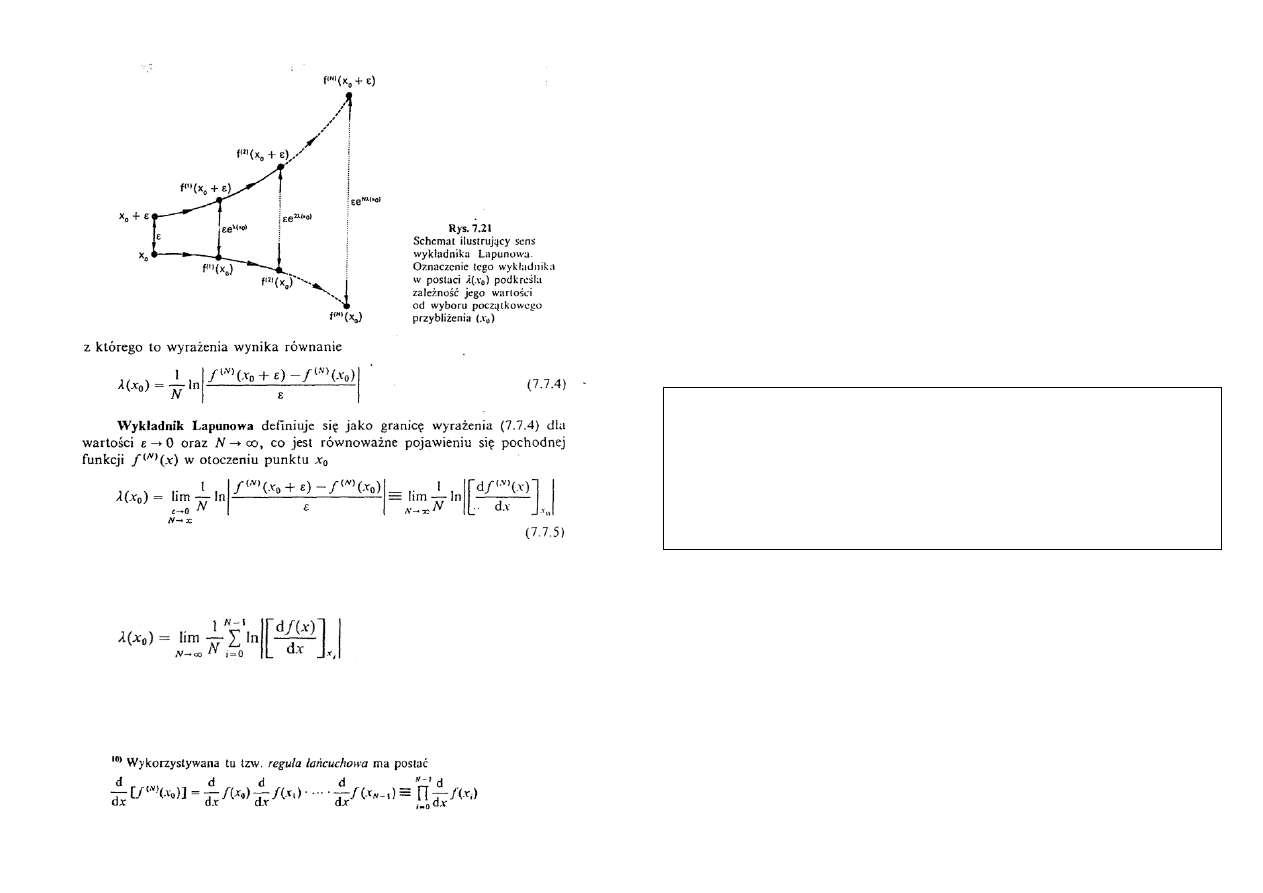
Korzystając z reguł różniczkowania funkcji złożonej
10)
, równanie (7.7.5)
można zapisać w innej równoważnej(a niejednokrotnie bardziej praktycznej)
postaci, operującej tylko pochodnymi pierwszego rzędu dla kolejnych wartości x
1
Z równania (7.7.6) można wywnioskować, iż między charakterem trajektorii a
wartością wykładnika Lapunowa istnieją następujące zależności (ograniczone
tymczasem do jednej współrzędnej x) :
-----------------------------
_____________
__________________
λ >0 oznacza trajektorie odpowiedzialną za generowanie chaosu deterministycznego
(dziwny atraktor) λ = O -trajektorię stanowiącą cykl graniczny, a λ < O — trajektorię
dążącą do stabilnego stanu stacjonarnego.
Powyższe rozważania trzeba uogólnić na układy wielowymiarowe. Układ
charakteryzuje się bowiem liczbą wykładników Lapunowa równą jego wymiarowi
(czyli liczbie równań różniczkowych opisujących dynamikę układu). W przypadku
opisanego wyżej układu Lorenza (czy zespołu przemian chemicznych z trzema
formami przejściowymi) otrzymuje się trzy wykładniki Lapunowa (dla trajektorii
A
-
,
y, z).
O wystąpieniu chaosu deterministycznego świadczy już to, że przynajmniej jeden z
nich jest dodatni, czyli to, że „widmo" znaków wykładników Lapunowa wygląda
następująco: ( + ,0, -). Zestawienie związków między znakami
X
x
, A
r
. A
z
a istnieniem
odpowiednich atraktorów podaje tabl. 7.1. Jeśli dodatnią wartość wykazuje więcej niż
jeden wykładnik Lapunowa, to obserwowane dynamiczne zachowanie określa się jako
hiperchaos [B7.32J. Odpowiadający mu dziwny atraktor rozwija się w odpowiednio
wielowymiarowej przestrzeni fazowej. Należy jednak pamiętać, że dla opisywanych
tu układów dynamicznych suma wszystkich wykładników Lapunowa powinna być
ujemna
(∑ λ
i
< 0
) [A3.I8].
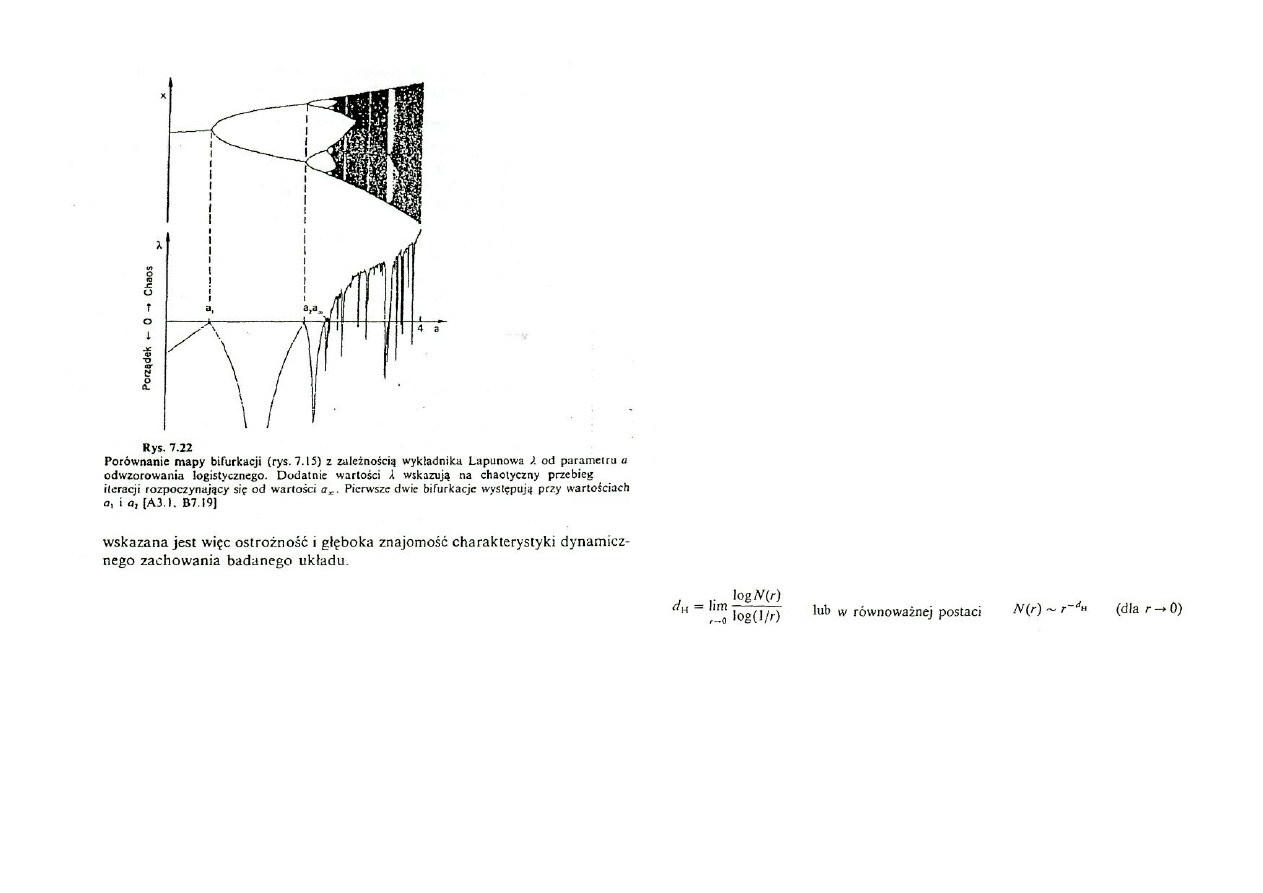
Jeśli opisaną wyżej koncepcję wykładnika Lapunowa zastosuje się do badania
chaosu w iteracjach odwzorowania logistycznego (p. 7.6), to otrzymuje się zależność /.
od parametru odwzorowania logistycznego a przedstawioną na rys. 7.22. Zestawienie
tego przebiegu z mapą bifurkacji z rys. 7.15, dla tego samego przedziału wartości
parametru a, dobitnie ukazuje opisane wyżej przejścia między porządkiem a chaosem w
procesie iteracji odwzorowania logistycznego [A3.1]. Dotychczasowe rozważania
dotyczyły idealnych, teoretycznych przebiegów trajektorii w przestrzeniach fazowych.
Istnienie czysto losowego szumu w zachowaniu układu może niestety w praktyce
prowadzić do otrzymania dodatniej wartości
A
max
11)
,
a zatem wyciągnięcia
wniosku o istnieniu chaosu deterministycznego, nawet jeżeli analizowany ruch jest
w istocie periodyczny lub quasi-periodyczny. Przy interpretacji wartości
A
max
---------------------------------------
11) Należy tu znowu wspomnieć o pozornie paradoksalnym efekcie nasilania porządku przez
oddziaływanie losowego szumu na niektóre układy chaotyczne, np. modelowy układ Bielousowa-
Żabotyńskiego (p. 7.8).
tablica 7
.1 ZESTAWIENIE RELACJI MIĘDZY ZNAKAMI WYKŁADNIKÓW LAPUNOWA (
λ
x
, λ
y
,
λ
z
) A CHARAKTEREM TRAJEKTORII W TRÓJWYMIAROWEJ PRZESTRZENI FAZOWEJ (
x, y, z
)
Charakter trajektorii — typ atraktora
Zestawienie znaków (A,, A,, A.)
Punktowy
( —, —, —)
Cykl graniczny
( O , -, -)
Quasi-peńodyczny (torus)
(0,0, —)
Chaotyczny (dziwny atraktor)
( + ,0,—)
7.7.2
_______________________________________
Fraktalna natura
dziwnych atraktorów. Rozszerzone pojęcie wymiaru
Jak wspomniano na początku tego rozdziału, wszystkie znane dziwne atraktory mają
strukturę fraktalną [A3.1, A3.6-A3.il, B7.17]. Czym jest fraktal ? Aby odpowiedzieć na to
pytanie, należy zdać sobie sprawę z tego, że zarówno dziwne atraktory, jak i inne obiekty,
wykazują strukturę, do opisu której znane ze szkoły klasyczne pojęcie wymiaru,
wywodzące się z prac Euklidesa (tzw. wymiar topologiczny), okazuje się niewystarczające.
Takie proste obiekty jak odcinki, gładkie krzywe, prostokąty, okręgi itp. nie opisują
dokładnie kształtu drzew, płatków śniegu, łańcuchów górskich czy wybrzeży morskich, lecz
znacznie je idealizują. A te ostatnie to właśnie są typowe obiekty fraktalne. Termin
„fraktal", stworzony przez ich odkrywcę — Benoit Mandelbrota [A3.10], nawiązuje do
łacińskiego słowa fractus (złamany). Fraktalami nazywane są więc dosłownie obiekty o
,,złamanym wymiarze", który często bywa ułamkowy. W dalszych rozważaniach
będzie mowa o atraktorach opisywanych przez modele ciągłe (równania różniczkowe)
i dyskretne (odwzorowania).
Atraktory opisywane układami równań różniczkowych
Warto powrócić do rozważań o dziwnym atraktorze Lorenza. O tym, że powinien on
mieć wymiar ułamkowy, świadczy analiza jego własności dla czasu dążącego do
nieskończoności, tj. gdy tworzy się tzw. graniczny zbiór punktów danej trajektorii. Okazuje
się, że objętość takiego granicznego zbioru (atrakto-ra) powinna wtedy dążyć do zera. W
przypadku atraktora regularnego np. stabilnego stanu stacjonarnego (punktu — wymiar
0) lub cyklu granicznego na płaszczyźnie (wymiar 2) warunek ten jest oczywiście spełniony.
W przypadku atraktora dziwnego, który przedstawiany był np. w trójwymiarowej
przestrzeni (x, y, z), problem objętości granicznego atraktora nieco się komplikuje. Jego
wymiar nie może być równy 3, bo oznaczałoby to niezerową jego objętość dla czasu
dążącego do nieskończoności. Nie może to być również wymiar równy zeru (jak dla
punktu), jedności (prosta) lub dwóm (płaszczyzna). Wykluczałoby to, na mocy
odpowiednich twierdzeń, dziwny charakter takiego atraktora. Przypisanie więc dziwnemu
atraktorowi wymiaru większego od 2, ale ułamkowego (potwierdzonego rozważaniami o
geometrii takiego obiektu), pozwala na spełnienie warunku o zerowej objętości
granicznego atraktora. Przykładowo, wymiar fraktalny opisanego wyżej atraktora
Lorenza wynosi 2,06. Jak jednak zdefiniować taki niecałkowity wymiar? Pod pojęciem
wymiaru fraktalnego rozumie się zwykle tzw. wymiar Hausdorffa
I2)
[A3.1, A3.16], określony
przez następujące rozumowanie. Zakłada się, że obiekt, którego wymiar (w ujęciu
Hausdorffa) chce się określić, ma wymiar topologiczny równy d
T
. Należy rozważyć, ile
potrzeba (
d
T
-
wymiarowych kul
13)
o promieniu r, aby pokryć (wypełnić) cały badany obiekt.
Jeśli ich liczbę oznaczy się przez N(r), to wymiar Hausdorffa
d
H
określony jest
wyrażeniem
Łatwo również zauważyć, że w przypadku tak „porządnych" obiektów jak punkt,
prosta (lub gładka krzywa) czy kwadrat, wymiar fraktalny jest zgodny z wymiarem
topologicznym:
d
H
=
d
T
(odpowiednio dla wymienionych obiektów: O, 1,2). Warto
rozważyć jednak obiekt zwany krzywą Kocha.
----------------------------
2)
Ściślej biorąc, wymiar Hausdorffa przedstawiony tu będzie w szczególnej postaci, zbieżnej z
pojęciem tzw. wymiaru pojemnościowego wprowadzonego przez Komiogorowa. Tożsamość
między tymi dwoma wymiarami jest spełniona przynajmniej dla większości trajektorii układów
dynamicznych.
13)
W przypadku, gdy
d
T
= 1
, kula staje się odcinkiem, a gdy
d
T
= 2
— kwadratem. Gdy
d
T
>
3,
równoważne są rozważania dla kuli i sześcianu.
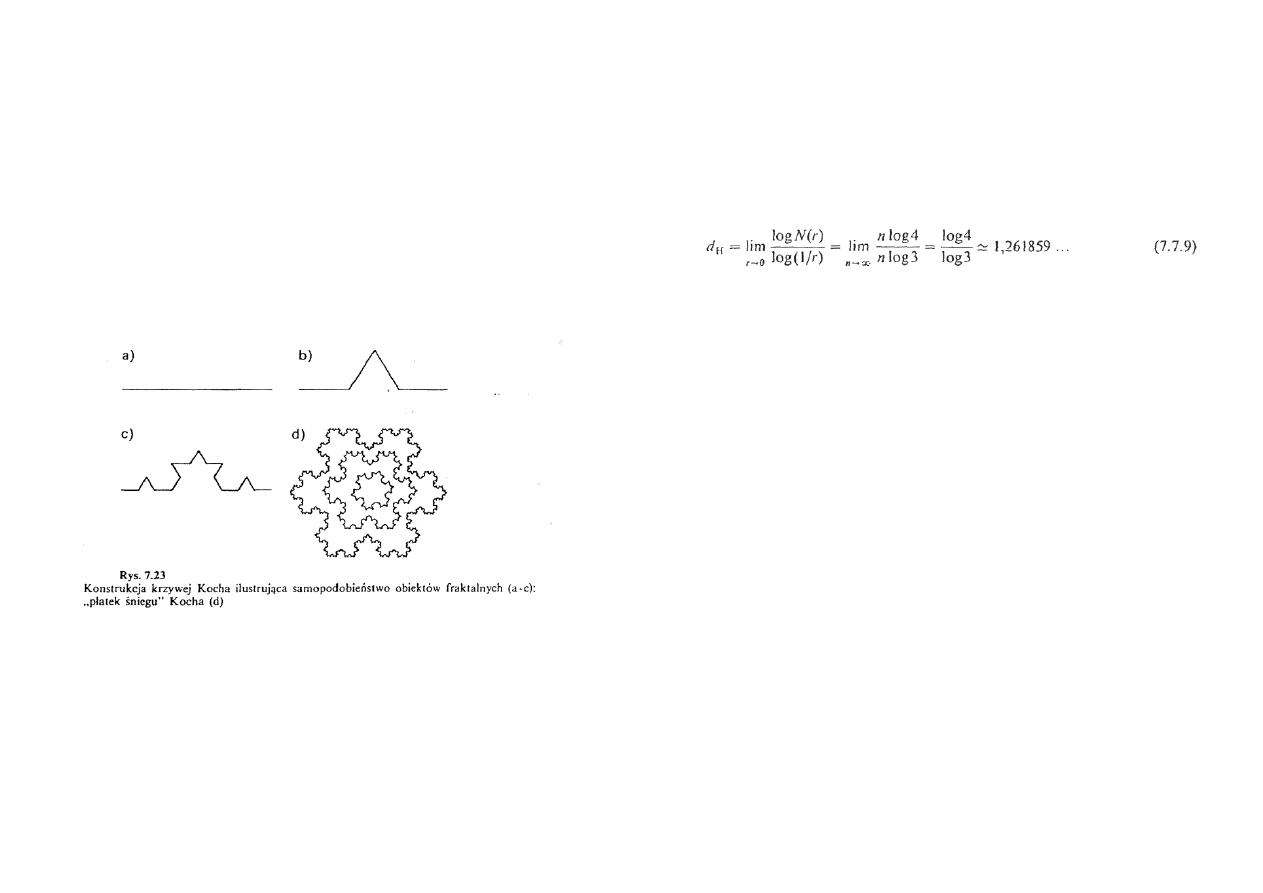
Krzywa Kocha jako typowy obiekt fraktalny
Krzywą Kocha konstruuje się następująco:
1.
obiektem wyjściowym (zwanym inicjatorem) jest odcinek o jedno stkowej
długości (rys. 7.23a);
2. jako generator przekształcania tego odcinka przyjmuje się operację
dzielenia odcinka na 3 części i usuwania części środkowej, z zastąpieniem jej
podwojoną długością usuniętego odcinka (rys. 7.23b);
3. analogiczną operację wykonuje się dla każdego z odcinków, otrzymując
obraz (rys. 7.23c);
operacje tę powtarza się „nieskończenie" wiele razy, otrzymując krzywą Kocha,
będącą łamaną złożoną z nieskończenie wielu odcinków.
Jeśli inicjatorem nie jest odcinek, ale trójkąt równoboczny (lub ich zespół),
otrzymuje się tzw. płatek śniegu Kocha (rys. 7.23d).
Przy okazji konstruowania tego obiektu można łatwo zauważyć pewną bardzo ważną
cechę większości fraktali, a co za tym idzie także rozważanych tu dziwnych
atraktorów. Jest nią samopodobieńsrwo, czyli powtarzanie schematu struktury
„makroskopowej" na poziomie bardziej „mikroskopowym". Inaczej mówiąc, mały
kawałek takiego obiektu, odpowiednio powiększony, jest nieodróżnialny od
większego, z którego został wycięty. Można to łatwo zauważyć na przykładzie opisanej
wyżej krzywej Kocha i dziwnych atraktorów. Jeśli bowiem program komputerowy
generujący dziwny atraktor napisze się tak, aby można było powiększać wybrane małe
fragmenty otrzymanej trajektorii, to otrzymuje się bezpośredni dowód na to, że
struktura „mikroskopowa" dziwnego atraktora jest identyczna ze strukturą bardziej
„makroskopową". Zatem jest to istotnie obiekt samopodobny, a więc należący do
fraktali.
Wracając do konstrukcji krzywej Kocha należy zauważyć, że z rysunków powyższych
wynika jasno, że dla r = 1/3, otrzymuje się N(r) = 4 odcinki krzywej. Druga operacja
oznacza podzielenie krzywej na 16 (4
2
) odcinków o długości 1/9 (czyli l/3
2
) każdy.
Można sprawdzić, że dla «-tej operacji r = 1/3
n
, a N (r) = 4
n
. Jak z tego wynika obliczanie
granicy wyrażenia (7.7.7) przy r 0 jest równoważne obliczaniu granicy tego
wyrażenia przy n ∞
Należy przypomnieć, że klasyczny (topologiczny) wymiar krzywej Kocha jest równy 1.
Otrzymana relacja
d
H
>
d
T
wydaje się dobrą definicją fraktala jako obiektu, dla którego
wymiar fraktalny jest wyższy od wymiaru topologicznego [A3.16]. Jak widać, definicja ta
nie narzuca warunku, że wymiar fraktalny ma wykazywać ułamkową wartość. W
rzeczy samej istnieją obiekty fraktalne, czyli spełniające warunek (7.7.10), ale między
dwiema liczbami całkowitymi, np. krzywa łamana powstająca jako ślad toru cząstki
poruszającej się bezładnym chaotycznym ruchem Browna (jej wymiar topologiczny jest
równy l, a wymiar fraktalny wynosi dokładnie 2). Można powiedzieć, że wymiar fraktalny
(Hausdorffa) uwidacznia złożoność struktury obiektu, której nie uwzględnia klasyczny
wymiar topologiczny. Dodatkowe informacje o fraktalach zawiera Uzupełnienie D.
Atraktory opisane przez równania iteracyjne (odwzorowania)
Wszystkie opisywane wyżej fraktalne cechy dziwnych atraktorów mają zastosowanie
do opisu chaosu w procesie iteracji odwzorowania logistycznego (scenariusz
Feigenbauma), opisanego samopodobnym „drzewkiem figowym" (rys. 7.15), z jednym
wyjątkiem. Uważnemu Czytelnikowi mogła zresztą nasunąć się poważna wątpliwość.
Atraktor Lorenza musiał mieć wymiar większy od 2, aby można było dopuścić jego
chaotyczną naturę. Czy więc atraktor Feigenbauma może być odpowiedzialny za
chaos, skoro jego wymiar z pewnością nie przekracza 2? Dla przykładu, wymiar
Hausdorffa dla atraktora Feigenbauma dla krytycznej wartości paramatru a, po
przekroczeniu której pojawia się chaos, jest równy 0,538... Nie wdając się jednak w
szczegóły matematyczne, należy podkreślić tylko, że istnieje różnica w wymaganiach
dotyczących wymiaru atraktora w przypadku, gdy jest on generowany przez układ
równań różniczkowych i przez iteracje [A3.1]. W tym drugim przypadku trajektorie mają
charakter nieciągły. Można wykazać, że wtedy nie ma sprzeczności między wymiarem
atraktora, mniejszym od 2, a jego chaotyczną naturą. Oprócz wymiaru Hausdorffa
istnieją też inaczej zdefiniowane wymiary, przydatne w analizie chaotycznego
zachowania układów: m.in. tzw. wymiar informacyjny d
1
oraz — szczególnie ostatnio
popularny w literaturze — wymiar korelacyjny Grassbergera i Procacci d
c
Wymiarom tym
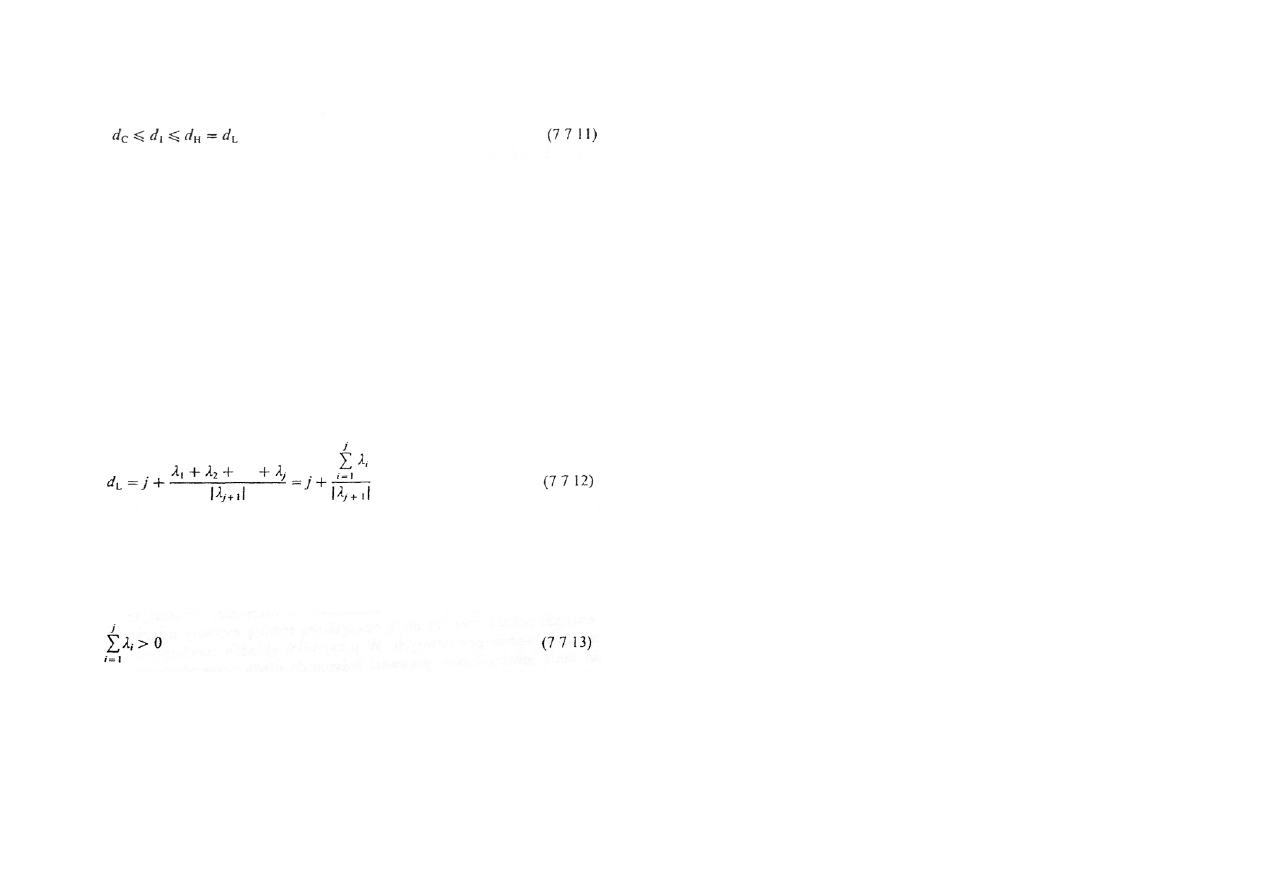
nie będzie poświęcona tutaj uwaga, tym bardziej, że są one często zbliżone wartościami
do wymiaru fraktalnego (Hausdorffa), zgodnie z relacją [B7 15, B7.32]
gdzie d
L
oznacza tzw wymiar Lapunowa, opisany w następnym rozdziale.
7.7.3 ___________________________________
Wykładnik Lapunowa a wymiar fraktalny
Po przeczytaniu ostatnich rozdziałów może pojawić się pytanie, czy miedzy dwiema
omówionymi wyżej a różnymi miarami chaosu: dynamiczną — w postaci wykładnika
Lapunowa i statyczną — w postaci wymiaru fraktalnego, istnieje jakikolwiek ścisły
związek. Okazuje się, że zależność taka została zaproponowana i znana jest w
literaturze jako hipoteza Kaplana i Yorke'a (A3.1, B7 15]. Zgodnie z nią, istnieje —
przynajmniej w wielu przypadkach - równość między wymiarem fraktalnym
d
H
i tzw.
wymiarem Lapunowa
d
L
Wymiar Lapunowa zdefiniowany jest za pomocą wykładników
Lapunowa ).
{
w następujący sposób
przy czym, aby obliczenie zostało wykonane prawidłowo, wykładniki Lapunowa
m u s z ą by ć u p o r z ą dk ow a n e w k o l e j n o ś c i m a le j ą c y c h w a r t o ś c i
(
λ
1
> λ
2
> …) Za j przyjmuje się największą liczbę całkowitą, dla której
spełniony jest warunek
Wymiar Lapunowa jest wielkością szczególnie wygodną do wyznaczania w
numerycznych symulacjach dla modeli teoretycznych. Trzeba jednak podkreślić, że
uniwersalność hipotezy Kapłana i Yorke'a nie została dotychczas potwierdzona.
Prawdopodobnie prawdziwa jest w ogólnym przypadku raczej nieostra
nierówność
d
H
≤ d
L
,
co jednak nie ma znaczenia dla prostych rozważanych tu dziwnych
atraktorów, dla których równość
d
H
= d
L
jest spełniana z wystarczającą
dokładnością.
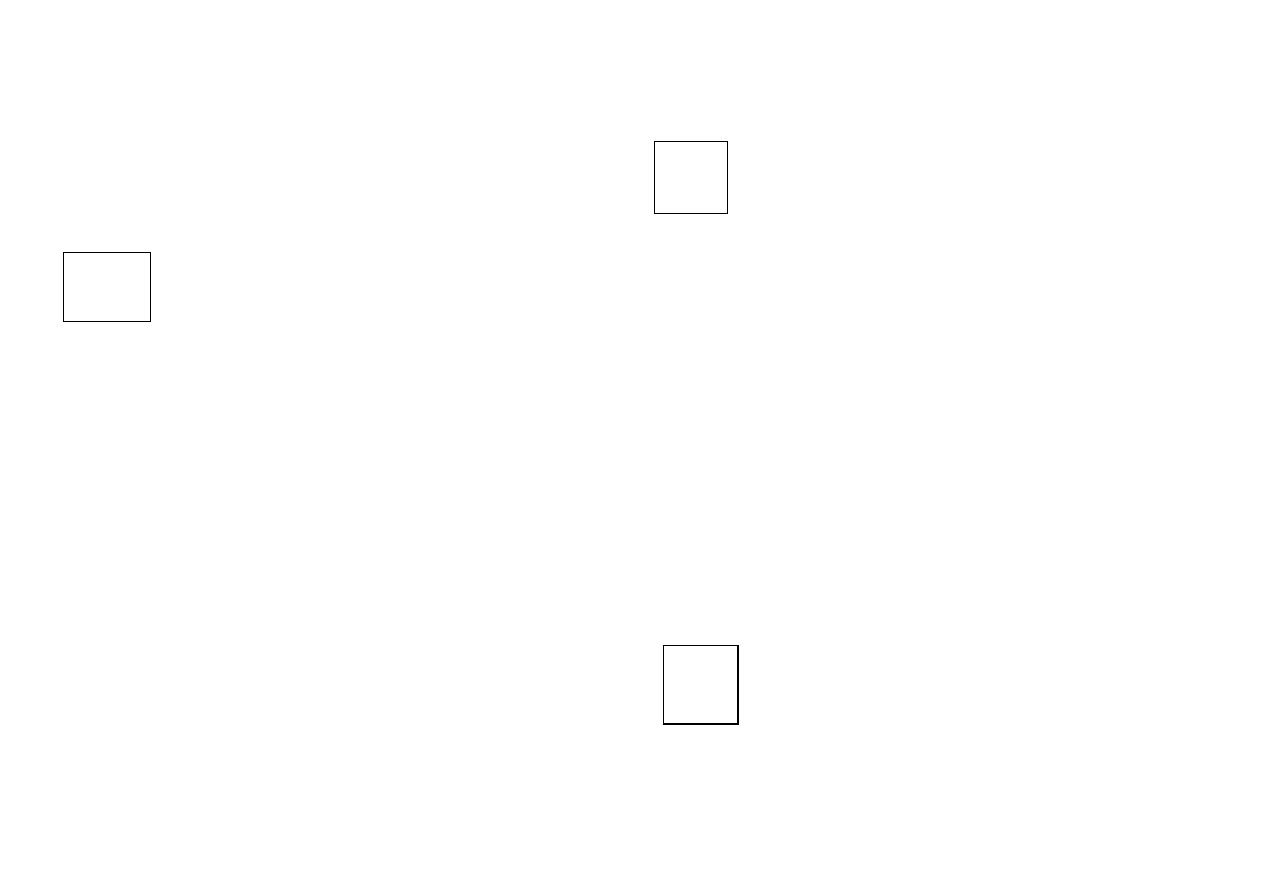
Rozdział 1 Czym są
fraktale?
Wprowadzenie
Człowiek jako istota obdarzona zdolnością myślenia, od zarania
swego istnienia starał się zrozumieć otaczający
go świat i rządzące nim
prawa. Pierwsze produkty działalności ludzkiej inspirowane tworami
natury, powstawały na zasadach prymitywnego empiryzmu, przez co w swym
wyglądzie nie odbiegały od otaczającego je świata przyrody. Z czasem zdolność
człowieka do myślenia abstrakcyjnego uległa zwiększeniu i każde zdejmowane z
nieboskłonu bóstwo zastępowała nowa teoria czy też hipoteza. Co więcej, z biegiem czasu
teorie opisujące istotę świata ulegały uproszczeniom, by od platońskiego podejścia
spirytualistycznego reprezentowanego
przez
starożytnych filozofów greckich przejść do
materializmu - nurtu w pełni empirycznego
wymaganego
przez dzisiejszą naukę. W 1610
roku Galileusz wyraził pogląd, że językiem natury jest matematyka, a , jej alfabetem są
trójkąty, koła i inne figury geometryczne"
-
tak więc matematyka stała się językiem
formalnym wszelkich teorii naukowych. Ale
czy
stwierdzenie Galileusza było słuszne? Czy
twory natury rzeczywiście
przypominają
kształty znane z geometrii klasycznej? Pablo
Picasso, Georges Braque i
inni kubiści krzyknęliby
głośno TAK!, lecz poglądowi temu
sprzeciwił się Benoit Man
delbrot, pionier w zakresie
badań nad nieregularnością
struktury rzeczywistego świata i
form geometrycznych
w nim
zawartych,
które nazwał
fraktalami. W swojej słynnej książce The Fractal
Geometry of
Nature opublikowanej w 1975
roku, .stwierdził: „Ani chmury nie
są
kulami, góry - stożkami,
-
linia brzegowa Kołem,
kora nie jest płaska, ani też błyskawica nie mknie po linii prostej". Zdanie to
przytaczane jest chyba we wszystkich publikacjach poruszających temat fraktali i w pełni
oddaje istotę rzeczy Dzisiejsze twory działalności człowieka, takie jak przedmioty_
codziennego użytku czy obiekty architektoniczne, proste w swej strukturze
geometrycznej, te twory kultu geometrii
klasycznej
wpajanej ludziom od najmłodszych lat,
przez co budującej podświadome
uwielbienie
dla trywialnej estetyki, zdają się zgodne z
galileuszowskim widzeniem
świata, lecz jakże
są odmienne od występujących w przyrodzie.
Dlatego opis tworów
natury za pomocą
fraktali, który
propaguje
Mandelbrot i jemu
podobni, wydaje się o wiele lepiej modelować ten aspekt rzeczywistości niż teorie mające
za narzędzie geometrię euklidesową.
Geneza fraktali
Jakże kręte i powikłane są drogi rozwoju nowych idei Powstawanie i rozwój teorii
zdaje się przypominać działanie ewolucji, tworzącej na zasadzie ślepego przypadku
nowe gatunki w przyrodzie, które to albo giną śmiercią naturalna zaraz po
powstaniu, albo trwają w swej egzystencji przez miliony lat jako formy ukryte, by nagle
po zmianie warunków środowiska naturalnego lub z powodu innych czynników wyjść w
pełnej krasie na światło dzienne. Analogia ta sprawdza się również i w przypadku
fraktali, jeśli prześledzić drogę rozwoju tej dziedziny wiedzy. Za narodziny fraktali
można przyjąć koniec wieku XIX i początek XX, kiedy to matematycy tacy jak Koch,
Hilbert czy Peano, zaczęli tworzyć krzywe wypełniające przestrzeń oraz krzywe, które
przecinają się w każdym punkcie. Współcześni im matematycy ograniczyli się jedynie
do określenia tych tworów czystej matematyki mianem patologiczne, monstrualne i nie
okazali im większego zainteresowania. Prace Kocha, Hilberta i Peana zostały
złożone w matematycznym lamusie. Ponowne zainteresowanie tematem nastąpiło
dopiero w latach sześćdziesiątych naszego wieku wraz z rozwojem badań nad
zachowaniem układów dynamicznych i zachodzących w nich procesów chaotycznych.
To właśnie chaos deterministyczny bo taką nazwę nadano temu obszarowi badań,
spowodował ponowne pojawienie się „monstrualnych" krzywych na scenie naukowej,
lecz tym razem pod nazwą dziwne atraktory/Jednak na początku związek między
dziwnymi atraktorami chaosu, a matematycznymi rojeniami Kocha, Hilberta i Peana,
nie został zauważony. Dopiero dzięki wyobraźni Mandelbrota tajemnicze krzywe i
twory chaosu scaliły się tworząc nowy byt o nazwie fraktal.
Definicja fraktala
Benoit Mandelbrot w swojej książce podaje definicję fraktala, jako
obiektu geometrycznego posiadającego cechę samopodobieństwa,
którego wymiar nie jest liczbą całkowitą. Zajmiemy się teraz głębszą
analizą tej definicji. Samopodobieństwo, oznacza, że część obiektu jest podobna do
całości. Jest to cecha charakterystyczna dla obiektów występujących w przyrodzie. Liść
paproci jest małą repliką całej paproci, powiększenie kory drzewa dalej przypomina korę,
a linia brzegowa pozostaje nie zachwiana w swojej strukturze niezależnie od skali mapy.
Natomiast tradycyjne kształty geometryczne - trójkąty, koła, sfery - tracą przy
1.1
1.
3
1.
2

powiększeniu swoje właściwości. Na przykład powiększenie ad itifitiititm wycinka okręgu
jest pozbawionym własności okręgu odcinkiem. Pojęcie wymiaru obiektu
geometrycznego jest znane chyba wszystkim absolwentom szkoły podstawowej. Tak
więc wymiar odcinka wynosi l, wymiar kwadratu wynosi 2, wymiar sześcianu 3, a
hipersześcianu 4. Ten rodzaj wymiaru nosi nazwę wymiaru topologicznego i jego
wartością jest nieujemna liczba całkowita. Cóż jednak oznacza sformułowanie „wymiar
niecałkowity"? Czy jest to kolejna imaginacja jakiegoś szalonego pisarza science-fiction,
która znalazła swoje miejsce w nauce? Istnieje wiele definicji wymiaru (wymiar
informacyjny, wymiar Lapunowa, wymiar korelacyjny itd.). Ten, o którym mowa, służy
opisowi stopnia chropowatości obiektu geometrycznego i jest znany jako wymiar
Hausdorffa-Besicovitcha. W celu lepszego zrozumienia tematu przyjrzyjmy się dwóm
przykładowym obiektom: domkniętemu wycinkowi okręgu i łamanej.
1
Wymiar topologiczny
obu tych obiektów jest równy i ma wartość l, lecz w sensie wymiaru Hausdorffa-Besicoyitcha
wymiar łamanej jest większy, ponieważ łamana lepiej zapełnia przestrzeń niż gładki
wycinek okręgu, a jednocześnie gorzej niż dwuwymiarowa po- wierzchnia. Zatem ma sens
wymiar zawarty gdzieś między wartościami l i 2>. Nie jest przypadkiem, że jako drugi z
przykładowych obiektów podano łamaną, ponieważ termin fraktal stworzony przez
Mandelbrota pochodzi od łacińskiego przymiotnika fractus, a odpowiadający mu
czasownik frangere znaczy „łamać", „tworzyć nieregularne fragmenty". Zatem wymiar jest
tym, co odróżnia w sposób ilościowy fraktale od obiektów geometrii euklidesowej.
Zastosowanie fraktali
W dzisiejszej nauce fraktale stosowane są do:
badania nieregularności powierzchni, opisu procesów chaotycznych
zachodzących w układach dynamicznych,
przetwarzania i kodowania obrazów cyfrowych - kompresja fraktalna,
modelowania tworów naturalnych dla celów realistycznej grafiki
komputerowej,
badania struktury łańcuchów DNA,
badania samopodobnych struktur harmonicznych występujących w
muzyce.
Jak już wspomniano wcześniej, natura nie tworzy form o strukturze gładkiej, lecz
charakteryzującej się większym lub mniejszym stopniem chropowatości powierzchni.
Odnosi się to zarówno do obiektów rozpatrywanych w skali mikroskopowej, jak i ma-
kroskopowej. Na przykład Douglas Rees i Mitchel Lewis ustalili, że powierzchnia białka
jest fraktalem o wymiarze około 2,4 i co więcej, że pewne jej obszary są bardziej
chropowate od innych, co implikuje, że mają one średnio większy wymiar. Jak się wydaje,
obszary te są miejscami, w których białka sklejają się ze sobą w procesie syntezy. natomiast
obszary bardziej gładkie są to miejsca aktywne dla enzymów, które wiążą się z białkami
znacznie gorzej. W latach sześćdziesiątych Mandelbrot, jeszcze jako pracownik naukowy
firmy IBM, zaproponował fraktalna koncepcję rozkładu galaktyk we wszechświecie.
Dowodził on mianowicie, że struktura wszechświata może być jednorodna, ale nie musi
wynikać stąd jednorodny rozkład materii, pod warunkiem, iż rozkład ten jest fraktalem.
Dzisiejsi znawcy tematu przyjmują, że wszechświat nie jest czysto fraktalny, ponieważ nie
wykazuje cechy samopodobieństwa we wszystkich rozpatrywanych skalach, lecz określają
go jako multifraktalny, to znaczy składający się
:
ze zbioru fraktali pomiędzy którymi nie
zachodzi relacja podobieństwa.
Fraktalny model natury i procesów w niej zachodzących wydaje się spełniać swoje
zadanie. Ale czy jest to model prawdziwy? Czy rzeczywiście przyroda działa na pod-
stawie zasad geometrii fraktalnej? Na tego typu pytania nigdy nie można dać odpowie-
dzi twierdzącej. Każda teoria jest tylko teorią, a to znaczy, że może zostać zastąpiona
modelem lepszym, sprawdzającym się w szerszym aspekcie rzeczywistości. Zastąpiona
nie znaczy jednak odrzucona. Jako przykład można podać mechanikę klasyczną Newto-
na, której prawa panowały niepodzielnie przez ponad dwa stulecia jako ostateczny opis
rzeczywistości. Wraz z rozwojem nauki odkryto, że nic sprawdzają się one jednak w
przypadku prędkości bliskich prędkości światła. Powstała nowa koncepcja - teoria
względności Alberta Einsteina. Nie wyparła ona jednak całkowicie mechaniki Newtona,
ponieważ w szerokim przedziale prędkości sprawdza się znakomicie i jest zupełnie wy-
starczająca. Fraktale, oprócz swych naukowych zastosowań, posiadają jeszcze jedną
ważną zaletę. Przede wszystkim są wizualnie piękne, co czyni je nieśmiertelnymi dopó-
ty, dopóki człowiek będzie hołdował nie tylko wartościom materialnym, lecz również
estetycznym.
1.
4
Wyszukiwarka
Podobne podstrony:
Chaos Deterministyczny p19 slides
Chaos Deterministyczny p3
Chaos, Fraktale oraz Euroatraktor 03 Zyczkowski p6
Bifurkacje, Chaos i Fraktale w Dynamice Wahadla 01 Szemplinska p32
Chaos, Fraktale oraz Euroatraktor 03 Zyczkowski p6
Fraktal & Chaos p7
Rajeev S G Advanced Mechanics From Eulers Determinism to Arnolds Chaos (OUP, 2013)(ISBN 978019967085
fraktale i chaos
biofiza cw 31
BIOFIZYKA
Biofizyka 4
Biochemia z biofizyką Seminarium 2
Determinanty dochodu narodowego
więcej podobnych podstron