PRZEDSTAWIANIE INFORMACJI

W KOMPUTERZE

wprowadzenie

PRZEDSTAWIANIE INFORMACJI

W KOMPUTERZE

wprowadzenie

ASCII

ASCII

Podstawy…

Informatyka nie jest (tylko) nauką o komputerach !!!!!!!!!!!!

O czym właściwie będziemy mówid…?

Przeciętny kandydat na informatyka zupełnie błędnie utożsamia sobie
zastosowania komputerów z informatyką i ma najczęściej całkiem fałszywe
wyobrażenie o tym, czym rzeczywiście jest informatyka. Interesują go
komputery, oprogramowanie użytkowe (przede wszystkim gry) i języki
programowania. Mamy tu do czynienia z sytuacją podobną, jak w przypadku
studiów astronomicznych, mających niewiele wspólnego z tym, o czym
marzy każdy miłośnik astronomii: patrzeniem w niebo. Informatyka nie jest
nauką o komputerach tak jak astronomia nie jest nauką o teleskopach.
Prawdziwy informatyk niekonieczne zna się na komputerach.

…z książki „Fascynujący świat komputerów”

O czym właściwie będziemy mówid…?

INFORMACJA

to, co umysł jest w stanie przetworzyd
i wykorzystad do własnych celów.

Informacja jest więc

interpretacją

otrzymanych sygnałów

Informacja

podlega przetwarzaniu

przez naszą wiedzę

i w efekcie możemy otrzymad inne informacje. Możliwe są
więc

różne interpretacje

tej samej informacji.

Systemy informatyki nie są bezpośrednio przystosowane do

przetwarzania informacji rozumianej w ten sposób…

O czym właściwie będziemy mówid…?

INFORMACJA

Zgodnie ze podejściem ścisłym, które wywodzi się z
fizyki i matematyki, informacja oznacza pewną

własnośd fizyczną lub strukturalną obiektów

.

Zgodnie z tym podejściem

informacja jest mierzona

jako prawdopodobieostwo zajścia zdarzenia

. Im

mniej prawdopodobne zdarzenie, tym więcej jest z
nim związanych informacji (lub więcej „daje”
informacji).

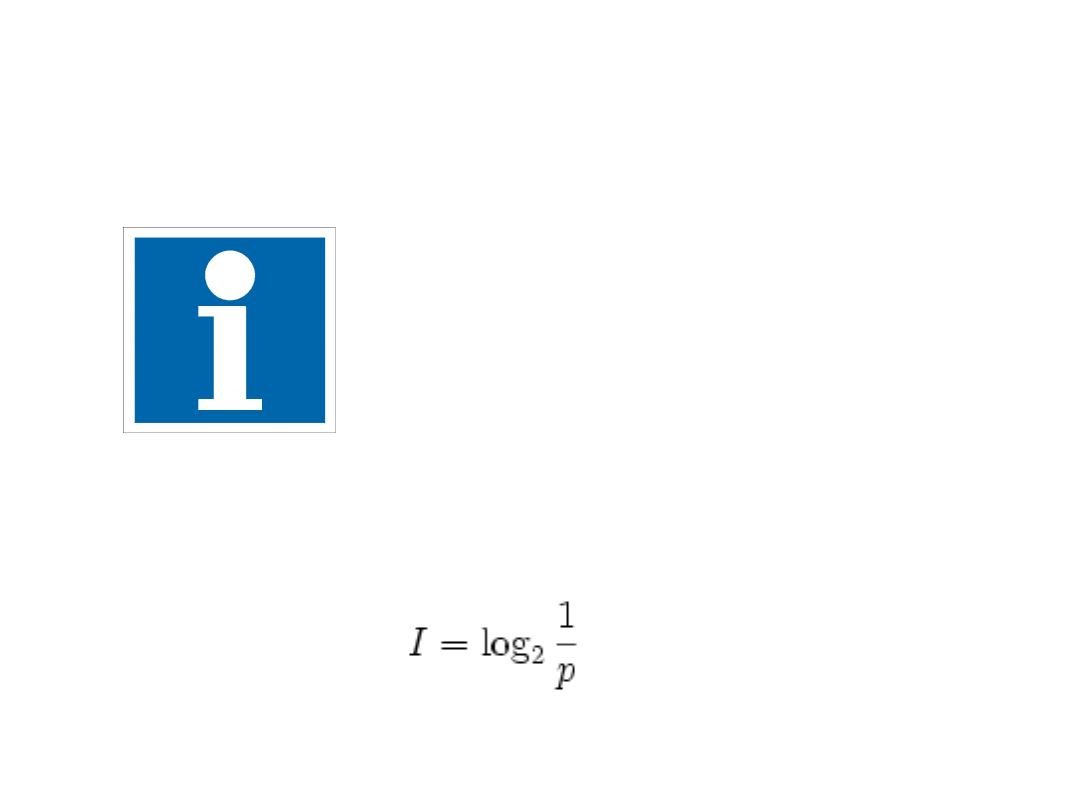
Wzór na „ilośd” informacji (w

bitach

) to

gdzie

p – prawdopodobieostwo

zdarzenia

I – liczba bitów

Ten sposób rozumienia informacji jest zgodny z tym,

jak „rozumieją” ją systemy informatyki.

?

?

?

Na początku była ciemnośd…

W takim „układzie” jest tylko jeden stan. Nic się nie dzieje.
Niczego nie trzeba opisywad.
Układ nie niesie ze sobą żadnych informacji.

-Który samochód jest Twój?
- Czerwony…

Informacja nie wyróżnia żadnego stanu.

Mój to ten czerwony…

W takim „układzie” mamy już dwa stany.
Jest to najprostszy układ,
w którym możemy je wyróżnid
i ponumerowad.

0

1

I stało się światło…:)

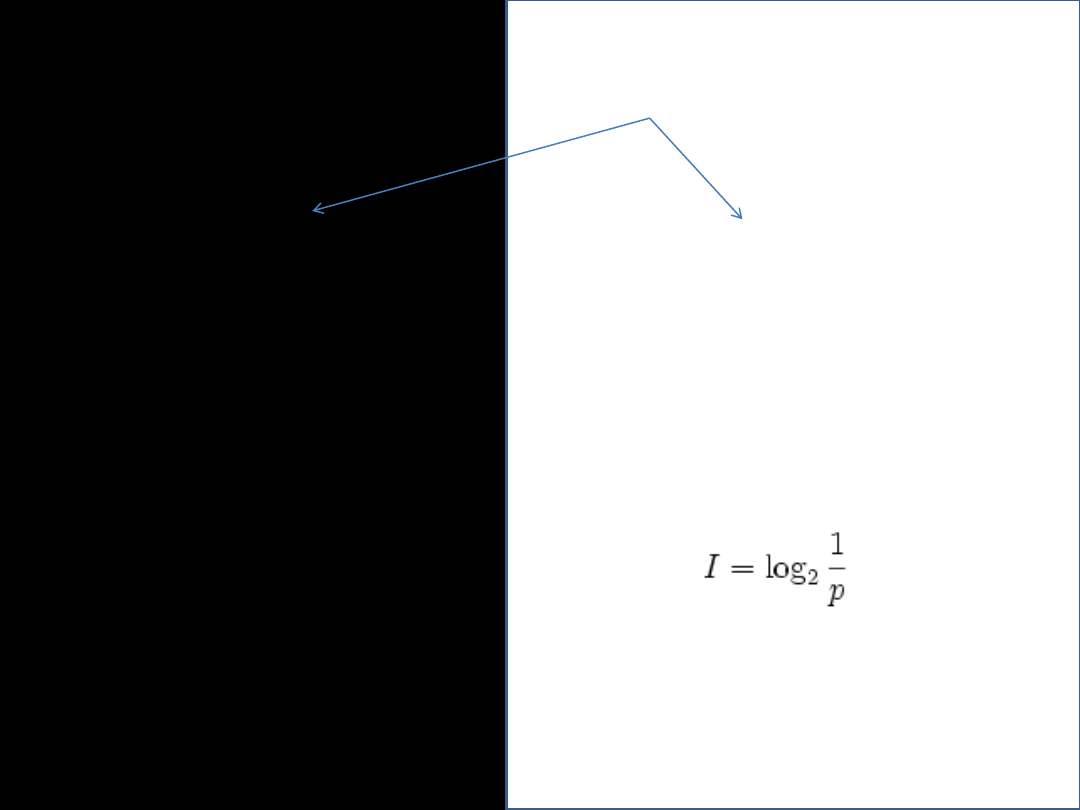
Aby się upewnid ile bitów potrzebujemy,
podstawmy do wzoru:



p=0,5, więc mamy log

2

(1/0,5) = log

2

2

Do jakiej potęgi należy podnieśd 2 aby
mied 2?  1

Mamy więc jeden bit informacji.

0

1

bit – elementarna jednostka informacji

W kontekście tego „układu” wartość 0
lub 1 stanowi informację o jego stanie.

Jednostkę taką nazywamy bit.

Dlaczego informatyk, gdy kładzie się spad, kładzie

obok siebie jedną szklankę pełną, a drugą pustą?

Bo albo mu się będzie chciało pid, albo nie…

Ponumerujmy
4 stany

00

01

10

11

Potrzebujemy 2 bitów do
zapisania wszystkich stanów.

A gdyby były 3 stany:

00

01

10

W tym wypadku
potrzebujemy około
log

2

(1/0,5) ~= 1,6 *bitów+.

Niestety nie ma bitów
„częściowych” więc musimy
wykorzystad dwa.

Jeden z ciągów (11) nie
będzie wykorzystany.

Dalej jest analogicznie:

10 stanów  4 bity
20 stanów  5 bitów
100 stanów  7 bitów
1000 stanów  10 bitów
50 000 stanów  16 bitów

itd….

Zapis taki nazywa się

zapisem binarnym

.

Organizacja informacji

OIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOIOIIOOOOOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOO
OIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOOOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIII
OIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOOOIIOOIOIOIIIIOOIIOIOIIOIOIIOIIIIOOIIOOOOOIOIIIOOOIIIIIO
OOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOOOOIIIIOOIIOI
OIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOOO
OIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIOIOII
OIOOOOOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOO
OIIIOIOIOIIOIOOOOOIIOOIOIOIIIIOOIIOIOIIOIOIIOIIIIOOIIOOOOOIOIIIOOOIIIIIOOOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOOOIIOIOO
OIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOOOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIO
OOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOOOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOII
IIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOOOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOI
OIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOOOIIOOIOIOIIIIOOIIOIOIIOIOIIOIIIIOOIIOOOOOI
OIIIOOOIIIIIOOOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOO
OOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIO
IOIIOIOOOOOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIII
OOOIIIOIOIOIIOIOOOOOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOI
OOOIOOIIIOOOIIIOIOIOIIOIOOOOOIIOOIOIOIIIIOOIIOIOIIOIOIIOIIIIOOIIOOOOOIOIIIOOOIIIIIOOOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOII
IOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOOOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIO
IOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOOOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOI
OIOIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOOOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIO
OIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIOIOIIOIOOOOOIIOOIOIOIIIIOOIIOIOIIOIOIIOIIIIO
OIIOOOOOIOIIIOOOIIIIIOOOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIOIIOIOOOIOOIIIOOOIIIOIO
IOIIOIOOOOOOIIIIOOIIOIOIIOIOIIOIIIIOOIIIIOIOIOIOOOIOOIOOIOIOIOIOIOOIOIOIIIIIOIOIIIOOOOIIOIOOOIOIIOIOIOIOIIIOIOIIIIOIOIIIOIOIOIIOIOIOI
OIOIOIOIIIIOIOIOIOIO

…

Informacja „wewnątrz” systemów
informatycznych zapisana jest
w postaci binarnej.

Jak nadad jej wartośd „użyteczną”???

Należy wprowadzid „jakiś porządek”

Organizacja informacji

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

…

Można dokonad podziału na fragmenty
stałej wielkości
(np. 8-bitowe)

ale…

„Jak bardzo” różni się
OOIIO

od

IIOO

od

OIOI

od

OIII …?

Organizacja informacji

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

…

Ważne są:

- wartośd bitu (o lub I)
- pozycja bitu

OOOI - jedynka na

prawej

pozycji

IOOO - jedynka na

lewej

pozycji

Organizacja informacji

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

…

Musimy przyjąd, która strona jest

ważniejsza

Bity z ważniejszej strony nazywamy

bardziej znaczącymi

Bity z mniej ważnej strony nazywamy

Mniej znaczącymi

OOOI - jedynka na

prawej

pozycji

IOOO - jedynka na

lewej

pozycji

Organizacja informacji

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

…

Jaką sumę wolelibyście mied na koncie:

11000011010100000 $

czy

00000001111101000 $

Najczęściej przyjmuje się lewą stroną

jako ważniejszą

Jaką sumę wolelibyście mied na koncie:

100 000 $

czy

1000 $

Organizacja informacji

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOI

IIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOI

OOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OLIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOO

O

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IO

OIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIO

O

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

OIIOIOOO

I

IOOIIIOO

I

…

Nie istnieje

JEDEN

unikalny sposób uporządkowania

bajtów

w pamięci lub w czasie transmisji.

Istnieją

DWA

BIG

end

ian

LITTLE

end

ian

Systemy komputerowe wykorzystują

obie koncepcje

…co często przyprawia informatyków

o zawrót głowy.

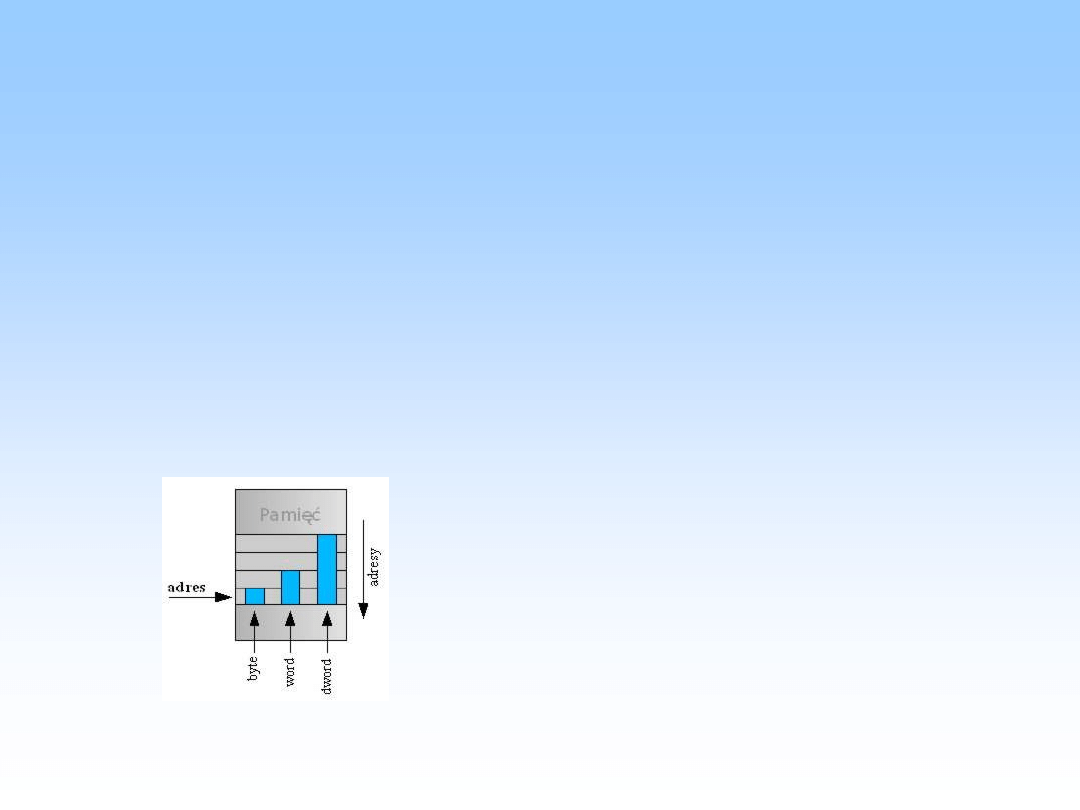
Big Endian

• Big endian (spotykane także "grubokońcowość") to forma zapisu

danych w której najbardziej znaczący bajt znajduje się jako pierwszy.
Na przykład słowo 0xA0B70708 (w zapisie szesnastkowym) zapisane
jest jako ciąg bajtów A0 B7 07 08. To znaczy, "najbardziej znaczący
bajt" (w tym przypadku A0) zapisanym jest w pamięci pod najniższym
adresem.

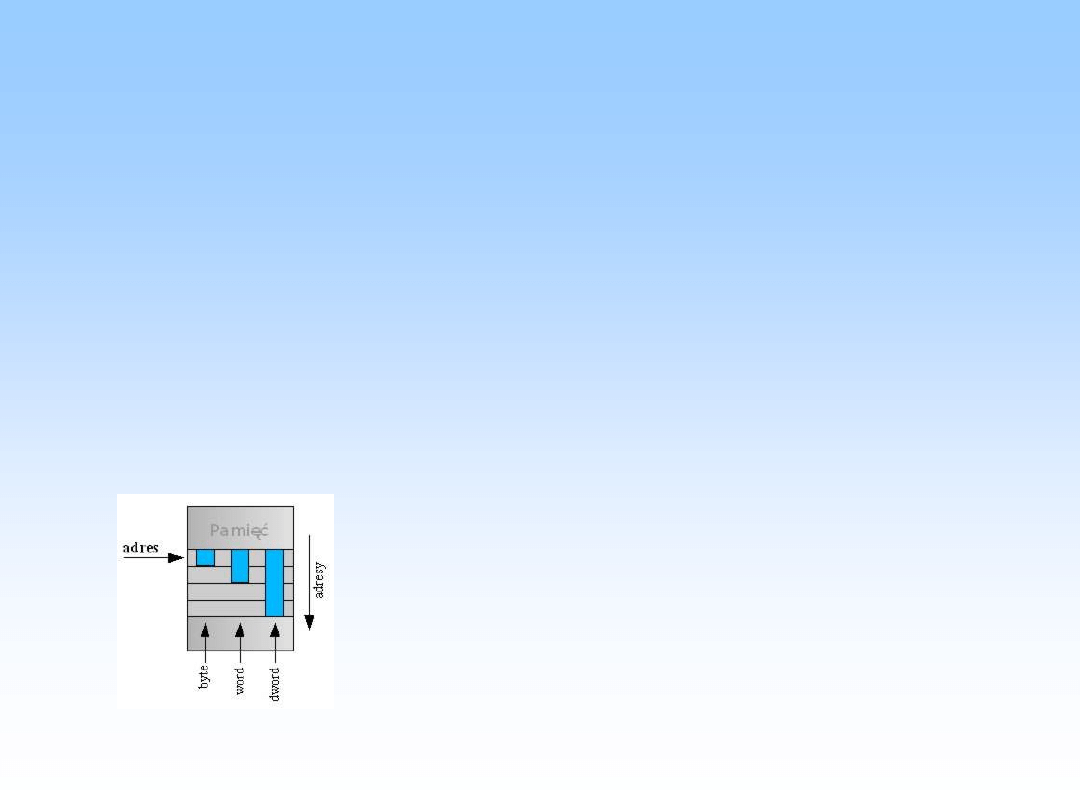
Little Endian

• Little endian (spotykane także "cienkokońcowość") to forma zapisu

danych w której mniej znaczący bajt znajduje się jako pierwszy. Na
przykład słowo 0xA0B70708 (w zapisie szesnastkowym) zapisane jest
jako ciąg bajtów 08 07 B7 A0. To znaczy, "najmniej znaczący bajt" (w
tym przypadku 08) zapisany jest w pamięci pod najniższym adresem.

Ciągom bitów przypisuje się konkretne wartości:

0

 0

10000

 16

1

 1

10001

 17

10

 2

10010

 18

11

 3

10011

 19

100

 4

10100

 20

101

 5

10101

 21

110

 6

10110

 22

111

 7

10111

 23

1000

 8

11000

 24

1001

 9

11001

 25

1010

 10

11010

 26

1011

 11

11011

 27

1100

 12

11100

 28

1101

 13

11101

 29

1110

 14

11110

 30

1111

 15

11111

 31

Zapis binarny jest ściśle związany z potęgami

liczby dwa

Wartości bitów na poszczególnych pozycjach w zapisie binarnym
odpowiadają kolejnym potęgom liczby

2

:

…0 1 1 0 1 0

…
2

5

= 32

2

4

= 16

2

3

= 8

2

2

= 4

2

1

= 2

2

0

= 1

=

0

*32 +

1

*16+

1

*8 +

0

*4 +

1

*2 +

0

*1

= 26

Bit, bajt, kilobajt, megabajt…

Ciągi symboli grupuje się w większe jednostki.
Szczególne znaczenie ma

8 bitów

, które tworzy

tzw.

BAJT

Bajt

przyjmuje wartości od

00000000

do

11111111

czyli od

0

do

255

dziesiętnie.

Np. 10101100  odpowiada wartości 172

Jednostki 4, 8, 16, 32 i więcej bajtów

nazywa się często

SŁOWAMI

lub

OKTETAMI

Bit, bajt, kilobajt, megabajt…

Co można zapamiętad w jednym bajcie?

- Liczby dziesiętne w małym przedziale, np. -100 do

200, czy 0 do 255;

- Pojedynczy znak z klawiatury (zgodnie z tzw. tabelą

ASCII

) np.: ‘a’, ‘4’, ‘*’;

Składając bajty w dłuższe ciągi można zapamiętywad

dowolne liczby czy teksty, np.:

„Ala ma kota” da się zapisad w 11 bajtach.

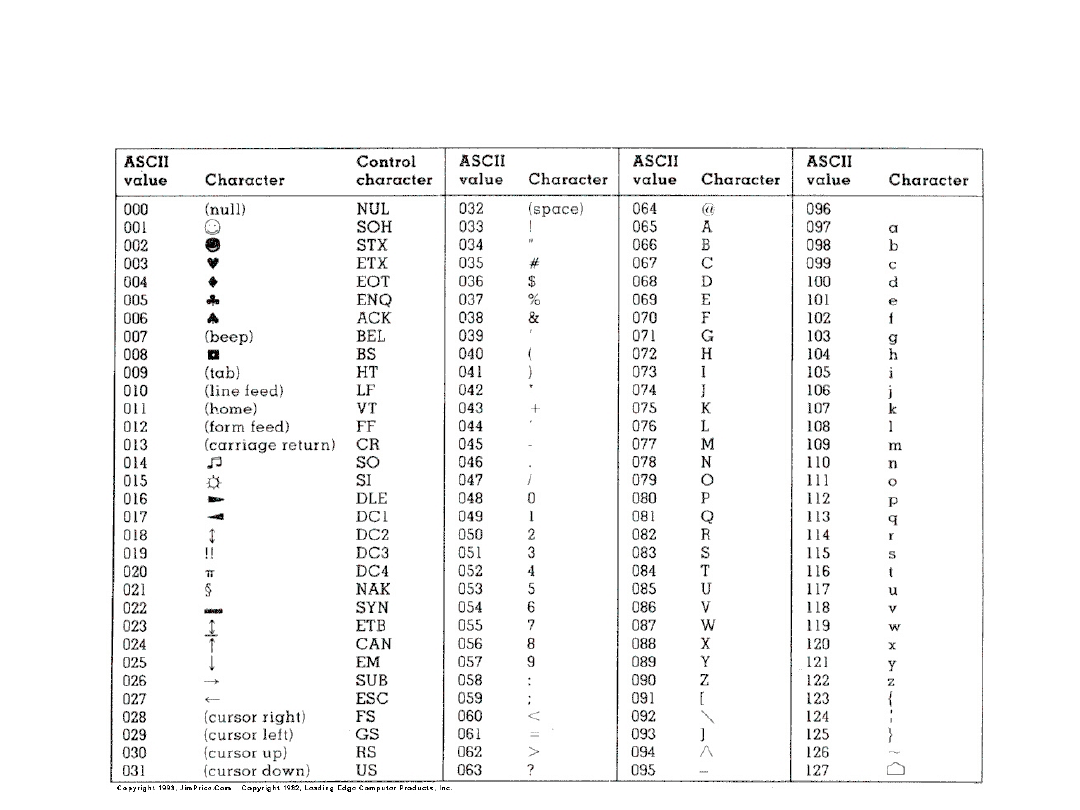
Tabela ASCII

Bit, bajt, kilobajt, megabajt…

Bajty grupowane są w większe jednostki.

1024 bajty to kilobajt [kb]
1024 kb to megabajt [Mb]
1024 Mb to gigabajt [Gb]
1024 Gb to terrabajt [Tb]

Do zastanowienia: dlaczego 1024 a nie 1000 ???

Rozmawia dwóch informatyków:

Pożycz mi 1000 złotych

…

Dobra…

Ale pożyczę ci 1024 złotych

dla równego rachunku.

Bit, bajt, kilobajt, megabajt…

Ile zmieści się w

kilobajcie?

Ala ma kota a kot ma Alę. To jest zbiór testowy. W tej perspektywie,
informacja

jest

indywidualną

lub

grupową

interpretacją

otrzymanego ciągu sygnałów (np. dźwiękowych czy optycznych) i

musi zawsze opisywad stan jakiejś dziedziny. Podejście

kognitywistyczno-systemowe w meta-teorii TOGA)[1] daje nam ścisłe

definicje rozróżniające dane, informacje, wiedzę i preferencje jako

podstawowe

funkcjonalne

elementy

procesów

myślowych

naturalnych i sztucznych (zobacz też: Sztuczna inteligencja). W tej

systemowej interpretacji, informacja jest przetwarzana przez naszą

wiedzę i w wyniku daje inną informację lub nową wiedzę. W

zależności od tzw. indywidualnego systemu konceptualizacji, ten sam

ciąg sygnałów/znaków (danych) może byd źródłem różnych

informacji dla różnych osób lub robotów. Jeśli grupa ludzi lub

społeczeostwo ma w pewnej dziedzinie ten sam system

konceptualizacyjny (np. teorie, zbiory poglądów, definicje), to te

same sygnały komunikacyjne odbierają w ten sam sposób, to znaczy

dostarczają im one tą samą informację do przetwarzania.

Ten tekst
zajmuje około 1kb.

Bit, bajt, kilobajt, megabajt…

Ile zmieści się w

megabajcie?

Szkoła podstawowa w Karlinie.
W 1Mb zmieszczą się szczegółowe
Informacje dotyczące wszystkich
uczących się dzieci.

oraz:

• tekst niewielkiej książki
• kilka niezbyt dużych zdjęd
•1000 tekstów piosenek
• 2000 dowcipów
• 5000 przysłów i powiedzonek
• 3 obszerne kazania teściowej

Bit, bajt, kilobajt, megabajt…

Ile zmieści się w

terrabajcie?

• odtworzenie filmów znajdujących się na płytach DVD o łącznej pojemności jednego
terabajta zajęłoby około pół roku

• w bardzo dużej bibliotece wszystkie książki zawierają łącznie około jednego
terabajta tekstu

Tak olbrzymie pojemności danych są już powszechnie dostępne!!!

Systemy liczbowe

System liczbowy

to zbiór reguł jednolitego zapisu liczb.

Do zapisywania liczb zawsze używa się pewnego

skooczonego zbioru znaków, zwanych cyframi, które

można zestawiad ze sobą na różne sposoby otrzymując

nieskooczoną liczbę kombinacji.

Najbardziej prymitywnym systemem liczbowym jest

jedynkowy system liczbowy

, w którym występuje tylko jeden

znak. Kolejne liczby są tworzone przez proste powtarzanie tego
znaku.
Np. 3 w tym systemie jest równe 111, a pięd 11111.
Systemem takim posługują się np.

PIGMEJE

.

Inne systemy liczbowe

Systemy liczbowe można podzielid na:

•

Addytywne, w których liczby tworzy się przez dodawanie kolejnych symboli i stąd

ich nazwa. Przykładem addytywnego systemu jest dobrze znany i wciąż stosowany

rzymski system liczbowy.

•

Pozycyjne, które posiadają symbole

n

liczb naturalnych: 0, 1, 2, ..., n − 1, gdzie n to

tzw.

podstawa systemu

, która może byd dowolną liczbą naturalną większą niż 1.

Sześddziesiątkowy system liczbowy

, stosowany był Mezopotamii,

w którym podstawowymi wielokrotnościami były 10 i 60. Był on
częściowo addytywny, częściowo pozycyjny.
W życiu codziennym spotykamy ślady babilooskiego systemu w
podziale godziny na 60 minut, a minuty na 60 sekund, oraz w
podziale kąta na minuty i sekundy kątowe.

Systemy pozycyjne

W systemach pozycyjnych

cyfry są umieszczane w ściśle określonych

pozycjach

i

mnożone przez odpowiednią potęgę n

dają odpowiednią

wartośd

.

W sytuacji, gdy dana potęga nie jest potrzebna do zapisu danej liczby,

wstawia się

specjalny symbol

. Współcześnie jest to cyfra 0.

Na przykład liczbę 5004 w dziesiętnym systemie liczbowym

(czyli systemie, którego podstawą jest 10) odczytuje się jako:

5×1000+0×100+0×10+4×1=5004.

Pytanie za 100 punktów:

Do którego z systemów zalicza się system binarny?

System dziesiętny

Dlaczego system dziesiętny jest dla ludzi tak naturalny?

System dziesiętny

Ciekawe, jaki system by się przyjął, gdyby ludzie mieli

inną liczbę palców?

System dwójkowy

System naturalny dla współczesnych maszyn cyfrowych.

• minimalizacja (do dwóch) liczby stanów pozwoliła na

zminimalizowanie przekłamao danych

;

• pasuje do cyfrowych urządzeo technicznych, na zasadzie:

jest

napięcie/nie ma napięcia

Liczby w systemach niedziesiętnych oznacza się często indeksem

dolnym zapisanym w systemie dziesiętnym, a oznaczającym

podstawę danego systemu. W celu podkreślenia, że liczba jest

dziesiętna można również napisad obok niej indeks.

Np. 1011

2

= 12

10

Stosuje się też inne oznaczenia –

dec

dla systemów dziesiętnych,

hex

dla szesnastkowych

System ósemkowy

Dawniej często wykorzystywany do skrócenia zapisu

binarnego.

Obecnie chętniej stosuje się zapis szesnastkowy.

144

8

= 1×8

2

+ 4×8

1

+ 4×8

0

= 64 + 32 + 4 = 100

10

System szesnastkowy

heksadecymalny (HEX)

Do zapisu liczb potrzebne jest szesnaście znaków.
Poza cyframi dziesiętnymi od

0

do

9

używa się pierwszych sześciu liter alfabetu

łacioskiego:

A, B, C, D, E, F

.

Hex

jest powszechnie używany w informatyce:

-

Zastępuje zapis binarny. Wartośd pojedynczego bajtu można opisad używając tylko

dwóch cyfr szesnastkowych. W ten sposób można kolejne bajty łatwo przedstawid

w postaci ciągu liczb HEX;

-

Służy do przeglądania zawartości „surowej” pamięci komputerów;

-

Służy do oznaczania kolorów w grafice komputerowej (kolory RGB zapisuje się jako 3

liczby HEX od 0 do FF(255) poprzedzone znakiem #, np. różowy - #FF8080). Zapis ten

stosuje np. w HTML (do opisu wyglądu stron internetowych);

65.536

dec

= 1.0000

hex

16.777.216

dec

= 100.0000

hex

65.535

dec

= FFFF

hex

4.294.967.295

dec

= FFFF.FFFF

hex

Reprezentacja ujemna liczb binarnych

Aby zapisad liczby ujemne w systemie

binarnym w komputerze stosuje się

kod

uzupełnieo do dwóch

.

W celu wyodrębnienia liczb ujemnych

pierwszy bit liczby binarnej stanowi o jej

znaku

: ‘0’ oznacza ‘+’, ‘1’ oznacza ‘–‘.

Ważne jest przy tym ustalenie ilości bitów

przeznaczonych na zapis liczby.

Algebra Bool’a

George Boole ur. 1815 roku

Przyszedł na świat jako syn szewca. Nauczył się greki, francuskiego,

niemieckiego i włoskiego. Postanowił zostad duchownym… najpierw jednak

założył prywatną szkołę. Zaczął też pracowad jako nauczyciel matematyki.

Opublikował wiele książek i artykułów z matematyki i logiki.

W wieku 35 lat poznał osiemastoletnią Mary Everest zaopiekował się nią i…

poślubił.

24 listopada 1864 Boole jak zwykle przebył pieszo trzy kilometry na uczelnię.

Tego dnia padał jednak ulewny deszcz, więc cały dzieo spędził w mokrym

ubraniu, co sprawiło że się przeziębił.

Mary Boole wierzyła, że najlepszym sposobem walki z chorobą jest wystawienie

chorego na jej przyczynę, regularnie polewała więc łóżko męża wodą.

George Boole nie przeżył kuracji, zmarł po dwóch tygodniach…

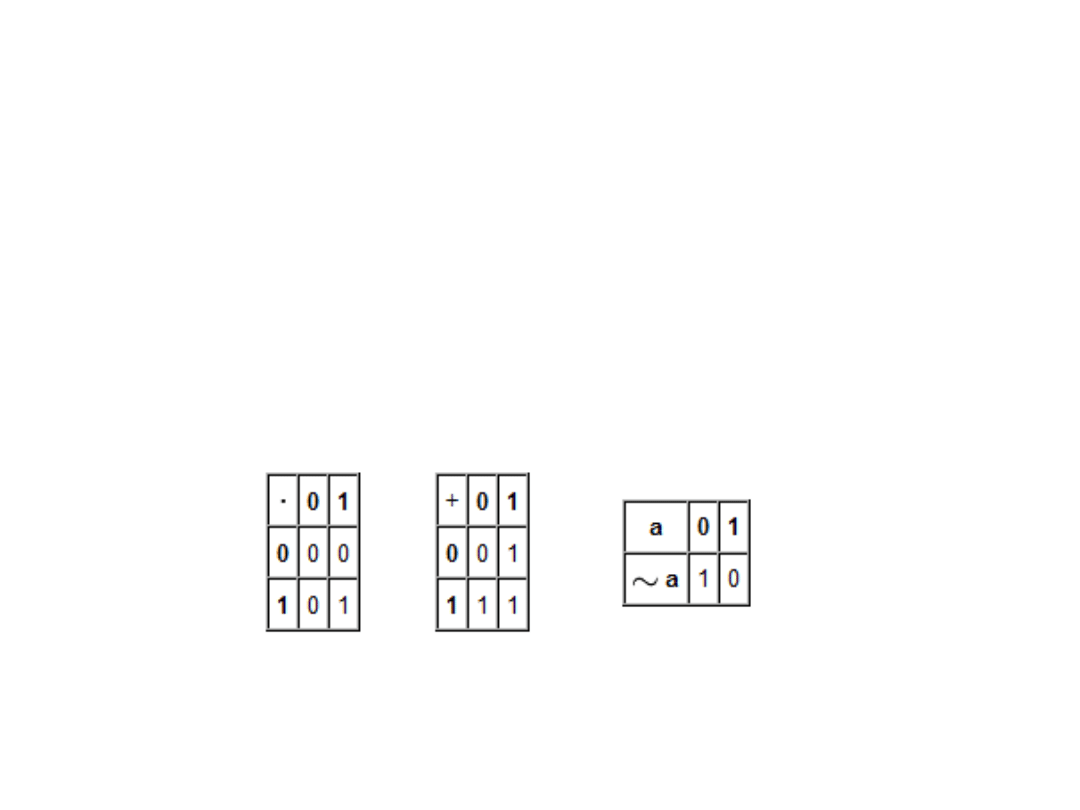
Algebra Bool’a

…pomijając ścisła definicję matematyczną

algebra Boole'a ma tylko dwa elementy, "

0

" i "

1

",

a operacje tej algebry są zdefiniowane przez
następujące tabele działao:

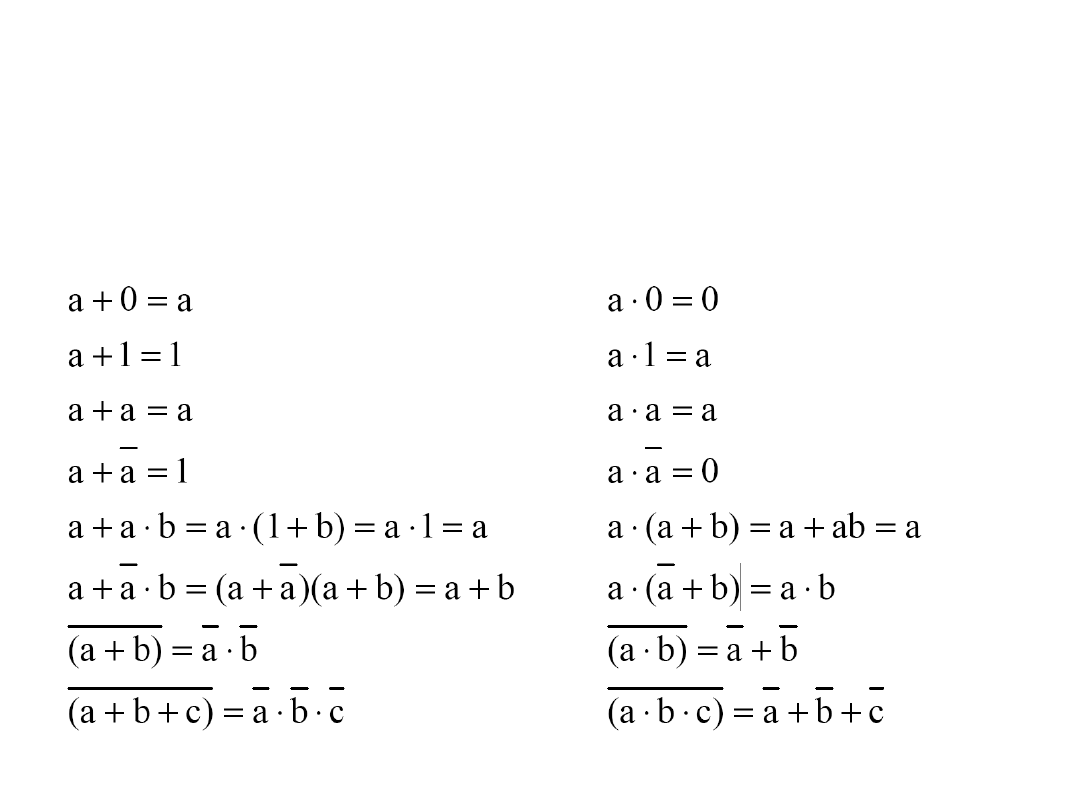
Algebra Bool’a

Podstawowe twierdzenia algebry Bool’a:

Algebra Bool’a

• Algebra Bool’a stanowi podstawę techniki cyfrowej.
• Elementarnymi podzespołami komputera są

bramki

,

działające zgodnie z zasadami algebry Bool’a. Są to elementy
wykonujące określone operacje na pojedynczych bitach
(AND, OR, NEGACJA)

• Budując złożone układy z bramek umożliwia się

przetwarzanie

informacji zapisanej w postaci binarnej

.

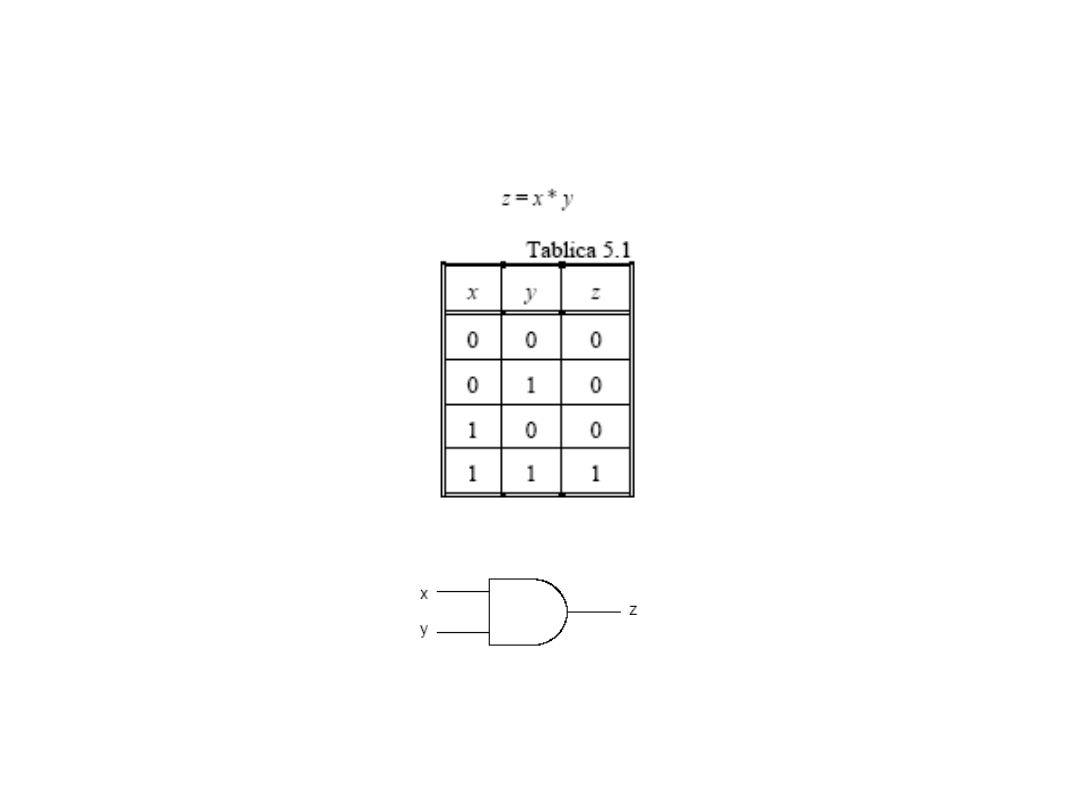
Bramka AND

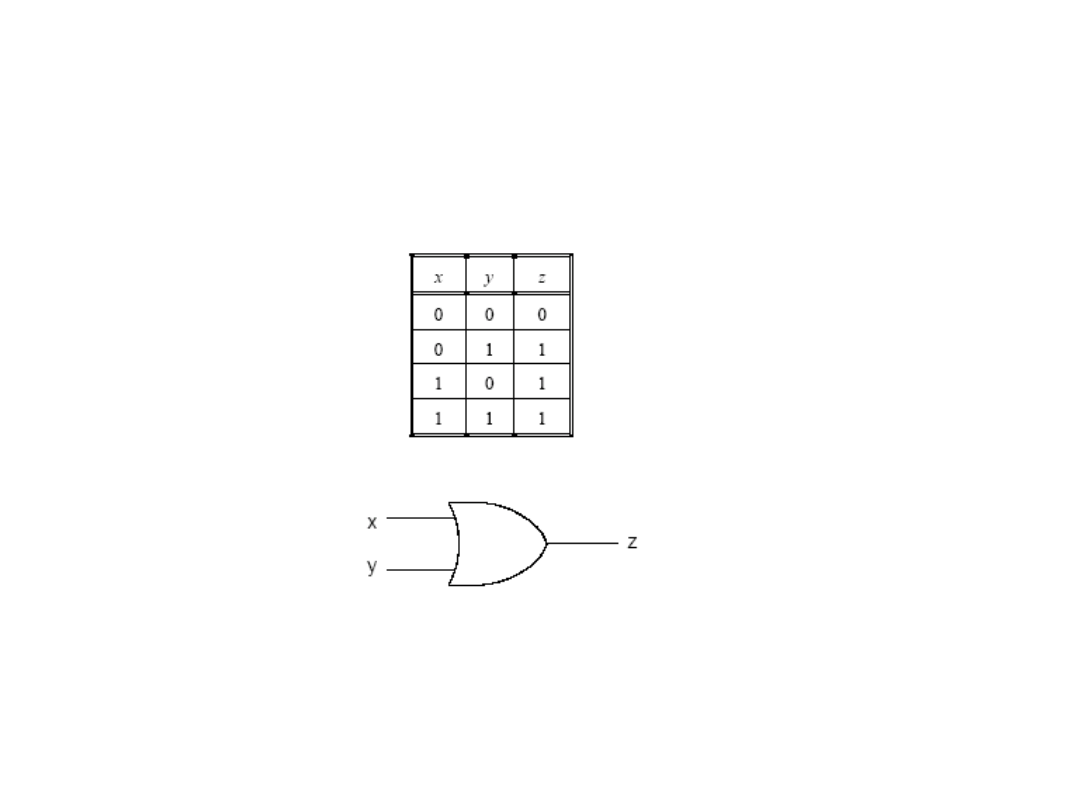
Bramka OR

Z = X + Y

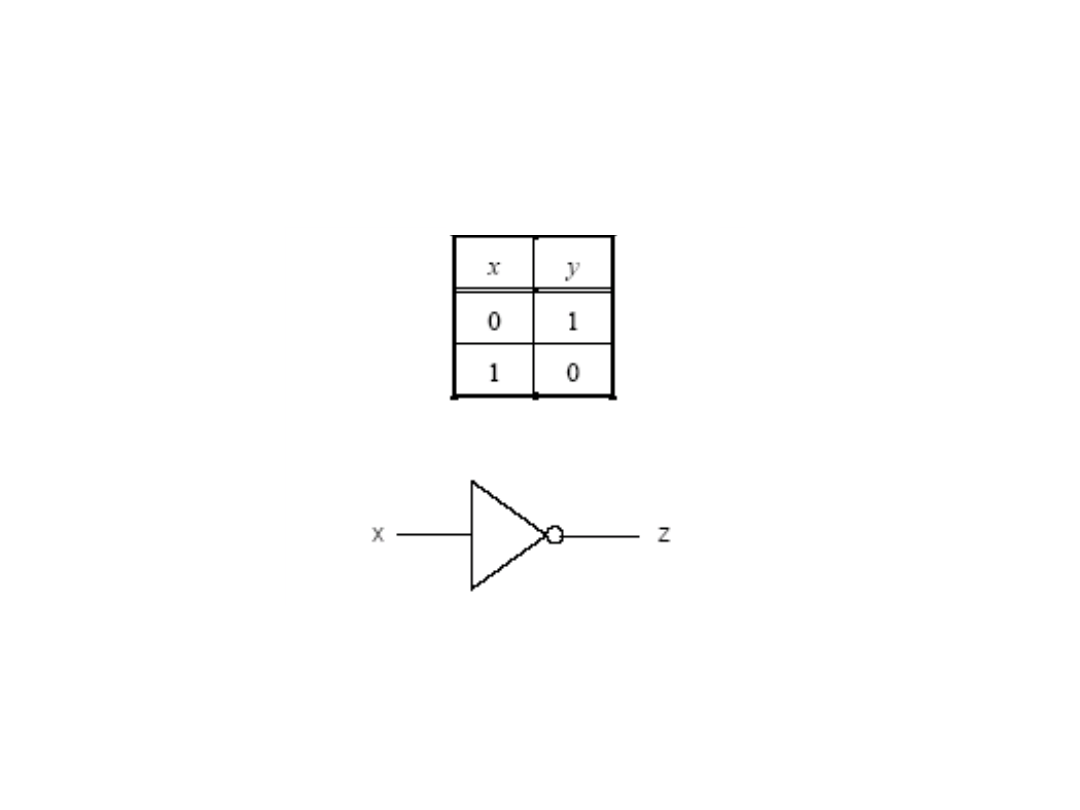
NEGACJA

Z = NIE X (~X)

Algebra Bool’a

Arytmetyka układów cyfrowych

• Realizację podstawowych działań arytmetycznych na

liczbach można sprowadzić do operacji bool’owskich na
ciągach binarnych.

• Różnica w stosunku do arytmetyki w klasycznej

informatyce są ograniczone zbiory liczb.

(na kalkulatorze też nie możemy np. mnożyć do
w nieskończoność)

Informacja

Podsumujmy:

• Informacja opisuje pewien stan.
• Przyjmuje się określony sposób zapisu informacji.
• Służą do tego systemy liczbowe.
• W systemach informatycznych najczęściej zapisuje się

informacje w postaci binarnej.

• Podstawą operacji na informacjach binarnych jest

algebra Bool’a

To wszystko dotyczyło

informacji

.

I co dalej…?

Problem językowy:

Angielską nazwę

computer science

można dosłownie tłumaczyd

jako nauka o komputerach. Jest to mylące
i krytykowane w środowiskach akademickich.

W języku polskim termin ten zaproponował w październiku 1968 r.
Romuald Marczyoski w Zakopanem na ogólnopolskiej
konferencji poświęconej "maszynom matematycznym"
(na wzór fr. informatique i niem. Informatik).

Informatyka

Informatyka

Przetwarzanie

Przechowywanie

Przesyłanie

Informatyka jest nauką o przechowywaniu,

przetwarzaniu i przesyłaniu informacji

A gdzie tu miejsce na komputery…?

Organizacji procesów przechowywania,

przetwarzania i przesyłania informacji służą

systemy informatyki.

Komputery są systemami informatyki

o określonym sposobie zapisu informacji

i algorytmów opierając się na odpowiedniej

strukturze urządzeniowej.

Przepis

Składniki

Czynności

Przetwarzanie informacji

Algorytmy

w znaczeniu potocznym są listą czynności

przeznaczonych do wykonania przez człowieka (bądź maszynę) na
określonych obiektach (składniki przyrządzanej potrawy, współczynniki
równania kwadratowego). Rezultatem wykonania tej listy jest wynik
(przyrządzona potrawa, rozwiązanie równania).

Słowo "algorytm" pochodzi od nazwiska
Muhammed ibn Musa Alchwarizmi (

) matematyka perskiego

z IX wieku

Przetwarzanie informacji

Komputery przetwarzają informacje z wykorzystaniem algorytmów.

Każdy algorytm komputerowy musi być wprowadzony do komputera

w bardzo rygorystycznie zdefiniowanym języku. Ludzie często

komunikując się przesyłają między sobą

informację wieloznaczne

.

Komputery mogą reagować tylko na całkowicie jednoznaczne instrukcje.

Do tego celu służą

języki programowania

, w których pisze się programy.

Program jest algorytmem zapisanym w języku zrozumiałym dla maszyny

.

Przetwarzanie informacji

Współczesne komputery pracują zgodnie z koncepcją von Neumana:

Polega na ścisłym podziale komputera na trzy podstawowe części:

• procesor (w ramach którego wydzielona bywa część sterująca oraz
część arytmetyczno-logiczna)
• pamięć komputera (zawierająca dane i sam program)
• urządzenia wejścia/wyjścia

…a to dokładniej w dalszej części wykładów o architekturze

systemów komputerowych

Przechowywanie informacji

Co dzień na głowę wody kubełek
oraz na trąbie zrobić supełek".
I chlust go wodą! Sekundę trwało
I w supeł związał trąbę wspaniałą!

Informację na ogół trzeba zapamiętać.

W zależności od ilości i rodzajów informacji sposoby

zapamiętywania będą się różnić.

Przechowywanie informacji

czy

Jak dużo informacji chcemy przechowywać?

Przechowywanie informacji

Czy mamy tyle czasu?

A może ważna jest trwałość?

Jak szybko możemy zapisać informacje?

Przechowywanie informacji

Na takiej żółtej karteczce
Był numer telefonu szefa…

Jak szybko odczytać informacje?

Przechowywanie informacji

Nawet w ujęciu systemów komputerowych problem przechowywania

informacji jest bardzo złożony i szeroki.

-Pamięci fizyczne: wewnętrzne, zewnętrzne…
-Struktury danych, rekordy, pliki…
-Systemy baz danych

Przesyłanie informacji

Sied komputerowa

-

grupa urządzeo połączonych ze

sobą w celu wymiany danych lub współdzielenia różnych zasobów

.

Różne języki…
Konieczność zapisania
informacji…
Adres…
Wybór drogi przez gońca…
Wymóg potwierdzenia
otrzymania…

…i to samo w drugą stronę

Milionów $ na koncie.

Kontekst informacji

„Czyta” informacja, zapisana w ciągach bitów, pozbawiona jest znaczenia (kontekstu).

Systemy informatyki z zasady przetwarzają informację bez zwracania
uwagi na jej znaczenie (semantykę).

Dla systemów informatyki informacje są jedynie ciągami bitów przetwarzanymi
przez odpowiednie operacje (algorytmy, programy).

Znaczenie nadają jej użytkownicy tych systemów.

0110 -> 6

informacja

kontekst

zł. w kieszeni.

o

C dziś w nocy.

Systemy liczbowe

Systemy liczbowe

Systemy liczbowe

to sposoby zapisywania i nazywania

liczb.

Rozróżnia się systemy liczbowe

pozycyjne

i

niepozycyjne

(addytywne).

W systemach liczbowych pozycyjnych liczbę przedstawia

się jako ciąg cyfr. Wartość jej jest zależna od położenia
(pozycji) cyfry w liczbie.

Do systemów pozycyjnych zaliczamy m.in.:

dziesiątkowy, dwójkowy, ósemkowy, szesnastkowy.

Do addytywnych systemów liczbowych zaliczamy m.in.:

rzymski, hieroglificzny, alfabetyczny, gdzie wartość
liczby jest sumą wartości jej znaków cyfrowych.

Definicja liczby

Liczba

– pojęcie abstrakcyjne, jedno z najczęściej

używanych w matematyce.

Określenie „liczba” bez żadnego przymiotnika jest

nieścisłe, gdyż matematycy nie definiują „liczb”, lecz
„liczby naturalne”, „liczby całkowite”, itp.

Poszczególne rodzaje liczb są definiowane za pomocą

aksjomatów lub konstruowane z bardziej podstawowych
pojęć, takich jak zbiór, czy typy liczb prostsze od
konstruowanego.

Pierwotnie liczby służyły do porównywania wielkości

zbiorów przedmiotów (liczby naturalne), później także
wielkości ciągłych (miary i wagi), obecnie w
matematyce są rozważane jako twory abstrakcyjne, w
oderwaniu od ewentualnych fizycznych zastosowań.

System pozycyjny – wzór ogólny

Ogólnie oznaczając przez

c

n

- cyfrę systemu pozycyjnego i

n

– pozycję cyfry

zaś przez:

p

- podstawę systemu,

wartość reprezentowaną przez symbol liczby zapisujemy

jako sumę iloczynów postaci:

c

n

*

p

n

+ . . . + c

2

*

p

2

+ c

1

*

p

1

+ c

0

*

p

0

System dziesiątkowy

(

decymalny

)

System dziesiątkowy

System dziesiątkowy

: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

- to wszystkim znane symbole cyfr arabskiego

dziesiątkowego, pozycyjnego systemu liczenia.

Każdemu z tych symboli przyporządkowana jest pewna

wartość.

Z tych prostych symboli tworzymy symbole bardziej

złożone wpisując cyfry na tzw. pozycje, w
uszeregowaniu od prawej do lewej.

I tak najbardziej skrajna prawa pozycja, to pozycja zerowa

(pozycja jedności), dalej pozycja pierwsza (pozycja
dziesiątek), dalej pozycja druga (pozycja setek), ... itd.

System dziesiątkowy

Zgodnie z przedstawioną zasadą, każdemu prostemu czy

złożonemu symbolowi układu można przyporządkować
wartość, zwaną liczbą.

Liczba to nie to samo co cyfra.

Cyfry to znaki graficzne służące do opisu liczb.

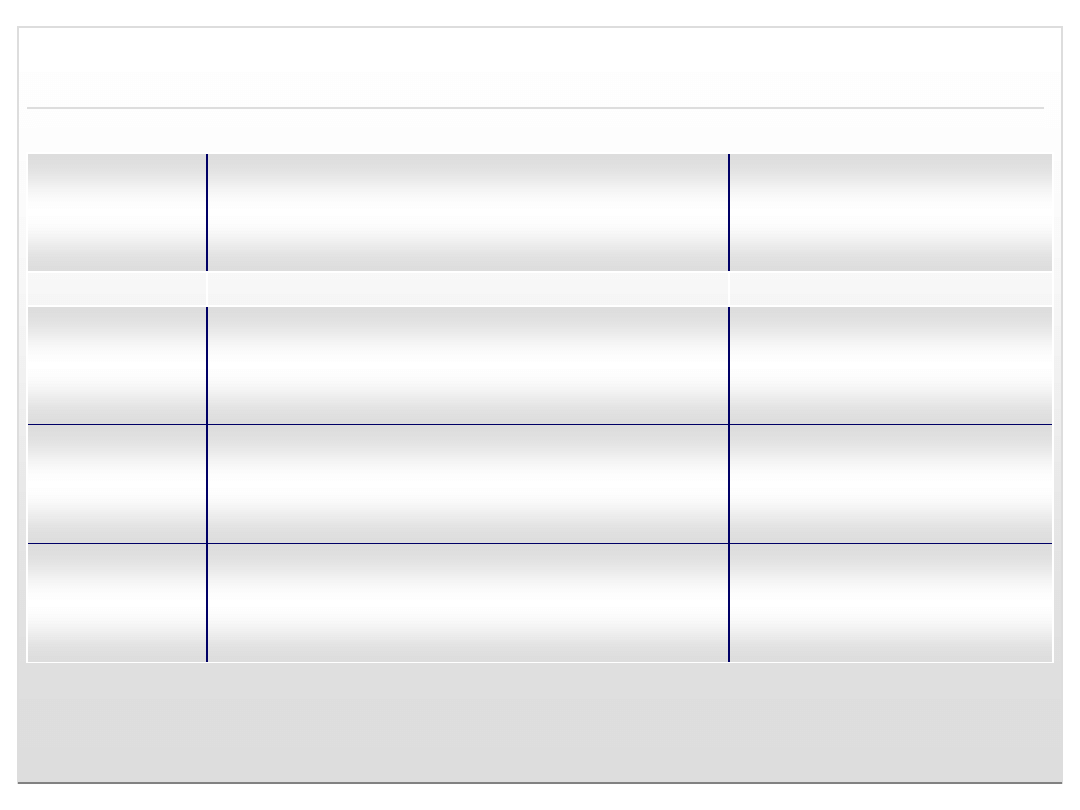
System dziesiątkowy

Symbol

Wartość w systemie Liczba

7

7 *10

0

siedem

56

5 * 10

1

+ 6 * 10

0

pięćdziesiąt sześć

342

3 * 10

2

+ 4 * 10

1

+2 * 10

0

trzysta
czterdzieści dwa

Konwersja liczb

Konwersja na dziesiątkowy:

(4013)

5

= 4 * 5

3

+ 0 * 5

2

+ 1 * 5

1

+ 3 * 5

0

= 500 + 5 + 3 = (508)

10

Konwersja z dziesiątkowego

System dwójkowy

(

binarny

)

System dwójkowy (binarny)

System dwójkowy

- zrewolucjonizował cały świat

techniki, dając podstawę rozwoju wiodącej obecnie
dziedzinie wiedzy jaką jest informatyka.

Cyframi tego systemu są: 0 i 1.

Symbolizują one dwa stany tzw.

0 -

stan niski

– (brak działania/brak sygnału)

1-

stan wysoki

– (działanie układu/sygnał)

Podstawą systemu jest 2.

Stąd też i nazwa układ dwójkowy.

Konwersja liczb

Ponieważ jest to również system pozycyjny, to możemy w
znany już sposób dokonywać konwersji liczby z systemu
dziesiątkowego na dwójkowy, np.

( 87)

10

= 87 : 2 = 43 1 = (1010111)

2

43 : 2 = 21 1
21 : 2 = 10 1
10 : 2 = 5 0
5 : 2 = 2 1
2 : 2 = 1 0
1 : 2 = 0 1

Konwersja liczb

Konwersja z systemu dwójkowego na dziesiątkowy:

(11011101)

2

= 1 * 2

7

+ 1 * 2

6

+ 0 * 2

5

+ 1 * 2

4

+ 1 * 2

3

+ 1 * 2

2

+ 0 * 2

1

+ 1 * 2

0

=

= 128 + 64 + 16 + 8 + 4 + 1 = (221)

10

System szesnastkowy

(

heksadecymalny

)

System szesnastkowy

Nawet niezbyt duża co do wartości liczba z systemu

dziesiątkowego zamieniona na postać dwójkową
(binarną) jest długim ciągiem jedynek i zer, a ponowne
przeliczenie jej na wartość w systemie dziesiątkowym
procesem żmudnym i długotrwałym.

Między innymi dla uproszczenia zapisu i szybkiego

przeliczenia wartości wprowadzono system pozycyjny,
którego podstawą jest 2

4

, czyli 16 i nazwano

systemem szesnastkowym (heksadecymalnym).

Cyframi tego systemu są:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

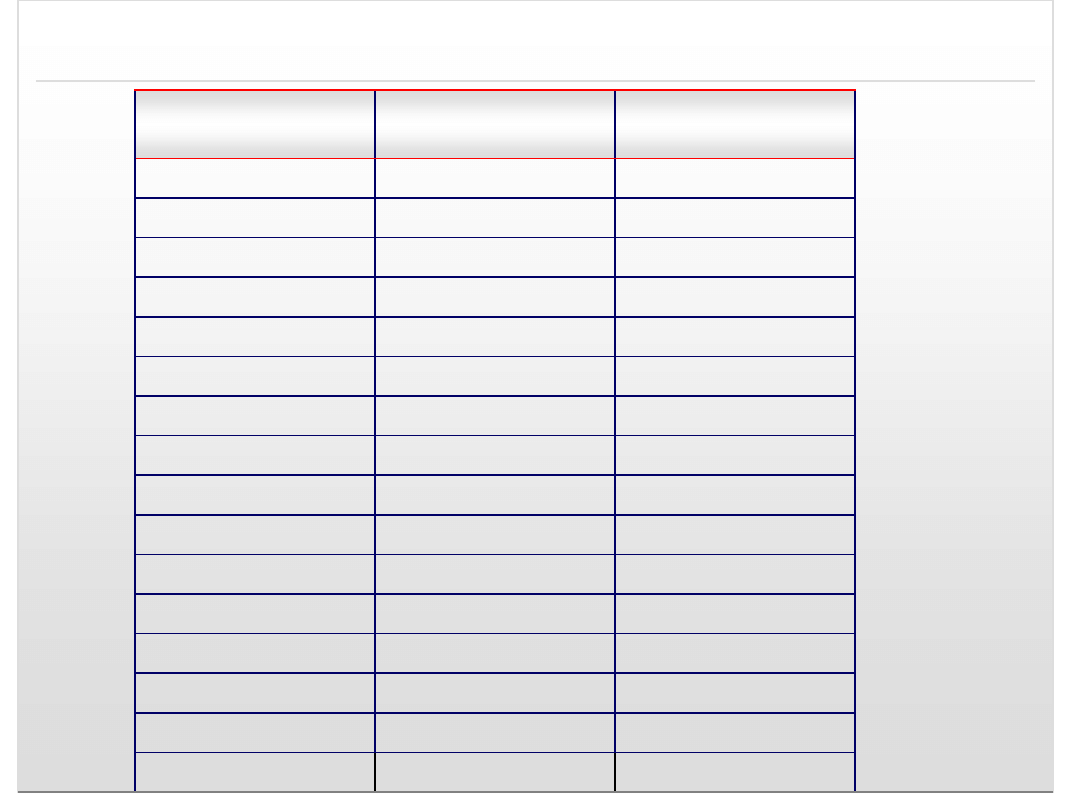
Zależność między liczbami

Cyfry systemu

szesnastkowego

Liczby systemu
dziesiątkowego

Liczby systemu

dwójkowego

0

0

0000

1

1

0001

2

2

0010

3

3

0011

4

4

0100

5

5

0101

6

6

0110

7

7

0111

8

8

1000

9

9

1001

A

10

1010

B

11

1011

C

12

1100

D

13

1101

E

14

1110

F

15

1111

Konwersje liczb na system binarny

Każdej cyfrze systemu szesnastkowego odpowiada cztero-

pozycyjna liczba systemu dwójkowego.

Zamiana postaci liczby z systemu dwójkowego na liczbę

systemu szesnastkowego polega na przypisaniu
każdemu kolejnemu cztero-pozycyjnemu pakietowi
układów zero-jedynkowych odpowiedniej cyfry układu
szesnastkowego, np.

(1011|0011|1010)

2

= (B3A)

16

Jeżeli w zapisie liczby dwójkowej ostatni /pakiet/ (z lewej)

ma mniej niż cztery pozycje zero-jedynkowe, to
uzupełniamy brakujące pozycje zerami, np.

(

11

|1011|1110)

2

= (

00

11|1011|1110)

2

= (3BE)

16

Konwersje liczb na system decymalny

Przeliczenie liczby z systemu szesnastkowego na wartość

liczby w systemie dziesiątkowym odbywa się według
znanego wzoru , np.

(3BE)

16

= 3 * 16

2

+ 11 * 16

1

+ 14 * 16

0

= 768 + 176 + 14 = (958)

10

Dodawanie dwójkowe

Dodawanie dwójkowe

Tabliczka dodawania binarnego

0

+

0

=

0

0

+

1

=

1

1

+

0

=

1

1

+

1

=

0

i

1

dalej

Ostatni wynik należy rozumieć następująco: 1 + 1 daje 0 w

bieżącej kolumnie i przeniesienie (ang. carry) jedynki do
następnej kolumny.

Przeniesienie dodawane jest do cyfry w następnej kolumnie -

zupełnie tak samo postępujemy w systemie dziesiętnym,
gdy wynik sumowania cyfr przekracza dziewięć.

Dodawanie dwójkowe

1101 13

+ 0010 +2

1111 15

0101 5

+ 0111 +7

1100 12

1001 9

+ 0011 +3

1100 12

Jeśli liczby binarne są zapisywane
ze stałym formatem (np. 8 bitów),
to może się zdarzyć, iż wynik
dodawania nie zmieści się w
dozwolonym zakresie liczb.
Sytuacja taka nazywa się

nadmiarem

(ang.

overflow

).

1010 10

+ 0110

+6

1

0000

16

Dodawanie dwójkowe

Wynik dodawania jest liczbą 5 bitową i nie mieści się w 4

bitach.

Jeśli ograniczymy go do 4 bitów, to otrzymamy wartość 0.

Wystąpił nadmiar.

Wynik został obcięty do reszty z dzielenia przez 16.

Zapamiętaj:

Nadmiar jest przekroczeniem górnej granicy zakresu liczb.
Dla liczb naturalnych mamy do czynienia z nadmiarem, gdy
pojawi się przeniesienie poza najstarszą pozycję liczby.

Dodawanie dwójkowe stałoprzecinkowe

W identyczny sposób dodajemy liczby stałoprzecinkowe.

Należy tylko pamiętać o ustawieniu przecinków w
jednej kolumnie i dopisaniu w razie konieczności zer
na początku części całkowitych i na końcu części
ułamkowych:

0011,011 3,375

+ 0111,110 + 7,750

1011,001

11,125

Odejmowanie dwójkowe

Odejmowanie dwójkowe

Tabliczka odejmowania binarnego

0

-

0

=

0

1

-

0

=

1

1

-

1

=

0

0

-

1

=

1

i pożyczka

Ostatni zapis należy rozumieć jako: 0 - 1 daje w bieżącej

kolumnie 1 i pożyczkę (ang. borrow) do następnej
kolumny.

Pożyczka jest odejmowana od cyfr w następnej kolumnie.

Odejmowanie dwójkowe

1111 15

- 0111 -7

1000 8

1011

11

- 0101 -5

0110 6

1101 13

+ 0011 +3

1010 10

0011 3

- 0100

-4

...11

1111

-1

Przy odejmowaniu wynik może
być liczbą ujemną. Ponieważ
omówione systemy zapisu liczb
binarnych nie uwzględniają
jeszcze liczb ujemnych, to w
takim przypadku wystąpi sytuacja
zwana

niedomiarem

(ang.

underflow

).

Odejmowanie dwójkowe

Zapamiętaj:

Niedomiar jest przekroczeniem dolnej granicy zakresu liczb.
Dla liczb naturalnych mamy do czynienia z niedomiarem,
gdy pojawi się pożyczka poza najstarszą pozycję liczby.

Liczba -1 leży poza zakresem liczb dla kodu 4 bitowego.
Dlatego nie może w tym kodzie być przedstawiona
prawidłowo i otrzymujemy wynik równy 15.

Wiodące jedynki powstają w tym przypadku w
nieskończoność, co zostało zaznaczone trzema
kropeczkami na początku wyniku odejmowania.

Mnożenie dwójkowe

Mnożenie dwójkowe

Tabliczka mnożenia binarnego

0

x

0

=

0

1

x

0

=

0

0

x

1

=

0

1

x

1

=

1

Mnożenie binarne wykonujemy identycznie jak w systemie

dziesiętnym - przemnażamy mnożną przez każdą cyfrę
mnożnika zapisując wyniki tego mnożenia odpowiednio
przesunięte.

Następnie wykonujemy dodawanie zgodnie z opisanym

wcześniej schematem:

Mnożenie dwójkowe

0011

3

x 0101

x 5

0011

0000

...

+ 0011

001111

15

Mnożenie dwójkowe

W systemie dwójkowym wynik mnożenia jest równy 1

tylko wtedy, gdy obie mnożone cyfry mają wartość 1.

W każdym innym przypadku otrzymujemy wartość 0.

Pozwala to znacznie uprościć schemat mnożenia.

Mnożną umieszczamy tylko w tych kolumnach, w których

w mnożniku występują cyfry 1.

Pozostałe kolumny pomijamy:

Mnożenie dwójkowe

1011

11

x 1101 x 13

1011

1011

33

+ 1011

+ 11

10001111

143

Uwagi na temat nadmiaru odnoszą się również do
mnożenia liczb binarnych.

Mnożenie dwójkowe

Mnożenie liczb
stałopozycyjnych
wykonujemy w
identyczny sposób, lecz
musimy pamiętać, aby
przy wyniku oddzielić
odpowiednią ilość cyfr
ułamkowych
przecinkiem - ilość ta
jest sumą liczby miejsc
po przecinku mnożnej i
mnożnika - tak samo jak
w systemie dziesiętnym.

10,1

2,5

x 11,01 x 3,25

101

125

101 50

+ 101

+ 75

1000001

1000,001

8125

8,125