1.

Zapisanie nierównoÊci w postaci:

x

x

2

5

3

2

-

-

-

G

.

1

Rozwiàzanie nierównoÊci w zbiorze liczb rzeczywistych:

,

x

4

3

3

4

1

!

c

m

.

1

Zapisanie wszystkich liczb ca∏kowitych spe∏niajàcych podanà nierównoÊç:

1

, ,

x

1 2 3

! #

-

.

2.

Zapisanie wielomianu w postaci

W x

a x

x

1

3

2

=

+

-

_

_

_

i

i

i

.

1

Wykorzystanie informacji

W 0

9

=

_ i

do podania wartoÊci wspó∏czynnika

d

1

i obliczenia wartoÊci wspó∏czynnika

a

:

,

d

a

9

1

=

=

.

Przekszta∏cenie wielomianu

W x

x

x

1

3

2

=

+

-

_

_

_

i

i

i

do postaci umo˝liwiajàcej

1

odczytanie wartoÊci pozosta∏ych wspó∏czynników i zapisanie:

,

b

c

5

3

= -

=

.

3.

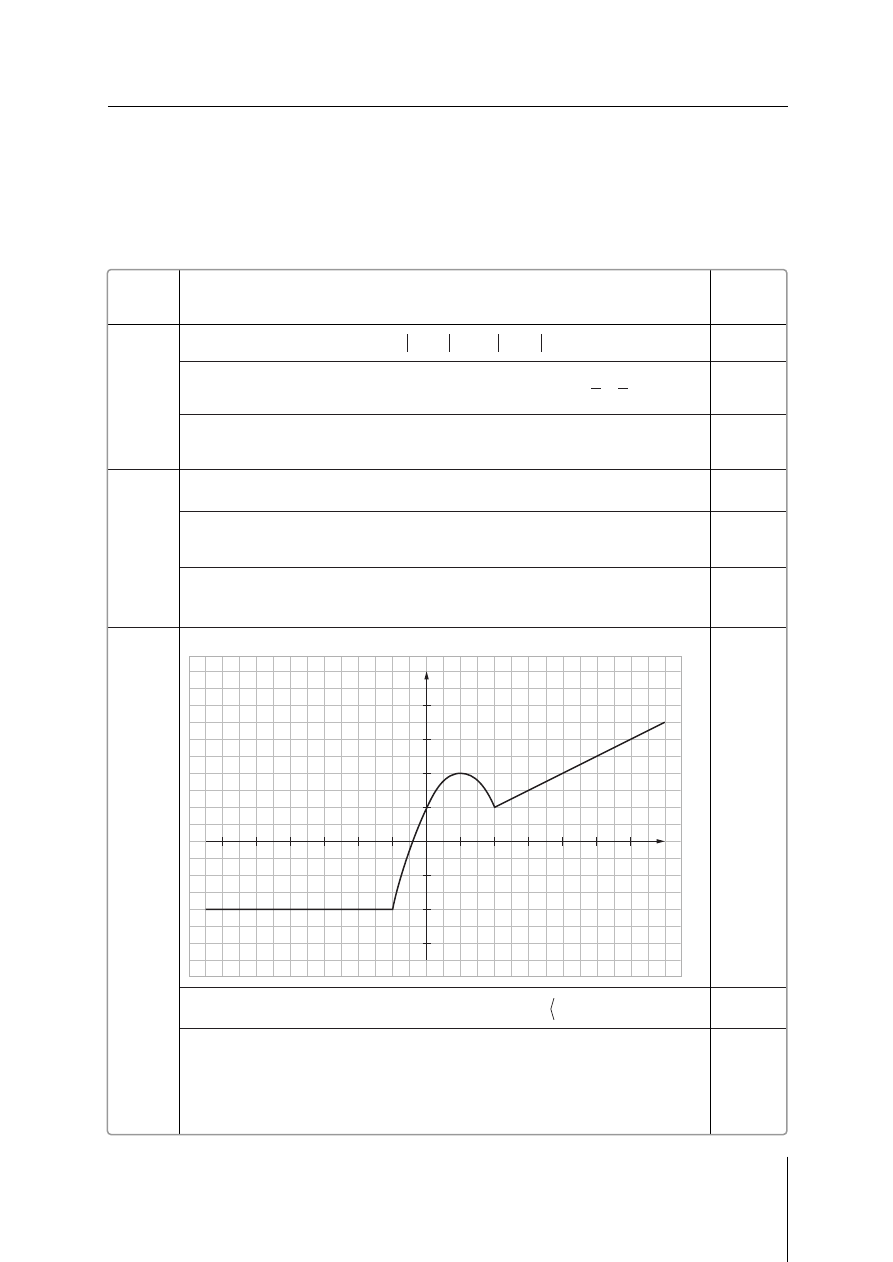
Narysowanie wykresu funkcji w zbiorze liczb rzeczywistych:

3

Zapisanie rozwiàzania nierównoÊci

f x

2

H

_ i

:

,

x

1

4

,

3

!

+

i

# -

.

1

Narysowanie wykresu funkcji

g

: np. przesuni´cie wykresu funkcji o

2

jednostki

2

w prawo

y

f x

2

=

-

_

i

i przekszta∏cenie otrzymanego wykresu w symetrii

wzgl´dem osi

OX g x

f x

2

= -

-

_

_

i

i

.

(po 1 pkt

za

narysowanie

wykresu

w ka˝dym

z przedzia-

∏ów)

X

Y

1

1

0

f

(po 1 pkt

za ka˝de

przekszta∏-

cenie)

1

w w w. o p e r o n . p l

Modele odpowiedzi do przyk∏adowego arkusza egzaminacyjnego

Matematyka

Poziom rozszerzony

Numer

Modelowe etapy rozwiàzywania zadania

Liczba

zadania

punktów

4.

Przedstawienie liczb

m

i

n

w postaci np.

m

k

r

7

=

+

,

n

l

r

7

=

+

, 1

gdzie

k

,

l

,

r

N

!

i

<

r

7

.

Wyznaczenie

(

)

m

n

k

l

kr

lr

7 7

7

2

2

2

2

2

2

-

=

-

+

-

.

1

Stwierdzenie, ˝e iloczyn liczb ca∏kowitych, w którym jednym z czynników jest

1

liczbà

7

jest podzielny przez

7

.

5.

Zapisanie za∏o˝eƒ:

sin

x

x

tg

i

0

0

!

!

lub

cos

sin

x

x

i

0

0

!

!

.

1

Zastosowanie wzoru

cos

sin

tg =

a

a

a

i przekszta∏cenie równania do postaci:

1

cos

cos sin

sin

x

x

x

x

2

2

1

-

=

-

.

Przekszta∏cenie równania do postaci iloczynowej:

cos

sin

x

x

2

1 1

0

-

-

=

_

_

i

i

.

1

Rozwiàzanie równania

sin x

1

=

dla

,

x

0 2

!

r

_

i

,

x

2

= r

i zapisanie, ˝e to

1

rozwiàzanie nie spe∏nia za∏o˝eƒ.

Rozwiàzanie równania

cos x

2

1

=

dla

,

x

0 2

!

r

_

i

i zapisanie rozwiàzania

1

równania

cos

sin

sin

x

x

x

x

tg

1

2

1

-

=

-

:

x

x

lub

3

3

5

=

=

r

r

.

6.

Wyznaczenie ró˝nicy ciàgu

(

)

a

n

:

r

2

=

.

1

Wyznaczenie pierwszego wyrazu ciàgu

(

)

a

n

:

a

11

1

= -

.

1

Wyznaczenie jedenastego wyrazu ciàgu

(

)

a

n

:

a

9

11

=

,

a

27

20

=

.

1

Zapisanie za pomocà równania warunku, ˝e ciàg

,

,

a a

a

8

11

20

_

i

jest ciàgiem

1

geometrycznym i podanie wniosku: np.

a

a a

11

2

8

20

$

=

, ciàg

,

,

a a

a

8

11

20

_

i

jest

geometryczny.

Podanie wzoru na wyraz ogólny ciàgu

(

)

a

n

:

a

n

2

13

n

=

-

.

1

Zapisanie wzoru na sum´ cz´Êciowà:

S

n

n

12

n

2

=

-

.

1

Wyznaczenie wartoÊci

n

, dla której

S

n

osiàga wartoÊç najmniejszà:

n

6

=

.

1

7.

Zapisanie logarytmów o podstawach

8

i

4

1

za pomocà logarytmu o podstawie 2:

1

2

log

log

log

3

3

1

27

2

1

9

2

2

2

-

-

.

Zastosowanie w∏asnoÊci logarytmów do zapisania wyra˝enia w postaci:

2

log 3

2

-

.

1

Obliczenie wartoÊci wyra˝enia

2

log

log

log

3

27

9

2

8

4

1

-

+

:

3

1

.

1

Zapisanie wniosku:

> ,

2

3

1

0 33

log

log

log

3

27

9

2

8

4

1

=

-

+

.

1

8.

Zapisanie mocy zbioru wszystkich zdarzeƒ elementarnych

X

:

n

2

=

X

e o

,

n

5

H

.

1

2

w w w. o p e r o n . p l

Matematyka. Poziom rozszerzony

Numer

Modelowe etapy rozwiàzywania zadania

Liczba

zadania

punktów

Zapisanie mocy zbioru zdarzeƒ elementarnych sprzyjajàcych zdarzeniu

A

: 1

A

5
2

= e o

.

Zapisanie równania wynikajàcego z treÊci zadania:

1

n

2

5
2

21

2

=

e

e

o

o

.

Przekszta∏cenie równania do postaci równania kwadratowego, np.:

1

n

n

210

0

2

-

-

=

.

Rozwiàzanie równania kwadratowego z uwzgl´dnieniem za∏o˝enia:

n

15

=

. 1

9.

Wyznaczenie równania prostej

AC

:

y

x

2

1

2

1

=

-

.

1

Wyznaczenie wspó∏rz´dnych punktu

S

, b´dàcego Êrodkiem odcinka

AC

: 1

,

S

1 0

=

_

i

.

Wyznaczenie równania prostej

BD

:

y

x

2

2

= -

+

.

1

Zapisanie zale˝noÊci pozwalajàcej wyznaczyç wspó∏rz´dne pozosta∏ych

1

wierzcho∏ków rombu: np.

x

x

3

2

4

5

2

2

+

+ -

+

=

_

_

i

i

.

Zapisanie wspó∏rz´dnych wierzcho∏ków

B

i

D

:

,

B

2

2

=

-

_

i

i

,

D

0 2

=

_

i

.

1

10.

Wyznaczenie wysokoÊci

h

trapezu:

h

6

=

.

1

Obliczenie d∏ugoÊci ramion

c

i

d

trapezu:

c

4 3

=

,

d

12

=

.

1

Wykorzystanie warunku opisywalnoÊci czworokàta na okr´gu do obliczenia

1

sumy d∏ugoÊci podstaw

a

i

b

trapezu:

a

b

4 3

12

+

=

+

.

Obliczenie pola trapezu:

P

12

3

3

=

+

`

j

.

1

11.

Wykonanie rysunku pomocniczego i zaznaczenie na nim przekroju p∏aszczyznà

1

równoleg∏à do p∏aszczyzny podstawy.

Obliczenie promienia przekroju sto˝ka p∏aszczyznà równoleg∏à do p∏aszczyzny

1

podstawy:

r

3

=

.

Obliczenie wysokoÊci sto˝ka, którego przekrój osiowy jest trójkàtem

1

równobocznym o boku d∏ugoÊci

6

:

h

3 3

=

.

Obliczenie obj´toÊci sto˝ka, którego przekrój osiowy jest trójkàtem

1

równobocznym o boku d∏ugoÊci

6

:

V

9

3

=

r

.

Zapisanie, ˝e obj´toÊç sto˝ka jest nie mniejsza od obj´toÊci sto˝ka, którego

1

przekrój osiowy jest trójkàtem równobocznym o boku d∏ugoÊci

6

, czyli jest

wi´ksza od

48

, bo

<

48

9

3

r

.

3

w w w. o p e r o n . p l

Matematyka. Poziom rozszerzony

Numer

Modelowe etapy rozwiàzywania zadania

Liczba

zadania

punktów