__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
1/21
Temat:
Oddziaływanie promieniowania z materią
Data opracowania: 15.10.95
Data ostat. zapisu: 15.10.95
Źródło 1:
autor -
J. Sobkowski
tytuł -
Chemia jądrowa
rodzaj źródła -
książka
strony -
104-117
wydawca -
PWN
rok wydania
1981
Źródło 2:
autor -
E. Skrzypczak, Z. Szefliński
tytuł -
Wstęp do fizyki jądra atomowego i cząstek elementarnych
rodzaj źródła -
książka
strony -
26-35
wydawca -
PWN
rok wydania
1995
Słowa kluczowe: efekt Comptona, efekt fotoelektryczny, efekt tworzenia par
Słowa dodatkowe:
UWAGI:
Liczba stron:
21
Mam (t/n):
tak
Gdzie mam
źródło:
dom
Zapis komputerowy:
Dysk nr:
FIZ_TECH
Etykieta dysku:
FIZ_TECH
Nazwa zbioru:
ODZIAL.DOC
Napisałem w:
Microsoft Word v 2.0 Pl
__________________________________________________________________________
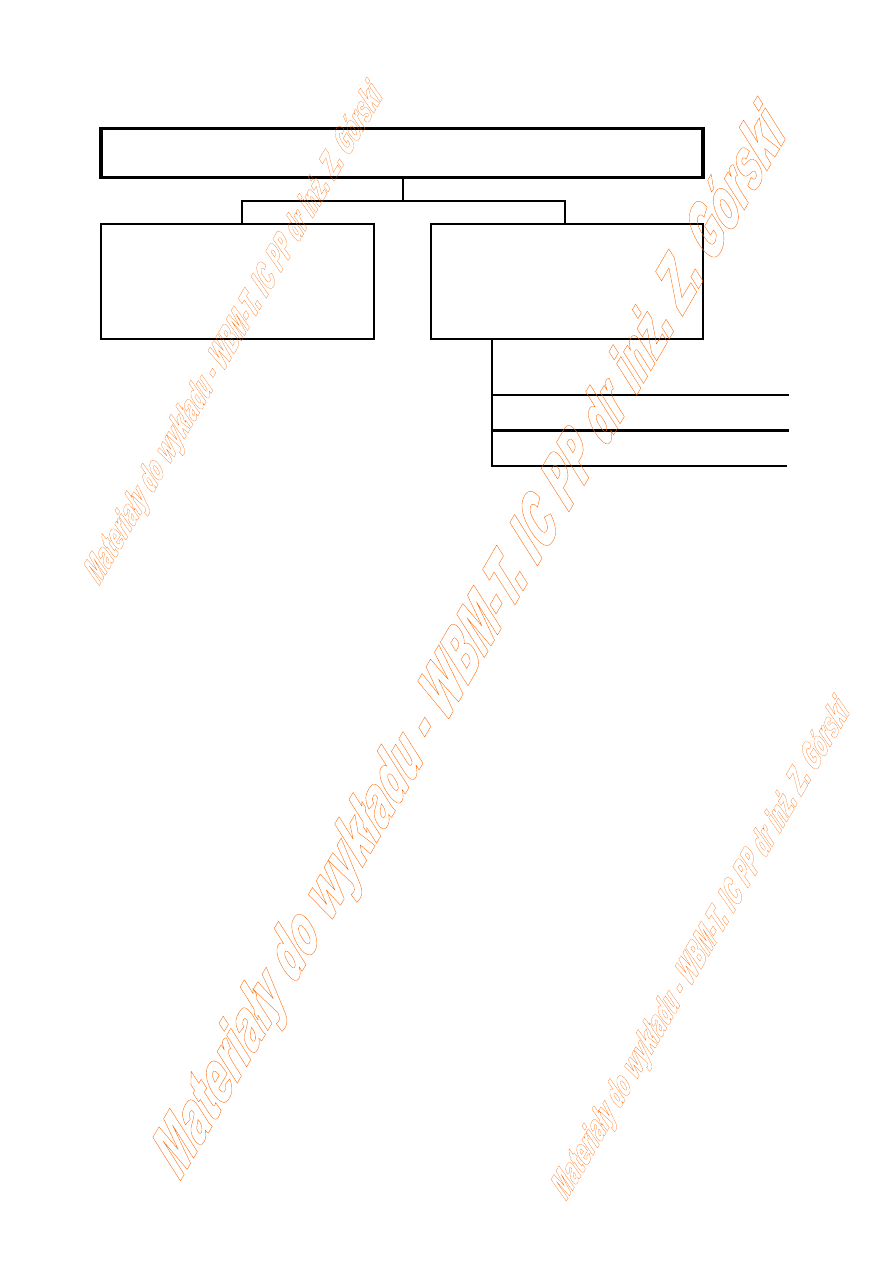
Zbigniew Górski OPRACOWANIA TEMATYCZNE
2/21
Oddziaływanie promieniowania i cząstek z materią
przemiany jądrowe
(reakcje jądrowe)
oddziaływanie
z elektronami powłok
elektronowych atomu
jonizacja atomów
Zmiany chemiczne
→
wzbudzenie cząsteczek
zerwanie wiązań w cząsteczce
Sposób oddziaływania zależy od :
•
rodzaju ładunku,
•
energii cząstek lub promieniowania,
•
właściwości substancji pochłaniającej.
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
3/21
Stopień jonizacji najłatwiej można określić w przypadku
absorbcji promieniowania przez gazy.
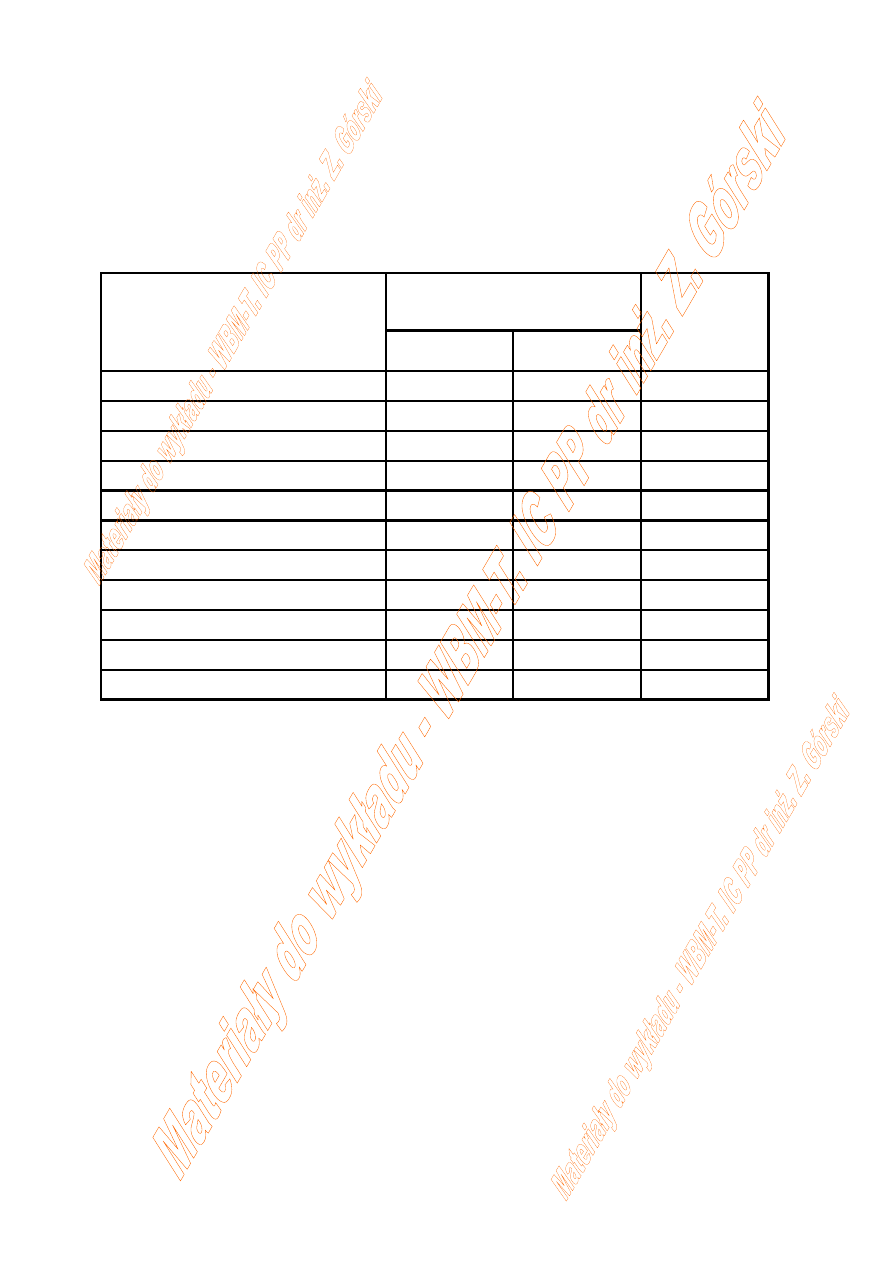
Zestawienie energii potrzebnej do utworzenia jednej pary
jonów (W) i energii jonizacji (I) dla różnych gazów.
Rodzaj gazu
W [eV/parę jonów]
I [eV]
cząstki
α
cząstki
β
Hel
44.4
41.4
24.6
Argon
26.4
26.1
15.8
Ksenon
21.9
22.1
12.1
Wodór
36.7
36.3
15.4
Tlen
32.4
31.1
12.1
Azot
36,5
34.7
15.6
Dwutlenek węgla
34.4
32.8
13.8
Metan
29.3
27.1
13.0
Etan
26.6
24.5
11.7
Etylen
28.0
26.1
10.5
Acetylen
27.5
25.7
11.4
Z porównania danych (W, I) zawartych w tabeli wynika, że
około
POŁOWA
pochłoniętej
ENERGII
jest zużywana
NA JONIZACJĘ
.
POZOSTAŁA CZĘŚĆ
pochłoniętej energii jest
przekazywana wybitym elektronom oraz zużyta na wzbudzenie
atomów i cząsteczek ośrodka.
Rodzaj promieniowania i jego energia mają niewielki wpływ
na wielkość W.
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
4/21
W wyniku oddziaływania z materią promieniowanie jonizujące
traci swoją energię.
Strata energii na jednostkę drogi nazywamy zdolnością
hamowania lub liniowym współczynnikiem przenoszenia energii
(LET)
jednostką LET jest [keV/cm]
LET zależy od rodzaju cząstek lub promieniowania oraz
od właściwości pochłaniającego ośrodka.
W pochłanianiu promieniowania decydującą rolę odgrywa gęstość
ośrodka by to uwzględnić wprowadza się MASOWĄ ZDOLNOŚĆ
HAMOWANIA.
MASOWA ZDOLNOŚĆ HAMOWANIA - strata energii na
jednostkę drogi podzielona przez gęstość ośrodka.
jednostką jest [keV*cm
-1
/g*cm
-3
]
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
5/21
WZGLĘDNA ZDOLNOŚĆ HAMOWANIA - stosunek zdolności
hamowania ośrodka do zdolności hamowania powietrza (S).
0
0
0
A
l
A
l
S
ρ
ρ
=
gdzie:
l - grubość,
ρ - gęstość,
A - liczba atomowa ośrodka
0 - wielkości dotyczące powietrza
UWAGA!!!
→ A
0
= 14.4
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
6/21
Hamowanie cząstek ciężkich (
α, p) w gazach jednoatomowych
opisuje równanie BETHEGO:
(
)
β
−
β
−
π
=
−
2
2
2
0
2
0
e
2
4
1
I
V
m
2
ln
V
m
n
z
e
4
dx
dE
β
ρ
=
=
=
V
c
n
Zn
Z N
A
e
a
gdzie:
z - ładunek cząstki,
V - prędkość cząstki,
n
e
- liczba elektronów w 1 cm
3
objętości ośrodka,
m
0
- masa spoczynkowa elektronu,
I - średnia
wartość
potencjałów
jonizacji
wszystkich elektronów atomów ośrodka,
c - prędkość światła,
n
a
- liczba atomów w 1 cm
3
,
N - liczba Avogadro
Z równania tego wynika, że strata energii jest proporcjonalna do
gęstości ośrodka i wielkości ładunku cząstki i odwrotnie
proporcjonalna do jej prędkości.
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
7/21
Zasięg cząstek (R)
obliczamy całkując równanie Bethego w granicach energii
początkowej od E
0
do 0
∫
∫
−
=
=
0
o
E
0
0
E
dx
dE
dE
dx
dE
dE
R
R uzyskane tą drogą są poprawne wyłącznie dla gazów
jednoatomowych.
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
8/21
Do obliczeń zasięgu cząstek (R) w absorbentach
"rzeczywistych" stosujemy różne wzory empiryczne.
np:
DLA CZĄSTEK
α, p i DEUTERONÓW (d)
o energiach
<0.1 do 100> MeV
, oraz dla absorbentów dla
których liczba atomowa
Z>10
można stosować wzór
(
)
−
+
+
=
A
E
log
Z
0086
.
0
06
.
0
Z
0275
.
0
90
.
0
R
R
pow
Z
gdzie:
R
z
- zasięg w ośrodku o liczbie atomowej Z,
R
pow
- zasięg w powietrzu,
Z - liczba atomowa ośrodka,
E - energia początkowa cząstki [MeV],
A - liczba masowa cząstki (dla
α = 4, d = 2)
Gdy absorbentem jest związek chemiczny
zakłada się,
że wartość absorbcji jest sumą absorbcji atomowych, atomów
wchodzących w skład związku:
1
R
w
R
m
i
i
i
=
∑
gdzie:
R
m
- zasięg promieniowania w związku chemicznym lub
mieszaninie,
R
i
- zasięg atomowy promieniowania (w pierwiastku chemicznym),
w - ułamek wagowy pierwiastka w absorbencie.
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
9/21
Absorpcja cząstek
α
Ponieważ masa spoczynkowa cząstek
α jest ok. 7.5 tys. razy
większa od masy spoczynkowej elektronu cząstka
α porusza się
w absorbującym ośrodku po linii prostej.
Zasięgi cząstek
α w ośrodkach skondensowanych są niewielkie.
Cząstki
α o energii 10 MeV są całkowicie zatrzymywane np przez:
Pb - 0.034 mm
H
2
O - 0.13 mm
Zdolność hamowania cząstki w danym ośrodku (-dE/dx) jest
proporcjonalna do jonizacji właściwej (dn/dx).
−
=
dE
dx
W
dn
dx
W - energia potrzebna do utworzenia jednej pary jonów.
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
10/21
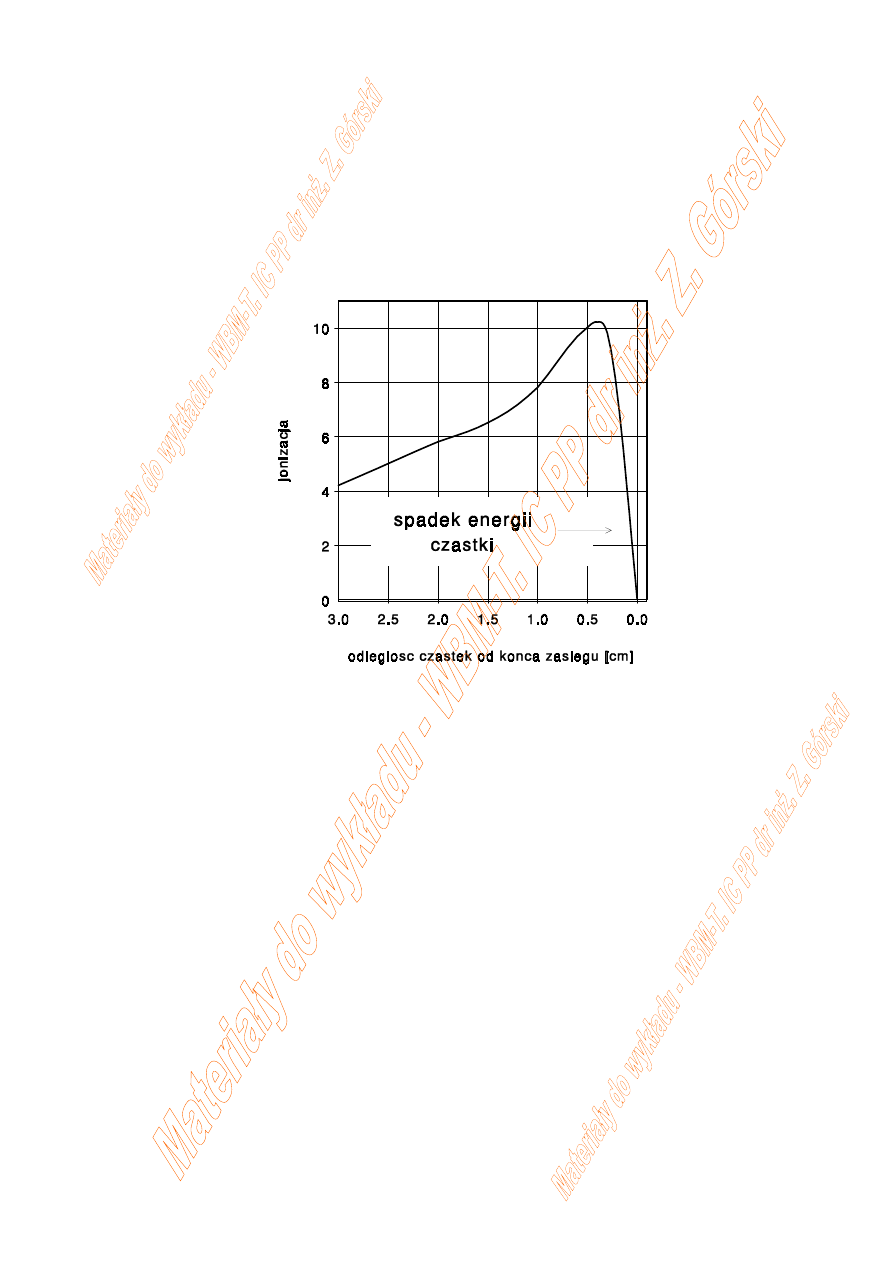
Zależność ilości powstających par jonów od przebytej przez
cząstkę
α drogi przedstawia krzywa Bragga.
Jonizacja rośnie wraz z przebytą drogą przechodząc przez
maksimum tuż przed końcem zasięgu cząstki
α.
__________________________________________________________________________
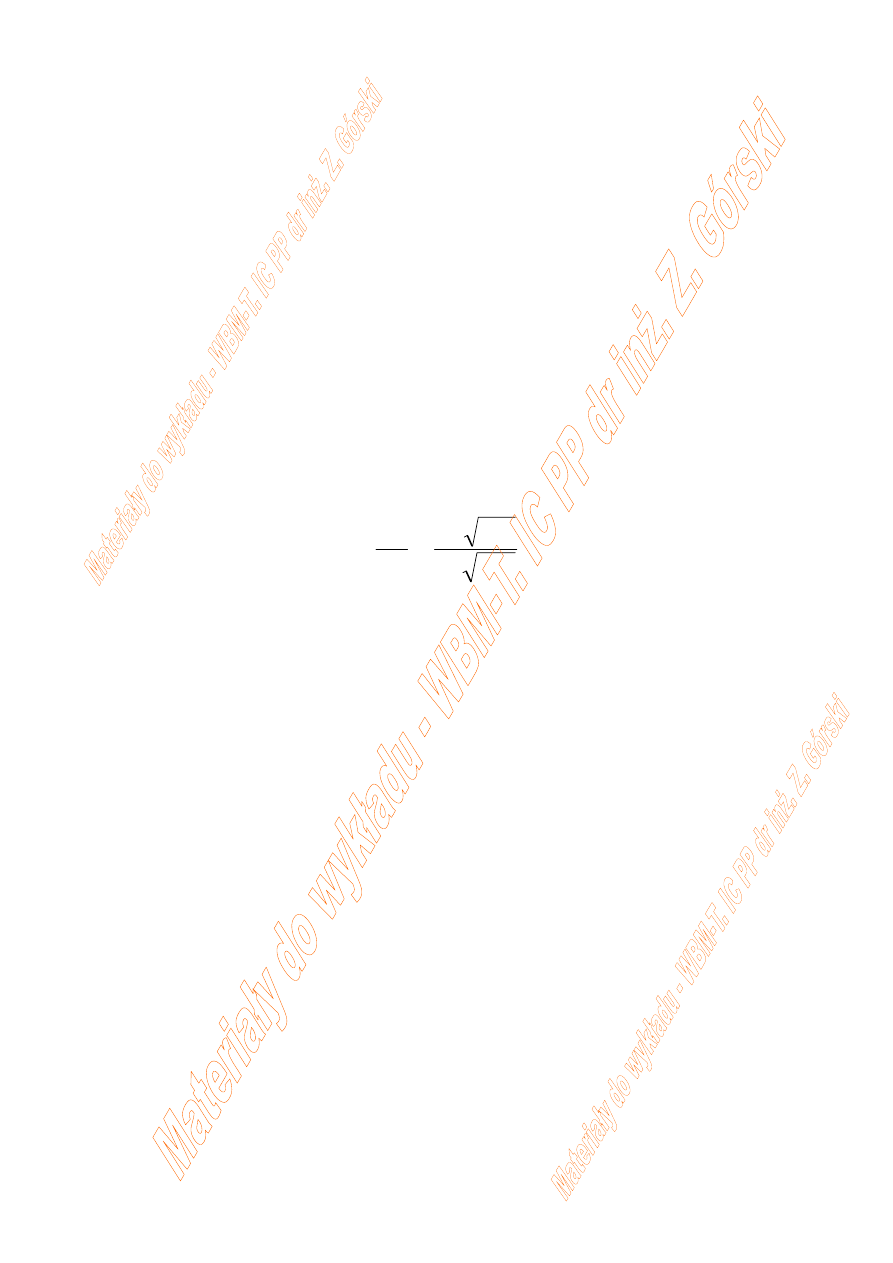
Zbigniew Górski OPRACOWANIA TEMATYCZNE
11/21
Zasięg cząstek
α można wyrazić przy pomocy masy
powierzchniowej.
M
pow
= R *
ρ [g/cm
2
]
Masa powierzchniowa jest wielkością tabelaryzowaną.
Znając zasięg cząstek
α w jakimś ośrodku możemy wyliczyć
zasięg w innym
R
R
M
M
1
2
2
1
1
2
=
ρ
ρ
gdzie:
R
1
- zasięg promieniowania w ośrodku 1,
R
2
- zasięg promieniowania w ośrodku 2,
σ - gęstość (odpowiednio ośrodka 1 i 2),
M - masa cząsteczkowa (odpowiednio ośrodka 1 i 2).
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
12/21
Pochłanianie cząstek
β
Ponieważ cząstka
β i elektrony mają te same masy i ładunki tor
cząstek
β w absorbencie ulega licznym zakrzywieniom.
(straty energii na zderzenia i odpychanie elektrostatyczne )
Jonizacja pierwotna stanowi 20-30% całkowitej jonizacji ośrodka
reszta to tzw. jonizacja wtórna.
(straty energii na jonizację wtórną - promieniowanie
δ )
W przypadku oddziaływania cząstek
β z ośrodkami o dużej liczbie
atomowej powstaje promieniowanie X - oddziaływanie z polem
elektrycznym jąder.
(straty energii na promieniowanie hamowania)
Jeżeli cząstka porusza się w przezroczystym ośrodku z prędkością
porównywalną z prędkością światła część energii jest tracona na
PROMIENIOWANIE CZERENKOWA (emisja światła).
(straty energii na promieniowanie Czerenkowa)
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
13/21
Dla elektronów stosunek strat energii wskutek emisji
promieniowania hamowania do energii traconej w skutek
jonizacji i wzbudzenia atomów wynosi
800
EZ
dx
dE
dx
dE
.
zderz
.
ham
.
prom
=
−
−
gdzie:
E - energia cząstek w [MeV],
Z - liczba atomowa.
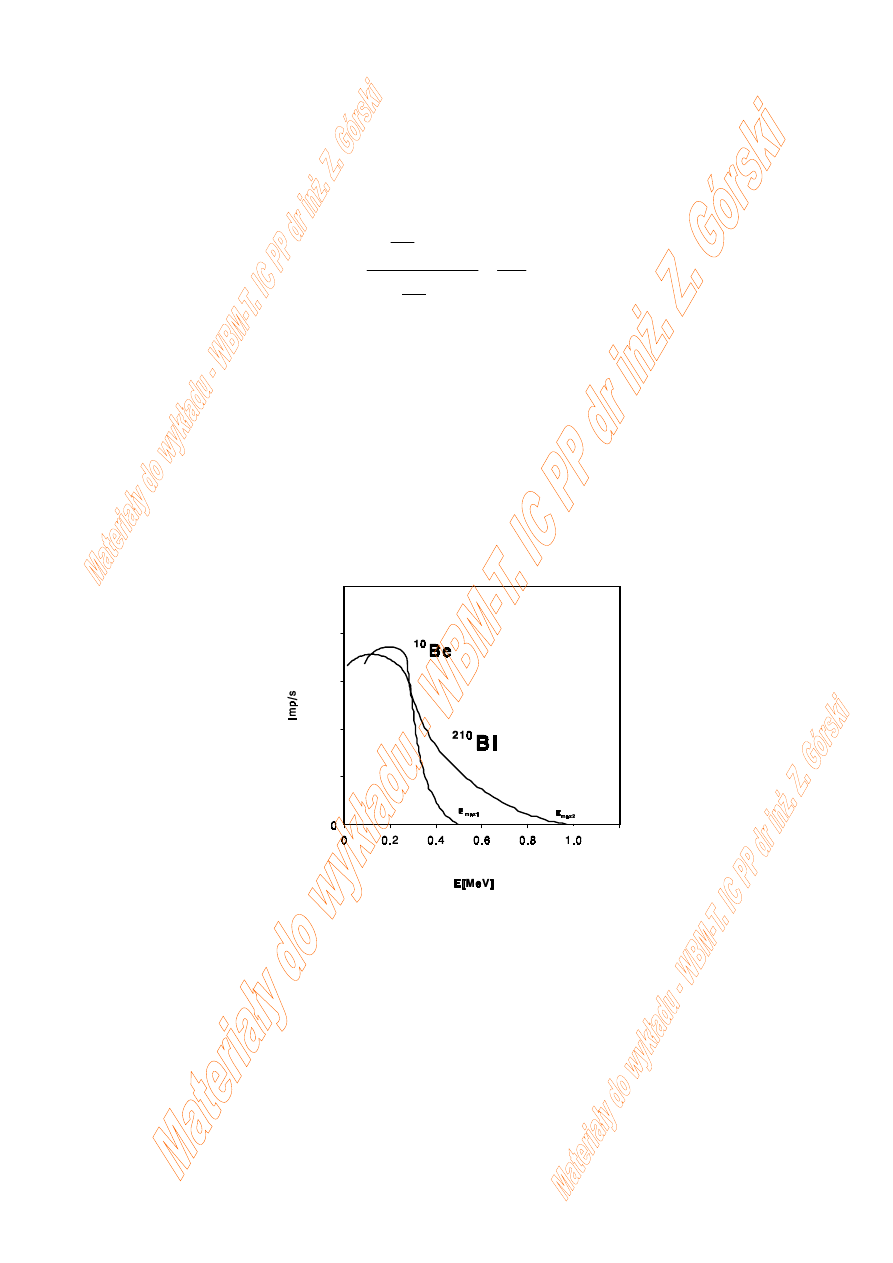
Przykładowe widma promieniowania
β
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
14/21
Pojawienie się promieniowania hamowania i ciągłość widma
cząstek
β emitowanych przez jądra powodują, że teoretyczne
obliczenia absorbcji cząstek
β jest skomplikowane i niedokładne.
Absorbcję cząstek
β można określić przez pomiar spadku ich
natężenia po przejściu przez określoną grubość warstwy.
Zmianę natężenia promieniowania możemy zapisać:
−
=
dI
I dl
µ
gdzie:
I - natężenie promieniowania,
I
0
- początkowe natężenie promieniowania,
l - grubość absorbenta,
µ - współczynnik absorbcji.
∫
∫
=
µ
=
−
l
0
l
I
I
dl
I
dI
0
gdzie:
I
0
- początkowe natężenie promieniowania,
ln
ln
I
I
l
=
−
0
µ
uzyskane równanie jest równaniem prostej o współczynniku
nachylenia
µ.
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
15/21
Ponieważ wartość współczynnika absorbcji (
µ), promieniowania β
o określonej energii, dla wszystkich lekkich pierwiastków, zależy
prawie liniowo od gęstości absorbenta wprowadzono
MASOWY WSPÓŁCZYNNIK ABSORBCJI:
ρ
µ
=
µ
ρ
g
cm
2
wyrażony w ten sposób wsp. absorbcji elektronów dla
promieniowania o określonej energii jest wielkością stałą.
(nie zależy od rodzaju materiału)
GRUBOŚĆ POŁÓWKOWA - jest to grubość absorbenta
zmniejszająca natężenie wiązki promieniowania o połowę
l
1 2
2
0 693
/
ln
.
=
=
µ
µ ρ
ρ
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
16/21
Zasięg cząstek
β
jest 5 do 10 razy większy od grubości połówkowej.
Można go obliczyć na podstawie wzorów empirycznych:
•
dla cząstek
β o E>0.8 MeV
[
]
MeV
cm
mg
165
E
536
R
2
max
↓
−
=
β
•
dla cząstek
β o energii <0.025, 2 MeV>
[
]
MeV
cm
mg
E
370
R
2
2
3
max
↓
=
β
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
17/21
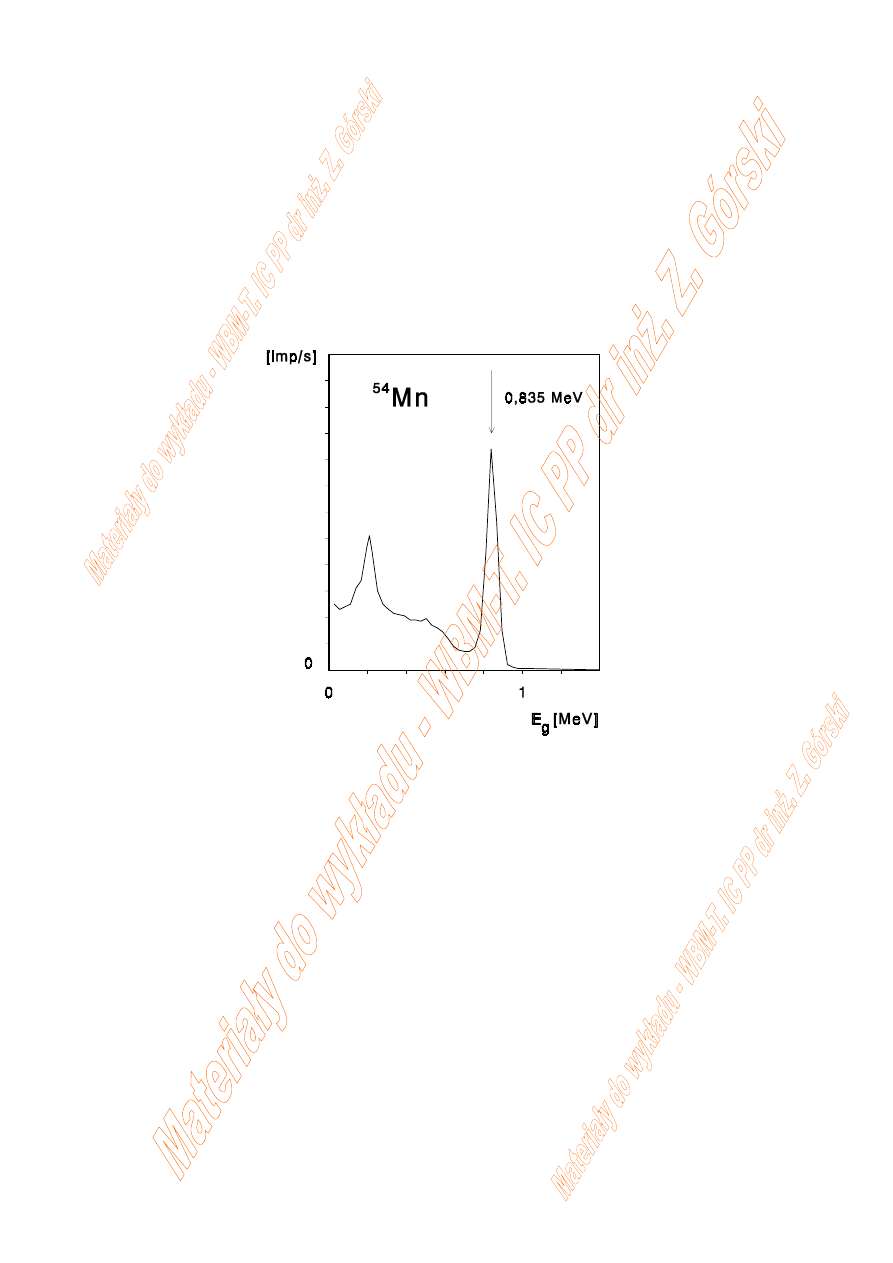
Pochłanianie promieniowania
γ
promieniowania
γ jest promieniowaniem elektro-
magnetycznym o długości fali od 0.025 do 0.0001 nm, co
odpowiada energią od 0.05 do kilku MeV
Widmo promieniowania emitowanego przez
54
Mn
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
18/21
Promieniowanie
γ można opisać równaniami podobnymi do
absorpcji światła chociaż mechanizm pochłaniania jest inny,
•
energię promieniowania świetlnego absorbują przede
wszystkim elektrony wiązań chemicznych,
•
energię promieniowania
γ absorbują wszystkie elektrony w
atomie
(decyduje o niej rodzaj pierwiastka)
Jeżeli:
→
→
→
→
→
→
I
0
I
µ
→
←
l
absorbent
to
I = I
0
exp(-l
µ)
gdzie:
µ - liniowy współczynnik osłabienia [cm
-1
]
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
19/21
Masowy współczynnik osłabienia -
ρ
µ
=
µ
ρ
g
cm
2
Atomowy współczynnik osłabienia -
ρ
µ
=
µ
=
µ
ρ
atom
cm
N
A
N
A
2
a
Elektronowy współczynnik osłabienia -
ρ
µ
=
µ
=
µ
elektron
cm
N
A
Z
Z
2
e
a
Cząsteczkowy współczynnik osłabienia -
M
N
.
czast
cm
cz
2
a
cz
µ
ρ
=
µ
µ
=
µ
∑
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
20/21
Pochłanianie promieniowania
γ zależy od energii kwantu, może
zachodzić poprzez:
•
efekt fotoelektryczny,
•
efekt Comptona,
•
efekt tworzenia par elektron-pozyton.
µ = τ + σ + κ
gdzie:
τ - współczynnik osłabienia poprzez efekt fotoelektryczny,
σ - współczynnik osłabienia poprzez efekt Comptona,
κ - współczynnik osłabienia poprzez efekt tworzenia par.
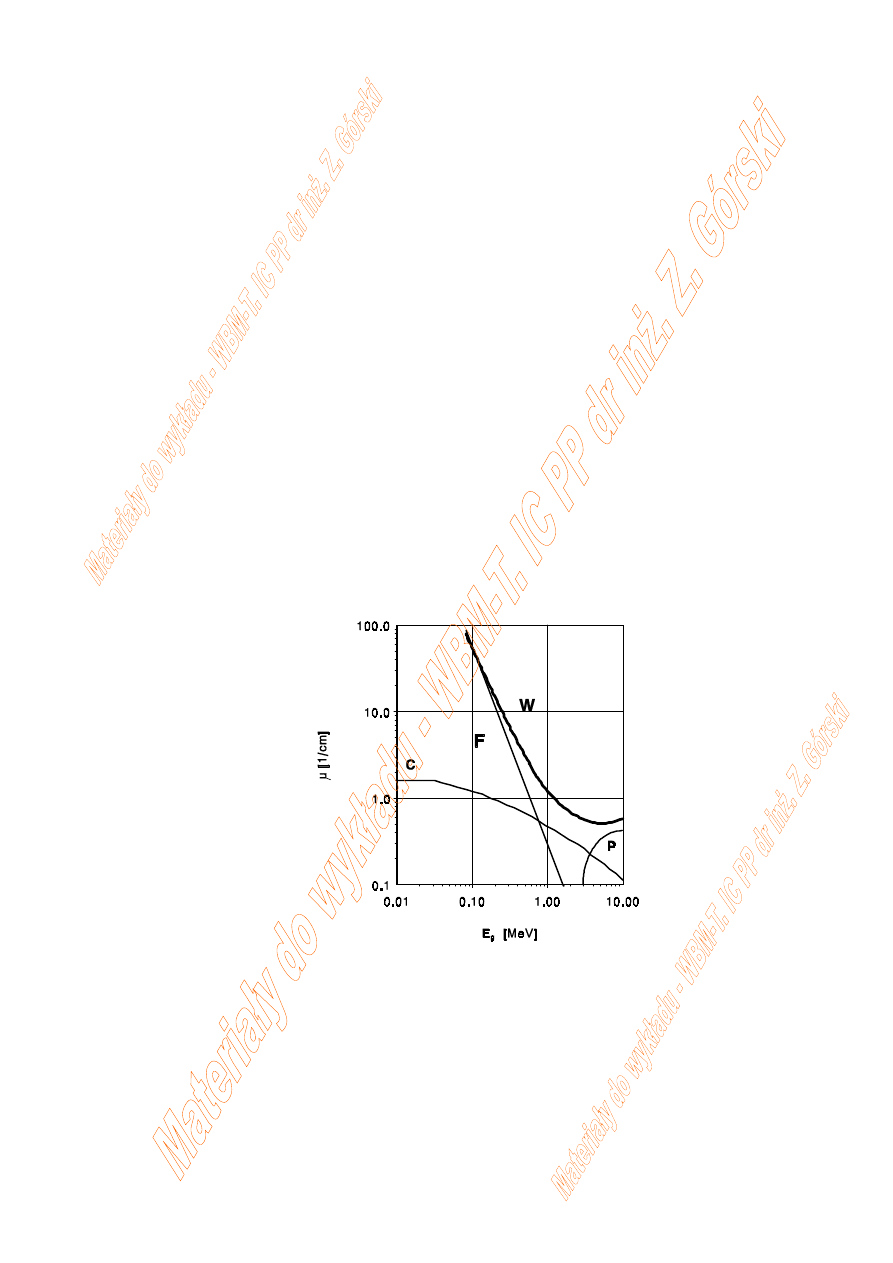
Zależność liniowego współczynnika osłabienia
µ oraz jego
składowych od energii kwantów
γ
F-efekt fotoelektryczny, C-efekt Comptona, P-efekt tworzenia
par.
__________________________________________________________________________
Zbigniew Górski OPRACOWANIA TEMATYCZNE
21/21
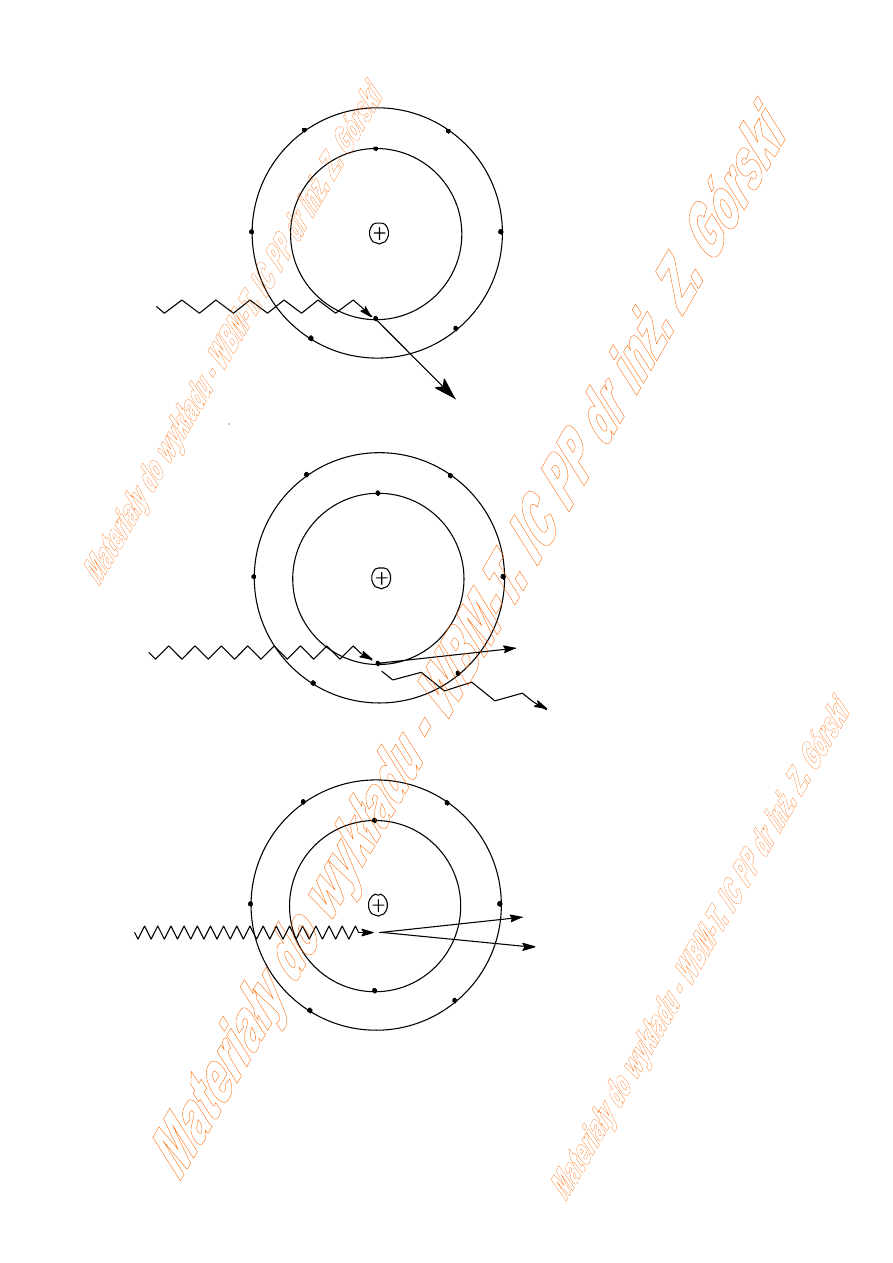
foton E=hν
fotoelektron
elektron
foton E=h
ν
elektron
foton E=h
ν
EFEKT FOTOELEKTRYCZNY
EFEKT COMPTONA
EFEKT TWORZENIA PAR
foton rozproszony
pozyton