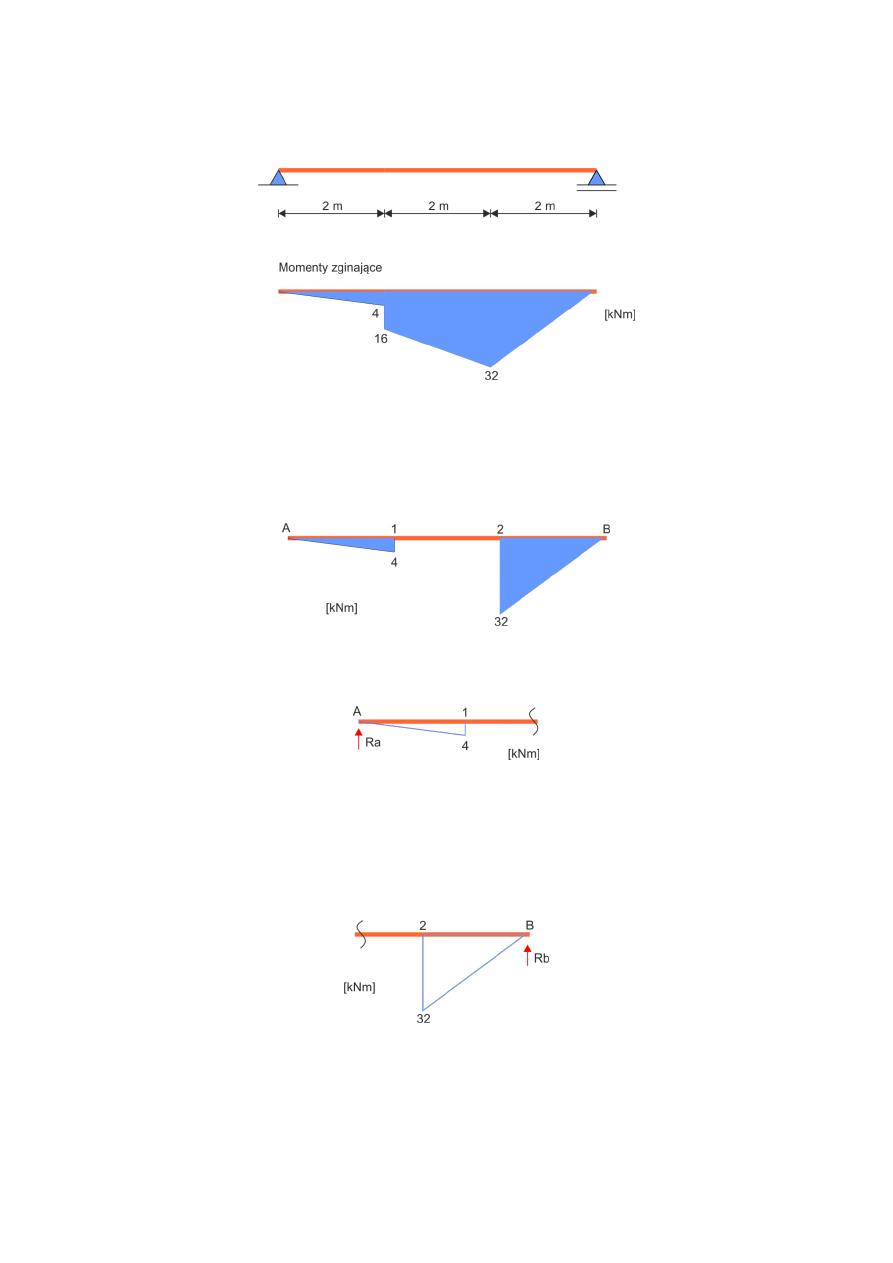
Zad. Na podstawie wykresu momentów zginających określić działające obciążenie oraz
narysować wykres sił tnących.

Należy zwrócić uwagę, że wszystkie funkcje opisujące momenty zginające w przekroju belki
są funkcjami liniowymi. W związku z tym od razu wiadomo, że na belce nie ma obciążenia
ciągłego.

Najłatwiej jest rozpatrzyć zawsze dwa przedziały na belce oznaczone, jako A-1 oraz 2-B:

W punktach A i B momenty zginające są zerowe, następnie następuje liniowy przyrost.
Można więc założyć, iż reakcje Ra i Rb są niezerowe. Rozpatrujemy przedział A-1:

Na 2 metrach moment przyrósł z 0 do 4 kNm:

2

4

2

Ra

m

kNm

Ra

kN







Rozpatrujemy przedział 2-B:

Na 2 metrach moment przyrósł z 0 do 32 kNm:

2

32

16

Rb

m

kNm

Rb

kN







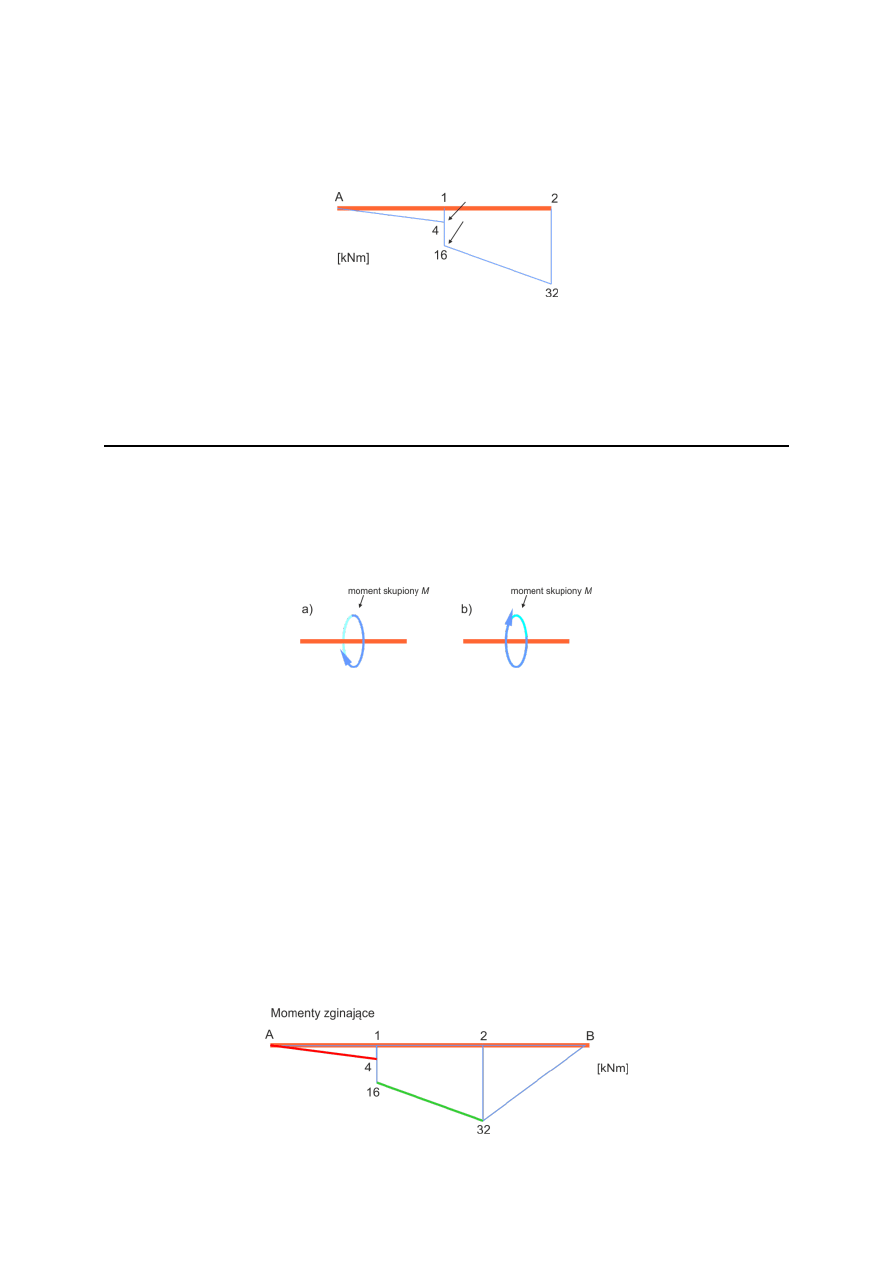
Kolejnym ważnym punktem na wykresie momentów jest punkt 1. Następuje tam dodatni
skok momentu zginającego. Skok momentu zginającego występuje tylko w wypadku
obciążenia w postaci momentu skupionego.

Wartość momentu skupionego M wynosi:

4

16

12

kNm

M

kNm

M

kNm







Moment skupiony jest dodatni, więc powoduje rozciąganie spodów belki.

Co to znaczy, że moment skupiony jest dodatni lub ujemny?

To zależy, od której strony rozpatrujemy belkę. Proszę zwrócić uwagę, że dodatni moment
zginający dla lewego i prawego końca belki mają przeciwne zwrotu pomimo tego samego
znaku.

Momenty skupione na powyższym rysunku mają ten sam znak i są dokładnie tym samym
momentem zginającym lecz może się wydawać, iż moment na rysunku a) rozciąga górę, a
monet na rysunku b) rozciąga spód. Należy podjeść do tego problemu w następujący sposób:
belkę rozpatrujemy od strony lewej do prawej związku z tum dodatni moment zginający to
ten, który kręci zgodnie z ruchem wskazówek zegara (patrz: konwencja znakowania sił
wewnętrznych).

W związku z tym wiemy, iż w punkcie 1 na belce działa moment skupiony o wartości 12
kNm i kręci on zgodnie z ruchem wskazówek zegara.

Kolejny ważny punkt, na który należy zwrócić uwagę: linie czerwona i zielona obrazujące
przebieg momentów zginających na długości belki nie są równolegle!

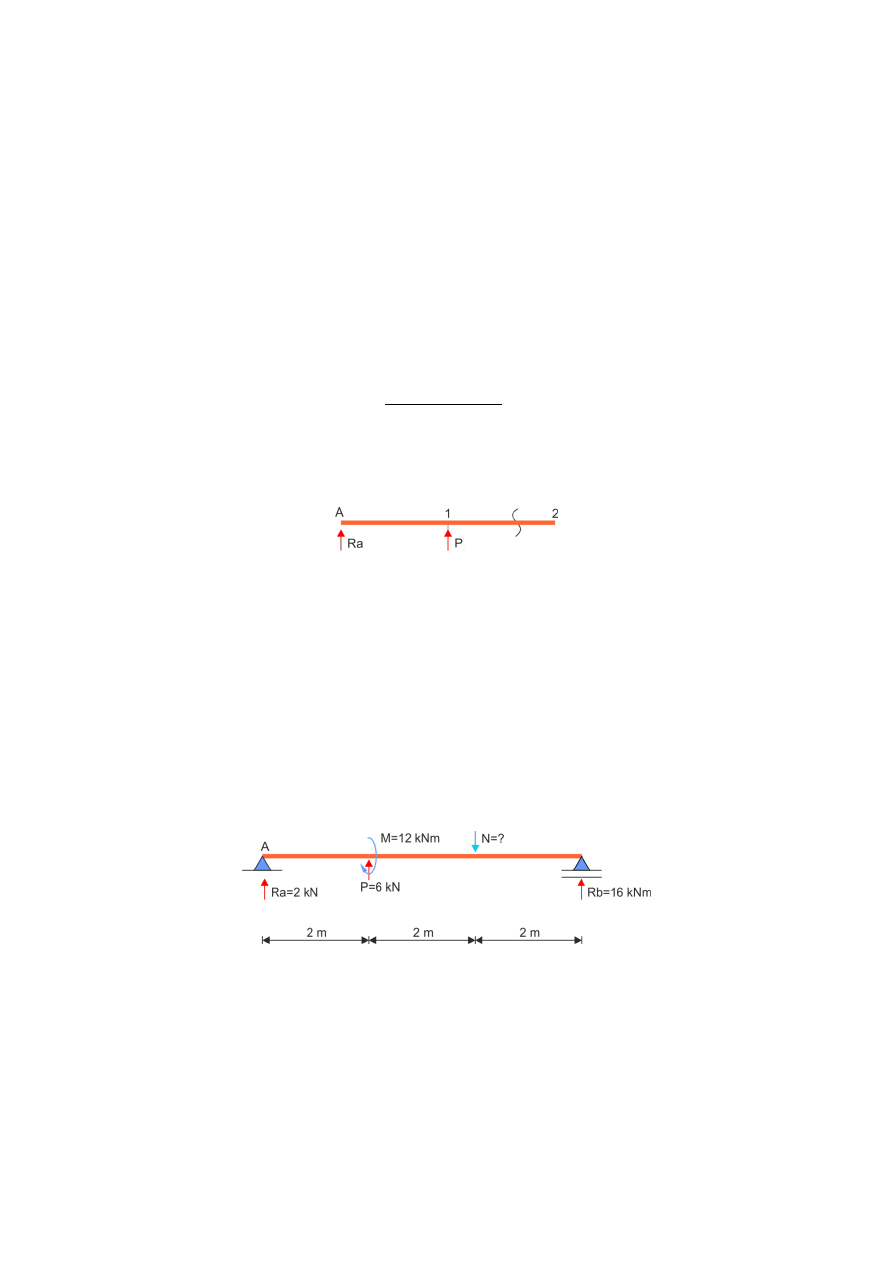
Skąd to wiadomo? Na odcinku A-1 moment zginający przyrósł o 4 kNm. Na odcinku 1-2
moment zginający przyrósł o 32-16 = 16 kNm. W związku z tym możemy wnioskować, że w
punkcie 1 oprócz momentu zginającego musi działać siła skupiona. Gdyby jej tam nie było,
linia czerwona i zielona pozostałyby równoległe i wynikałyby jedynie działania reakcji Ra.

Gdyby zaś nie było momentu skupionego, zauważalne byłoby załamanie wykresu momentów
świadczące o obecności siły skupionej.

Kolejnym wnioskiem jest to, że zwrot tej siły jest taki sam jak zwrot reakcji Ra, ponieważ
mamy przyrost momentów zginających – musi więc rozciągać spód belki.

Siła tnąca na odcinku 1-2 wynosi:

1 2

32

16

8

2

kNm

kNm

T

kN

m









Należy zauważyć, że siła tnąca jest sumą reakcji Ra i nieznanej siły P przyłożonej w punkcie
1:

1 2

8

6

T

Ra

P

kNm

P

kNm





 



Ostatni krok: na wykresie momentów zginających widoczne jest załamanie wykresu
momentów. Takie załamania występują w przypadku obciążeń skupionych. Sposób załamania
tego wykresu zdradza kierunek działania obciążenia. Kolokwialnie można stwierdzić, że
„czub” pokazuje kierunek działającej siły skupionej.

Najprostszym sposobem obliczenia brakującej siły skupionej jest skorzystanie z równania
sumy rzutów na kierunek y i wtedy nie ma konieczności zastanawiania się nad zwrotem siły
skupionej  :

0

0

y

P

Ra

Rb

P

N

 



  



2

6

16

24

N

kN

kN

kN

N

kN









Ostateczne rozwiązanie w postaci obciążenia belki:

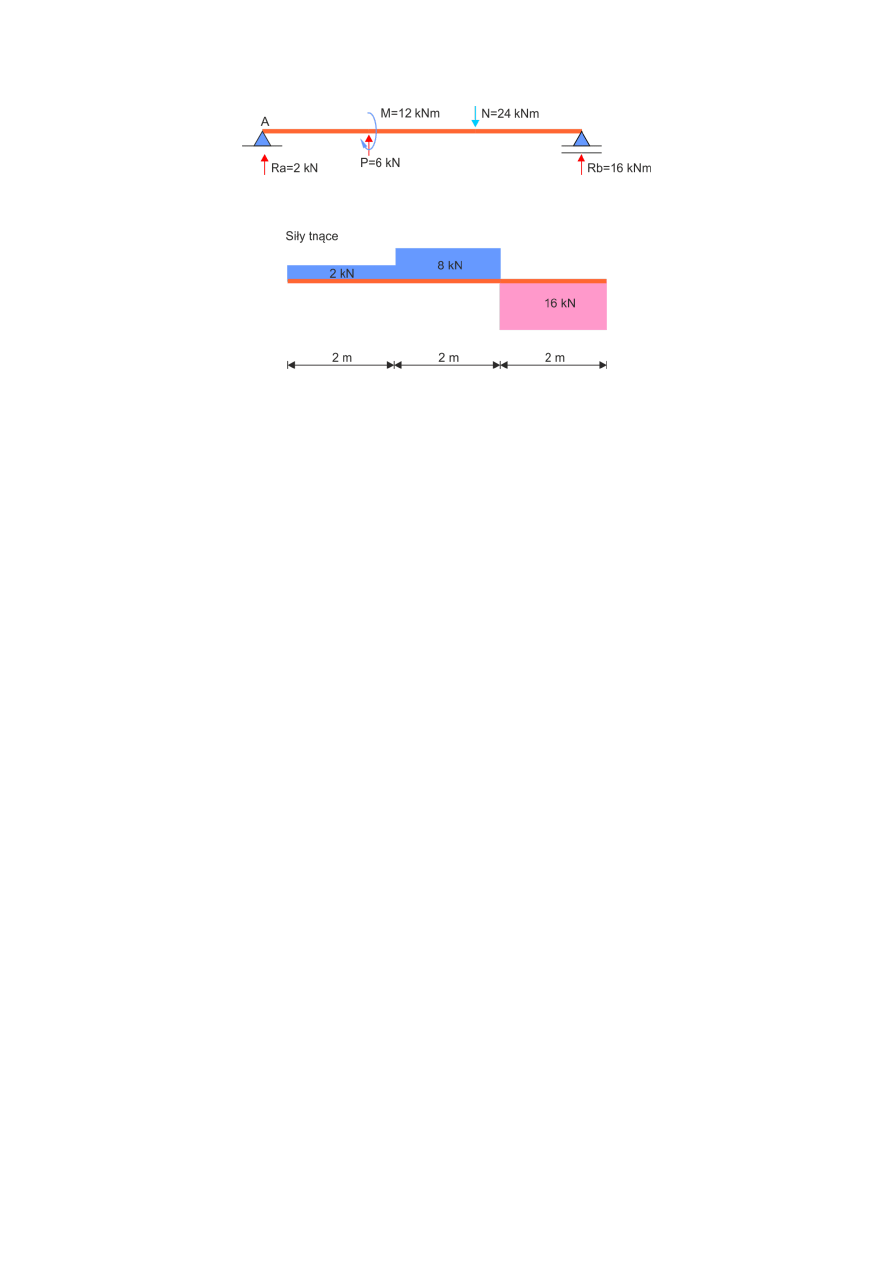
Oraz wykres sił tnących: