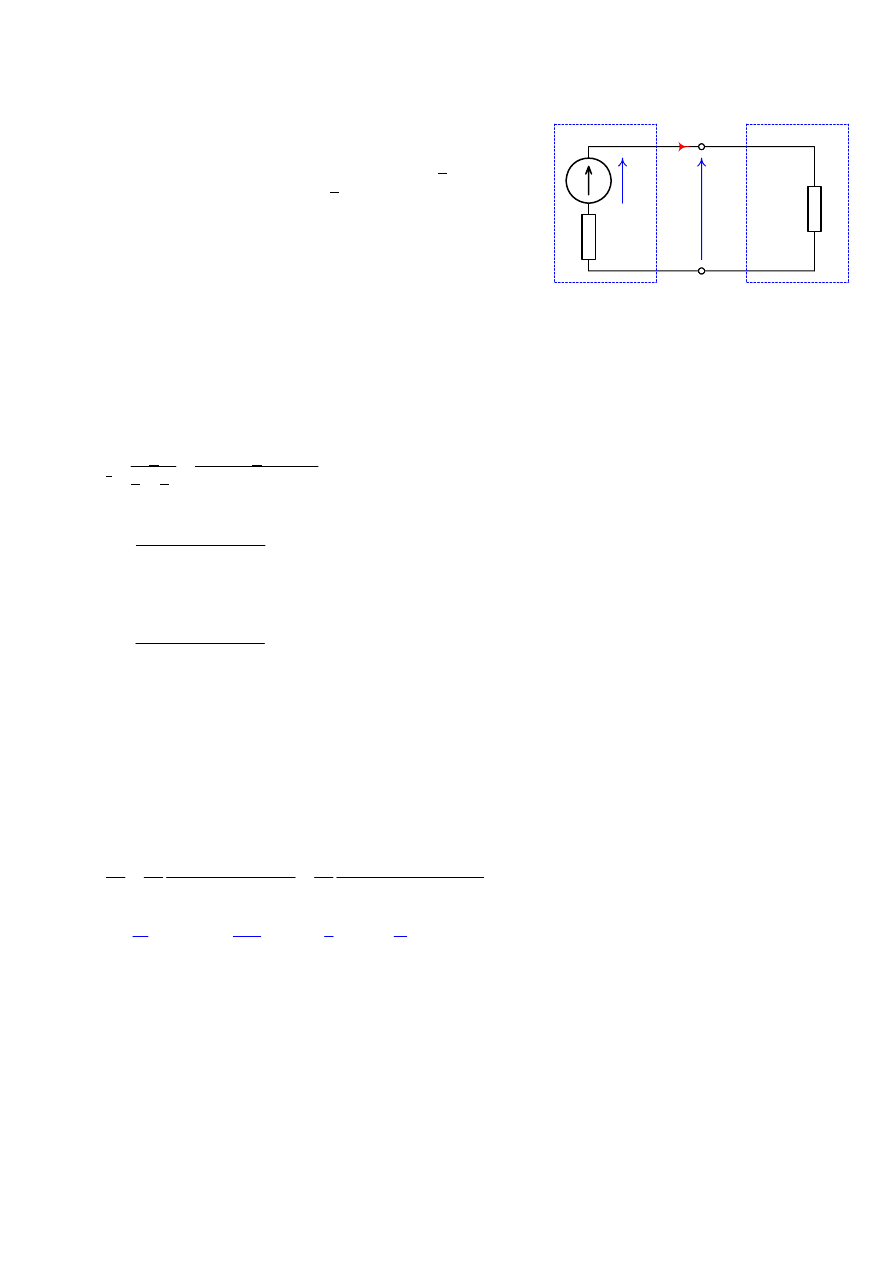
1.3 Dopasowanie odbiornika do źródła 

 
 Do źródła napięcia sinusoidalnie zmiennego o wartości 
skutecznej  E oraz impedancji wewnętrznej  Z

w

 = R

w

 + jX

w 

przyłączono odbiornik o impedancji Z = R + jX (Błąd! Nie można 
odnaleźć źródła odwołania.). 
 

Jakie powinny być parametry odbiornika, aby moc czynna 

pobierana ze danego źródła napięcia była największa? 
 
Rozwiązanie 
  Moc czynna odbiornika o impedancji Z jest opisana równaniem: 
 
  P = R I

2

 

 
gdzie R jest rezystancją odbiornika. 
 
Prąd płynący w obwodzie wynosi: 
 

  I = 

E

Z + Z

w

 = 

E

(R+R

w

) + j(X+X

w

)

  

 
czyli 

  I

2

 = 

E

2

(R+R

w

)

2

 + (X+X

w

)

2

 

 
 Równanie 

opisujące moc czynną odbiornika przyjmuje postać: 

 

  P = 

R E

2

(R+R

w

)

2

 + (X+X

w

)

2

   

(*) 

 
  W celu wyznaczenia maksimum mocy czynnej odbiornika w 
zależności od rezystancji obciążenia  R oraz reaktancji obciążenia 
X, należy: 
 - 

zróżniczkować wyrażenie na moc czynną P raz względem X, a 

drugi raz względem R.  
 - 

przyrównać do zera otrzymane równania na pochodną mocy. 

 
  Pochodna mocy względem reaktancji obciążenia wynosi: 
 

 

dP
dX

 = 

d

dX

 

R E

2

(R+R

w

)

2

 + (X+X

w

)

2

 = 

d

dX

 

-2 (X+X

w

) R E

2

[(R+R

w

)

2

 + (X+X

w

)

2

]

2

  

 

 y 

= 

1

x

m

    

y’ = - 

m

x

m+1

    

y = 

u

v

   

y’ = 

1

v

2

 (u’ v - u v’) 

 Powyższe równie jest równe zeru tylko, gdy licznik tego 
równania jest równy zeru, czyli gdy 
 
  X = 

−

X

w

 

 
 
 

Z

w

E

I

Z

U

A

B

 

Rys. 9.  Źródło sem i odbiornik 

 

 
 Pochodna wyrażenia na moc (*) względem rezystancji 
odbiornika R, gdy reaktancja odbiornika spełnia warunek X = - X

w

 

jest opisana równaniem: 
 

 

dP
dR

 = 

d

dR

 

R E

2

(R+R

w

)

2

 = 

E

2

 (R

2

 + R

w

)

2

 - RE

2

 2(R+R

w

)

(R+R

w

)

4

 = 

 

    = 

E

2

 (R

2

 + 2RR

w

 + R

w

2

 - 2R

2

 - 2RR

w

)

(R+R

w

)

4

 = 

E

2

 (R

w

2

 - R

2

)

(R+R

w

)

2

 = 0 

 

 Przyrównując do zera powyższe równanie otrzymujemy: 
 
 

(

R

w

 

−

  R

)(

R

w

 + R

)

 = 0 

 
 Jeżeli R

w

 

>

 0 oraz R 

>

 0, to warunek jest spełniony tylko wtedy, 

gdy zachodzi poniższa równość: 
 
 

R = R

w 

 

Wniosek: 
  Odbiornik jest dopasowany do źródła o napięciu źródłowym 
sinusoidalnie zmiennym, gdy rezystancja odbiornika jest 
równa rezystancji wewnętrznej  źródła, a reaktancja 
odbiornika jest równa reaktancji wewnętrznej  źródła ze 
znakiem przeciwnym. 
 

  Z = Z

w

*

 

 

  Sprawność obwodu elektrycznego  złożonego ze źródła 
napięcia i odbiornika jest opisana równaniem: 
 

 

η

 = 

P

odb

P

odb

 + 

Δ

P

w

  

 
gdzie: 
 

Δ

P

w

 

− straty mocy w źródle, 

 

P

odb

 

− moc wydzielająca się w odbiorniku. 

 
 Sprawność rozpatrywanego układu możemy wyznaczyć znając 
rezystancję wewnętrzną źródła oraz rezystancję obciążenia: 
 

 

η

 = 

R

R + R

w

  

 

 Jeżeli uwzględnimy,  że w stanie 
dopasowania odbiornika do źródła zachodzi 
równość: 
 
 

R = R

w

 

 
to sprawność układu wynosi: 
 
 

 

η

 = 0,5 

 
Wniosek: 
  Przy dopasowaniu odbiornika do 
źródła sprawność układu wynosi  50 

%