1
Fundamentowanie - ćwiczenia
Część 9 – Obliczanie zakotwień ścianek szczelnych
(dr hab. inż. Adam Krasiński)
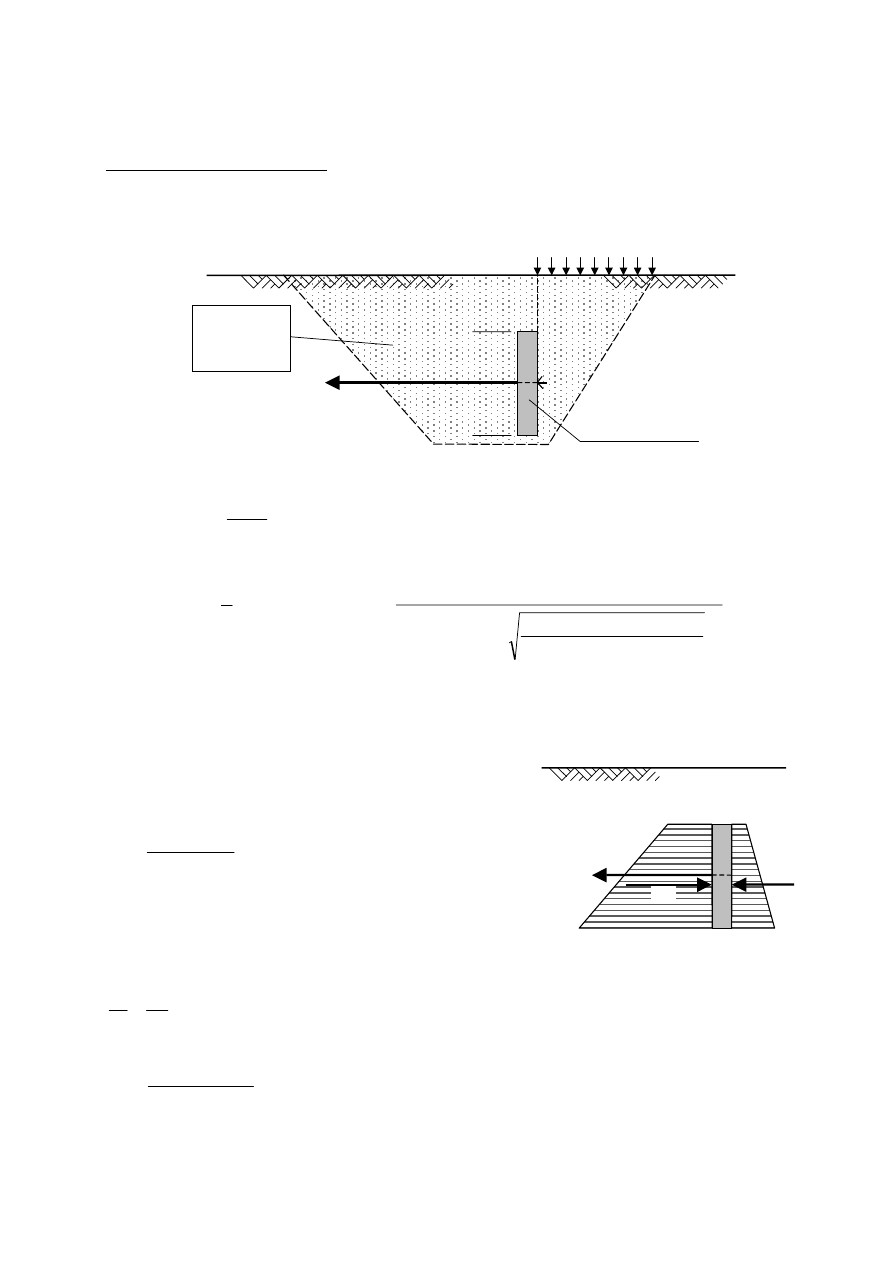
Zadanie przykładowe nr 9.1.
Polecenie: Jaką maksymalną siłę S ze ściągu może przenieść płyta kotwiąca przedstawiona na
rysunku poniżej.
Współczynnik parcia gruntu:
277
,
0
)
2
5
,
34
45
(
tan
2
=
°
−
°
=
a
K
Współczynnik odporu gruntu:
przyjęto
°
=
⋅
−
=
17
5
,
34
2
1
p
δ
→
972
,
6
)
17
cos(
5
,
34
sin
)
17
5
,
34
sin(
1
)
17
cos(
5
,
34
cos
2
2
=
°
−
°
⋅
°
+
°
−
⋅
°
−
°
=
p
K
zredukowana składowa pozioma współczynnika:
667
,
5
)
17
cos(
972
,
6
85
,
0
=
°
−
⋅
⋅
=
′
ph
K
Wartości jednostkowe parcia gruntu za płytą kotwiącą:
72
,
6
277
,
0
)
5
,
18
5
,
0
0
,
15
(
1
=
⋅
⋅
+
=
a
e
kPa
87
,
12
277
,
0
)
5
,
18
7
,
1
0
,
15
(
2
=
⋅
⋅
+
=
a
e
kPa
Wypadkowa parcia gruntu:
1
,
14
2
,
1
2
,
1
2
87
,
12
72
,
6
=
⋅
⋅
+
=
a
E
kN
Wartości odporu gruntu przed płytą kotwiącą:
42
,
52
667
,
5
5
,
18
5
,
0
1
=
⋅
⋅
=
p
e
kPa
23
,
178
667
,
5
5
,
18
7
,
1
2
=
⋅
⋅
=
p
e
kPa
Współczynnik
β
przestrzennego działania odporu i szerokość zastępcza płyty b
z
:
42
,
1
2
,
1
7
,
1 =
=
h
H
→
β
= 2,2
→
64
,
2
2
,
1
2
,
2
=
⋅
=
z
b
m > a = 2,4 m
→ b
z
= a = 2,4 m
Wypadkowa odporu:
1
,
332
4
,
2
2
,
1
2
23
,
178
42
,
52
=
⋅
⋅
+
=
p
E
kN
Obliczeniowa wartość maksymalnej siły w ściągu:
S
max
=
⋅
−
⋅
=
⋅
−
⋅
=
1
,
14
2
,
1
1
,
332
8
,
0
2
,
1
8
,
0
a
p
E
E
248,8 kN
p = 15 kN/m
2
S
max
= ?
grunt zasypowy:
Ps, I
D
= 0,75
γ
= 18,5 kN/m
3
φ
= 34,5
°
płyta 1,2
×1,2×0,15 m
rozstaw a = 2,4 m
-0,5
-1,7
0,0
S
max
e
a1
e
a2
e
p1
e
p2
E
a
E
p
2
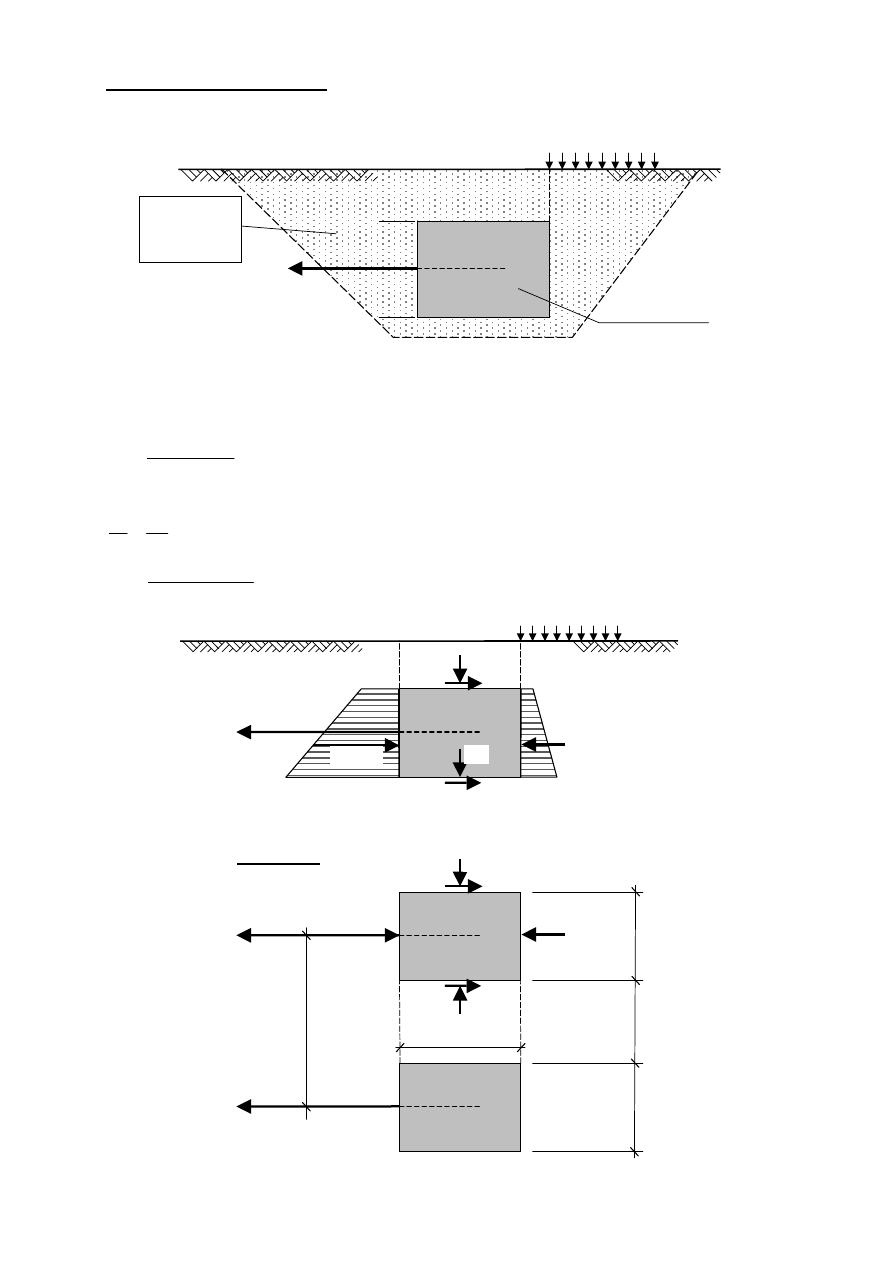
Zadanie przykładowe nr 9.2.
Polecenie:
Policzyć nośność kotwiącą bloku betonowego przedstawionego poniżej.
Warunki gruntowe takie same jak w przykładzie wyżej stąd:
277
,
0
=
a
K
,
667
,
5
=
′
ph
K
72
,
6
277
,
0
)
5
,
18
5
,
0
0
,
15
(
1
=
⋅
⋅
+
=
a
e
kPa,
87
,
12
277
,
0
)
5
,
18
7
,
1
0
,
15
(
2
=
⋅
⋅
+
=
a
e
kPa
1
,
14
2
,
1
2
,
1
2
87
,
12
72
,
6
=
⋅
⋅
+
=
a
E
kN
42
,
52
667
,
5
5
,
18
5
,
0
1
=
⋅
⋅
=
p
e
kPa,
23
,
178
667
,
5
5
,
18
7
,
1
2
=
⋅
⋅
=
p
e
kPa
42
,
1
2
,
1
7
,
1 =
=
h
H
→
β
= 2,2
→
64
,
2
2
,
1
2
,
2
=
⋅
=
z
b
m > a = 2,4 m
→ b
z
= a = 2,4 m
1
,
332
4
,
2
2
,
1
2
23
,
178
42
,
52
=
⋅
⋅
+
=
p
E
kN
p = 15 kN/m
2
S
max
= ?
grunt zasypowy:
Ps, I
D
= 0,75
γ
= 18,5 kN/m
3
φ
= 34,5
°
blok 1,2
×1,2×1,5 m
rozstaw a = 2,4 m
-0,5
-1,7
0,0
p = 15 kN/m
2
S
max
e
a1
e
a2
e
p1
e
p2
Q
1
= E
p
Q
2
= E
a
G
1
Q
3
Q
4
G
2
S
max
Q
1
= E
p
Q
2
= E
a
E
0
Q
5
Q
5
E
0
S
max
Widok z góry
a =
2,4 m
1,2 m
1,2 m
1,2 m
1,5 m
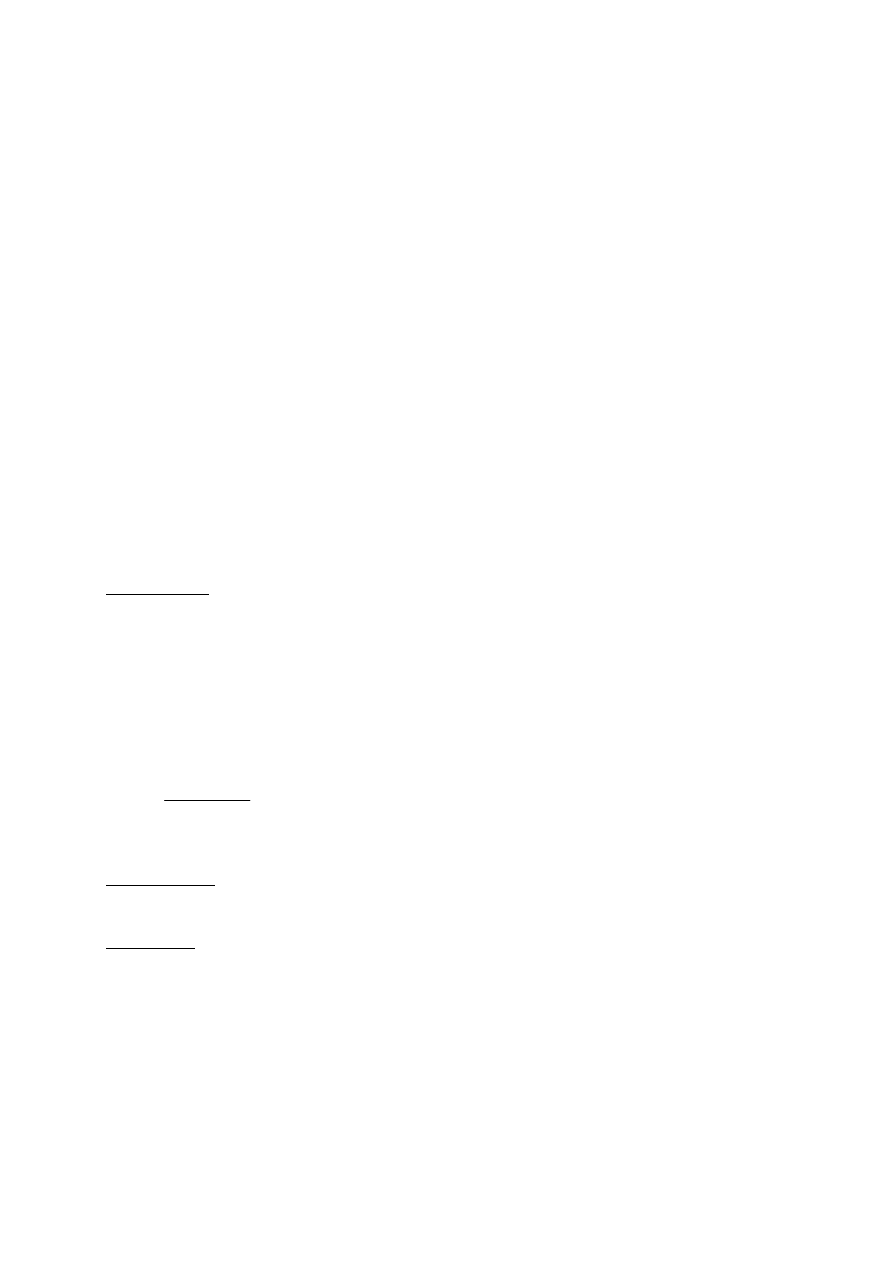
3
Wartości sił Q
i
:
1
,
332
1
=
=
p
E
Q
kN
1
,
14
2
−
=
−
=
a
E
Q
kN
Q
3
- pominięto ze względu na małą wartość
Obliczenie siły Q
4
- siła tarcia podstawy bloku o grunt
Przyjęto kąt tarcia gruntu o podstawę bloku:
δ
4
=
φ
= 34,5
° (blok betonowany wprost na gruncie)
Ciężary:
65
,
16
5
,
18
5
,
0
5
,
1
2
,
1
1
=
⋅
⋅
⋅
=
G
kN
84
,
51
0
,
24
2
,
1
5
,
1
2
,
1
2
=
⋅
⋅
⋅
=
G
kN
49
,
68
84
,
51
65
,
16
2
1
=
+
=
+ G
G
kN
1
,
47
5
,
34
tan
49
,
68
tan
)
(
4
2
1
4
=
°
⋅
=
⋅
+
=
δ
G
G
Q
kN
Obliczenie siły Q
5
Wariant I - siła Q
5
pochodzi od tarcia na ścianach bocznych bloku
Wariant II - siła Q
5
pochodzi od tarcia pod podstawą bryły gruntu miedzy blokami
Decyduje ten wariant, który da mniejszą wartość siły Q
5
Ad. Wariant I:
Przyjęto kąt tarcia gruntu o ściany bloku:
δ
5
=
φ
/2 = 34,5°/2 = 17° (blok betonowany w deskowaniu systemowym)
Parcie spoczynkowe gruntu na ściany boczne bloku:
434
,
0
5
,
34
sin
1
sin
1
0
=
°
−
=
−
=
φ
K
kN
01
,
4
434
,
0
5
,
18
5
,
0
01
=
⋅
⋅
=
e
kPa
65
,
13
434
,
0
5
,
18
7
,
1
02
=
⋅
⋅
=
e
kPa
89
,
15
5
,
1
2
,
1
2
65
,
13
01
,
4
0
=
⋅
⋅
+
=
E
kN
72
,
9
17
tan
89
,
15
2
tan
2
5
0
5
=
°
⋅
⋅
=
⋅
⋅
=
δ
E
Q
I
kN
Ad. Wariant II:
9
,
38
5
,
34
tan
)
2
,
1
5
,
1
5
,
18
7
,
1
(
tan
5
=
°
⋅
⋅
⋅
⋅
=
⋅
=
φ
g
II
G
Q
kN
Ostatecznie:
72
,
9
5
5
=
=
I
Q
Q
kN
Nośność bloku:
S
max
=
=
⋅
=
+
+
−
⋅
=
⋅
∑
72
,
374
8
,
0
)
72
,
9
1
,
47
1
,
14
1
,
332
(
8
,
0
8
,
0
i
Q
300,0 kN
Wniosek: stosowanie bloków jest mało opłacalne w stosunku do płyt kotwiących.
Wyszukiwarka
Podobne podstrony:
Fundamentowanie cw cz 2 id 181 Nieznany
Fundamentowanie ćw cz 2
Fundamentowanie cw cz 8 cd id Nieznany
Fundamentowanie ćw cz 1
Fundamentowanie cw cz 8 id 181 Nieznany
Fundamentowanie cw cz 5 id 181 Nieznany
Fundamentowanie ćw cz 2
więcej podobnych podstron