1
Fundamentowanie - ćwiczenia
Część 5 – Nośność pali – metoda
α
i
β
(dr inż. Adam Krasiński, mgr inż. Tomasz Kusio)
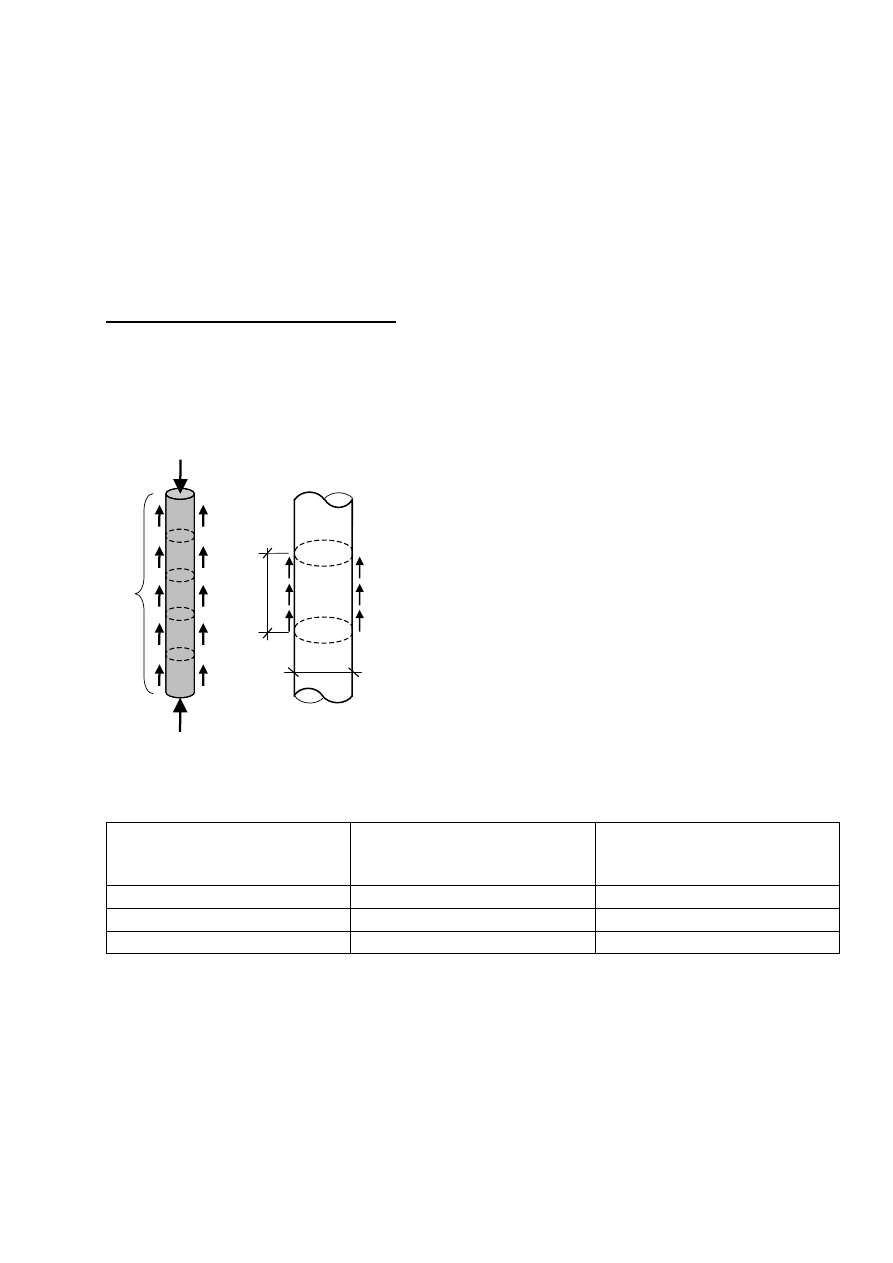
Nośność pala jest sumą nośności pobocznicy i podstawy pala:
b
i
si
b
s
c
R
R
R
R
R
+
=
+
=
∑
gdzie: R
s
– nośność charakterystyczna pobocznicy pala, która jest sumą nośności wszystkich
odcinków obliczeniowych wzdłuż pobocznicy pala
si
R ,
R
b
– nośność charakterystyczna podstawy pala.
Metoda
α - nośność krótkoterminowa
Korzystając z tej metody można oszacować nośność pojedynczego pala pracującego w warunkach
bez odpływu. Oznacza to, że metoda może być zastosowana tylko w przypadku zagłębienia pala w
gruntach spoistych. Opór gruntu zależy głównie od wytrzymałości gruntu na ścinanie w warunkach
bez odpływu C
u
.
Nośność pobocznicy pala dla i-tego odcinka obliczenio-
wego:
i
si
si
si
si
si
si
h
D
f
S
A
f
S
R
⋅
⋅
⋅
⋅
=
⋅
⋅
=
π
gdzie: f
si
– opór gruntu na pobocznicy i-tego odcinka
obliczeniowego pala.
Dla warunków bez drenażu f
si
=
α
i
· C
ui
w którym
α
i
wyznaczany wg tablicy 1,
A
si
– pole powierzchni bocznej i-tego odcinka
obliczeniowego pala,
S
si
– współczynnik technologiczny.
Dla pali:
- wierconych w rurach S
s
= 1,0;
- pali CFA S
s
= 1,2;
- Vibro i wkręcanych S
s
= 1,4;
- pali prefabrykowanych S
s
= 1,0.
Tablica 1. Współczynnik
α
wg Viggiani’ego (1993).
Wytrzymałość gruntu na
ścinanie bez odpływu
C
u
[kPa]
Pale przemieszczeniowe,
wbijane i wkręcane
Pale wiercone i CFA
≤25
α
= 1,0
α
= 0,7
25÷70
α
= 1,0 – 0,011· (C
u
– 25)
α
= 0,7 – 0,008· (C
u
– 25)
>70
α
= 0,5
α
= 0,35
Nośność podstawy pala:
2
25
,
0
D
q
S
A
q
S
R
b
b
b
b
b
b
⋅
⋅
⋅
⋅
=
⋅
⋅
=
π
gdzie: q
b
= 9 · C
ub
– opór gruntu pod podstawą pala wg Skempton’a (1959) ,
A
b
– powierzchnia podstawy pala ( dla pali Vibro D jest średnicą „buta” stalowego),
S
b
– współczynnik technologiczny.
Dla pali:
- wierconych i CFA S
b
= 1,0;
- wkręcanych S
b
= 1,1;
- prefabrykowanych S
b
= 1,2;
- Vibro S
b
= 1,3.
h
i
D
f
si
Q
c
R
b
Σ
R
Si
=
R
s
R
si
2
Metoda
β
– nośność długoterminowa
Korzystając z tej metody można oszacować nośność pojedynczego pala pracującego w warunkach z
odpływem w gruntach spoistych i niespoistych. Opór gruntu zależy od stanu naprężenia
efektywnego w gruncie. Metodę
β
stosuje się do wszystkich rodzajów gruntów.
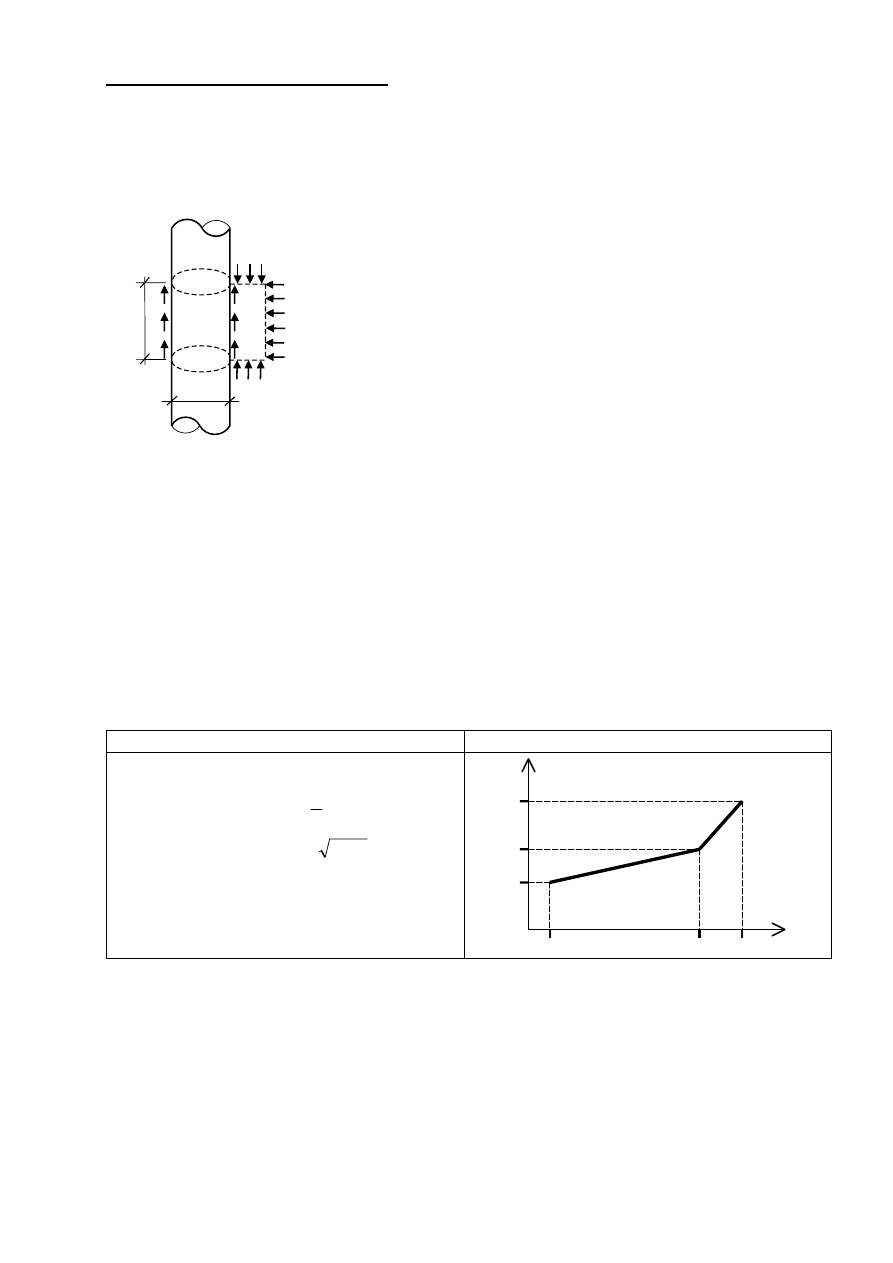
Nośność pobocznicy pala dla i-tego odcinka obliczeniowego:
i
si
si
si
si
si
si
h
D
f
S
A
f
S
R
⋅
⋅
⋅
⋅
=
⋅
⋅
=
π
gdzie: f
si
– opór gruntu na pobocznicy i-tego odcinka pala.
Dla warunków z odpływem f
si
=
β
i
·
σ
’
vi
,
A
si
– pole powierzchni bocznej i-tego odcinka
obliczeniowego pala,
S
si
– współczynnik technologiczny.
Dla pali:
- wierconych w rurach S
s
= 0,9;
- CFA S
s
= 1,0;
- Vibro S
s
= 1,4;
- wkręcanych S
s
= 1,3;
- prefabrykowanych S
s
= 1,1.
Wyznaczanie oporu gruntu f
si
na pobocznicy pala:
Opór gruntu na pobocznicy pala wyraża się wzorem:
vi
i
i
vi
i
i
vi
i
si
K
K
f
'
tan
'
'
0
0
σ
δ
σ
µ
σ
β
⋅
⋅
=
⋅
⋅
=
⋅
=
; 200
'
≤
vi
σ
kPa
gdzie:
σ
’
vi
– jest średnim, efektywnym naprężeniem pionowym, działąjącym w i-tej obliczeniowej
warstwie gruntu. Jednak ze względu na zjawisko głębokości krytycznej, w obliczeniach
przyjmujemy maksymalnie
σ
’
vi
= 200 kPa.
β
i
– jest współczynnikiem zależnym od efektywnego naprężenia poziomego, działąjącego w i-tej
obliczeniowej warstwie gruntu (
vi
i
hi
K
'
'
0
σ
σ
⋅
=
)
oraz szorstkości powierzchni pobocznicy pala
(
i
i
δ
µ
tan
=
). Współczynnik należy przyjmować wg tablicy 2.
Tablica 2. Współczynnik
β
.
Grunty spoiste; wg Burlanda (1973)
Grunty niespoiste; wg Meyerhofa (1976)
⋅
⋅
=
'
3
2
tan
0
φ
β
K
(
)
OCR
K
⋅
−
=
'
sin
1
0
φ
OCR – współczynnik prekonsolidacji
(wyznaczony na podstawie badań
laboratoryjnych bądź in situ)
Nośność podstawy pala:
2
25
,
0
D
q
S
A
q
S
R
b
b
b
b
b
b
⋅
⋅
⋅
⋅
=
⋅
⋅
=
π
gdzie: q
b
– opór gruntu pod podstawą pala,
A
b
– powierzchnia podstawy pala ( dla pali Vibro D jest średnicą „buta” stalowego),
S
b
– współczynnik technologiczny
Dla pali:
- wierconych i CFA S
b
= 1,0;
- wkręcanych S
b
= 1,2;
- prefabrykowanych S
b
= 1,3;
- Vibro S
b
= 1,4.
β
1,20
0,75
0,44
28°
35°
37°
φ
’
h
i
D
σ
vi
’
σ
hi
’
f
si
3
Wyznaczanie oporu gruntu q
b
pod podstawą pala:
Opór gruntu pod podstawą pala przyjmujemy wg rozwiązania Terzaghi’ego:
c
b
q
vb
b
N
c
N
q
⋅
+
⋅
=
'
'
σ
gdzie:
σ′
vb
– naprężenie efektywne w poziomie podstawy pala, przy czym ze względu na zjawisko
głębokości krytycznej w obliczeniach przyjmujemy maksymalnie
σ′
vi
= 200 kPa,
c’
b
– spójność efektywna gruntu w poziomie posadowienia,
N
c
, N
q
– współczynniki nośności:
(
)
(
)
b
e
N
b
b
q
'
tan
2
2
2
'
tan
1
'
tan
φ
η
φ
φ
⋅
⋅
⋅
+
+
=
gdzie:
÷
=
π
π
η
5
3
3
1
Kąt wypierania gruntu
η
spod podstawy pala. Przyjmujemy w przedziale od
π
3
1
dla plastycznych
gruntów spoistych do
π
5
3
dla zagęszczonych piasków.
b
q
c
N
N
'
cot
)
1
(
φ
⋅
−
=
Nośność projektowa pala
Nośność projektową pala wyznaczamy w następujący sposób:
b
b
s
s
d
b
d
s
d
c
R
R
R
R
R
γ
γ
+
=
+
=
;
;
;
Współczynniki częściowe do nośności (podejście obliczeniowe 2, kombinacja 1, zalecane przez
PKN):
γ
s
=
γ
b
= 1,1
Warunek nośności:
Q
v;d
≤ R
c;d
Wpływ zmiany warstwy gruntowej na nośność podstawy pala
Wyżej podane wzory w metodach
α
i
β
, dotyczące nośności podstaw pali, są ważne dla przypadku
podłoża jednorodnego. W przypadku podłoża uwarstwionego, w sytuacji gdy występuje zmiana
warstwy o różnych parametrach wytrzymałościowych, na granicy obu warstw może pojawić się
przeskok w nośności podstawy. Taki przeskok jest nierzeczywisty. Zmiany nośności podstaw
przebiegają w rzeczywistości stopniowo. Można zastosować zmodyfikowaną propozycję
Meyerhofa (1983), przedstawioną na rysunkach poniżej.
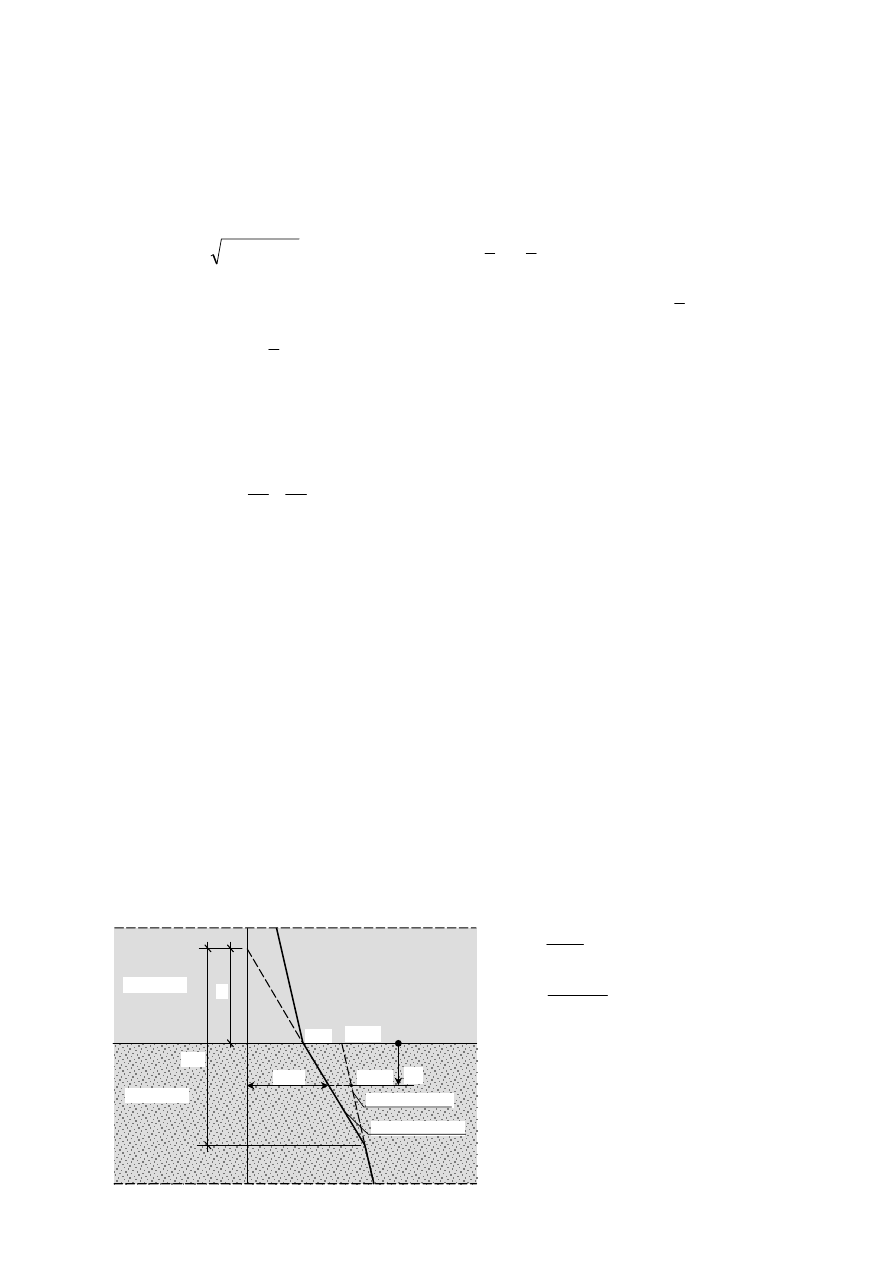
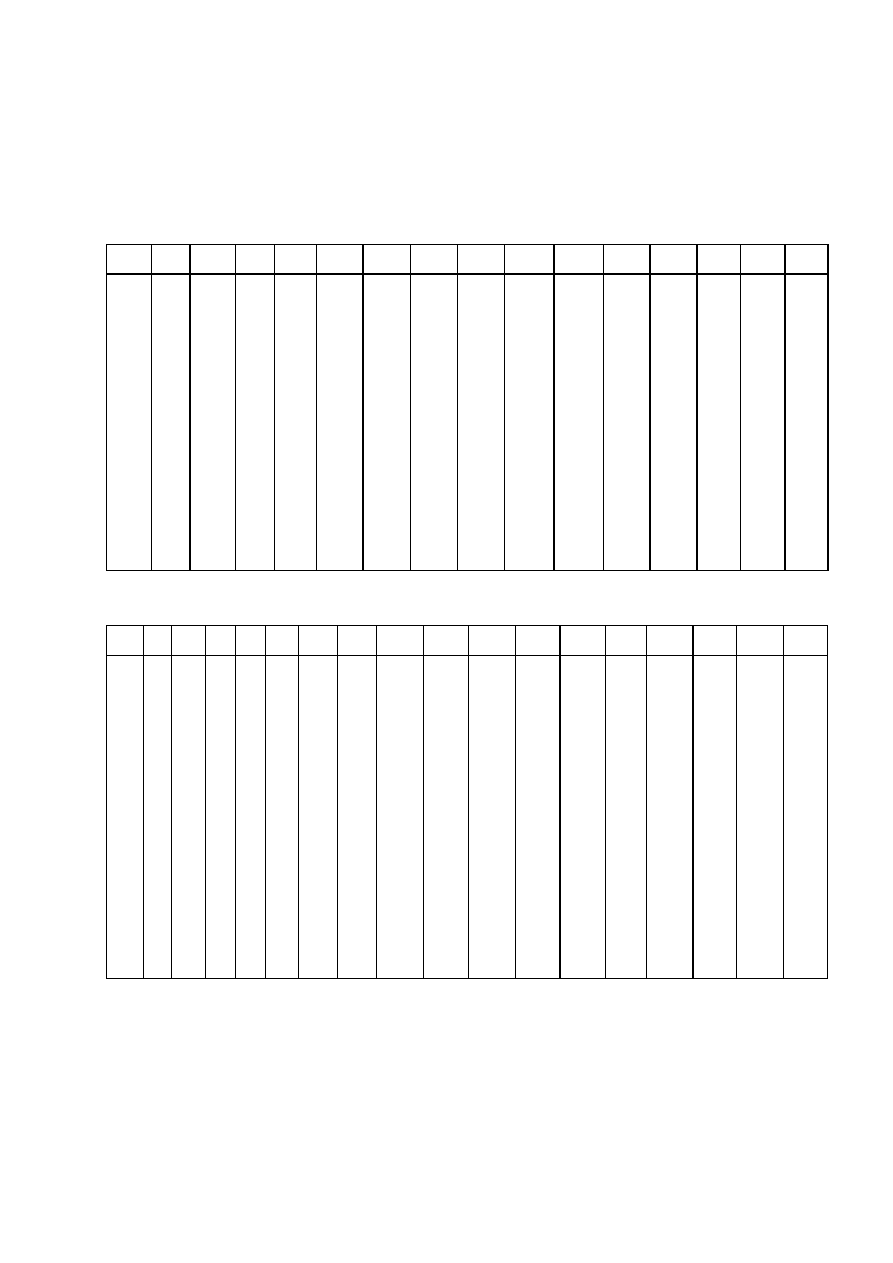
Przypadek 1
– warstwa górna (1) o mniejszej nośności niż warstwa dolna (2)
D
R
R
h
b
b
z
10
1
2
2
1
⋅
′
=
−
−
; D – średnica pala
0
,
1
10
2
2
≤
∆
+
=
D
z
h
z
η
Skorygowana nośność podstawy pala
w warstwie 2:
2
2
2
)
(
b
b
R
z
R
′
⋅
=
η
Wartość R
′
b2
(z) oblicza się według wzorów
na str. 1 i 2.
h
z
10D
R
b1-2
R
′
b2-1
R
b2
(z)
R
′
b2
(z)
∆
z
2
wykres teoretyczny
wykres skorygowany
warstwa 1
warstwa 2
4
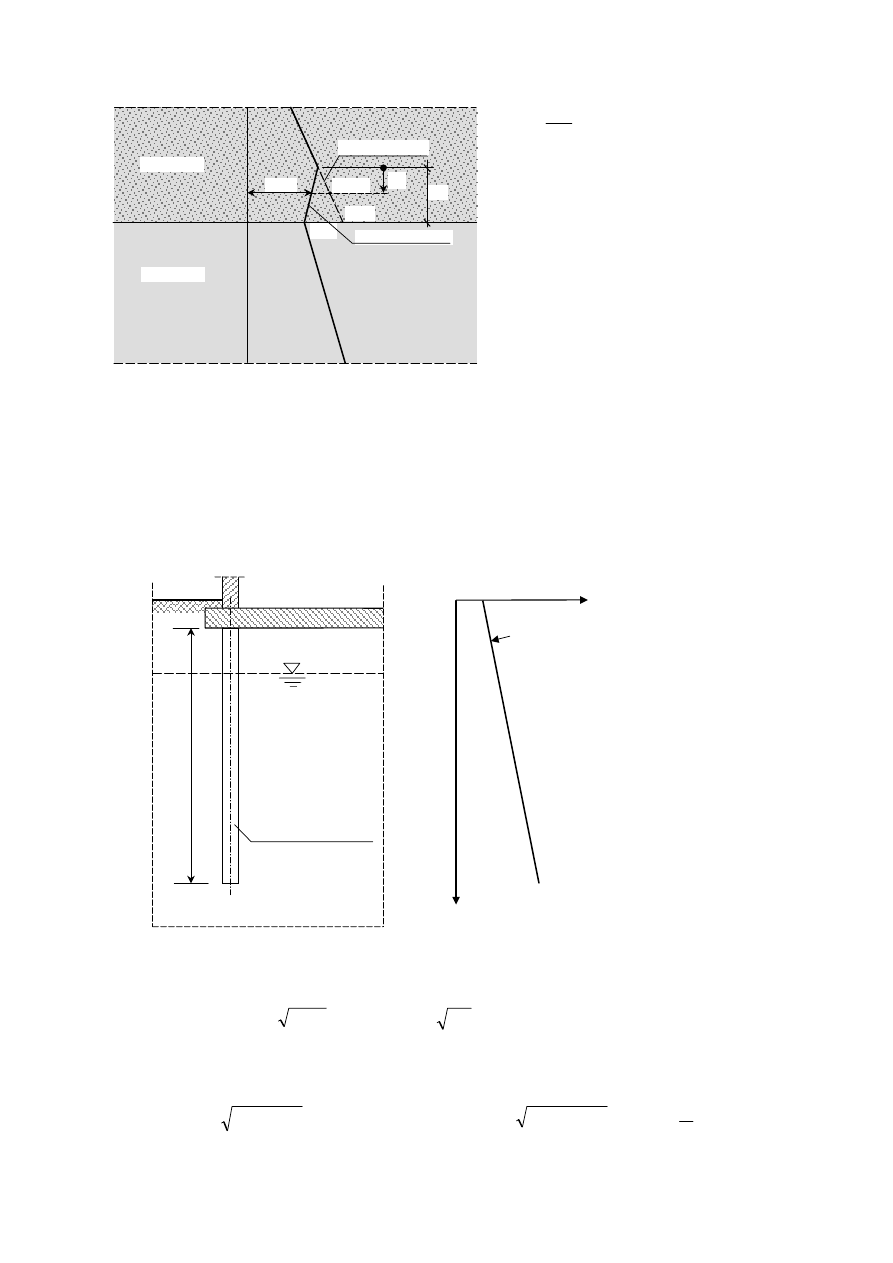
Przypadek 2
– warstwa górna (1) o większej nośności niż warstwa dolna (2)
0
,
1
3
1
1
≤
∆
=
D
z
η
; D – średnica pala
Skorygowana nośność podstawy pala
w warstwie 1:
)
(
)
(
)
(
1
2
2
1
1
1
1
−
−
−
′
⋅
−
′
=
b
b
b
b
R
R
z
R
z
R
η
Wartość R
′
b1
(z) oblicza się według wzorów
na str. 1 i 2.
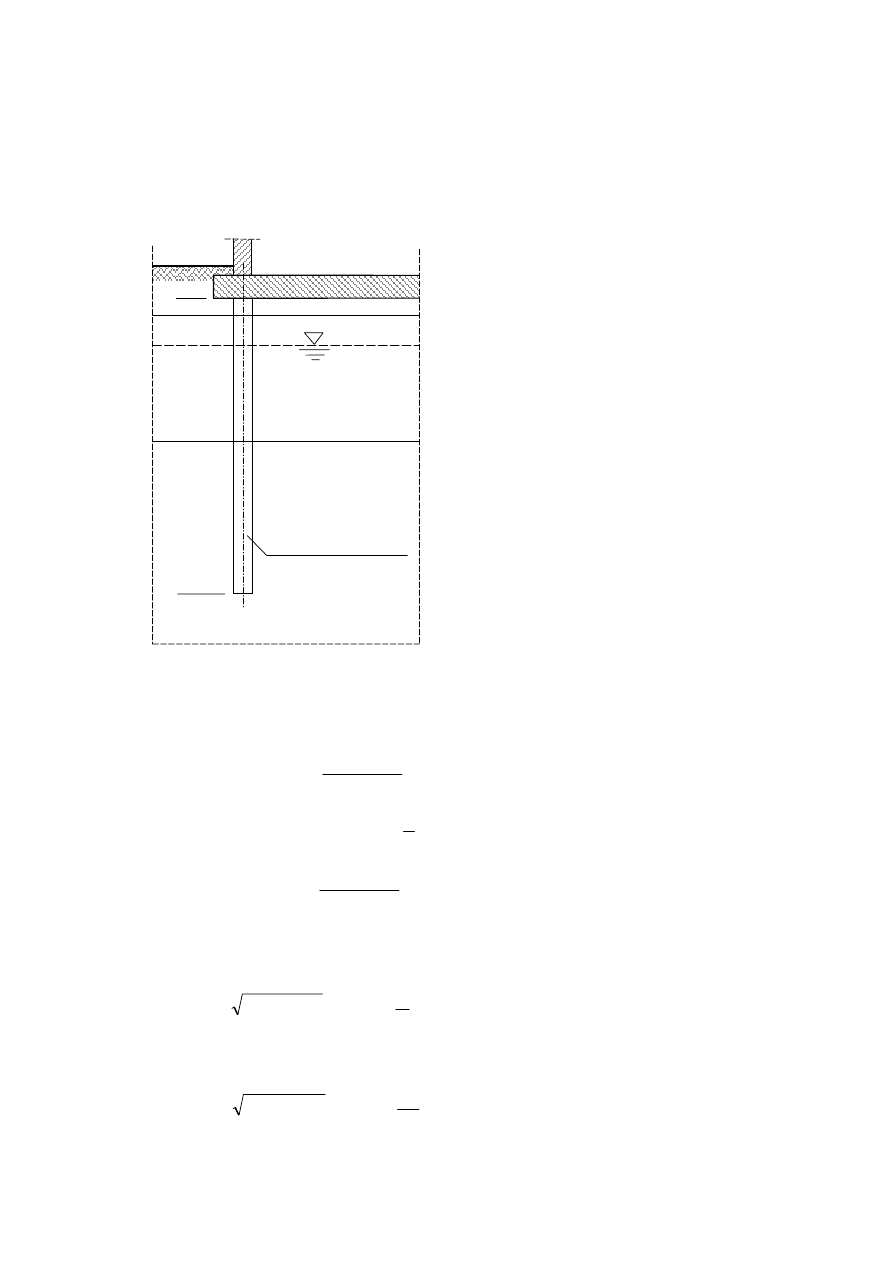
Zadanie przykładowe 5.1.
Dobrać długość L pala wierconego
φ800 mm, aby w zadanych warunkach gruntowych uzyskał
nośność wystarczającą do przeniesienia obciążenia projektowego Q
d
= 1500 kN. Obliczenia
wykonać metodą
α
i
β
z uwzględnieniem zaleceń Eurokodu 7 (EC7).
Obliczenia wielkości pomocniczych
Współczynnik parcia spoczynkowego:
977
,
0
0
,
2
)
18
sin
1
(
)
sin
1
(
0
=
⋅
°
−
=
⋅
′
−
=
OCR
K
φ
Współczynniki nośności gruntu pod podstawą pala:
przyjęto
η
=
π
/2
(
)
(
)
255
,
5
)
18
tan
2
2
exp(
18
tan
1
18
tan
)
tan
2
exp(
tan
1
tan
2
2
2
2
=
°
⋅
⋅
⋅
°
+
+
°
=
′
⋅
⋅
′
+
+
′
=
π
φ
η
φ
φ
q
N
(
)
(
)
1
,
13
18
cot
1
255
,
5
cot
1
=
°
⋅
−
=
′
⋅
−
=
φ
q
c
N
N
zwg
0,0
-1,0
-3,0
ił pylasto-piaszczysty
I
L
=0,30
γ
= 20 kN/m
3
γ
′ = 10 kN/m
3
φ
′ = 18°, c′=45 kPa
OCR = 2,0
Profil geotechniczny
L
= ?
pal wiercony
φ
800 mm
C
u
[kPa]
z [m ppt]
25
0
C
u
(z) = 25 + 5,0
⋅z [kPa]
R
b2-1
R
′
b1-2
R
b1
(z)
wykres teoretyczny
wykres skorygowany
warstwa 1
warstwa 2
3D
∆
z
1
R
′
b1
(z)
5
Współczynniki technologiczne:
do metody
α
: S
s
= 1,0; S
b
= 1,0
do metody
β
: S
s
= 0,9; S
b
= 1,0
Współczynniki korekcyjne do nośności (wg EC7): przyjęto
ξ
3
= 1,25/1,1 = 1,14
Współczynniki częściowe do nośności (podejście obliczeniowe 2 wg EC7):
γ
s
= 1,1;
γ
b
= 1,1
Obliczenie nośności pala metodą
α
z
h
i
C
ui
α
i
f
si
R
si
R
s
q
bi
R
b
R
c
R
s;k
R
b;k
R
c;k
R
s;d
R
b;d
R
c;d
[m ppt]
[m]
[kPa]
[kPa]
[kN]
[kN]
[kPa]
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]
0,0
0,0
25,0
0,70
1,0
0,0
30,0
0,66
18,7
0,0
0,0
3,0
2,0
40,0
0,58
21,5
108,1
108,1
6,0
3,0
55,0
0,46
24,3
182,8
290,9
9,0
3,0
70,0
0,35
24,9
187,7
478,7
630,0
316,7
795,3
419,9
277,8
697,7
381,7
252,5
634,2
12,0
3,0
85,0
0,35
27,1
204,5
683,2
765,0
384,5
1067,7
599,3
337,3
936,6
544,8
306,6
851,4
15,0
3,0
100,0
0,35
32,4
244,1
927,3
900,0
452,4
1379,7
813,4
396,8 1210,2
739,5
360,8 1100,2
16,0
1,0
105,0
0,35
35,9
90,2
1017,4
945,0
475,0
1492,4
892,5
416,7 1309,2
811,4
378,8 1190,1
17,0
1,0
110,0
0,35
37,6
94,6
1112,0
990,0
497,6
1609,6
975,4
436,5 1412,0
886,8
396,8 1283,6
18,0
1,0
115,0
0,35
39,4
99,0
1211,0 1035,0
520,2
1731,2
1062,2
456,4 1518,6
965,7
414,9 1380,5
19,0
1,0
120,0
0,35
41,1
103,4
1314,3 1080,0
542,9
1857,2
1152,9
476,2 1629,1 1048,1
432,9 1481,0
20,0
1,0
125,0
0,35
42,9
107,8
1422,1 1125,0
565,5
1987,6
1247,4
496,0 1743,5 1134,0
450,9 1585,0
21,0
1,0
130,0
0,35
44,6
112,2
1534,2 1170,0
588,1
2122,3
1345,8
515,9 1861,7 1223,5
469,0 1692,5
22,0
1,0
135,0
0,35
46,4
116,6
1650,8 1215,0
610,7
2261,5
1448,1
535,7 1983,8 1316,4
487,0 1803,4
Obliczenie nośności pala metodą
β
z
h
i
σ
vi
φ
'
i
c'
i
β
i
f
si
R
si
R
s
q
bi
R
b
R
c
R
s;k
R
b;k
R
c;k
R
s;d
R
b;d
R
c;d
[m ppt] [m] [kPa]
[
o
]
[kPa]
[kPa]
[kN]
[kN]
[kPa]
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]
0,0
0,0
0,0
1,0
0,0
20,0 18,0 45,0
0,21
4,15
0,0
0,0
3,0
2,0
60,0 18,0 45,0
0,21
8,31
37,6
37,6
6,0
3,0
90,0 18,0 45,0
0,21
15,58
105,7
143,3
9,0
3,0 120,0 18,0 45,0
0,21
21,81
148,0
291,2
1220,0
613,2
904,5
255,5
537,9
793,4
232,2
489,0
721,3
12,0
3,0 150,0 18,0 45,0
0,21
28,04
190,2
481,5
1377,6
692,5
1174,0
422,3
607,4
1029,8
384,0
552,2
936,2
13,0
1,0 160,0 18,0 45,0
0,21
32,19
72,8
554,3
1430,2
718,9
1273,2
486,2
630,6
1116,8
442,0
573,3
1015,3
14,0
1,0 170,0 18,0 45,0
0,21
34,27
77,5
631,8
1482,7
745,3
1377,1
554,2
653,8
1208,0
503,8
594,3
1098,2
15,0
1,0 180,0 18,0 45,0
0,21
36,34
82,2
714,0
1535,3
771,7
1485,7
626,3
676,9
1303,3
569,4
615,4
1184,8
16,0
1,0 190,0 18,0 45,0
0,21
38,42
86,9
800,9
1587,8
798,1
1599,0
702,5
700,1
1402,7
638,7
636,5
1275,1
17,0
1,0 200,0 18,0 45,0
0,21
40,50
91,6
892,5
1640,4
824,5
1717,0
782,9
723,3
1506,2
711,7
657,5
1369,2
18,0
1,0 210,0 18,0 45,0
0,21
41,53
93,9
986,4
1640,4
824,5
1811,0
865,3
723,3
1588,6
786,6
657,5
1444,2
19,0
1,0 220,0 18,0 45,0
0,21
41,53
93,9
1080,4
1640,4
824,5
1904,9
947,7
723,3
1671,0
861,6
657,5
1519,1
20,0
1,0 230,0 18,0 45,0
0,21
41,53
93,9
1174,3
1640,4
824,5
1998,9
1030,1
723,3
1753,4
936,5
657,5
1594,0
21,0
1,0 240,0 18,0 45,0
0,21
41,53
93,9
1268,3
1640,4
824,5
2092,8
1112,5
723,3
1835,8
1011,4
657,5
1668,9
22,0
1,0 250,0 18,0 45,0
0,21
41,53
93,9
1362,2
1640,4
824,5
2186,8
1194,9
723,3
1918,2
1086,3
657,5
1743,8
Wniosek z obliczeń:
Wartości nośności pala otrzymane z obu metod obliczeniowych są zbliżone do siebie.
Zadecydował wynik obliczeń metodą
α
Potrzebna długość pala: L = 20,0 - 1,0 = 19,0 m
Warunek nośności: Q
d
= 1500 kN < R
c;d
= 1585 kN
6
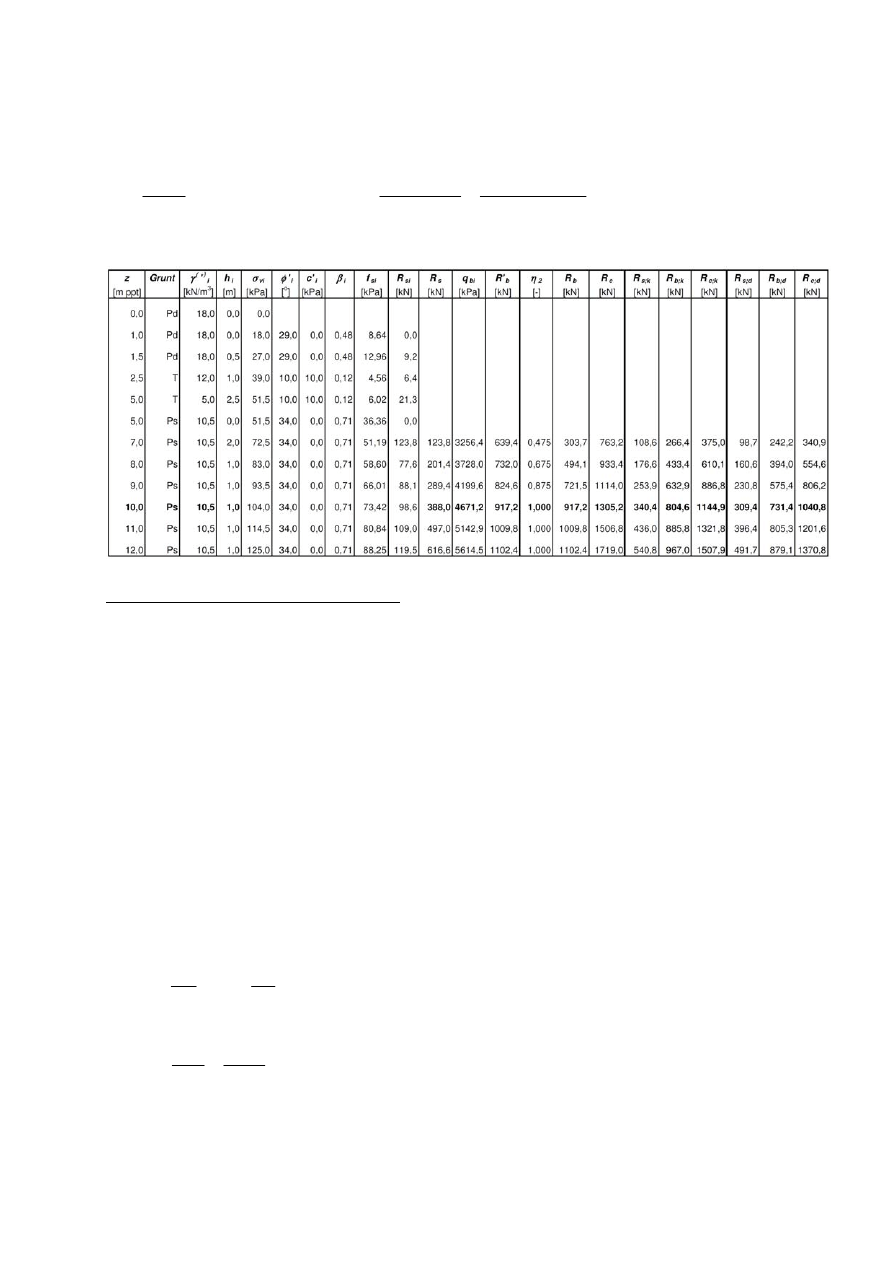
Zadanie przykładowe 5.2.
Policzyć nośność na wciskanie i wyciąganie pala wierconego
φ500 mm, przedstawionego na
rysunku poniżej. Obliczenia wykonać metodą
β
z uwzględnieniem zaleceń Eurokodu 7 (EC7).
Założyć działanie tarcia negatywnego.
Obliczenia wielkości pomocniczych
Współczynnik
β
(według Meyerhofa):
Pd,
φ
' = 29
° →
48
,
0
)
28
29
(
28
35
44
,
0
75
,
0
44
,
0
=
−
⋅
−
−
−
=
β
T,
φ
' = 10
° , K
0
= 1,0
→
117
,
0
10
3
2
tan
0
,
1
=
°
⋅
⋅
=
β
Ps,
φ
' = 34
° →
706
,
0
)
34
35
(
28
35
44
,
0
75
,
0
75
,
0
=
−
⋅
−
−
−
=
β
Współczynnik nośności gruntu pod podstawą pala:
1) Warstwa T - przyjęto
η
= 1/3
π
(
)
05
,
2
369
,
0
exp
42
,
1
)
10
tan
3
2
exp(
10
tan
1
10
tan
2
2
=
⋅
=
°
⋅
⋅
⋅
°
+
+
°
=
π
q
N
95
.
5
10
cot
)
1
05
,
2
(
=
°
⋅
−
=
c
N
2) Warstwa Pd - przyjęto
η
= 3/5
π
(
)
0
,
45
543
,
2
exp
537
,
3
)
34
tan
5
3
2
exp(
34
tan
1
34
tan
2
2
≅
⋅
=
°
⋅
⋅
⋅
°
+
+
°
=
π
q
N
Powierzchnia 1mb pobocznicy pala: A
s
(1mb) =
π⋅0,5 = 1,571 m
2
Powierzchnia podstawy pala: A
b
= 0,25
⋅π⋅0,5
2
= 0,196 m
2
zwg
0,0
-1,0
-2,5
Torf
γ
′ = 10,5 kN/m
3
φ
′ = 34°
η
= 3/5
π
Profil geotechniczny
pal wiercony
φ500 mm
L = 9,0 m
-10,0
-1,5
-2,5
-5,0
Pd,
φ
'= 29
°,
γ
= 18 kN/m
3
γ
= 12 kN/m
3
γ
′ = 5 kN/m
3
φ
′ = 10°, c′=10 kPa
K
0
= 1,0 kPa
Ps
Przyjęto współczynniki:
S
s
= 0,9; S
b
= 1,0, S
s;t
= 0,7
γ
s
= 1,1;
γ
b
= 1,1;
γ
s;t
= 1,15
ξ
3
= 1,25/1,1 = 1,14
Współczynnik obciążenia do tarcia
negatywnego:
γ
Tn
= 1,2
7
Granica warstw na głębokości z = 5,0 m ppt.
1
,
165
95
,
5
0
,
10
05
,
2
5
,
51
2
1
=
⋅
+
⋅
=
−
b
q
kPa
→
4
,
32
1
,
165
196
,
0
2
1
=
⋅
=
−
b
R
kN
5
,
2317
0
,
45
5
,
51
1
2
=
⋅
=
−
b
q
kPa
→
2
,
454
5
,
2317
196
,
0
1
2
=
⋅
=
′
−
b
R
kN
Wysokość zastępcza h
z
:
357
,
0
0
,
5
2
,
454
4
,
32
=
⋅
=
z
h
m
→
0
,
5
357
,
0
0
,
5
10
0
,
5
2
+
−
=
+
−
=
z
D
h
z
z
η
Obliczenie nośności pala na wciskanie metodą
β
Obliczenie wartości tarcia negatywnego:
Tarcie negatywne równa się sumie sił R
si
w warstwach Pd i T
T
n,k
= 9,2 + 6,4 + 21,3 = 36,9 kN
Wartość projektowa tarcia negatywnego:
T
n,d
= 36,9
⋅1,2 = 44,3 kN
Warunek nośności pala na wciskanie:
Q
d
+ T
n,d
≤ R
c;d
= 1040,8 kN
Dopuszczalna wartość projektowej siły wciskającej pal:
Q
d
≤ R
c;d
– T
n,d
= 1040,8 - 44,3 = 996,5 kN
Nośność pala na wyciąganie:
Wartość charakterystyczna:
0
,
265
4
,
340
9
,
0
7
,
0
;
;
;
=
⋅
=
⋅
=
k
s
s
t
s
k
ct
R
S
S
R
kN
Wartość projektowa:
=
=
=
15
,
1
0
,
265
;
;
;
t
s
k
ct
d
ct
R
R
γ
230,0 kN
Do powyższej wartości nośności na wyciąganie można dodać ciężar pala:
4
,
29
)
0
,
10
0
,
25
(
196
,
0
5
,
7
0
,
25
196
,
0
5
,
1
=
−
⋅
⋅
+
⋅
⋅
=
p
G
kN