Dr inż. Krzysztof Schabowicz

BUDOWNICTWO OGÓLNE

WYKŁAD 13

.

Zasady obliczania elementów z drewna litego w dachach

rozporowych i bezrozporowych.

Zasady obliczania stropów na belkach.

Zasady obliczania nadproży.

Zasady obliczania murów niezbrojonych i zbrojonych

.

WROCŁAW 2010

Zasady obliczania elementów

z drewna litego w dachach

rozporowych i bezrozporowych.

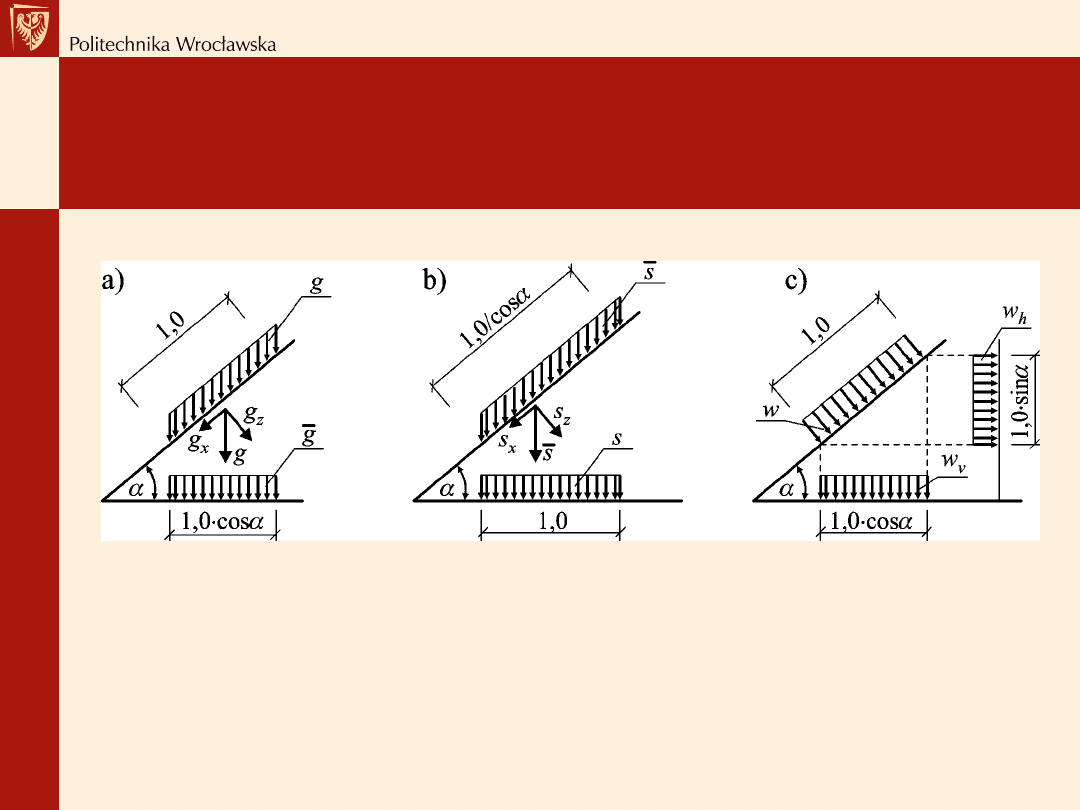
Rozkład obciążeń na pochyłych połaciach



cos

g

g

z





sin

g

g

x





2

cos

s

s

z







cos

sin

s

s

x





cos

w

w

v





sin

w

w

h



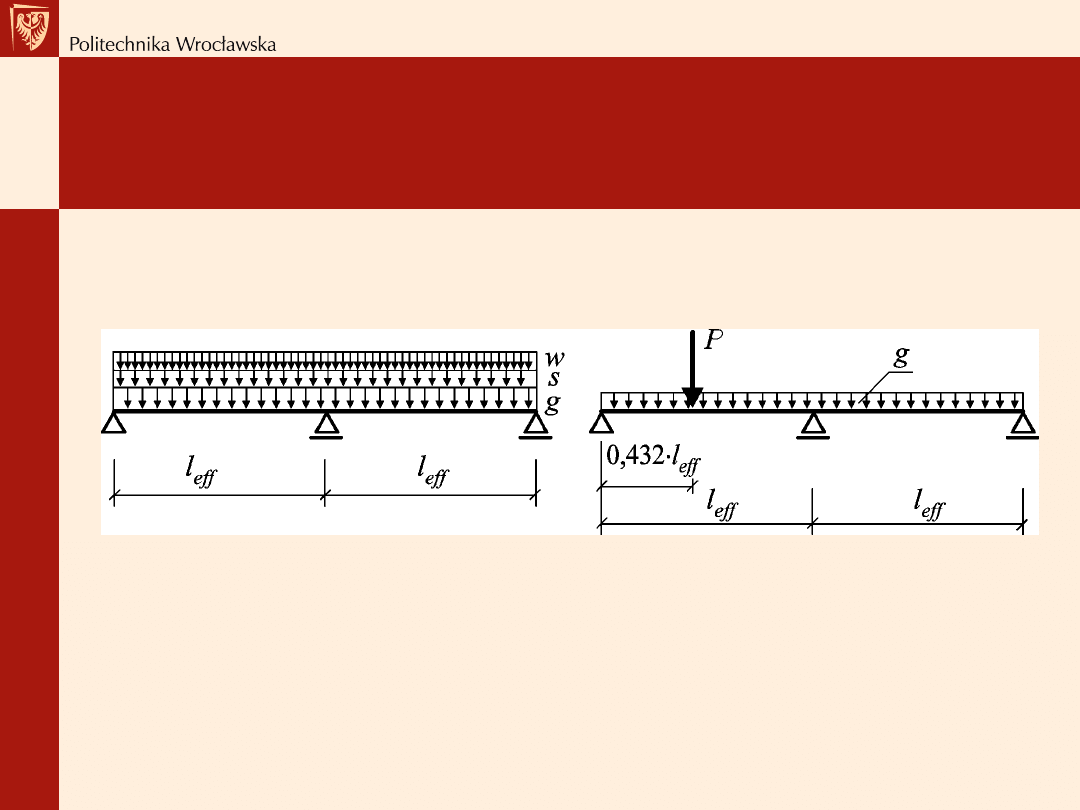
Łata lub deskowanie

I wariant obciążeń

II wariant obciążeń

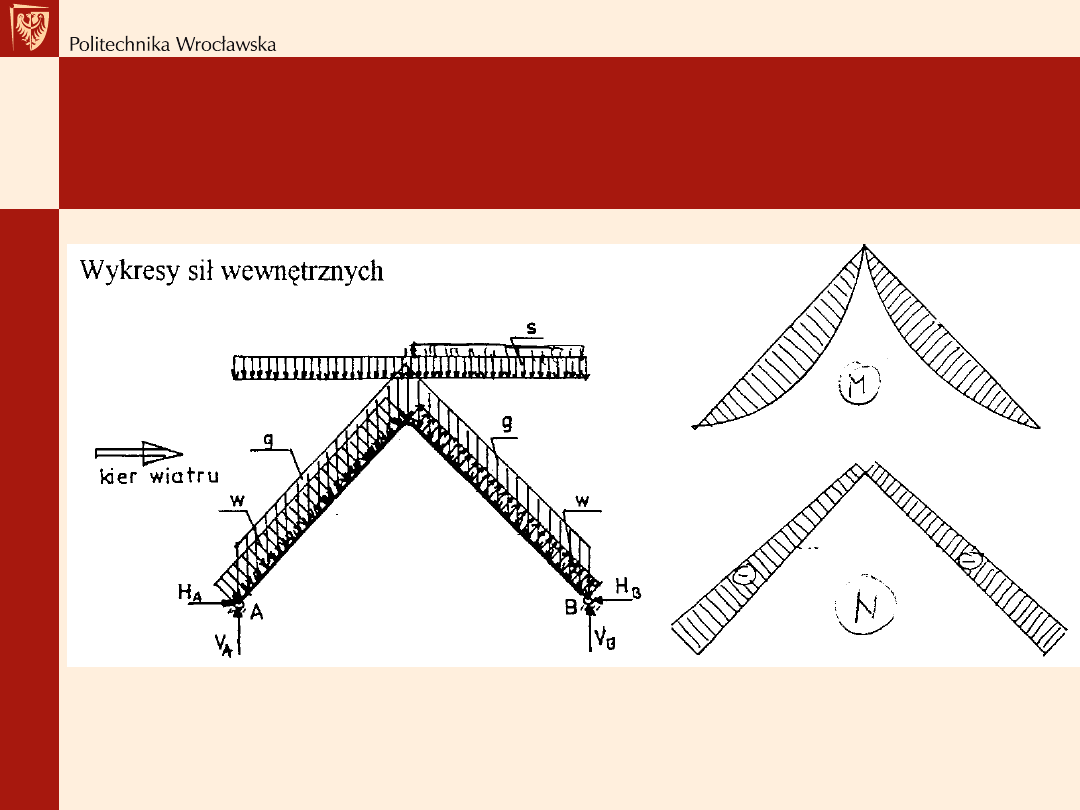
Wiązar rozporowy – wiązar krokwiowy

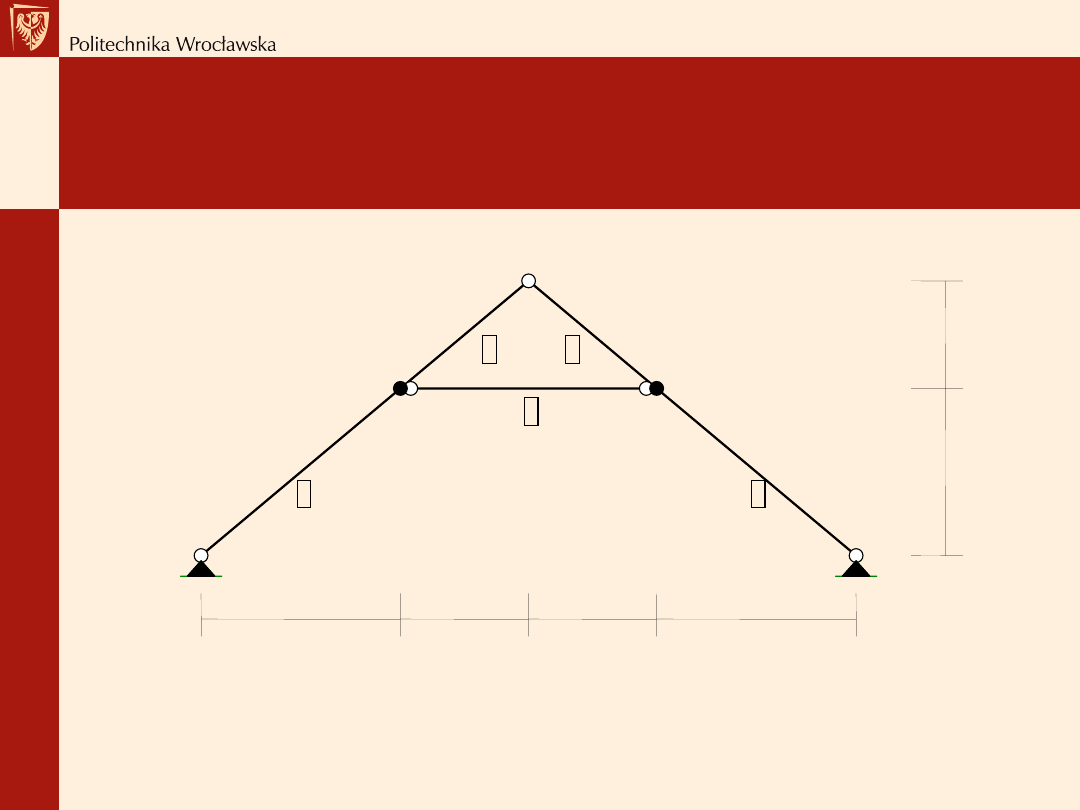
Wiązar rozporowy – wiązar jętkowy

1

2

3

4

5

2740

1760

1760

2740

H=9000

2299

1477

V=3776

1

2

5

4

3

schemat statyczny

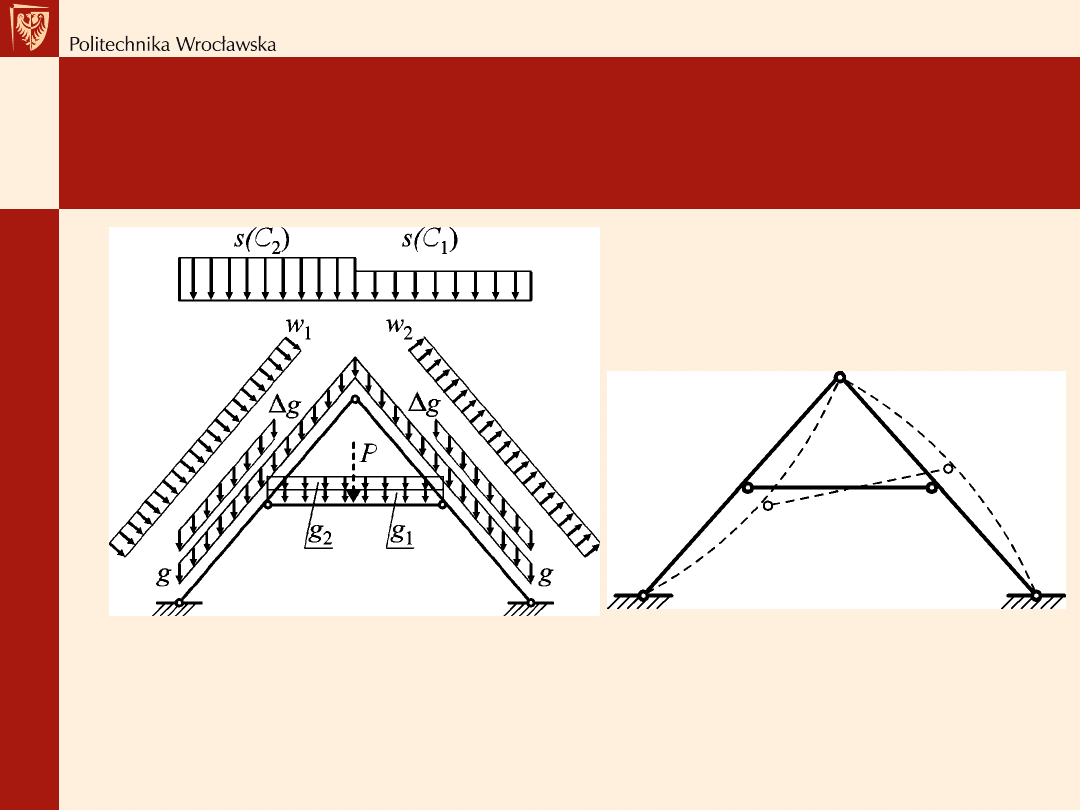
Wiązar rozporowy – wiązar jętkowy

Obciążenia działające na wiązar jętkowy nad poddaszem mieszkalnym: g – ciężar
konstrukcji dachu i pokrycia dachowego,

Δg – dodatkowy ciężar ocieplenia i obudowy

poddasza, g

1

– ciężar stropu na jętce, g

2

– obciążenie użytkowe, s – obciążenie

śniegiem, w – obciążenie wiatrem, P – ciężar człowieka (gdy nie występuje g

2

)

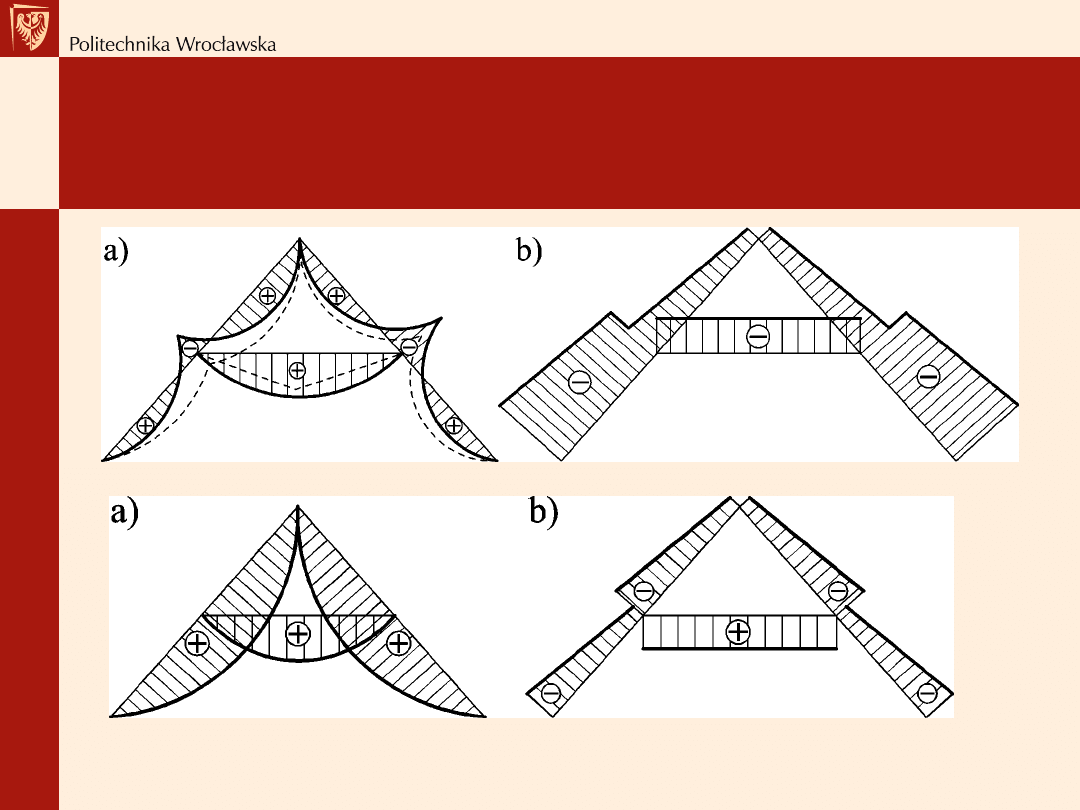
Wiązar rozporowy – wiązar jętkowy

MURŁAT

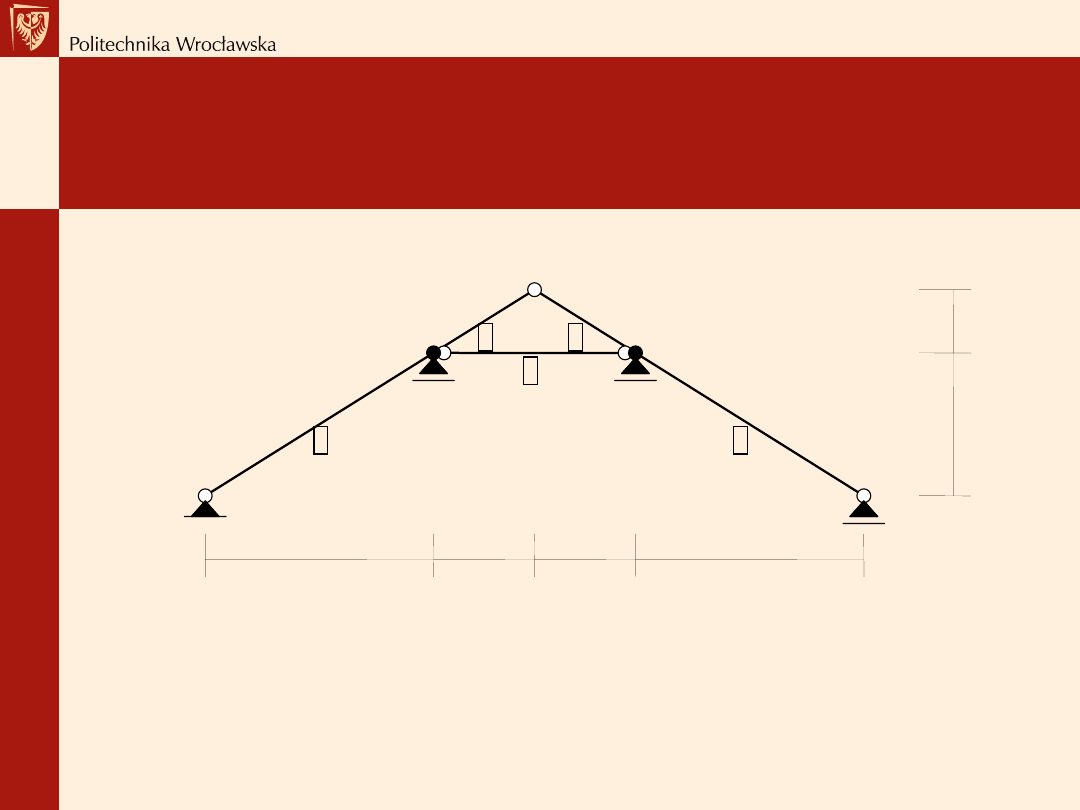
Wiązar płatwiowo-kleszczowy

1

2

3

4

5

4160

1840

1840

4160

H=12000

2599

1150

V=3749

1

2

3

4

5

schemat statyczny

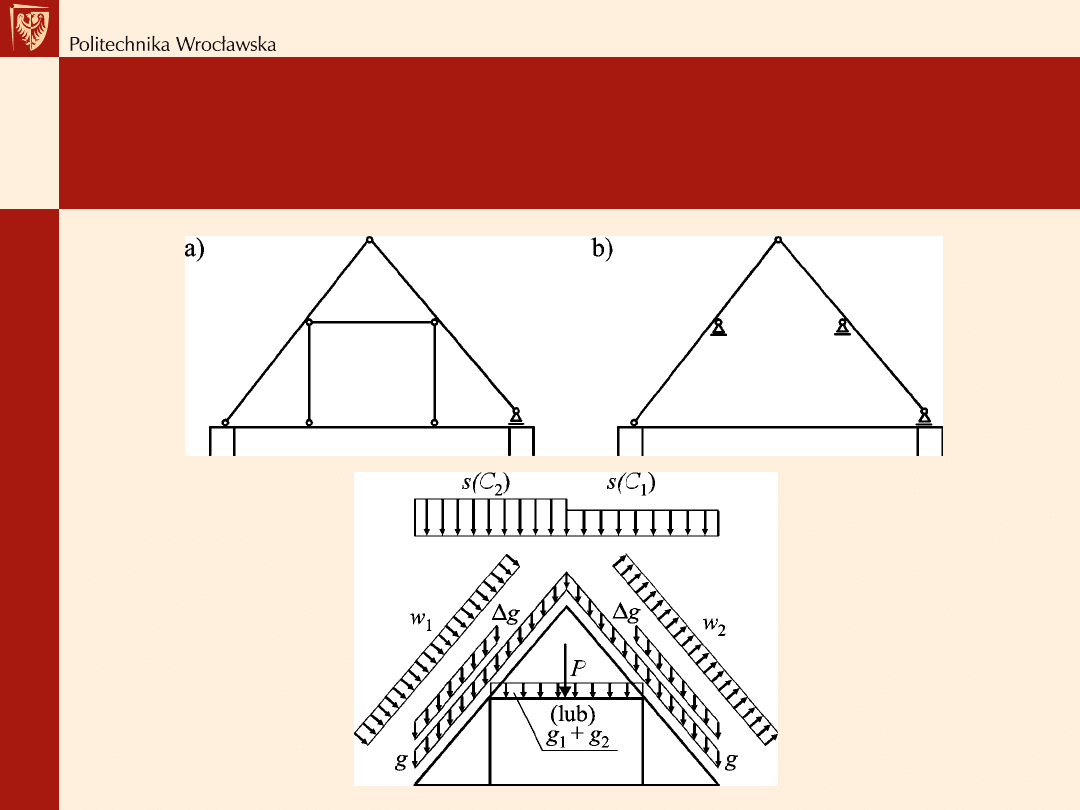
Wiązar płatwiowo-kleszczowy

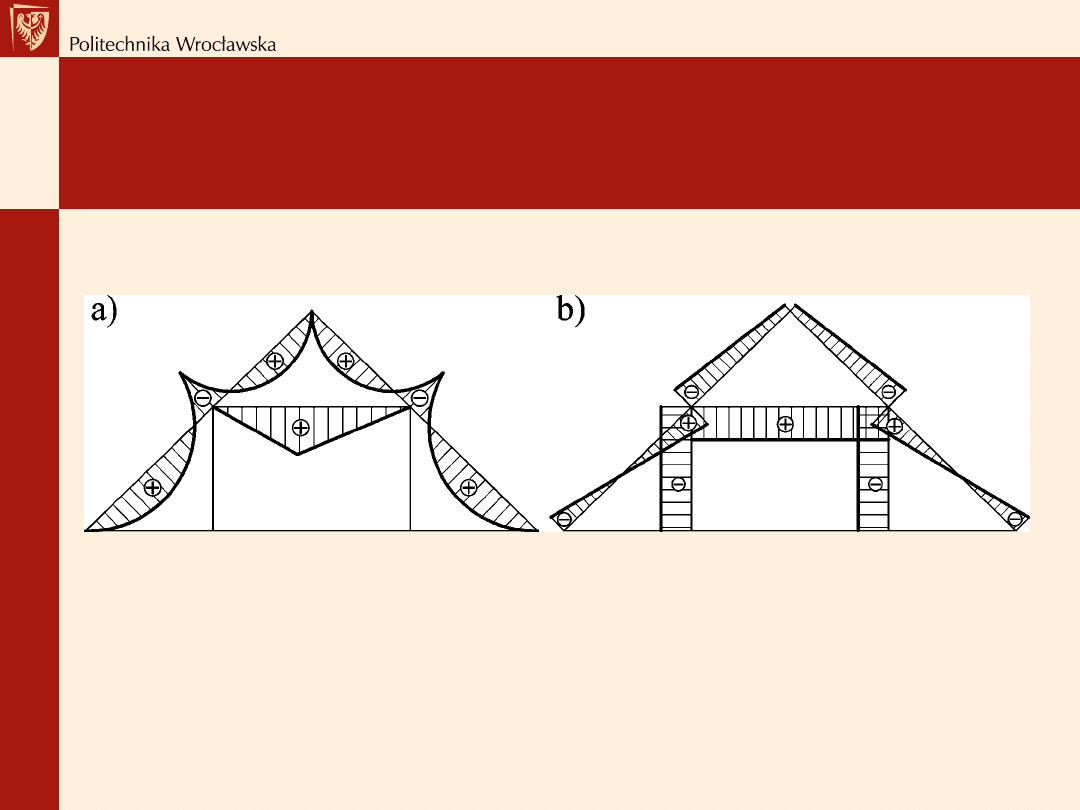
Wiązar płatwiowo-kleszczowy

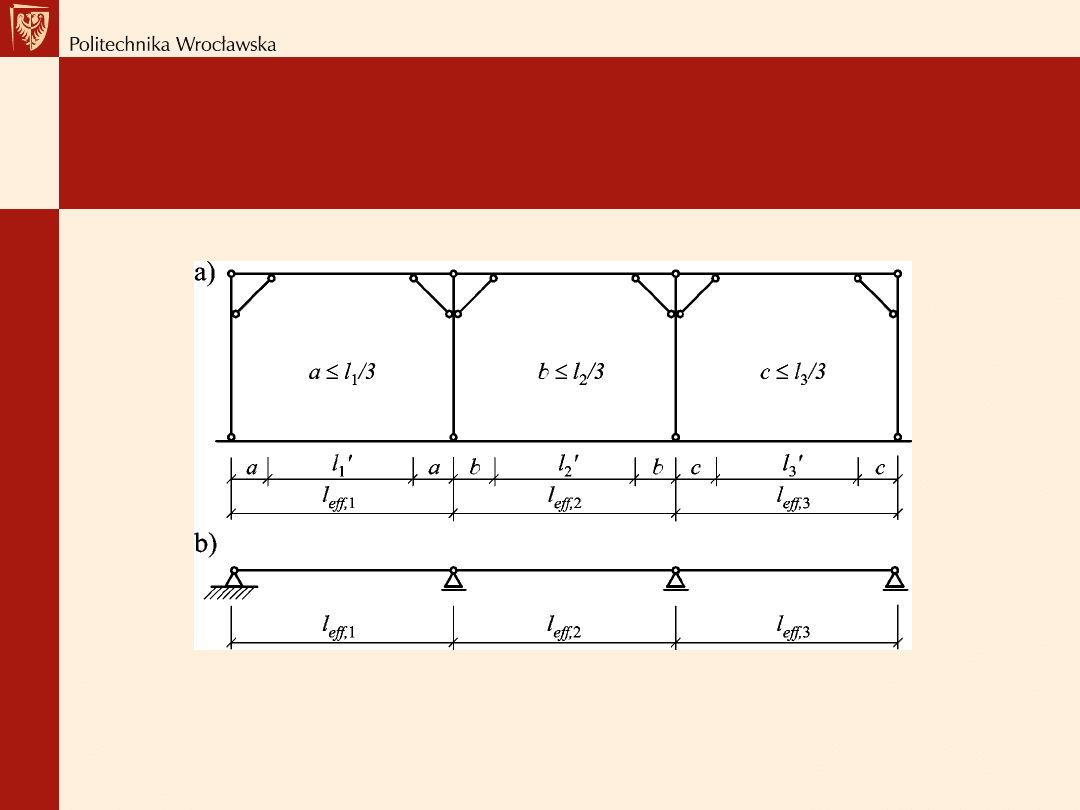
Wiązar płatwiowo-kleszczowy

Przykładowy schemat statyczny ramy (ścianki) stolcowej:

a) w płaszczyźnie x-z, b) w płaszczyźnie x-y

Zestawienie obciążeń

Obciążenie

Wartość

charaktery-

styczna

[kN/m]

Współ-

czynnik

obciążenia



f

[-]

Wartość

obliczeniowa

[kN/m]

Składowe prostopadłe

obciążenia

Składowe równoległe

obciążenia

wartość

charaktery-

styczna

[kN/m]

wartość

obliczeniowa

[kN/m]

wartość

charaktery-

styczna

[kN/m]

wartość

obliczeniowa

[kN/m]

Ciężar własny dachu z
uwzględnieniem ciężaru
krokwi i deskowania
0,35



0,85

g

k

= 0,298

1,2

g

d

= 0,358

g

k



= 0,253

g

d



= 0,304

g

k||

= 0,158

g

d||

= 0,190

ciężar własny krokwi
0,08



0,18



5,5

g

k1

= 0,079

1,1

g

d1

= 0,087

g

k



1

= 0,067

g

d



1

= 0,074

g

k||1

= 0,042

g

d||1

= 0,046

Śnieg
połać lewa
S

k

= Q

k



C

2

= 0,9



1,12



0,85

połać prawa
S

k

= Q

k



C

1

= 0,9



0,75



0,85

S

k

= 0,857

S

k

= 0,574

1,5
1,5

S

d

= 1,200

S

d

= 0,803

S

k



= 0,616

S

k



= 0,413

S

d



= 0,863

S

d



= 0,578

S

k||

= 0,385

S

k||

= 0,258

S

d||

= 0,539

S

d||

= 0,361

Wiatr
połać nawietrzna
p

k1

= q

k



C

e



C



=

= 0,35



0,8



0,28



1,8



0,85

połać zawietrzna
p

k2

= q

k



C

e



C



=

= 0,35



0,8



(-

0,4)



1,8



0,85

p

k1

= +0,120

p

k2

= -0,171

1,3
1,3

p

d1

= +0,156

p

d2

= -0,223

p

k



1

= +0,108

*

p

k



2

= -0,154

*

p

d



1

= +0,140

*

p

d



2

= -0,200

*

-
-

-
-

Ciężar własny kleszczy
2



0,038



0,115



5,5

g

k2

= 0,048

1,1

g

d2

= 0,053

-

-

-

-

Obciążenie skupione
(człowiek obciążający
kleszcze)[kN]

P

k

= 1,00

1,2

P

d

= 1,20

-

-

-

-

*

Uwzględniono współczynnik jednoczesności obciążeń



o

= 0,9

Zasady obliczania stropów na belkach.

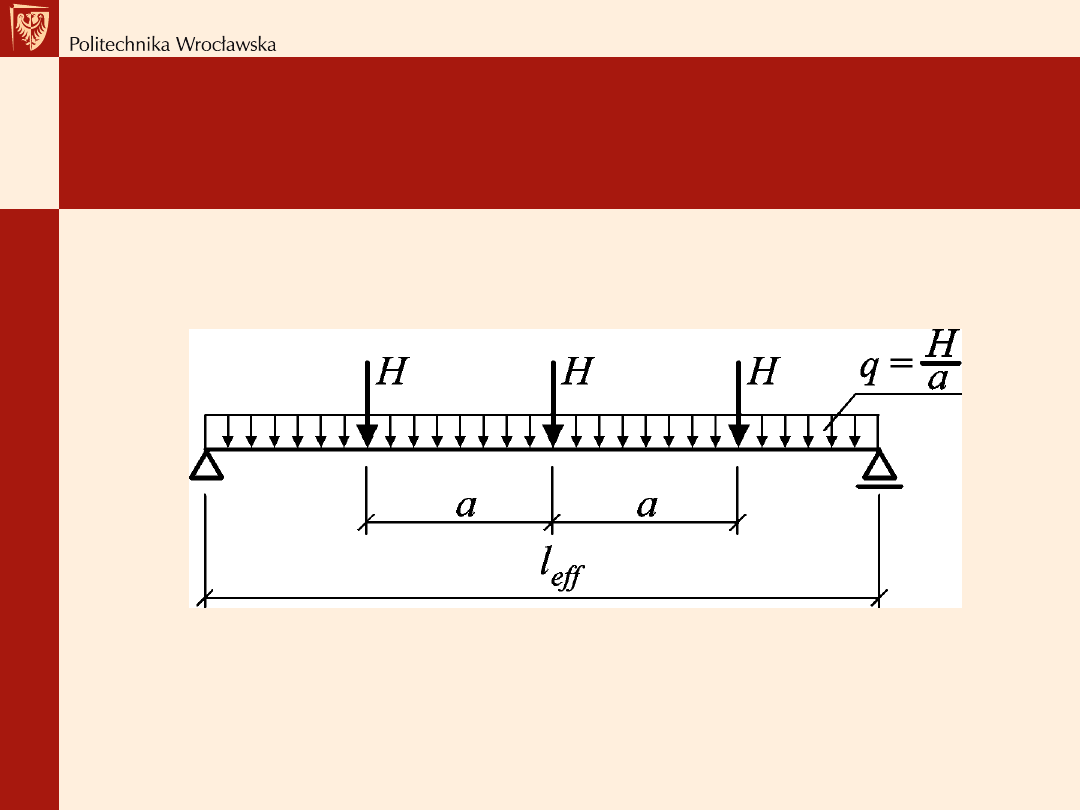
Rozpiętość obliczeniowa

l

eff

= l

n

+ a

1

+ a

2

l

n

-

rozpiętość elementu w świetle podpór,

a

1

i a

2

-

odległości teoretycznych punktów podparcia elementu od krawędzi

podpór określone na postawie odpowiednich wartości a

i

z rysunków

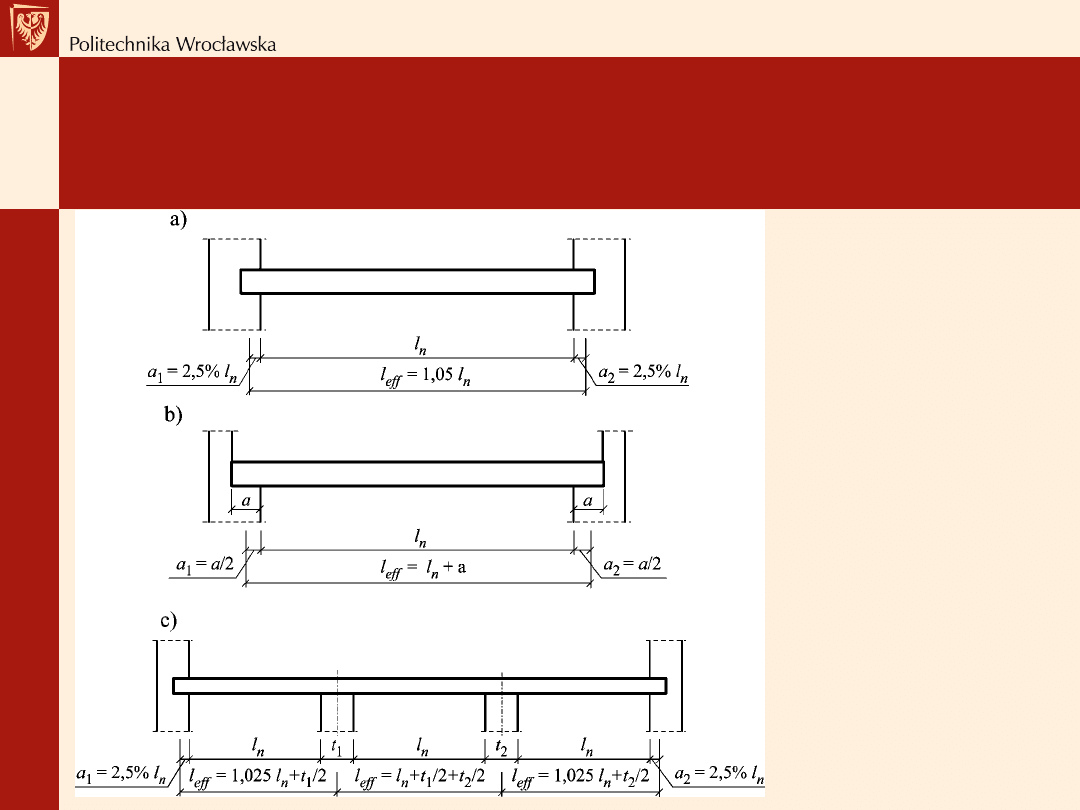
Rozpiętość obliczeniowa

Rozpiętość
obliczeniowa l

eff

belek

opartych na murze:
a)

jednoprzęsłowych
wolnopodpartych
lub częściowo
utwierdzonych,

b)

jednoprzęsłowych
wolnopodpartych
prefabrykowanych

c)

wieloprzęsłowych

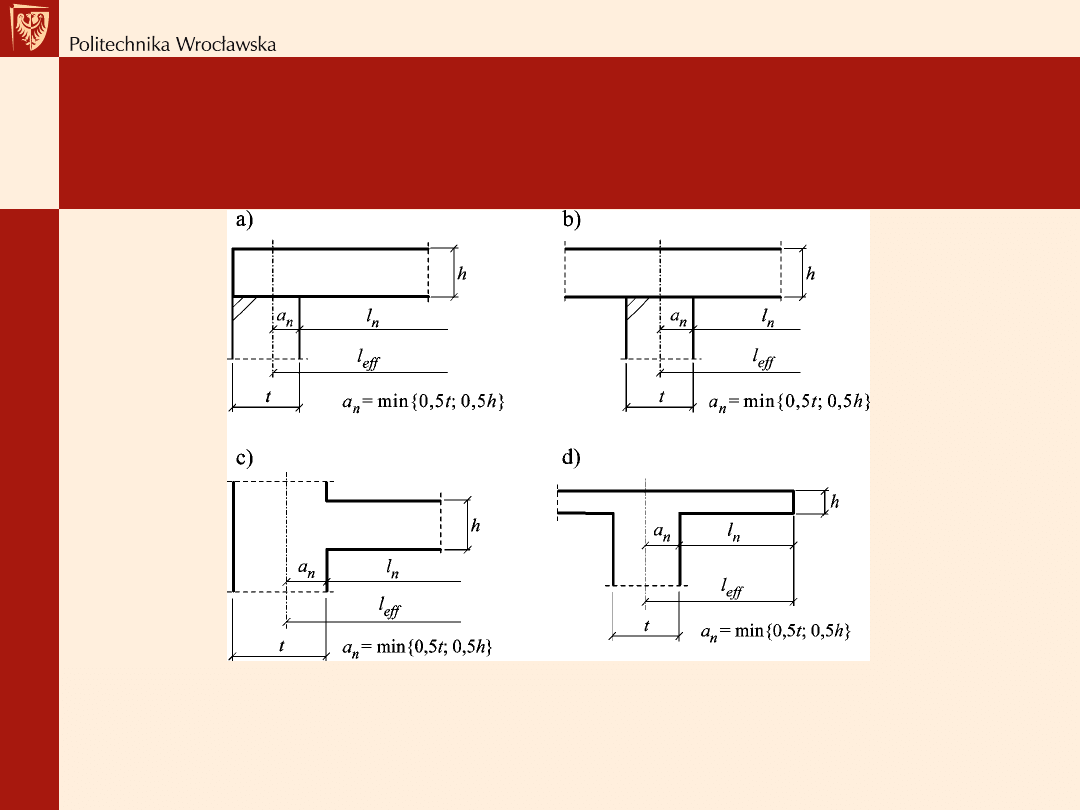
Rozpiętość obliczeniowa

Wyznaczenie rozpiętości obliczeniowej l

eff

belek wg wzoru dla różnych

warunków podparcia na murze: a) podpora skrajna swobodnie podparta,
b) podpora pośrednia w elemencie ciągłym, c) podpora skrajna z pełnym
zamocowaniem, d) podpora skrajna przy wsporniku

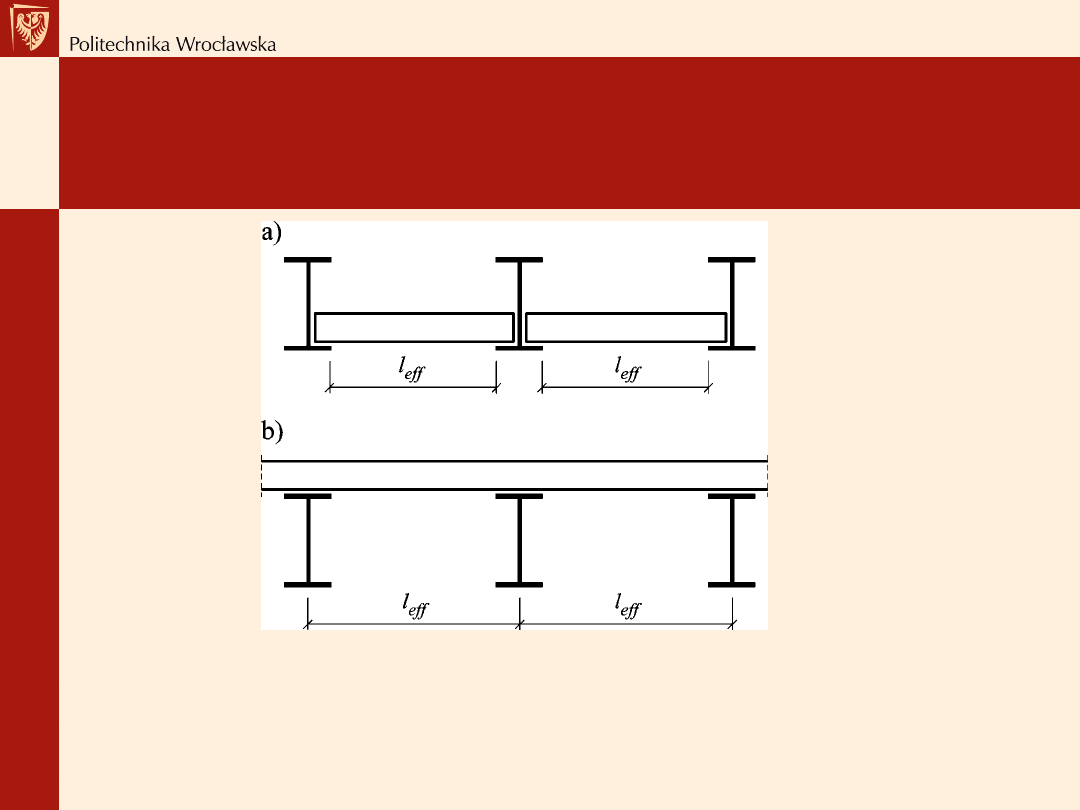
Rozpiętość obliczeniowa

Rozpiętość obliczeniowa l

eff

płyt ceglanych i żelbetowych opartych na

belkach stalowych: a) płyty jednoprzęsłowe, b) płyta wieloprzęsłowa

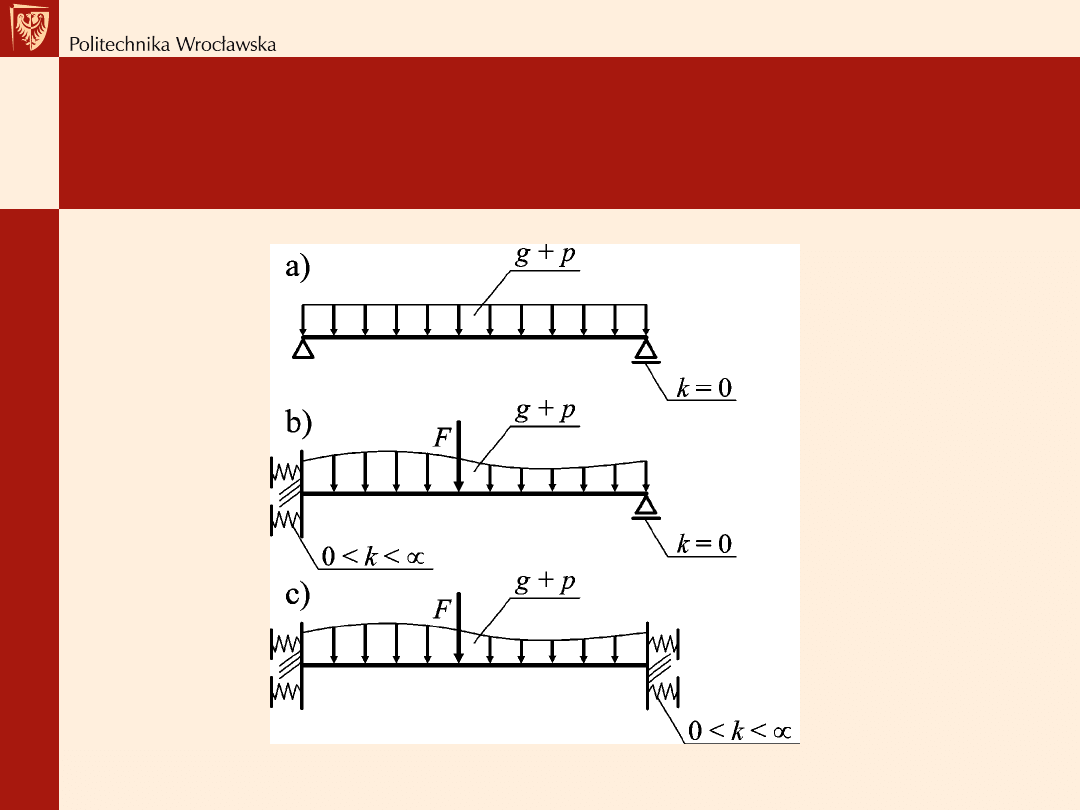
Schemat statyczny

Schemat statyczny – warunki częściowego
utwierdzenia

(1)

powyżej stropu i pod stropem wymurowana jest ściana, a średnie naprężenie
obliczeniowe jej muru



cd



0,25 MPa,

(2) strop jest oparty na ścianie za pośrednictwem wieńca żelbetowego o
szerokości c równej grubości ściany t i nie mniejszej od wysokości konstrukcji
stropu h

, tak by zapewnione było odpowiednie ramię pary sił mocujących,

(3) z końców żeber wypuszczone są pręty zbrojenia górnego (o przekroju
wystarczającym do przeniesienia momentu utwierdzenia) zaopatrzone w haki
wchodzące w wieniec (przy użyciu stali żebrowanej, haków nie stosuje się).

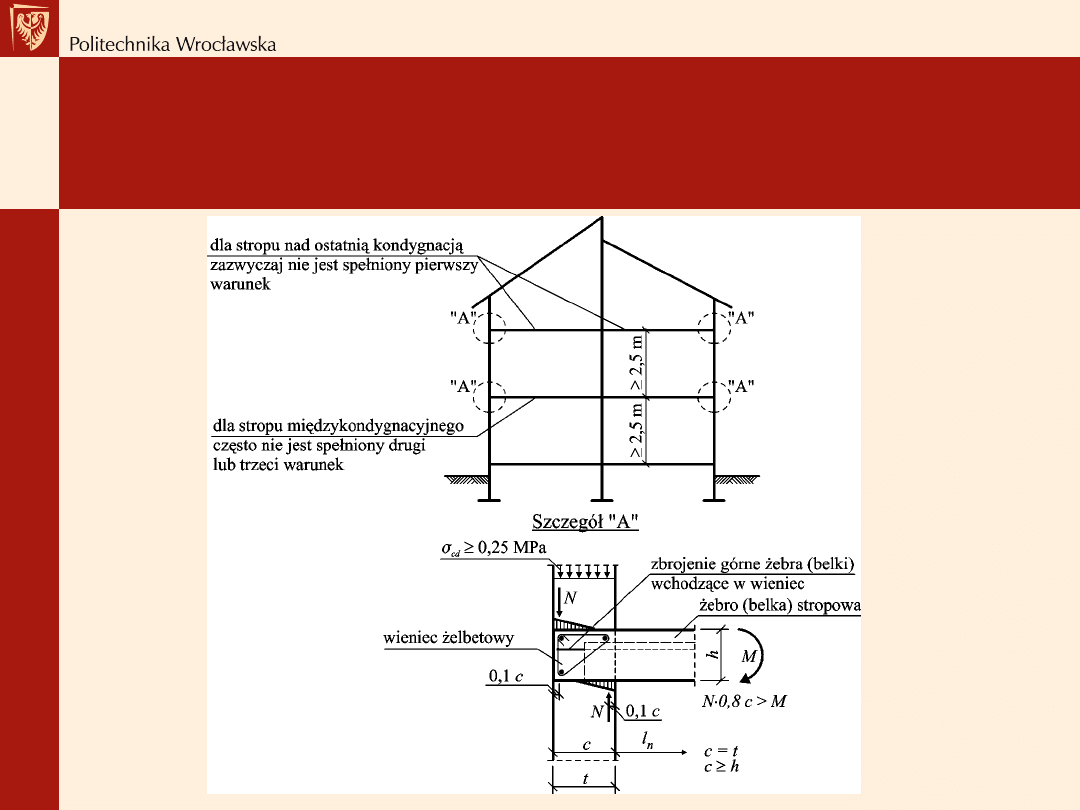
Schemat statyczny

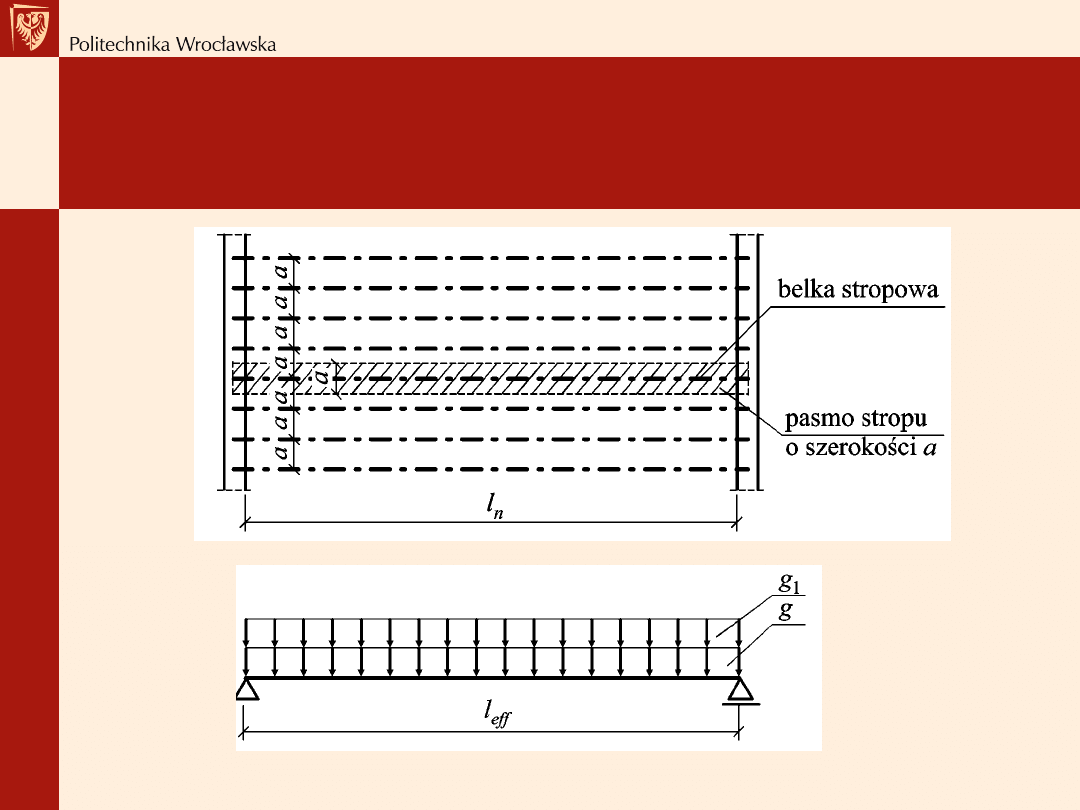
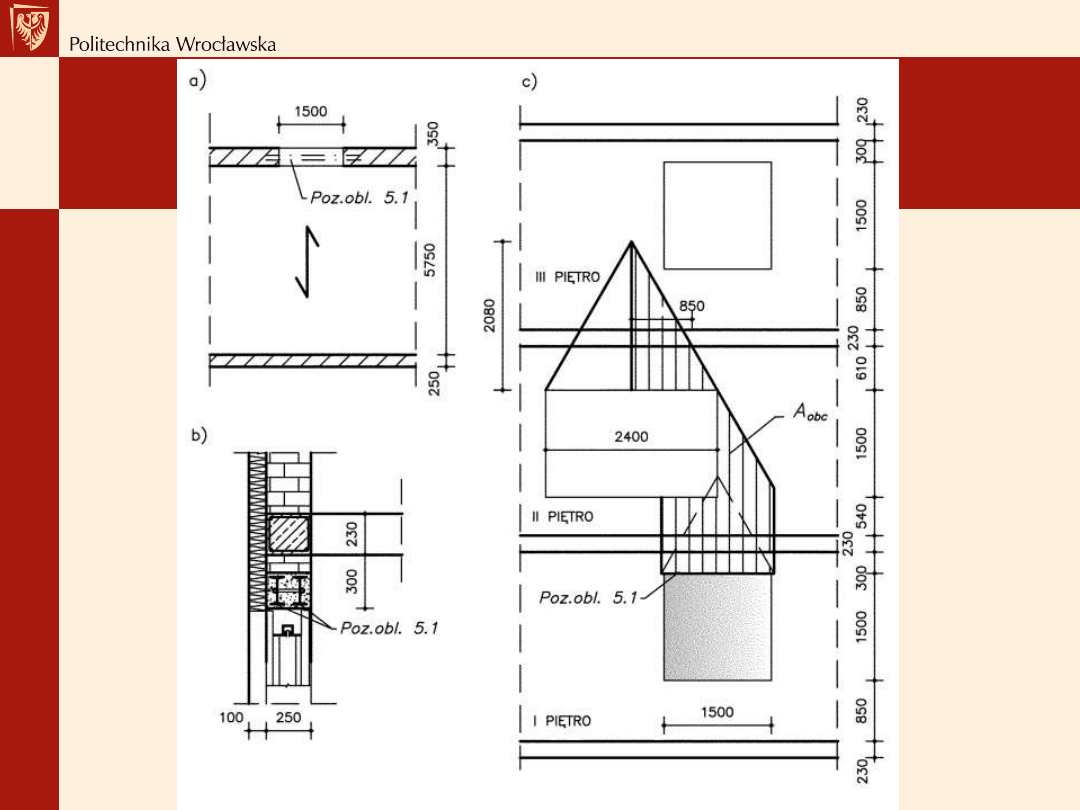
Przykłady

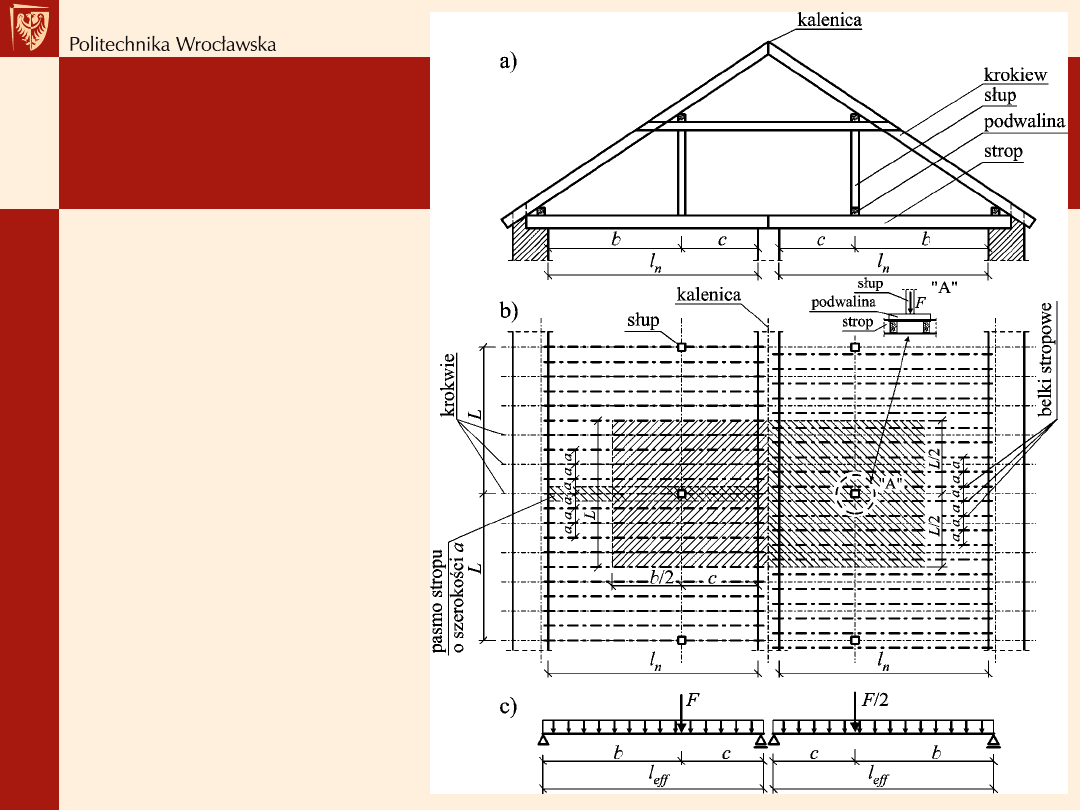
Przykłady

Schemat obciążenia belki
stropowej stropu poddasza:

a) przekrój przez dach,
b) obszar obciążenia belki
stropowej siłą skupioną
przekazywaną przez słup (po
lewej -

oparty bezpośrednio na

belce, po prawej - oparty na
belkach za pośrednictwem
podwaliny),
c) schemat obciążenia belki
stropowej,

g -

ciężar konstrukcji stropu,

p -

obciążenie użytkowe

poddasza,
F -

obciążenie przekazywane na

belkę stropową przez słup (ciężar
konstrukcji dachu wraz z
ciężarem śniegu i wiatru)

Strop Akermana

Obciążenie

Wartość

charakterystyczna

[kN/m

2

]

Współczynnik

obciążenia



f

[-]

Wartość

obliczeniowa

[kN/m

2

]

g – Obciążenie stałe

wykładzina PCW na kleju grubości
0,07
gładź cementowa grubości
0,035



21,0

folia polietylenowa
styropian grubości
0,02



0,45

warsta wyrównawcza grubości
0,01



21,0

strop Akermana wg tabeli 2.4

2,88

tynk cementowo-wapienny grubości

0,015



19

0,07

0,735

-

0,01

0,21

2,88

0,285

1,2

1,3

-

1,2

1,3

1,1

1,3

0,084

0,956

-

0,012

0,273

3,168

0,371

RAZEM

4,190

4,864

p – Obciążenie zmienne technologiczne

1,5
obciążenie zastępcze od ścianek działowych
0,25

1,5

0,25

1,4

1,2

2,1

0,30

RAZEM g+p

5,940

7,264

Zasady obliczania nadproży.

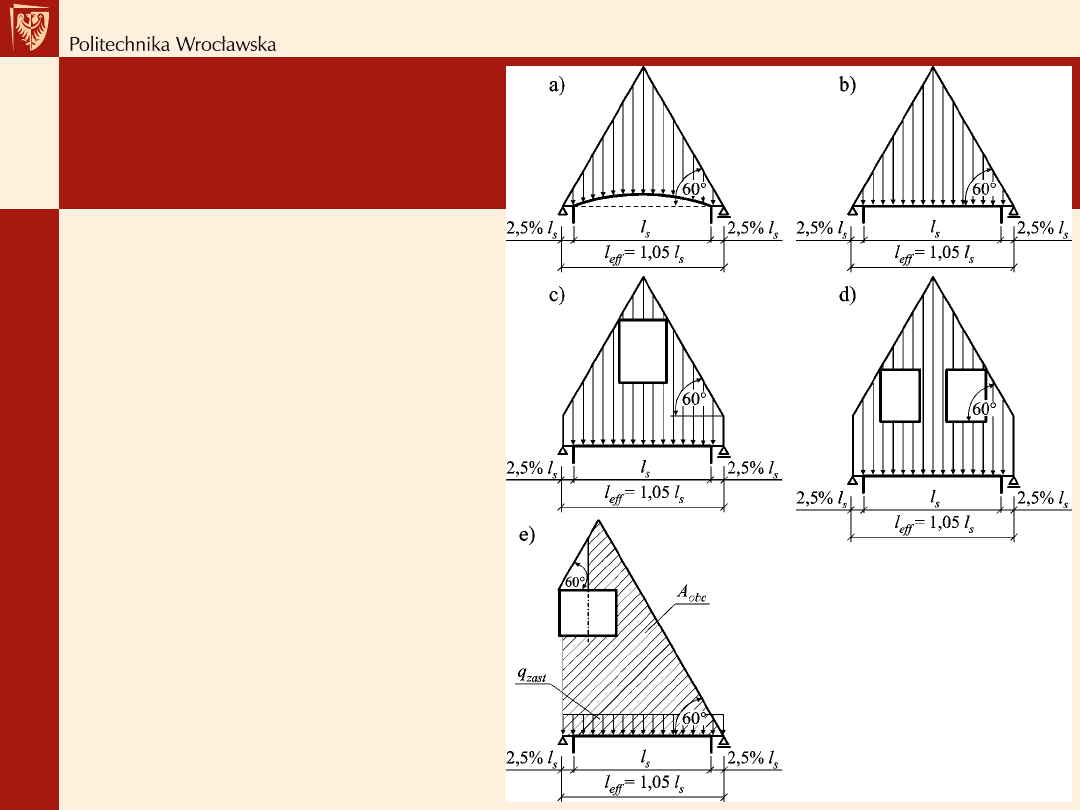
Schemat
obciążenia nadproża

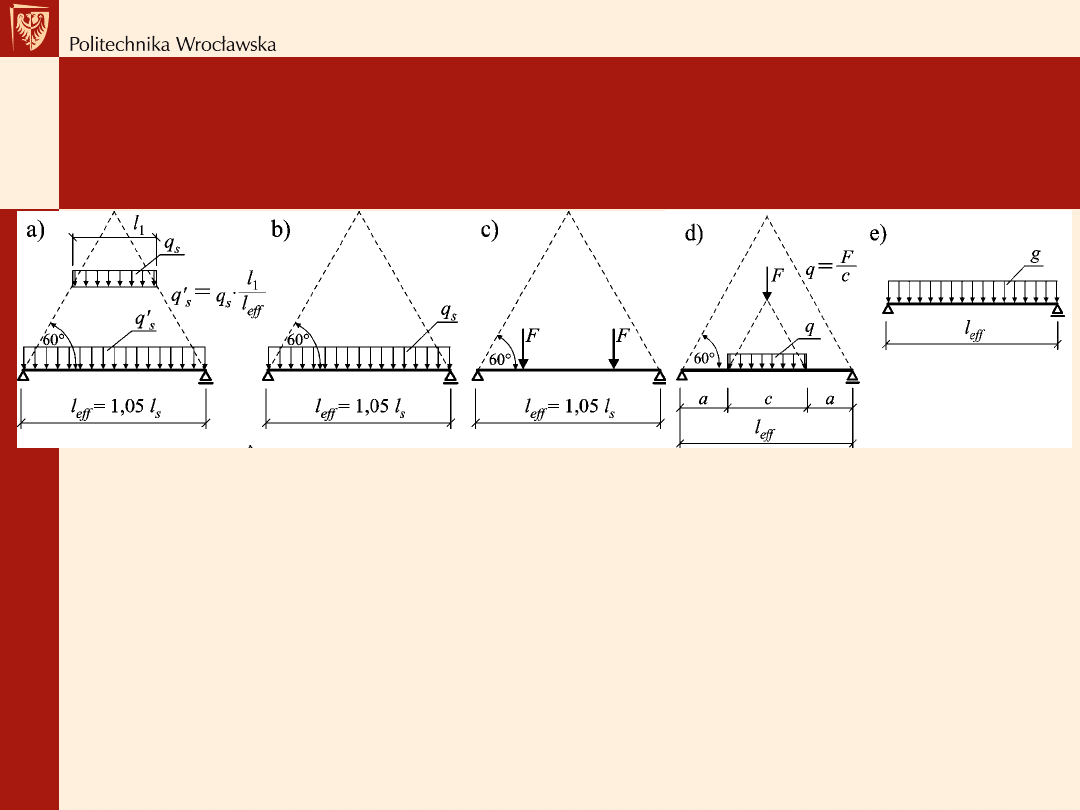
Schemat obciążenia nadproża:
a) i b) ścianą murowaną bez
otworu,
c) i d) ścianą murowaną z
otworami,
e) ścianą murowaną (z otworami)
o nieforemnej powierzchni

Schemat obciążenia nadproża

Schemat obciążenia nadproża: a) obciążeniem równomiernie rozłożonym
q’

s

, od stropu opartego za pośrednictwem wieńca na ścianie powyżej

nadproża, b) obciążeniem równomiernie rozłożonym q

s

od stropu opartego

za pośrednictwem wieńca bezpośrednio na nadprożu, c) siłami skupionymi
F

, pochodzącymi od belek stropowych opartych bezpośrednio na nadprożu,

d) obciążeniem równomiernie rozłożonym q, od siły skupionej F
pochodzącej od belki stropowej opartej na ścianie powyżej nadproża, e)
obciążeniem równomiernie rozłożonym g, od ciężaru własnego nadproża.

Zasady obliczania murów

niezbrojonych.

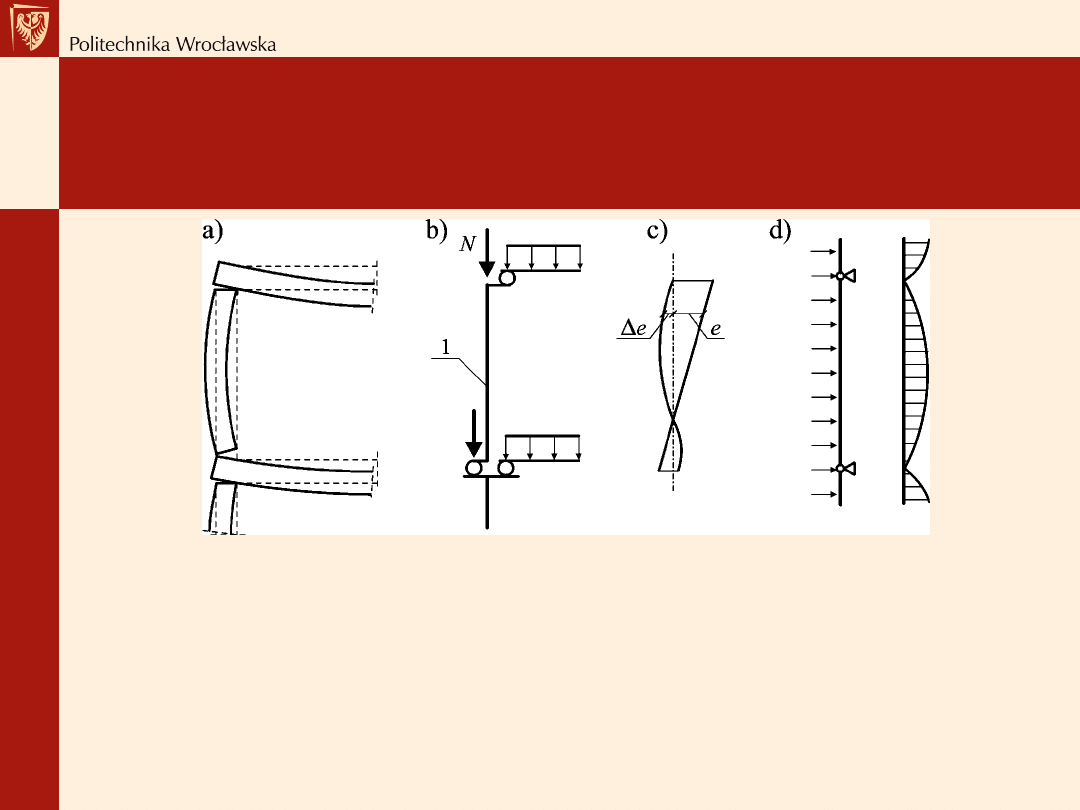
Modele obliczeniowe ścian

Ściana zewnętrzna na najwyższej kondygnacji budynku obciążona głownie
pionowo:
a)

odkształcenia ścian i stropów,

b)

przyjęty model obliczeniowy,

c)

mimośrody działania siły pionowej spowodowane obciążeniem od stropów,

d)

oddziaływanie obciążenia poziomego;

1-

nominalna oś ściany (przechodząca przez środek ciężkości przekroju)

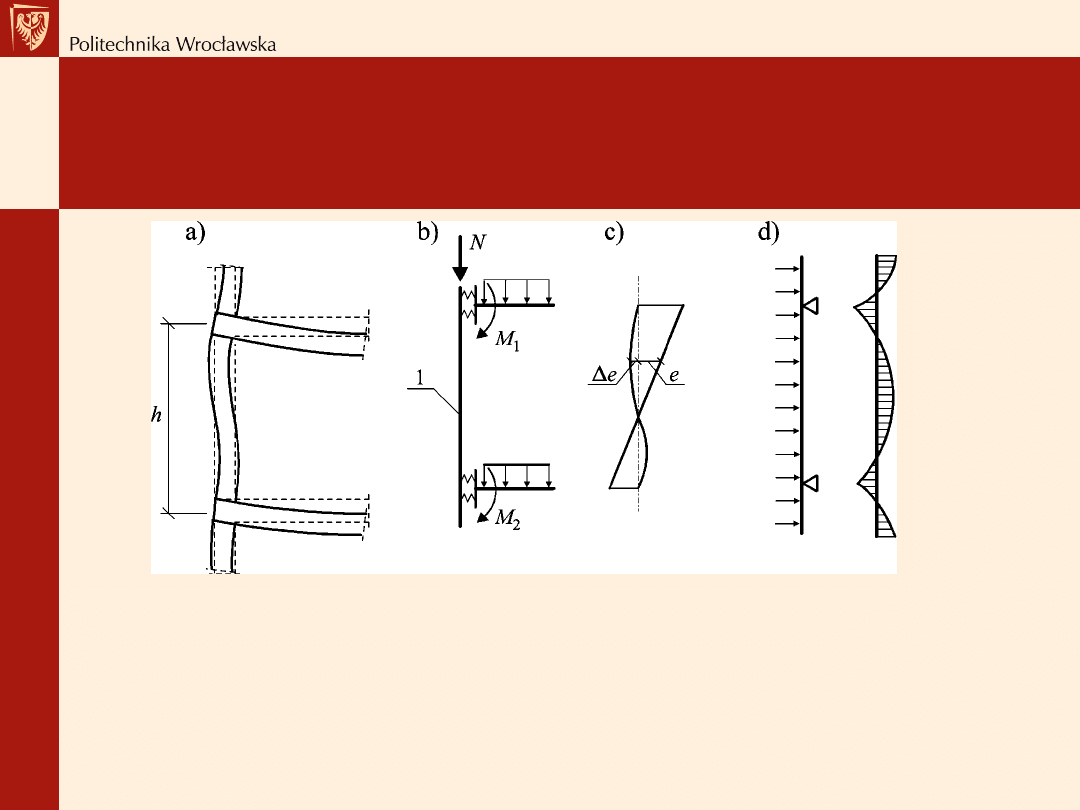
Modele obliczeniowe ścian

Ściana zewnętrzna na niższych kondygnacjach budynku obciążona głownie
pionowo:
a) odkształcenia ścian i stropów,
b) przyjęty model obliczeniowy,
c) mimośrody działania siły pionowej spowodowane obciążeniem od stropów,
d) oddziaływanie obciążenia poziomego; 1- nominalna oś ściany

Modele obliczeniowe ścian

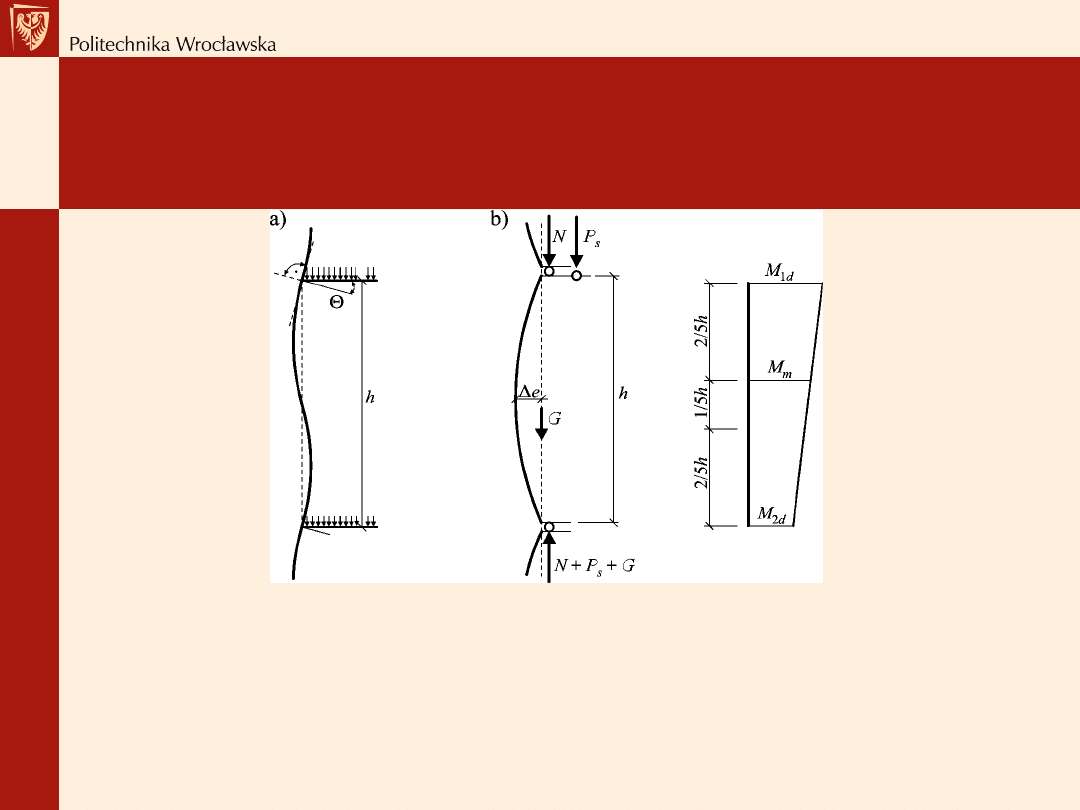
Schematy statyczne przyjmowane w obliczeniach ścian murowanych;

a)

model ciągły,

b)

model przegubowy i wykres momentów w ścianie;

h

– wysokość obliczeniowa ściany, θ – kąt obrotu osi stropu na podporze, N,

P

s

, G

– składowe obciążenia ściany, Δe – mimośród II rzędu, M

1d

– wartość

momentu pod stropem, M

2d

– wartość momentu nad stropem, M

m

–

maksymalna wartość momentu w środkowym odcinku ściany

Model ciągły

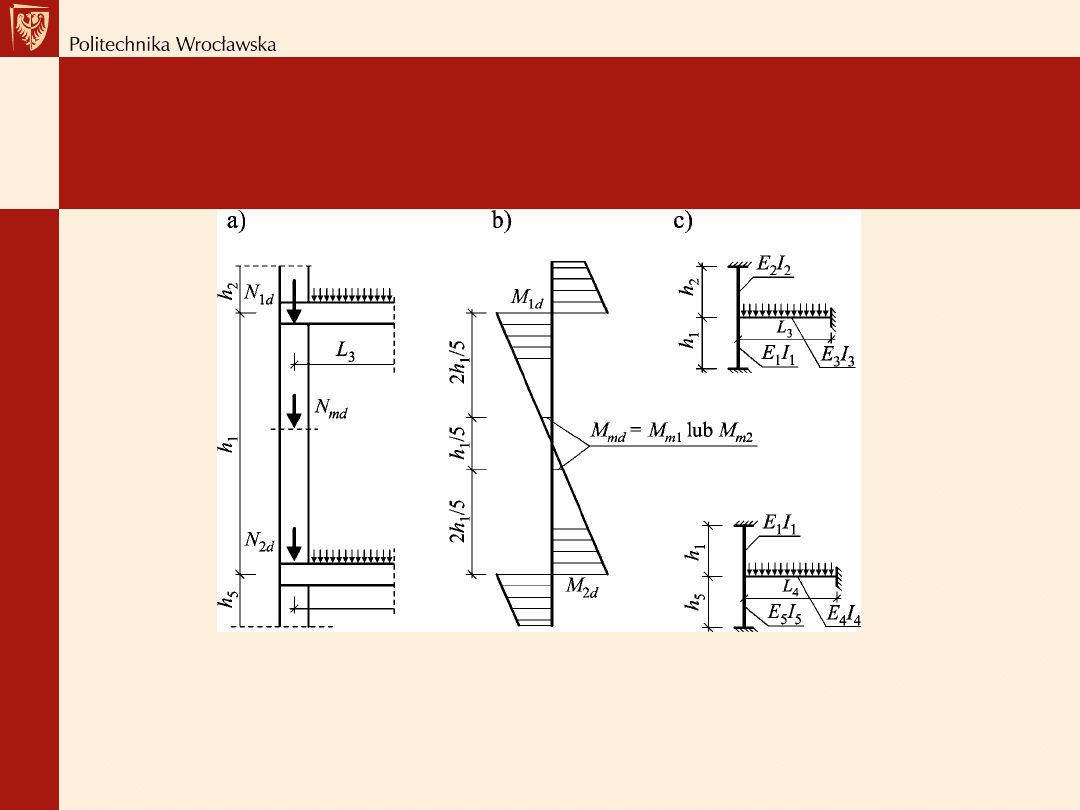
Model ciągły ściany obciążonej jednostronnie: a) schemat ściany, b) momenty
wywołane mimośrodowym obciążeniem ściany, c) uproszczone modele
obliczeniowe dla wyznaczenia momentu pod stropem M

1d

i nad stropem M

2d

oraz w środkowej strefie ściany M

md

Model przegubowy

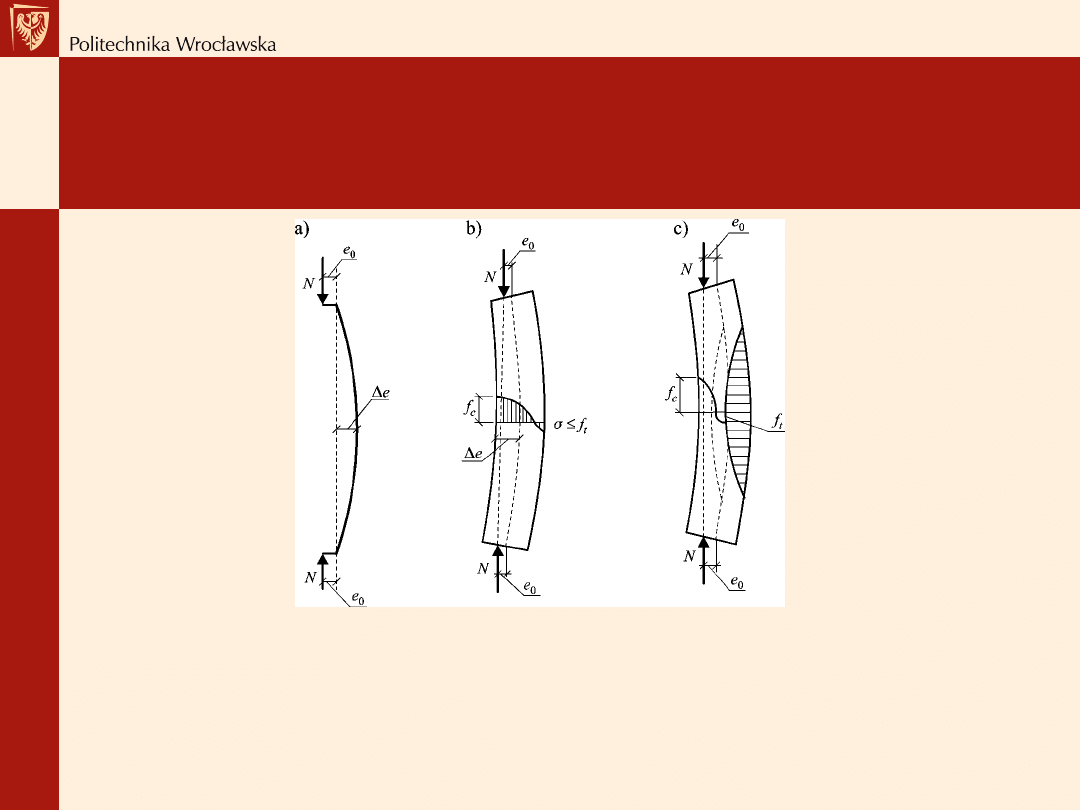
Schemat przegubowy przyjmowany dla ściany murowanej nośnej: a) model
zastępczego pręta przegubowego z mimośrodowym przekazaniem reakcji
stropu, b) wykres momentów zginających w ścianie, c) model zniszczenia
ściany w strefie rozciąganej; e

0

– mimośród początkowy obciążenia N, Δe –

mimośród II rzędu, f

c

– wytrzymałość muru na ściskanie, f

t

– wytrzymałość

muru na rozciąganie

Model
przegubowy

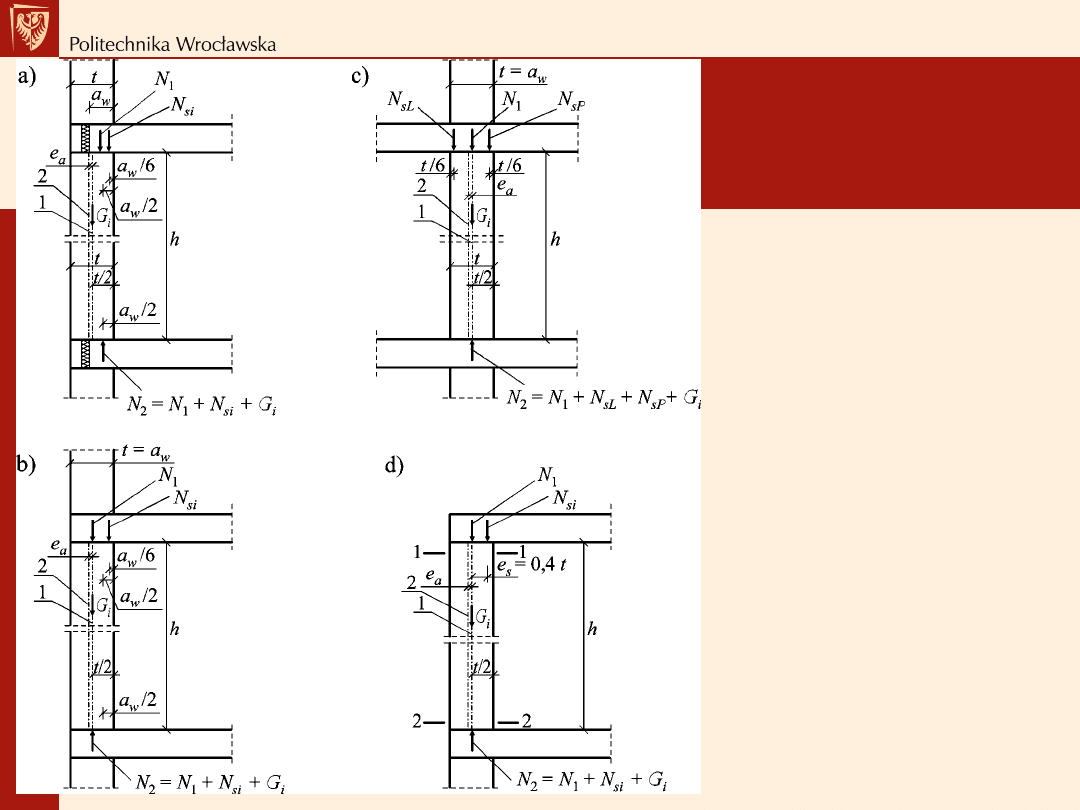
Miejsca przyłożenia sił z górnych
kondygnacji N

1

oraz od stropu

nad rozpatrywaną ścianą N

Si

w

modelu przegubowym:

a)

ściana zewnętrzna z
wieńcem o szerokości
mniejszej od grubości ściany
(a

w

< t),

b)

ściana zewnętrzna z
wieńcem o szerokości
równej grubości ściany (a

w

=

t),

c)

ściana wewnętrzna
obciążona stropami z dwóch
stron (a

w

= t),

d)

ściana zewnętrzna
najwyższej kondygnacji;

1-

oś nominalna ściany

(przechodząca przez środek
ciężkości przekroju), 2- oś
obliczeniowa dla modelu ściany,
a

w

– szerokość wieńca, N

1

–

obciążenie z górnych
kondygnacji budynku, N

Si

–

obciążenie ze stropu nad
rozpatrywanym odcinkiem
ściany, G

i

– ciężar

rozpatrywanego odcinka ściany,
t

– grubość ściany, e

a

–

mimośród przypadkowy, e

s

–

mimośród obciążenia ze stropu