Wydział Badań i Ewaluacji CKE

Warszawa, listopad 2007

Wydanie 2., uzupełnione

A

A

A

N

N

N

A

A

A

L

L

L

I

I

I

Z

Z

Z

A

A

A

I

I

I

I

I

I

N

N

N

T

T

T

E

E

E

R

R

R

P

P

P

R

R

R

E

E

E

T

T

T

A

A

A

C

C

C

J

J

J

A

A

A

W

W

W

Y

Y

Y

N

N

N

I

I

I

K

K

K

Ó

Ó

Ó

W

W

W

O

O

O

C

C

C

E

E

E

N

N

N

I

I

I

A

A

A

N

N

N

I

I

I

A

A

A

I

I

I

E

E

E

G

G

G

Z

Z

Z

A

A

A

M

M

M

I

I

I

N

N

N

O

O

O

W

W

W

A

A

A

N

N

N

I

I

I

A

A

A

Opracowanie:

Jolanta Czarnotta-Mączyńska, Marta Firsiuk,

Małgorzata Lipska, Zofia Lisiecka

Redaktor cyklu:

Zofia Lisiecka

Wydawca: Wydział Badań i Ewaluacji CKE

00-842 Warszawa, ul. Łucka 11

tel. [phone]

e-mail: [e-mail]

Wydanie 2., uzupełnione

Warszawa, listopad 2007

A

A

A

N

N

N

A

A

A

L

L

L

I

I

I

Z

Z

Z

A

A

A

I

I

I

I

I

I

N

N

N

T

T

T

E

E

E

R

R

R

P

P

P

R

R

R

E

E

E

T

T

T

A

A

A

C

C

C

J

J

J

A

A

A

W

W

W

Y

Y

Y

N

N

N

I

I

I

K

K

K

Ó

Ó

Ó

W

W

W

O

O

O

C

C

C

E

E

E

N

N

N

I

I

I

A

A

A

N

N

N

I

I

I

A

A

A

I

I

I

E

E

E

G

G

G

Z

Z

Z

A

A

A

M

M

M

I

I

I

N

N

N

O

O

O

W

W

W

A

A

A

N

N

N

I

I

I

A

A

A

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

3

Cykl broszur Teoria i praktyka egzaminowania powstał w odpowiedzi na zapotrzebowanie

uczestników procesu egzaminowania na syntetyczne, popularyzatorskie ujęcie trudnej

problematyki związanej z diagnostyką edukacyjną, w szczególności zaś z ocenianiem

wewnątrzszkolnym i egzaminowaniem zewnętrznym. W kolejnych publikacjach przybliżo-

ne zostaną kwestie związane z planowaniem badań osiągnięć uczniów, jakością

materiałów egzaminacyjnych, metodą pomiaru dydaktycznego, organizacją i przepro-

wadzaniem egzaminów, analizą i interpretacją wyników egzaminu, wykorzystaniem

wyników egzaminów w podnoszeniu jakości pracy szkoły, etc.

Cykl przeznaczony jest przede wszystkim dla nauczycieli i dyrektorów szkół, ale może też

stanowić pomoc dla tych, którym nieobojętna jest jakość polskiej edukacji – wizytatorów,

opiekujących się szkołami pracowników jednostek samorządów terytorialnych, rodziców,

dziennikarzy.

Mamy nadzieję, że niniejsza broszura, w swojej strukturze przypominająca ilustrowany

słownik tematyczny, przybliży Państwu podstawy statystyki, dostarczając licznych

przykładów, jak można wyniki prowadzonych analiz wykorzystać w praktyce. Liczymy też,

iż ilustrujące pojęcia statystyczne cytaty z publikacji przygotowanych przez Centralną

Komisję Egzaminacyjną dopomogą w niełatwej drodze od teorii do praktyki oceniania i

egzaminowania.

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

4

SPIS TREŚCI

Podstawowe parametry statystyczne pomocne w analizie ilościowej wyników................s. 5

Miary położenia............................................................................................................s. 7

Miary tendencji centralnej.......................................................................................s. 7
Modalna....................................................................................................…..........s. 8
Mediana...................................................................................................................s.8
Średnia arytmetyczna.............................................................................................s. 8
Średnia ważona......................................................................................................s. 9
Kwantyle.................................................................................................................s. 9
Kwartyle..................................................................................................................s. 9

Zastosowanie podstawowych miar tendencji centralnej..................s. 12

Miary rozproszenia (zróżnicowania) ....................................................................s. 14
Rozstęp................................................................................................................s. 14
Wariancja..............................................................................................................s. 14
Odchylenie standardowe.......................................................................................s.15

Miary współzmienności..............................................................................................s. 16
Korelacja...............................................................................................................s. 16
Przykładowe zestawienie wyników egzaminu zewnętrznego....................................s. 17

Podstawowe parametry statystyczne pomocne w analizie ilościowej wyników zadań
egzaminacyjnych i testu..................................................................................................s. 18
Rozkład liczebności..............................................................................................s. 18

Łatwość zadania/testu..........................................................................................s. 19

Trudność zadania/testu........................................................................................s. 22
Frakcja

opuszczeń................................................................................................s. 22

Moc

różnicująca zadania......................................................................................s. 23

Rzetelność pomiaru..............................................................................................s. 23
Efekt

standardowy................................................................................................s. 25

Wynik

standardowy..............................................................................................s. 26

Skale znormalizowane....................................................................................................s. 28

Pojęcie normy............................................................................................................s. 28
Normalizacja

wyników

testowania........................................................................s. 29

Obszar wyników typowych.........................................................................s. 29

Definicje wybranych skal znormalizowanych.............................................................s. 32
Skala

staninowa...................................................................................................s. 32

Standardowa

„piątka”...........................................................................................s. 34

Skala

centylowa....................................................................................................s. 36

Skala akademicka CEEB.....................................................................................s. 37

Przykłady analiz wyników egzaminów zewnętrznych.....................................................s. 42

Analiza i interpretacja wyników staninowych uczniów i szkół....................................s. 42
Analizy porównawcze i korelacyjne...........................................................................s. 57
Zastosowanie wybranych skal znormalizowanych w analizie wyników matury podczas
rekrutacji na wyższe uczelnie....................................................................................s. 59

Źródła danych.................................................................................................................s. 62

Polecana literatura..........................................................................................................s. 62

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

5

PODSTAWOWE PARAMETRY STATYSTYCZNE
POMOCNE W ANALIZIE ILOŚCIOWEJ WYNIKÓW

Analiza ilościowa wyników polega na zebraniu, zestawieniu, statystycznym opracowaniu
i interpretacji danych uzyskanych podczas badań edukacyjnych, psychologicznych, spo-
łecznych, itp. Opiera się na analizie statystycznej, dzięki czemu uzyskujemy możliwość
dokładniejszego porównania i opisu badanych grup lub zjawisk

0F0F0F0F

1

. Tabela 1. zawiera cha-

rakterystykę podstawowych wskaźników pomocnych w prowadzeniu analiz i interpretowa-
niu wyników oceniania osiągnięć uczniów.

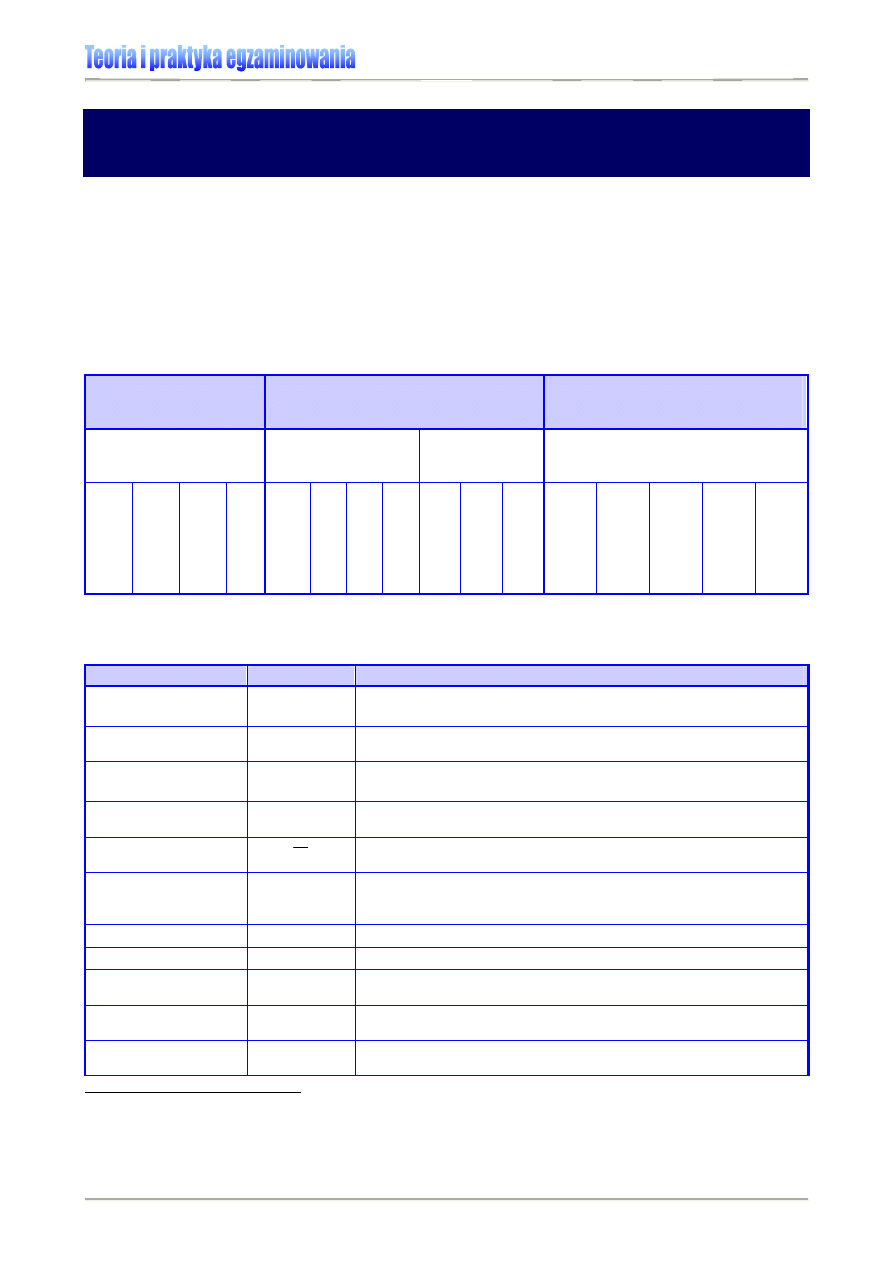
Tabela 1. Podstawowe parametry statystyczne wykorzystywane w analizie i prezentacji wyników osiągnięć
edukacyjnych [6]

1F1F1F1F

2

Parametry statystyczne

służące do analizy

zadań i testu

Parametry statystyczne

służące do analizy

wyników testowania

Sposoby porządkowania

i grupowania

wyników testowania

Analiza zadania/testu

Ustalenie miar

położenia

Ustalenie miar

rozproszenia

Porządkowanie i grupowanie zaob-

serwowanych wartości zmiennej

(tu: wyników testowania uczniów)

Łatwo

ść

Trud

no

ść

Wa

rian

cja

zad

ania

Moc

ró

żnicuj

ąca

śre

dnia

aryt

m

et

ycz

na

Modaln

a

Median

a

Kwantyl

e

Ro

zst

ęp

Wa

rian

cja

tes

tu

Odchyl

enie

stand

ard

owe

Ro

zk

ład

pun

ktowy

Ro

zk

ład

liczebno

ści

Ro

zk

ład

stanin

owy

Ro

zk

ład

cent

ylo

w

y

Sk

ala CEEB

Tabela 2. Podstawowe parametry statystyczne wykorzystywane w analizie i prezentacji wyników osiągnięć
edukacyjnych – charakterystyka [6]

Nazwa parametru Oznaczenie

Objaśnienie

frakcja opuszczeń

zadania

f

o

stosunek liczby uczniów, którzy nie podjęli się rozwiązania danego
zadania (opuścili je) w teście do liczby egzaminowanych uczniów

łatwość zadania/testu

p

stosunek liczby punktów uzyskanych przez ucznia/ów do maksy-
malnej liczby punktów możliwych do zdobycia za zadanie lub test

trudność zadania

q

stosunek liczby uczniów, którzy nieprawidłowo rozwiązali zadanie
w teście do liczby egzaminowanych uczniów

moc różnicująca

zadania

np. D

50,

R

pb

zdolność zadania (zadań testowych) do odróżniania uczniów o
wyższych i niższych osiągnięciach egzaminacyjnych

średnia arytmetyczna

wyników

X

średni wynik uzyskany przez badaną grupę uczniów (np. klasę
szkolną)

mediana

Me

wynik środkowy zbioru wyników egzaminowania określonej popu-
lacji (np. klasy szkolnej), uporządkowanych w kolejności malejącej
lub rosnącej

kwartyle

Q

układ wyników w procentowych przedziałach 25, 50 i 75

modalna (dominanta)

Mo

wynik najczęściej występujący w badanej grupie

rozstęp

(obszar zmienności)

R

różnica pomiędzy najwyższym a najniższym wynikiem uzyskanym
przez daną grupę uczniów podczas badania

wariancja

s

2

x

średnia arytmetyczna kwadratów odchylenia wyników uzyskanych
przez uczniów od ich średniej wartości

odchylenie

standardowe

s

x

miara rozrzutu wyników, pozwalająca na ustalenie przedziału wy-
ników typowych

1

Por. W.P. Zaczyński, Statystyka w pracy badawczej nauczyciela, Warszawa 1997, Wydawnictwo „Żak”, s.

3-5.

2

Cyfry w nawiasach kwadratowych wskazują źródło danych, których wykaz zamieszczono na końcu

opracowania.

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

6

obszar wyników

typowych

OWT

przedział wyników na skali mieszczący się pomiędzy sumą
a różnicą średniej arytmetycznej i odchylenia standardowego

rzetelność

np. alfa

Cronbacha

wskaźnik powtarzalności wyników testowania; dokładność
pomiaru

skala staninowa

-

dziewięciostopniowa skala znormalizowanego rozkładu wyników

„standardowa piątka”

-

pięciostopniowa skala znormalizowanego rozkładu wyników

skala centylowa

-

dziewięćdziesięciodziewięciostopniowa skala znormalizowanego
rozkładu wyników

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

7

MIARY POŁOŻENIA

Miary położenia wskazują miejsce, w którym leży wartość (liczba) najlepiej reprezentująca
wszystkie wielkości wchodzące w skład danego zbioru wyników.

Miary tendencji centralnej

Terminem tendencja centralna określa się wartość, która położona jest najbliżej najwięk-
szego skupienia wartości i dlatego można ją uznać za typową dla całego zbioru badanych.
Do najczęściej stosowanych miar należą: średnia arytmetyczna, wartość modalna i
mediana

2F2F2F2F

3

.

Przykład:

Prezentowane przez system egzaminacyjny

3F3F3F3F

4

doroczne wyniki szkół zawierają informa-

cje o tych miarach:

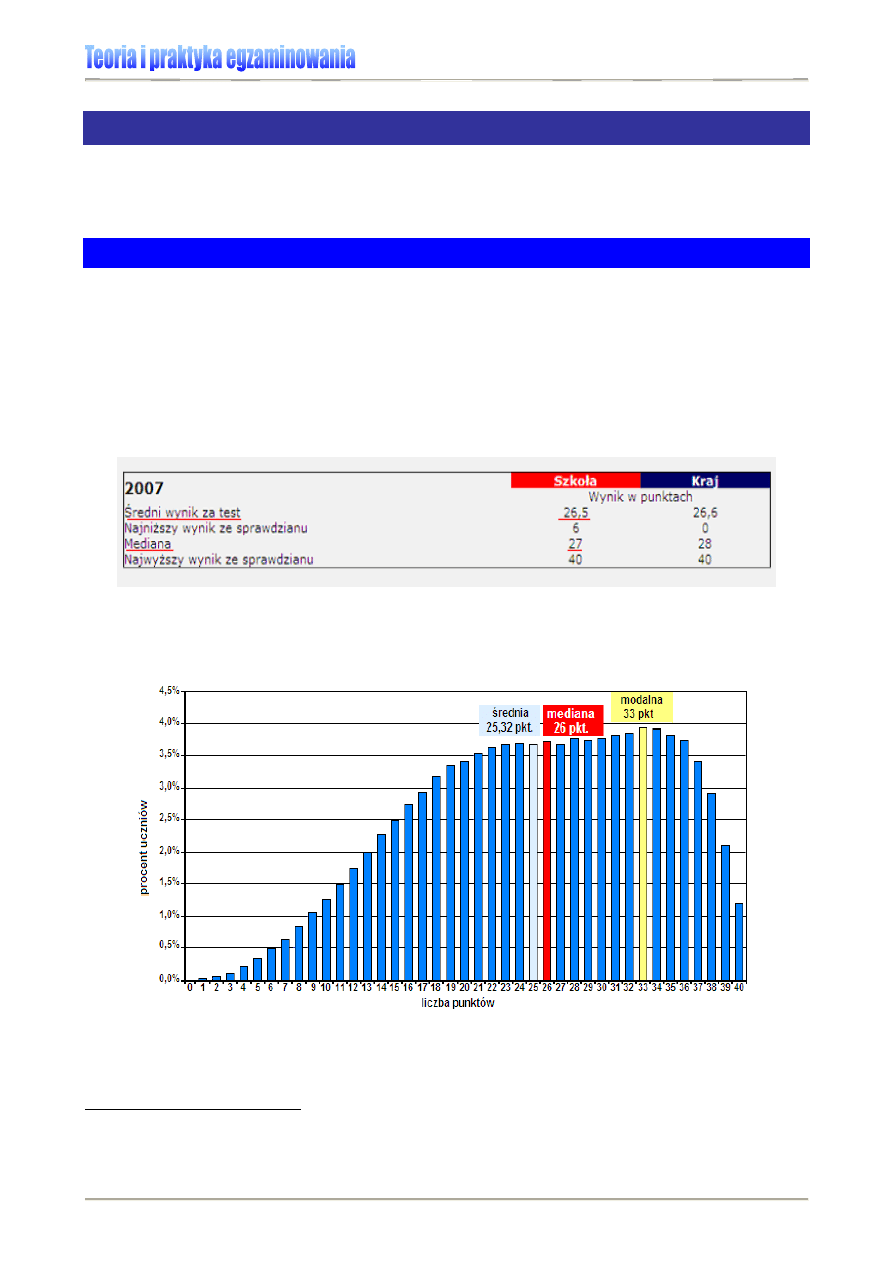
Tabela 3. Miary tendencji centralnej dla wyników sprawdzianu 2007 Szkoły Podstawowej w M. [7]

Miary tendencji centralnej służą do wyznaczenia wartości, wokół której grupują się dane

4F4F4F4F

5

.

Wykres 1. pozwoli nam wskazać te parametry dla sprawdzianu 2006.

Wykres 1. Rozkład wyników krajowych sprawdzianu 2006 [2]

3

G.A. Ferguson, Y. Takane, Analiza statystyczna w psychologii i pedagogice, PWN, Warszawa 2004, s.69.

4

Zob.: www.cke.edu.pl – tu: Wyniki szkół.

5

W. Starzyńska, Statystyka praktyczna, PWN, Warszawa 2002, s.47.

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

8

N

Xi

X

∑

=

Modalna (dominanta, moda)

Modalna (oznaczana często symbolem D lub M

o

) jest wynikiem, który w badanej populacji

występuje najczęściej, tzn. jest np. najczęściej uzyskaną liczbą punktów, najczęściej wy-
bieraną odpowiedzią.

Na sprawdzianie w 2006 roku modalna przyjęła wartość 33, co oznacza, że taką liczbę
punktów uzyskało najwięcej uczniów piszących ten sprawdzian.

Mediana

Mediana (Me, M) jest wartością dzielącą wyniki pomiaru uporządkowane od najwyższego
do najniższego (lub odwrotnie) dokładnie na połowy. Aby ją wyznaczyć, porządkujemy
wszystkie wyniki określonej populacji (np. klasy szkolnej, szkoły, uczniów szkół w woje-
wództwie, czy też wszystkich uczniów w kraju, którzy np. przystąpili do egzaminu) w kolej-
ności malejącej lub rosnącej. Następnie otrzymany zbiór dzielimy na pół. W przypadku
nieparzystej liczby badanych (wyników), medianę stanowi wartość środkowa.

Przykład:

Testowaniu zostało poddanych trzynastu uczniów.

Ich wyniki zostały uporządkowane od

najniższego do najwyższego: 2, 3, 4, 4, 6, 8,

9

, 11, 12, 15, 16, 16, 18. Zatem medianą będzie wy-

nik siódmy, czyli 9 punktów.

Jeżeli liczba badanych (wyników) jest parzysta, medianę wyznaczamy, obliczając średnią
dwóch środkowych wyników

5F5F5F5F

6

.

Przykład:

. Testowaniu zostało poddanych dwunastu uczniów.

Ich wyniki zostały uporządkowane

od najniższego do najwyższego: 2, 3, 4, 4, 6,

8

,

9

, 11, 12, 15, 16, 16. Zatem medianą będzie wynik

szósty i siódmy, czyli 8,5 punktu [8 + 9 = 8,5].

Podczas sprawdzianu przeprowadzonego w 2006 roku, mediana przyjęła wartość 26
punktów (patrz: Wykres 1.) i była nieznacznie wyższa niż średnia, co oznacza, że dla du-
żej części uczniów sprawdzian ten okazał się dość łatwy. Dowodzi tego też „najpopular-
niejszy” wynik, czyli modalna – 33 punkty.

Średnia arytmetyczna

Średnia arytmetyczna informuje o tym, ile punktów teoretycznie otrzymałby każdy uczeń
za rozwiązanie testu, gdyby wszystkie uzyskane przez badanych punkty rozdzielić między
nich po równo. Zatem statystyczny uczeń, który przystąpił do sprawdzianu 2006 (patrz:
Wykres 1.) średnio uzyskał 25,32 pkt. Średnią arytmetyczną oznacza się najczęściej sym-
bolem X i oblicza według wzoru

6F6F6F6F

7

:

6

B. Niemierko, Testy osiągnięć szkolnych. Podstawowe pojęcia i techniki obliczeniowe. WSiP, Warszawa

1975, s. 56-57.

7

Por. G.A. Ferguson, Y. Takane, op.cit., s.69-70.

gdzie:

Xi

∑

oznacza sumę wszystkich mierzonych wartości (punktów), a N liczbę pomiarów

(uczniów).

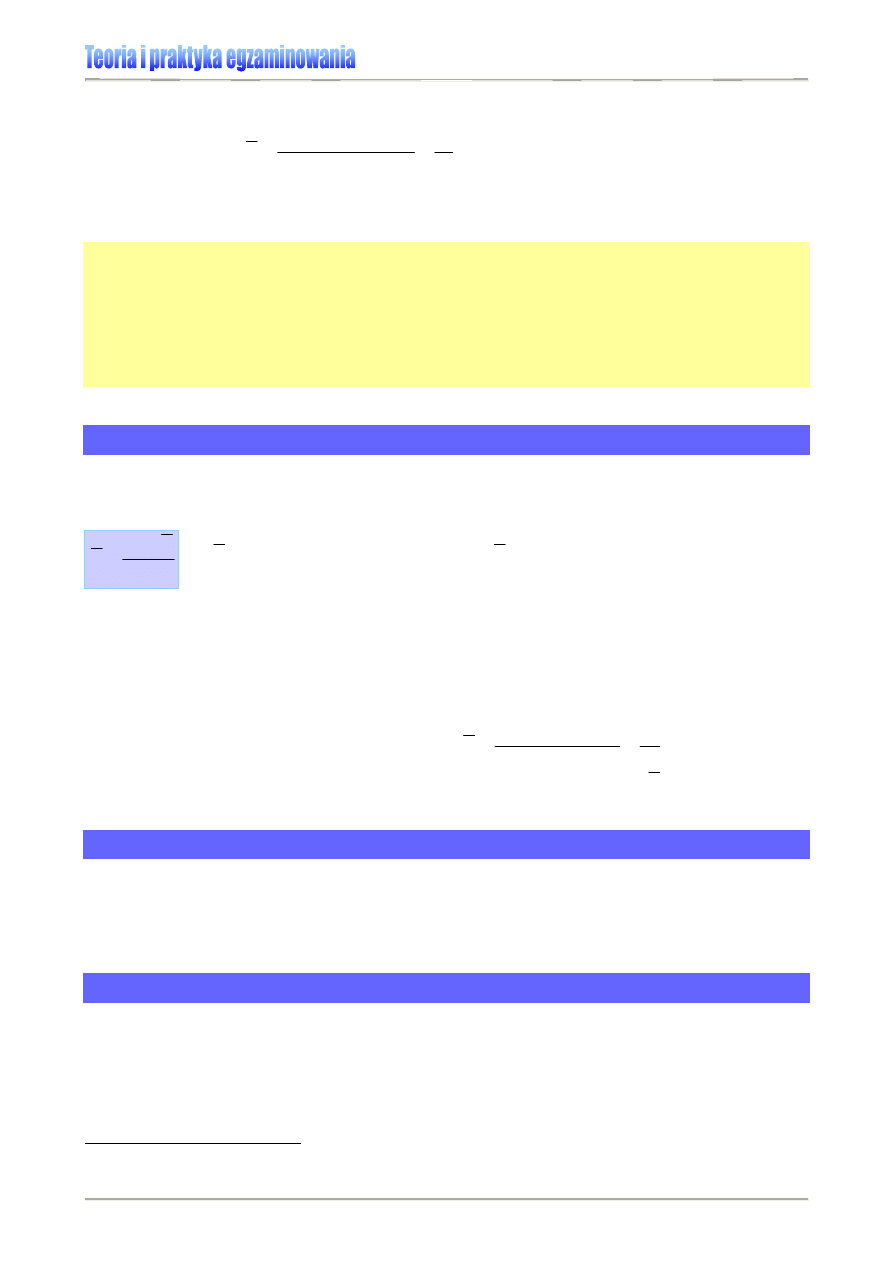
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

9

∑

∑

=

N

X

ni

X

Przykład:

Mamy liczby: 1, 2, 3, 2, 2, 6. Średnią z tych liczb otrzymamy, sumując je i dzieląc przez

liczbę ich wystąpień:

67

,

2

6

16

6

6

2

2

3

2

1

=

=

+

+

+

+

+

=

X

W powszechnym użyciu średnia arytmetyczna zastępowana jest słowem przeciętna, jak
np. przeciętna ocen.

Uwaga: Należy pamiętać o tym, że średnia arytmetyczna jest miarą bardzo wrażliwą na
wyniki skrajne (tj. najniższe i najwyższe). Jeżeli mamy pojedynczy wynik znacząco niższy
lub wyższy od pozostałych, to wpłynie on na wartość średniej

7F7F7F7F

8

, zwłaszcza w przypadku

niewielkiej grupy badanych. Na przykład w zespole klasowym, w którym przeważa grupa
uczniów o bardzo wysokich wynikach kształcenia, niski wynik pojedynczego ucznia zna-
cząco wpłynie na obniżenie średniej, a wynik żadnego ucznia nie będzie zbliżony do śred-
niej.

Średnia ważona

Średnią ważoną liczymy wówczas, gdy poszczególne wartości mają różne wagi (rangi), tj.
wyższe znaczenie, nierównorzędną ważność. Obliczamy ją według wzoru:

Przykład:

Uczeń uzyskał następujące oceny szkolne: ze sprawdzianu – 5, z pracy domowej – 3, z

odpowiedzi – 4 i 3 (średnia 3,5). Załóżmy, że większą wartość informacyjną dla nauczyciela o
osiągnięciach edukacyjnych ucznia mają stopnie uzyskane ze sprawdzianu niż z odpowiedzi ust-
nej, dlatego poszczególnym aktywnościom ucznia podlegającym ocenie nadajemy odpowiednią
rangę (w statystyce – wagę). Dajmy na to, że sprawdzianowi nadajemy wagę 3, pracy domowej 1,
odpowiedziom ustnym 2. Sumę tych wartości - 6 wpisujemy w mianowniku.

Średnią ważoną obliczamy w następujący sposób:

17

,

4

6

25

2

1

3

2

5

,

3

1

3

3

5

=

=

+

+

⋅

+

⋅

+

⋅

=

X

Gdybyśmy obliczali tylko średnią arytmetyczną, uzyskalibyśmy wynik niższy:

X

=3,75.

Kwantyle

Kwantyle to wartości, które dzielą badaną zbiorowość na części pozostające ze sobą w
odpowiednim stosunku. Do najczęściej stosowanych należą kwartyle, dzielące zbioro-
wość na 4 części, decyle (na 10 części) i percentyle (na 100 części).

Kwartyle

Definiuje się je jako wartości cechy badanej zbiorowości, przedstawionej w postaci szere-
gu statystycznego (czyli uporządkowanego według określonego kryterium, np. od naj-
mniejszego do najwyższego wyniku), które dzielą zbiorowość na cztery części pod wzglę-
dem liczby jednostek. Części te pozostają do siebie w określonych proporcjach. Kwartyle
są wartościami granicznymi w szeregu wyników wyznaczających te części.

8

B. Niemierko, op.cit., s.52.

gdzie:

X

ni

to iloczyn średniej i rangi (wagi), a

∑

X

ni

oznacza sumę tych iloczynów;

∑

N

to su-

ma wag poszczególnych wartości.

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

10

Kwartyl zerowy to wartość minimalna uzyskana przez badanych (patrz: rozstęp wyników).
Kwartyl pierwszy „odcina” dolną ćwiartkę uporządkowanego zbioru wyników, czyli 25%
wyników ma od niego mniejszą wartość, a 75% większą. Z kolei kwartyl drugi dzieli zbiór
na połowę i stanowi medianę. Trzeci kwartyl wyznacza górną ćwiartkę wyników, czyli 75%
wyników ma od niego mniejszą wartość, a 25% wyższą. Natomiast kwartyl czwarty to war-
tość maksymalna wyników.

Podanie kwartyli wzbogaca informację o łatwości danego arkusza. Im trudniejszy test dla
uczniów, tym niższe będą wartości poszczególnych kwartyli.

8F8F8F8F

9

Rozstęp ćwiartkowy jest różnicą wyniku pomiędzy trzecim i pierwszym kwartylem. Mierzy
on poziom zróżnicowania tylko części jednostek, pozostałych po odrzuceniu 25%
jednostek o wartościach najmniejszych (Q1) i 25% jednostek o wartościach największych
(Q3). Ponieważ między pierwszym i trzecim kwartylem znajduje się z definicji 50%
wyników, dlatego im większy jest rozstęp, tym większe zróżnicowanie badanej cechy.

Przykład:

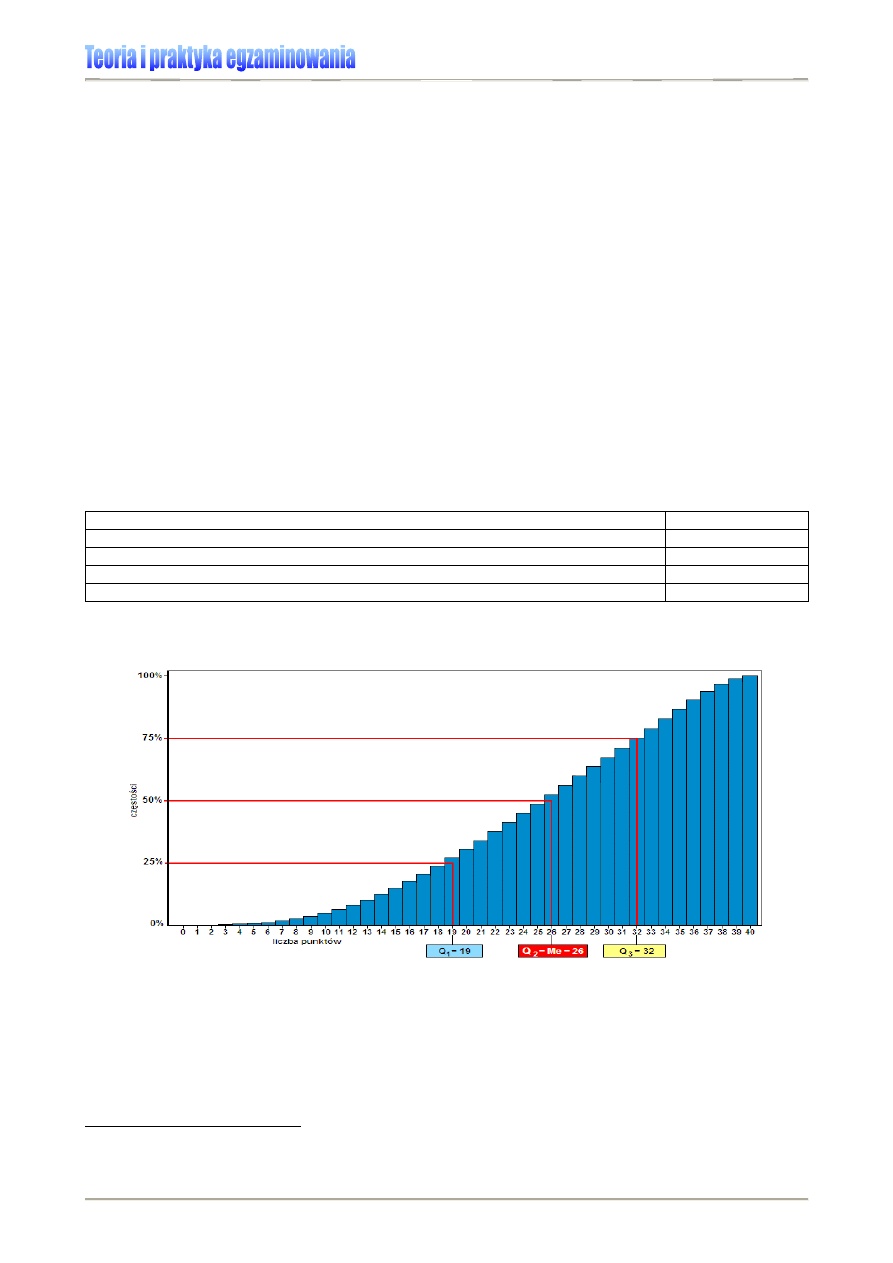
Tabela 4. przedstawia podział na kwartyle obliczony dla sprawdzianu 2006 (por. też

Rysunek 1.). Rozstęp ćwiartkowy wynosi 13, bo kwartyl trzeci przyjął wartość liczbową 32, a
kwartyl pierwszy – 19 [32 – 19 = 13].

Tabela 4. Podział kwartylowy i rozstęp ćwiartkowy wyników sprawdzianu 2006 [6]

1. kwartyl – najwyższy wynik uczniów z pierwszej ćwiartki (25%) wyników

19

2. kwartyl (mediana) – wynik środkowy w zbiorze wyników sprawdzianu

26

3. kwartyl – najwyższy wynik uczniów z trzeciej ćwiartki (75%) wyników

32

4. kwartyl – najwyższy wynik ze sprawdzianu

40

rozstęp ćwiartkowy (3. kwartyl minus 1. kwartyl)

13

Kwartyle możemy wyznaczyć graficznie, tak jak to pokazano na Rysunku 1.

Rysunek 1. Wyznaczanie kwartyli dla wyników sprawdzianu 2006 [6]

Dla przykładu przeanalizujmy i zinterpretujmy wyniki sprawdzianu 2006 uczniów pewnej
szkoły podstawowej.

Przykład:

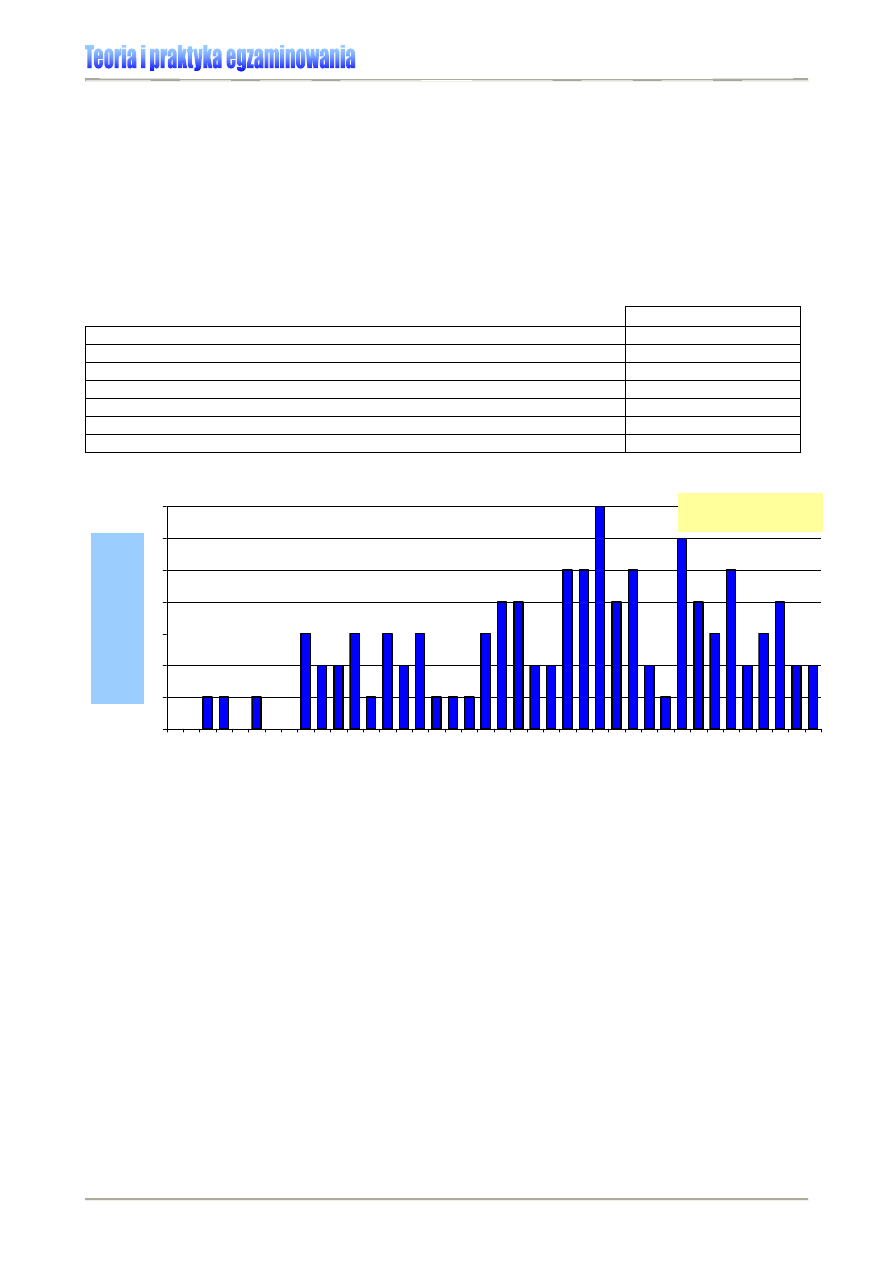
W Szkole Podstawowej w Iksowie sprawdzian pisało stu uczniów. Informacji o rozkła-

dzie ich wyników dostarczą nam: Tabela 5., Wykres 2. oraz Rysunek 1. Rozstęp wyników (40 pkt.
– 3 pkt. = 37 pkt.) dowodzi, że w tej szkole sprawdzian pisała dość zróżnicowana populacja
uczniów, gdyż znalazł się wśród nich i taki, którego wynik to zaledwie 3 pkt., ale jest też dwóch

9

H. Szaleniec, M.K. Szmigel, Doskonalenie kompetencji nauczycieli w zakresie oceniania zewnętrznego,

Wydawnictwo Zamiast korepetycji, Kraków 2001, s.62-63

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

11

uczniów o wyniku maksymalnym. Widać jednak wyraźnie, że grupa 25% dzieci o najsłabszych
wynikach z testu, to uczniowie o bardzo zróżnicowanych osiągnięciach, bo należą do niej zarówno
ci, którzy zdobyli zaledwie 3 czy 4 punkty, jak i ci, którzy uzyskali ich 17, 18 czy 19. Bardziej jedno-
rodną grupę stanowią uczniowie o wynikach najwyższych, bo ich wyniki zawierają się w przedziale
od 33 do 40 punktów. Przeciętny wynik ucznia w tej szkole to 26 punktów (tyle wynosi mediana).
Rozstęp ćwiartkowy pokazuje nam wynik grupy 50% uczniów, którzy napisali test średnio (pamię-
tajmy – w porównaniu z wynikami innych uczniów tej szkoły, a nie „w ogóle”). Zróżnicowanie ich
wyników jest mniejsze (13 punktów) niż w grupie uczniów o najniższych osiągnięciach (17 punk-
tów). W tej szkole największa liczba uczniów (siedmiu) uzyskała 27 punktów (to modalna).

Tabela 5. Rozkład wyników sprawdzianu 2006 w SP w Iksowie (N=100) [6]

Wynik

0. kwartyl – najniższy wynik ze sprawdzianu

3 pkt.

1. kwartyl – najwyższy wynik uczniów z pierwszej ćwiartki (25%) wyników

19 pkt.

2. kwartyl (mediana) – wynik środkowy w zbiorze wyników sprawdzianu

26 pkt.

3. kwartyl – najwyższy wynik uczniów z trzeciej ćwiartki (75%) wyników

32 pkt.

4. kwartyl – najwyższy wynik ze sprawdzianu

40 pkt.

rozstęp (wynik najwyższy minus wynik najniższy) 37

pkt.

rozstęp ćwiartkowy (3. kwartyl minus 1. kwartyl)

13 pkt.

Wykres 2. Rozkład wyników sprawdzianu 2006 w SP w Iksowie (N=100) [6]

liczba egzaminowanych:

N=100

0

1

2

3

4

5

6

7

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

liczba punktów uzyskanych przez uczniów za test

cz

ę

sto

ść

(liczba uczniów, którzy uzyskali

dany wynik)

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

12

Zastosowanie podstawowych miar tendencji centralnej

Rysunek 2. Rozkład symetryczny

Rysunek 3. Rozkład u-kształtny

Rysunek 4. Rozkład asymetryczny lewostronnie

Rysunek 5. Rozkład asymetryczny prawostronnie

Rysunek 6. Rozkład dwumodalny

Na Rysunku 2. przedstawiony jest rozkład wyników, gdzie
średnia, mediana i modalna (dominanta) przyjęły tę samą
wartość, tj. znajdują się w tym samym miejscu. Rozkład wy-
ników w związku z tym jest symetryczny. Rozkłady syme-
tryczne rzadko występują w praktyce szkolnej związanej z
badaniem osiągnięć uczniów. Najczęściej mamy do czynienia
z wykresami asymetrycznymi.

Jeżeli średnia jest niższa od modalnej i mediany, uzyskuje-
my rozkład wyników asymetryczny ujemnie (patrz: Rysunek
4.). Rozkład zwany ujemnieskośnym lub lewoskośnym,
oznacza że uczniowie w większości uzyskali wysokie wyniki
w teście lub na egzaminie.

Rozkład, w którym modalna jest niższa od mediany, a me-
diana niższa od średniej, nazywany jest dodatnioskośnym
lub prawoskośnym (Rysunek 5.). Taki rozkład wyników
oznacza, że większość uczniów uzyskała niskie wyniki w te-
ście lub na egzaminie, bo rozwiązywane zadania okazały się
dla nich trudne.

Rozkład, w którym wystąpiły dwie dominanty
(modalne) nazywamy dwumodalnym. Taki
rozkład wyników oznacza, że w badaniu ma-
my do czynienia z dwiema grupami uczniów o
różnych osiągnięciach. Rysunek 6. przedsta-
wia przykłady trzech typowych, symetrycz-
nych układów dwumodalnych.

Rozkład stanowiący lustrzane odbicie rozkładu zaprezento-
wanego na Rysunku 2., w którym dominują wyniki skrajne –
najwyższe i najniższe, nazywamy u-kształtnym (Rysunek
3.). W wypadku rozkładu normalnego u-kształtnego media-
na i średnia mają wartości najniższe i pokrywają się ze so-
bą. Taki układ wyników często wynika z użycia niezbyt traf-
nego narzędzia pomiarowego (testu).

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

13

Przykład:

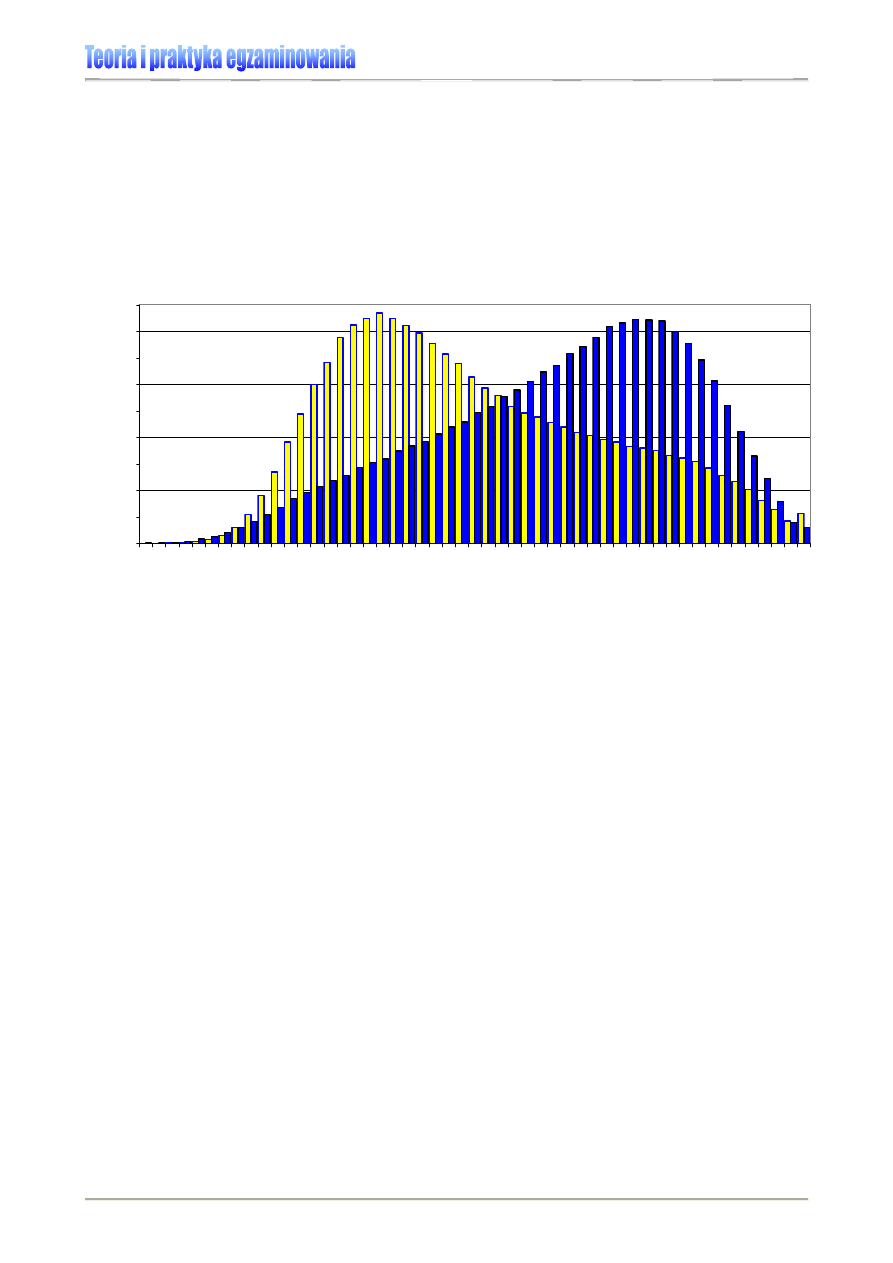
Wykres 3. prezentuje rozkłady wyników przeprowadzonych w 2007 r. dwóch części eg-

zaminu gimnazjalnego. Ich odmienne ukształtowanie zwraca uwagę na różnicę w rozkładzie wyni-
ków z części humanistycznej i matematyczno-przyrodniczej egzaminu – lewoskośny rozkład wyni-
ków z części humanistycznej (kolor niebieski) świadczy o większej liczbie w populacji wyników
wysokich, prawoskośność rozkładu wyników z części matematyczno-przyrodniczej (kolor żółty)
wskazuje zaś na dominację wyników niskich i średnich. Tak więc, mimo że oba testy pisali ci sami
uczniowie, sprawiły im one różną trudność.

Wykres 3. Egzamin gimnazjalny 2007 – rozkład wyników krajowych w części humanistycznej (kolor
niebieski) i matematyczno-przyrodniczej (kolor żółty) [4]

0,0%

0,5%

1,0%

1,5%

2,0%

2,5%

3,0%

3,5%

4,0%

4,5%

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50

punkty

% l

iczebno

ści

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

14

MIARY ROZPROSZENIA (ZRÓŻNICOWANIA)

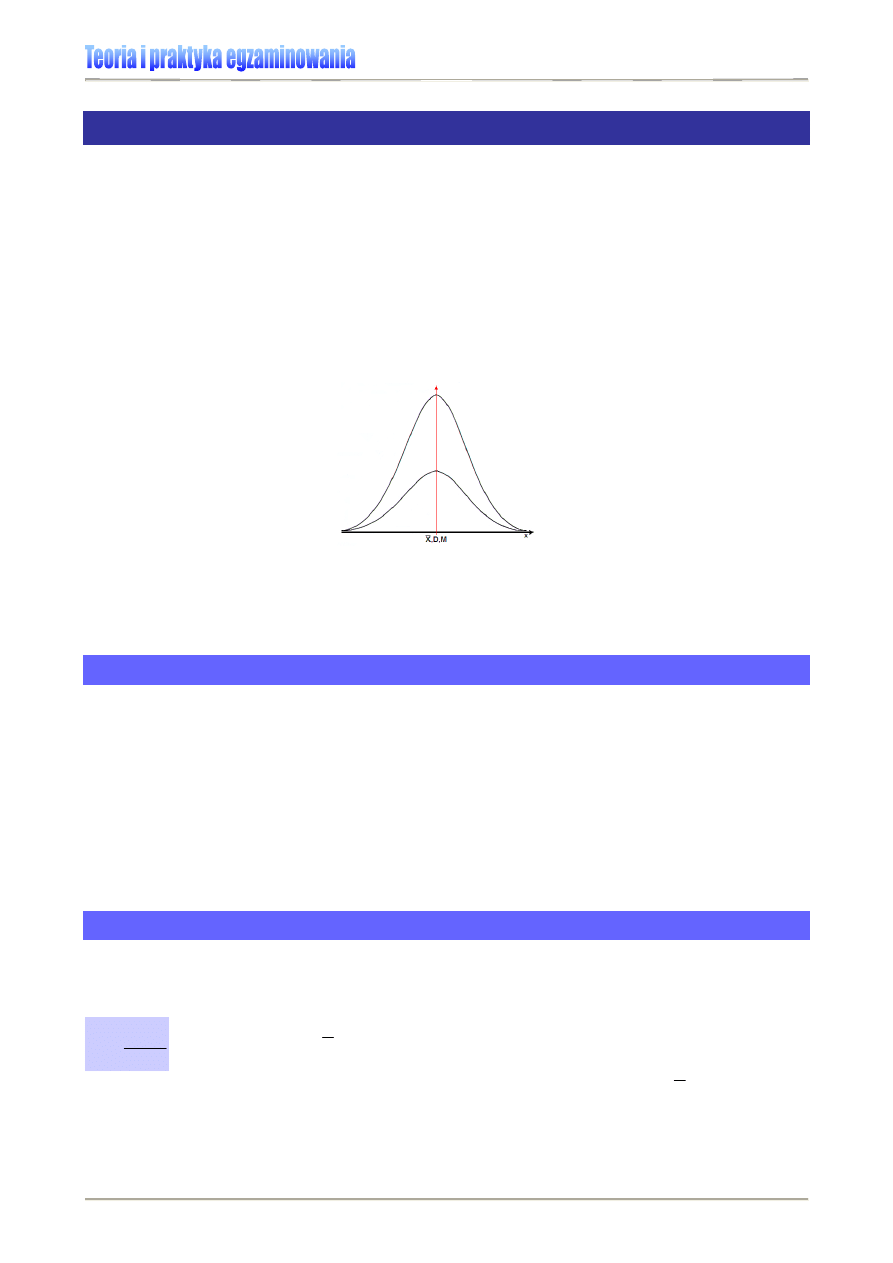
Miary tendencji centralnej nie wystarczają, aby w pełni scharakteryzować i porównać ba-
dane cechy populacji. Może się bowiem zdarzyć, że w kolejnych pomiarach, mimo iż śred-
nia, mediana i modalna przyjmą identyczną wartość, wyniki będą różnić się w istotny spo-
sób (zob. Rysunek 7.). Stąd, by dokładniejszej scharakteryzować badane grupy, oblicza
się miary rozproszenia (rozrzutu), które opisują, jak bardzo wyniki te odchylają się od war-
tości centralnej, jak bardzo są zróżnicowane. Są to wskaźniki dyspersji. Należą do nich:
rozstęp wyników pomiaru, wariancja i odchylenie standardowe. Im mniejszą wartość
liczbową przyjmuje współczynnik dyspersji, tym większe jest skupienie wyników pomiarów
wokół średniej i tym mniej są one zróżnicowane.

Rysunek 7. Przykład różnic rozkładów przy identycznej wartości centralnej

Jeśli wariancja jest mała, wówczas wyniki poszczególnych pomiarów leżą w pobliżu war-
tości średniej (rozkład w kształcie wąskiego dzwonu). Jeżeli jest ona duża, to wyniki są
bardziej rozproszone (rozkład przyjmuje kształt szerokiego dzwonu).

Rozstęp

Rozstęp jest różnicą między najwyższym i najniższym wynikiem. Pokazuje, jak różne wy-
niki uzyskali badani uczniowie.

Przykład:

Mamy kolejne liczby: 4, 8, 9, 45, 32, 13. Rozstęp liczymy, odejmując od najwyższej licz-

by liczbę najniższą w szeregu: 45 – 4 = 41.

W przypadku wyników sprawdzianu 2006 (Wykres 1.), wynikiem najniższym był wynik mi-
nimalny – 0 punktów (uzyskało go 23 uczniów na 473 924 zdających), zaś wynik maksy-
malny to 40 punktów – ten wynik uzyskało 5498 osób (1,2%). Zatem rozstęp wynosi 40.

Wariancja

Wariancja jest kwadratem odchylenia standardowego, gdzie

∑

oznacza sumę obserwacji

(wyników).

N

x

s

∑

=

2

2

gdy

(

)

2

2

∑

∑

−

=

X

X

x

gdzie:

∑

2

x

to suma kwadratów odchyleń, N – liczebność populacji, X – wynik ucznia,

X

– średnia arytme-

tyczna z testu (egzaminu).

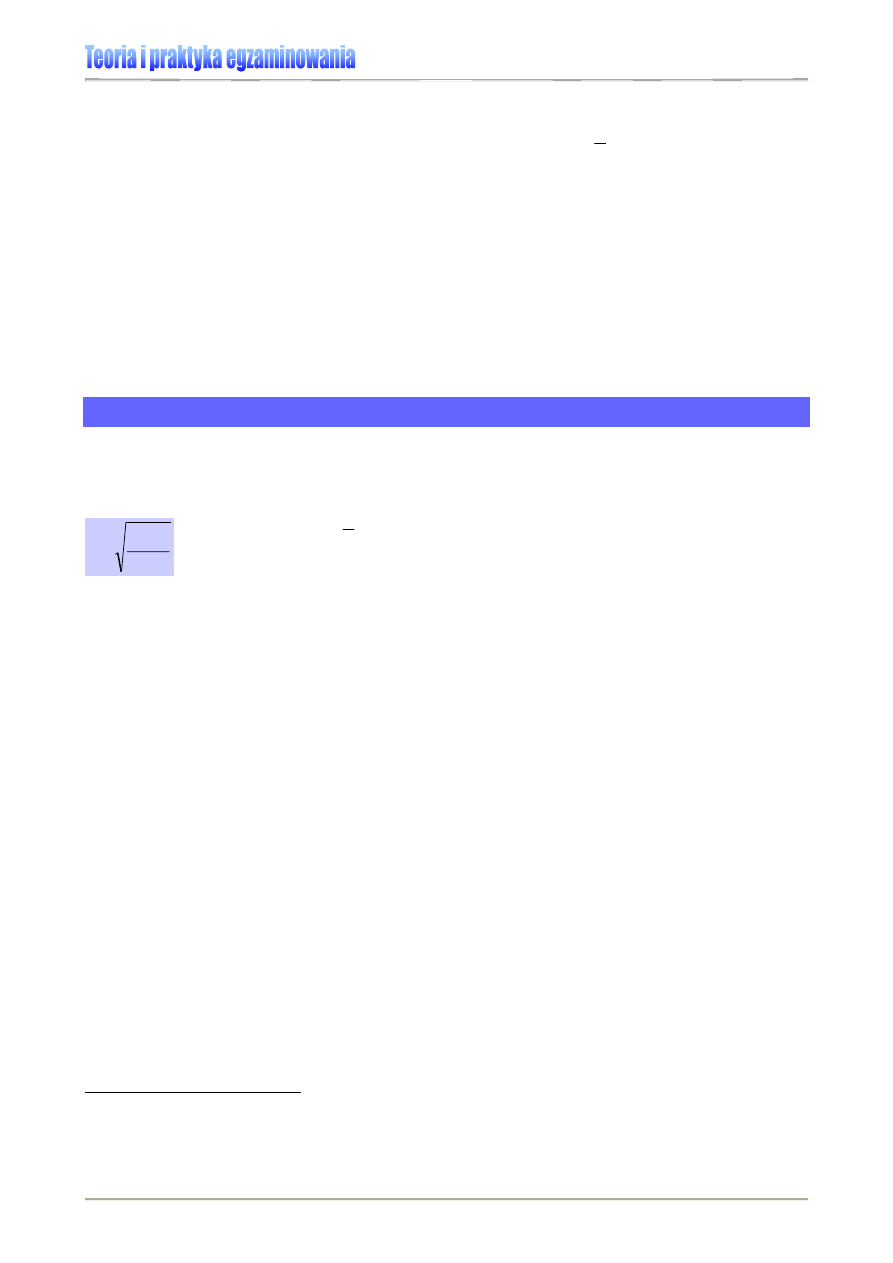
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

15

W celu uzyskania

∑

2

x

, należy:

obliczyć odchylenie od średniej dla każdego ucznia

(

)

X

X

−

,

sprawdzić, czy suma odchyleń od średniej równa się zero,

podnieść do kwadratu każde odchylenie od średniej, żeby zlikwidować wartości
ujemne,

zsumować wszystkie odchylenia od średniej.

9F9F9F9F

10

Wariancja opisuje wielkość błędu, jaki popełniamy wtedy, kiedy średni wynik traktujemy
jako dobre odzwierciedlenie wszystkich wyników indywidualnych. Mała wariancja (niewiel-
kie zróżnicowanie wyników wokół wartości średniej) wskazuje, że średni wynik dobrze od-
zwierciedla wyniki indywidualne. Duża wariancja informuje, że wartości średniej nie można
traktować jako rzetelnej miary wyników indywidualnych.

10F10F10F10F

11

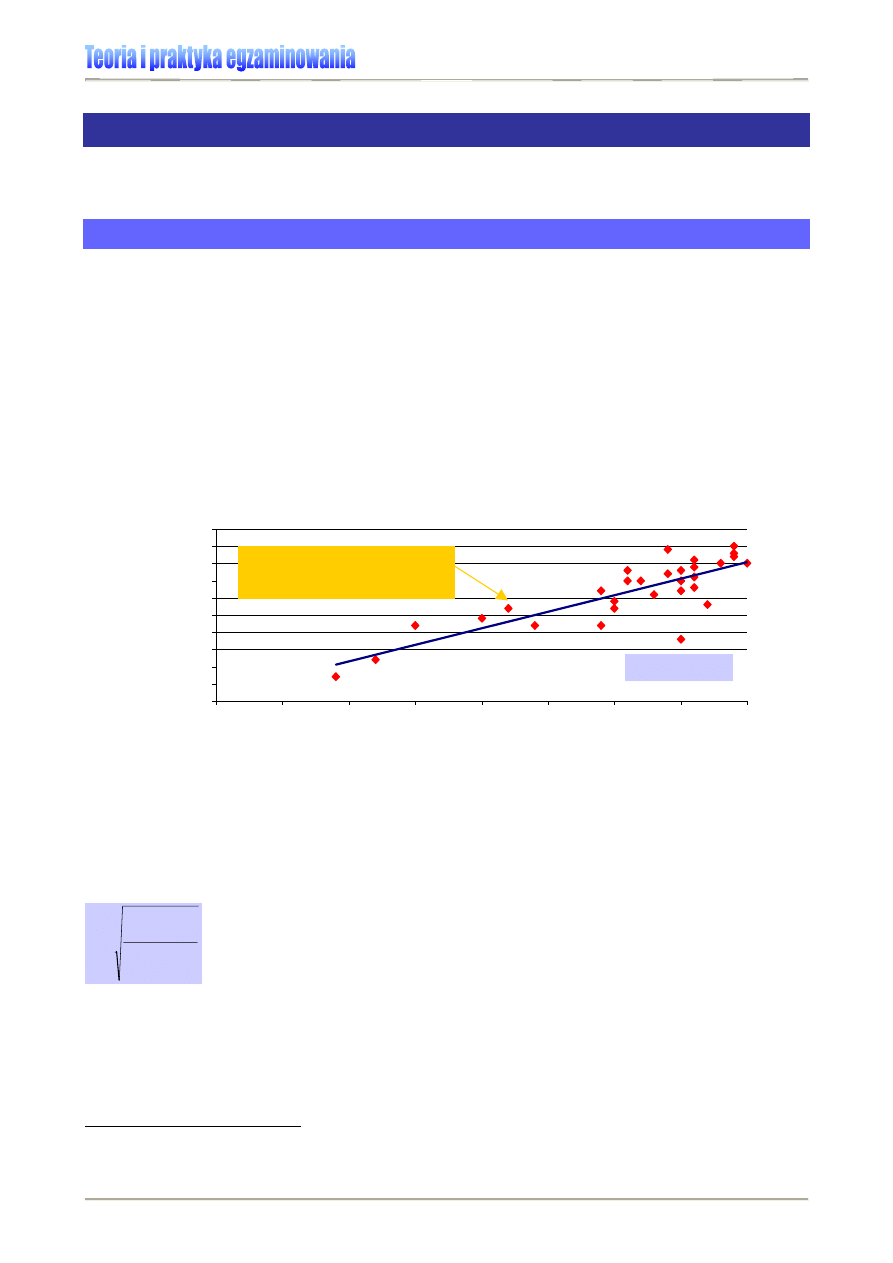
Odchylenie standardowe

Odchylenie standardowe, które jest kwadratowym pierwiastkiem z wariancji, określa
zmienność wyników w obrębie średniej. Służy m.in. do opisu zróżnicowania wyników.
Obliczamy je następująco:

N

x

s

∑

=

2

Gdy zmienność wyników rośnie, zwiększa się odległość pomiaru od średniej, czyli im
większe odchylenie standardowe, tym rozproszenie wyników większe. Im mniejsze jest
odchylenie standardowe, tym większe jest skupienie wartości zmiennej wokół średniej. Im
większe odchylenie standardowe, tym mniej precyzyjna informacja wynika z porównania
analizowanego wyniku do średniej (patrz: Rysunek 7.)

Najlepiej odchylenie standardowe można opisać na rozkładzie normalnym, o którym
w dalszej części materiałów.

Przykład:

Odchylenie standardowe wyników sprawdzianu 2006 (patrz: Wykres 1.) wynosi 8,6 pkt.

10

D. Sołtys, M.K. Szmigel, Doskonalenie kompetencji nauczycieli w zakresie diagnozy edukacyjnej,

Wydawnictwo „Zamiast korepetycji”, Kraków 1997, s. 55

11

Elżbieta Hornowska, Testy psychologiczne. Teoria i praktyka, Wydawnictwo Naukowe SCHOLAR,

Warszawa 2003, s. 70.

gdy

(

)

2

2

∑

∑

−

=

X

X

x

gdzie:

∑

2

x

to suma kwadratów odchyleń, a N – liczebność populacji.

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

16

MIARY WSPÓŁZMIENNOŚCI

Miary współzmienności opisują stopień, w jakim są ze sobą związane dwie zmienne.

Korelacja

Korelacja (łac. wzajemny związek) to współzależność jakichś zjawisk lub obiektów. Anali-
zy korelacyjne prowadzimy wówczas, gdy chcemy zbadać związki między niejednorodny-
mi zmiennymi. W systemie egzaminacyjnym coraz częściej szuka się powiązań między
wynikami różnych egzaminów.

Oto

przykład

analizy wyników 30 uczniów jednego z oddziałów szkolnych Gimnazjum

w L., uzyskanych na sprawdzianie 2004 i egzaminie gimnazjalnym 2007. Każdy z punktów
obrazuje pozycję na skali wyników jednego ucznia, opisaną dwiema zmiennymi: wynikiem
sprawdzianu (maks. 40 pkt.) oraz jednej z części egzaminu gimnazjalnego (maks. 50 pkt.).
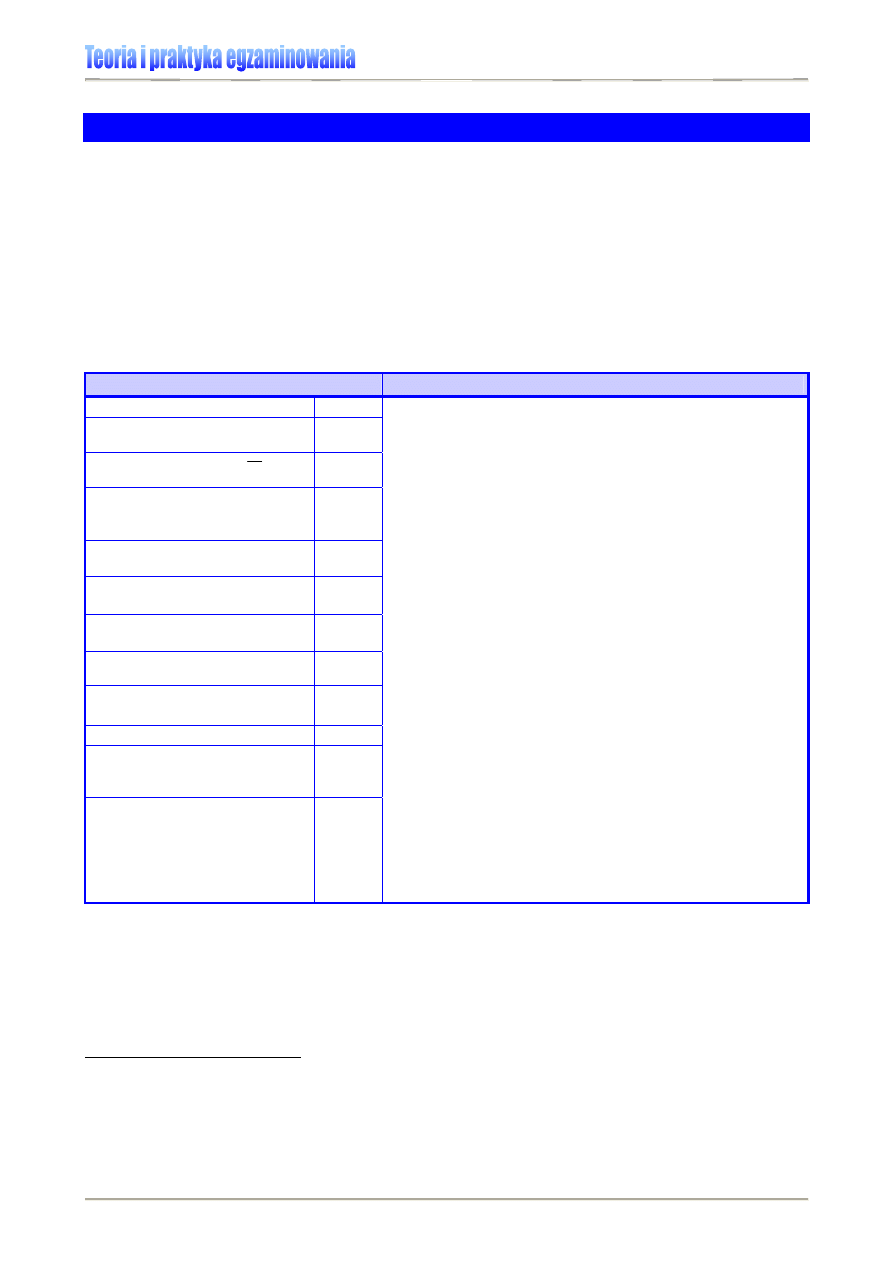
By uchwycić ogólną prawidłowość, możemy wykreślić linię trendu, zwaną linią regresji,
która powinna być jak najlepiej dopasowana do wszystkich 30 punktów.

Wykres 4. Korelacja wyników sprawdzianu i egzaminu gimnazjalnego klasy IIId Gimnazjum w L. [6]

0

5

10

15

20

25

30

35

40

45

50

0

5

10

15

20

25

30

35

40

wynik sprawdzianu

wynik cz

ęś

ci humanistyczn

egzaminu gimnazjalnego

Najczęściej używanym wskaźnikiem korelacji jest współczynnik r korelacji liniowej Pe-
arsona. Odzwierciedla on stopień liniowej zależności pomiędzy dwoma zbiorami danych,
dając możliwość porównania zróżnicowania wartości zmiennej wokół linii regresji z całym
zróżnicowaniem wartości tej zmiennej.

11F11F11F11F

12

Jego wartość mieści się w zakresie od -1,0 do

1,0 włącznie i informuje o sile związku pomiędzy zmiennymi (1 – całkowita korelacja, 0 –
jej brak). Liczymy go wg wzoru (może nas w tym zastąpić komputer):

∑

∑

=

−

=

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

±

=

n

i

i

n

i

i

Y

y

y

y

r

1

2

1

2

'

Znak przy współczynniku zależy od nachylenia linii regresji. Gdy jest rosnąca (jak na Wy-
kresie 4.), znak jest dodatni. Mówimy wtedy, że korelacja jest dodatnia (im większa war-
tość X, tym większa wartość Y). Gdy linia regresji jest malejąca, mamy do czynienia z ko-
relacją ujemną (im większa wartość X, tym mniejsza Y).

12

Zob. K. Konarzewski, Jak uprawiać badania oświatowe. Metodologia praktyczna, WSiP, Warszawa 2002,

s. 186-189.

r = 0,82488

Wynik Kamila J.:

22 pkt. na sprawdzianie,

27 pkt na egzaminie gimnazjalnym.

gdzie r to pierwiastek z ułamka, w którego liczniku mamy sumę kwadratów odległości
poszczególnych przypadków od linii regresji, a w mianowniku – sumę kwadratów odle-
głości od średniej; y’ to punkt na linii regresji odpowiadający wartości x

i

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

17

Przykładowe zestawienia wyników egzaminu zewnętrznego

Po zebraniu wszystkich wyników pomiaru (testowania, egzaminowania), otrzymujemy „su-
rowy” materiał statystyczny

12F12F12F12F

13

, który, aby móc go właściwie zinterpretować w odniesieniu

do badanej populacji, powinien być usystematyzowany i odpowiednio opisany. Analiza
wartości parametrów statystycznych umożliwi scharakteryzowanie badanych zbiorowo-
ści w sposób systematyczny.

Przykład:

Aby trafnie wnioskować o osiągnięciach edukacyjnych uczniów przystępujących do eg-

zaminów zewnętrznych, oblicza się – biorąc pod uwagę liczbę zdających – następujące parametry
statystyczne:

Tabela 6. Podstawowe dane i parametry statystyczne sprawdzianu 2006 [2] [6]

Parametry

Komentarz

Liczba egzaminowanych (N)

473 924

►

Sprawdzian 2006 pisało prawie pół miliona uczniów.

Łatwość testu egzaminacyjnego
(p)

0,62

►

Łatwość testu na poziomie 0,62 wskazuje na fakt, iż był on
umiarkowanie trudny dla uczniów.

Średnia arytmetyczna (

X

)

25 pkt.

►

Statystyczny uczeń zdający ten egzamin uzyskał 25 na 40
punktów możliwych do uzyskania.

Mediana (Me, M)

26 pkt.

►

Uczeń, który uzyskał wynik plasujący się w środku wyników
rozkładu uporządkowanego rosnąco otrzymał 26 punktów,
czyli 65% punktów możliwych do uzyskania.

Modalna (dominanta) (Mo, D)

33 pkt.

►

Na sprawdzianie 2006 uczniowie uzyskiwali najczęściej 33
punkty.

Maksymalny wynik (x

max

) 40

pkt.

►

Maksymalna liczba punktów możliwa do uzyskania w
sprawdzianie to 40 punktów.

Najwyższy wynik

40 pkt.

►

W 2006 roku 5498 uczniów w kraju uzyskało ze spraw-
dzianu wynik maksymalny.

13F13F13F13F

14

Najniższy wynik

0 pkt.

►

Najniższy wynik 0 pkt. na sprawdzianie miało tylko 23

uczniów.

Rozstęp (R)

40 pkt.

►

W r. 2006 rozstęp wyników wyniósł 40 pkt., przybierając

wielkość maksymalną.

Wariancja (s

2

x

) 73,3

Odchylenie standardowe (s

x

)

8,6 pkt.

►

68% uczniów osiągnęło wynik w przedziale wyników typo-
wych (stanowiącym 2/3 wszystkich wyników), uzyskując od
17 do 34 punktów.

Kwartyle

1. – 25%
2. – 50%
3. – 75%

18 pkt.
26 pkt.
32 pkt

.

►

Rozkład wyników egzaminu zbliżony jest do normalnego,

z wyraźnym przesunięciem w stronę wyższych wyników.
25% uczniów uzyskało wynik równy lub niższy od 19 punk-
tów; 50% uczniów uzyskało wynik równy lub niższy od 26
punktów; 75% uczniów uzyskało wynik równy lub niższy od
32 punktów.

13

„Surowy” wynik testowania to suma punktów uzyskanych przez badanego za rozwiązanie testu. Por. B.

Niemierko, Testy osiągnięć szkolnych. Podstawowe pojęcia i techniki obliczeniowe, Warszawa 1975, WSiP,
s. 116.

14

Najwyższy wynik z testu nie zawsze oznacza wynik maksymalny (liczba punktów możliwa do uzyskania za

rozwiązanie całego testu). Może się np. zdarzyć, że żaden z piszących sprawdzian uczniów w szkole nie
uzyska 40 punktów.

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

18

PODSTAWOWE PARAMETRY STATYSTYCZNE
POMOCNE W ANALIZIE ILOŚCIOWEJ WYNIKÓW
ZADAŃ EGZAMINACYJNYCH I TESTU

Rozkład liczebności

Rozkład liczebności to najprostsza forma przedstawiania wyników testowania. Polega na
uporządkowaniu danych od wyniku najwyższego do najniższego (lub odwrotnie) w formie
tabeli bądź wykresu, z uwzględnieniem liczebności zaobserwowanych wartości zmiennej
(wyników).

14F14F14F14F

15

Przykład:

Klasa szkolna liczy 25 uczniów. W wyniku klasyfikacji śródrocznej z matematyki jeden

uczeń uzyskał ocenę celującą, trzech ocenę bardzo dobrą, sześciu ocenę dobrą, dziesięciu ocenę
dostateczną, trzech dopuszczającą i dwóch niedostateczną. Rozkład liczebności przedstawia się
więc następująco:

Tabela 7., Wykres 5

.

Rozkład wyników oceniania wewnątrzszkolnego za I okres w klasie Ib SP w B. [6]

Ocena

Liczba uczniów

celująca 1
bardzo dobra

3

dobra 6
dostateczna 10
dopuszczająca 3
niedostateczna 2

razem

25

Rozkład liczebności ocen w klasie VI b

1

3

6

10

3

2

0

2

4

6

8

10

12

celująca

bardzo dobra

dobra

dostateczna

dopuszczająca

niedostateczna

liczba uczniów

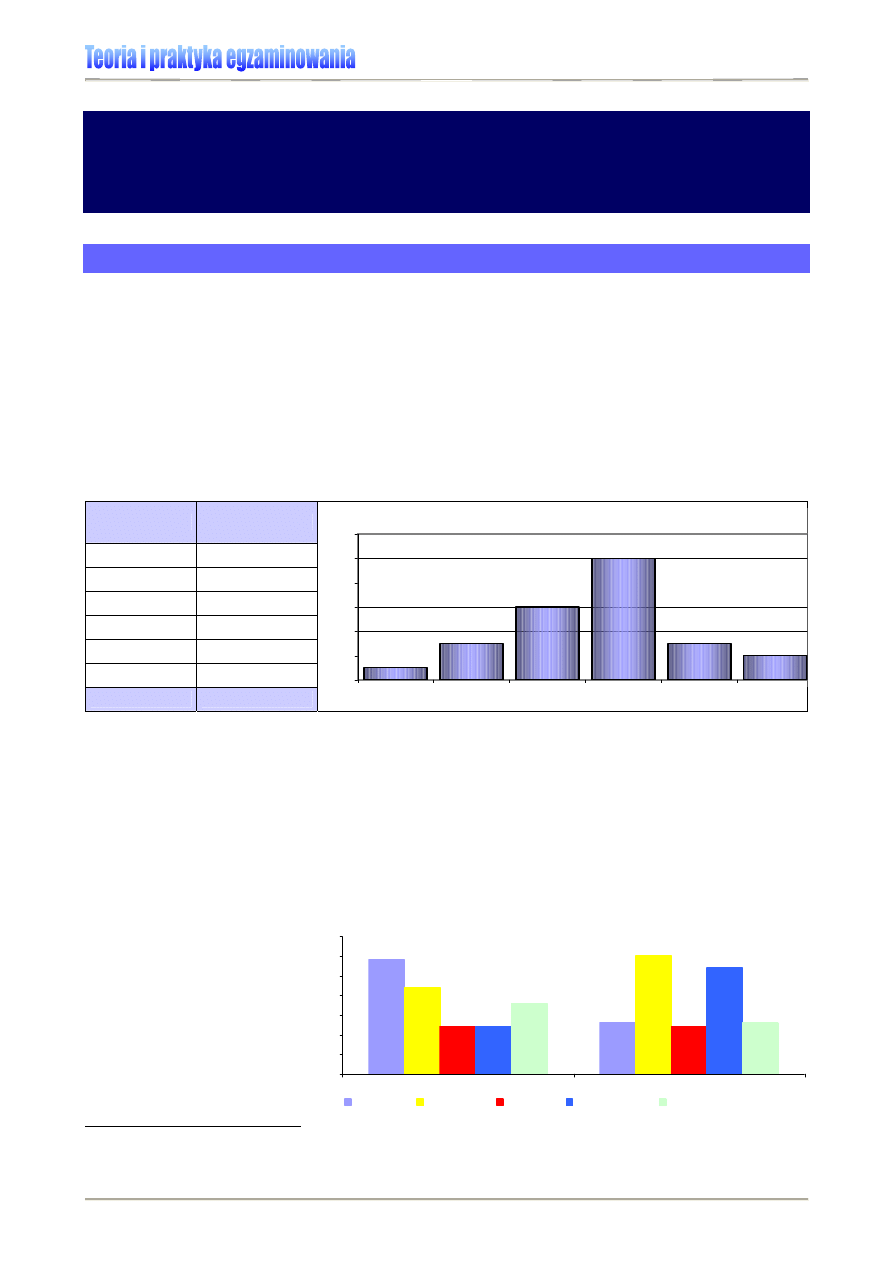
W pomiarze dydaktycznym rozkład liczebności wykorzystywany jest do graficznej prezen-
tacji wyników, najczęściej w postaci wykresu słupkowego, gdzie na osi poziomej umiesz-
czona jest liczba punktów, a na pionowej podana jest liczba albo procent uczniów, którzy
dany wynik uzyskali. Wyniki mogą być prezentowane co 1 punkt lub pogrupowane w klasy.

Przykład:

Rozkład liczebności wykorzystywany jest w raportach CKE do prezentacji wyników eg-

zaminów (zobacz np. Rozkład wyników krajowych sprawdzianu 2006 przedstawiony na Wykresie
1.) lub charakterystyki zróżnicowania populacji, czego przykładem może być Wykres 6., ukazujący
zależność między płcią maturzysty 2007 a wyborem przedmiotu zdawanego na maturze.

Wykres 6. Wybór przedmiotów
obowiązkowych a płeć
maturzysty 2007 – histogram.
[5]

15

B. Niemierko, Testy osiągnięć..., s. 50. Sposób grupowania wyników testowania został również opisany w

części Normalizacja wyników testowania.

29%

13%

22%

30%

12%

12%

12%

27%

18%

13%

0%

5%

10%

15%

20%

25%

30%

35%

kobiety

mężczyźni

biologia

geografia

historia

matematyka

wiedza o społeczeństwie

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

19

Łatwość zadania / testu

Łatwość zadania (bądź całego testu) jest wskaźnikiem używanym zarówno podczas ana-
lizy wyników egzaminów zewnętrznych, jak i wyników testowania wewnątrzszkolnego. Jest
to wskaźnik pozytywny, tzn. taki, którego wartość rośnie wraz ze wzrostem osiągnięć.

15F15F15F15F

16

Łatwość zadania (testu), rozumiana jako stosunek sumy punktów uzyskanych przez zda-
jących za zadanie lub test do iloczynu liczby egzaminowanych uczniów i maksymalnej
liczby punktów możliwych do uzyskania za zadanie lub test, liczona jest według wzoru:

Przykład:

30 uczniów rozwiązywało zadanie punktowane w skali 0-3. Maksymalną liczbę punktów

(3 pkt.) uzyskało dziewięciu uczniów, 2 punkty – trzech, 1 punkt – piętnastu, a pozostałych trzech –
0 p. Zatem suma punktów uzyskanych za rozwiązanie zadania wynosi: 9 x 3 + 3 x 2 +15 x 1 = 48.
Natomiast za poprawne rozwiązanie tego zadania wszyscy uczniowie mogli uzyskać 90 punktów:
30 x 3 = 90. Współczynnik łatwości zadania wynosi więc 0,53 [48 : 90 = 0,53].

W przypadku zadań punktowanych 0-1, łatwość zadania jest stosunkiem liczby uczniów,
którzy prawidłowo rozwiązali to zadanie, do liczby uczniów biorących udział w testowaniu.
Wyraża to wzór:

Przykład:

30 uczniów rozwiązywało zadanie punktowane w skali 0-1. Prawidłowej odpowiedzi

udzieliło 14. Zatem współczynnik łatwości zadania wynosi 0,47 [14 : 30 = 0,47].

Wskaźnik łatwości zadania/testu pozwala określić stopień trudności zadania dla ucznia lub
grupy uczniów, pokazując poziom opanowania badanej czynności. Jego wartości gra-
niczne to 0 (nikt nie sprostał zadaniu) i 1 (wszyscy piszący rozwiązali je prawidłowo). In-
terpretację współczynnika łatwości przedstawia Tabela 8.

Tabela 8. Interpretacja współczynnika łatwości

16F16F16F16F

17

0 – 0,19

0,20 – 0,49

0,50 – 0,69

0,70 – 0,89

0,90 – 1,00

zadanie

bardzo trudne

zadanie

trudne

zadanie

umiarkowanie

trudne

zadanie

łatwe

zadanie

bardzo łatwe

Łatwość zadania wyrażamy ułamkiem dziesiętnym (0,7) lub w procentach (70%).

16

B. Niemierko, Pomiar wyników kształcenia, WSiP, Warszawa 1999, s. 152-154.

17

Jw.

nk

x

p

x

∑

=

gdzie:

∑

x

– suma punktów uzyskanych za rozwiązanie zadania lub testu

n – liczba egzaminowanych uczniów
k – maksymalna liczba punktów możliwych do uzyskania przez ucznia za rozwiązanie
danego zadania lub całego testu

gdzie:
p – oznacza łatwość zadania punktowanego 0-1
n

p

– liczba uczniów, którzy rozwiązali zadanie

n – liczba uczniów testowanych

n

n

p

p

=

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

20

Rysunek 8. Przykładowa prezentacja wyniku uzyskanego za rozwiązanie zadania ze sprawdzianu 2006 [2]

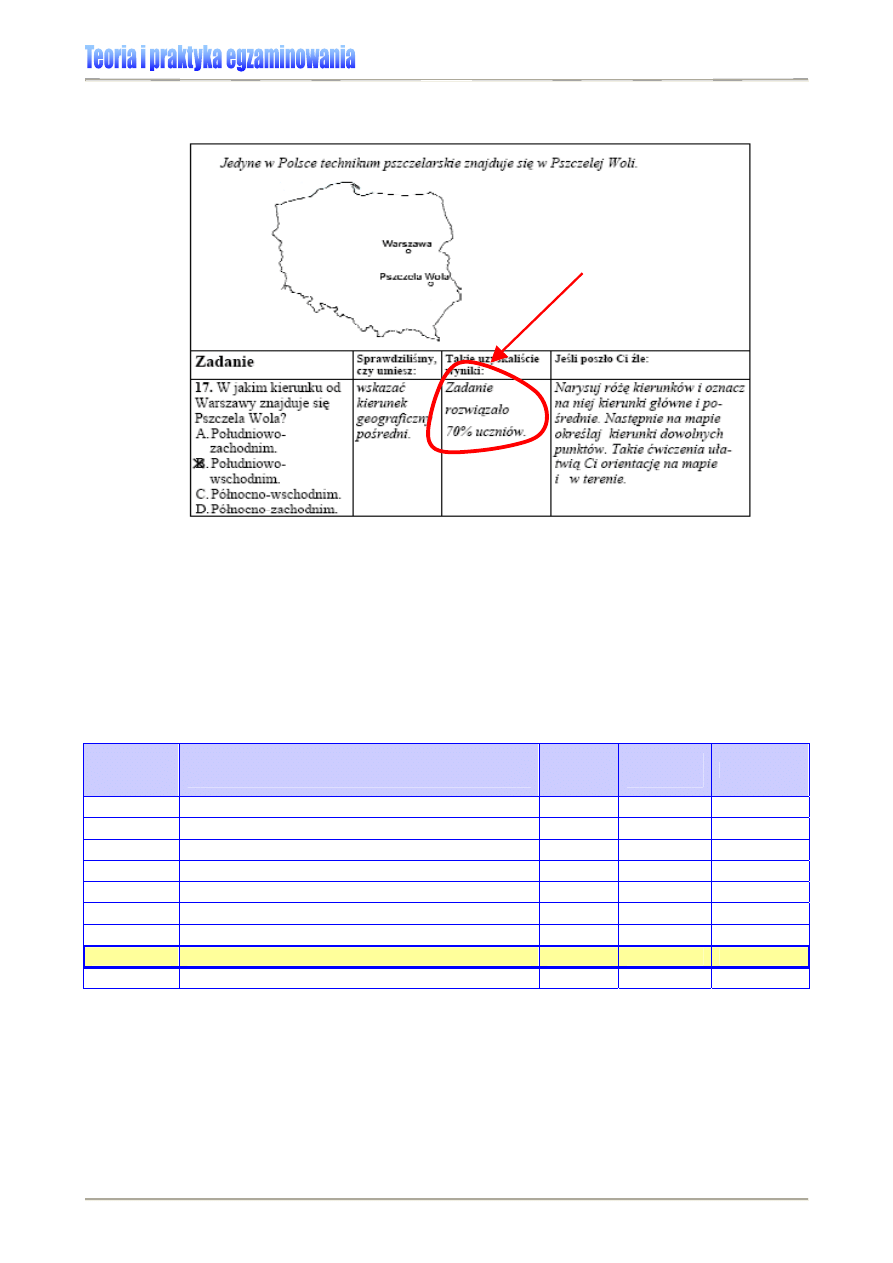
Interpretując wskaźnik łatwości, trzeba zawsze pamiętać o tym, że jego wartość odnosi się
do stopnia opanowania czynności badanej danym zadaniem (zgodnie z zapisem w karto-
tece testu) i w ten sposób powinna być rozumiana.

Przykład:

W 2006 roku 70% uczniów klas VI opanowało umiejętność odczytywania danych

z mapy (potrafiło wskazać kierunek geograficzny pośredni) badaną zadaniem 17. – patrz: Rysunek
8. i Tabela 9. Oznacza to równocześnie, że współczynnik łatwości tego zadania przyjął wartość 0,7
i mieści się w obszarze zadań łatwych.

Tabela 9. Fragment kartoteki (planu) testu S-A1 sprawdzianu 2006 ze wskaźnikami łatwości

zadań/czynności [2]

Nr zadania

Sprawdzana czynność ucznia

Uczeń:

Maks.
liczba

pkt.

Nr

standardu

Łatwość

1

odczytuje tekst popularnonaukowy

1

1.1

0,90

2

odczytuje tekst popularnonaukowy

1

1.1

0,85

3

odczytuje tekst popularnonaukowy

1

1.1

0,78

4

wykonuje obliczenia dotyczące temperatury

1

5.3

0,48

... ....

15

wykorzystuje w sytuacji praktycznej własności liczb

1

5.5

0,62

16

sprawdza wyniki z warunkami zadania

1

3.9

0,52

17

odczytuje dane z mapy

1

1.4

0,70

18

wykonuje obliczenia dotyczące długości 1

5.3

0,55

Wskaźnik łatwości obliczany jest również np. dla obszarów standardów egzaminacyjnych.
W tym przypadku interpretujemy go w odniesieniu do stopnia opanowania umiejętności
badanych danym standardem. Tak przedstawiane bywają wyniki uczniów i szkół w
raportach OKE i CKE (Rysunek 8.), tak prezentowane są zainteresowanym w Internecie
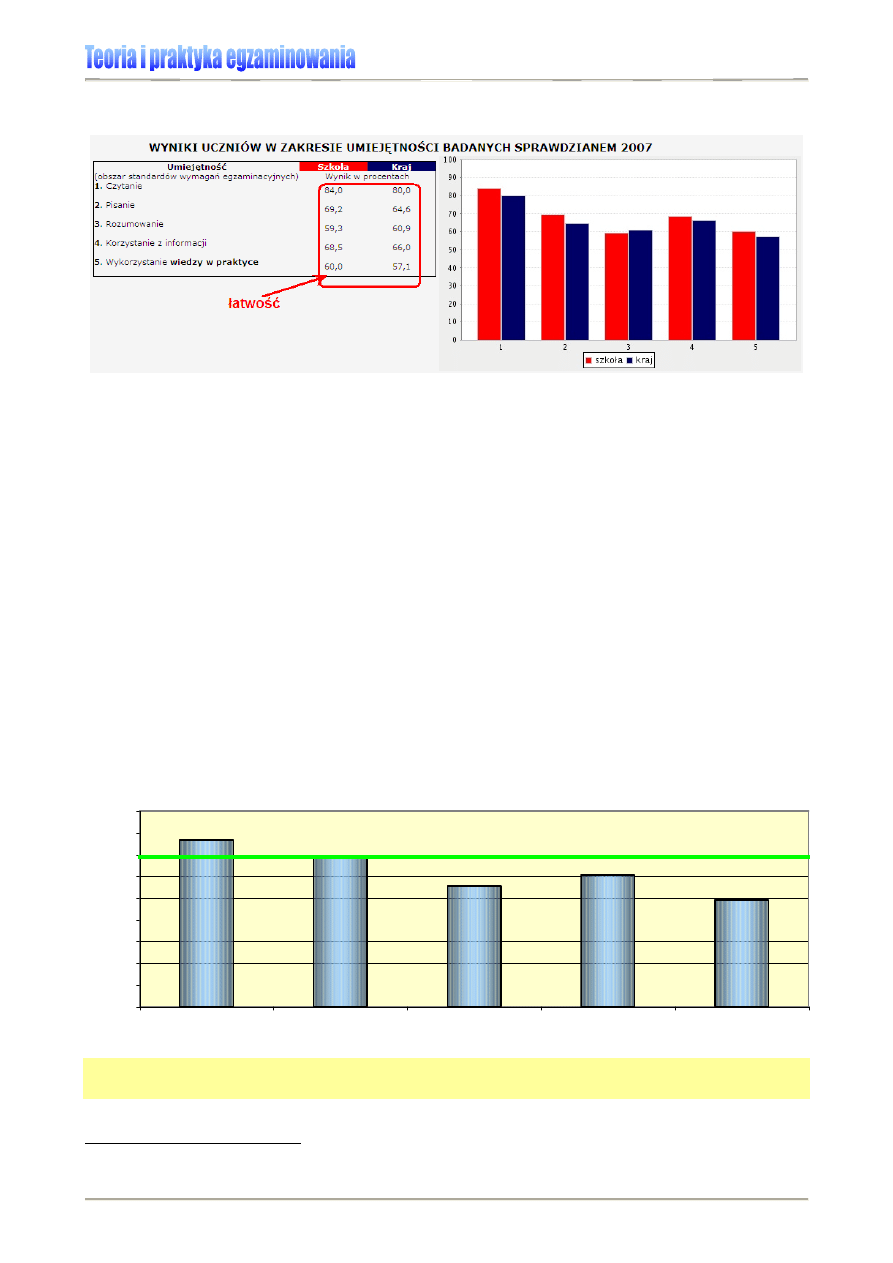
(Tabela 10. i Rysunek 9.).

łatwość

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

21

Tabela 10., Rysunek 9. Przykład prezentacji osiągnięć uczniów szkoły w R. na sprawdzianie 2007 [7]

Aby zinterpretować wyniki uczniów wyrażone wskaźnikiem łatwości, konieczne jest ustale-
nie umownego progu, którego osiągnięcie pozwoli uznać, że dana umiejętność jest opa-
nowana zadowalająco. Określenie progu „zaliczenia” umożliwi tym samym zidentyfikowa-
nie najważniejszych potrzeb edukacyjnych (braków) uczniów i podjęcie decyzji dotyczą-
cych zmian/modyfikacji w procesie kształcenia. Zgodnie z propozycją prof. Bolesława
Niemierki można przyjąć, że normę biegłości stanowić będzie 70% punktów możliwych do
uzyskania za rozwiązanie zadań/testu

17F17F17F17F

18

, nie znaczy to jednak, że wewnątrzszkolny sys-

tem oceniania szkoły nie może stanowić inaczej.

Przykład:

W 2006 roku uczniowie przystępujący do sprawdzianu uzyskali 63,3% punktów

możliwych do uzyskania. Zatem test zastosowany na egzaminie okazał się dla zdających
umiarkowanie trudny, bo łatwość testu przyjęła wartość 0,63. W stopniu zadowalającym uczniowie
opanowali umiejętności z obszaru standardów „Czytanie” (patrz: Wykres 7.). W pozostałych nie
osiągnęli progu 70%. Wobec tego wszelkie zmiany lub modyfikacje procesu dydaktycznego w
szkole powinny przede wszystkim dotyczyć kształcenia umiejętności opisanych w pozostałych
obszarach standardów wymagań egzaminacyjnych, szczególnie w obszarze „Wykorzystanie
wiedzy w praktyce”.

Wykres 7. Wyniki sprawdzianu 2006 w obszarach umiejętności (dla uczniów rozwiązujących arkusz
standardowy) [2]

Co potrafi statystyczny szóstoklasista 2006?

76,6%

68,5%

55,6%

49,1%

60,5%

0%

10%

20%

30%

40%

50%

60%

70%

80%

90%

czytanie

pisanie

rozumowanie

korzystanie z informacji wykorzystanie wiedzy w

praktyce

procent punktów

☺

Uwaga: Analizując wyniki egzaminów, należy pamiętać, że co roku stosuje się testy, które
mogą obejmować inne treści i mieć różny stopień trudności. Nie należy zatem wprost po-

18

Por. B. Niemierko, Pomiar sprawdzający w dydaktyce, Warszawa 1990, s. 357.

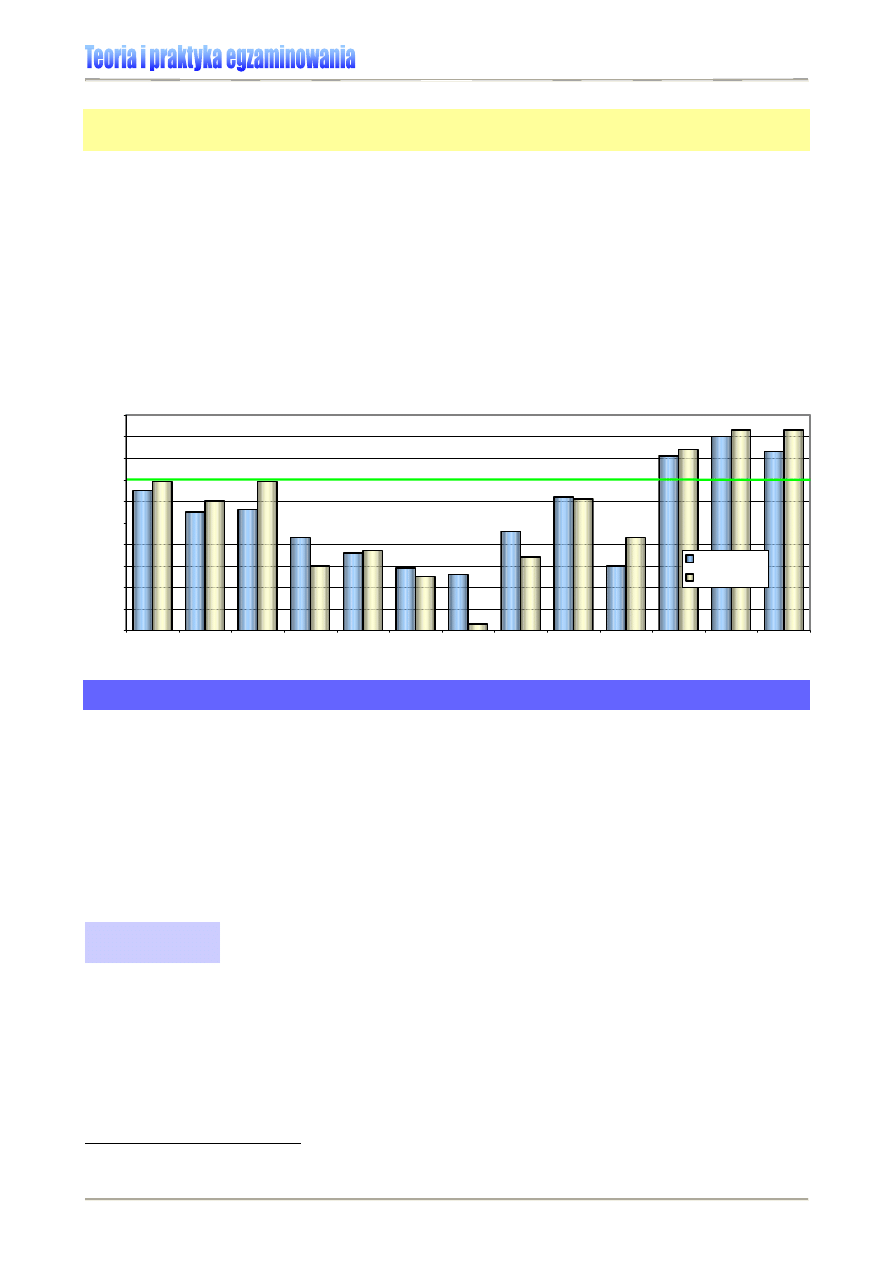
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

22

q = 1 - p

równywać surowych (punktowych lub procentowych) wyników z kolejnych lat, w zamian
posługując się skalą znormalizowaną.
Wskaźnik łatwości jest użyteczny również w różnorodnych analizach porównawczych pro-
wadzonych w ramach wewnątrzszkolnych badań osiągnięć edukacyjnych uczniów.

Przykład:

Analizując zestawienie wyników wewnątrzszkolnych badań osiągnięć edukacyjnych

uczniów klasy VIa Szkoły Podstawowej w C. – Wykres 8.), łatwo możemy wskazać zadania, które
sprawiły uczniom szczególne kłopoty (np. zad. 4-8, 10), i te, które pokazały, że czynności nimi ba-
dane opanowane zostały w stopniu zadowalającym (zad. 11-13). Jakie to czynności – wskaże kar-
toteka, czyli zestawienie czynności sprawdzanych testem. Bez sięgnięcia do niej, nauczyciel nie
jest w stanie ocenić efektywności swej pracy z uczniem.

Wykres 8. Fragment wewnątrzszkolnej analizy wyników badań osiągnięć edukacyjnych uczniów klasy VIa na
tle wyników Szkoły Podstawowej w C. [6]

Trudność zadania / testu

W analizach wyników testu złożonego z zadań punktowanych 0-1, wartości liczbowe
wskaźnika łatwości zadania wykorzystuje się do obliczania wskaźnika trudności tegoż za-
dania. Dostarcza on jakościowej informacji o stopniu trudności zadania testowego, bo im
niższy jest wskaźnik łatwości zadania, tym jest ono trudniejsze (tzn. rozwiązuje go mniej
uczniów). Inaczej mówiąc, parametr trudność zadania jest odwrotnością łatwości, bo
wskazuje, jaki odsetek uczniów nie rozwiązał danego zadania. Test, w którym dominują
zadania o takich wartościach, prowadzi do skośności dodatniej rozkładu wyników testo-
wych.

Trudność zadania punktowanego 0-1 jest to stosunek liczby uczniów,
którzy nie rozwiązali prawidłowo tego zadania, do liczby uczniów
biorących udział w testowaniu

18F18F18F18F

19

.

Przykład:

Trudność zadania, które ma współczynnik łatwości 0,73, wynosi 0,27, bo 1 – 0,73=0,27.

Jest to wskaźnik rzadziej stosowany w analizach wyników testowania niż łatwość zadania,
stąd jego mniejsza popularność w szkolnych analizach statystycznych.

19

B. Niemierko, Pomiar wyników ..., op. cit., s. 153.

Stopień opanowania czynności badanych testem przez uczniów klasy VI a

0,65

0,55

0,56

0,43

0,36

0,29

0,26

0,46

0,62

0,30

0,81

0,90

0,83

0,69

0,60

0,69

0,30

0,37

0,25

0,03

0,34

0,61

0,43

0,84

0,93

0,93

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1

1

2

3

4

5

6

7

8

9

10

11

12

13

numer zadania

łatwo

ść

zadania

wynik szkoły
wynik klasy

gdzie: p – łatwość zadania/testu, q – trudność zadania/testu.

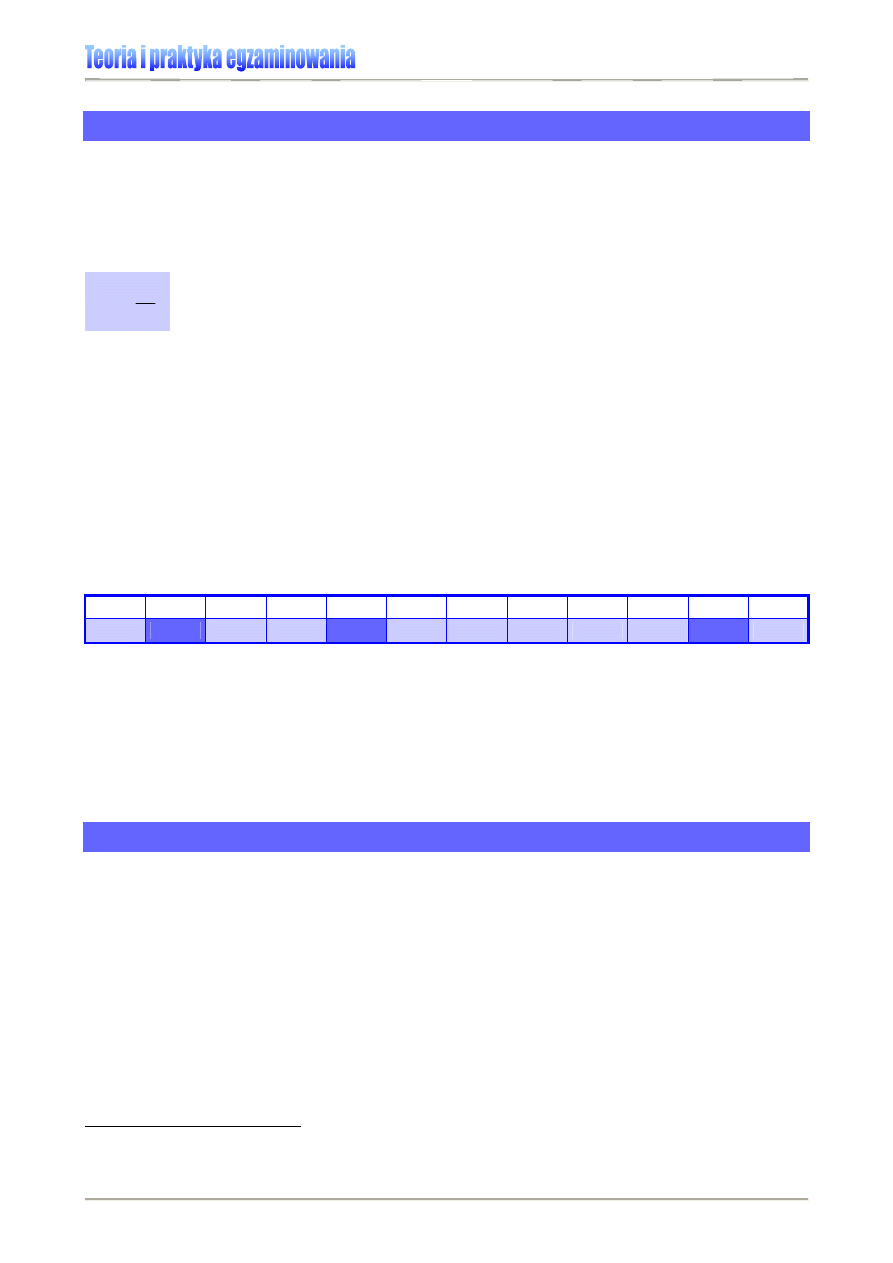
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

23

n

n

f

o

o

=

Frakcja opuszczeń

W analizie poprawności dydaktycznej i stosowności zadań testowych uwzględnia się rów-
nież zadania, które uczniowie pominęli, czyli pozostawili bez odpowiedzi z powodu braku
czasu, utraty motywacji lub zbyt wysokiej trudności zadania.

Frakcja opuszczeń zadania wyrażona jest stosunkiem liczby uczniów, którzy opuścili za-
danie, do liczby egzaminowanych uczniów.

Frakcja opuszczeń zadania nie powinna przekraczać 0,15. Jeżeli jest większa, zadanie
może nie być poprawne dydaktycznie (merytorycznie, redakcyjnie lub pod względem trud-
ności)

19F19F19F19F

20

, należy mu się ponownie przyjrzeć przed następnym zastosowaniem, zwracając

uwagę również na jego kategorię taksonomiczną (np. zadania sprawdzające czynności z
kategorii A, badającej zapamiętywanie wiadomości, mogą być opuszczane częściej, po-
nieważ uczniowie nie zapamiętali szczegółowych informacji) oraz na ich miejsce w teście
(zadania opuszczane w końcowej części mogą świadczyć o braku czasu na ich rozwiąza-
nie). Frakcja opuszczeń to informacja ważna przede wszystkim dla konstruktorów testów
(także nauczycielskich).

Przykład:

Do potrzeb analizy wyników testowania sporządzono zbiorczą tabelę (Tabela 11.).

Tabela 11. Fragment analizy zbiorczej wyników testowania [6]

Nr

1 2 3 4 5 ... .... 17 18 19

20

f

0

0,19

0,05

0,05

0,17

0,00

...

...

0,02

0,11

0,18

0,03

Z prezentowanego zestawienia wynika, że frakcja opuszczeń zadań nr 1, 4, 19 przyjęła wartość
powyżej 0,15. Zatem zadania 1 i 4 wymagają pogłębionych analiz konstrukcyjnych, ponieważ są to
zadania umieszczone na początku testu, w związku z tym powód ich opuszczenia jest inny niż
brak czasu na rozwiązanie zadania przez ucznia. Również zadanie 19. należy poddać dodatko-
wym analizom jakościowym, ponieważ to nie jego umieszczenie pod koniec testu spowodowało
brak rozwiązania. Uczniowie podejmowali próbę zmierzenia się z ostatnim zadaniem (frakcja
opuszczeń 0,03), a więc można przypuszczać, że na pracę mieli wystarczająco dużo czasu.

Moc różnicująca zadania

Moc różnicująca zadania jest informacją o związku wyniku tego zadania z wynikami in-
nych zadań danego testu. Jest mierzona korelacją wyników zadania z wynikami testu, któ-
rego jest częścią. Miara ta posiada zdolność do odróżniania uczniów o wyższych i niż-
szych osiągnięciach. Przyjmuje wartość od -1 do +1

20F20F20F20F

21

. Jest wskaźnikiem wykorzystywa-

nym w procesie konstruowania testu po pierwszym zastosowaniu narzędzia (po testowa-
niu próbnym lub na etapie standaryzacji). Informuje o zdolności zadania do rozróżniania
uczniów na podstawie ich osiągnięć, czyli odpowiada na pytanie, jak zadanie rozróżnia
egzaminowanych uczniów. Im wyższy wskaźnik mocy różnicującej, tym zadanie jest kon-
strukcyjnie lepsze. Zadanie o wysokiej mocy różnicującej rozwiązują uczniowie lepsi, na-
tomiast słabsi nie. Natomiast ujemny wskaźnik oznacza, że zadanie jest prawdopodobnie
niepoprawnie skonstruowane i wymaga pogłębionej analizy jakościowej.

20

Ibidem, s. 152.

21

Ibidem, s.154-155.

gdzie:
f

o

– frakcja opuszczeń, n

o

– liczba opuszczeń, n – liczba uczniów.

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

24

Moc różnicująca zadania punktowanego 0-1 obliczana jest według wzoru:

W praktyce często stosowany jest prostszy, ale mniej doskonały wskaźnik zastępczy mocy
różnicującej zadania punktowanego 0-1, oznaczany D

50

i

obliczany według wzoru:

Przykład:

Aby obliczyć wskaźnik mocy różnicującej D

50

, należy uszeregować wyniki od najwyż-

szego do najniższego. Otrzymany zbiór dzielimy na połowy i obliczamy wskaźnik łatwości dla wyż-
szej (lepszej) i dla niższej (słabszej) połówki rozwiązań, a następnie znajdujemy różnicę.

Załóżmy, że współczynnik łatwości dla uczniów w „lepszej” połowie (tych, którzy uzyskali lepszy
wynik w teście) rozwiązujących dane zadanie wyniósł 0,75, a dla radzących sobie słabiej – 0,31.
Moc różnicująca zadania wyrażona wskaźnikiem D

50

wyniesie więc 0,44. Jeżeli test składał się z co

najmniej 25 zadań, to przykładowe zadanie dobrze różnicuje osiągnięcia uczniów. Gdyby wartość
wskaźnika mocy różnicującej wyniosła 0, znaczyłoby to, iż liczba poprawnych odpowiedzi w obu
grupach uczniów jest jednakowa.

Interpretacja wskaźnika mocy różnicującej jest skomplikowana

21F21F21F21F

22

. Najczęściej rozważane

są trzy zależności wyznaczające wartość tego wskaźnika:

1. zależność od łatwości zadania (np. zadania najtrudniejsze i najłatwiejsze nie różni-

cują osiągnięć uczniów),

2. zależność od rodzaju kryterium,
3. zależność od długości danego testu.

Przybliżone progi zadowalających wartości wskaźnika mocy różnicującej przedstawia Ta-
bela 12.

Tabela 12. Interpretacja wskaźnika mocy różnicująca zdań w testach o różnej długości

22F22F22F22F

23

Liczba zadań w teście

Minimalna moc różnicująca zadań

Zadowalająca moc różnicująca zadań

100 0,10

0,22

25 0,20

0,42

10 0,32

0,60

5 0,45

0,75

22

Więcej na ten temat można przeczytać w: Pomiar wyników..., s. 156-158.

23

Za: B. Niemierko, ibidem, s. 158.

q

p

s

x

x

r

t

p

pb

−

=

D

50

= p

L

-p

S

gdzie:
r

pb

– wskaźnik mocy różnicującej, tzw. punktowo-dwuseryjny, korelacyjny

x

p

– średnia arytmetyczna wyników uczniów, którzy wykonali zadanie

x

– średnia arytmetyczna wyników testu

s

t

– odchylenie standardowe wyników egzaminowania

p – łatwość zadania
q – trudność zadania

gdzie:
D

50

– wskaźnik mocy różnicującej, tzw. połówkowy

p

L

– łatwość zadania w lepszej połowie wyników egzaminu

p

S

– łatwość zadania w słabszej połowie wyników egzaminu

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

25

Rzetelność pomiaru

Rzetelność jest miarą dokładności pomiaru dokonywanego za pomocą testu. Najogólniej
rozumiana jest jako powtarzalność (stałość) wyników pomiaru w określonych warunkach.
Oznacza to, że uczniowie badani ponownie po jakimś czasie w porównywalnych warun-
kach tym samym testem uzyskują podobne wyniki

23F23F23F23F

24

.

Jednym ze sposobów szacowania rzetelności jest obliczenie alfy Cronbacha wg wzoru:

W przypadku wewnętrznej zgodności testu k jest liczbą zadań w teście,

2

i

α

wariancją wy-

ników i-tego zadania, zaś

2

x

α

wariancją wyników testowania.

W przypadku zadań punktowanych 0-1, rzetelność szacuje się z wykorzystaniem wzoru
KR20 (Kudera i Richardson nr 20):

Współczynnik rzetelności może przybierać wartości w przedziale 0-1. Wartość 0 oznacza,
że cała zmienność wyników pochodzi z błędów pomiaru, zatem różnice między osiągnię-
ciami uczniów są wyłącznie losowe, a test niewiele mierzy. Natomiast wartość 1 oznacza,
że wyniki testowania są wolne od błędów pomiaru

24F24F24F24F

25

. Ponieważ nie ma idealnego testu,

należy wiedzieć, jak duży popełniamy błąd, stosując konkretne narzędzie badawcze i
określić granice interpretacji otrzymanego wyniku testowego. Innymi słowy, rzetelność
pomiaru jest to wielkość błędu, jaki możemy popełnić, interpretując wyniki danego testu

25F25F25F25F

26

.

Efekt standardowy

26F26F26F26F

27

Do zmierzenia wpływu określonego czynnika na wynik całej badanej populacji wykorzystu-
je się wskaźnik zwany efektem standardowym, który obliczany jest według wzoru:

24

Ibidem, s.192.

25

Ibidem, s.196.

26

Więcej na ten temat można przeczytać w: B. Niemierko, Pomiar wyników..., s. 192-219.

27

Przykłady w: Ewa Stożek, O czym mówi efekt standardowy?, [w:] Holistyczne i analityczne metody dia-

gnostyki edukacyjnej, Perspektywy informatyczne egzaminów szkolnych, red. B. Niemierko, G. Szyling, Fun-
dacja Rozwoju UG, Gdańsk 2005, s.520-525; także: www.ptde.org.pl

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

−

=

∑

2

2

1

1

x

i

k

k

α

α

α

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

−

=

∑

2

1

1

x

i

i

tt

q

p

m

m

r

α

s

x

x

d

2

1

−

=

gdzie:
α – współczynnik rzetelności (alfa Cronbacha)
k – liczba pomiarów cząstkowych składających się na zmienną x

∑

2

i

α

– suma wariancji wyników k pomiarów cząstkowych

2

x

α

– wariancja zmiennej x

gdzie:
r

tt

– współczynnik rzetelności KR20

m – liczba zadań w teście (długość testu)
p

i

– łatwość i-tego zadania

2

x

α

– wariancja wyników testowania

q

i

– trudność i-tego zadania

gdzie:
d – efekt standardowy

1

x

– średnia grupy pierwszej (eksperymentalnej, którą będziemy porównywać)

2

x

– średnia grupy drugiej (kontrolnej, bazowej, do której będziemy porównywać)

s – odchylenie standardowe

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

26

Odchylenie obliczane jest wg wzoru:

Efekt standardowy pozwala m. in. na porównywanie uzyskanej przewagi bez względu na
właściwości skali i rozkładu wyników.
Pozwala na porównywanie wyników różnych grup (np. równoległych oddziałów klasowych)
pod względem określonej cechy, umiejętności. Proponuje się następującą skalę siły efek-
tu:

Tabela 13. Skala siły efektu według Cohena

27F27F27F27F

28

d = 0,2

d = 0,5

d = 0,8

mały efekt (wpływ)

średni efekt (wpływ) duży efekt (wpływ)

Efekt standardowy jest corocznie wykorzystywany w prezentacji wyników sprawdzianu. Z
jego pomocą analizowany jest między innymi wpływ na wynik egzaminu płci czy też wiel-
kości miejscowości.

Dla przykładu,

fragment sprawozdania ze sprawdzianu 2007, dotyczący wpływu płci na wynik

egzaminu: „Analiza efektu standardowego płci w latach 2002-2007 wykazuje, że do roku 2004
przewaga dziewcząt rosła, w kolejnych dwóch latach nieznacznie zmalała, a w bieżącym roku po-
nownie wzrosła.”

28F28F28F28F

29

.

Wykres 9. Efekt standardowy na sprawdzianie 2002-2007 [3]

Wynik standardowy

Wynik standardowy jest wskaźnikiem zbliżonym do efektu standardowego. Pozwala na
umieszczenie wyniku pojedynczego ucznia na skali, niezależnie od wielkości średniej i
odchylenia standardowego. Jest informacją o tym, w jakiej odległości od średniej mierzo-
nej w odchyleniach standardowych znajduje się wynik ucznia. Wyniki standardowe mają
średnią 0 i odchylenie standardowe 1. O ile efekt standardowy służy do porównywania
grup, wynik standardowy umożliwia porównywanie wyników ucznia w obrębie badanej
grupy.

29F29F29F29F

30

Wyniki standardowe stosuje się w celu porównania wyników uzyskanych przy

użyciu różnych narzędzi pomiaru, np. wyniku ucznia uzyskanego w części humanistycznej

28

Za: E. Stożek, ibidem.

29

Osiągnięcia uczniów kończących szkołę podstawową w roku 2007. Sprawozdanie ze sprawdzianu 2007,

Centralna Komisja Egzaminacyjna, Warszawa, maj 2007, s. 15.

30

E. Stożek, op.cit., s. 523-524.

2

)

1

(

)

1

(

2

1

2

2

2

2

1

1

−

+

−

+

−

=

=

N

N

s

N

s

N

s

s

pooled

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

27

i matematyczno-przyrodniczej egzaminu gimnazjalnego. Wynik standardowy jest obliczany
według wzoru

30F30F30F30F

31

:

s

x

x

z

−

=

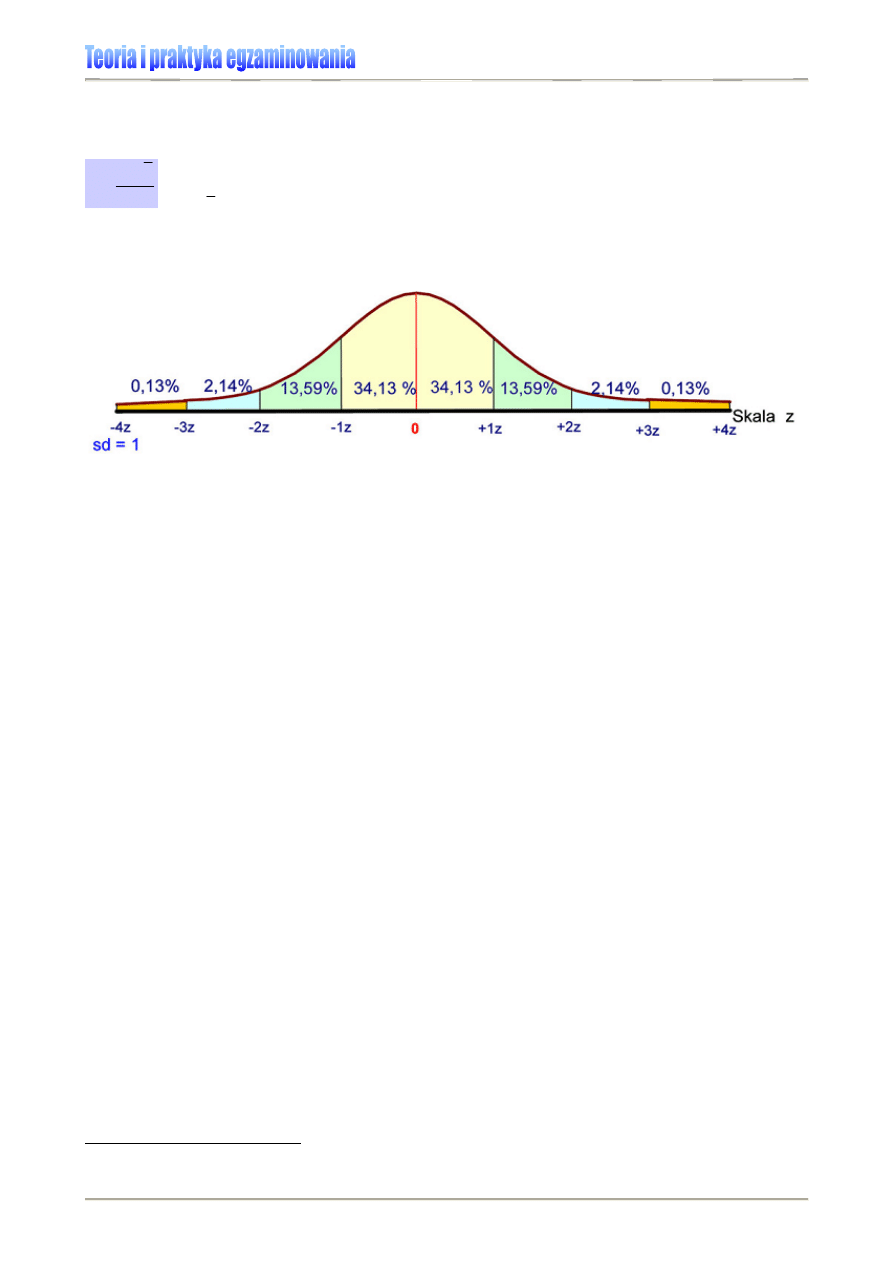
Rysunek 10. Rozkład normalny wyników standardowych

31

G.A. Ferguson, Y. Takane, op. cit., s.92-93.

gdzie:
x – wynik pojedynczego ucznia

x

– średni wynik z testu

s – odchylenie standardowe w teście

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

28

SKALE ZNORMALIZOWANE

Skale znormalizowane są stosowane w statystycznych analizach danych uzyskiwanych w
badaniach, które obejmują duże próby. W związku z tym nie normalizuje się wyników
egzaminów zewnętrznych ani na poziomie szkoły, ani tym bardziej na poziomie kla-
sy szkolnej, wykorzystuje się je natomiast w analizach np. na poziomie kraju.

Pojęcie normy

W powszechnym rozumieniu termin norma oznacza ustaloną, przyjętą zasadę, wzór, regu-
łę, kanon lub ilość, miarę, granicę przewidzianą jako wymaganą lub obowiązującą w ja-
kimś zakresie. Z pojęciem tym nierozerwalnie łączą się takie właściwości, jak powszech-
ność, masowość, częstość występowania określonej cechy lub zachowania w badanej
populacji (por. Hornowska, 2003). Natomiast z punktu widzenia statystyki normą jest to, co
opisywane jest jako zachowanie większości, czy też jako zachowanie średnie lub przecięt-
ne. Inaczej mówiąc, normą jest typowy wynik w teście otrzymany przez określoną grupę
badanych osób. Dzięki niemu można ustalić np. rzeczywistą wartość surowego wyniku
testowego, uzyskanego przez ucznia w stosunku do wyników otrzymanych przez pozosta-
łe badane osoby, bowiem norma nie oznacza, że test został dobrze rozwiązany, ale opisu-
je poziom typowego wykonania tegoż testu.

Przystąpiwszy do egzaminów zewnętrznych, uczeń otrzymuje wynik punktowy (spraw-
dzian i egzamin gimnazjalny) lub procentowy (matura). Jest to tzw. wynik surowy, które-
go bez określonego punktu odniesienia nie można interpretować, zatem oceniać, czy to
wynik wysoki, czy też niski. Dopiero przeniesienie wyników surowych na wspólną skalę
pozwoli na ustalenie norm, dokonywanie porównań i nadanie wynikom znaczenia treścio-
wego, tj. określenie, jaka jest np. pozycja wyniku pojedynczego ucznia (szkoły) względem
wyników innych zdających (szkół).

W badaniach używa się różnych sposobów przedstawiania norm. Punktem wyjścia w ich
ustalaniu jest rozkład normalny wyników, tzw. krzywa Gaussa-Laplace’a. Do najczęściej
spotykanych należą normy standardowe, rangowe lub równoważnikowe

31F31F31F31F

32

.

Dla przykładu: w Polsce do interpretacji wyników egzaminów zewnętrznych stosuje się
standardową skalę staninową, zaś skala centylowa służy do analizy wskaźnika eduka-
cyjnej wartości dodanej (EWD). Natomiast do interpretacji wyników uzyskanych w Pro-
gramie Międzynarodowej Oceny Umiejętności Uczniów OECD (PISA) wykorzystuje się
skalę równoważnikową CEEB. Trwają prace nad zastosowaniem tej skali w komuniko-
waniu wyników matury 2008.

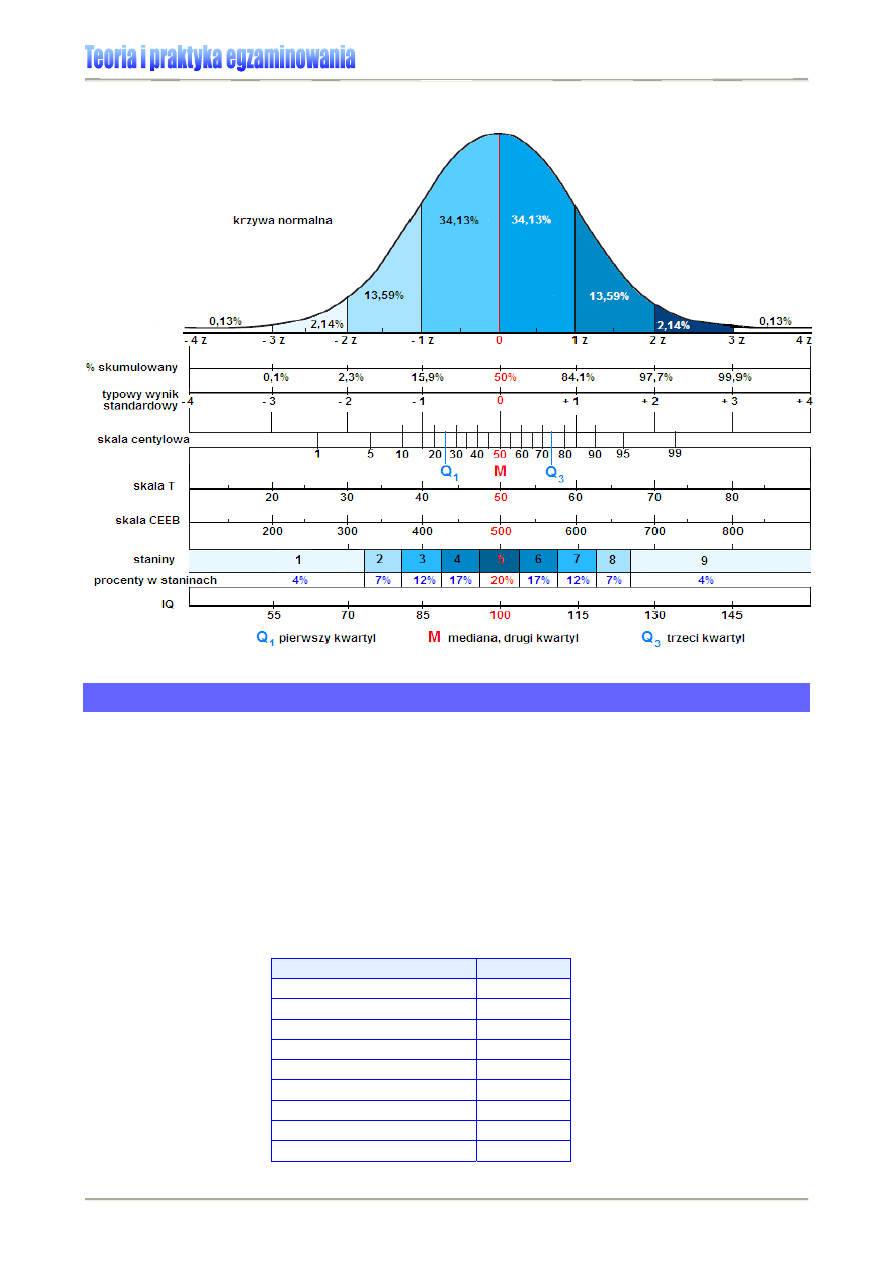
Rysunek 11. przedstawia wybrane skale wykorzystywane w badaniach psychologicznych
i pedagogicznych.

32

Elżbieta Hornowska, op. cit., s.134

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

29

Rysunek 11. Wybrane normy typu standardowego

Normalizacja wyników testowania

Rozkład normalny, stanowiący podstawę do tworzenia skal znormalizowanych, uzyskuje
się przez dopasowanie krzywej do wyników testowania ujętych w przedziały, graficznie
przedstawione za pomocą histogramu. Zatem wynik w skali standardowej jest przekształ-
ceniem (przy użyciu odpowiedniej funkcji) wyniku surowego w zmienną, której kształt roz-
kładu z góry ustalamy. Należy pamiętać, że rozkład normalny jest rozkładem idealnym,
teoretycznym.
„Przepis” na wyznaczenie rozkładu normalnego:
1. Uporządkuj wartości zmiennej (rosnąco) – oblicz częstości wartości zmiennej przypa-
dające na każdą z kategorii:

Tabela 14.

Wartości zmiennej

Częstość

0 2
1 3
2 2

11 13
28 15
32 2
39 10
40 2
45 5

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

30

2. Umieść wyniki w przedziałach (podziel wartości zmiennej na przedziały, pamiętając, że
liczba przedziałów nie powinna być mniejsza od 5 i większa od 20).

Wartości zmiennej

Częstość

0 - 10

7

10 - 20

13

20 - 30

15

30 - 40

12

Tabela 15.

40 - 50

7

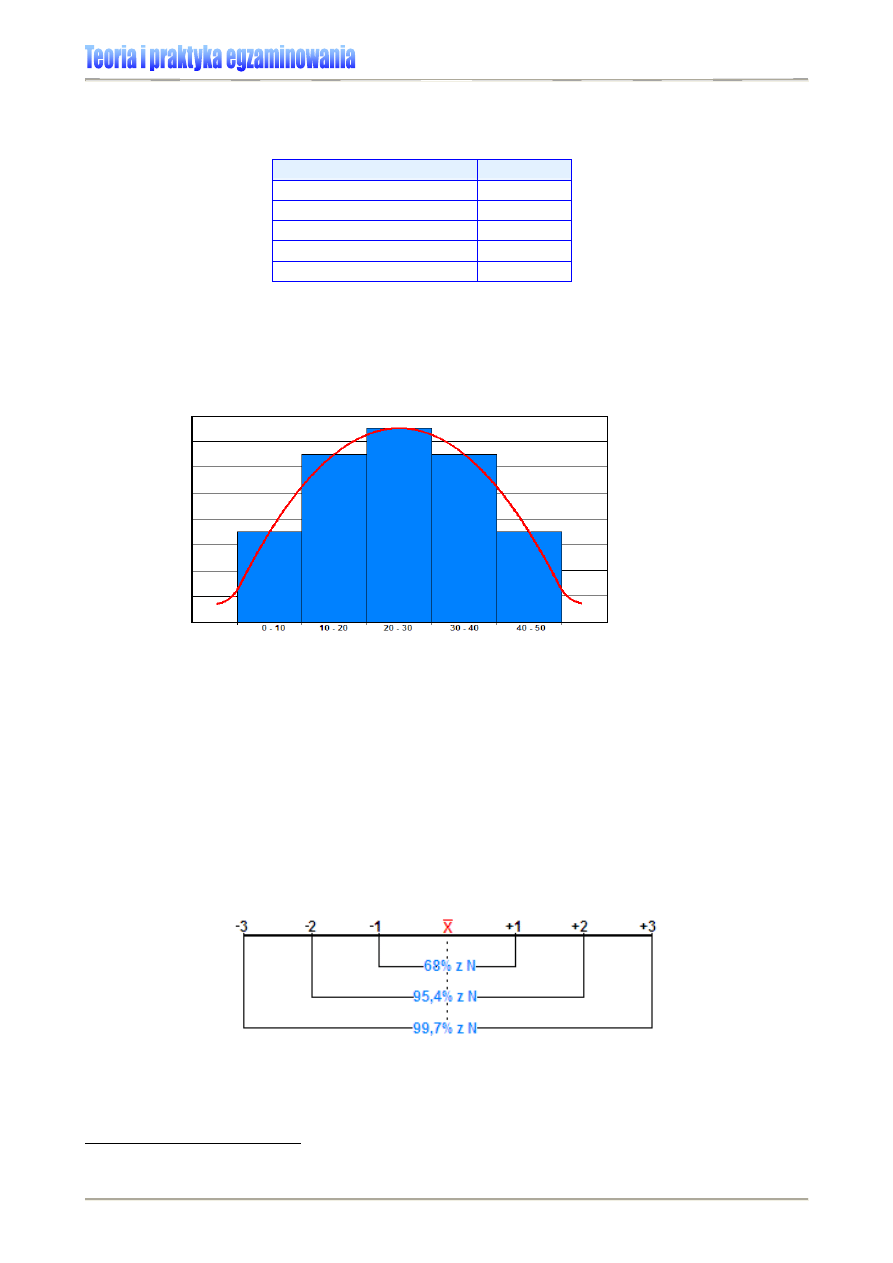
3. Na tej podstawie narysuj histogram, który przedstawia rozkład zmiennej.
Przedziały, które wcześniej zostały ustalone, zaznacza się na osi współrzędnych. Często-
ści wyznaczają wysokość (w obrębie określonego przedziału – oś y). Na osi x zaznaczone
są wyniki.

Rysunek 12. Histogram

Histogram umożliwia poznanie typu rozkładu zbiorowości statystycznych wg badanej ce-
chy

.

4. Przez środek przedziałów wyznaczonych w punkcie 2. przeprowadź krzywą, która nigdy
nie łączy się z zerem, ale dąży do nieskończoności.
5. Wyznaczona krzywa to krzywa normalna. Obszar pod krzywą posiada określone wła-
ściwości: od +1 do -1 odchylenia standardowego rozciąga się obszar wyników typowych
obejmujących ok. 68% wszystkich przypadków; od +2 do -2 odchyleń standardowych za-
wiera się ok. 95% wszystkich wyników, od +3 do -3 odchyleń zawiera się ok. 99% wszyst-
kich przypadków. Innymi słowy, w przypadku rozkładu normalnego procent wartości wyni-
ków między obliczonymi współczynnikami odchylenia standardowego jest stały

32F32F32F32F

33

.

Rysunek 13. Procent wartości wyników między współczynnikami odchylenia standardowego w rozkładzie
normalnym.

33

W.P. Zaczyński, Statystyka w pracy badawczej nauczyciela, Warszawa 1997, s. 19.

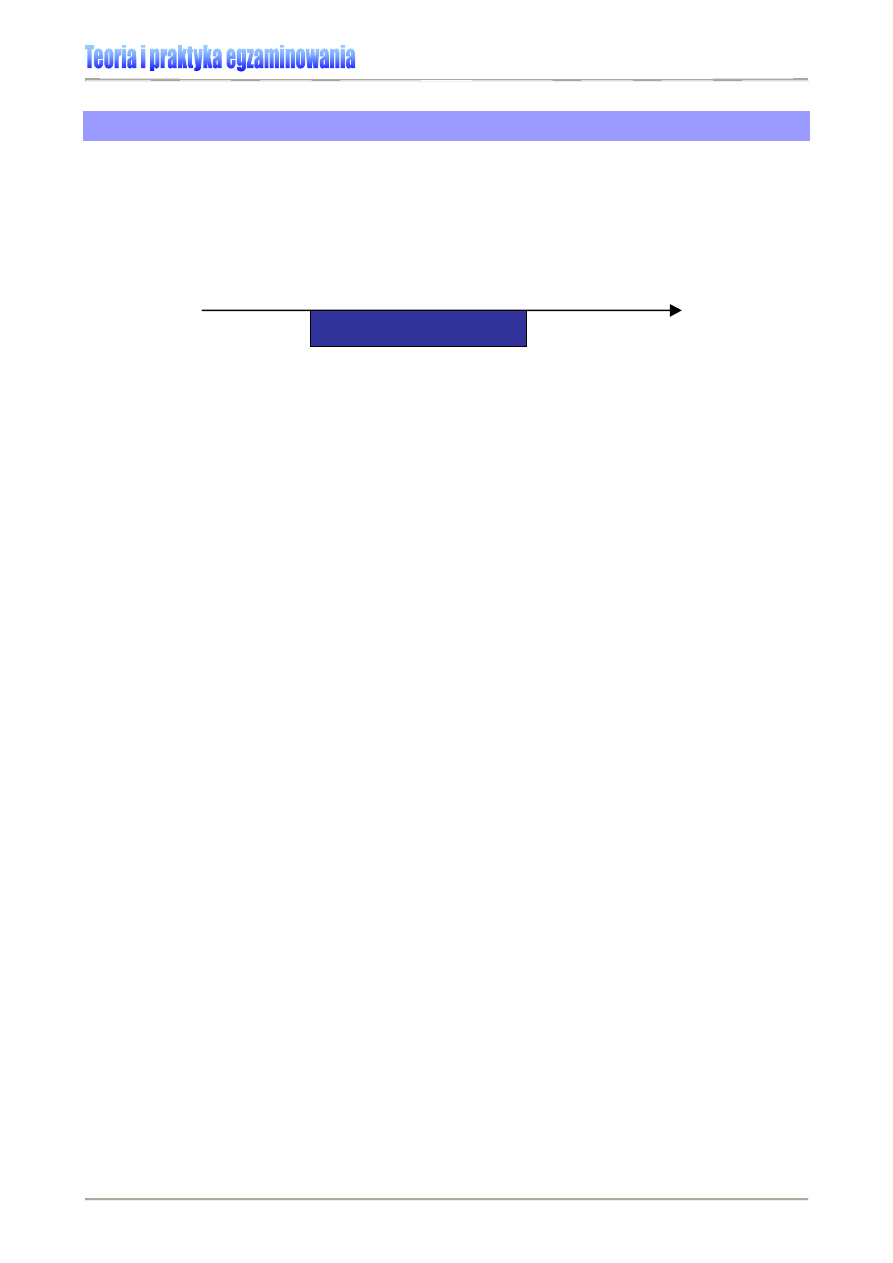
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

31

Obszar wyników typowych

Obszar wyników typowych (OWT) przy rozkładzie normalnym obejmuje 2/3 wszystkich
wyników (ok. 68%). Jego granice stanowią wartości, które obliczamy z jednej strony
odejmując od średniej arytmetycznej wartość odchylenia standardowego, z drugiej –
dodając te dwa współczynniki do siebie.

Rysunek 14. Wyznaczanie obszaru wyników typowych

Przykład:

Obszar wyników typowych sprawdzianu 2006 (patrz: Wykres 1.) mieści się w przedziale

od 16,7 do 33,9 punktów. Wyznaczyliśmy go, odejmując i dodając od/do średniej (25,3 pkt.)
wartość odchylenia standardowego (8,6 pkt.). [25,3 – 8,6 = 16,7; 25,3 + 8,6 = 33,9]

Ponieważ wyniki egzaminu są wyrażane liczbą całkowitą, po zaokrągleniu wyników, rezultaty
typowe dla uczniów piszących sprawdzian 2006 zawrą się w przedziale <17; 34>.

_

x - s

x

_

x

_

x + s

x

OWT

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

32

Definicje wybranych skal znormalizowanych

Skala staninowa

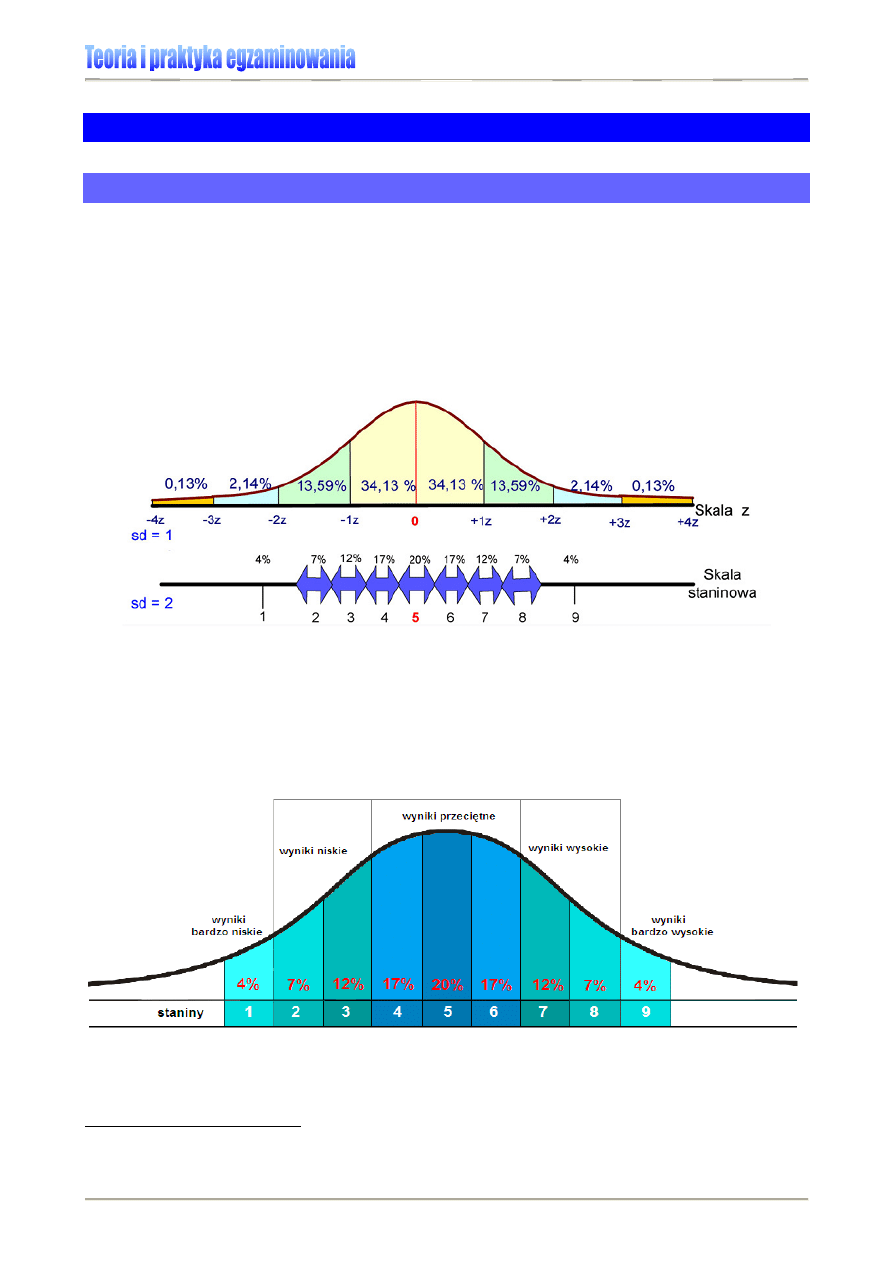
Skala staninowa (od ang. standard nine), zwana także standardową dziewiątką, jest ska-
lą dziewięciostopniową, zaproponowaną w 1942 r. przez Guilforda. Średnia arytmetycz-
na staninów wynosi 5, a odchylenie standardowe 2 (dokładnie 1,96). Staniny wewnętrzne,
od drugiego do ósmego, mają jednakową długość, wynoszącą połowę odchylenia stan-
dardowego, i rozciągają się od -1,75 do +1,75 odchylenia standardowego wyników
w rozkładzie normalnym. Staniny zewnętrzne, pierwszy i dziewiąty, nie mogą być unor-
mowane co do długości, bo muszą zawierać minimalny i maksymalny wynik na tej skali.

33F33F33F33F

34

Rysunek 15. Skala staninowa

Skalę staninową wyników budujemy poprzez uporządkowanie wyników surowych od wyni-
ku najniższego do najwyższego i podzielenie ich na 9 przedziałów, które kolejno zawiera-
ją: 4% wyników najniższych, 7% wyników bardzo niskich, 12% wyników niskich, 17% wy-
ników niżej średnich, 20% wyników średnich oraz analogicznie w górę 17% wyników wyżej
średnich, 12% wyników wysokich, 7% wyników bardzo wysokich i 4% wyników najwyż-
szych.

Rysunek 16. Rozkład normalny a skala staninowa wyników egzaminu

34F34F34F34F

35

Następnie dla kolejnych staninów wyznacza się przedziały punktowe. Polega to na ustale-
niu liczby punktów uzyskanych przez uczniów zdających egzamin w danym roku, którzy
uzyskali wynik mieszczący się w danym przedziale.

34

B. Niemierko, Pomiar wyników ..., op. cit., s. 271-272.

35

E. Hornowska, op. cit., s.137.

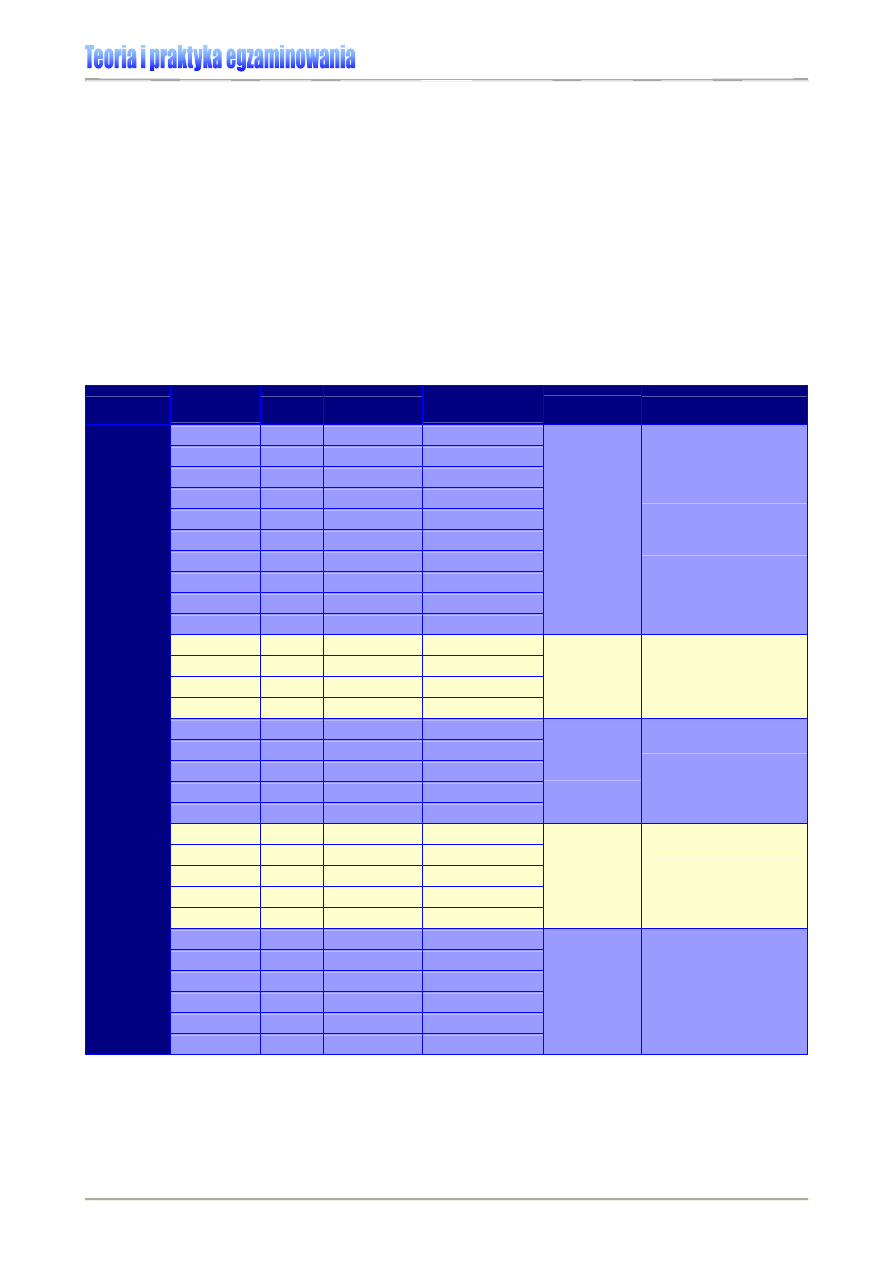
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

33

Przykład:

Dla stanina 1. będzie to przedział zawierający wyniki punktowe 4% uczniów, którzy uzy-

skali najniższe wyniki na teście. Analizując wyniki zdających (patrz: Tabela 15.), stwierdzimy, iż do
czteroprocentowej grupy uczniów, którzy na sprawdzianie 2006 wypadli najsłabiej, zaliczają się ci,
którzy za rozwiązanie testu uzyskali od 0 do 9 punktów; są to 23 osoby, które mają wynik zerowy,
68 uczniów, którzy zdobyli jeden punkt, 210 uczniów, którzy uzyskali dwa punkty, 470 – trzy, itd.,
aż do wyniku 4829 uczniów, którzy zdobyli dziewięć punktów, czyli do zbliżenia się w kolumnie
„Procent skumulowany” do granicy 4% badanej populacji. Granica odcięcia 1. stanina w przypadku
sprawdzianu 2006 przebiegnie na poziomie 3,688% populacji (niedobór 0,312% jest tu niższy niż
w przypadku, gdybyśmy do przedziału punktowego dla stanina 1. zechcieli zaliczyć także wynik 10
punktów, co dałoby nam aż 0,961% powyżej graniczne 4%). Analogicznie postępujemy, wyznacza-
jąc przedziały następnych staninów – drugi na granicy 11% populacji (4% dla pierwszego stanina +
7% dla drugiego), trzeci – 23% (4%+7%+12%), itd.

Tabela 16. Rozkład staninowy wyników sprawdzianu 2006 [1]

Egzamin

Liczba

punktów

Częstość

Procent

Procent

skumulowany

Stanin

Opis skali

0

23

0,0049

0,0049

1

68

0,0146

0,0196

2

210

0,0452

0,0648

3

470

0,1011

0,1659

4

946

0,2035

0,3694

5

1540

0,3313

0,7007

6

2271

0,4886

1,1893

7

2922

0,6286

1,8180

8

3863

0,8311

2,6491

9

4829

1,0389

3,6880

1

wynik

najniższy

4%

10

5917

1,2730

4,9610

11

6954

1,4961

6,4571

12

8114

1,7457

8,2028

13

9232

1,9862

10,1890

2

bardzo niski

7%

14

10531

2,2657

12,4546

15

11540

2,4828

14,9374

16

12700

2,7323

17,6697

17

13626

2,9315

20,6012

18

14715

3,1658

23,7671

3

niski

12 %

19

15486

3,3317

27,0988

20

15866

3,4135

30,5122

21

16429

3,5346

34,0468

22

16872

3,6299

37,6767

23

17010

3,6596

41,3363

4

niżej średni

17 %

24

17126

3,6845

45,0208

25

17098

3,6785

48,6994

26

17301

3,7222

52,4215

27

17087

3,6761

56,0977

28

17436

3,7512

59,8489

Sprawd

zian 2006

29

17321

3,7265

63,5754

5

średni

20 %

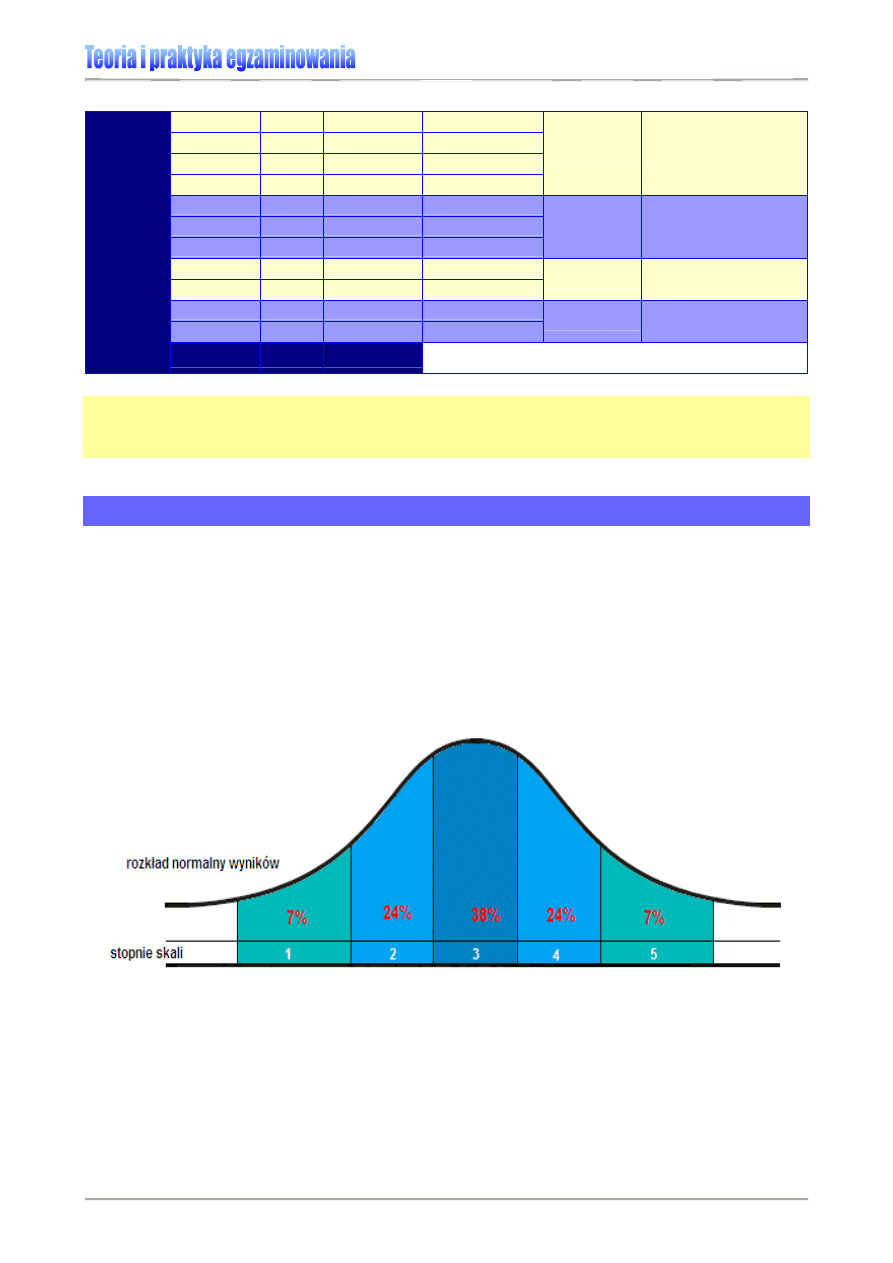
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

34

30

17478

3,7603

67,3357

31

17733

3,8151

71,1508

32

17931

3,8577

75,0086

33

18398

3,9582

78,9668

6

wyżej średni 17%

34

18135

3,9016

82,8684

35

17728

3,8141

86,6824

36

17420

3,7478

90,4302

7

wysoki 12%

37

15775

3,3939

93,8241

38

13510

2,9066

96,7307

8

bardzo wysoki 7%

39

9698

2,0865

98,8171

40

5498

1,1829

100

9

najwyższy 4%

Ogółem 464807

100,00

Uwaga: Wyniki egzaminów normalizowane są corocznie, dlatego – choć przedziały pro-
centowe dla staninów są stałe – to przedziały punktowe w poszczególnych latach różnią
się między sobą tak, jak różnią się wyniki uczniów lub szkół w danym roczniku.

Standardowa „piątka”

Podobnie jak skalę staninową, tworzy się pięciostopniową skalę zwaną „standardową piąt-
ką”. Różnica między skalami polega na tym, że zamiast dziewięciu, tworzy się pięć prze-
działów, które kolejno zawierają: 7%, 24%, 38%, 24%, 7% wyników uporządkowanych od
wyniku najniższego do najwyższego. Poszczególne stopnie skali charakteryzowane są
następująco: niski, niżej średni, średni, wyżej średni, wysoki. Średnia w skali pięcio-
stopniowej wynosi 3, a odchylenie standardowe 1. Za pomocą tej skali prezentowane są
wyniki mniejszych zbiorów.

Rysunek 17. Rozkład wyników w pięciostopniowej skali standardowej

Skalę tę wykorzystywano do prezentacji wyników egzaminów zewnętrznych w powiatach.
Przykładowo – jak na Rysunku 18.

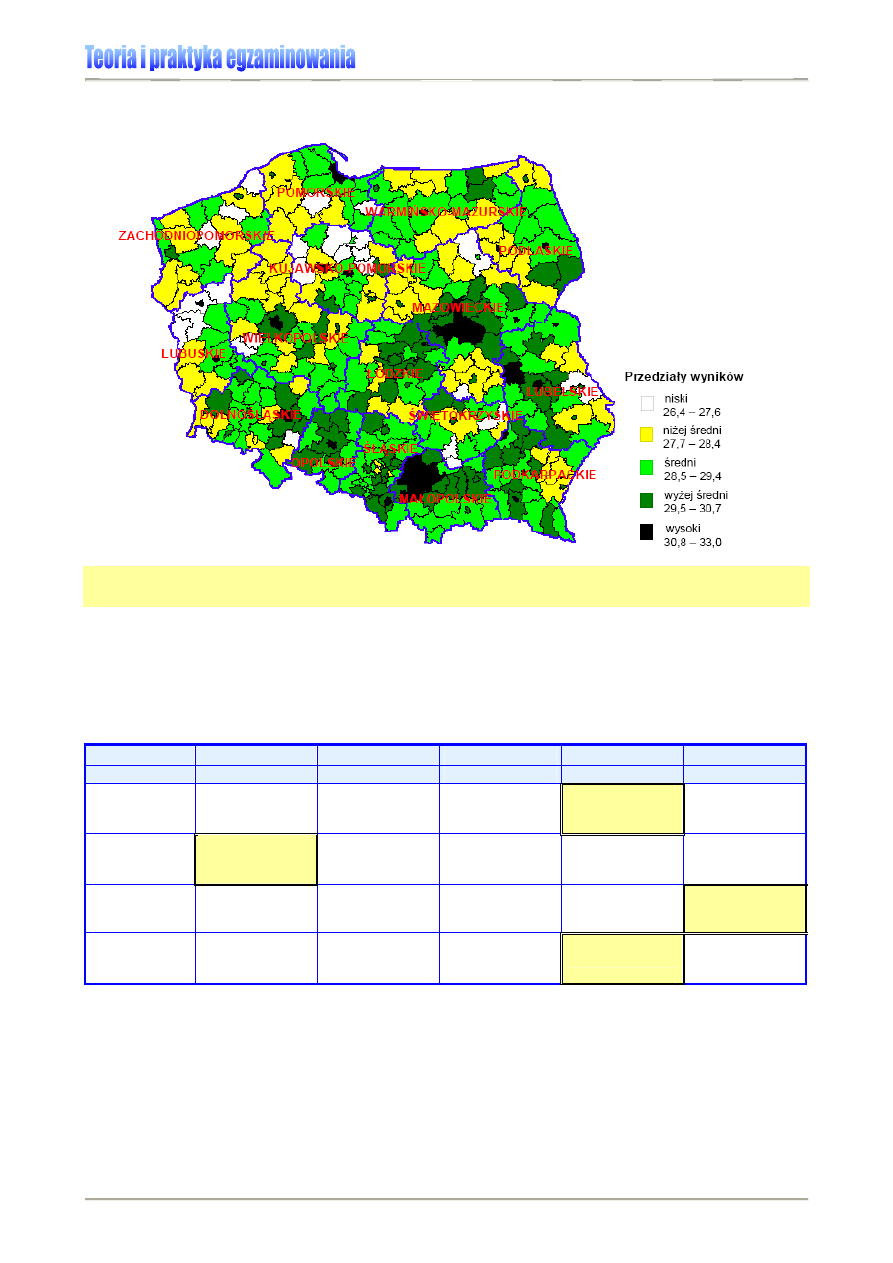
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

35

Rysunek 18. Średnie wyniki sprawdzianu 2005 w powiatach [1]

Uwaga: Należy pamiętać, że przedziały punktowe wyników prezentowane w tej skali,
w kolejnych latach będą się zmieniały, podobnie jak w przypadku skali staninowej.

Przykład:

Tabela 17. pokazuje, że osiągnięcia szkół podstawowych w powiecie X w stosunku do

innych szkół w kraju w kolejnych latach zdecydowanie różniły się, choć szkoły te co roku uzyskiwa-
ły średni wynik 27 punktów.

Tabela 17. Znormalizowane średnie wyniki szkół podstawowych w powiatach w skali pięciostopniowej w
latach 2004-2007 [1] [6]

]

Stopień skali

1

2

3

4

5

Wynik

niski

niżej średni

średni

wyżej średni

wysoki

Przedział

punktowy

2004 r.

21,8-23,5 23,6-24,5 24,6-25,5 25,6-27,0

27,1-29,4

Przedział

punktowy

2005 r.

26,4-27,6

27,7-28,4 28,5-29,4 29,5-30,7 30,8-33,0

Przedział

punktowy

2006 r.

21,6-23,2 23,3-24,2 24,3-25,3 25,4-26,9 27,0-29,6

Przedział

punktowy

2007 r.

23,7-24,7 24,8-25,5 25,6-26,5 26,6-28,0

28,1-30,4

Podobnie jak w przypadku skali staninowej, prezentacja wyników w skali pięciostopniowej
pozwala np. władzom powiatu zorientować się, jakie miejsce zajmują prowadzone przez
nich szkoły pośród wyników krajowych. Dla szkół z terenu danego powiatu oznacza to, że
jeżeli np. ich wynik znajduje się w 3. przedziale, to 31% powiatów w kraju uzyskało wynik
niższy niż te szkoły, 38% wynik porównywalny, a w 31% powiatów wyniki piszących
sprawdzian były wyższe.

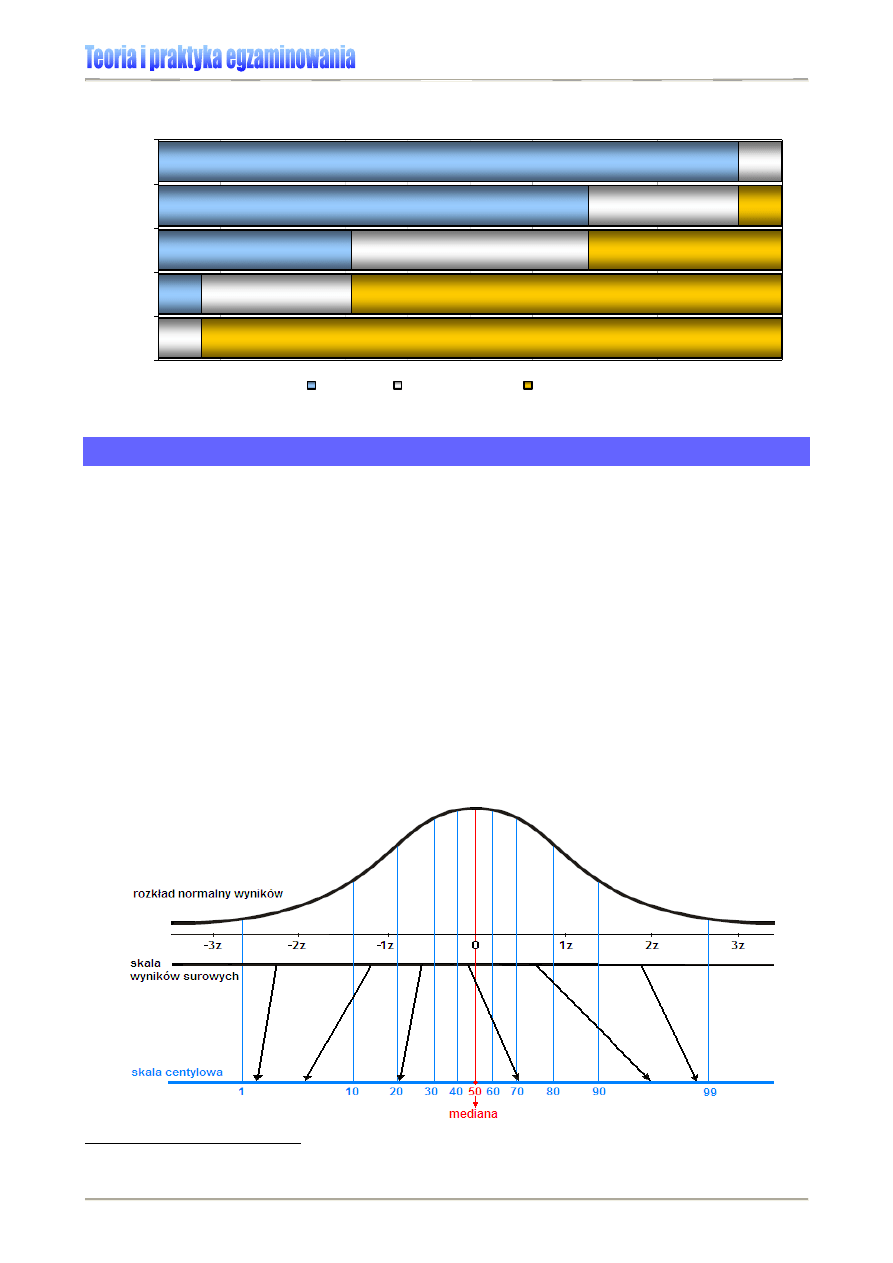
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

36

Wykres 10. Ranga wyniku w stosunku do innych wyników badania w skali „standardowej piątki” [6]

7%

31%

69%

93%

7%

24%

38%

24%

7%

93%

69%

31%

7%

1

2

3

4

5

skala pi

ęciost

opniowa

wynik niższy

wynik porównywalny

wynik wyższy

Skala centylowa

Skala centylowa jest skalą rangową, w której otrzymane wyniki dzielone są na 99 prze-
działów (centyli). W celu ustalenia wartości tych przedziałów, porządkuje się wyniki
wszystkich zdających od wyniku najniższego do najwyższego, a następnie otrzymany
zbiór przelicza na 100 równych części. Potem określa się granice między tymi częściami
na skali wyników i oznacza je jako centyle. Każdy centyl obejmuje około 1% wyników.
Ponieważ skala centylowa rozpoczyna się od 0, w całości składa się ona ze 101 jedno-
stek. Środek skali, a więc jego medianę, wyznacza centyl 50. Oznacza to, że powyżej 50
centyla znajdują się wyniki odnoszące się do większego niż przeciętny poziomu wykona-
nia testu, a poniżej do słabszego. Zatem centyl to punkt na skali, poniżej którego leży
określony odsetek rozkładu.

Mimo że centyl definiowany jest jako odsetek, nie jest tym samym co wynik procentowy,
mówi nam bowiem o odsetku osób, które znajdują się poniżej określonego centylem punk-
tu na skali

35F35F35F35F

36

, a nie o poprawności wykonania zadań w teście.

Rysunek 19. Związek między centylami a rozkładem normalnym

36

Elżbieta Hornowska, op. cit., s.146-147.

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

37

Numer kolejny najbliższego centyla stanowi rangę centylową danego wyniku, czyli okre-
śla procent uczniów o wyniku niższym niż dany wynik. Rangi centylowe są miarami pozy-
cyjnymi osiągnięć uczniów. Wskazują miejsce uczniów w grupie uczniów uporządkowanej
według wyników testowania. Należy pamiętać o tym, że pozycja wyniku nie oznacza speł-
nienia wymagań programowych. Często występującym błędem jest mylenie rang centylo-
wych z procentem rozwiązanych zadań

36F36F36F36F

37

.

Skala akademicka (CEEB)

Skala CEEB (College Entrance Examination Board), tzw. skala akademicka, stosowana
jest w amerykańskim Teście Uzdolnień Akademickich (American College Test) oraz w
programie OECD/PISA.

Podobnie jak inne prezentowane tu skale, oparta jest na modelu rozkładu normalnego –
przy średnim wyniku 500 pkt., ok. 2/3 uczniów ma wynik mieszczący się w przedziale 400-
600 punktów. Pełna skala obejmuje przedział od 200 do 800 punktów.

Skala ta konstruowana jest też w oparciu o normy typu równoważnikowego, dla których
punktem odniesienia są najczęściej wiek ucznia lub rok i miesiąc nauczania w roku szkol-
nym.

37F37F37F37F

38

Równoważniki wieku lub klasy to liczby, które wskazują na rok i miesiąc życia

bądź kolejne lata i miesiące nauki, odpowiadające średniej arytmetycznej lub medianie
wykonania testu na danym etapie rozwoju. Innymi słowy, równoważnik ucznia będącego
typowym przedstawicielem swojej grupy, który z testu otrzymał np. 40 punktów, może wy-
nosić 3,6. Oznacza to, że taki właśnie wynik osiągają przeciętnie uczniowie w trzecim mie-
siącu nauki w VI klasie. Zatem równoważniki klasy (lub wieku) wskazują opóźnienia albo
przyspieszenie w uczeniu się, bądź to w stosunku do średnich osiągnięć uczniów tej samej
klasy, bądź w stosunku do rówieśników.

Przedstawiona na Rysunku 20. skala równoważników lat nauki szkolnej ma średnią
odpowiadającą 12 latom nauki. Zatem nieco ponad 95% wyników odchyla się, w górę lub
w dół od średniej, nie więcej niż o 6 klas nauki, a około 68% odchyla się nie więcej niż o
trzy klasy.

37

Bolesław Niemierko, Pomiar wyników..., s.267-271.

38

Zob. Elżbieta Hornowska, op. cit., s.150-154 oraz Bolesław Niemierko, Koncepcje matury, „Dyrektor

Szkoły” nr 1 i 2, 2007.

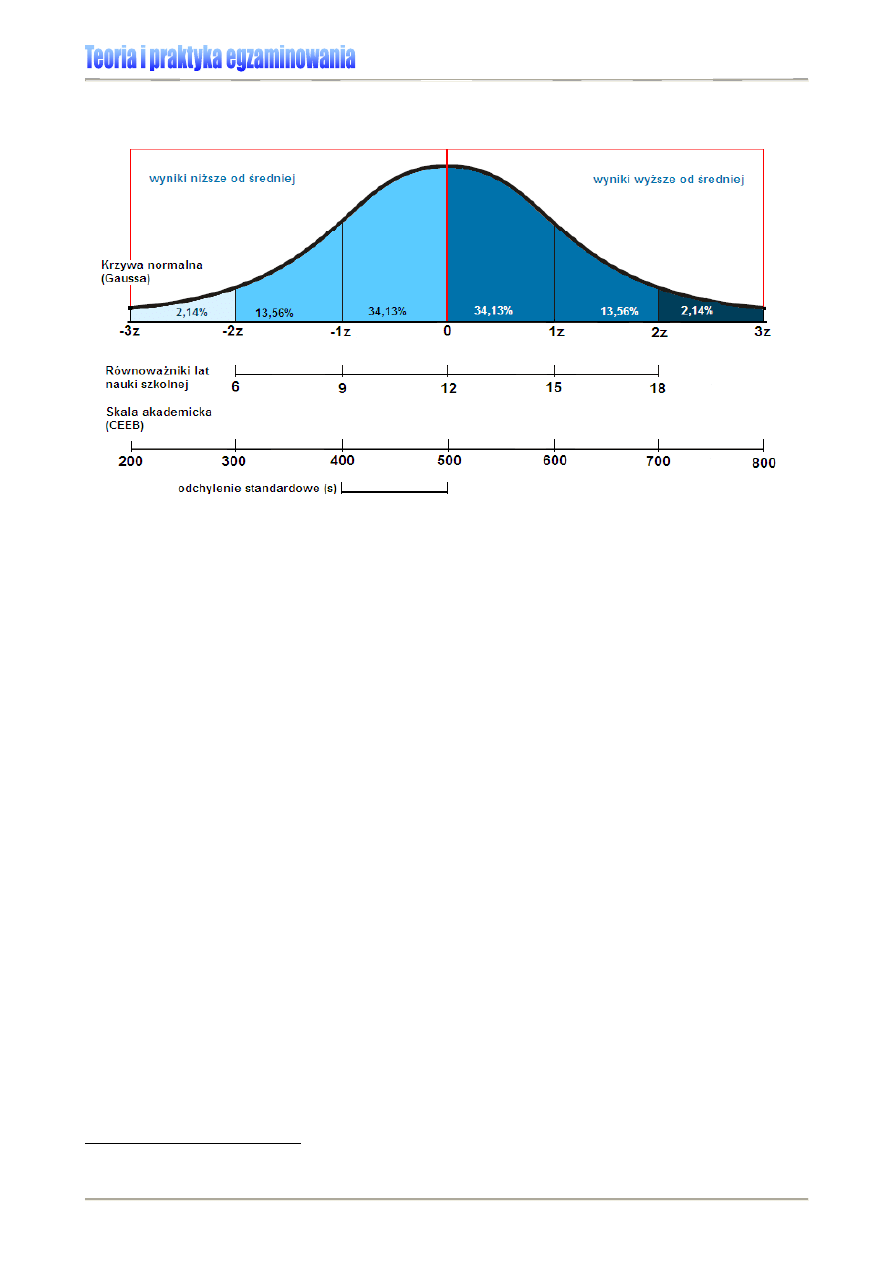
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

38

Rysunek 20. Związek między skalą równoważnikową i skalą CEEB a rozkładem normalnym

38F38F38F38F

39

W najbliższych planach CKE przewiduje komunikowanie wyników egzaminu maturalnego
polskich uczniów z użyciem także tej skali.

39

Bolesław Niemierko, Koncepcje matury...

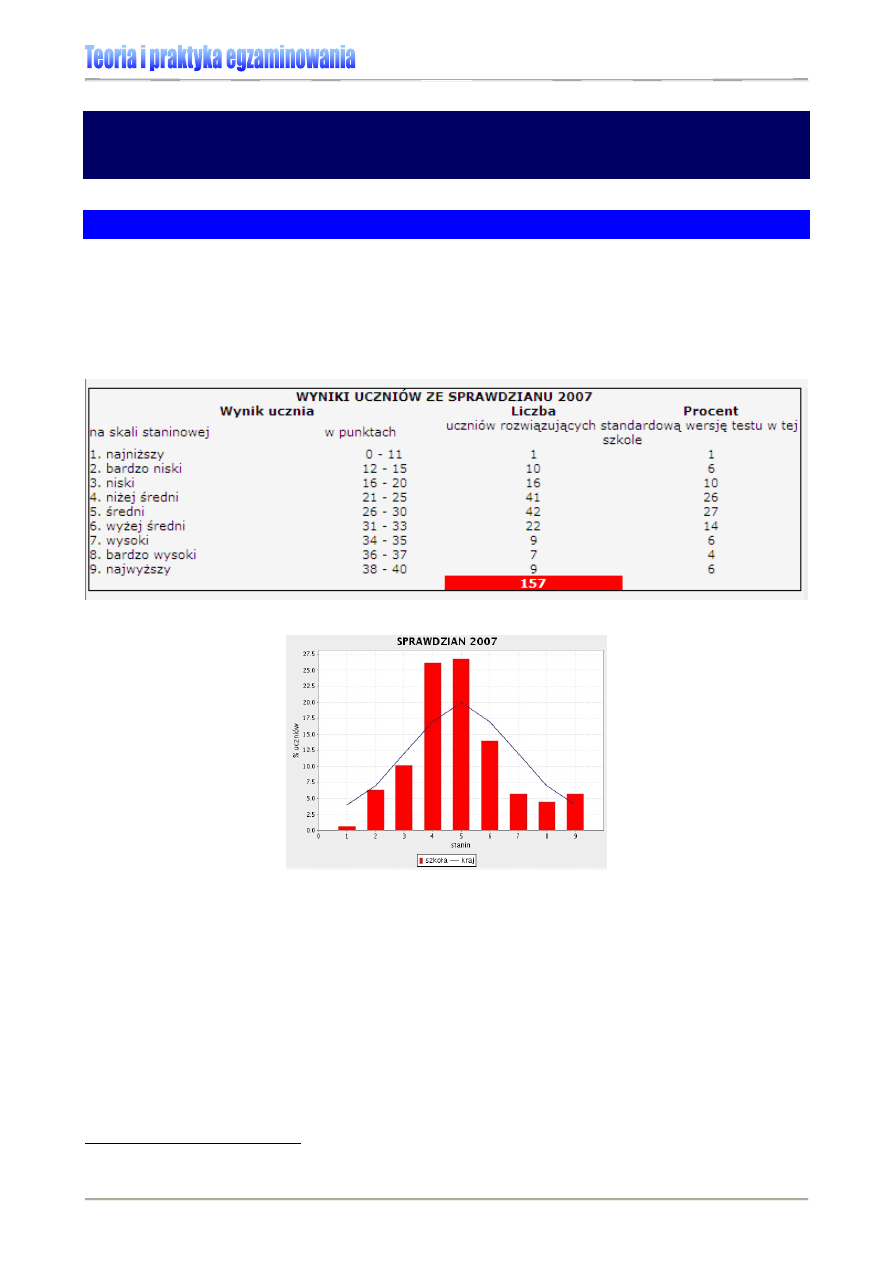
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

39

PRZYKŁADY ANALIZ
WYNIKÓW EGZAMINÓW ZEWNĘTRZNYCH

Analiza i interpretacja wyników staninowych uczniów i szkół

Znormalizowana skala staninowa wykorzystywana jest zarówno w przypadku analizy
wyników

indywidualnych

, jak i

zbiorowości

(np. uczniów danej szkoły).

Przykład:

Prezentując doroczne wyniki szkół w Internecie

39F39F39F39F

40

, ukazano wyniki surowe uczniów tej

szkoły pomieszczone na skali staninowej

Tabela 18., Rysunek 21. Sposób prezentowania wyników szkoły [7]

oraz porównano rezultaty uzyskane przez uczniów tej szkoły do wyników innych szkół w Polsce:

Analiza

indywidualnego

wyniku w odniesieniu do innych zdających jest niezbędna

szczególnie wtedy, gdy chcemy porównać wyniki uczniów zdających egzamin w różnych
latach.

Przykład:

Uczennica kończąca szkołę podstawową, która na sprawdzianie uzyskała 32 punkty, w

kolejnych latach ze swoim wynikiem punktowym lokowałaby się w różnych staninach: w 2002 roku
uzyskałaby piąty stanin (wynik średni), w 2003 – szósty (wyżej średni), w 2004 – siódmy (wysoki),
w 2005 piąty (średni), a 2006 i 2007 – roku szósty (wyżej średni). (Por. Tabela 19.)

40

www.cke.edu.pl - tu: Wyniki szkół

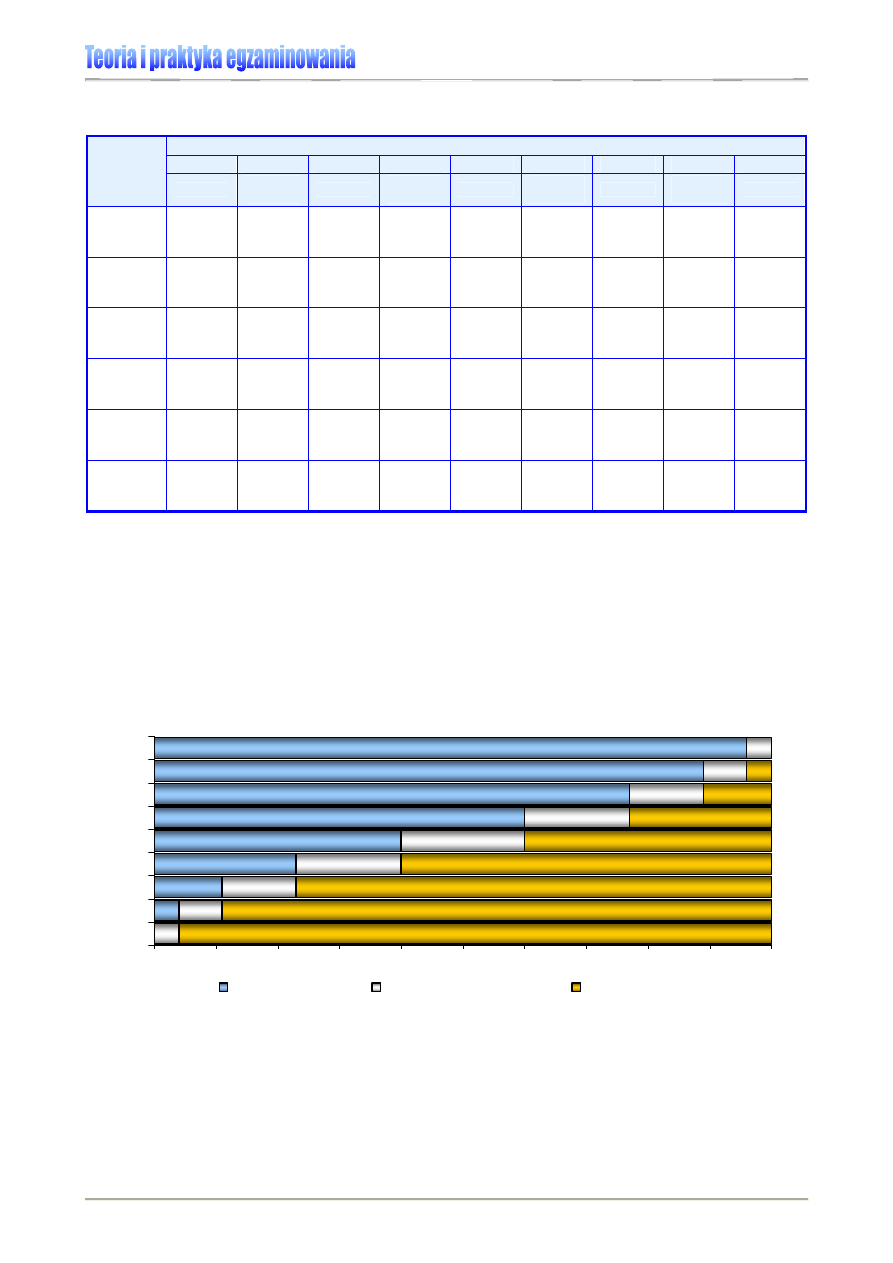
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

40

Tabela 19. Przedziały punktowe skali staninowej dla wyników uczniów na sprawdzianie w latach 2002-07 [3]

Stanin

1

2

3

4

5

6

7

8

9

Wynik

najniższy

bardzo

niski

niski

niżej

średni

średni

wyżej

średni

wysoki

bardzo
wysoki

najwyższy

Przedział

punktowy

2002 r.

0 – 15

16 – 20

21 – 24

25 – 28

29 – 32

33 – 35

36 – 37

38

39 – 40

Przedział

punktowy

2003 r.

0 – 15

16 – 19

20 – 23

24 – 27

28 – 31

32 – 34

35 – 36

37 – 38

39 – 40

Przedział

punktowy

2004 r.

0 – 10

11 – 15

16 – 19

20 – 23

24 – 27

28 – 31

32 – 34

35 – 37

38 – 40

Przedział

punktowy

2005 r.

0 – 13

14 – 18

19 – 23

24 – 28

29 – 32

33 – 35

36 – 37

38

39 – 40

Przedział

punktowy

2006 r.

0 – 9

10 – 13

14 – 18

19 – 23

24 – 29

30 – 33

34 – 36

37 – 38

39 – 40

Przedział

punktowy

2007 r.

0 – 11

12 – 15

16 – 20

21 – 25

26 – 30

31 – 33

34 – 35

36 – 37

38 – 40

Prezentacja wyników egzaminów zewnętrznych na skali staninowej pozwala uczniowi zo-
rientować się, jakie miejsce zajmuje ze swymi wynikami wśród wyników innych
uczniów, którzy zdawali egzamin w danym roku, a szkole – jaka jest jej pozycja
względem innych szkół. Dla ucznia X oznacza to, że jeżeli np. jego wynik znajduje się w
2. staninie, to 4% uczniów uzyskało wynik niższy niż ten, który był jego udziałem, 7% uzy-
skało wynik porównywalny z jego wynikiem, a 89% wszystkich uczniów piszących egzamin
miało wynik wyższy niż osiągnięty przez niego.

Wykres 11. Ranga wyniku w stosunku do innych wyników badania w skali staninowej [6]

Porównanie wyniku ucznia/szkoły z wynikami innych zdających/szkół

0%

4%

11%

23%

40%

60%

77%

89%

96%

4%

7%

12%

17%

20%

17%

12%

7%

4%

96%

89%

77%

60%

40%

23%

11%

4%

0%

0%

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

1

2

3

4

5

6

7

8

9

stanin

wynik niższy

wynik porównywalny

wynik wyższy

Nauczyciele i rodzice powinni przyjrzeć się wynikom uczniów szczególnie bacznie, gdyż
pokazują one nie tylko stan uczniowskich osiągnięć „na dziś”, ale też są dobrym progno-
stykiem sukcesów w uczeniu się na kolejnych etapach edukacyjnych. W Tabeli 20. i
na Rysunku 22. kolorami zaznaczono strefy wyników: niskich (kolor czerwony), średnich
(żółty) i wysokich (zielony), wyodrębniając obszar zagrożenia niskimi osiągnięciami oraz
wskazując grupę uczniów, których wynik świadczy o znacznym potencjale edukacyjnym.

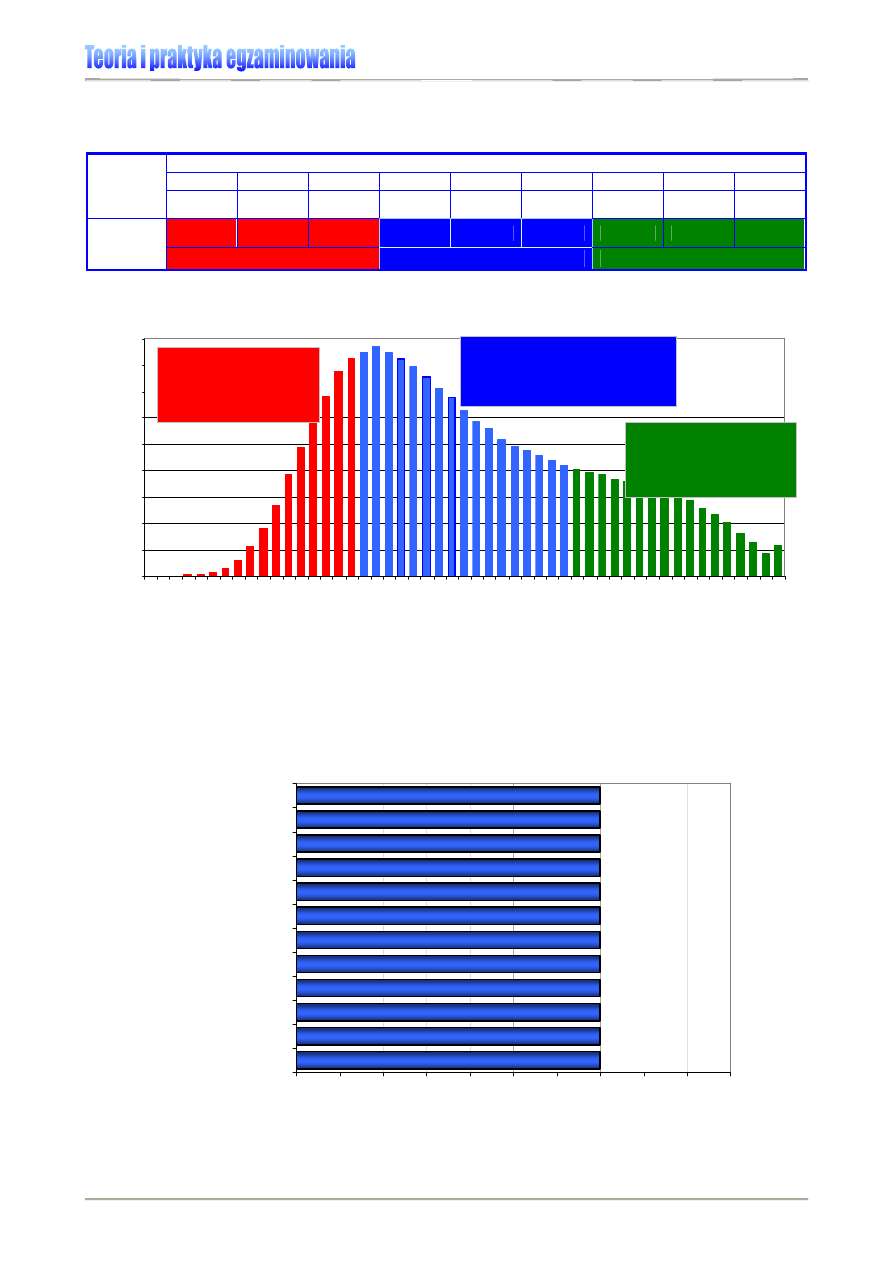
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

41

Tabela 20. Przedziały punktowe skali staninowej dla wyników części matematyczno-przyrodniczej egzaminu
gimnazjalnego 2007 r.[4] [6]

Stanin

1 2 3 4 5 6 7 8 9

Wynik

najniższy

bardzo

niski

niski

niżej

średni

średni

wyżej

średni

wysoki

bardzo
wysoki

najwyższy

0 – 10

11 – 13

14 – 16

17 – 20

21 – 26

27 – 33

34 – 40

41 – 45

46 – 50

Przedział

punktowy

2007 r.

strefa wyników niskich

strefa wyników średnich

strefa wyników wysokich

Rysunek 22. Rozkład wyników części matematyczno-przyrodniczej egzaminu gimnazjalnego 2007 z
wyodrębnieniem stref wyników: niskich, średnich i wysokich [4] [6]

0,0%

0,5%

1,0%

1,5%

2,0%

2,5%

3,0%

3,5%

4,0%

4,5%

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

punkty

% lic

zebno

ści

Możliwość porównania własnych osiągnięć edukacyjnych z osiągnięciami innych
zdających egzaminy zewnętrzne jest szczególnie ważna w przypadku matury, ponieważ
pozwala uczniowi na określenie własnych szans w rywalizacji o przyjęcie na studia.

Przykład:

Oto surowe (w procentach) wyniki Anny Kowalskiej zdającej maturę w 2006 r.

Wykres 12. Indywidualny wynik procentowy z egzaminu maturalnego 2006 [6]

Wyniki procentowe egzaminu maturalnego 2006 Anny Kowalskiej

70%

70%

70%

70%

70%

70%

70%

70%

70%

70%

70%

70%

0%

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

język polski ustny O

język polski pis. O P

język polski pis. O R

język angielski ustny O R

język angielski pis. O P

język angielski pis. O R

geografia O P

geografia O R

język rosyjski ustny D R

język rosyjski pis. D R

historia D R

wiedza o społ. D R

O – przedmiot wybrany jako obowiązkowy, D – przedmiot dodatkowy, P – poziom podstawowy, R – poziom rozszerzony

STREFA WYNIKÓW

NISKICH

Uczniowie zagrożeni niskimi

osiągnięciami – pomóżmy im

to zmienić!

STREFA WYNIKÓW ŚREDNICH

Warto bacznie monitorować postępy

tych uczniów, bo stagnacja bądź regres

osiągnięć są dla nich groźne.

STREFA WYNIKÓW

WYSOKICH

To uczniowie o znacznym

potencjale - nie zgubmy tych

pereł!

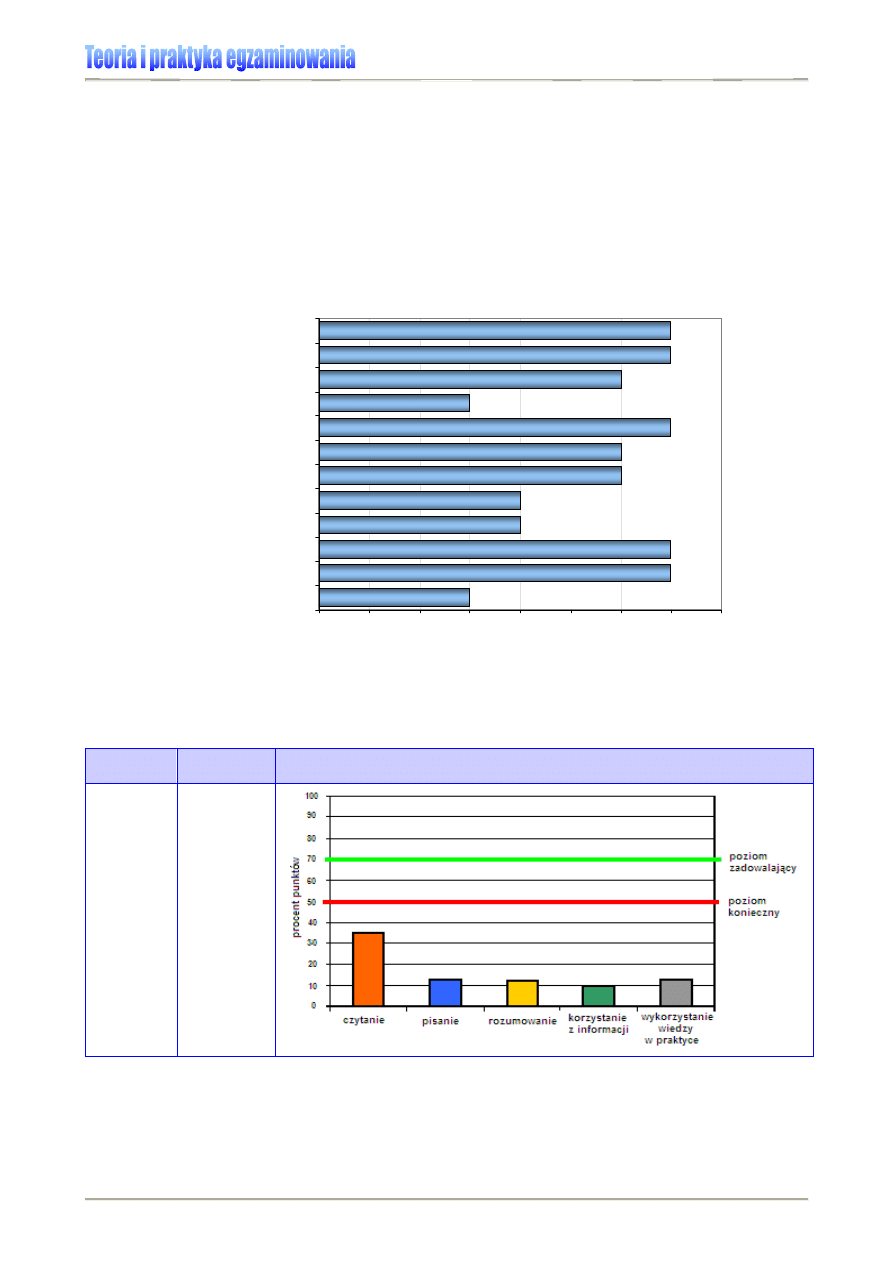
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

42

Gdyby Anna poprzestała na ich analizie, mogłaby pozostawać w przekonaniu, iż jej osiągnięcia są
nie tylko stabilne (ze wszystkich zdawanych przedmiotów uzyskała ten sam wynik), ale i dość wy-
sokie (70% punktów możliwych do uzyskania). Gdy jednak odniesiemy jej wyniki do wyników in-
nych osób zdających dany przedmiot, może się okazać, iż ubiegając się o przyjęcie np. na oblega-
ną filologię angielską, mogłaby mieć ograniczone szanse, ponieważ większość jej konkurentów
uzyskała wynik lepszy od jej wyników. Znormalizowane wyniki uczniów powinny też zainteresować
ich nauczycieli, gdyż pokazują, czy kształcą efektywnie, przyczyniając się do sukcesu w przyjęciu
na studia.

Wykres 13. Indywidualny wynik staninowy egzaminu maturalnego 2006 [6]

Wyniki staninow e egzam inu maturalnego 2006 Anny Kow alskiej

4

8

8

5

5

7

7

8

4

7

8

8

1

2

3

4

5

6

7

8

9

język polski ustny O

język polski pis. O P

język polski pis. O R

język angielski ustny O R

język angielski pis. O P

język angielski pis. O R

geografia O P

geografia O R

język rosyjski ustny D R

język rosyjski pis. D R

historia D R

wiedza o społ. D R

Aby stwierdzić, jakie osiągnięcia mają uczniowie, których wyniki mieszczą się w poszcze-
gólnych przedziałach skali staninowej, dokonuje się pogłębionej analizy statystycznej ich
wyników.

Tabela 21. Wyniki w obszarach a poziomy osiągnięć uczniów (fragment analizy) [2]

Przedział

punktowy

Nazwa

wyniku

Obraz osiągnięć uczniów

Stanin 1.

1- 9 p

NAJNIŻSZY

(uzyskany

przez 3,7%

uczniów)

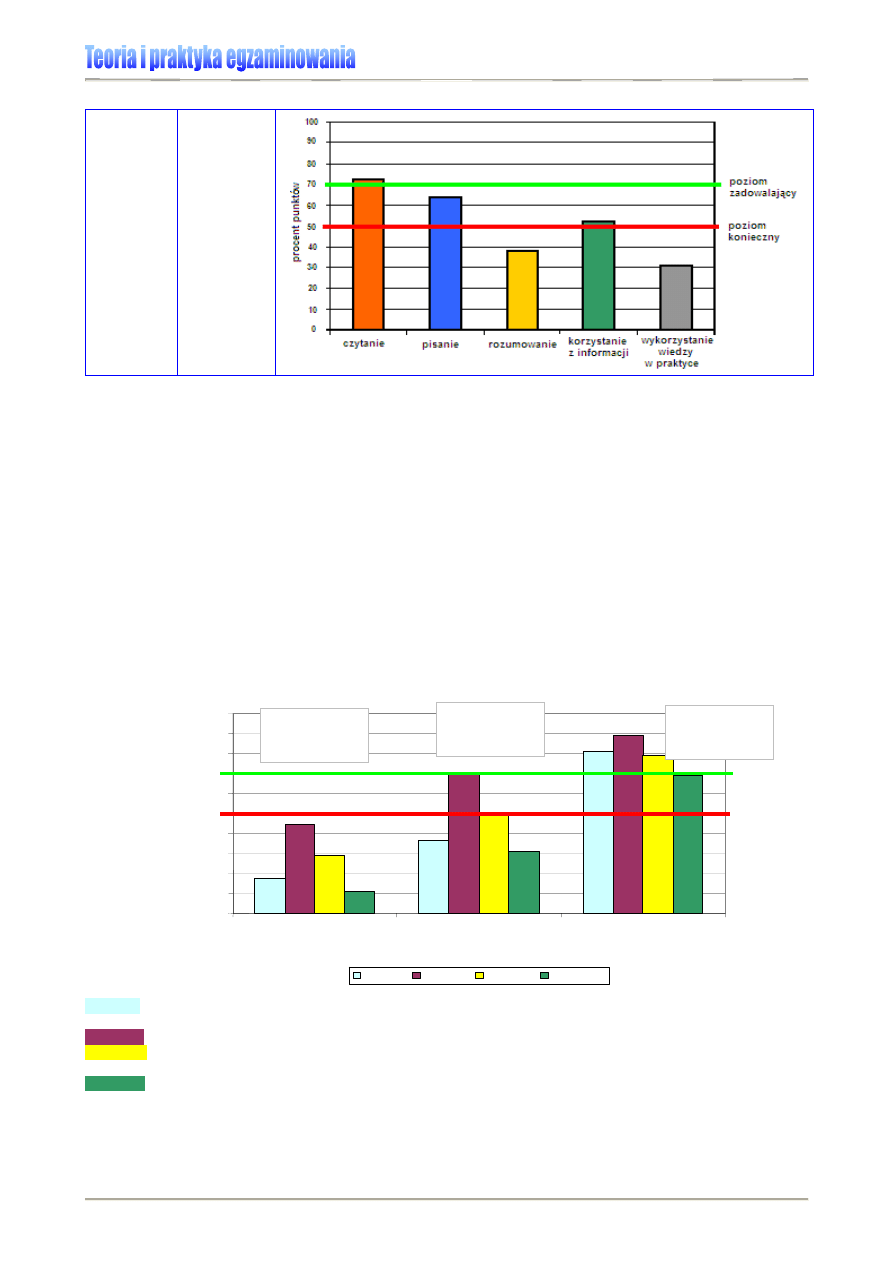
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

43

Stanin 4.

19- 23 p

NIŻEJ

ŚREDNI

(uzyskany

przez 17,6%

uczniów)

Przykłady:

Na podstawie analizy wyników i zadań zastosowanych na sprawdzianie, CKE ustaliła

następujące normy osiągnięć szóstoklasistów zdających sprawdzian w 2006 r: poziom konieczny
– 20 punktów (50% punktów możliwych do uzyskania) i poziom zadowalający – 28 punktów (70%
punktów możliwych do uzyskania). Analizując Tabelę 21. widzimy, iż uczniowie z najsłabszymi
wynikami z testu (1. stanin), nie osiągnęli poziomu koniecznego w żadnym z badanych obszarów
standardów wymagań egzaminacyjnych. W obszarze „Czytanie” poziom zadowalający osiągnęli
dopiero uczniowie z 4. staninem (na egzaminie otrzymali od 19 do 23 punktów). Natomiast ci sami
szóstoklasiści nie opanowali na poziomie koniecznym umiejętności z obszaru „Rozumowanie” i
„Wykorzystanie wiedzy w praktyce”.

Podobnej analizie możemy poddać poziom osiągnięć uczniów w obszarach umiejętności badanych
testami gimnazjalnymi. Oto co potrafią gimnazjaliści, którzy na egzaminie w 2007 r. z przedmiotów
matematyczno-przyrodniczych uzyskali wyniki niskie (0-16 pkt.), średnie (17-33 pkt.) i wysokie (34-
50 pkt.).

Wykres 14. Osiągnięcia uczniów z części matematyczno-przyrodniczej egzaminu gimnazjalnego 2007 w
obszarach wymagań egzaminacyjnych [4] [6]

0

1 0

2 0

3 0

4 0

5 0

6 0

7 0

8 0

9 0

1 0 0

1 7 -3 3

3 4 -5 0

p rz e d z ia ł w y n ik ó w (w p u n k ta c h )

poz

io

m

opa

no

wan

ia

o b s z a r I

o b s z a r II

o b s z a r III

o b s z a r IV

Obszar I

Umiejętne stosowanie terminów, pojęć i procedur z zakresu przedmiotów matematyczno-
przyrodniczych

niezbędnych w praktyce życiowej i dalszym kształceniu

Obszar II

Wyszukiwanie i stosowanie informacji

Obszar III

Wskazywanie i opisywanie faktów, związków i zależności, w szczególności przyczynowo-skutkowych,
funkcjonalnych, przestrzennych i czasowych

Obszar IV

Stosowanie zintegrowanej wiedzy i umiejętności do rozwiązywania problemów

STREFA

WYNIKÓW

WYSOKICH

STREFA

WYNIKÓW

NISKICH

STREFA

WYNIKÓW

ŚREDNICH

0-16

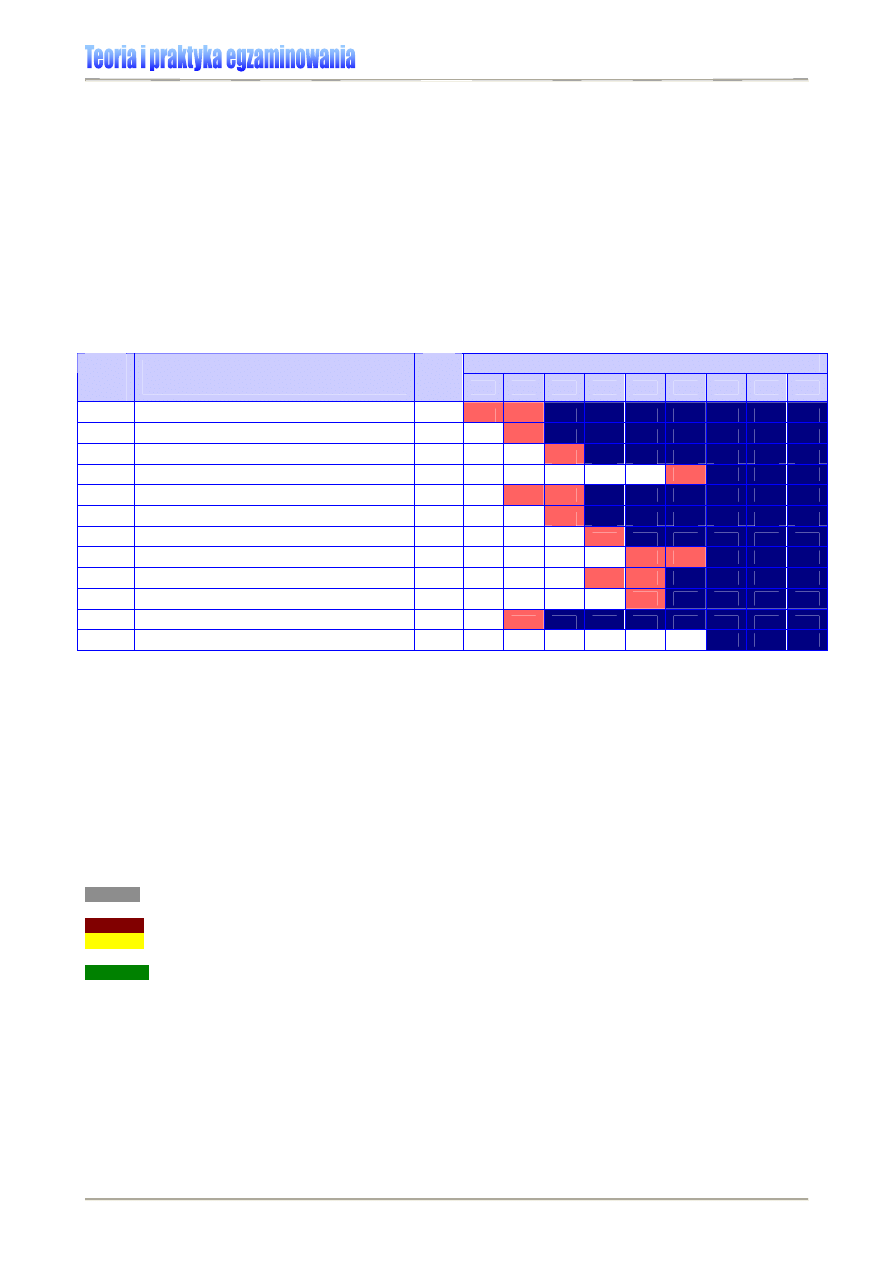
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

44

Bardziej szczegółowych informacji o poziomie osiągnięć uczniów dostarczy analiza
wskaźników łatwości poszczególnych zadań w arkuszu egzaminacyjnym, dokonana w od-
niesieniu do pozycji wyniku ucznia na skali staninowej.

Przykład:

Staniny uporządkowane od najniższego (1.) do najwyższego (9.), grupują uczniów, któ-

rzy coraz lepiej opanowali poszczególne umiejętności (opisane w kartotece testu) badane na
sprawdzianie 2006. Z przedstawionego fragmentu zestawienia wynika, iż poziom osiągnięć ko-
niecznych oraz zadowalających tych zdających jest nierównomierny, bo niektóre umiejętności są
opanowane w stopniu koniecznym przez uczniów uzyskujących wynik w 1. staninie, a w zadowala-
jącym w 3., zaś inne – dopiero przez uczniów osiągających wyniki powyżej średniej (6 stanin –
poziom konieczny) i wynik wysoki (7. stanin – poziom zadowalający).

Tabela 22. Pogłębiona analiza statystyczna wykonania zadań sprawdzianu 2006 (fragment zestawienia) [2]

Łatwość zadania/kryterium w staninach

Nr

zadania/

kryte-

rium

Badana czynność ucznia

(z numerem standardu)

Maks.

liczba

pkt

1

2

3

4

5

6

7

8

9

1

odczytuje tekst popularnonaukowy (1.1)

1

0,51

0,69

0,81

0,90

0,95 0,97 0,99

0,99

1,00

2

odczytuje tekst popularnonaukowy (1.1)

1

0,45

0,58

0,71

0,83

0,91 0,95 0,98

0,99

1,00

3

odczytuje tekst popularnonaukowy (1.1)

1

0,34 0,49 0,62

0,74

0,83 0,89 0,94

0,97

0,99

4

wykonuje obliczenia dotyczące

temperatury

(5.3)

1 0,14 0,17 0,21 0,31 0,48 0,65

0,78

0,89

0,97

5

odczytuje tekst popularnonaukowy (1.1)

1

0,41

0,56

0,67

0,79

0,87

0,93

0,96

0,98

0,99

6

odczytuje tekst popularnonaukowy (1.1)

1

0,27 0,44 0,62

0,78

0,89 0,95 0,98

0,99

1,00

7

umieszcza datę w przedziale czasowym (3.1)

1

0,09 0,19 0,36 0,59

0,79 0,90 0,95

0,98

0,99

8

rozpoznaje własności figur geometrycznych (3.6)

1

0,14

0,21

0,28

0,38

0,50

0,61

0,72

0,82

0,95

9

rozpoznaje własności figur geometrycznych (3.6)

1

0,17

0,26

0,37

0,52

0,68

0,78

0,85

0,91

0,97

10

odczytuje tekst poetycki (1.1)

1

0,20

0,26

0,33

0,45

0,60

0,73

0,84

0,93

0,98

11

posługuje się czynnie terminami (1.2)

1

0,43

0,60

0,71

0,81

0,87 0,92 0,95

0,98

0,99

... .....

... ... ... ... ... ... ...

...

...

...

Pole białe – uczniowie nie osiągnęli poziomu koniecznego; pole czerwone – uczniowie osiągnęli poziom konieczny;
pole granatowe – uczniowie osiągnęli poziom zadowalający.

Przykład:

Nauczyciele znający pozycję wyników poszczególnych uczniów z danej klasy na skali

staninowej, mogą przeanalizować ich osiągnięcia bardzo dokładnie, w odniesieniu do każdego
rozwiązywanego na teście zadania. Mogą je także porównać z osiągnięciami statystycznego pol-
skiego ucznia. Oto łatwość zadań (ich poziom opanowania) z gimnazjalnego testu matematyczno-
przyrodniczego 2007 – dla uczniów, których wyniki są odpowiednio w pierwszym (Wykres 15.),
piątym (Wykres 16.) i dziewiątym (Wykres 17.) staninie.

Wykresy 15.-17. Poziom opanowania umiejętności badanych zadaniami testu gimnazjalnego 2007 w części
matematyczno-przyrodniczej przez ucznia, którego wynik za cały test mieści się w 1., 5. i 9. staninie [4]

Legenda:

Obszar I

Umiejętne stosowanie terminów, pojęć i procedur z zakresu przedmiotów matematyczno-
przyrodniczych

niezbędnych w praktyce życiowej i dalszym kształceniu

Obszar II

Wyszukiwanie i stosowanie informacji

Obszar III

Wskazywanie i opisywanie faktów, związków i zależności, w szczególności przyczynowo-skutkowych,
funkcjonalnych, przestrzennych i czasowych

Obszar IV

Stosowanie zintegrowanej wiedzy i umiejętności do rozwiązywania problemów

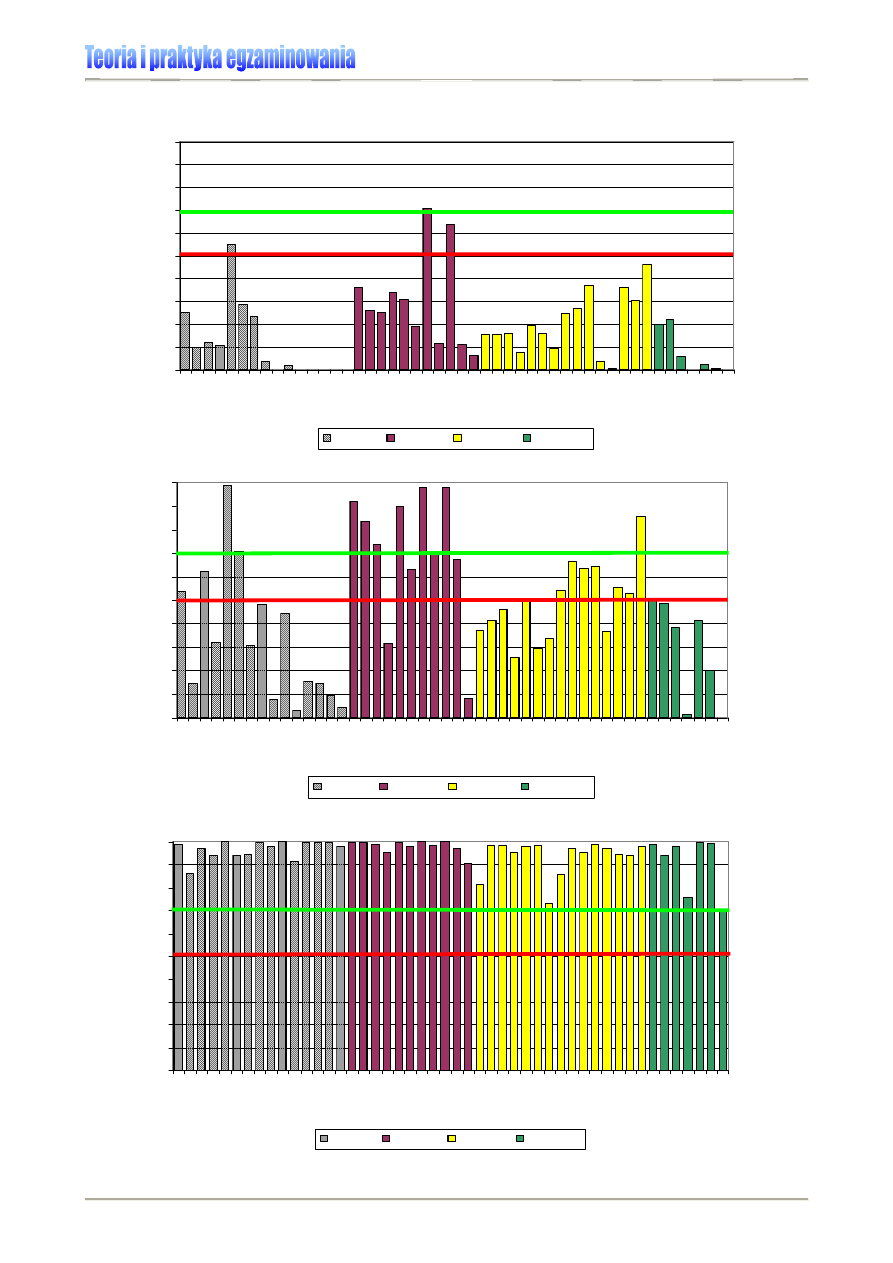
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

45

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

7 8 9 10 11 17 18

30.

1

30.

2

30.

3

30.

4

33.

1

33.

2

33.

3

33.

4 1 2 3 4 5 6 26 27

31.

1

31.

2

31.

3 13 14 15 16 19 20 21 23 24 25

29.

1

29.

2

34.

1

34.

2

34.

3 12 22 28

32.

1

32.

2

32.

3

32.

4

umiejętność

po

zi

om

opanow

ani

a

obszar I

obszar II

obszar III

obszar IV

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

7 8 9 10 11 17 18

30.

1

30.

2

30.

3

30.

4

33.

1

33.

2

33.

3

33.

4 1 2 3 4 5 6 26 27

31.

1

31.

2

31.

3 13 14 15 16 19 20 21 23 24 25

29.

1

29.

2

34.

1

34.

2

34.

3 12 22 28

32.

1

32.

2

32.

3

32.

4

umiejętność

po

zi

om

o

panow

an

ia

obszar I

obszar II

obszar III

obszar IV

0,0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

7 8 9 10 11 17 18

30.

1

30.

2

30.

3

30.

4

33.

1

33.

2

33.

3

33.

4 1 2 3 4 5 6 26 27

31.

1

31.

2

31.

3 13 14 15 16 19 20 21 23 24 25

29.

1

29.

2

34.

1

34.

2

34.

3 12 22 28

32.

1

32.

2

32.

3

32.

4

umiejętność

poz

iom

o

pano

w

ani

a

obszar I

obszar II

obszar III

obszar IV

1. stanin

5. stanin

9. stanin

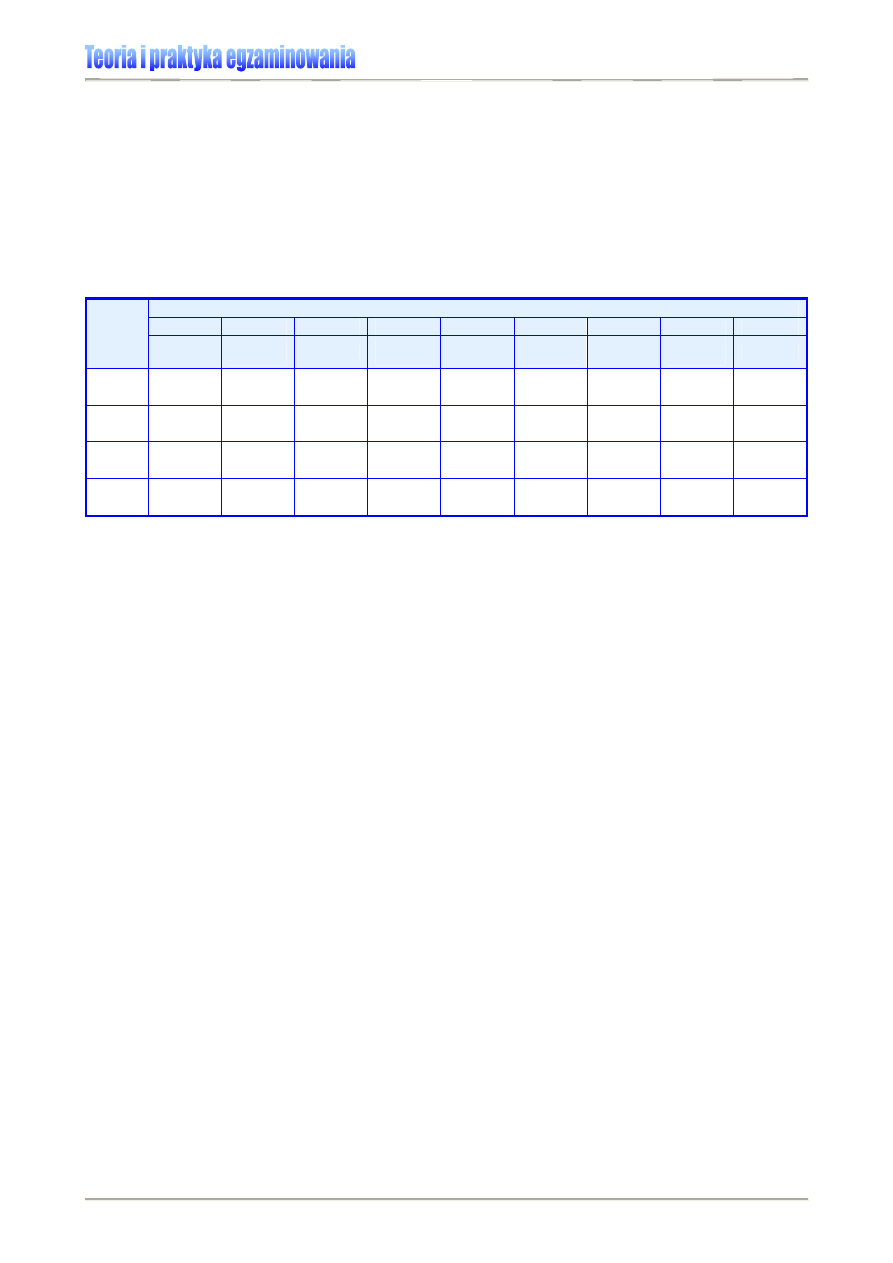
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

46

Analiza wyników egzaminacyjnych uczniów rozpoczynających naukę w szkole programo-
wo wyższej okazuje się niezbędna w procesie diagnozy wstępnej, może też ułatwić
przydział uczniów do poszczególnych oddziałów szkolnych, a później posłużyć do
analiz porównawczych, pomocnych w badaniu efektywności kształcenia.

Przykład:

Oto rozkład wyników ze sprawdzianu uczniów przyjętych do klas pierwszych w Gimna-

zjum w Igrekowie. Zastosowanie skali staninowej pozwala kontrolować potencjał klasy „na wej-
ściu”, pozwoli także dokonać analizy postępów tych uczniów po trzech latach nauki w szkole:

Tabela 23. Rozkład wyników „na wejściu” uczniów Gimnazjum w Igrekowie [6]

Stanin

1

2

3

4

5

6

7

8

9

Wynik

najniższy

bardzo

niski

niski

niżej

średni

średni

wyżej

średni

wysoki

bardzo
wysoki

najwyższy

I a

Ania B.

I b

I c

I d

Karol C.

Rozkład wyników uczniów z poszczególnych oddziałów dowodzi, iż podczas przyjmowania
uczniów do poszczególnych klas zastosowano segregację szkolną, co szczególnie jaskrawo wi-
dać na przykładzie klas Ic (językowej) i Id (ogólnej). W pierwszej z nich nie ma uczniów z niskim
potencjałem; odmiennie rzecz ma się w przypadku Id, w której zgromadzono uczniów z niskimi i
średnimi wynikami. Szczególnie pilnie należałoby śledzić osiągnięcia Karola C., który w tym od-
dziale szkolnym może mieć trudności z czynieniem postępów na swoją miarę.

Analiza wyników egzaminacyjnych nowo przyjętych uczniów może też pomóc nauczycielom w
planowaniu pracy dydaktycznej z uczniami w poszczególnych oddziałach.

Postępy, które poczynili uczniowie w trakcie trzyletniej nauki w gimnazjum w Igrekowie, można
zbadać na różne sposoby. Oprócz pogłębionych badań jakościowych, przydatnej informacji może
dostarczyć analiza porównawcza wyników uczniów „na wejściu” i „na wyjściu” – ze sprawdzianu i
egzaminu gimnazjalnego.

Przeanalizujmy to na przykładzie klasy oznaczonej literą „b”. Oto wyniki staninowe 31 uczniów
tego oddziału, uzyskane na sprawdzianie 2004 oraz na egzaminie gimnazjalnym 2007 (przykład
ograniczono tu do wyników z części matematyczno-przyrodniczej tego egzaminu).

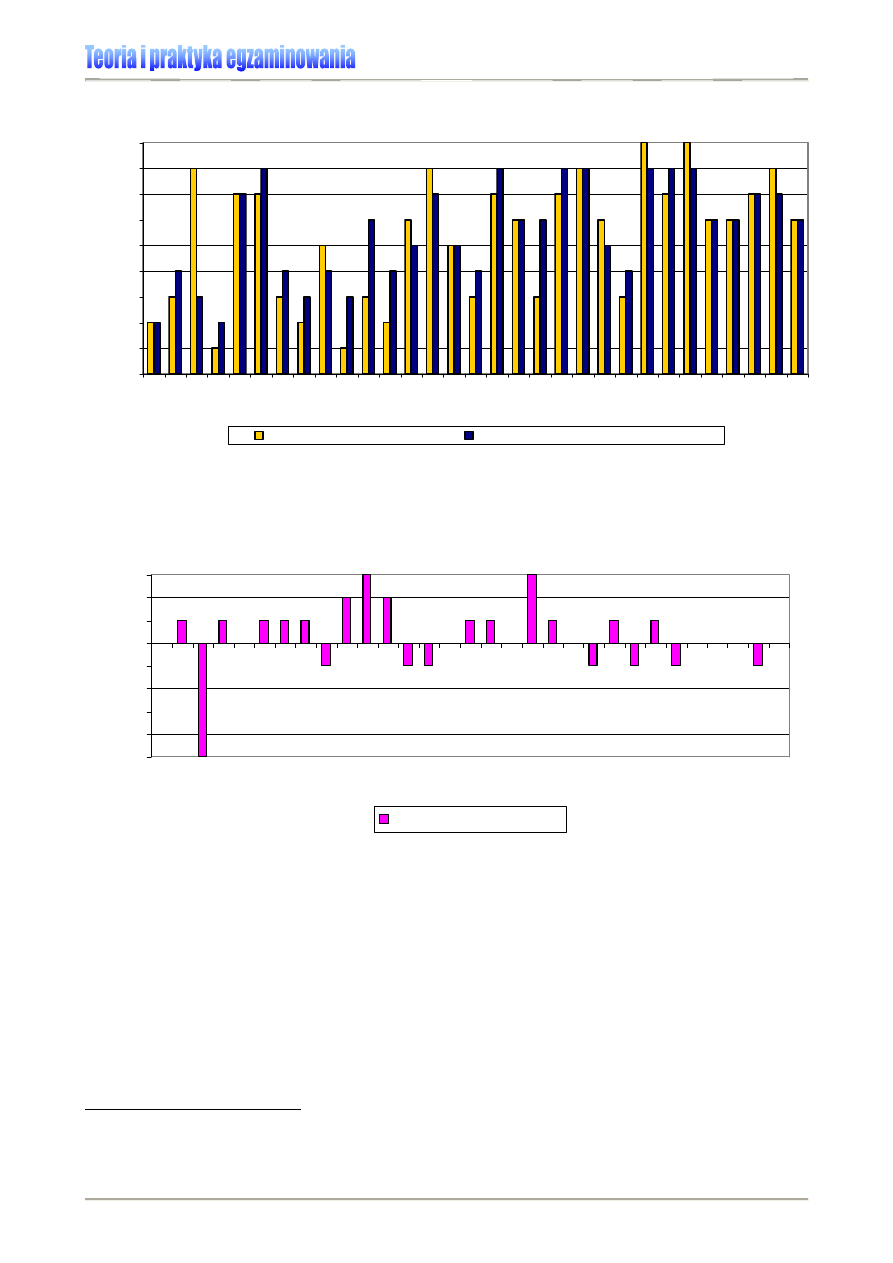
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

47

Wykres 18. Wyniki absolwentów klasy IIIb „na wejściu” i „na wyjściu” z gimnazjum [6]

2

3

8

1

7

7

3

2

5

1

3

2

6

8

5

3

7

6

3

7

8

6

3

9

7

9

6

6

7

8

6

2

4

3

2

7

8

4

3

4

3

6

4

5

7

5

4

8

6

6

8

8

5

4

8

8

8

6

6

7

7

6

0

1

2

3

4

5

6

7

8

9

1

2

3

4

5

6

7

8

9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

nr ewidencyjny ucznia

stani

n

wynik sprawdzianu 2004

wynik cz. mat.-przyr. egz. gimn. 2007

Różnica pomiędzy wynikami sprawdzianu i egzaminu gimnazjalnego poszczególnych uczniów po-
zwala wstępnie ocenić efektywność kształcenia w tej klasie. Bardziej precyzyjnie uczynić to moż-
na, posługując się wskaźnikiem edukacyjnej wartości dodanej.

40F40F40F40F

41

Wykres 19. Postępy uczniów klasy IIIb Gimnazjum w Igrekowie [6]

0

1

-5

1

0

1 1 1

-1

2

3

2

-1 -1

0

1 1

0

3

1

0

-1

1

-1

1

-1

0 0 0

-1

0

-5

-4

-3

-2

-1

0

1

2

3

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

Uczniow ie

Post

ę

p

postęp (S2004 - MPG2007)

Wykres 20. ukazuje miarę postępu w tym oddziale szkolnym. Wartości dodatnie oznaczają postęp
(w przypadku ucznia oznaczonego nr 11 i 19. aż o 3 staniny), zero – stagnację, zaś wartości
ujemne – regres (w skrajnym przypadku ucznia o nr. 3. aż o 5 staninów!). W klasie IIIb, w porów-
naniu ze stanem wejściowym mierzonym wynikami sprawdzianu, niższe wyniki „na wyjściu” ze
szkoły miało 8 osób, 9 osób ukończyło szkołę z wynikiem staninowym identycznym jak uzyskane 3
lata wcześniej, zaś aż 14 osób zdobyło wynik wyższy.

41

Więcej na temat EWD w 14. numerze Biuletynu Badawczego Egzamin na stronie www.cke.edu.pl oraz w

dalszej części materiałów. Kalkulator do obliczania edukacyjnej wartości dodanej w gimnazjum – także na
stronie domowej CKE.

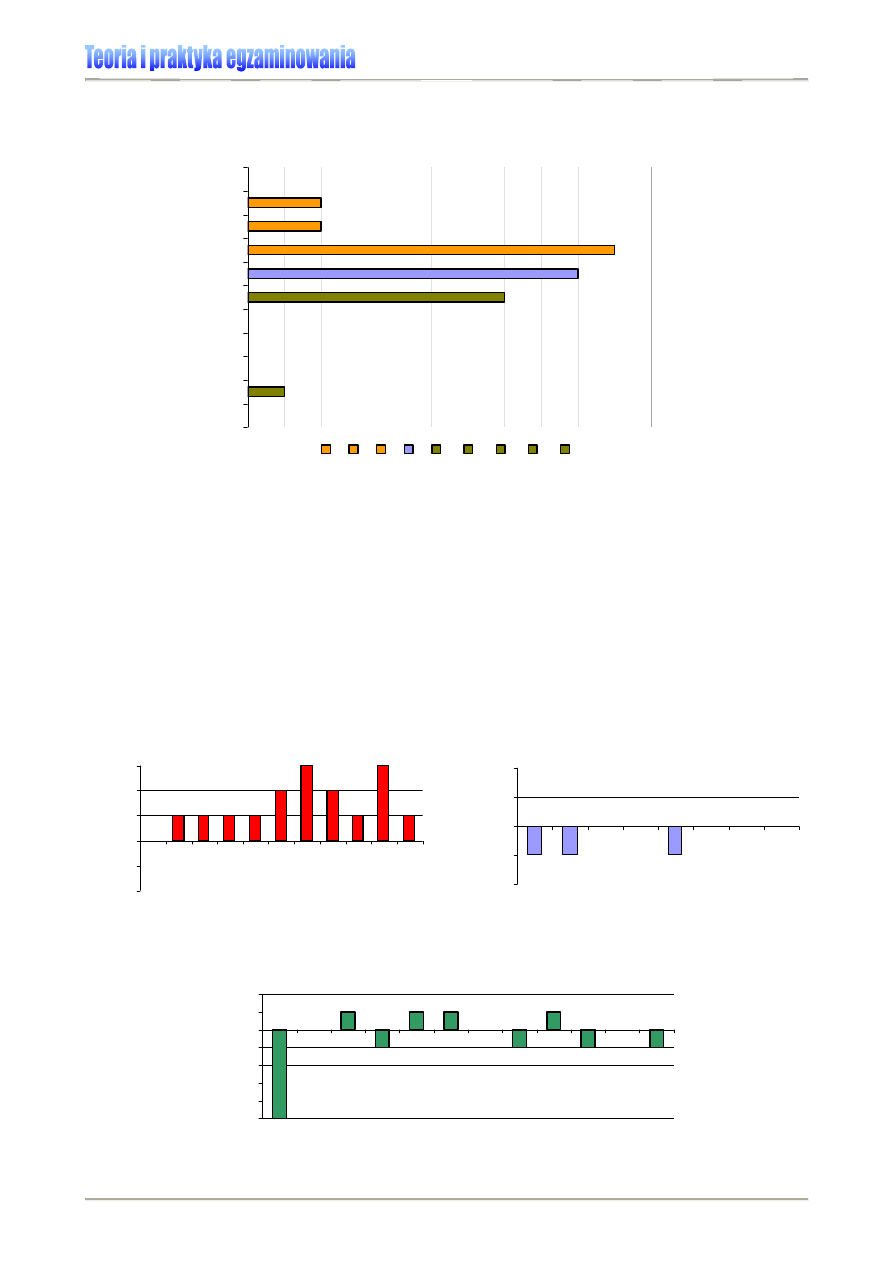
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

48

Wykres 20. Postępy uczniów klasy IIIb Gimnazjum w Iksowie [6]

0

2
2

10

9

7

0
0
0

1

0

3
2
1
0

-1
-2
-3
-4
-5

post

ęp

liczba uczniów

3

2

1

0

-1

-2

-3

-4

-5

Wykresy 21.-23. szczegółowo pokazują, jak w klasie „b” pracowano z uczniami, którzy przyszli do
szkoły z wynikami niskimi (1.-3. stanin), średnimi (4.-6. stanin) i wysokimi (7.-9. stanin). Ich analiza
pokazuje, że szczególnie zajęto się w tej klasie wyrównywaniem szans edukacyjnych uczniów
najsłabszych – żadna spośród 11 osób nie uzyskała na egzaminie gimnazjalnym wyniku niższego
niż na sprawdzianie, 2 miały identyczny i aż 10 – wyższy. Mniej skutecznie pracowano z grupą
uczniów o wynikach mieszczących się w staninach środkowych (4.-6.) – postępów nie poczynił
żaden z nich. Wyniki uczniów o najwyższym potencjale edukacyjnym okazały się najbardziej
zróżnicowane – 4 osoby poczyniły postępy, 5 uzyskało wyniki gorsze niż w szkole podstawowej,
reszta z 12-osobowej grupy pozostała z wynikiem uzyskanym 3 lata wcześniej.

Wykresy 21.-23. Efektywność pracy z uczniami o niskim, średnim i wysokim potencjale edukacyjnym „na
wejściu” [6]

Postępy uczniów ze strefy w yników niskich

(1-3 stanin)

0

1

1

1

1

2

3

2

1

3

1

-2

-1

0

1

2

3

1

2

3

4

5

6

7

8

9

10 11

uczeń

post

ę

p

Postępy uczniów ze strefy w yników

średnich (4-6 stanin)

-1

-1

0

0

-1

0

0

0

-2

-1

0

1

2

1

2

3

4

5

6

7

8

uczeń

post

ę

p

Postępy uczniów ze strefy wyników wysokich (7-9 stanin)

-5

0

1

-1

1

1

0

-1

1

-1

0

-1

-5

-4

-3

-2

-1

0

1

2

1

2

3

4

5

6

7

8

9

10

11

12

uczeń

post

ę

p

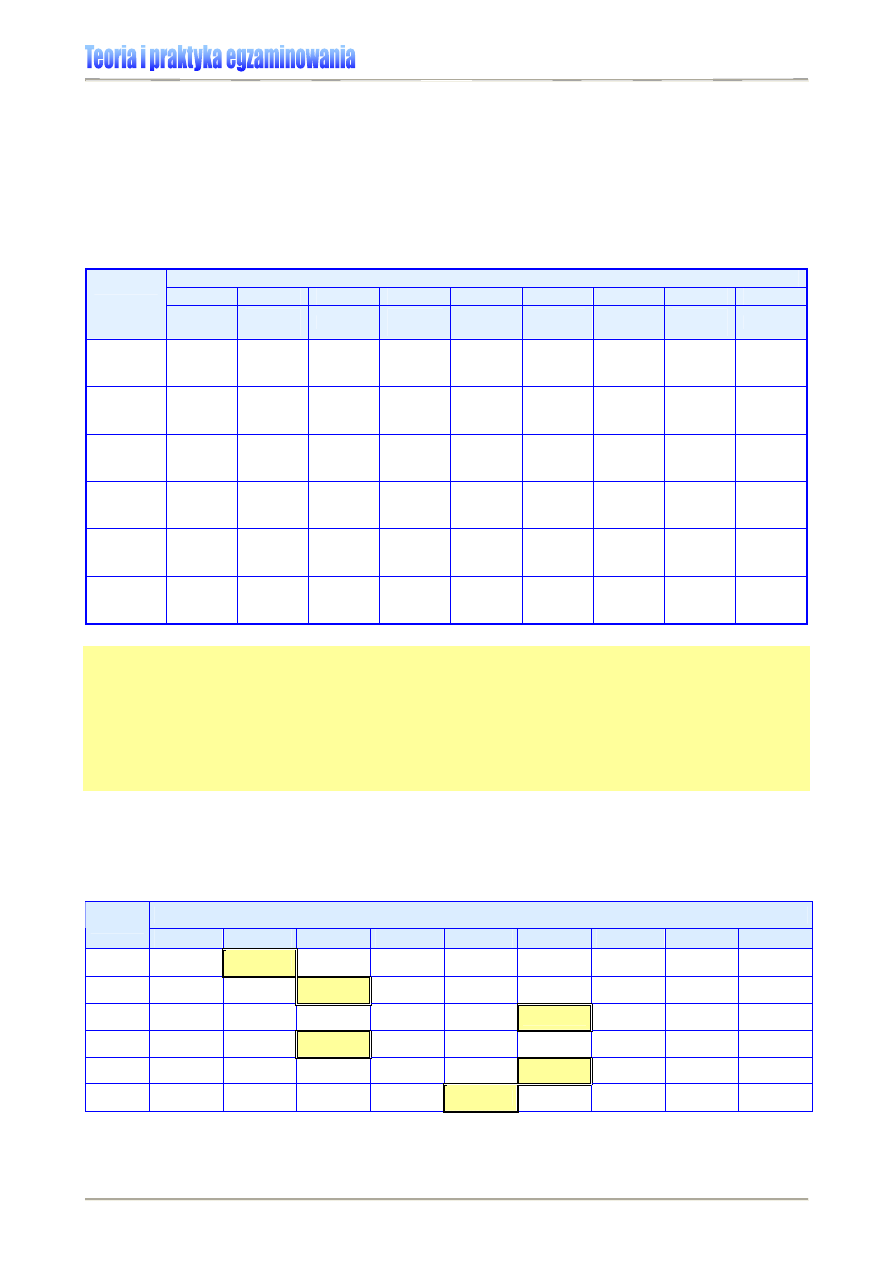
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

49

Identycznie jak dla uczniów, wyznacza się przedziały punktowe w kolejnych staninach dla

szkół

, z tą tylko różnicą, że przy podziale na stopnie skali uwzględnia się średnie wyniki

punktowe szkoły. Zatem np. w 2002 roku w pierwszym staninie lokowały się te szkoły
podstawowe, których średni wynik punktowy znalazł się w przedziale od 7,5 aż do 24,2
punktów, a w 2006 r., kiedy to szkół z niskim wynikiem przybyło, przedział ten zaczynał się
od 4 punktów jako średniej dla szkoły, a kończył już na 19,1 pkt.

Tabela 24. Skala staninowa średnich wyników szkół dla sprawdzianu 2002-2007 [3]

Stanin

1

2

3

4

5

6

7

8

9

Wynik

najniższy

bardzo

niski

niski

niżej

średni

średni

wyżej

średni

wysoki

bardzo
wysoki

najwyższy

Przedział

punktowy

2002 r.

7,5-24,2 24,3-26 26,1-27,4 27,5-28,7 28,8-30 30,1-31,3 31,4-32,8 32,9-34,6 34,7-39,5

Przedział

punktowy

2003 r.

7,7-23,1 23,2-24,9 25,0-26,3 26,4-27,6 27,7-28,9 29,0-30.1 30,2-31,3 31,4-32,8 32,9-39,0

Przedział

punktowy

2004 r.

2,0-19,6 19,7-21,4 21,5-22,9 23,0-24,3 24,4-25,7 25,8-27,2 27,3-28,9 29,0-31,2 31,3-39,5

Przedział

punktowy

2005 r.

11,0-23,7 23,8-25,6 25,7-27,0 27,1-28,4 28,5-29,7 28,8-31,0 31,1-32,3 32,4-33,8 33,9-39,2

Przedział

punktowy

2006 r.

4,0

-19,1 19,2-20,9 21,0-22,6 22,7-24,1 24,2-25,7 25,8-27,3 27,4-29,0 29,1-31,3 31,4-39,0

Przedział

punktowy

2007 r.

7,2-20,8 20,9-22,6 22,7-24,1 24,2-25,4 25,5-26,8 26,9-28,2 28,3-29,7 29,8-31,7 31,8-39,5

Uwaga: Zainteresowani analizą wyników egzaminów zewnętrznych poszczególnych szkół
(a są nimi nie tylko nauczyciele, ale także rodzice, nadzór pedagogiczny, samorządy
lokalne, media), nie powinni poprzestawać na oglądzie parametrów związanych z
prezentacją wyników surowych (te bowiem podlegają corocznym wahaniom związanym
choćby z łatwością egzaminu czy liczbą piszących), ale muszą sięgać także do wyników
znormalizowanych. Jest to szczególnie istotne, kiedy pragniemy porównywać wyniki danej
szkoły w kolejnych latach.

Przykład:

Tabela 25. pokazuje, że osiągnięcia Szkoły Podstawowej w R. w stosunku do innych

szkół w kraju w kolejnych latach zdecydowanie różniły się, choć szkoła ta wciąż uzyskiwała
identyczny wynik surowy

26

punktów.

Tabela 25. Znormalizowane wyniki Szkoły Podstawowej w R. w kolejnych latach, a surowy wynik 26 pkt. [6]

stanin

Rok

1

2

3

4

5

6

7

8

9

2002

7,5-24,2

24,3-26,0

26,1-27,4 27,5-28,7 28,8-30,0 30,1-31,3 31,4-32,8 32,9-34,6 34,7-39,5

2003

7,7-23,1 23,2-24,9

25,0-26,3

26,4-27,6 27,7-28,9 29,0-30,1 30,2-31,3 31,4-32,8 32,9-39,0

2004

2,0-19,6 19,7-21,4 21,5-22,9 23,0-24,3 24,4-25,7

25,8-27,2

27,3-28,9 29,0-31,2 31,3-39,5

2005

11,0-23,7 23,8-25,6

25,7-27,0

27,1-28,4 28,5-29,7 28,8-31,0 31,1-32,3 32,4-33,8 33,9-39,2

2006

4,0-19,1 19,2-20,9 21,0-22,6 22,7-24,1 24,2-25,7

25,8-27,3

27,4-29,0 29,1-31,3 31,4-39,0

2007

7,2-20,8 20,9-22,6 22,7-24,1 24,2-25,4

25,5-26,8

26,9-28,2 28,3-29,7 29,8-31,7 31,8-39,5

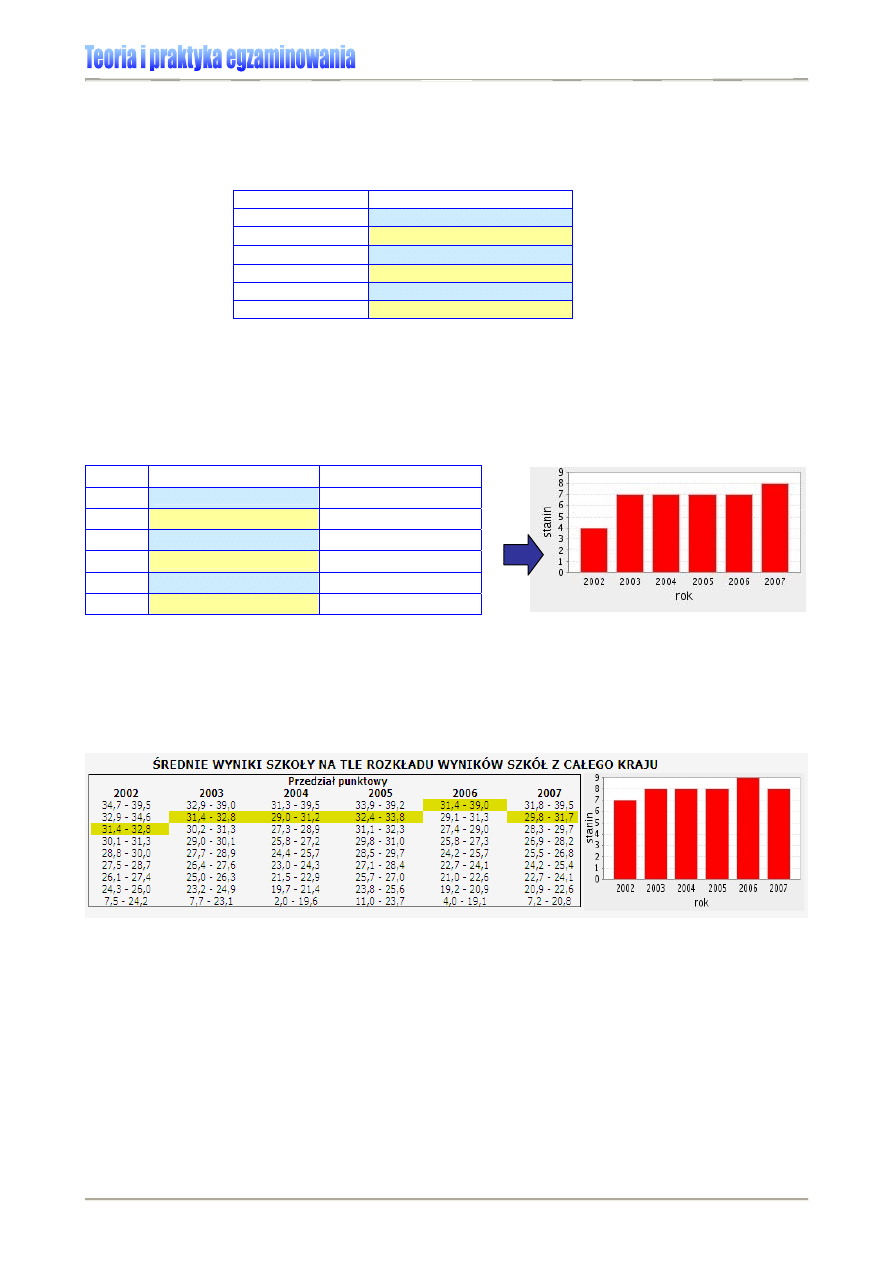
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

50

Z kolei Tabela 26. zawiera wyniki szkoły D, której efektywność niektórzy postrzegali jako niestabil-
ną, gdyż na kolejnych sprawdzianach uzyskiwała na przemian: 27,5 pkt. od 31,1 pkt.

Tabela 26. Surowe wyniki sprawdzianu w szkole D (średnia punktów uzyskanych przez uczniów) w latach
2002-2007 [6]

rok wynik

szkoły (śr. pkt.)

2002

27,5 pkt.

2003

31,1 pkt.

2004

27,5 pkt.

2005

31,1 pkt.

2006

27,5 pkt.

2007

31,1 pkt.

Opinia ta jest krzywdząca, gdyż w porównaniu z innymi placówkami w Polsce, szkoła D jest pla-
cówką, której osiągnięcia systematycznie rosną – od „kapitału początkowego” 4. stanina, poprzez
kolejne cztery lata utrzymywania wysokiego wyniku (7. stanin), po kolejny wzrost w roku 2007,
pozwalający na osiągnięcie wyniku bardzo wysokiego (8. stanin):

Tabela 27., Rysunek 23. Surowe (średnia punktów uzyskanych przez uczniów) oraz znormalizowane (stani-
nowe) wyniki sprawdzianu w szkole D w latach 2002-2007 [6] [7]

rok wynik

szkoły (śr. pkt.) wynik szkoły (stanin)

2002

27,5 pkt.

4

2003

31,1 pkt.

7

2004

27,5 pkt.

7

2005

31,1 pkt.

7

2006

27,5 pkt.

7

2007

31,1 pkt.

8

W celu ułatwienia analizy osiągnięć edukacyjnych uczniów w danej szkole w kolejnych
latach, pod adresem

0H0H0H0H

www.cke.edu.pl, w zakładce Wyniki szkół, prezentowane jest

zestawienie wyników tejże szkoły w odniesieniu do znormalizowanych wyników krajowych:

Tabela 28., Rysunek 24. Wyniki szkoły Z ze sprawdzianów 2002-2007 na tle osiągnięć innych szkół w
Polsce [7]

Szkoła powinna analizować swoje wyniki jeszcze dokładniej, badając np. efektywność
pracy grup nauczycieli. Oto przykład takiej szkolnej analizy.

Przykład:

Tabela 29. przedstawia wyniki staninowe szkoły K., która – gdybyśmy analizowali

jedynie jej wyniki surowe: zawsze

28

punktów z każdej części egzaminu – pracowała z kolejnymi

rocznikami uczniów jednakowo efektywnie. Analiza wyników odniesionych do osiągnięć innych
szkół w kraju dowodzi, że ta rzekoma stabilizacja nie jest prawdą ani w przypadku nauczycieli
przedmiotów matematyczno-przyrodniczych (stały wzrost w latach 2002-2004 oraz utrzymanie
wysokiej pozycji – 7. stanin – przez 4 kolejne lata), ani tym bardziej w przypadku nauczycieli
przedmiotów humanistycznych.

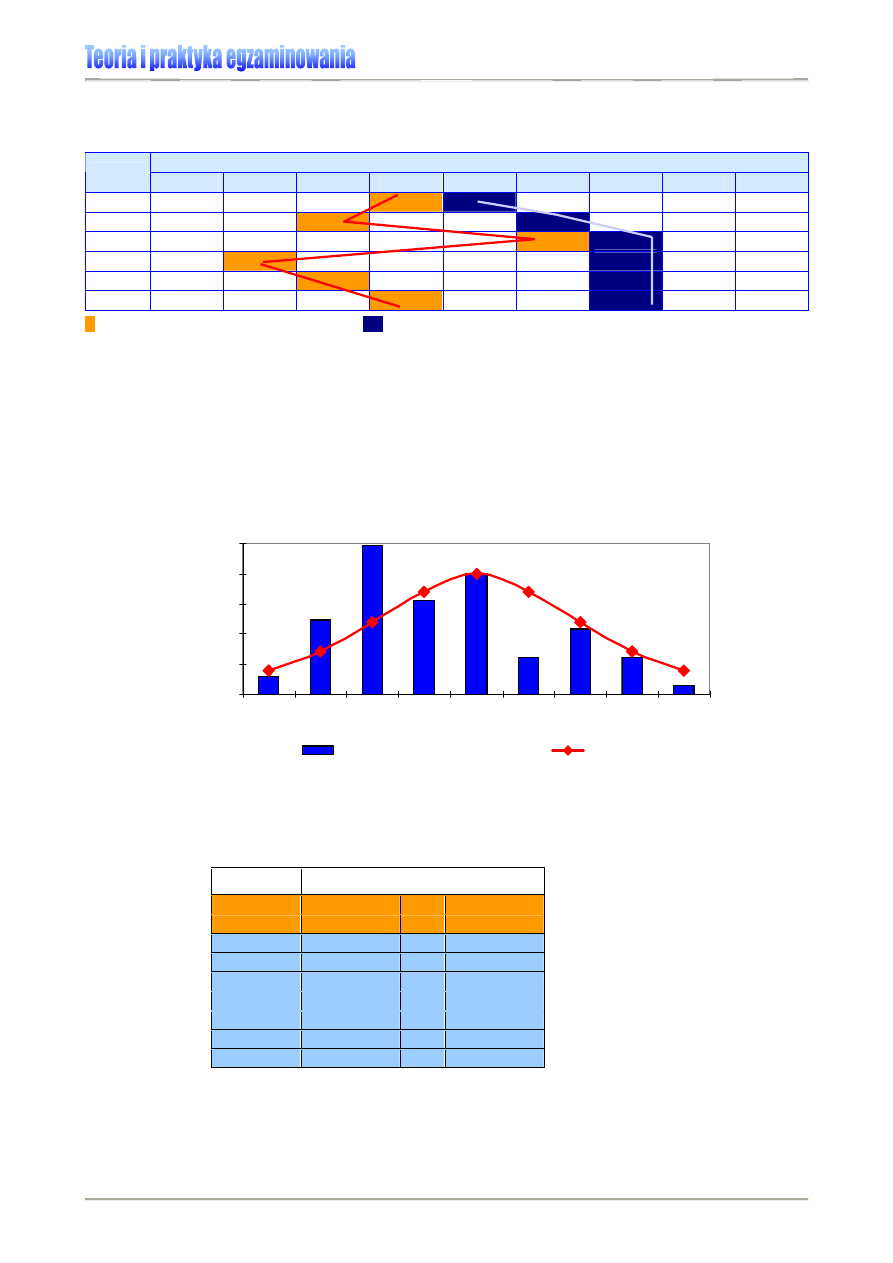
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

51

Tabela 29. Znormalizowane wyniki szkoły K. z obu części egzaminu gimnazjalnego 2002-2007, uzyskującej
stały wynik 28 pkt. [6]

stanin

rok

1

2

3

4

5

6

7

8

9

2002

H

MP

2003

H

MP

2004

H

MP

2005

H

MP

2006

H

MP

2007

H

MP

H

wynik części humanistycznej egzaminu

MP

wynik części matematyczno-przyrodniczej

egzaminu

Wnikliwa analiza wyników egzaminu pozwala też zbadać efektywność kształcenia w po-
szczególnych oddziałach szkolnych.

Przykład:

Oto wyniki matury 2007 z biologii zdawanej na poziomie podstawowym w LO w Matu-

rowie. Egzamin zdawało 65 osób z wszystkich 8 oddziałów tej szkoły. Wykres 24. przedstawia ich
osiągnięcia – najczęściej uzyskiwanym wynikiem w szkole okazał się 3. stanin (uzyskało go 15
uczniów, czyli prawie ¼ zdających). Wysokie wyniki (staniny 7.-9.) uzyskało tylko 12 osób (18,5%).

Wykres 24. Wyniki matury 2007 w LO w Maturowie z biologii na poziomie podstawowym na tle rozkładu
krajowego [6]

3

12,3

24,6

15,4

20

6,2

10,8

6,2

1,5

4

7

12

17

20

17

12

7

4

0

5

10

15

20

25

1

2

3

4

5

6

7

8

9

w ynik staninow y

cz

ę

sto

ść

(%)

szkoła (%)

kraj

Korzystając z „Karty wyników matury 2007” można odczytać, iż próg zdawalności egzaminu (30%)
zbiega się w tym przypadku z wynikiem granicznym dla 2. stanina:

Tabela 30. Karta wyników matury z biologii na poziomie podstawowym w 2007 r. [5]

Oznacza to, że aż 10 uczniów tej szkoły (15% zdających) nie przekroczyło tego progu:

Stanin

Wyniki na świadectwie

1

0%

-

20%

2

21%

-

30%

3

31%

-

40%

4

41%

-

50%

5

51%

-

61%

6

62%

-

70%

7

71%

-

78%

8

79%

-

84%

9

85%

-

100%

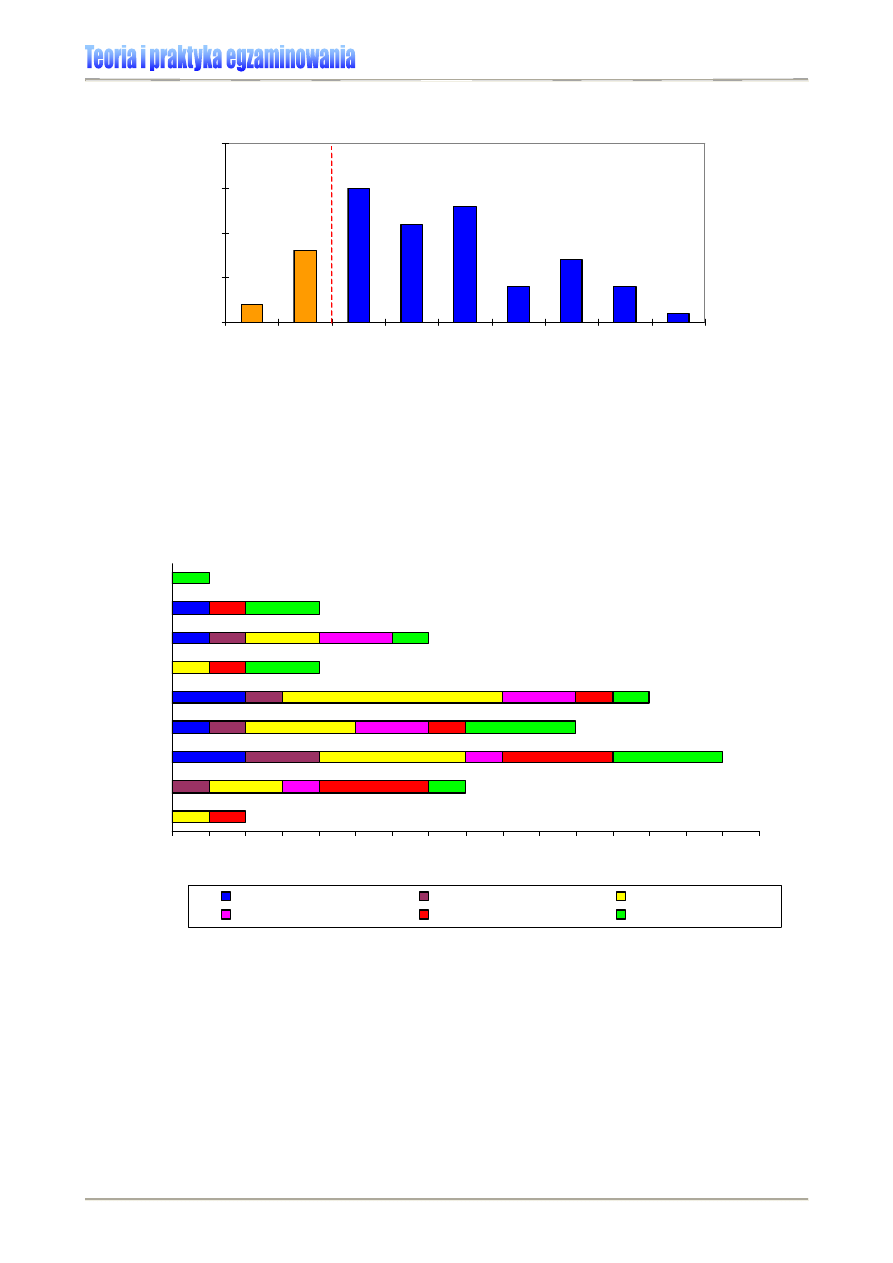
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

52

Wykres 25. Wyniki matury 2007 w LO w Maturowie z biologii na poziomie podstawowym w 2007 r. [6]

2

8

15

11

13

4

7

4

1

0

5

10

15

20

1

2

3

4

5

6

7

8

9

w ynik staninow y

lic

ze

bno

ść

Wykres 26. dostarcza szczegółowych informacji o efektywności kształcenia w poszczególnych
oddziałach szkolnych. Zdecydowanie poniżej oczekiwań (przeważająca liczba wyników średnich i
niskich, najwyższy wynik w 7. staninie) wypadła klasa IIIc, ekologiczna, w której realizowano
rozszerzony program nauczania biologii. Z klasy IIIa, ukierunkowanej na przedmioty ścisłe, maturę
z biologii pisało zaledwie 7 osób. Dwie z nich poradziły sobie z egzaminem dobrze (7. i 8. stanin),
wyniki pozostałych zaś mieszczą się w strefie wyników średnich. Jeśli uczniowie ci wybierali się na
studia medyczne, wyniki te raczej nie zapewniły im sukcesu w rekrutacji.

Wykres 26. Wyniki matury 2007 w LO w Maturowie z biologii na poziomie podstawowym dla poszczególnych
oddziałów szkolnych [6]

2

1

2

1

11

2

1

1

1

1

2

4

3

6

1

2

1

1

2

2

2

1

3

3

1

1

1

1

1

3

3

1

2

1

2

1

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

1

2

3

4

5

6

7

8

9

wyni

k stani

nowy

liczebność

IIIa – mat.-inf.

IIIb – humanist.

IIIc – ekologiczna

IIId – ekonomiczna

IIIe – artystyczna

IIIf – turyst.-sport.

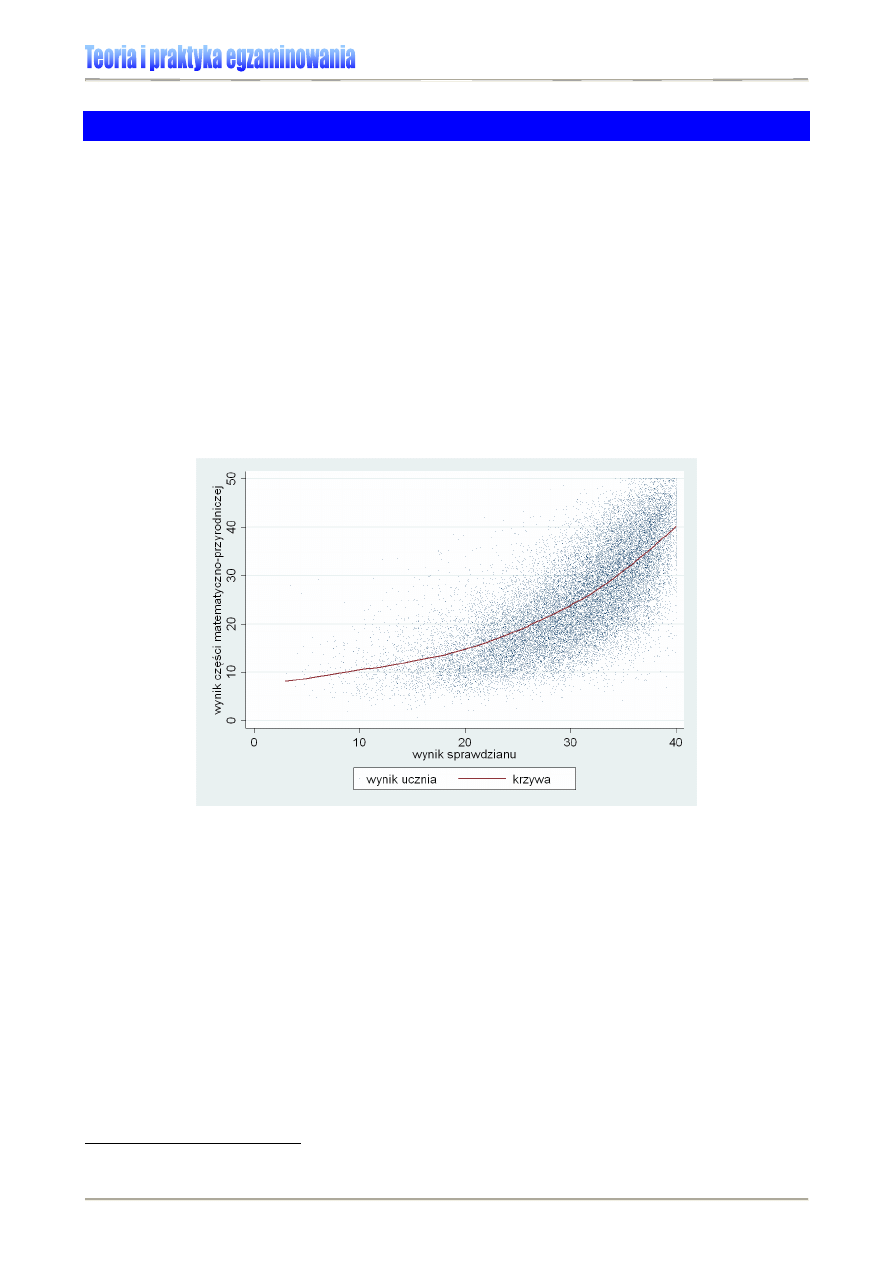
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

53

Analizy porównawcze i korelacyjne

Dzięki temu, iż już kilka roczników uczniów przystępowało do egzaminów po kolejnych
etapach edukacyjnych, możemy szukać związków pomiędzy poszczególnymi wynikami
egzaminów pisanych przez tych samych uczniów.

Poszukiwanie związku pomiędzy wynikami egzaminów pisanych przez tych samych
uczniów stanowi podstawę badania efektywności pracy szkoły. Najbardziej zaawansowa-
ną metodologię stosuje się w przypadku obliczania wskaźnika edukacyjnej wartości do-
danej, opartej na analizie regresji wyników z egzaminów „na wejściu” (np. ze sprawdzia-
nu) i „na wyjściu” (z egzaminu gimnazjalnego). Wykres 27. przedstawia wyniki całej popu-
lacji uczniów piszących sprawdzian w 2003, a egzamin gimnazjalny w 2006 r. (prawie pół
miliona obserwacji). Dopasowana do „chmury” wyników krzywa dzieli ów zbiór na wyniki
wyższe niż oczekiwane (powyżej linii regresji), zgodne z oczekiwaniami (leżące na krzy-
wej) oraz poniżej oczekiwań (wyniki pod krzywą).

Wykres 27. Sprawdzian a wynik części matematyczno-przyrodniczej egzaminu gimnazjalnego [8]

Dokonanie szczegółowych analiz wyników danej szkoły umożliwia zastosowanie Kalkula-
tora EWD, udostępnionego na stronie internetowej CKE.

41F41F41F41F

42

Pozwala on na wprowadzenie

nie tylko takich podstawowych danych, jak wynik egzaminu ucznia, ale uwzględnia też ta-
kie zmienne, jak płeć czy dysleksja.

Szkoły mogą także posiłkować się analizami wyników, które same gromadzą.

Przykład:

Oto wyniki uczniów Gimnazjum nr 1 w K. uzyskane na sprawdzianie i obu częściach

egzaminu gimnazjalnego. 33 obserwacje (kolorowe punkty) na Wykresie 28. obrazują związek
miedzy dwoma wynikami ucznia – ze sprawdzianu i egzaminu gimnazjalnego (odrębnie dla obu
części tego egzaminu).

42

W chwili obecnej możliwe jest obliczenie EWD dla r. 2005 i 2006 w gimnazjach.

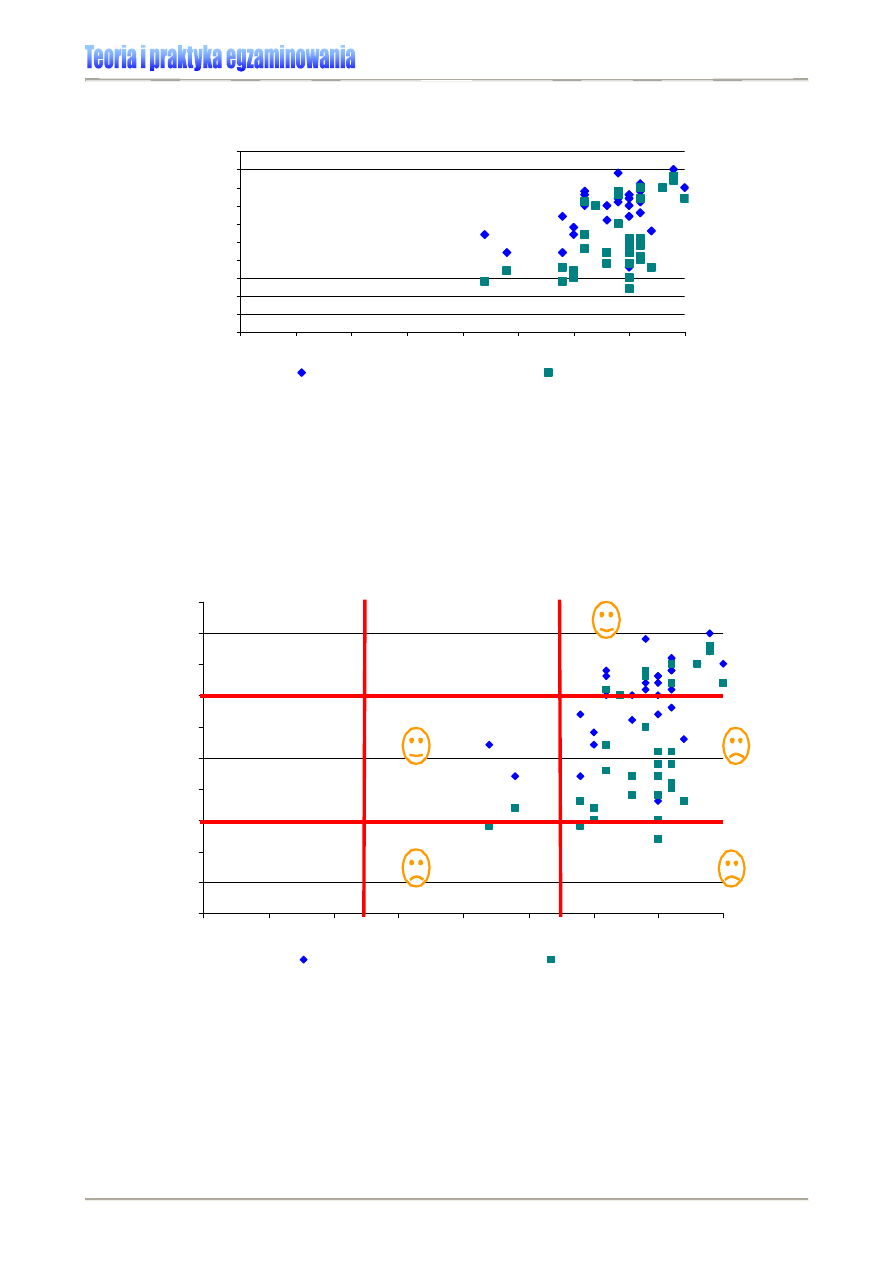
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

54

Wykres 28. Wyniki uczniów Gimnazjum nr 1. w K. „na wejściu” i „na wyjściu” [6]

0

5

10

15

20

25

30

35

40

45

50

0

5

10

15

20

25

30

35

40

sprawdzian

egzamin gimnazjalny

wynik GH

wynik GMP

Jeśli obszar wykresu podzielimy na pola ukazujące zależności pomiędzy wynikiem wyjściowym i
wejściowym (np. pole nr 1 – niski wynik ze sprawdzianu, ale wysoki wynik z egzaminu gimnazjal-
nego; pole nr 3 – wysoki ze sprawdzianu i wysoki wynik gimnazjalny; pole nr 9 – wysoki wynik ze
sprawdzianu, zaprzepaszczony w gimnazjum – tu niski wynik), uzyskamy wstępną informację o
efektywności kształcenia w danej szkole. Już na tej podstawie możemy bowiem zadawać sobie
pytania o skuteczność kształcenia np. w odniesieniu do uczniów, których wyniki po gimnazjum
okazały się zdecydowanie poniżej oczekiwań związanych z wynikiem „na wejściu”.

Wykres 29. Wyniki uczniów w Gimnazjum nr 1. w K. „na wejściu” i „na wyjściu” w obszarach wyników: ni-
skich, średnich i wysokich [6]

0

5

10

15

20

25

30

35

40

45

50

0

5

10

15

20

25

30

35

40

spraw dzian

egzamin gimnazjalny

w ynik GH

w ynik GMP

1

2

5

4

3

9

8

7

6

W sprawozdaniach CKE z 2007 r. znajdziemy kolejne przykłady takich porównań. Oto kil-
ka z nich.

Przykład

:

Tabele 31. i 32. pokazują istotny związek pomiędzy wynikami ucznia z obu części eg-

zaminu gimnazjalnego, zdeterminowany ich wysoką korelacją. Uważna analiza obu tabel pozwa-
la też obalić funkcjonujący przez lata mit o „zdeklarowanych humanistach”, którzy w szkole nie
radzą sobie z przedmiotami ścisłymi – tylko nieznaczny odsetek populacji (0,1%-0,2%) uzyskał
wyniki skrajne: wysoki z jednej, a niski z drugiej części egzaminu.

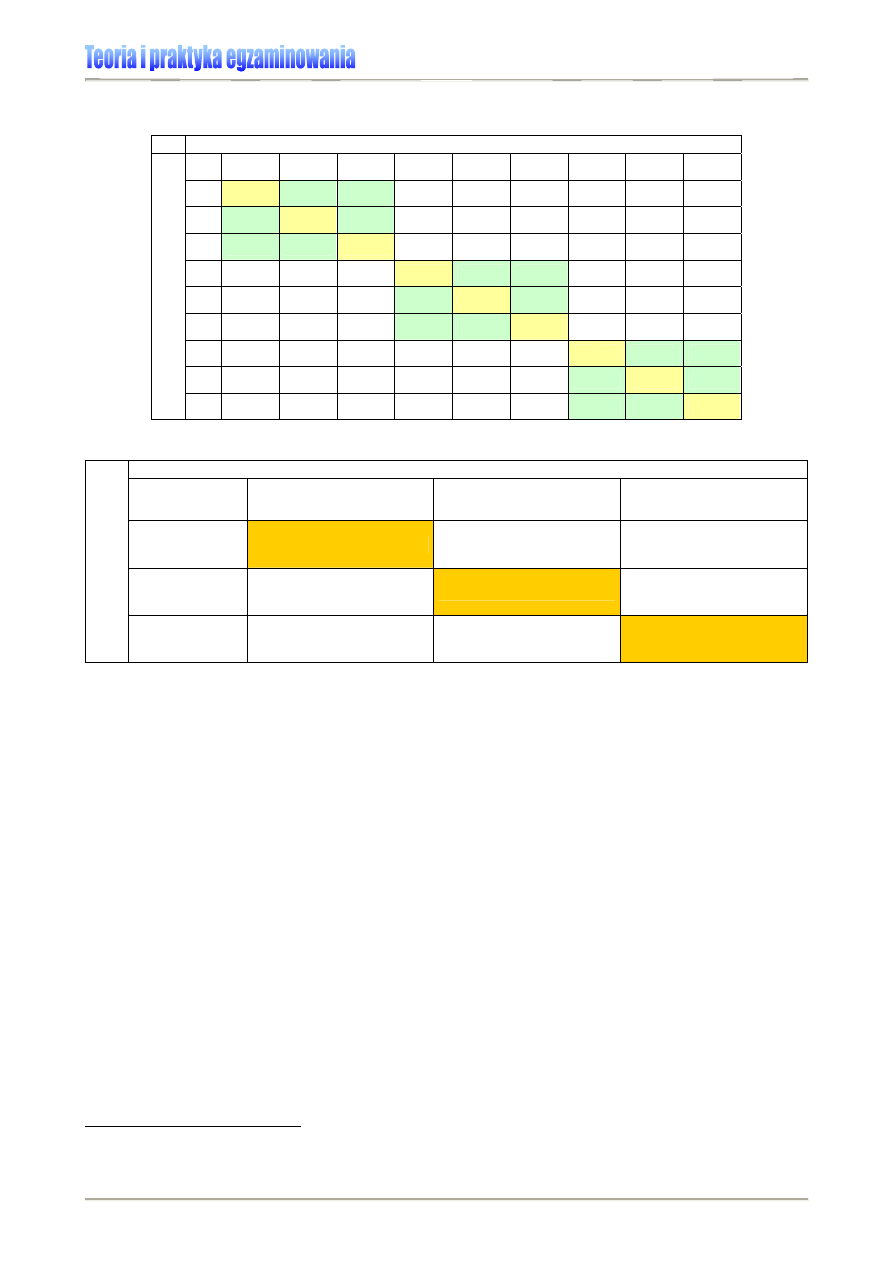
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

55

Tabela 31. Wyniki uczniów z obu części egzaminu gimnazjalnego 2007 [4]

staniny – część matematyczno-przyrodnicza 2007

1 2 3 4 5 6 7 8 9

1

1,3%

1,4%

1,0%

0,5% 0,1% 0%

0%

0%

0%

2

0,9%

1,8%

1,9%

1,3% 0,5% 0,1% 0%

0%

0%

3

0,7%

2,1%

3,1%

3,3% 1,8% 0,4% 0,1% 0%

0%

4

0,3% 1,4% 3,0% 4,8%

4,3%

1,6%

0,5% 0,1% 0%

5

0,1% 0,6% 1,9% 4,6%

7,0%

4,7%

2,3% 0,6% 0,1%

6

0% 0,1% 0,5% 1,7%

4,2%

4,7%

3,6% 1,6% 0,5%

7

0% 0%

0,1% 0,5% 1,9% 2,9% 3,1%

1,8%

0,8%

8

0%

0%

0%

0,2% 0,8% 1,7% 2,3%

1,7%

1,0%

stanin

y – cz.

humanis

ty

cz

na 20

07

9

0%

0%

0%

0% 0,2% 0,6% 1,2%

1,2%

1,0%

Tabela 32. Wyniki uczniów z obu części egzaminu gimnazjalnego 2007 [4]

część matematyczno-przyrodnicza egzaminu gimnazjalnego w roku 2007

Strefa wyników niskich

(0-16 pkt.)

Strefa wyników średnich

(17-33 pkt.)

Strefa wyników wysokich

(34-50 pkt.)

Strefa wyników

niskich

(0-23 pkt.)

14%

8% 0,1%

Strefa wyników

średnich

(24-39 pkt.)

8%

38%

9%

cz

ęś

ć hu

ma

nistyc

zn

a

w roku 20

07

Strefa wyników

wysokich

(40-50 pkt.)

0,2% 9% 14%

Liczne analizy porównawcze można czynić także, porównując

wyniki egzaminu gimna-

zjalnego i matury. Oto kilka przykładów ze sprawozdania CKE Osiągnięcia maturzystów
w 2007 r.

42F42F42F42F

43

Przykład:

Maturzyści 2007 zdawali egzamin gimnazjalny w latach 2002-2004. Większość z nich to

tegoroczni absolwenci liceów ogólnokształcących, którzy przystępowali do tego egzaminu w roku
2004. W komputerowych bazach okręgowych komisji egzaminacyjnych odszukano wyniki wszyst-
kich obecnych maturzystów wraz z informacją, do jakiej strefy należą. Z poniższego wykresu moż-
na odczytać, że duża część uczniów z niskimi wynikami egzaminu gimnazjalnego nie kontynuowa-
ła nauki w szkołach kończących się maturą, wybierając zasadnicze szkoły zawodowe. Tylko ok.
10% uczniów o niskim potencjale edukacyjnym trafiło do liceów i techników.

43

Osiągnięcia maturzystów w roku 2007. Sprawozdanie z egzaminu maturalnego 2007, Centralna Komisja

Egzaminacyjna, czerwiec 2007, s. 119-125.

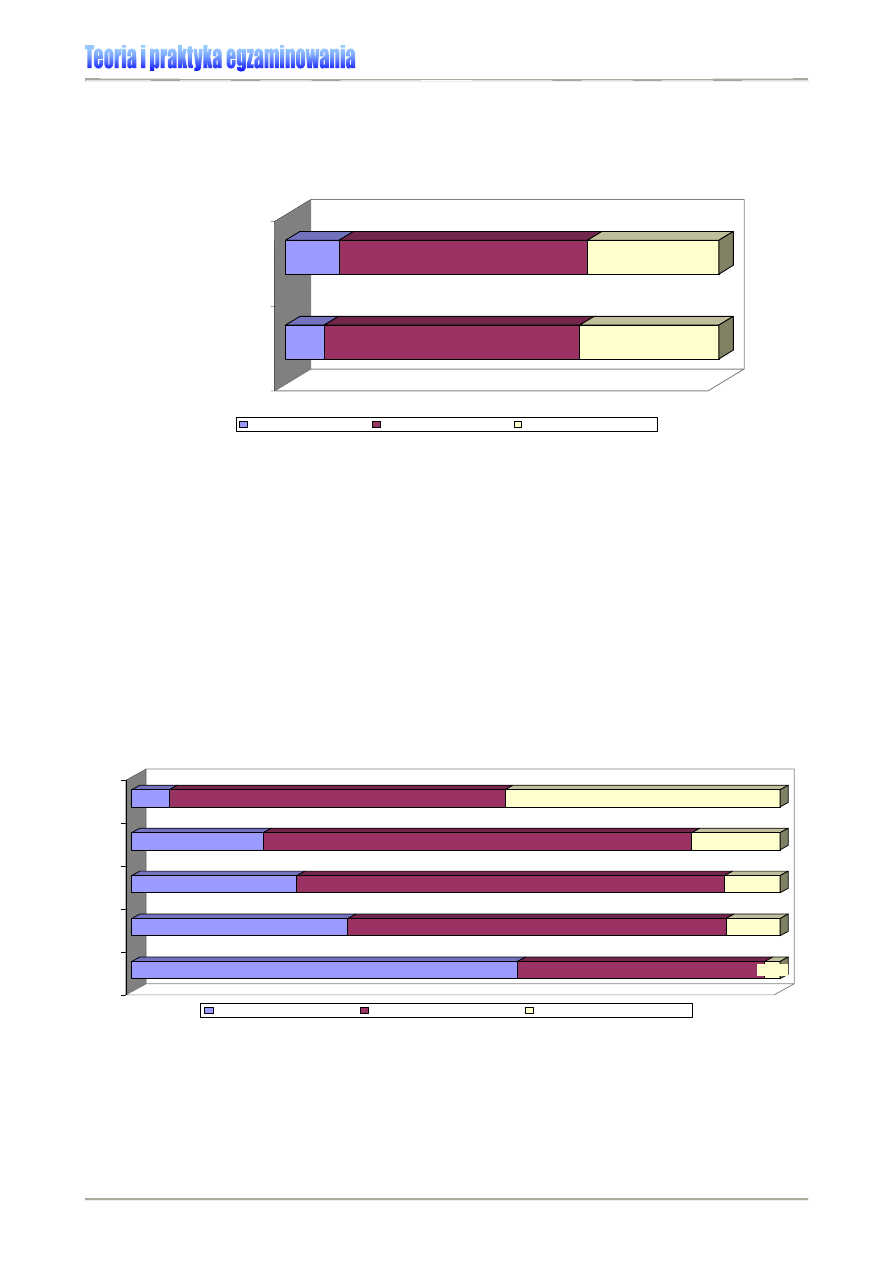
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

56

Wykres 30. Wyniki egzaminu gimnazjalnego zdawanego przez maturzystów 2007 [5]

8,9%

59%

32,1%

12,4%

57,3%

30,3%

część humanistyczna

część matematyczno -

przyrodnicza

Procent populacji maturzystów 2007, którzy na swoim egzaminie

gimnazjalnym mieli wyniki znajdujące się we wskazanych strefach

strefa niskich wyników

strefa średnich wyników

strefa wysokich wyników

Warto tu przypomnieć, że z konstrukcji skali staninowej wynika, iż strefa wyników niskich danej
części egzaminu gimnazjalnego w każdym roku obejmuje 23% populacji zdających, strefa wyników
średnich – 54%, strefa wyników wysokich – 23%.

Absolwenci gimnazjów z lat 2002-2004 kontynuowali naukę w szkole ponadgimnazjalnej: liceum
ogólnokształcącym (LO), liceum profilowanym (LP), technikum (T) czy zasadniczej szkole
zawodowej. Absolwenci szkół zawodowych też mogli kontynuować naukę w liceum (LU) bądź
technikum uzupełniającym (TU) i po jego ukończeniu przystąpić do matury. Sprawdzono, w jakich
strefach (niskich, średnich, wysokich) znajdowały się wyniki egzaminu gimnazjalnego
tegorocznych maturzystów, absolwentów pięciu typów szkół. Zwracają uwagę znaczne różnice w
strukturze wyników gimnazjalnych populacji uczniów wybierających różne typy szkoły kończące się
maturą.

Wykres 31. Wyniki egzaminu gimnazjalnego zdawanego przez maturzystów 2007 a ich wybór typu szkoły [5]

5 9 , 5 %

3 8 ,1 %

2 ,4 %

3 3 ,3 %

5 8 , 3 %

8 ,3 %

2 5 , 5 %

6 6 , 0 %

8 ,6 %

2 0 , 3 %

6 6 , 1 %

1 3 , 6 %

5 , 8 %

5 1 , 8 %

4 2 ,4 %

L U

T U

L P

T

L O

P r o c e n t m a t u r z y s t ó w 2 0 0 7 , a b s o lw e n t ó w p o s z c z e g ó ln y c h t y p ó w s z k ó ł,

k t ó r z y m ie li w y n ik i c z ę ś c i m a t e m a t y c z n o - p r z y r o d n ic z e j

e g z a m in u g im n a z ja ln e g o w e w s k a z a n y c h s t r e f a c h

s t r e f a n is k ic h w y n ik ó w

s t r e fa ś r e d n ic h w y n ik ó w

s tr e f a w y s o k ic h w y n ik ó w

Przykład:

Każdy z maturzystów roku 2007 wybierał jeden egzamin obowiązkowy spośród siedmiu

przedmiotów ogólnych (biologia, chemia, fizyka i astronomia, geografia, historia, matematyka lub
wiedza o społeczeństwie) bądź trzech przedmiotów artystycznych (historia muzyki, historia sztuki,
wiedza o tańcu). Populacje zdających obowiązkowe egzaminy z tych przedmiotów są rozłączne.
Trudno więc wprost porównywać wyniki matur z tych przedmiotów. Korzystając z możliwości po-
działu populacji maturzystów 2007 na grupy zdających ten sam egzamin gimnazjalny zbadano, jaki

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

57

potencjał na wejściu do szkoły ponadgimnazjalnej mieli abiturienci zdający różne obowiązkowe
egzaminy. Zwracają uwagę znaczne różnice w strukturze grup zdających. Biorąc pod uwagę
wspólny punkt odniesienia, jakim są wyniki tego samego egzaminu gimnazjalnego, można stwier-
dzić, że najsłabszy potencjał mieli zdający obowiązkowo wos i geografię, najmocniejszy – zdający
obowiązkowo fizykę.

Wykres 32. Wyniki egzaminu gimnazjalnego zdawanego przez maturzystów 2007 a ich wybór typu szkoły [5]

0 , 6 %

2 4 , 3 %

7 5 , 1 %

1 , 1 %

3 6 , 3 %

6 2 , 6 %

2 , 5 %

4 2 , 7 %

5 4 , 9 %

6 , 0 %

5 5 , 8 %

3 8 , 2 %

1 3 , 8 %

5 9 , 5 %

2 6 , 7 %

1 6 , 0 %

6 6 , 2 %

1 7 , 8 %

2 0 , 0 %

6 4 , 1 %

1 5 , 9 %

f iz y k a z a s t r o n o m ią

m a t e m a t y k a

c h e m ia

h is t o r ia

b io lo g ia

g e o g r a f ia

w i e d z a o s p o łe c z e ń s t w ie

P r o c e n t m a t u r z y s t ó w 2 0 0 7 , z d a j ą c y c h w s k a z a n e e g z a m i n y o b o w i ą z k o w e ,

k t ó r z y m i e l i w y n i k i c z ę ś c i m a t e m a t y c z n o - p r z y r o d n i c z e j e g z a m i n u

g i m n a z ja l n e g o w e w s k a z a n y c h s t r e f a c h

s t r e f a n is k ic h w y n ik ó w

s t r e f a ś r e d n ic h w y n ik ó w

s t r e f a w y s o k ic h w y n ik ó w

Przykład:

Po zakończeniu egzaminu maturalnego zbadano powiązania między wynikami obu

egzaminów – matury i egzaminu gimnazjalnego – dla poszczególnych zdających. W roku 2007
maturzyści przystępujący do egzaminu z tego samego przedmiotu na różnych poziomach
(podstawowym albo rozszerzonym) stanowili rozłączne grupy. Ponownie korzystając z możliwości
podziału populacji maturzystów 2007 na grupy zdających ten sam egzamin gimnazjalny zbadano,
jaki potencjał na wejściu do szkoły ponadgimnazjalnej mieli abiturienci zdający egzamin z tego
samego przedmiotu na różnych poziomach.

W poniższych tabelach w kolumnach jest podział na strefy wyników pisemnego egzaminu
maturalnego ze wskazanego przedmiotu na wskazanym poziomie, w wierszach – podział na strefy
wyników odpowiedniej części egzaminu gimnazjalnego. Porównanie sum kolejnych wierszy
pozwala na charakteryzację potencjału „na wejściu” zdających maturę na danym poziomie.
Możliwe są porównania zarówno w obrębie jednego przedmiotu (różne poziomy egzaminu), jak i
obrębie jednego poziomu (różne przedmioty). Warto zwrócić uwagę na łączny procent tych,
których wyniki obu egzaminów (matury i egzaminu gimnazjalnego) znajdują się w tej samej strefie.

Tabele 33., 34. Wyniki egzaminu gimnazjalnego i matury 2007 [5]

Strefa wyników

niskich z matematyki

na poziomie

podstawowym

Strefa wyników

średnich z

matematyki na

poziomie

podstawowym

Strefa wyników

wysokich z

matematyki na

poziomie

podstawowym

Strefa wyników niskich

na egzaminie

gimnazjalnym w części

matematyczno-

przyrodniczej

1%

0%

0%

Strefa wyników

średnich na egzaminie

gimnazjalnym w części

matematyczno-

przyrodniczej

16%

33%

3%

Strefa wyników

wysokich na egzaminie

gimnazjalnym w części

matematyczno-

przyrodniczej

4%

32%

10%

egzamin maturalny

eg

zam

in g

im

n

azj

a

ln

y

Strefa wyników

niskich z biologii na

poziomie

podstawowym

Strefa wyników

średnich z biologii na

poziomie

podstawowym

Strefa wyników

wysokich z biologii na

poziomie

podstawowym

Strefa wyników niskich

na egzaminie

gimnazjalnym w części

matematyczno-

przyrodniczej

13%

6%

0%

Strefa wyników

średnich na egzaminie

gimnazjalnym w części

matematyczno-

przyrodniczej

17%

44%

6%

Strefa wyników

wysokich na egzaminie

gimnazjalnym w części

matematyczno-

przyrodniczej

1%

7%

5%

egzamin maturalny

e

g

za

mi

n

g

imn

a

zj

a

ln

y

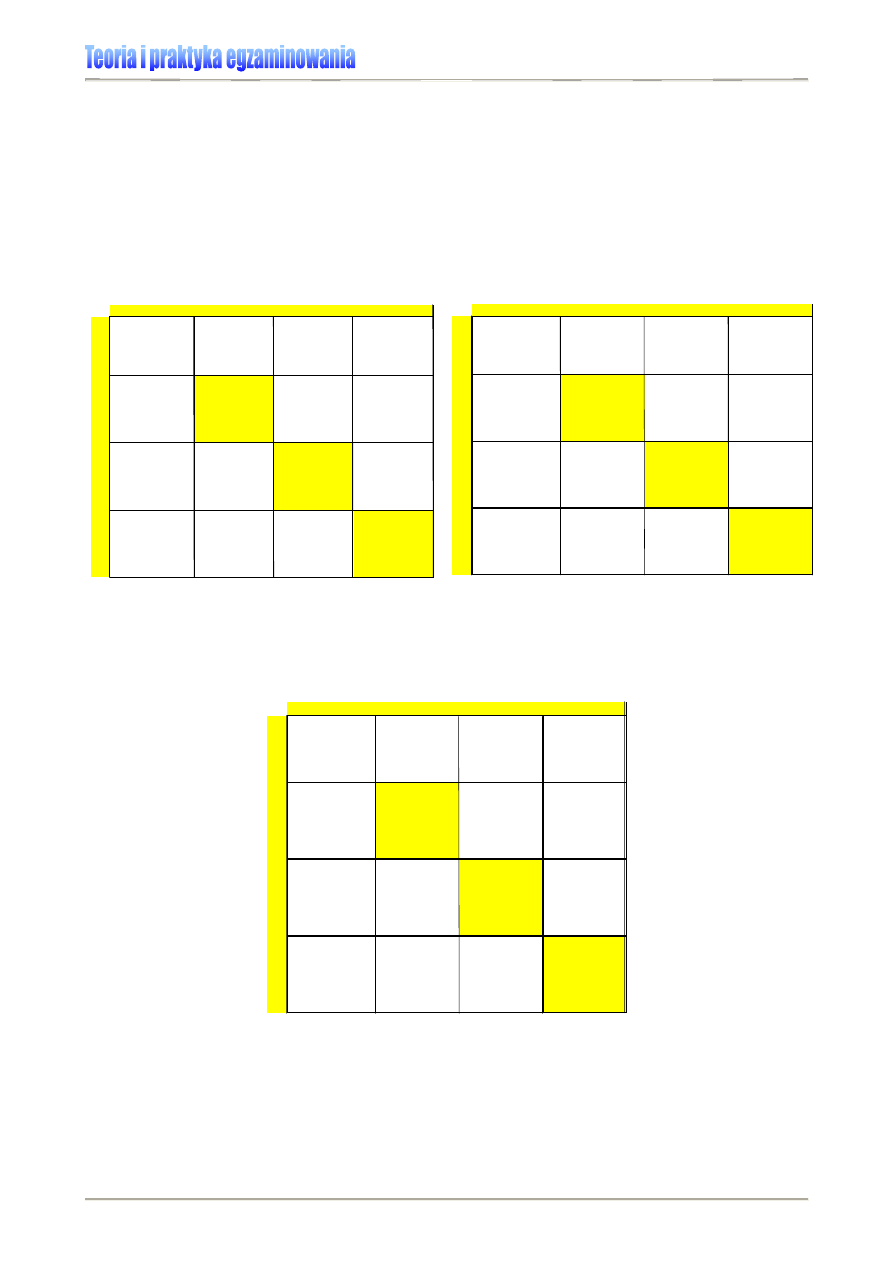
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

58

Przykład:

Wszyscy maturzyści obowiązkowo zdają pisemny egzamin z języka polskiego. Biorąc

pod uwagę ten punkt odniesienia, podjęto próbę porównania wyników maturzystów zdających na
tym samym poziomie (podstawowym albo rozszerzonym) pisemne egzaminy z różnych przedmio-
tów obowiązkowych (są to rozdzielne populacje).

Widać dużą zgodność wyników matury na poziomie podstawowym z przedmiotu wybranego
i z języka polskiego. Ponad połowa zdających ma wyniki dokładnie w tej samej strefie z obu tych
przedmiotów. Dla maturzystów ze średnimi wynikami poziomu podstawowego z języka polskiego
matematyka była trudniejsza niż historia.

Tabele 35., 36. Związek pomiędzy wynikami zdającego maturę 2007 z różnych przedmiotów [5]

Strefa wyników

niskich z języka

polskiego na

poziomie

podstawowym

Strefa wyników

średnich z języka

polskiego na

poziomie

podstawowym

Strefa wyników

wysokich z języka

polskiego na

poziomie

podstawowym

Strefa wyników niskich

z historii na poziomie

podstawowym

6%

5%

0%

Strefa wyników

średnich z historii na

poziomie

podstawowym

13%

42%

14%

Strefa wyników

wysokich z historii na

poziomie

podstawowym

1%

8%

9%

egzamin maturalny

egzam

in

m

at

u

ral

n

y

Strefa wyników

niskich z języka

polskiego na

poziomie

podstawowym

Strefa wyników

średnich z języka

polskiego na

poziomie

podstawowym

Strefa wyników

wysokich z języka

polskiego na

poziomie

podstawowym

Strefa wyników niskich

z matematyki na

poziomie

podstawowym

9%

15%

2%

Strefa wyników

średnich z matematyki

na poziomie

podstawowym

9%

40%

14%

Strefa wyników

wysokich z matematyki

na poziomie

podstawowym

1%

6%

5%

egzam in m aturalny

e

g

za

mi

n

ma

tu

ra

ln

y

Połowa populacji maturzystów zdających na poziomie rozszerzonym zarówno język polski
(pisemnie) jak i historię ma wyniki dokładnie w tej samej strefie. Do wyjątków należą przypadki, w
których niskim wynikom z historii (języka polskiego) towarzyszą wysokie wyniki z drugiego
przedmiotu. Układ wyników (średni i wysoki) przeważa nad układem (średni i niski).

Tabela 37. Związek pomiędzy wynikami zdającego maturę 2007 z różnych przedmiotów [5]

Strefa wyników

niskich z języka

polskiego na

poziomie

rozszerzonym

Strefa wyników

średnich z języka

polskiego na

poziomie

rozszerzonym

Strefa wyników

wysokich z języka

polskiego na

poziomie

rozszerzonym

Strefa wyników niskich

z historii na poziomie

rozszerzonym

6%

11%

2%

Strefa wyników

średnich z historii na

poziomie

rozszerzonym

8%

31%

14%

Strefa wyników

wysokich z historii na

poziomie

rozszerzonym

1%

13%

13%

egzamin maturalny

e

g

za

mi

n

ma

tu

ra

ln

y

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

59

Zastosowanie wybranych skal znormalizowanych w analizie
wyników matury podczas rekrutacji na wyższe uczelnie

Załóżmy, że Wyższa Szkoła Nauk Wszelakich w X ustaliła, iż w 2007 r. rekrutacja na Wy-
dział Rozwoju Kariery prowadzona będzie na podstawie wyników egzaminu maturalnego
z:

matematyki na poziomie rozszerzonym,

języka obcego na poziomie podstawowym,

jednego z następujących przedmiotów zdawanych na poziomie podstawowym: wos,
historia, biologia, chemia, fizyka, geografia.

Nim rekrutacja się odbędzie, Senat uczelni zlecił swoim pracownikom naukowym analizę
porównawczą wyników maturalnych osób ubiegających się o przyjęcie na ten wydział w
roku 2006, z zastosowaniem różnych skal rozkładu wyników, oraz poprosił o zarekomen-
dowanie skali, w której powinny być wyrażone wyniki maturalne kandydatów.

Przykład:

Podczas rekrutacji na rok akademicki 2006/07 do Wyższej Szkoły Rozwoju Kariery bra-

no pod uwagę następujące wyniki egzaminu maturalnego:

matematyka na poziomie podstawowym,

matematyka na poziomie rozszerzonym,

język obcy na poziomie podstawowym,

język obcy na poziomie rozszerzonym,

do wyboru przez kandydata jeden z przedmiotów: wos, historia, biologia, chemia, fizyka lub
geografia – zdawany na poziomie podstawowym.

Tu przyjrzyjmy się wynikom jedynie czworga kandydatów, w dodatku zdających maturę zarówno w
2006, jak i w 2005 roku (mogli ubiegać się o przyjęcie na studia na równych prawach, ponieważ
zdawali tzw. nową maturę). Tak się składa, iż każdy z nich uzyskał ze wszystkich branych pod
uwagę przedmiotów 70% punktów.

Tabela 38. Wyniki procentowe (x

%

) kandydatów na studia w Wyższej Szkole Nauk Wszelakich [6]

Beata Kowalewska

matura 2005

Bartosz Nowak

matura 2005

Kajetan Mądry

matura 2006

Kinga Szmit

matura 2006

Wybrane

przedmioty

1 2 3 4

matematyka

P

70% 70% 70% 70%

matematyka R

70% 70% 70% 70%

język angielski P

70%

język angielski R

70%

język niemiecki P

70%

język niemiecki R

70%

język francuski P

70%

język francuski R

70%

język hiszpański P

70%

język hiszpański R

70%

wos P

70%

historia P

70%

geografia P

70%

biologia P

70%

chemia P

fizyka P

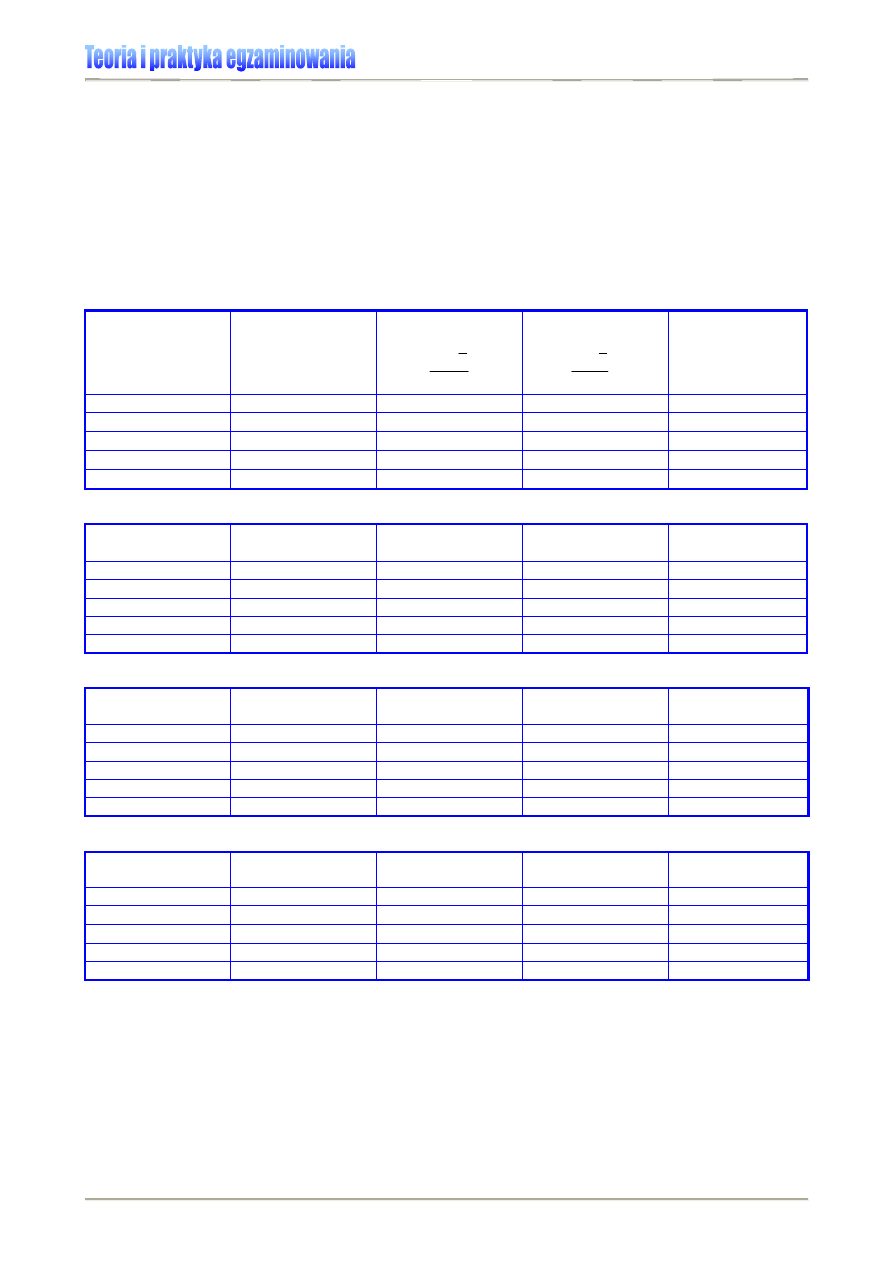
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

60

Jak wybrać najlepszych? Analiza surowego wyniku odpada, bo procentowy nie różnicuje (przypo-
mnijmy – wszyscy zdobyli 70% punktów), a punktowy nie nadaje się do porównań ze względu na
różną liczbę punktów możliwych do uzyskania na egzaminach z różnych przedmiotów (stąd na
świadectwie podaje właśnie wynik procentowy).

Podjęty trud znormalizowania wyników pozwala na zaistnienie wyników indywidualnych
kandydatów na studia w kontekście osiągnięć ich konkurentów. Oto wyniki czworga naszych
kandydatów: staninowy, standardowy, centylowy oraz na skali CEEB.

Tabela 39. Znormalizowane wyniki kandydatów na studia w Wyższej Szkole Nauk Wszelakich [6]

Kandydatka 1. Beata Kowalewska – matura 2005

Wybrane

przedmioty

Wynik staninowy

x

st.nine

Wynik

standardowy

s

x

x

−

Wynik

CEEB

100

500

×

−

+

s

x

x

Wynik

centylowy

x

centyl

matematyka P

6

0,7

569

72

matematyka R

8 1,8 676

95

język angielski P

4 -0,4 461 31

język angielski R

5 0,3 528

57

historia P

7 1,0 603

83

Kandydat 2. Bartosz Nowak – matura 2005

Wybrane

przedmioty

Wynik

staninowy

Wynik

standardowy

Wynik

CEEB

Wynik

centylowy

matematyka P

6

0,7

569

72

matematyka R

8 1,8 676

95

język niemiecki P

5 -0,1 488 42

język niemiecki R

6 0,5 553

68

geografia P

6 0,7 573

74

Kandydat 3. Kajetan Mądry – matura 2006

Wybrane

przedmioty

Wynik

staninowy

Wynik

standardowy

Wynik

CEEB

Wynik

centylowy

matematyka P

5

0,2

524

69

matematyka R

7 1,3 626 69

język francuski P

4 -0,4 459 70

język francuski R

6 0,5 545

69

biologia P

7 1,2 620

70

Kandydatka 4. Kinga Szmit – matura 2006

Wybrane

przedmioty

Wynik

staninowy

Wynik

standardowy

Wynik

CEEB

Wynik

centylowy

matematyka P

5

0,2

524

69

matematyka R

7

1,3 626 69

język hiszpański P

3

-0,6 445 70

język hiszpański R

5 0,3 529

69

wos P

6 0,5 554

69

Porównanie wyników znormalizowanych może przynieść rezultat w postaci tzw. listy rankingowej,
wykorzystywanej w rekrutacji studentów. Tabela 20. pokazuje miejsce kandydata, na którym
plasuje się jego wynik wyrażony w każdej z wyżej wskazanych skal.

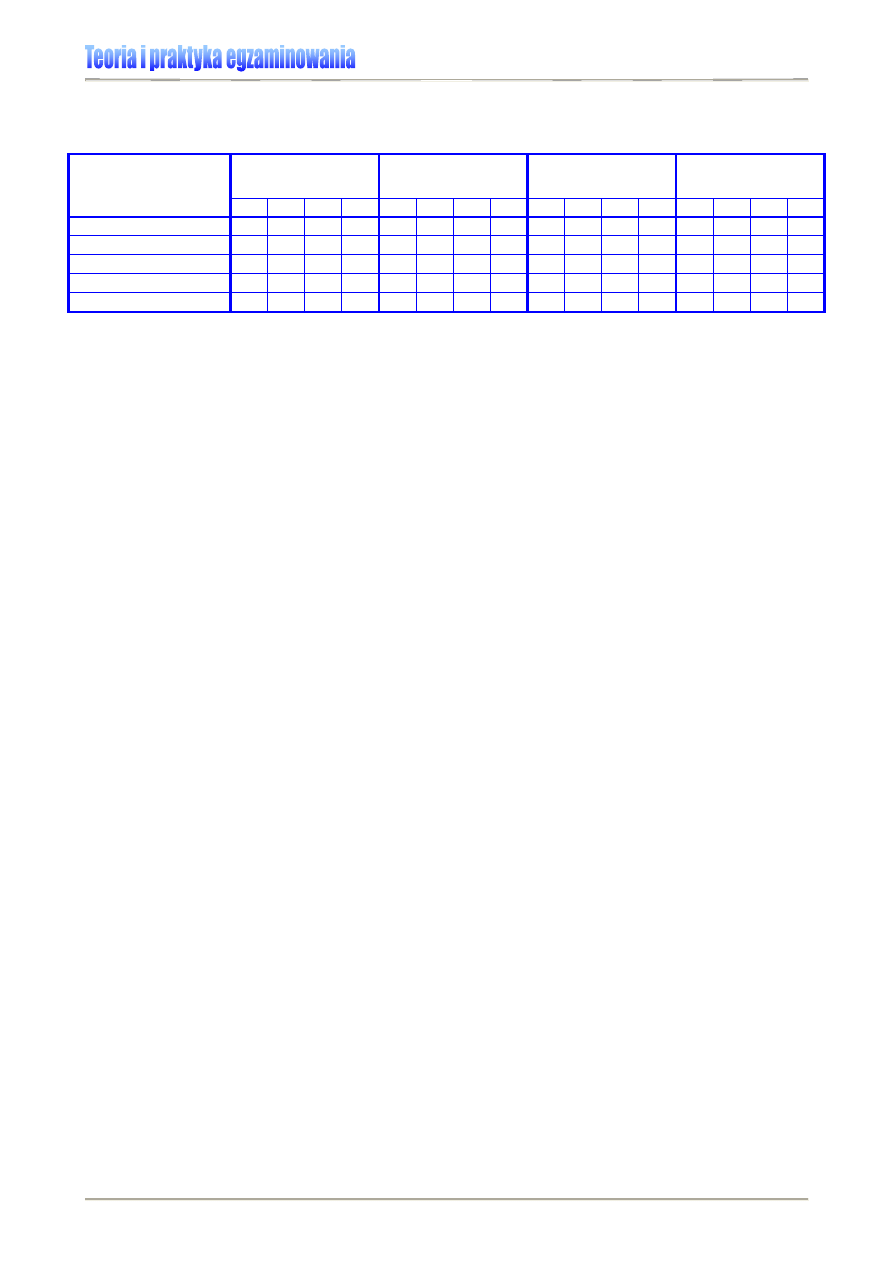
A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

61

Tabela 40. Pozycja rankingowa

kandydatów na studia w Wyższej Szkole Nauk Wszelakich w roku 2006 ze

względu na przyjętą skalę normalizacji wyników

Beata Kowalewska

matura 2005

Bartosz Nowak

matura 2005

Kajetan Mądry

matura 2006

Kinga Szmit

matura 2006

Wybrane przedmioty

SN SD CB CE SN SD CB CE SN SD CB CE SN SD CB CE

matematyka P

I I I I I I I I II II II II II II II II

matematyka R

I I I I I I I I II II II II II II II II

język obcy P

II II II III I I I II II II III I III III IV I

język obcy R

II II IV III I I I II I I II I II II III I

przedmiot wybrany P

I II II I II III III II I I I I II IV IV III

gdzie: P – poziom podstawowy egzaminu maturalnego, R – poziom rozszerzony

SN – wynik staninowy, SD – wynik standardowy, CB – wynik na skali CEEB, CE – wynik centylowy,

I, II, III, IV

– pozycja w rankingu

Oczywiście podczas rekrutacji, przede wszystkim z przyczyn czasowych, uczelnia nie może wyko-
rzystywać wielu skal. Decydując się na jedną z nich, trzeba by odrzucić te, które słabo różnicują
(tu: staninową). W przypadku Wyższej Szkoły Nauk Wszelakich, zaproponowano Senatowi uczel-
ni, by podczas rekrutacji prowadzonej w kolejnych latach wykorzystywać wyniki uczniów wyrażone
z użyciem akademickiej skali CEEB.

Mimo iż przykład Wyższej Szkoły Nauk Wszelakich jest przykładem wymyślonym, wiele
wskazuje na to, iż w niedalekiej przyszłości podczas rekrutacji uczelnie coraz chętniej bę-
dą sięgać po wyniki znormalizowane.

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

62

ŹRÓDŁA DANYCH

[1] Sprawdzian 2006. Sprawozdanie Centralnej Komisji Egzaminacyjnej, Warszawa 2006; zob. też:
www.cke.edu.pl/images/stories/Sprawdzian/raport_ws_akt.pdf
[2] Osiągnięcia uczniów kończących szkołę podstawową w roku 2007. Sprawozdanie Centralnej
Komisji Egzaminacyjnej, Warszawa 2006; zob. też:
www.cke.edu.pl/images/stories/Sprawdzian/raport_ws_akt.pdf
[3] Osiągnięcia uczniów kończących gimnazjum w roku 2007. Sprawozdanie z egzaminu
maturalnego 2007. Centralna Komisja Egzaminacyjna. Warszawa, czerwiec 2007; zob. też:

1H1H1H1H

www.cke.edu. pl/index.php?option=content&task=view&id=141&Itemid=122
[4] Osiągnięcia maturzystów w roku 2007. Sprawozdanie z egzaminu maturalnego 2007.
Centralna Komisja Egzaminacyjna. Warszawa, czerwiec 2007; zob. też:
www.cke.edu.pl/images/stories /Wyniki07mat/sprawozdanie_ogolne_a.pdf
[5] Opracowania własne Wydziału Badań i Ewaluacji Centralnej Komisji Egzaminacyjnej
[6] Wyniki szkół ze sprawdzianów i egzaminów 2002-07 oraz matury 2007 –

2H2H2H2H

www.cke.edu.pl - tu:

Wyniki szkół
[7] Edukacyjna wartość dodana, cz. 2. Biuletyn Badawczy Egzamin, nr 14/2007,

3H3H3H3H

www.cke.edu.pl -

tu: Badania, analizy, wyniki

POLECANA LITERATURA

Blalock H.M. Statystyka dla socjologów, Warszawa 1977, Wydawnictwo Naukowe PWN

Brzeziński J. Metodologia badań psychologicznych, Warszawa 1996, Wydawnictwo Naukowe
PWN

Brzeziński J. Trafność i rzetelność testów psychologicznych. Wybór tekstów, Gdańsk 2005,
Gdańskie Wydawnictwo Psychologiczne

Ferguson G. A., Takane Y. Analiza statystyczna w psychologii i pedagogice, Warszawa 2003,
Wydawnictwo Naukowe PWN

Guilford J.P. Podstawowe metody statystyczne w psychologii i pedagogice, Warszawa 1964,
Wydawnictwo Naukowe PWN

Hornowska E. Testy psychologiczne. Teoria i praktyka, Warszawa 2003, Wydawnictwo Na-
ukowe „Scholar”

Konarzewski K. Jak uprawiać badania oświatowe. Metodologia praktyczna, Warszawa 2002,
WSiP

Luszniewicz A. Statystyka nie jest trudna, Warszawa 2001, Polskie Wydawnictwo Ekonomicz-
ne

Łomnicki A. Wprowadzenie do statystyki dla przyrodników, Warszawa 2003, Wydawnictwo
Naukowe PWN

Nawojczyk M. Przewodnik po statystyce dla socjologów, Kraków 2002, SPSS Polska

Niemierko B. Pomiar wyników kształcenia, Warszawa 1999, WSiP

Niemierko B. Testy osiągnięć szkolnych. Podstawowe pojęcia i techniki obliczeniowe, Warsza-
wa 1975, WSiP

Sołtys D., Szmigel M.K., Doskonalenie kompetencji nauczycieli w zakresie diagnozy edukacyj-
nej, Kraków 1997., Wydawnictwo „Zamiast korepetycji”

Starzyńska W. Statystyka praktyczna, Warszawa 2002, Wydawnictwo Naukowe PWN

Szaleniec H., Szmigel M.K., Doskonalenie kompetencji nauczycieli w zakresie oceniania ze-
wnętrznego, Kraków 2001, Wydawnictwo „Zamiast korepetycji”

Wieczorkowska G., Kochański P., Eljaszuk M. Statystyka. Wprowadzenie do analizy danych
sondażowych i eksperymentalnych, Warszawa 2003, Wydawnictwo Naukowe „Scholar”

Zaczyński W.P. Praca badawcza nauczyciela, Warszawa 1995, WSiP

Zaczyński W.P. Statystyka w pracy badawczej nauczyciela, Warszawa 1997, Wydawnictwo
„Żak”

A n a l i z a i in te r p r e t a cj a w y n i k ó w o c e n i a ni a i egz a m i n o w a nia

W y d z i a ł B a d a ń i E w a l u a c ji C K E

63

NOTATKI