1

Arkusz kalkulacyjny wspomagający wyznaczanie planów
przemieszczeń ram obciążonych statycznie

Wyznaczanie planów przemieszczeń jest istotnym i chyba najtrudniejszym elementem
rozwiązania zadania metodą przemieszczeń. Aby ułatwić opanowanie tej czynności proponuje
się czytelnikowi wykorzystanie arkusza kalkulacyjnego MSExcel o nazwie „Plan_s.xls”,
który umożliwia sprawdzenie samodzielnie wykonanych obliczeń. O postaci planów
przemieszczeń decyduje poprawne przyjęcie wahaczy odbierających możliwość przechyłów
ramy. Zakłada się, że użytkownik arkusza wahacze dobiera samodzielnie, a z jego pomocą
sprawdza poprawność swojego wyboru. Arkusz pełni nie tylko funkcję weryfikującą, ale
także wykonuje automatycznie obliczenia związane z wyznaczaniem planów przemieszczeń.
Oprócz tego arkusz został wyposażony w szereg innych funkcji. Są one opisane w dalszej
części rozdziału.

Na początek kilka uwag natury ogólnej:

1. Aby zmniejszyć liczbę przechyłów ramy wskazane jest ograniczenie liczby

elementów statycznie wyznaczalnych. W praktyce jest to bardzo łatwe do
spełnienia, gdyż elementy takie można zredukować we wstępnej analizie
statycznej konstrukcji. Trzeba je tylko zastąpić znanymi reakcjami w miejscach
połączenia z resztą konstrukcji.

2. Arkusz został gruntownie sprawdzony pod względem poprawności wyników

otrzymywanych z jego pomocą. Dlatego pomyślne zakończenie obliczeń,
potwierdzone odpowiednim komunikatem, daje w efekcie zawsze poprawne
wyniki. Aczkolwiek trzeba pamiętać, że wyniki te odpowiadają danym
wprowadzonym podczas edycji arkusza. Błędne dane wpływają na otrzymane
wyniki. Stąd też wynika apel o bardzo staranne wprowadzanie danych.

3. Aby zapewnić spójność pomiędzy danymi i wynikami, po kończącym obliczenia

naciśnięciu przycisku <Oblicz> uniemożliwiono zmianę którejkolwiek z danych.
Wprowadzanie poprawek możliwe jest dopiero po zamknięciu arkusza i
ponownym jego otworzeniu. Następnie krok po kroku trzeba dojść do ponownego
przeliczenia arkusza za pomocą przycisku <Oblicz>.

4. Aby arkusz działał poprawnie musi być włączona obsługa makr.
5. Zaleca się żeby każde rozwiązane zadanie za pomocą arkusza zapisać nadając mu

nową nazwę. Dzięki temu oryginał arkusza pozostanie niezmieniony.
Zignorowanie tego zalecenia pociąga za sobą konieczność „posprzątania” po
poprzednim rozwiązaniu.

Prześledźmy szczegółowo zasady korzystania z arkusza analizując wyznaczenie planów
przemieszczeń w zadaniu 1

2

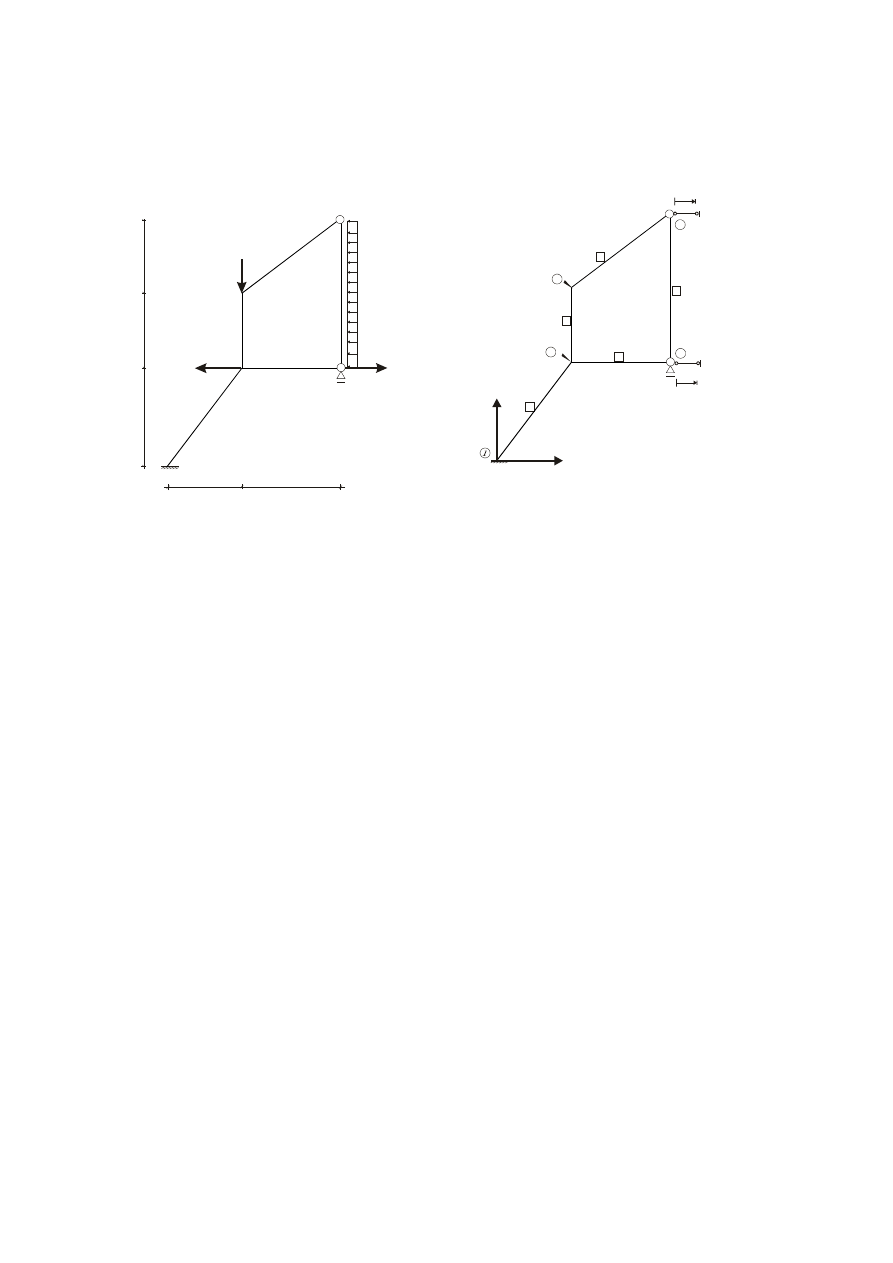
Zadanie 1
Zapisać równania równowagi ramy jak na Rysunku 1. Uwzględnić wpływ dużych sił
osiowych S. Przyjąć stałą sztywność EJ wszystkich prętów.

Rozwiązanie.

1. Załóżmy bez dowodu, że duże siły S nie powodują zginania danej ramy. Założenie to

w rozpatrywanym zadaniu jest prawdziwe i umożliwia wyznaczenie z elementarnej
równowagi węzłów dużych sił osiowych we wszystkich prętach(DSO). Siły te są
następujące.

.

0

,

0

,

4

,

,

5

5

4

3

2

1













S

S

S

S

S

S

S

S

Oczywiście punkt ten nie występuje w zadaniach zwykłego zginania bez udziału DSO.
2. Przed otworzeniem arkusza należy przyjąć układ geometrycznie wyznaczalny(UGW).

Dla arkusza istotne są tylko wahacze odbierające możliwość przechyłów ramy,
wskazujące na nieznane przemieszczenia translacyjne, ponumerowane w sposób
ciągły i oznaczane literą w. Do dalszych rozważań przyjęto wstępnie jeden z wielu
możliwych UGW(p. Rys. 2).

3. Układ współrzędnych kartezjańskich Oxy ma dowolnie położony początek. Pozioma

oś x układu musi być zwrócona w prawo, a oś y pionowo do góry.

4. Teraz można otworzyć arkusz. Po wybraniu opcji <Tak> w odpowiedzi na pytanie

„Czy nowe zadanie?”, trzeba w komórce A1 wpisać liczbę węzłów ramy, w tym także
węzłów podporowych. Opcję <Nie> wybieramy tylko wtedy, gdy zamierzamy poddać
edycji dane wcześniej wprowadzone, por. p.3 uwag podanych we wstępie opisu
arkusza. Następnie klikamy myszką sąsiedni przycisk <Liczba węzłów OK >. W
następstwie kliknięcia przycisku powinna odsłonić się tabela z listą węzłów.

5. Odsłoniętą tabelę należy starannie wypełnić. Jeśli tabela zawiera stare, nieaktualne

dane, trzeba je najpierw wyczyścić. Następnie należy wpisać aktualne współrzędne
węzłów, a zaraz obok opisać więzy odbierające składowe przemieszczeń

Rys. 1.

Rys. 2.

4

a

3

a

3a

4a

3

a

4S

4S

S

q

1

2

3

4

5

w

1

w

2

2

5

3

4

x

y

O

3

translacyjnych węzła. Cyfrą 0 oznacza się wszystkie więzy rzeczywiste(podpory), a
kolejnymi cyframi(<=5) oznacza się ponumerowane wahacze fikcyjne. Odebrane
przemieszczenia wzdłuż osi x opisuje się w kolumnie D, natomiast przemieszczenia
wzdłuż osi y opisuje się w kolumnie E. W arkuszu ograniczono liczbę niezależnych
przechyłów ramy do pięciu. Edycję tabeli trzeba zakończyć kliknięciem myszką
przycisku <Tylko więzy x y>, co ustawia kierunki więzów tak, że odpowiadające im
przemieszczenia w

i

są zgodnie ze zwrotami osi układu Oxy. Jeżeli faktycznie zwroty

wszystkich przemieszczeń wskazywanych przez więzy pokrywają się z kierunkami osi
układu Oxy można przejść do następnego punktu. W przypadku, gdy zwrot któregoś
wektora przemieszczenia nie pokrywa się z jednym ze zwrotów osi Oxy, należy w
komórce przesuniętej w prawo o dwie kolumny wpisać, podaną w radianach, wartość
kąta nachylenia wektora przemieszczenia do osi Ox(jest to kąt skierowany w układzie
Oxy). Wskazówka: najwygodniej jest wstawić dostępną w Excelu funkcję atan() z
odpowiednim argumentem będącym tangensem kąta. Zatem jeśli zachodzi taka
konieczność kąty te wpisuje się w kolumnie F lub G.

6. W komórce A24 trzeba wpisać liczbę prętów ramy. Następnie kliknąć myszką sąsiedni

przycisk <Liczba prętów OK>, po czym powinna odsłonić się tabela z listą prętów.

7. Tabelę należy wypełnić równie starannie jak tabelę dotyczącą węzłów. Ponieważ także

i ta tabela może zawierać stare, nieaktualne dane, trzeba je najpierw wyczyścić.
Następnie wpisuje się przypisane do każdego pręta właściwe numery węzłów,
początkowego i końcowego. Tymczasowo pozostaje jeszcze tylko wpisanie w
odpowiednich kolumnach niezerowych wartości wstępnej siły osiowej i sztywności
EJ, przypisanych do poszczególnych prętów. Wartości te wyrażone są w wielkościach
porównawczych.

8. Arkusz został zaprojektowany tak aby mógł automatycznie wskazywać pręty, których

kąty obrotu cięciw mogą być kondensowane statycznie. Ta opcja działa poprawnie o
ile zostaną w ramie wskazane wszystkie pręty geometrycznie wyznaczalne
obustronnie podparte przegubowo. Pamiętajmy, że pręt o takim sposobie podparcia
jest geometrycznie wyznaczalny, pod warunkiem że nie działa na niego DSO. Zatem
jeśli pręty geometrycznie wyznaczalne występują w ramie trzeba je wskazać poprzez
wpisanie cyfry jeden w odpowiedniej komórce kolumny H.

9. Na zakończenie wystarczy kliknąć myszką przycisk < Oblicz >. Teraz pojawi się seria

komunikatów. Każdy z nich trzeba przeczytać i zaakceptować odpowiednim
przyciskiem.

4

Dalsze rozważania są poświęcone interpretacji otrzymanych wyników. W tabeli poniżej
zestawiono znaczenie komunikatów pojawiających się w trakcie obliczeń.

Treść komunikatu/informacji

Znaczenie

UGW jest OK.

Przyjęto układ geometrycznie wyznaczalny,
w którym poprawnie odebrano możliwość
wszystkich przechyłów ramy.

Można skondensować kąty obrotu cięciw
prętów: nr1, nr2,…..nrk

Znaczenie tej informacji jest oczywiste, a
dodatkowo jest ona wyświetlana w komórce
C102. Uwaga: informacja jest prawdziwa o
ile wcześniej wskazano wszystkie pręty
geometrycznie wyznaczalne obustronnie
podparte przegubowo.

Poza wskazanymi kątami innych
kondensować nie można

Jeśli nie wskazano żadnego pręta do
kondensacji, komunikat oznacza
niemożność jakiejkolwiek kondensacji kąta
obrotu cięciwy. Uwaga: komunikat ten jest
prawdziwy o ile wcześniej wskazano
wszystkie pręty geometrycznie wyznaczalne
obustronnie podparte przegubowo.

UGW jest błędny.
Informacja towarzysząca: zbyt dużo więzów
fikcyjnych lub w nieodpowiednim miejscu

Znaczenie komunikatu wyjaśnia informacja
towarzysząca wyświetlana także w komórce
C102

UGW jest błędny

Przyjęto układ geometrycznie wyznaczalny,
w którym nie odebrano możliwości
wszystkich przechyłów ramy.

W ramie dublują się więzy!

Komunikat nie jest krytyczny dla
pozostałych obliczeń i jest także wyświetlany
w komórce B102. Oznacza on tylko tyle, że
w ramie nie można obliczyć wszystkich sił
podłużnych. Jest to efekt dublowania się
więzów wynikających z założenia o
podłużnej nieodkształcalności i sposobu jej
podparcia. Mimo to w ramach tego typu
można obliczyć siły poprzeczne i momenty
.zginające.

Treść innych komunikatów jest na tyle zrozumiała, że pominięto je w powyższej tabeli.
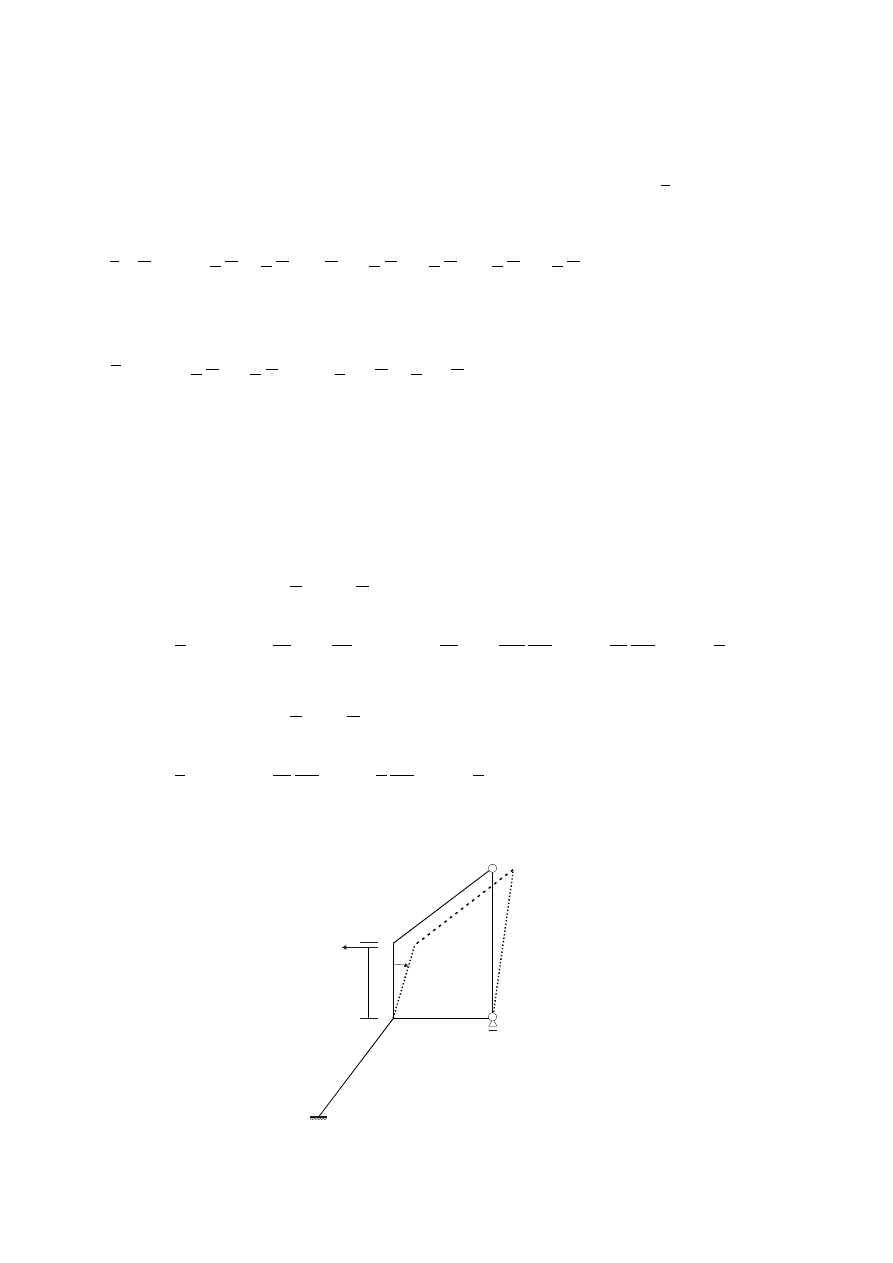
Stan arkusza po zakończeniu obliczeń przedstawia rysunek 3. Na rysunku począwszy od
wiersza 45 widać obliczone kąty obrotu cięciw wszystkich prętów. Otrzymane wartości

interpretuje się następująco. Np. kąt obrotu cięciwy pręta 3
wynosi.

2

1

3

3

1

48

7













5

są kątami porównawczymi kolejnych przechyłów ramy, zaś

symbol a oznacza jednostkę długości. W tej samej konwencji pokazane są po dwie

składowe przemieszczeń (u i v) wszystkich węzłów, wyskalowane w jednostce długości a.
Znajdują się one w górnej części arkusza, po prawej stronie. Składowa u jest zwrócona
zgodnie ze zwrotem osi x, a składowa v zgodnie ze zwrotem osi y. Inne użyteczne
informacje znajdują się w tabeli edycyjnej prętów. Można tam znaleźć automatycznie

obliczone długości prętów oraz wartości parametrów 

i

wyrażonych poprzez parametr

porównawczy . Czerwonym kolorem wyeksponowano wartości zespolone.
W zadaniach z udziałem DSO występuje tzw. macierz geometryczna, mająca swój udział
w macierzy sztywności. Macierz geometryczna, widoczna w dolnej części arkusza, jest
obliczana automatycznie. Po odpowiednim wyskalowaniu współczynniki tej macierzy
wyrażają pracę DSO na przemieszczeniach wirtualnych łańcucha kinematycznego, a
zatem są składnikami równań równowagi. Np. współczynniki w pierwszym wierszu tej

macierzy występują jako mnożniki przy niewiadomych

2

1

,





w równaniu równowagi

stowarzyszonym z pierwszym przechyłem ramy.
Pierwsza grupa równań jest stowarzyszona z kątami obrotu węzłów.

.

0

,

0

4
4

3
4

3
2

2
2

1

2





















a

w

a

w

2

2

1

1

,









Rys. 3. Widok arkusza – rozwiązanie 1

6

Zanim zredagujemy równania stowarzyszone z przechyłami ramy konieczne jest obliczenie
pracy obciążeń zewnętrznych na przemieszczeniach wirtualnych łańcucha kinematycznego.
W rozpatrywanym zadaniu pracę wykonuje tylko wypadkowa obciążenia ciągłego. Dlatego w
pierwszej kolejności konieczne jest obliczenie przemieszczenia wirtualnego

u w środku pręta

nr 5.

a

a

a

a

a

a

w

u

2

1

2

1

1

2

1

1

2

1

2

1

2

1

2

1

6

1

6

1

3













































Zatem praca sił zewnętrznych wynosi.

2

2

1

2

2

1

2

3

2

3

2

1

2

1

6









qa

qa

a

a

qa

L

z

























W przypadku występowania DSO wymagane jest także obliczenie pracy tych sił na
przemieszczeniach wirtualnych łańcucha kinematycznego. Te obliczenia pominięto, gdyż jak
wspomniano składnikami pracy DSO są, automatycznie obliczane w arkuszu, współczynniki
macierzy geometrycznej.
Brakujące równania równowagi stowarzyszone z przechyłami ramy otrzymuje się przyjmując
następujące wielkości wirtualne.

a)

Stan wirtualny





0

,

1

2

1











prowadzi do równania.









.

0

2

3

12

7

96

161

16

3

48

7

16

3

4

1

2

2

2

1

2

4
4

3
4

3
2

2
2

1

2

1
1

































qa

a

EJ

a

EJ









b)

Stan wirtualny





1

,

0

2

1











prowadzi do równania.





.

0

2

3

3

4

12

7

3

1

2

2

2

1

2

3
4

3
2

















qa

a

EJ

a

EJ









Z wyjątkiem wartości pracy sił zewnętrznych wszystkie współczynniki liczbowe
występujące w ostatnich dwóch równaniach można odczytać z arkusza roboczego. Na tym

3



qa

3

Rys. 4. Kondensacja statyczna

7

kończy się rozwiązanie zadania i opis zasadniczych funkcji arkusza. Oprócz tego ma on
jeszcze kilka funkcji dodatkowych. Jedną z nich jest udzielanie wskazówek dotyczących
możliwości przeprowadzenia kondensacji statycznych kątów obrotu cięciw prętów. Stanie
się to zrozumiałe gdy powrócimy do analizowanego zadania. Z dotąd przeprowadzonych
obliczeń wynika, że rama jest dwuprzechyłowa, a zatem czterokrotnie geometrycznie
niewyznaczalna. Do parametrów opisujących dwa niezależne przechyły ramy dochodzą
dwa kąty obrotu węzłów. Zauważmy jednak, że można przeprowadzić kondensację
statyczną kąta obrotu cięciwy pręta 3. Potwierdza to rysunek 5, który przedstawia plan
przemieszczeń na którym obraca się cięciwa pręta nr 3, a cięciwy pozostałych prętów, z
wyjątkiem geometrycznie wyznaczalnego pręta nr 5, są nieobrócone.
Zabieg kondensacji pozwala zmniejszyć liczbę niewiadomych geometrycznych zadania
do trzech. Niestety w dotąd wykonanych obliczeniach nie ma żadnej informacji o
możliwości przeprowadzenia wspomnianej kondensacji. Jest to spowodowane tym, że
podczas edycji arkusza pominięto wskazanie prętów geometrycznie wyznaczalnych
obustronnie podpartych przegubowo. W analizowanej ramie występuje jeden taki pręt,
mianowicie pręt nr 5. Aby mógł być on uznany za geometrycznie wyznaczalny nie może
na niego działać DSO. Tutaj warunek ten jest spełniony. Wobec tego należy chwilowo
zamknąć arkusz w taki sposób żeby nie utracić wprowadzonych dotąd danych, a następnie
otworzyć go ponownie. Teraz po kliknięciu myszką kolejno przycisków <Liczba węzłów
OK > a zaraz potem przycisku <Liczba prętów OK> uzyskuje się możliwość ponownej
edycji wprowadzonych danych. Aby wskazać geometryczną wyznaczalność pręta nr 5
trzeba wpisać cyfrę 1 w komórce H30. Wystarczy teraz kliknąć myszką przycisk < Oblicz
>, a w efekcie pojawi się spodziewany komunikat o możliwości kondensacji statycznej
kąta obrotu cięciwy pręta nr 3. Wynika stąd, że aby uniknąć konieczności wielokrotnego
otwierania arkusza powinno się wskazać pręty geometrycznie wyznaczalne podczas
pierwszej edycji arkusza. W związku z możliwą kondensacją statyczną kąta obrotu
cięciwy przedstawiono inną wersję rozwiązania analizowanego zadania. Zatem dalej
postępuje się zgodnie z treścią komunikatu dotyczącego kondensacji, czyli trzeba wskazać
kąt obrotu cięciwy tego pręta jako kondensowany statycznie. Odbywa się to poprzez
wpisanie cyfry 0 w odpowiedniej komórce kolumny H. Oznacza to konieczność
powtórzenia tych samych czynności, jak przy wskazywaniu pręta geometrycznie
wyznaczalnego. Tym razem rzecz jednak nie jest tak prosta, ponieważ kondensacja
statyczna prowadzi w praktyce do eliminacji jednego fikcyjnego wahacza w przyjętym
UGW. W rozpatrywanym przykładzie jest to wahacz wskazujący na przemieszczenie w

2

.

Dlatego w kolejnym kroku po zamknięciu i ponownym otworzeniu arkusza należy
wyczyścić zawartość komórki D7. Jeśli tego nie zrobimy w efekcie końcowym obliczeń
pojawi się komunikat błędu. W innych zadaniach czasami trzeba będzie także
przenumerować pozostałe więzy fikcyjne, gdyż ich numeracja powinna być ciągła i
zaczynać się od 1. Teraz po ponownym przeliczeniu arkusza za pomocą przycisku

8

< Oblicz > otrzymuje się nowe wyniki udokumentowane rysunkiem 5.

Rys. 5. Widok arkusza – rozwiązanie 2

Zwraca się uwagę, że kąt obrotu cięciwy pręta 3, na skutek kondensacji statycznej, stał się
nieokreślony. W stanie przemieszczeń wirtualnych przyjmuje się wartość tego kąta jako
równą zeru. Numer takiego pręta w tabeli kątów obrotu cięciw zostaje wyróżniony
kolorem czerwonym. Należy także pamiętać, że z powodu nieokreślonej wartości kąta
obrotu cięciwy trzeciego pręta, opis składowych przemieszczeń węzłów musi być
uzupełniony o wartości wynikające z planu przemieszczeń rzeczywistych towarzyszących
kondensacji(p. rysunek 4). Zatem równania równowagi w tej wersji rozwiązania są jak
następuje.
Pierwsza grupa równań, stowarzyszona z kątami obrotu węzłów, pozostaje bez zmian.

.

0

,

0

4
4

3
4

3
2

2
2

1

2





















Ostatnie brakujące równanie stowarzyszone teraz z jednym przechyłem wymaga także
obliczenia pracy obciążeń zewnętrznych na przemieszczeniach wirtualnych łańcucha
kinematycznego: W tym przypadku pracę wykonuje także tylko wypadkowa obciążenia
ciągłego. Dlatego też konieczne jest obliczenie przemieszczenia wirtualnego

u w środku

pręta nr 5.

a

a

a

a

w

u

1

1

1

1

1

32

23

32

9

32

3

3

































9

Zatem praca sił zewnętrznych wynosi.

1

2

1

16

69

32

23

6





qa

a

qa

L

z









Teraz stan wirtualny





1

1







prowadzi do ostatniego równania równowagi.





.

0

16

69

64

91

16

3

16

3

4

1

2

1

2

4
4

2
2

1

2

1
1























qa

a

EJ





Na zakończenie w uzupełnieniu opisu arkusza dodajmy jeszcze dwie uwagi:

1. W koszarze roboczym arkusza(p. Rys. 3 i 5) znajdują się dwa przyciski w

ciemnoszarym kolorze. Są to przyciski formatujące. Poprzez kliknięcie myszką
jednego z nich wybiera się naukowy lub ułamkowy format reprezentacji liczb.

2. W pierwszym wierszu arkusza, od kolumny I na prawo, znajdują się komórki, w

których można wpisać współczynniki skalujące kąty porównawcze przechyłów
ramy. Dodajmy od razu, że zalecanym współczynnikiem jest liczba 1. Nie zaleca
się stosowania wartości ujemnych, a liczba 0 jest niedopuszczalna. Należy to
rozumieć w taki sposób, że jeśli współczynnikiem skalującym i-tego przechyłu jest
liczba k

i

, to kąt porównawczy tego przechyłu

wyraża się wzorem.

Wydaje się, że najwięcej problemów w użytkowaniu arkusza może sprawić kondensacja
statyczna kątów obrotu cięciw prętów. Aby nieco rozjaśnić ten aspekt proponuje się
rozwiązanie zadania nr 2. Zanim to nastąpi warto przytoczyć podstawowe zasady
korzystania z kondensacji statycznej kątów obrotu cięciw prętów. Zastosowanie
suwakowego schematu obliczeniowego pręta(kondensacja statyczna kąta obrotu cięciwy
pręta) może być opłacalne wtedy, gdy potrafimy narysować(wyznaczyć tak jak niejawnie
dzieje się to w arkuszu) zgodny z więzami plan przemieszczeń na którym obraca się
cięciwa tylko wybranego pręta, a kąty obrotu cięciw pozostałych prętów są równe zeru.
Na takim planie dopuszcza się obroty cięciw prętów obustronnie podpartych przegubowo
o ile nie działa na nie DSO. Kondensacja kąta obrotu cięciwy eliminuje jeden z fikcyjnych
wahaczy UGW, zastępując go również fikcyjnym założeniem o zerowej wartości tego
kąta. Założenie to trzeba uwzględnić definiując UGW.
Arkusz kalkulacyjny zaprojektowano w taki sposób, że ww. kondensacja staje się
możliwa dopiero po odebraniu wszystkich przechyłów ramy za pomocą zwykłych
wahaczy wskazujących na nieznane przemieszczenia translacyjne węzłów. Wahacze te
należy opisać w arkuszu kolejnymi liczbami naturalnymi. Następnie arkusz trzeba
przeliczyć (kliknąć przycisk <Oblicz>). Jeśli dobrano odpowiednie wahacze w efekcie
obliczeń wykonanych przez arkusz w komórce C102 pojawi się komunikat informujący o
tym które kąty obrotu cięciw mogą być kondensowane statycznie. Po przeczytaniu
komunikatu arkusz trzeba zamknąć zachowując wprowadzone zmiany. Teraz dopiero

.

5

,

,

1

,









i

a

k

w

i

i

i



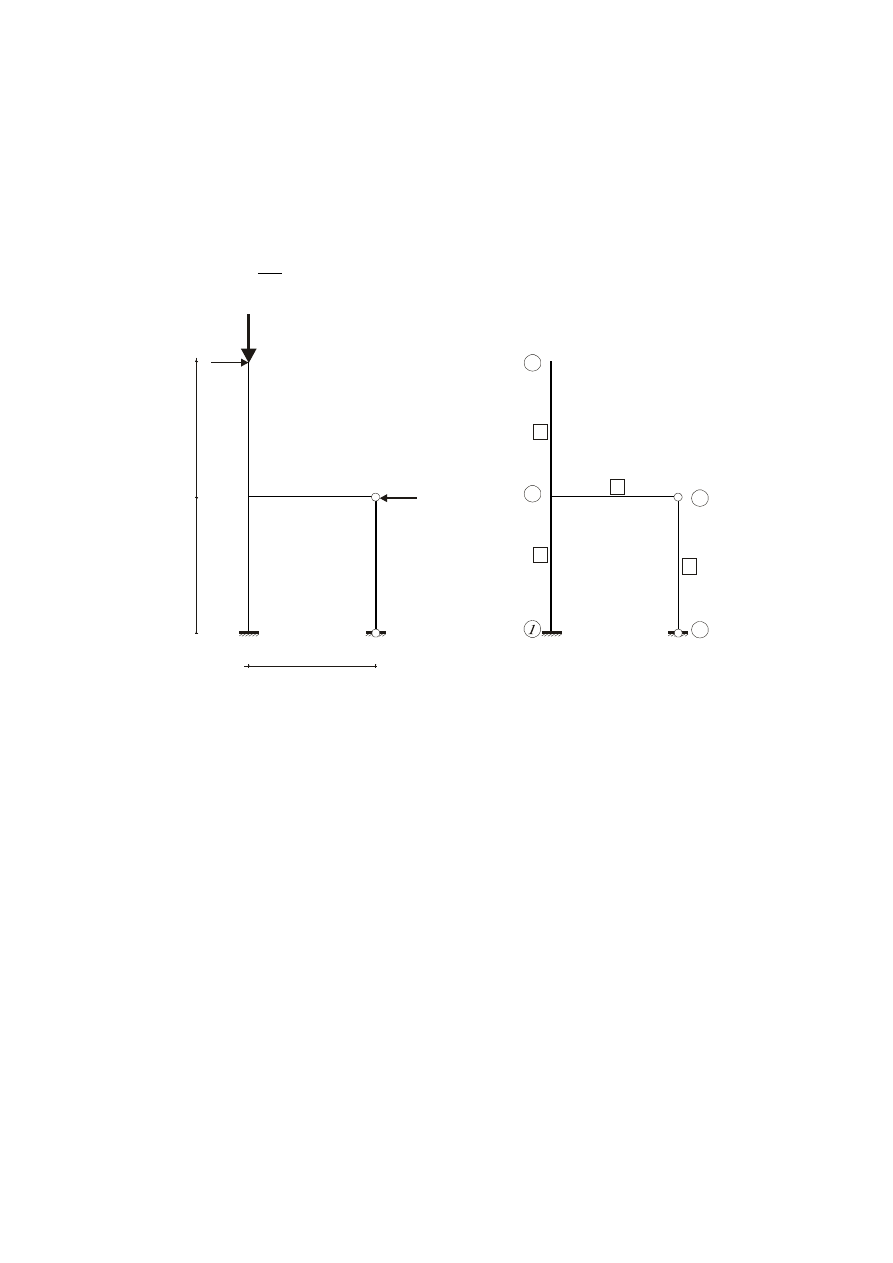
10

można zająć się kondensacją kątów obrotu cięciw. W tym celu trzeba ponownie otworzyć
arkusz. Należy tylko pamiętać aby w odpowiedzi na pojawiające się pytanie „Czy nowe
zadanie?” wybrać opcję <Nie>. W razie pomyłki trzeba będzie powtórzyć czynności z
poprzedniego kroku.

Zadanie 2

Znaleźć wartości momentów przywęzłowych w ramie jak na rysunku 6. Uwzględnić dużą

siłę osiową

2

1

a

EJ

S 

. Przyjąć stałą sztywność EJ wszystkich prętów.

Rozwiązanie.

Numerację prętów i węzłów przedstawia rysunek 6. Ponieważ duża siła S nie powoduje
zginania ramy, zatem wstępne siły osiowe, wyznaczone z elementarnej równowagi
węzłów, są następujące.

.

0

,

4

3

2

1









S

S

S

S

S

Zwróćmy uwagę, że nie wolno redukować pręta nr 2 z uwagi na dużą siłę osiową
występującą w tym pręcie. Bez DSO pręt ten byłby statycznie wyznaczalny, a wówczas
taka redukcja byłaby wręcz wskazana.
Teraz trzeba przyjąć układ geometrycznie wyznaczalny przestrzegając dwóch zasad.

1. Wskazać wszystkie pręty geometrycznie wyznaczalne obustronnie podparte

przegubowo. W rozpatrywanym przykładzie jest to pręt nr 4.

2. Nałożyć fikcyjne wahacze w taki sposób aby odebrać swobodę przemieszczania

wszystkich, bez wyjątku, węzłów. Zalecenie to także dotyczy węzła nr 3. Proszę

a

a

a

P

P

S

1

2

4

2

5

3

4

3

Rys. 6

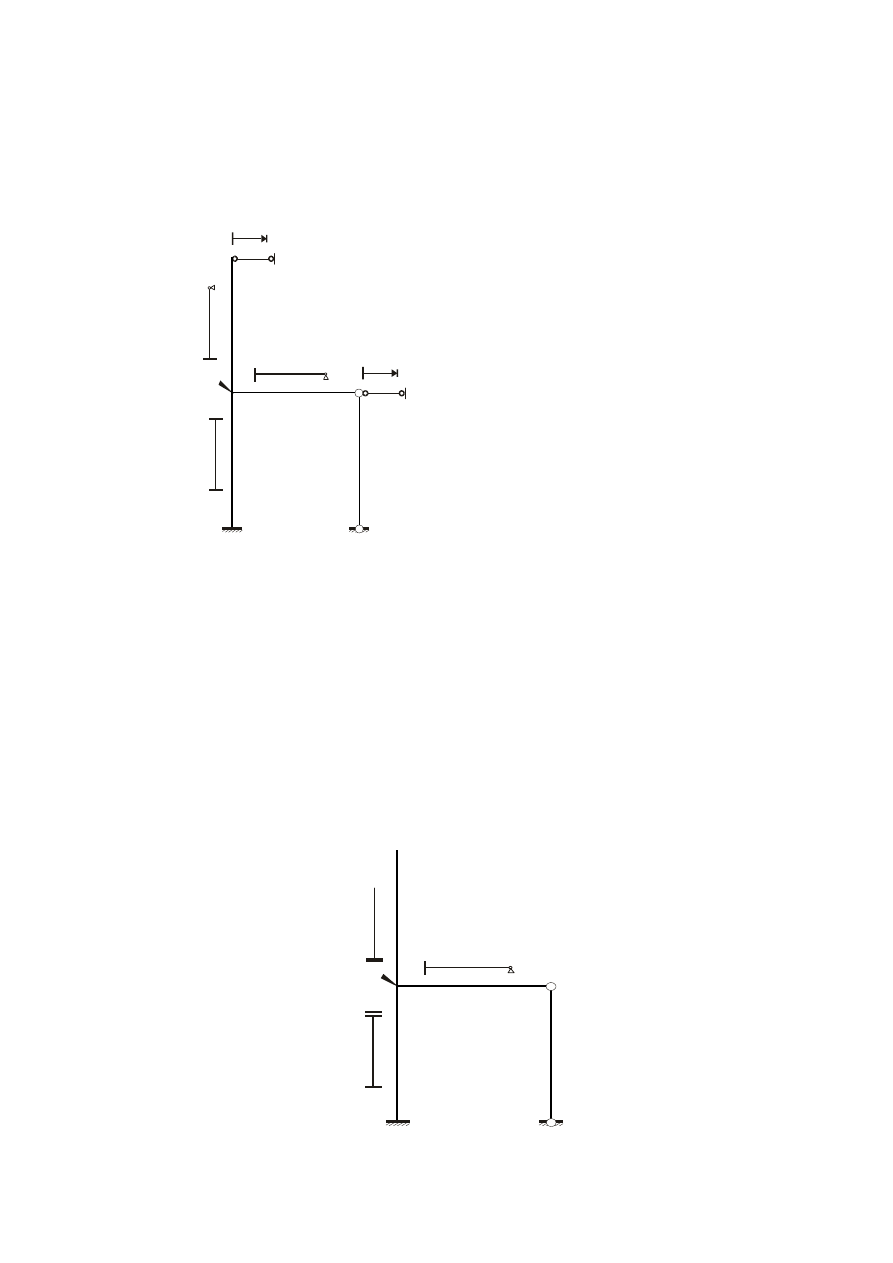
11

}

{

:

2



Niewiadome

Rys. 8. UGW – wersja 2

zapamiętać, że arkusz uznaje za poprawny tylko taki UGW w którym wszystkie
węzły mają odebraną swobodę przemieszczeń translacyjnych.

Oznacza to przyjęcie układu geometrycznie wyznaczalnego w pierwszej wersji jak na
rysunku 7. Na rysunku tym pokazano także schematy obliczeniowe prętów wynikające z

przyjętego UGW. Pomijając wszystkie szczegóły związane z użyciem arkusza, stwierdzamy
że odpowiednie obliczenia wykonane w arkuszu potwierdzają poprawność tego UGW. W
arkuszu pojawia się także następujący komunikat „Można skondensować kąty obrotu cięciw
prętów 1; 2;”. Zanim użytkownik zastosuje się do ostatniego komunikatu powinien
przeanalizować opłacalność proponowanych kondensacji. Bezkrytyczne zastosowanie się do
tego komunikatu prowadzi do UGW jak na rysunku 8. Niewątpliwym plusem
przeprowadzenia proponowanych kondensacji jest znaczna redukcja liczby niewiadomych.

w

1

w

2

)}

(

),

(

,

{

:

2

2

1

1

2

w

w

Niewiadome







Rys. 7. UGW – wersja 1

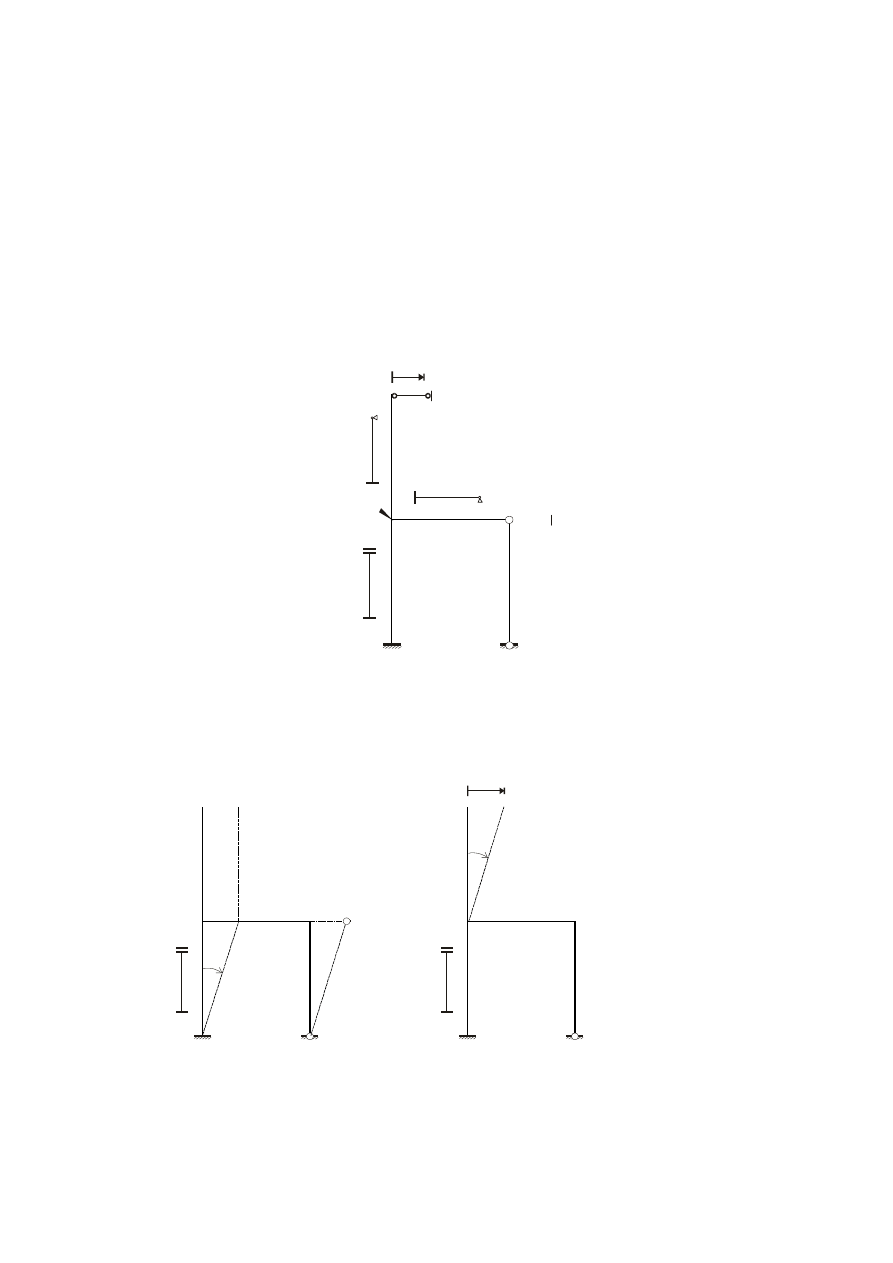
12

Pozostaje tylko jedna niewiadoma. Minusem jest konieczność obliczenia momentu

wyjściowego

o

2
2



od siły P obciążającej koniec wspornika. Aby uniknąć tej niedogodności

proponuje się rezygnację z przeprowadzania kondensacji kąta obrotu cięciwy drugiego pręta.
Natomiast bez dodatkowych utrudnień obliczeniowych warto skondensować kąt obrotu
cięciwy pręta nr 1. W konsekwencji dochodzi się do UGW jak na rysunku 9.
Z uwagi na kondensację kąta obrotu cięciwy pręta pierwszego wymagany jest rysunek 10a)
potwierdzający zasadność tej kondensacji. W dalszej kolejności trzeba wyznaczyć plan
przemieszczeń towarzyszący przechyłowi w

1

. Do wyznaczenia ostatniego planu

przemieszczeń można posłużyć się arkuszem kalkulacyjnym (p. rysunek 11) lub też

przedstawić go tak jak na rysunku 10b. Proszę zwrócić uwagę, że w arkuszu nie występuje
wahacz nr 2, a kąt obrotu cięciwy pręta pierwszego został skondensowany statycznie o czym

w

1

)}

(

,

{

:

1

1

2

w

Niewiadome





Rys. 9. UGW-wersja3

1



a)

b)

w

1

2



Rys. 10. Plany przemieszczeń

13

świadczy zero wpisane w komórce H26. Tak lub inaczej wyznaczony plan przemieszczeń
opisują następujące zależności.

.

,

1

1

1

2

a

w

gdzie











Teraz można zapisać równania równowagi. Pierwsze równanie ma następującą postać.

.

0

3
2

2
2

1

2













Przed zapisaniem drugiego równania związanego z przechyłem ramy trzeba obliczyć pracę sił
zewnętrznych oraz pracę DSO na przemieszczeniach wirtualnych łańcucha kinematycznego.
Prace te wynoszą odpowiednio.

1

1

1

1

1

,











a

EJ

Sa

L

Pa

L

S

z







.

Teraz przyjmując wartość wirtualną





1

1







otrzymuje się drugie równanie równowagi.

.

0

1

2
2











Pa

a

EJ



Zwróćmy uwagę, że wartość pracy

S

L występująca w tym równaniu odpowiada

współczynnikowi macierzy geometrycznej, gdyż dla

2

a

EJ

S 

parametr

.

1

2





Rys. 11. Widok arkusza

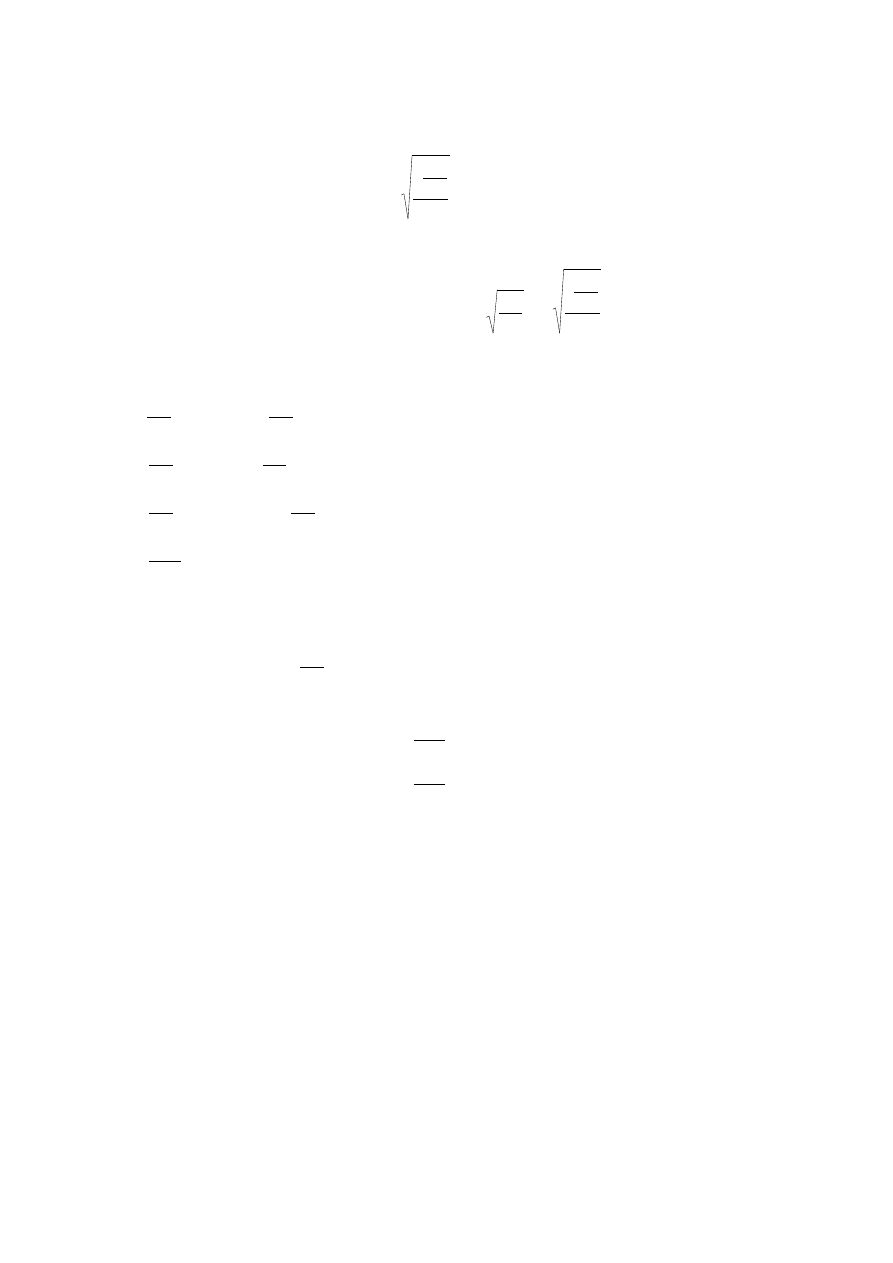
14

Przed zapisaniem wzorów transformacyjnych trzeba jeszcze obliczyć parametry

i

 prętów.

.

0

,

1

1

4

3

2

2

1



















EJ

a

EJ

a

Wartości te także można odczytać w kolumnie G tabeli edycyjnej prętów obliczając

uprzednio wartość parametru porównawczego

1

1

2







EJ

a

EJ

a

EJ

S

a



.

Zatem wzory transformacyjne przedstawiają się następująco.

























.

3

,

2.7940

2.7940

)

1

(

'

,

0.6421

)

1

(

''

,

1.1884

-

)

1

(

2

3
2

1

2

1

2

2
2

2

2

1

2

2

2

''

1
1

























a

EJ

a

EJ

a

EJ

a

EJ

a

EJ

a

EJ

a

EJ





























Powyższe wzory podstawione do równań równowagi prowadzą do układu równań.

.

1

0

1.7940

2.7940

-

2.7940

-

6.4361

1

2

Pa

a

EJ













































Rozwiązanie układu równań

















EJ

Pa

EJ

Pa

2

1

2

2

1.7209

0.7471





podstawione do wzorów transformacyjnych

daje wartości momentów przywęzłowych.

.

2.241Pa

,

-2.721Pa

,

0.480Pa

,

-0.888Pa

3
2

2
2

1

2

1
1















