POLITECHNIKA

WYDZIAŁ TRANSPORTU

Katedra Logistyki i Transportu

Ś

R O D K I

T

EMAT

:

W

YDAJNOŚĆ MASZYN TRAN

RUCHU CIĄGŁYM I OBLI

Sekcja: …………………………

Ocena: …………………………

Data: …………………………

KATOWICE 2012

POLITECHNIKA ŚLĄSKA

WYDZIAŁ TRANSPORTU

Katedra Logistyki i Transportu

Przemysłowego

R O D K I

T

R A N S P O R T U

P R O J E K T

ŚĆ

MASZYN TRANSPORTOWYCH PRACUJ

GŁYM I OBLICZENIA NAPĘDU METODĄ PODSTAWOW

PRACUJĄCYCH W

PODSTAWOWĄ

KATEDRA LOGISTYKI I

Dobrać parametry przenoś
określonej wydajności i wyznaczy
przenośnika.

Dane do projektu:

•

materiał: ………………………………………………….…..,

•

wydajność praktyczna: ……………………………………....

•

długość przenośnika, (L=100

Tok obliczeniowy:

1.

Obliczyć wydajność teoretyczn

2.

Przyjąć kąt naturalnego usypu :
transportowanych w górnictwie, energetyce i budownictwie).

3.

Przyjąć kąt nachylenia przeno
przenośnika powinien być mniejszy od k

4.

Założyć granulację a dla zadanego materiału sypkiego

5.

Przyjąć prędkość v taśmy przeno

6.

Obliczyć rzeczywistą szerokość

7.

Dobrać typ zestawu krążnikowego
nosiwa F

n

(z wzóru 3), w przypadku braku pasuj

szerokość taśmy (z uwzględni

8.

Dobrać kąt niecki

β

zestawu kr

9.

Dobrać typ zestawu dolnego do danej szeroko

10.

Obliczyć nominalny przekrój nosiwa
przenośnikowej B.

11.

Sprawdzić rzeczywistą wydajno

12.

Dobrać taśmę przenośnikową

13.

Obliczyć masę taśmy w jednym ci

14.

Wyznaczyć masę obracających si

15.

Obliczyć współczynnik oporu ruchu c, w

16.

Wyliczyć moc napędu,

17.

Narysować schemat kinematyczny układu nap

18.

Wykonać rysunek przenośnika oraz przekroju zestawów kr
wielkości

Obliczenia przenośników

Dobór szerokości taśmy na podstawie wydajno

Do prawidłowego doboru taśmy niezb

•

rodzaj transportowanego materiału, jego granulacja i g
ziaren, temperatura,

KATEDRA LOGISTYKI I TRANSPORTU PRZEMYSŁOWEGO

parametry przenośnika taśmowego transportującego materiał sypki o

wyznaczyć moc niezbędną do zainstalowania dla tego

materiał: ………………………………………………….…..,

praktyczna: ……………………………………....

nika, (L=100

÷

2500[m]),……………………,

teoretyczną (wzór 1).

t naturalnego usypu :

ρ

=15

o

(założenie to jest słuszne dla większo

transportowanych w górnictwie, energetyce i budownictwie).

t nachylenia przenośnika od 0° do 30° zgodnie z tablicą 2 (kąt nachylenia

ć

mniejszy od kąta naturalnego usypu).

dla zadanego materiału sypkiego (tablica 1).

my przenośnikowej i jej szerokość B na podstawie danych (tabl.

szerokość taśmy przenośnikowej B (wzór 5).

ąż

nikowego górnego wedle tablicy 7, wyznaczając wst

3), w przypadku braku pasującego zestawu przyjąć odpowiednio inn

ę

dnieniem zmiany prędkości tablica 4).

zestawu krążnikowego (tablica 5, 7).

typ zestawu dolnego do danej szerokości taśmy.

nominalny przekrój nosiwa F

n

(wzory 6-10) dla danego zestawu i szeroko

wydajność przenośnika taśmowego (wzór 3).

nikową o wyznaczonej szerokości,

my w jednym cięgnie,

ą

cych się części krążników zestawu dolnego i górnego, m

ółczynnik oporu ruchu c, współczynnik tarcia f,

schemat kinematyczny układu napędowego.

ś

nika oraz przekroju zestawów krążnikowych dla obliczonych

my na podstawie wydajności

ś

my niezbędne są takie podstawowe informacje, jak:

rodzaj transportowanego materiału, jego granulacja i gęstość, wilgotno

Strona 2 z 12

cego materiał sypki o

do zainstalowania dla tego

ę

kszości materiałów

ą

t nachylenia

na podstawie danych (tabl. 3, 4).

ą

c wstępnie przekrój

ąć

odpowiednio inną

) dla danego zestawu i szerokości taśmy

ników zestawu dolnego i górnego, masę nosiwa,

nikowych dla obliczonych

, jak:

, wilgotność, ostrość krawędzi

KATEDRA LOGISTYKI I

•

wydajność praktyczna, teoretyczna

•

parametry drogi transportowej
między punktami załadunku i wyładunku, zakrzywienia przeno

•

prędkość taśmy,

•

obliczenie oporów ruchu przeno

Wydajność teoretyczną urządze
jednostkach masy [t] lub w jednostkach
przemieszczonego w jednostce czasu.

W praktyce rzeczywista wydajno

teoretycznej.

gdzie

ϕ

- wsp. korygujący wydajno

ϕ

3

= 0.65

ϕ

4

ϕ

5

= 0,8

÷

-

Szerokość, prędkość taśmy i kąt niecki dobiera si

Dla materiału transportowanego

teoretyczna wydajność masowa przeno

W

t

gdzie:
W

t.

- nominalna teoretyczna wydajno

podłużnego nachylenia przenośnika

v - prędkość taśmy, [m/s],

γ

- gęstość

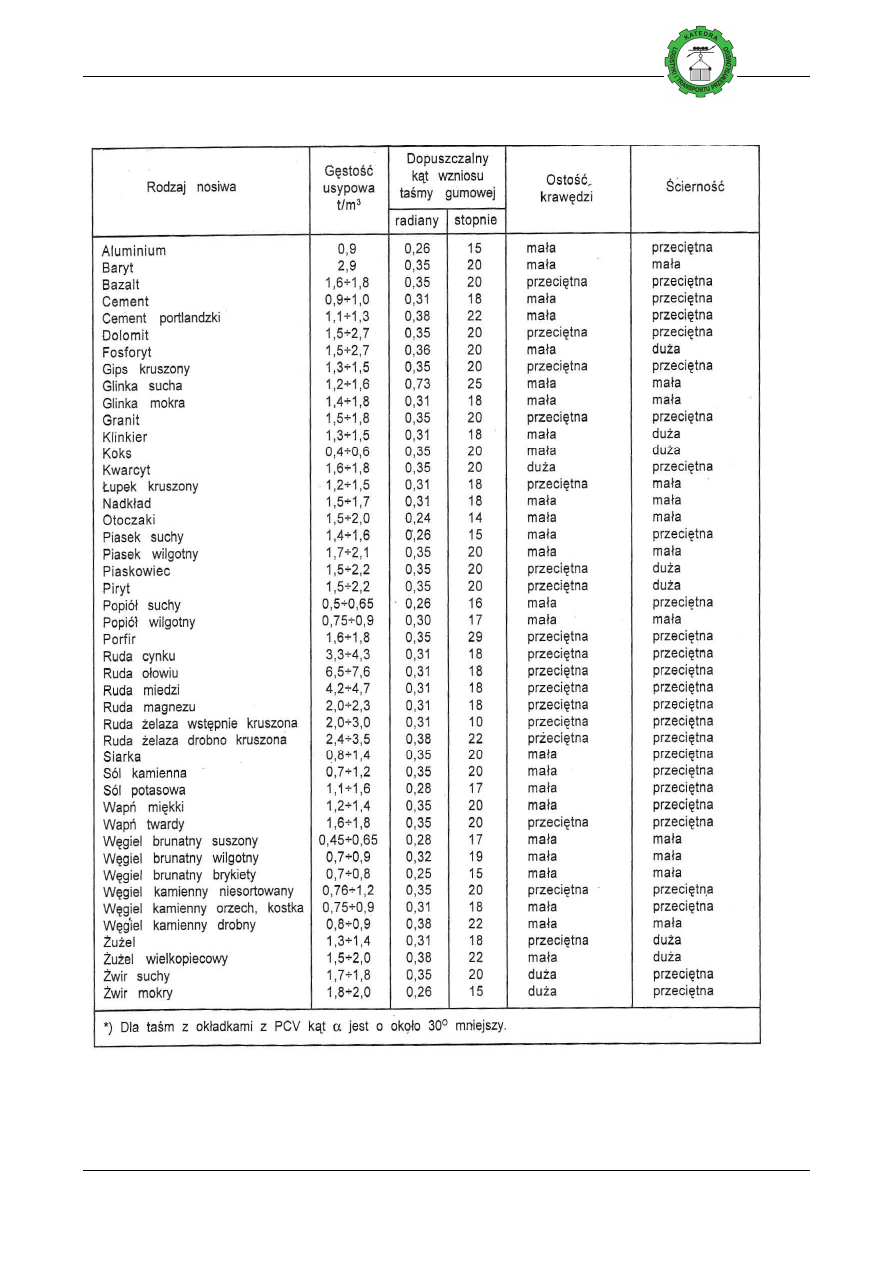
Tablica 1. Zakres granulacji materiału

L.p. Materiały:

1.

pyłowe

2.

proszkowe

3.

ziarniste

4.

drobnokawałkowe

5.

średniokawałkowe

6.

wielkokawałkowe

7.

bryłowe

KATEDRA LOGISTYKI I TRANSPORTU PRZEMYSŁOWEGO

praktyczna, teoretyczna (maksymalna i średnia),

parametry drogi transportowej (rys.2), takie jak: długość przenośnika, ró

dzy punktami załadunku i wyładunku, zakrzywienia przenośnika (profil trasy),

obliczenie oporów ruchu przenośnika i zapotrzebowanie mocy.

urządzeń transportowych (W

t

) o ruchu ciągłym okre

w jednostkach objętości [m

3

] transportowanego materiału (nosiwa)

przemieszczonego w jednostce czasu. Za jednostkę czasu zazwyczaj przyjmuj

W praktyce rzeczywista wydajność przenośników (W

p

) jest mniejsza od wydajno

ϕ

⋅

=

T

P

W

W

cy wydajność ze względów techniczno-organizacyjnych

0.65

÷

0,75 – wsp. nierytmiczności dostaw

= 0.8

÷

1,0 – wsp. sprawności obsługi

- wsp. zależny od ∢

∢∢

∢ pochylenia przenośnika

ą

t niecki dobiera się w ten sposób, aby został spełniony warunek (2):

T

P

W

W

<

łu transportowanego (przepływającego nieprzerwaną jednakow

przenośnika wynosi:

γ

α

⋅

⋅

⋅

⋅

=

v

F

k

n

3600

.









h

t

nominalna teoretyczna wydajność masowa, [t/h], k

α

- współczynnik uwzglę

nika na F

n

(tablica 4; )F

n

– nominalny przekrój nosiwa na ta

stość usypowa nosiwa [t/m

3

] (tablica 1 ).

Tablica 1. Zakres granulacji materiału transportowanego, w zależności od wielkości wi

Zakres:

Przykład:

a<0,05 mm

(cement),

0,05<a<0,5 mm

(piasek),

0,5<a<9 mm

(drobny żwir),

10<a<60 mm

(żwir),

60< a<160 mm

(węgiel),

161< a<320 mm

(ruda),

a>320 mm

(głazy).

Strona 3 z 12

ś

nika, różnica poziomów

nika (profil trasy),

o ruchu ciągłym określa się w

transportowanego materiału (nosiwa)

czasu zazwyczaj przyjmuje się godzinę [h],

jest mniejsza od wydajności

(1)

organizacyjnych

(2)

w ten sposób, aby został spełniony warunek (2):

(3)

nieprzerwaną jednakową strugą)

(4)

współczynnik uwzględniający wpływ kąta

nominalny przekrój nosiwa na taśmie [m

2

],

ci większości brył

(drobny żwir),

KATEDRA LOGISTYKI I

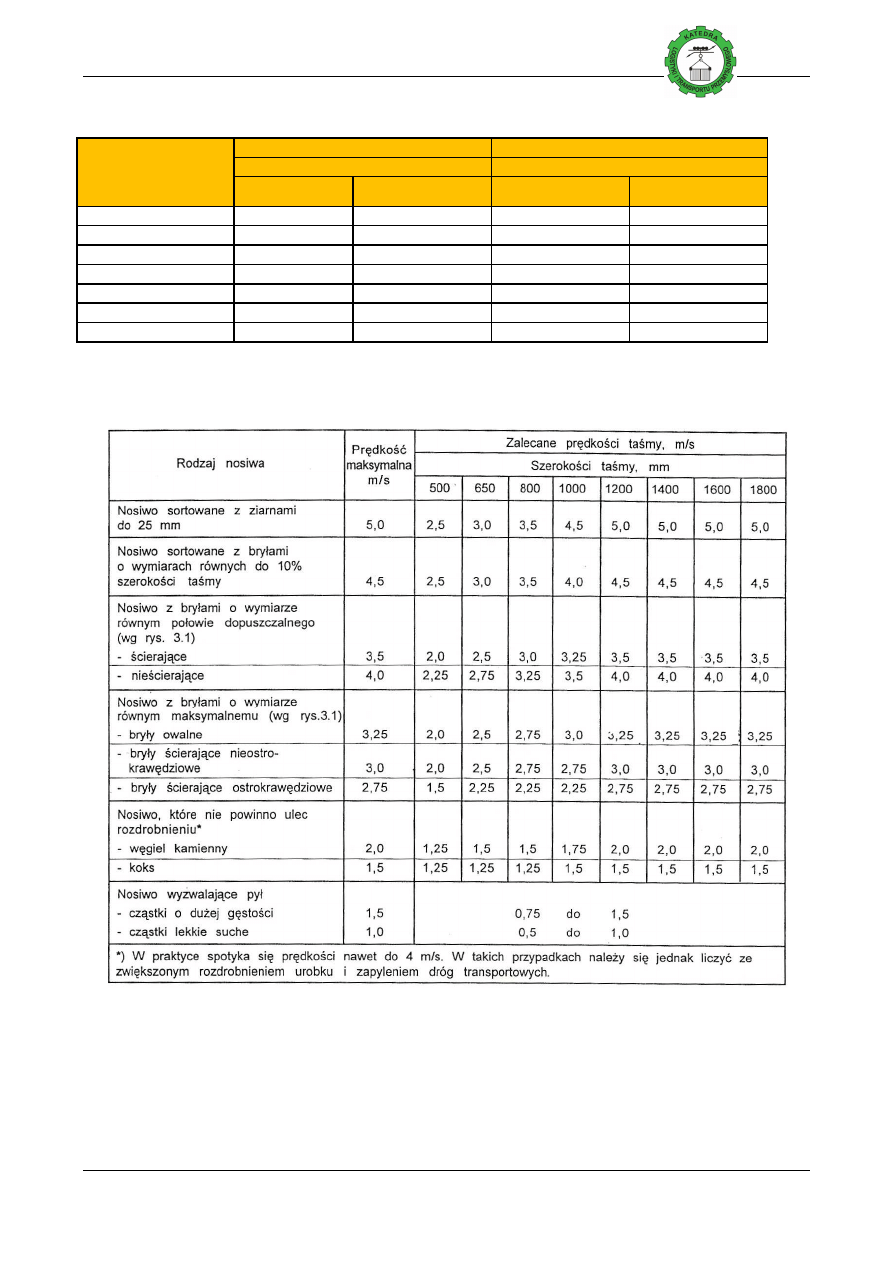
Tablica 2 Ważniejsze własności ró

Z wzoru (4) wyznaczamy pole przekroju strugi F.
W zależności od własności fizykochemicznych transportowanego nosiwa i wielko
zalecane i maksymalne prędkości ta

KATEDRA LOGISTYKI I TRANSPORTU PRZEMYSŁOWEGO

ci różnych nosiw

wyznaczamy pole przekroju strugi F.

ci fizykochemicznych transportowanego nosiwa i wielko

ś

ci taśm v dla różnych jej szerokości B

T

podane zastały

Strona 4 z 12

ci fizykochemicznych transportowanego nosiwa i wielkości jego brył a

podane zastały w tablicy

KATEDRA LOGISTYKI I

Tablica 3. Maksymalne prędkości taś

Szerokość taśmy, B

T

[m]

Skała luźna

Nachylenie przeno

o

8

≤

0,8

4,0

1,0

4,5

1,2

5,0

1,4

5,6

1,6

6,3

1,8

7,5

2,0

7,5

Tablica 4. Zalecane i maksymalne pr
transportowanego nosiwa

KATEDRA LOGISTYKI I TRANSPORTU PRZEMYSŁOWEGO

ci taśm v

max

[m/

s]

Skała zwięzła

Nachylenie przenośnika

Maksymalny wymiar brył, a

o

8

≥

>0,05

<0,05

3,2

1,6

2,5

4,0

2,0

3,2

4,5

2,0

3,2

5,0

2,5

4,0

6,3

3,2

4,5

6,3

3,2

4,5

7,5

3,2

4,5

Tablica 4. Zalecane i maksymalne prędkości taśmy w zależności od własności fizykomechanicznych

Strona 5 z 12

Maksymalny wymiar brył, a

max

[m]

<0,05

2,5

3,2

3,2

4,0

4,5

4,5

4,5

ci od własności fizykomechanicznych

KATEDRA LOGISTYKI I

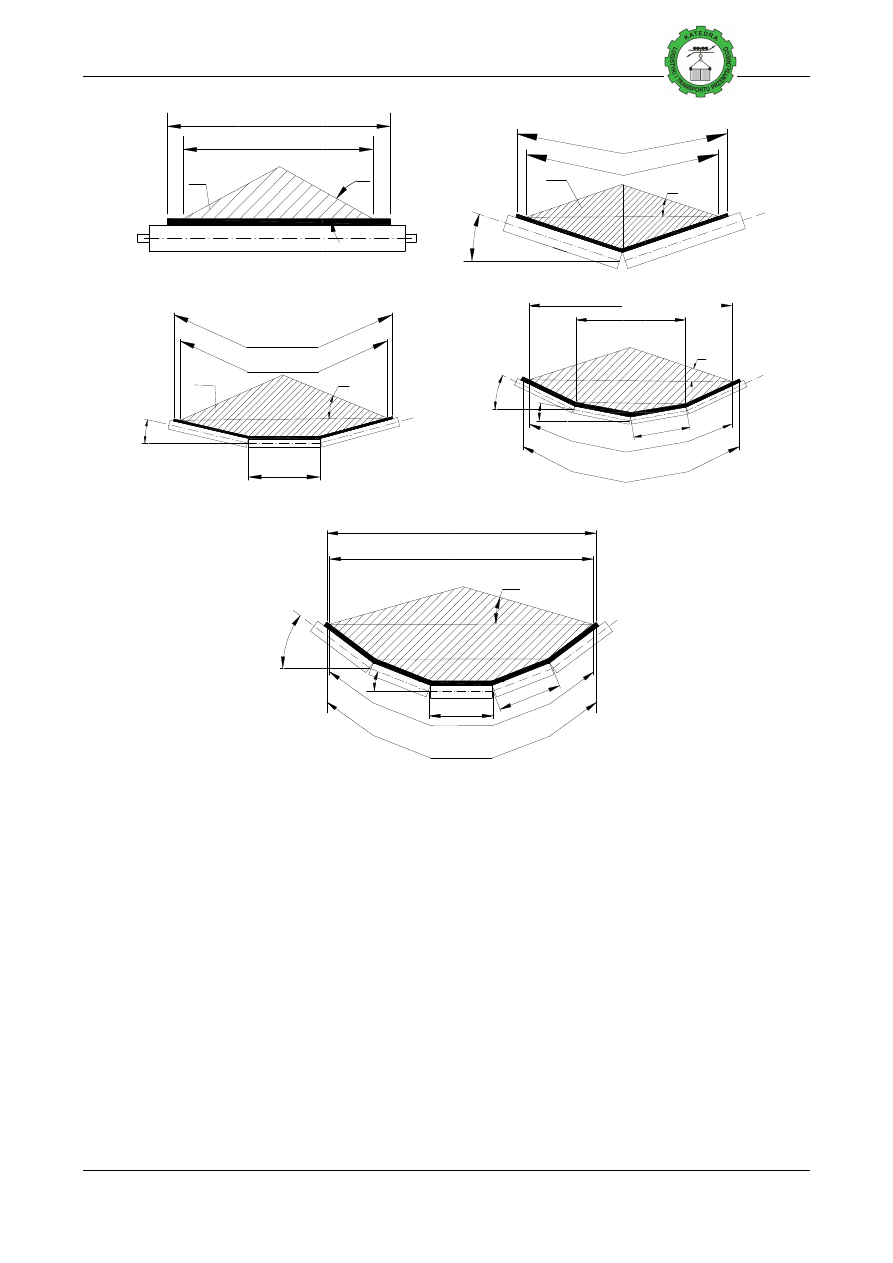
a)

n

B

B

γ

n

B

B

β

1

l

γ

c)

1

β

e)

Rys. 1. Nominalny (obliczeniowy) przekrój poprzeczny nosiwa na ta

a – jednokrążnikowego,

d – czterokrążnikowego, e –

Nominalny przekrój poprzeczny nosiwa na ta

Powierzchnię przekroju nosiwa okre

prostymi nachylonymi do poziomu pod k
materiałów transportowanych w górnictwie, energetyce i budownictwie), a od dołu krzyw
wyznaczoną przez ułożenie skrajnych kr

Aby uniknąć rozsypywania si

od szerokości taśmy B. Szerokość

9

,

0

=

n

B

KATEDRA LOGISTYKI I TRANSPORTU PRZEMYSŁOWEGO

ρ

b)

n

B

B

β

γ

ρ

n

B

B

1

β

2

β

2

b

1

b

d)

n

B

B

2

β

1

b

2

b

1

l

2

l

ρ

. Nominalny (obliczeniowy) przekrój poprzeczny nosiwa na taśmie F

nikowego, b – dwukrążnikowego, c – trójkrążnikowego,

– pięciokrążnikowego.(kąt β

1

przyjąć45°kąt β

Nominalny przekrój poprzeczny nosiwa na taśmie jest przekrojem umownym (rys.

przekroju nosiwa określa się zakładając, że z góry jest ona ograniczona

prostymi nachylonymi do poziomu pod kątem

ρ

=15

o

(założenie to jest słuszne dla wi

materiałów transportowanych w górnictwie, energetyce i budownictwie), a od dołu krzyw

enie skrajnych krążników nośnych w zestawie krążnikowym.

rozsypywania się nosiwa przyjmuje się szerokość zapełnienia

. Szerokość tę dla B

T

<2.0 [m] określa zależność:

05

,

0

9

−

⋅

T

B

[ ]

m

Strona 6 z 12

ρ

1

l

ρ

mie F

n

dla zestawu:

nikowego,

β

2

jak z tablicy 3)

mie jest przekrojem umownym (rys. 1).

e z góry jest ona ograniczona dwoma

enie to jest słuszne dla większości

materiałów transportowanych w górnictwie, energetyce i budownictwie), a od dołu krzywą łamaną

ąż

nikowym.

zapełnienia taśmy B

n

mniejszą

(5)

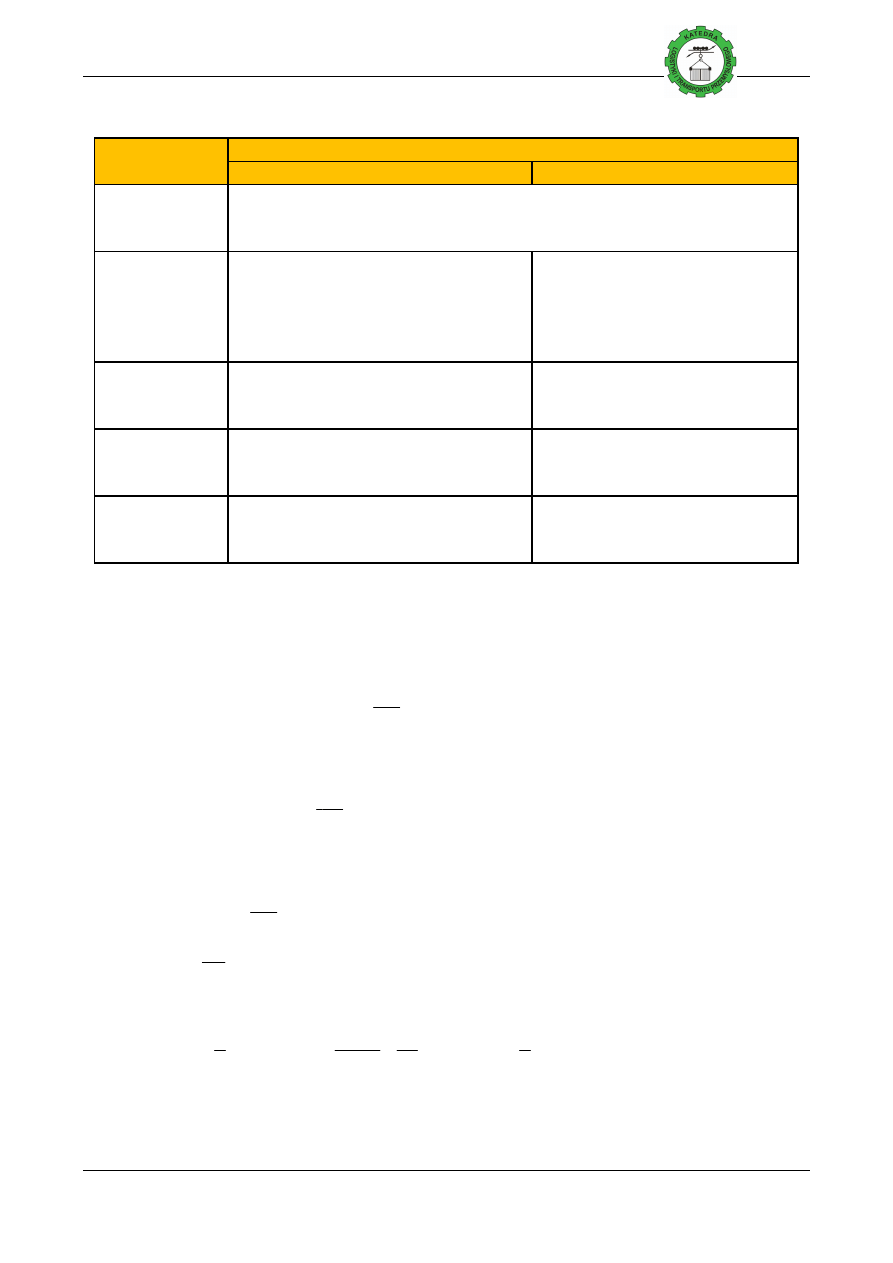
KATEDRA LOGISTYKI I

Tablica 5. Kąty niecki taśmy przenoś

Kształt niecki

Gałąź górna ta

Niecka płaska

W przenośnikach odbieraj
opakowanych (pudła, skrzynki, baga
skrzynkową lub inn

Niecka

dwukrążnikowa

Dla taśm o szeroko

do 30[

o

](w zale

szerokości ta

specjalnych k

szerokoś

Niecka

trójkrążnikowa

Im węższa i im sztywniejsza poprzecznie

taśma tym mniejszy k

kąty od 20[

Niecka

czterokrążnikowa

Taśmy szerokie do

kąty niecki

Niecka

pięciokrążnikowa

Taśmy sztywne o szeroko

[m], kąt niecki

Nominalny przekrój nosiwa F

n

wyznacza się korzystając z zależno

- dla zestawu jednokrążnikowego (ta

- dla zestawu dwukrążnikowego

B

F

n

=

- dla zestawu trójkrążnikowego

[cos

4

2

β

B

F

n

n

⋅

=

gdzie:

n

B

l

1

=

λ

- dla zestawu czterokrążnikowego

β

l

b

F

n

+

⋅

⋅

⋅

=

1

1

1

sin

2

1

gdzie:

1

1

1

cos

2

β

⋅

⋅

=

l

b

[

m

],

2

=

b

KATEDRA LOGISTYKI I TRANSPORTU PRZEMYSŁOWEGO

przenośnikowej β

Zastosowanie

górna taśmy

Gałąź dolna taśmy

ś

nikach odbierających nosiwo spod zbiorników, transport materiałów

opakowanych (pudła, skrzynki, bagaże podróżne, w przenośnikach z ta

lub inną specjalną.

m o szerokości do 0,8 [m] kąt niecki

](w zależności do konstrukcji i

ś

ci taśmy); w rozwiązaniach

specjalnych kąt niecki do 45[

o

] przy

szerokościach taśmy do 1,2 [m].

Dla dowolnej szeroko

niecki 10[

o

zapewnienia centrowania ta

i im sztywniejsza poprzecznie

ma tym mniejszy kąt niecki; stosowane

od 20[

o

] do 45[

o

] (50[

o

])

Dla dowolnej szeroko

niecki 10[

o

zapewnienia centrowania ta

my szerokie dość sztywne poprzecznie,

ą

ty niecki od 45[

o

] do 55[

o

]

Dla dowolnej szeroko

niecki 10[

o

zapewnienia centrowania ta

my sztywne o szerokości powyżej 1,8

[m], kąt niecki od 45[

o

] do 60[

o

]

Dla dowolnej szeroko

niecki 10[

o

zapewnienia centrowania ta

n

[m

2

] dla szerokości zapełnienia taśmy B

c z zależności:

ążnikowego (taśma płaska) (rys. 1a),

ρ

tg

B

F

n

n

⋅

=

4

2

ążnikowego (rys. 1b),

)

cos

cos

(sin

4

2

2

ρ

β

β

β

tg

B

n

⋅

+

⋅

⋅

nikowego (rys. 1c),

]

)

(

)

cos

1

(

2

2

β

λ

ρ

β

β

λ

β

tg

tg

tg

⋅

−

+

⋅

−

⋅

+

ążnikowego (rys. 1d),

ρ

β

tg

b

l

B

b

b

n

⋅

⋅

+

⋅

−

⋅

+

+

2

2

2

1

2

1

4

1

sin

)

2

(

2

2

1

1

cos

)

2

(

β

⋅

⋅

−

+

=

l

B

b

n

[

m

],

Strona 7 z 12

dolna taśmy

cych nosiwo spod zbiorników, transport materiałów

ś

nikach z taśma

Dla dowolnej szerokości taśmy kąt

o

] do 15[

o

] w celu

zapewnienia centrowania taśm

Dla dowolnej szerokości taśmy kąt

o

] do 15[

o

] w celu

zapewnienia centrowania taśm

Dla dowolnej szerokości taśmy kąt

o

] do 15[

o

] w celu

zapewnienia centrowania taśm

Dla dowolnej szerokości taśmy kąt

o

] do 15[

o

] w celu

zapewnienia centrowania taśm

B

n

[m] i kąta niecki

β

[

2

m

]

(6)

[

2

m

]

(7)

[

2

m

]

(8)

[

2

m

]

(9)

KATEDRA LOGISTYKI I

- dla zestawu pięciokrążnikowego (rys.

2

2

(

4

ρ

tg

tg

b

F

n

+

⋅

=

gdzie:

1

2

1

1

cos

2

β

⋅

⋅

+

=

l

l

b

[

m

],

ρ

- kąt usypu nosiwa w ruchu

b

1

, b

2

, l

1

, l

2

- wielkości geometryczne zaznaczone na rysunk

Rys. 2 Maksymalny wymiar brył nosiwa w funkcji szeroko

Tablica 6. Wartości współczynnika k

Kąt podłużnego nachylenia przeno

0-3

4

6

8

10

12

14

16

18

20

22

24

26

28

30

KATEDRA LOGISTYKI I TRANSPORTU PRZEMYSŁOWEGO

ążnikowego (rys. 1e),

1

2

1

2

1

2

1

2

4

)

(

4

)

β

β

β

β

tg

l

tg

tg

b

tg

⋅

−

−

⋅

+

],

1

2

1

2

1

1

2

cos

2

cos

)

2

1

(

β

β

⋅

⋅

+

+

⋅

⋅

−

−

=

l

l

l

B

b

n

[

m

],

t usypu nosiwa w ruchu (°),

β

,

β

1

,

β

2

- kąt nachylenia krążników (°)

ś

ci geometryczne zaznaczone na rysunku 3.

Maksymalny wymiar brył nosiwa w funkcji szerokość taśmy B i udziału w nosiwie brył o

wymiarze a

max

ci współczynnika k

α

w funkcji kąta podłużnego nachylenia przenośnika

nego nachylenia przenośnika

α

[

o

]

Wartość współczynnika k

1

0,99

0,98

0,97

0,95

0,93

0,91

0,89

0,85

0,81

0,76

0,71

0,66

0,61

0,56

Strona 8 z 12

[

2

m

]

(10)

ników (°),

my B i udziału w nosiwie brył o

nego nachylenia przenośnika

współczynnika k

α

KATEDRA LOGISTYKI I

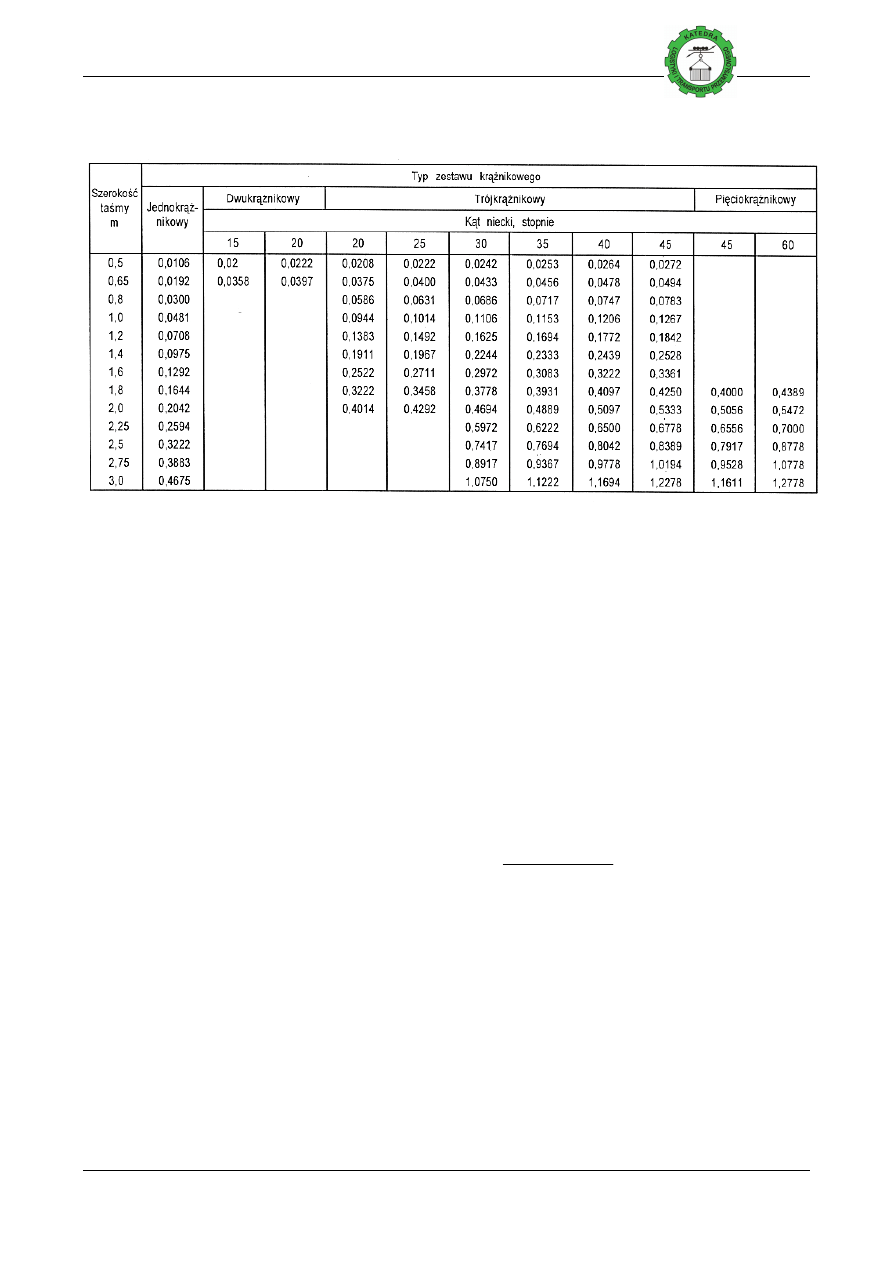
Tablica 7. Nominalne przekroje nosiwa F
taśmy B i kąta niecki β (dla ρ=15°)

2. Obliczenia mocy napędu metod

Opory ruchu przenośnika ta

zastosowanej metody otrzymujemy obliczony wynik ko
dokładnością. Jedynym dokładnym sposobem obliczania oporów ruchu przeno
metoda oporów jednostkowych
W praktyce stosuje się metod
ruchu jako całość. Do metody tej nale
których opory ruchu oblicza się
zadawalającą dokładność oblicze
długości od 60 do 2500 m.

Opory ruchu taśmy przeno

ustalonym:

m

m

g

f

C

W

D

K

n

+

⋅

⋅

=

[

gdzie:

C, f - współczynniki oporów ruchu, m
obrotowych krążników w ci

cięgnie dolnym, [kg], m
nachylenie przenośnika, Q

prędkość taśmy, [m/s

].

Masa taśmy wynosi (jedno ci

gdzie:

B - szerokość taśmy, [m],

KATEDRA LOGISTYKI I TRANSPORTU PRZEMYSŁOWEGO

. Nominalne przekroje nosiwa F

n

[m

2

] dla różnych zestawów krążnikowych

ędu metodą podstawową

nika taśmowego można obliczyć wieloma metodami.

zastosowanej metody otrzymujemy obliczony wynik końcowy z wię

. Jedynym dokładnym sposobem obliczania oporów ruchu przenoś

metoda oporów jednostkowych, która polega na obliczaniu poszczególnych składowych oporów.

metodę obliczeń oporów przenośników taśmowych ujmuj

. Do metody tej należy metoda podstawowa, obejmuje wszystkie te metody, w

oblicza się jak dla tarcia suchego. Metoda podstawowa pozwala uzyska

obliczeń oporów ruchu przenośnika taśmowego

my przenośnikowej obciążonej transportowanym materiałem w ruchu

V

g

L

Q

m

m

P

n

T

D

⋅

⋅

⋅

⋅

+

⋅

+

⋅

+

6

,

3

sin

]

cos

)

2

(

α

α

[N]

współczynniki oporów ruchu, m

T

- masa taśmy w jednym cięgnie, [kg], m

ników w cięgnie górnym, [kg], m

D

- masa części obrotowych kr

m

n

- masa nosiwa, [kg], g - przyspieszenie ziemskie, [m/s

nika, Q

p

– wydajność praktyczna, [t/h], L – długość przeno

my wynosi (jedno cięgno):

j

t

T

m

B

L

m

.

⋅

⋅

=

[kg]

my, [m], m

t.j

- masa jednostkowa taśmy, [kg/m

2

].

Strona 9 z 12

nikowych w funkcji szerokości

wieloma metodami. W zależności od

cowy z większą lub mniejszą

. Jedynym dokładnym sposobem obliczania oporów ruchu przenośnika taśmowego jest

h składowych oporów.

mowych ujmujące opory

obejmuje wszystkie te metody, w

oda podstawowa pozwala uzyskać

mowego dla przenośników o

onej transportowanym materiałem w ruchu

[N]

(11)

gnie, [kg], m

K

-masa części

ci obrotowych krążników w

przyspieszenie ziemskie, [m/s

2

],

α

-

ść przenośnika [m], V –

(12)

KATEDRA LOGISTYKI I

Masę obracających się częś

rozstawie, wyznacza się wzorem:

K

m

gdzie:

n

g

, n

e

- liczba zestawów kr

zestawie nośnym i nadawowym, m

nadawowego, [kg].

Masę obracających się częś

gdzie:

n

d

- liczba zestawów kr

m

d

- masa części obrotowych kr

Przy obliczaniu masy urobku nale

długości taśmy przenośnikowej.

gdzie:

L

i

- długość odcinka, na którym ta

jednostkowej m

i

, m

i

-

Masę jednostkową materiału transportowanego na rozpatrywanej długo

wynosi:

gdzie:

Q

m

- wydajność przenoś

Wielkość współczynnika oporów ruchu

od długości przenośnika. Wystę
Zależnie od sposobu rozpatrywania tych oporów (wzór 1) nale
(tablica 8, rys. 3) w funkcji długo

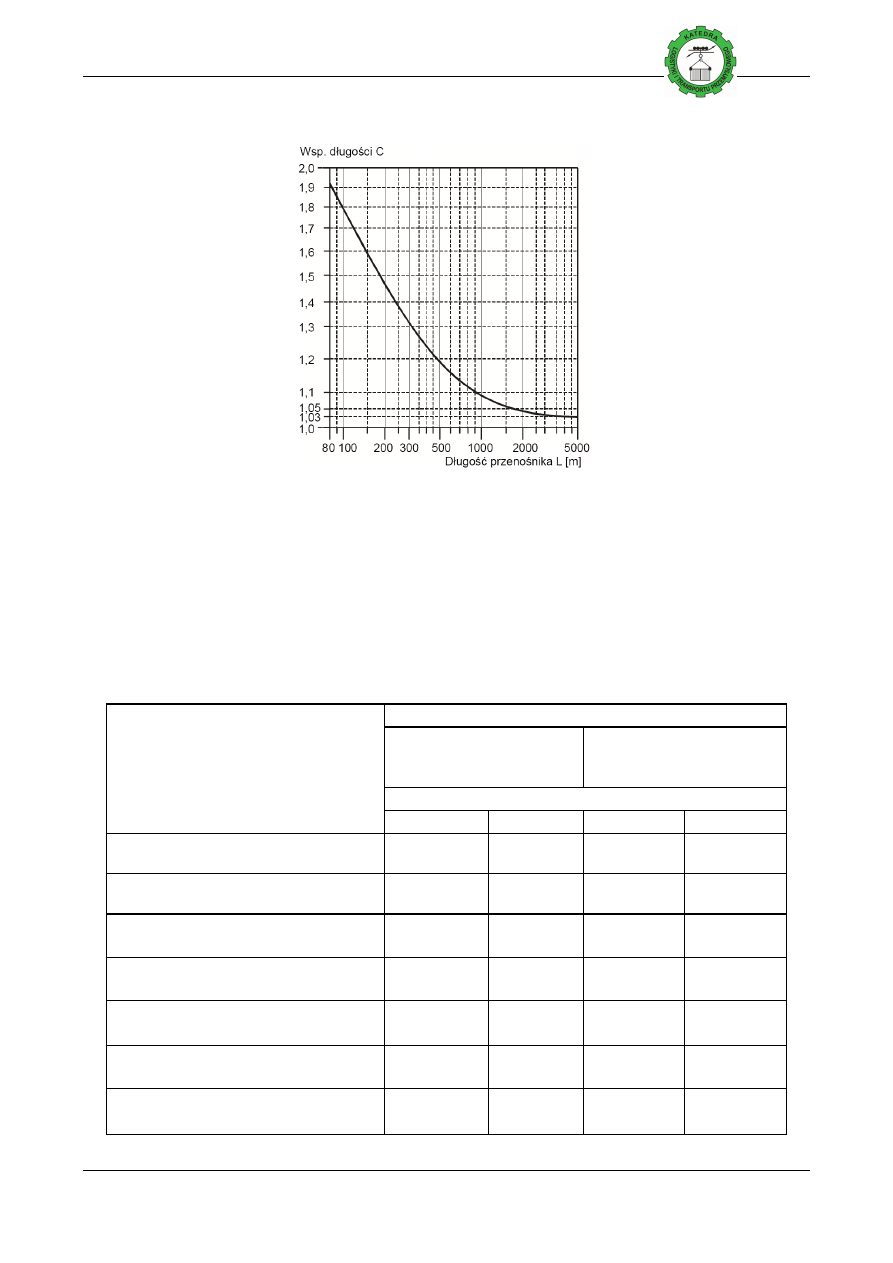
Tablica 8. Współczynnik oporów ruchu C

Współczynnik

80

100

C

1,92 1,78

KATEDRA LOGISTYKI I TRANSPORTU PRZEMYSŁOWEGO

ę

części krążników górnych przy znanej liczbie zestawów oraz ich

wzorem:

e

e

e

g

g

g

m

z

n

m

z

n

⋅

⋅

+

⋅

⋅

=

[kg]

liczba zestawów krążników nośnych i nadawowych, z

g

, z

e

- liczba kr

nym i nadawowym, m

g

, m

e

- masa części obrotowych kr

ę

części krążników dolnych oblicza się ze wzoru:

d

d

d

D

m

z

n

m

⋅

⋅

=

[kg]

liczba zestawów krążników dolnych, z

d

- liczba krążników w zestawie dolnym,

ci obrotowych krążnika dolnego, [kg].

Przy obliczaniu masy urobku należy założyć, że jest ona równomiernie rozło

nikowej. Zatem wzór na masę nosiwa ma postać:

∑

⋅

=

i

i

n

m

L

m

[kg]

odcinka, na którym taśma jest obciążona urobki

masa jednostkowa urobku, [kg/m].

materiału transportowanego na rozpatrywanej długo

V

Q

m

m

i

=

[kg/m]

przenośnika, [kg/s], V – prędkość taśmy, [m/s].

współczynnika oporów ruchu C uwzględnia opory skupione, które s

nika. Występują one zazwyczaj na stacji czołowej lub na stacji

obu rozpatrywania tych oporów (wzór 1) należy okreś

) w funkcji długości.

Współczynnik oporów ruchu C

Długość przenośnika L, [m]

150

200

300

400

500

600

700

1,58 1,45 1,31 1,25 1,20 1,17 1,14

Strona 10 z 12

ników górnych przy znanej liczbie zestawów oraz ich

(13)

liczba krążników w

ci obrotowych krążnika nośnego i

ze wzoru:

(14)

ników w zestawie dolnym,

e jest ona równomiernie rozłożona na całej

(15)

ona urobkiem o masie

materiału transportowanego na rozpatrywanej długości przenośnika

(16)

dnia opory skupione, które są niezależne

one zazwyczaj na stacji czołowej lub na stacji zwrotnej.

y określić współczynnik C

800

900 1000

1,12 1,10 1,09

KATEDRA LOGISTYKI I

Rysunek

Zalecane wartości dla współczynnika

podane przedziały wartości uwa
uwzględnić pracę przenośnika w niskich temperaturach, poniewa
temperatury rosną opory ruchu. Pona
obciążenia taśmy przenośnika nosiwem. Zwi
przenośnikach krótkich lub nie wykorzystania mocy w urz

Tablica 9. Współczynnik oporów ruchu

Rozmieszczenie przenośników

Przenośniki w budynkach i na

osłoniętych konstrukcjach nośnych

Przenośniki stacjonarne w kopalniach

odkrywkowych, na składowiskach

Przenośniki przesuwne w kopalniach

odkrywkowych

Przenośniki pracujące w skrajnie

niskich temperaturach

Przenośniki opadające

Przenośniki transportu głównego w

kopalniach podziemnych

Pozostałe przenośniki w kopalniach

podziemnych

KATEDRA LOGISTYKI I TRANSPORTU PRZEMYSŁOWEGO

Rysunek 3 - Współczynnik oporów ruchu C

ci dla współczynnika f podano w tablicy 9. W warunkach normalnych

ci uważane są za bezpieczne. Dobierając współczynnik

nika w niskich temperaturach, ponieważ wraz ze obni

opory ruchu. Ponadto należy brać pod uwagę zmienno

nika nosiwem. Związane jest to z możliwością przeci

nikach krótkich lub nie wykorzystania mocy w urządzeniach o większych długo

Współczynnik oporów ruchu f

ś

ników

Warunki eksploatacji

Wysoki poziom eksploatacji,

skutecznie działający

mechanizm napinania.

Niski poziom eksploatacji,

duż

Temperatura otoczenia, w której przeno

>0

o

C

<0

o

C

>0

o

C

ś

nych

0,016

÷

0,018

0,018

÷

0,021

0,022

÷

0,024

niki stacjonarne w kopalniach

odkrywkowych, na składowiskach

—

0,018

÷

0,022

—

niki przesuwne w kopalniach

—

0,020

÷

0,024

—

ce w skrajnie

—

do 0,035

—

0,012

÷

0,014

0,014

÷

0,016

—

niki transportu głównego w

0,025

÷

0,027

—

0,027

÷

0,028

niki w kopalniach

0,028

÷

0,030

—

0,031

÷

0,033

Strona 11 z 12

. W warunkach normalnych

c współczynnik f należy

wraz ze obniżaniem się

zmienność oraz rozkład

ą

przeciążenia napędu w

ę

kszych długościach.

Warunki eksploatacji

Niski poziom eksploatacji,

duże zwisy taśmy

Temperatura otoczenia, w której przenośnik pracuje

C

<0

o

C

0,024

0,025

÷

0,027

0,026

÷

0,028

0,029

÷

0,031

—

—

0,028

—

0,033

—

KATEDRA LOGISTYKI I

Moc napędu przenośnika taśmowego wynosi:

gdzie:

η

c

– sprawność mechanizmu nap

gdzie:

η

sp

- sprawność sprzę

(n – liczba stopni),

η

B

Moc zainstalowanych silników jest z reguły wi

gdzie:

k

N

= 1,05 ÷ 1,1 – współczynnik rezerwy mocy (przy dwóch b

k

N

=1,05, przy trzech lub wi

gdzie: N

zs

– moc znamionowa poszczególnych silników:

KATEDRA LOGISTYKI I TRANSPORTU PRZEMYSŁOWEGO

mowego wynosi:

]

[

1000

kW

V

W

N

c

n

n

⋅

⋅

=

η

mechanizmu napędowego.

B

R

sp

c

η

η

η

η

⋅

⋅

=

sprzęgła (

η

sp

=0,99),

η

R

- sprawność przekładni (

B

- sprawność bębna (

B

η

=0,94

÷

0,96)

Moc zainstalowanych silników jest z reguły większa od mocy wymaganej:

N

n

Z

k

N

N

⋅

≥

współczynnik rezerwy mocy (przy dwóch bębnach nap

=1,05, przy trzech lub większej liczbie bębnów k

N

= 1,1)

∑

=

ZS

Z

N

N

moc znamionowa poszczególnych silników:

Strona 12 z 12

(17)

(18)

przekładni (

η

R

=0,98

n

),

(19)

ę

bnach napędowych

(20)