ZADANIE 1
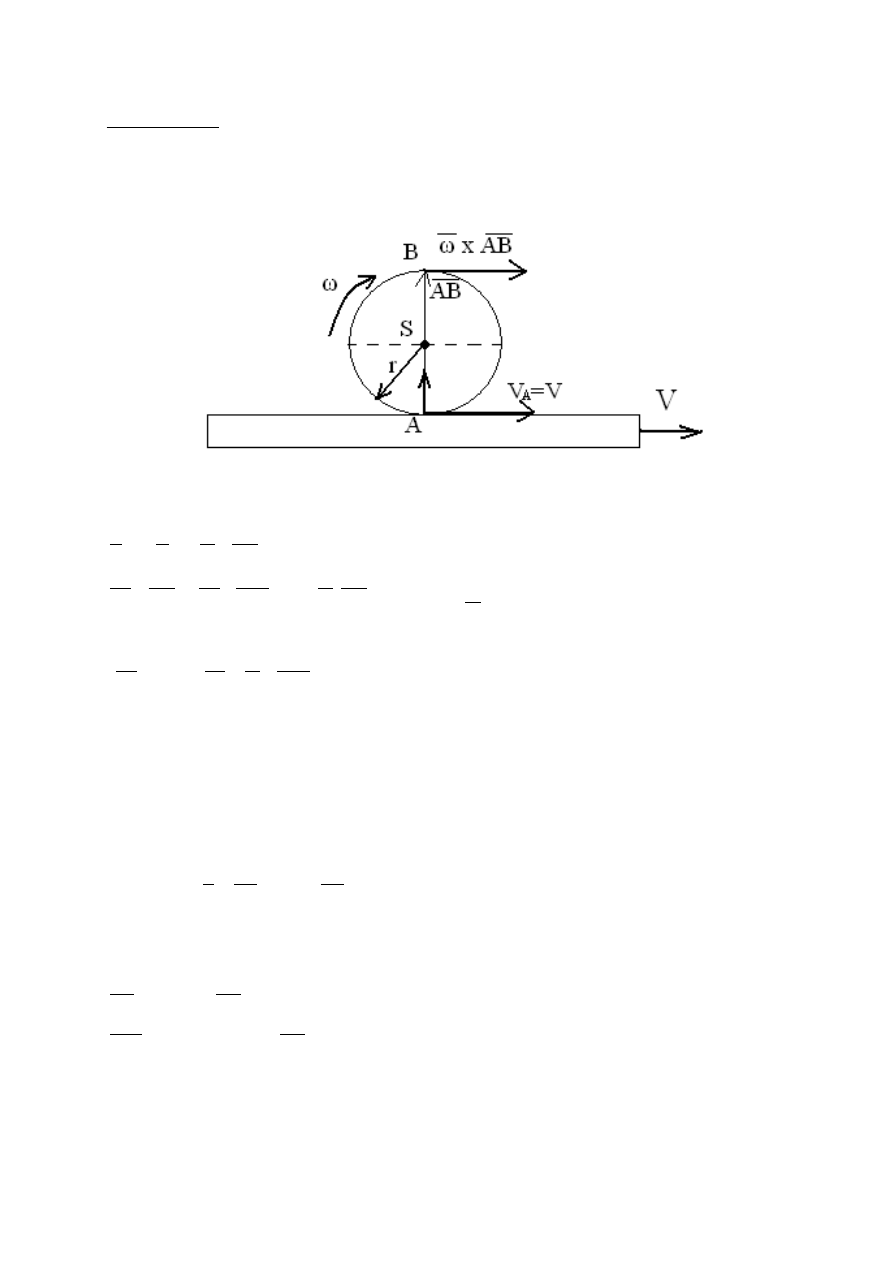
Koło pojazdu o promieniu r=0,2 [m] poruszają się bez poślizgu po poziomym
moście o ω=16 [rad/s] pomost porusza się z prędkością V=ω·r. Oblicz prędkość
całkowitą punktu B koła i przyśpieszenie punktu A stycznego koła z pomostem.
V
V
A
=
Prędkość dowolnego punktu koła:
V
V
i
bysmy
odejmowali
to
strone
przeciwna
w
krecilo
sie
by
koło
Jeżeże
V
V
r
V
ponieważ
V
r
r
AB
V
V
V
r
r
AB
AB
AB
AB
V
V
B
B
A
B
B
A
B
=
=
⋅
=
=
+
=
×
+
=
=
=
⋅
=
⋅
⋅
=
×
×
+
=
_
_
_
_
_
_
_
_
_
_
3
:
3
2
|
|
|
|
2
2
sin
2
)
,
sin(
|
|
|
|
|
|
ϖ
ϖ
ϖ
ϖ
ϖ
π
ϖ
ϖ
ϖ
ϖ
ϖ
Przyśpieszenie dowolnego punktu koła np. A
SA
SA
a
a
S
A
⋅
−
×
+
=
2
ϖ
ε
Ponieważ V
S
= const to a
S
=0 [m/s
2
]
Ponieważ ω= const to ε=0 [rad/s
2
]
r
SA
a
a
SA
a
A
A
A
2
2
2
|
|
|
|
ϖ
ϖ
ϖ
=
⋅
−
=
=
⋅
−
=
ZADANIE 2
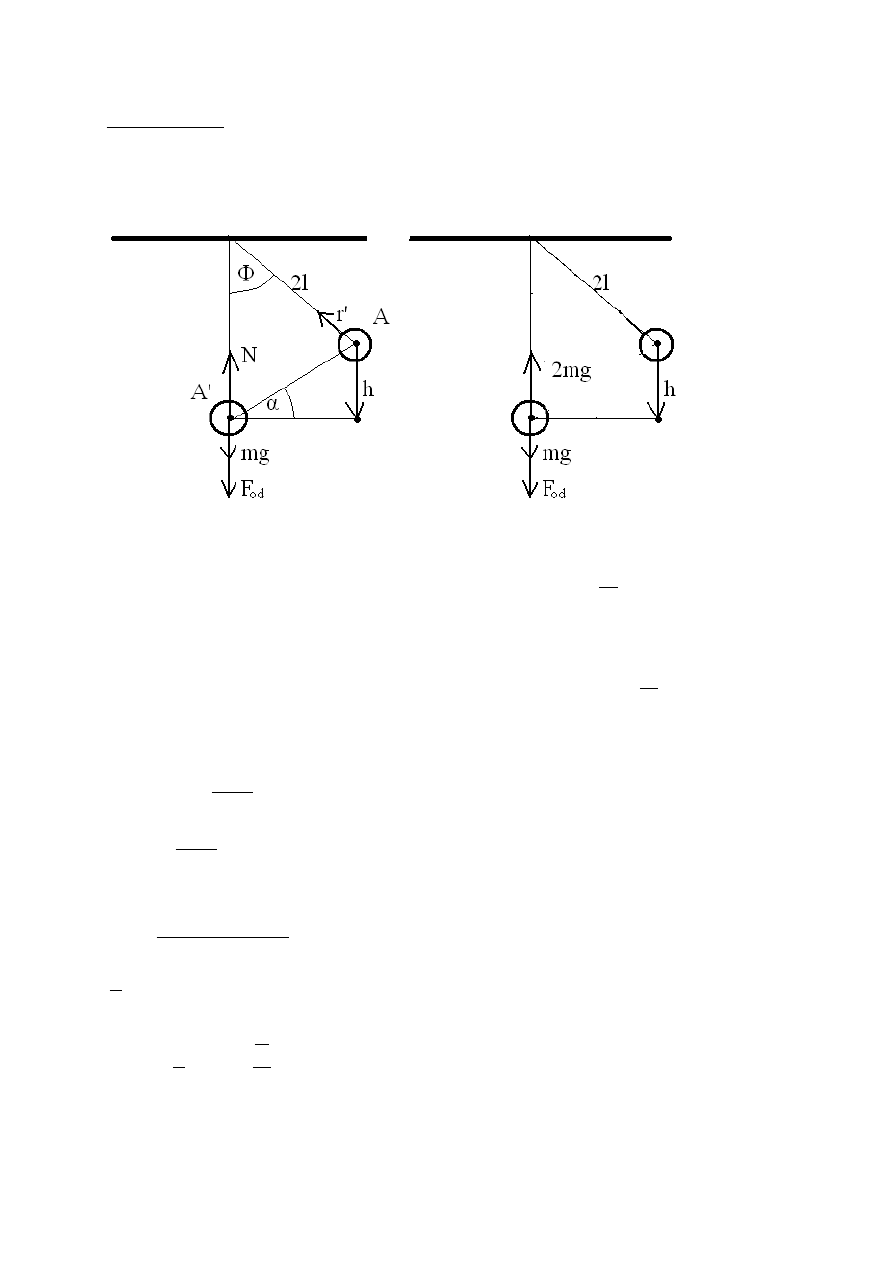
O jaki kąt φ trzeba odchylić od równowagi wahadlo matematyczne o długości 2l
i masie kulki m aby naciąg nieważkiej nici przy przejściu wahadła przez dane
położenie był dwukrotnie większy od ciężaru kulki.
mg
l
m
r
mg
r
mg
r
+
=
=
=
2
'
2
'
cos
2
ϖ
ϕ
l
r
V
m
F
l
m
F
r
V
r
V
od
od
2
)
(
2
2
2
⋅
=
⋅
=
=
=
ϖ
ϖ
ϖ
3
2
1
cos
cos
1
2
1
2
)
cos
1
(
)
cos
1
(
2
2
2
2
2
)
cos
1
(
2
cos
2
2
2
2
2
π
α
α
α
α
α
α
α
=
= >
=
−
=
−
=
=
−
=
+
=
−
=
−
=
l
l
mgh
mg
V
ghl
mV
mgh
l
mV
mg
mg
l
l
l
h
ZADANIE 3
Punkt materialny porusza się w płaszczyźnie XY z przyśpieszeniem
]
,
[
y
x
a
a
a
=
gdzie a
x
=-sint, a
Y
=-2cost. Wyznacz położenie i prędkość punktu w chwili t
1
=Π/2
[s], w chwili t=0.
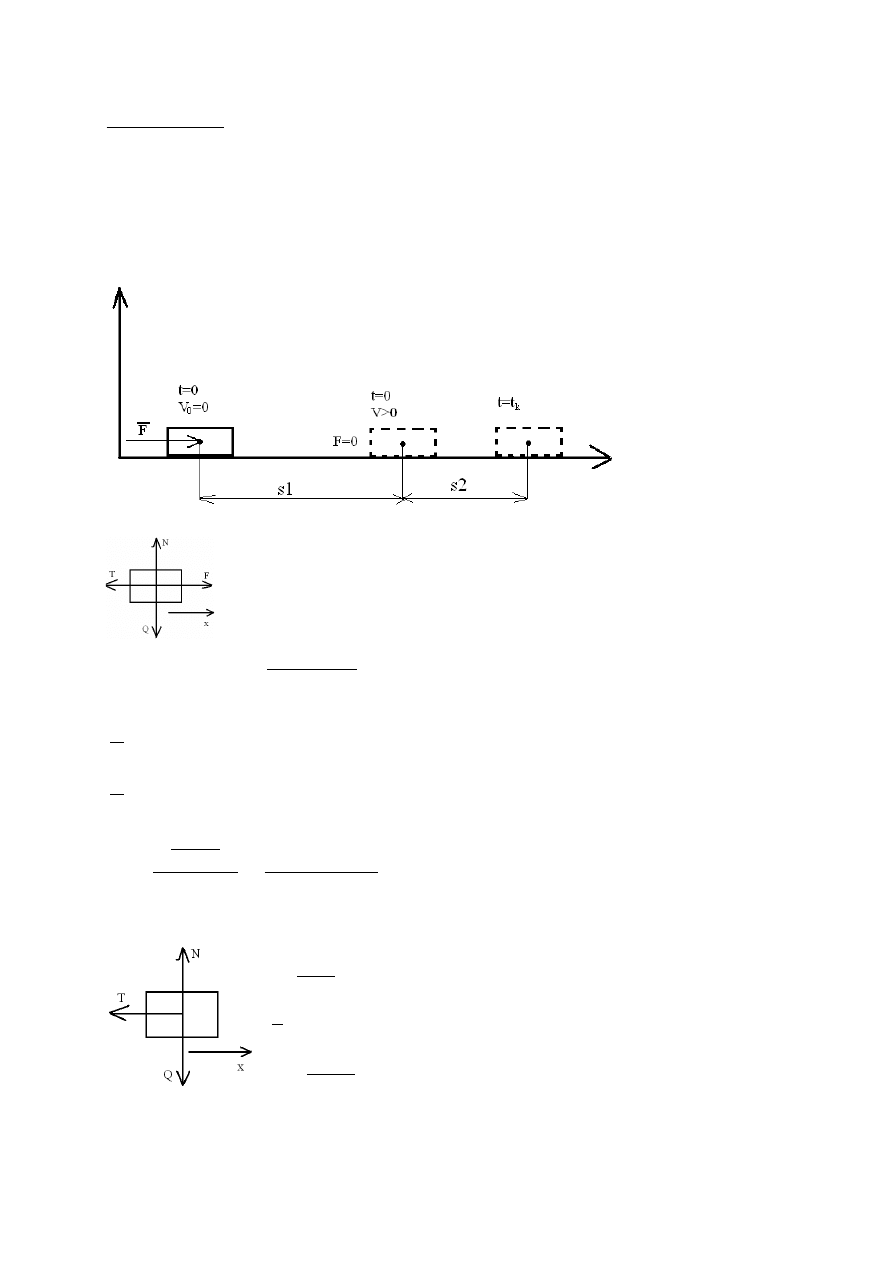
ZADANIE 4
Do suwaka o masie m=5[kg] znajdującego się na chropowatej prowadnicy
poziomej przyłożono w chwili t=0 siłę F=20[N] działającą poziomo. W jakiej
odległości s od płożenia początkowego zatrzyma się suwak jeśli podczas
działania siły T=3[s]. Współczynnik tarcia μ=0,3, w chwili początkowej
prędkość suwakaV
0|t0
=0
I FAZA
Z zasady zachowania Pędu
m
T
mg
F
V
T
mg
F
mV
T
T
F
m
mV
t
F
p
p
x
x
x
)
(
)
(
)
(
0
)
(
)
0
(
)
1
(
µ
µ
−
=
−
=
−
=
−
Σ
=
−
Z Zasady zachowania energii kinetycznej
)
(
2
2
)
(
2
1
)
(
0
2
1
2
2
1
1
2
1
2
mg
F
mV
mg
F
mV
s
s
mg
F
mV
s
mg
F
mV
µ
µ
µ
µ
−
=
−
=
−
=
−
=
−
II FAZA
Z zasady zachowania energii kinetycznej
g
V
s
s
g
V
s
mg
mV
µ
µ
µ
−
=
⋅
−
=
⋅
−
=
−
2
2
1
2
0
2
2
2
2
2
2
S=s1+s2
ZADANIE 5
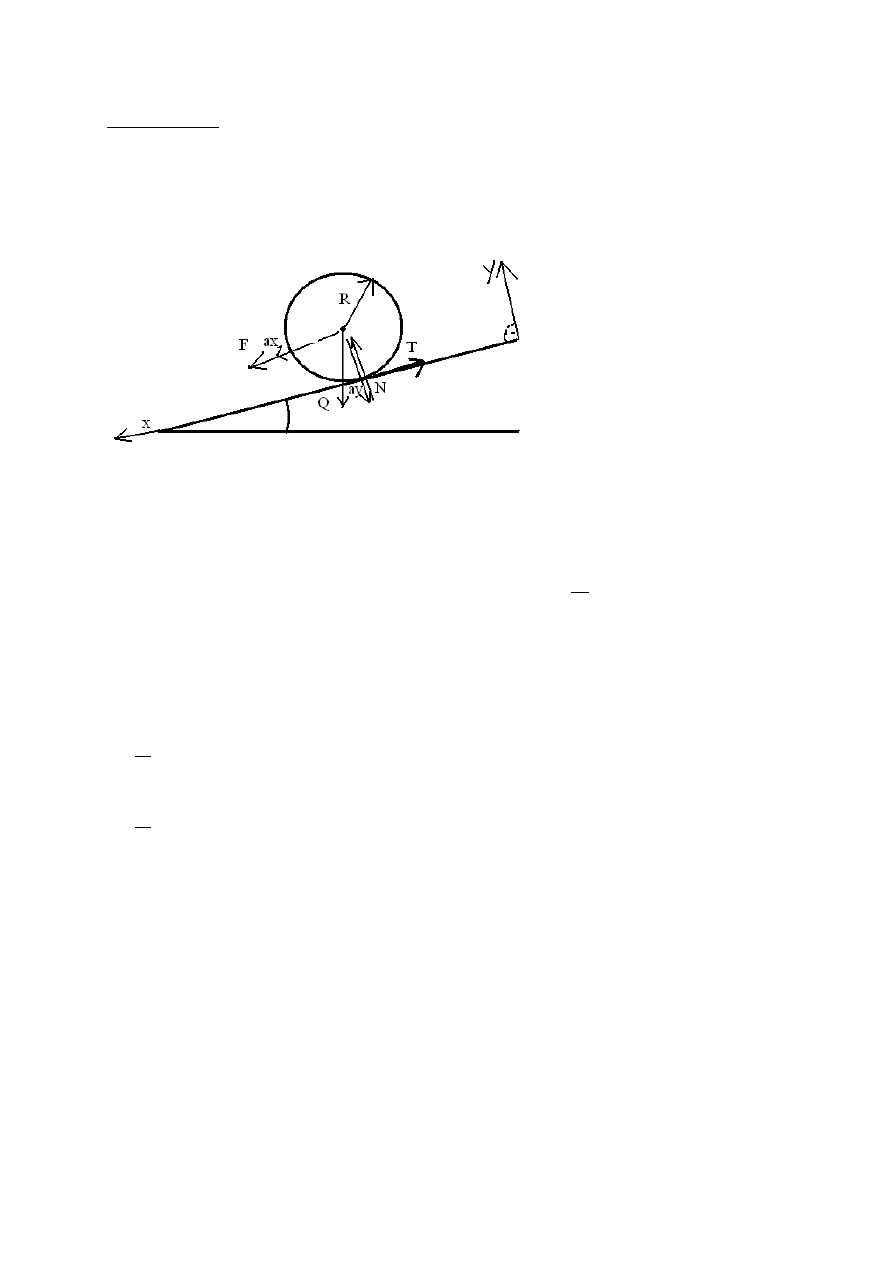
Koła pojazdu szynowego traktowane jak tarcza kołowa jednorodna ma promień
R i masę m, toczy się bez poślizgu po torze o kącie nachylenia α, współczynnik
tarcia między kołami a torem wynosi μ. Jaki warunek musi spełnić siła
pociągowa F przyczepiona w środku aby koło toczyło się bez poślizgu.
Z równań ruchu płaskiego
(1)
α
µ
α
cos
sin
..
..
mg
mg
F
x
m
T
Qx
F
x
m
s
s
−
+
=
⋅
−
+
=
⋅
R
a
R
a
a
x
=
⋅
=
=
ε
ε
..
(2)
α
µ
ε
α
µ
ε
α
µ
ε
α
µ
ε
ε
cos
2
cos
2
1
cos
2
1
cos
2
g
R
g
R
mg
R
mR
mg
R
Is
T
R
Is
=
⋅
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
α
µ
ε
cos
2
..
..
g
x
R
x
s
s
=
⋅
=
α
α
µ
α
µ
α
α
µ
sin
cos
3
cos
sin
cos
2
mg
mg
F
mg
mg
F
mg
−
=
−
+
=
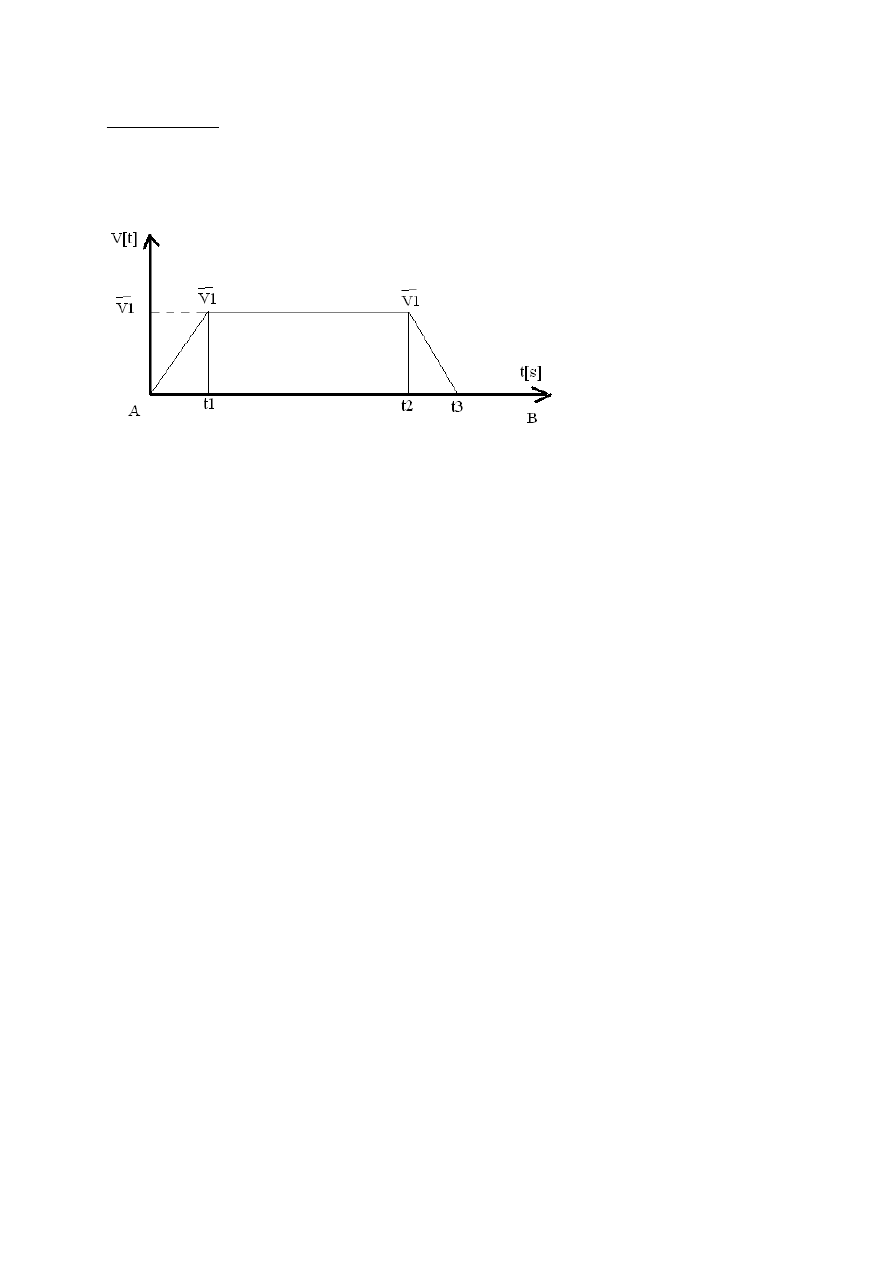
ZADANIE 6
Przebieg prędkości pociągu w funkcji czasu między stacjami AB przedstawia
wykres. Wyznacz odległość s[m] między tymi stacjami jeśli t1=2[min];
t2=12[min]; t3=15[min]; V=72[km/h]
s- całkowita odległość między stacjami
s=s1+S2+s3
s1- droga od czasu 0 do czasu t1
s1=1/2·V·t1
s2- droga od czasu t1 do t2
s2=V(t2-t1)
s3- droga od czasu t2do t3
s3=1/2·V·(t3-t2)
dodajemy wszystkie czasy
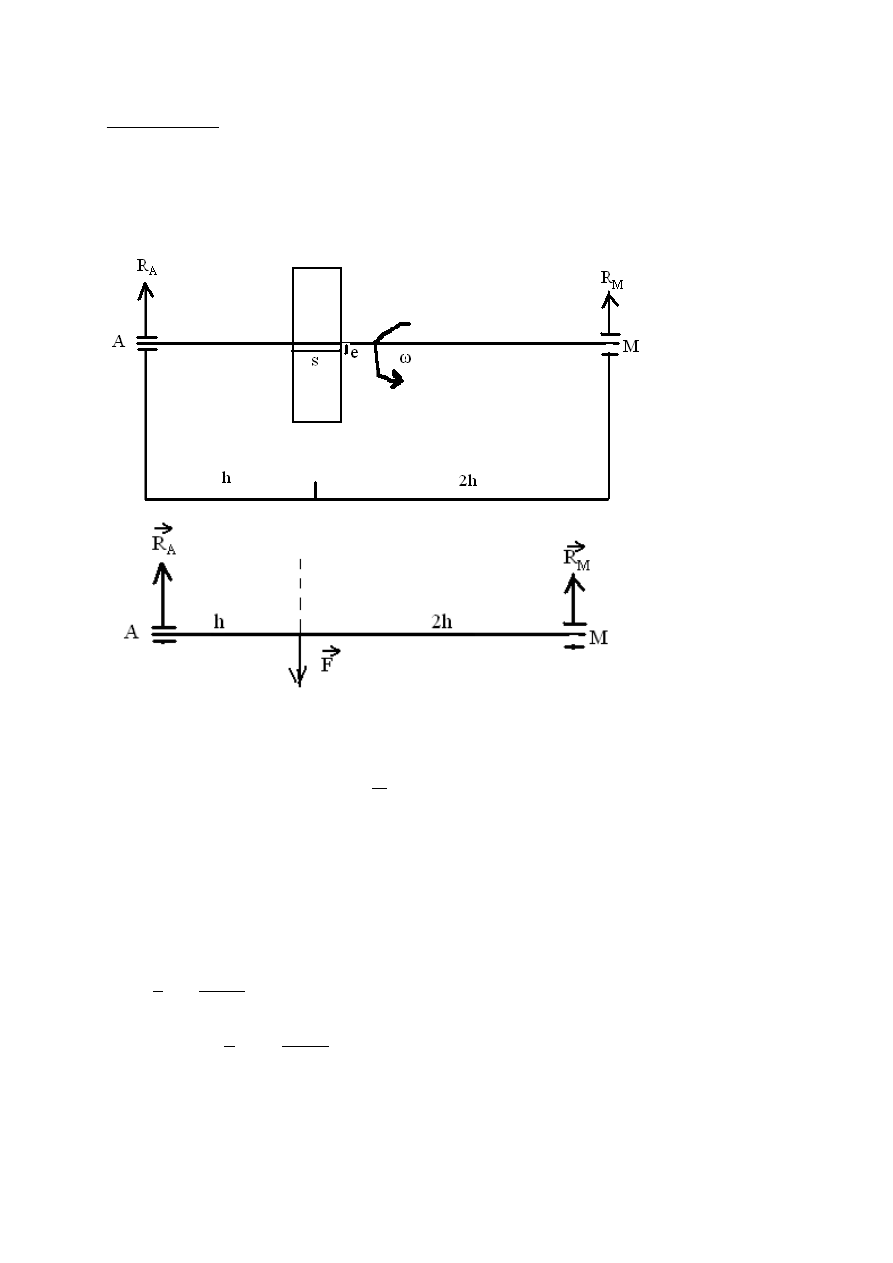
ZADANIE 7
Koło pasowe o ciężarze Q=100[N] i promieniu r=0,12 [m] jest obsadzone na
łożyskach osi AM i obraca się z częstotliwością=50Π[Hz]. Geometryczna oś
obrotu jest przesunięta względem osi symetrii koła o e=1[mm] obliczyć reakcję
łożysk.
R
A
, R
B
– szukane reakcje
F- siła odśrodkowa
e
g
Q
e
m
F
2
2
ϖ
ϖ
=
=
Warunki równowagi
0
3
)
2
0
)
1
=
−
⋅
=
Σ
=
+
−
=
Σ
h
R
h
F
M
R
F
R
Fy
M
A
M
A
Z 2) równania otrzymujemy
g
e
Q
F
R
F
R
g
e
Q
F
R
M
A
M
3
2
3
2
3
3
1
2
2
ϖ
ϖ
=
=
−
=
=
=
]
/
[
96
,
986
50
2
2
s
rad
f
=
Π
⋅
Π
=
Π
=
ϖ
ϖ
ϖ
WYLICZAMY RA i RM
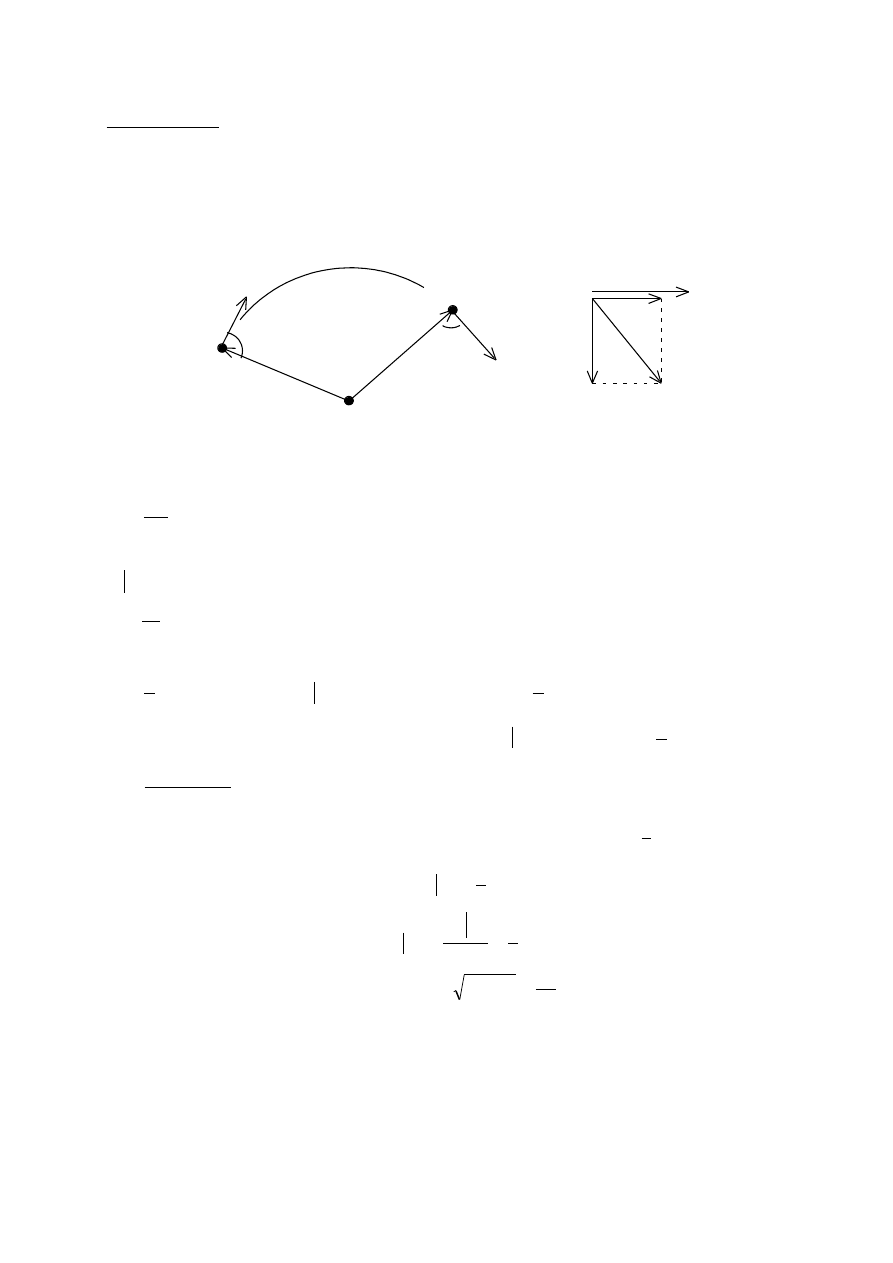
ZADANIE 7
Pociąg mający prędkość początkową V
o
= 54[km/h], przejechał drogę s
1
=
600[m] w ciągu czasu t
1
= 30[s]. Zakładając stałe przyspieszenie styczne
pociągu, obliczyć jego prędkość i przyspieszenie całkowite w końcu trzydziestej
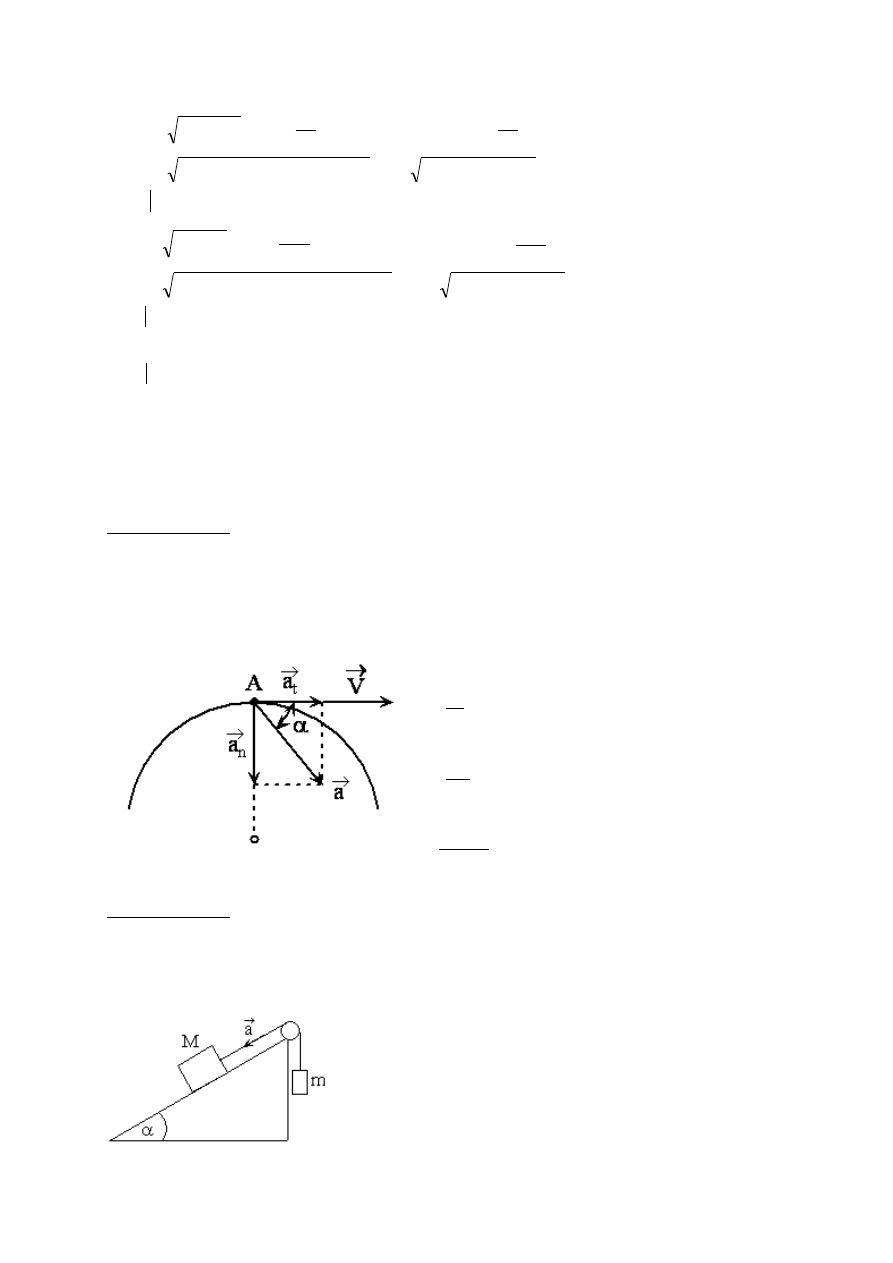
sekundy, jeżeli ruch odbywał się po łuku o promieniu R=1[km].
R
o
V
1
V
R
s
1
V
→
a
t
→
a
n
→
a
→
.
.
→
→
a
t
−
przyspieszenie styczne,
a
n
−
przyspieszenie normalne,
a
−
przyspieszenie całkowite.
C
t
a
V
C
dt
a
dV
C
dt
a
dV
dt
a
dV
dt
dV
a
t
t
t
t
t
+
=
→
+
=
→
+
=
→
=
→
=
∫
∫
∫
∫
C
−
stała zależna od warunku początkowego,
0
t
V
=
= V
o
→ C = V
o
→ V = a
t
t + V
o
(1)
∫
∫
∫
∫
∫
∫
+
+
=
→
+
+
=
→
+
=
→
=
→
=
1
o
t
1
o
t
1
C
dt
V
tdt
a
s
C
)dt
V
t
(a
ds
C
Vdt
ds
Vdt
ds
dt
ds
V
C
1
−
stała zależna od warunku początkowego,
1
o
2
t
C
t
V
t
a
2
1
s
+
+
=
→
0
t
s
=
= 0 → C
1
= 0 →
t
V
t
a
2
1
s
o
2
t
+
=
Z ostatniego równania wyliczamy a
t
: →
1
t
t
s
=
= s
1
→
1
o
2
1
t
1
t
V
t
a
2
1
s
+
=
→
2
1
1
o
1
t
t
)
t
V
2(s
a
−
=
Podstawiając dane liczbowe (V
o
= 15 [m/s]) otrzymujemy:
]
[m/s
3
1
a
2
t
=
Liczymy V w chwili t
1
ze wzoru (1):
[m/s]
25
15
30
3
1
V
1
t
t
=
+
=
=
a
n
w chwili t
1
liczymy ze wzoru:
8
5
R
V
a
1
1
t
t
2
t
t
n
=
=
=
=
[m/s
2
]
całkowite przyspieszenie w chwili t
1
:
24
17
a
a
a
2
n
2
t
=
+
=
[m/s
2
].
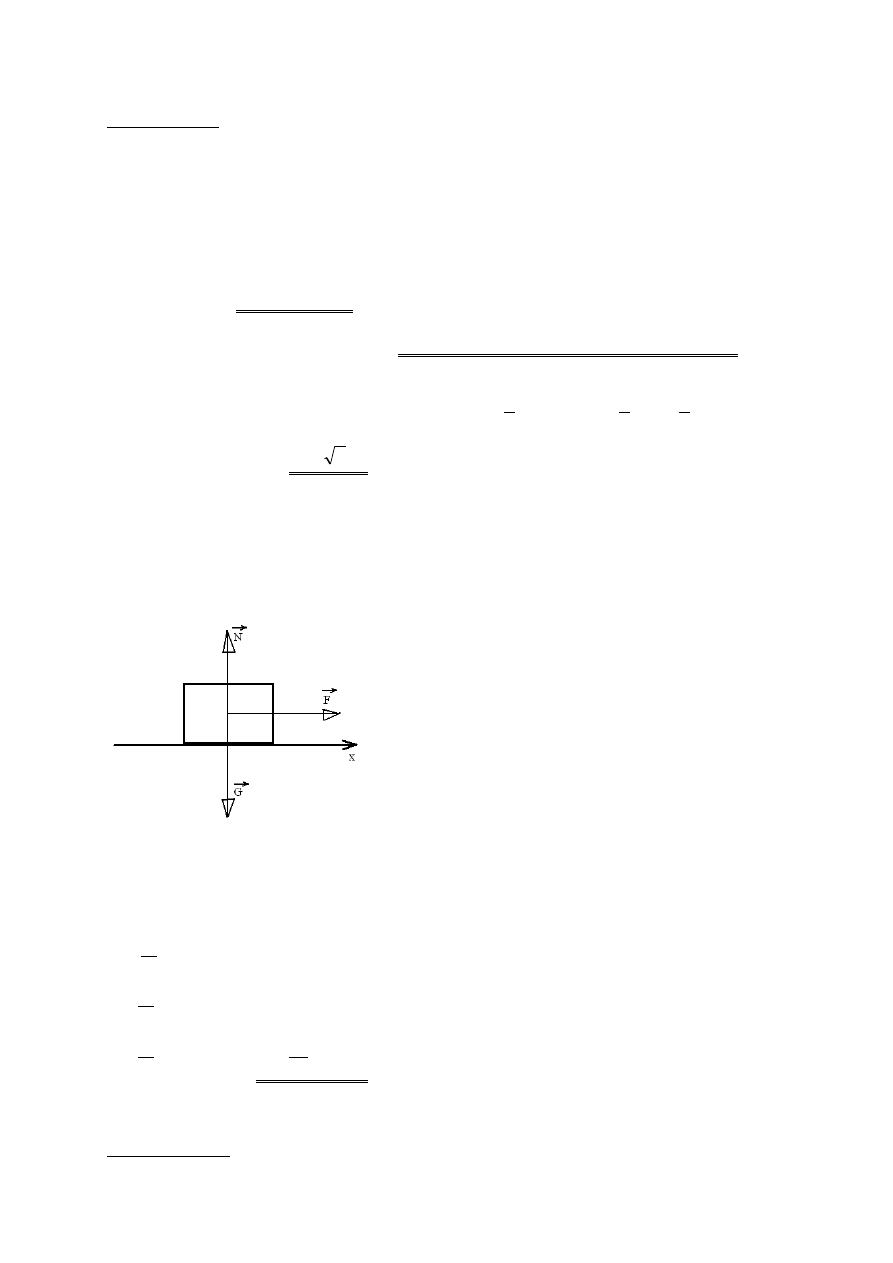
ZADANIE 8
Punkt materialny porusza się po płaszczyźnie Oxy zgodnie z równaniami:
)
sin(
)
(
cos
),
sin(
2
t
t
y
t
x
Π
−
Π
=
Π
=
Wyznacz tor punktu orazjego przyśpieszenie dla t1=3/2 [s]
)
sin(
)
(
cos
2
)
(
sin
2
)
cos(
)
sin(
)
cos(
2
)
sin(
),
cos(
_
1
)
(
)
sin(
)
(
sin
1
2
2
2
2
2
2
2
2
t
t
t
y
t
t
t
y
t
x
t
x
RUCHU
TOR
x
x
x
y
t
t
y
Π
Π
+
Π
Π
−
Π
Π
=
Π
Π
−
Π
Π
Π
−
=
Π
Π
−
=
Π
Π
=
−
+
−
−
=
⇒
Π
−
Π
−
=
•
•
•
•
•
•
Podstawiamy za t => t1=3/2 i otrzymujemy
2
1
2
3
cos
;
0
2
3
sin
−
=
Π
=
Π
stąd:
2
1
2
1
..
2
1
..
2
Π
=
Π
=
Π
=
a
y
x
ZADANIE 9
Ładunek o masie m=2[kg] znajdujący się na poziomej platformie porusza się
pod wpływem poziomej siły F(t)=2t [N]. Oblicz drogę jaką pokonał ładunek
ciała zatrzymanego w ciągu t1=3 [s]. Tarcie pomijamy
]
[
36
6
6
|
;
6
0
;
6
0
;
2
2
2
)
(
3
1
1
1
3
2
2
1
3
1
1
2
m
s
s
x
t
x
c
c
t
c
t
x
c
c
t
V
tdt
dV
t
V
t
F
V
m
t
t
=
=
⇒
=
=
=
+
+
=
=
+
=
=
→
=
→
=
=
•
•
ZADANIE 10
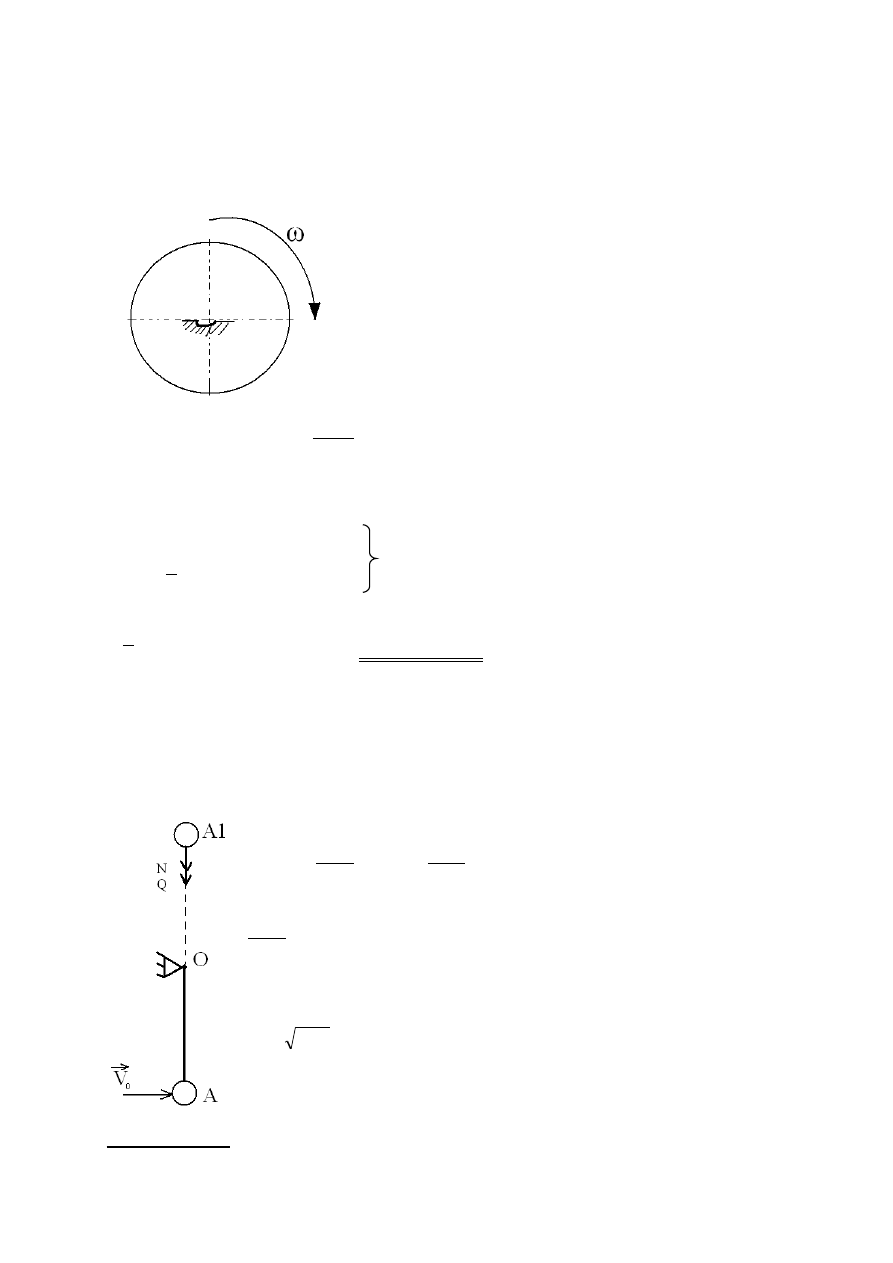
Wirnik obraca się ze stałą prędkością kątową ω
0
. Jego moment bezwładności
względem osi obrotu wynosi J. Po wyłączeniu prądu prędkość kątowa winrnika
spada na skutek momentu oporów ruchu M=h/(b+t) gdzie h,b – stałe, t – czas.
Po jakim czasie prędkość kątowa wirnika spadnie dwukrotnie?
b
h
J
c
c
t
b
h
J
t
t
b
h
J
t
M
J
ln
;
)
ln(
0
;
)
(
0
1
1
⋅
+
=
→
+
+
⋅
−
=
≥
+
−
=
→
−
=
•
•
ϖ
ϖ
ϖ
ϖ
0
1
0
2
1
|
)
ln(
ln
)
(
ϖ
ϖ
ϖ
ϖ
=
+
⋅
−
=
⋅
−
−
=
t
t
t
b
h
b
h
J
)
1
(
)
ln(
ln
2
1
2
/
0
1
1
0
−
=
→
+
⋅
=
⋅
−
−
h
J
e
b
t
t
b
h
b
h
J
ϖ
ϖ
ZADANIE 11
Wahadło matematyczne o długości 2l i masie kulki m znajduje się w środku
równowagi. Jaką prędkość początkową należy nadać kulce aby naciąg linki przy
przejściu przez górne położenie wahadła był równy zero?
Z zasady zachowania energii mechanicznej:
)
1
(
2
2
2
2
2
2
0
mV
mgl
mV
mgl
+
=
+
−
W położeniu górnym:
mg
Q
gdzie
Q
N
l
mV
=
+
=
:
2
2
Ma być N=0
:
)
1
(
)
2
(
)
2
(
2
2
>
−
→
=
mgl
mV
po podstawieniu otrzymujemy:
gl
V
10
0
=
ZADANIE 12
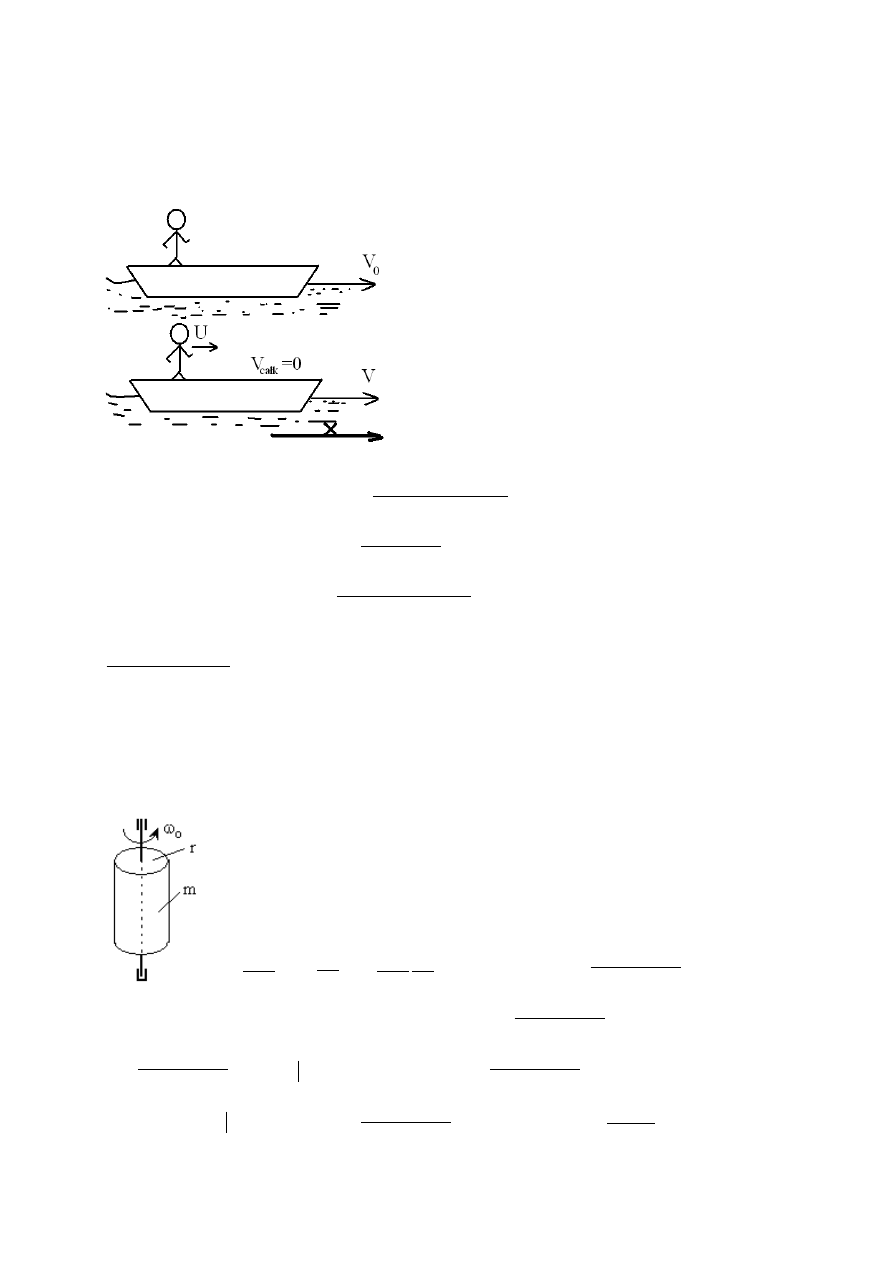
Łódź ze stojącym na niej człowiekiem ma prędkośćV
0
. Pomijając opór wody
znaleźć prędkość łodzi V i jej równanie ruchu s=s(t), jeśli człowiek porusza się
do przodu względem łodzi ze stałą prędkością U. Dla jakiej wartości prędkości
V
0
łódź nie będzie się przemieszczać.
m- masa człowieka
M – masa łodzi
Pęd początkowy p
1
=(m+M)V
0
Pęd końcowy p
2
=MV+m(U+V)
Z zasady zachowania pędu wynika równanie:
(m+M)V
0
=MV+m(U+V)
(m+M)V
0
=MV+mU+MV
(M+m)V=(m+M)V
0
-mU
Wyliczamy i otrzymujemy: V=
m
M
mU
V
M
m
+
−
+
0
)
(
- prędkość łodzi
m
V
m
M
U
mU
V
m
M
V
0
0
)
(
)
(
0
+
=
⇒
=
+
⇔
=
-przy takiej prędkości łódź w spoczynku
Równanie ruchu: s(t)=Vt =
t
m
M
mU
V
M
m
⋅
+
−
+
0
)
(
ZADANIE 14
Jednorodny walec o masie m = 30[kg] i promieniu r = 0,1[m] został ze stanu
spoczynku wprawiony w ruch obrotowy wokół swej nieruchomej osi symetrii
uzyskując prędkość kątową
ω
1
=
120[rad/s] w ciągu t
1
= 8[s]. Wiedząc, że
moment oporowy ruchu M
t
= 0,2[Nm], oblicz moment napędowy zakładając
jego stałą wartość.
Dynamiczne równanie ruchu:
t
n
M
M
ε
I
−
=
gdzie:
I
−
moment bezwładności walca
względem osi obrotu
ε
−
przyspieszenie kątowe
M
n
−
szukany moment napędowy
2
r
m
I
2
=
,
dt
dω
ε
=
→
t
n
2
M
M
dt
dω
2
r
m
−
=
→
dt
r
m
)
M
M
2(
dω
2
t
n
−
=
całkujemy obustronnie ostatnie równanie:
∫
∫
+
−
=
C
dt
r
m
)
M
M
2(
dω
2
t
n
C
t
r
m
)
M
M
2(
ω
2
t
n
+
−
=
,
0
ω
0
t
=
=
→ C = 0 →
t
r
m
)
M
M
2(
ω
2
t
n
−
=
z treści zad:
1
t
t
ω
ω
1
=
=
→
1
2
t
n
1
t
r
m
)
M
M
2(
ω
−
=
stąd:
1
2
1
t
n
2t
mr
ω
M
M
+
=
= 2,45 [Nm].
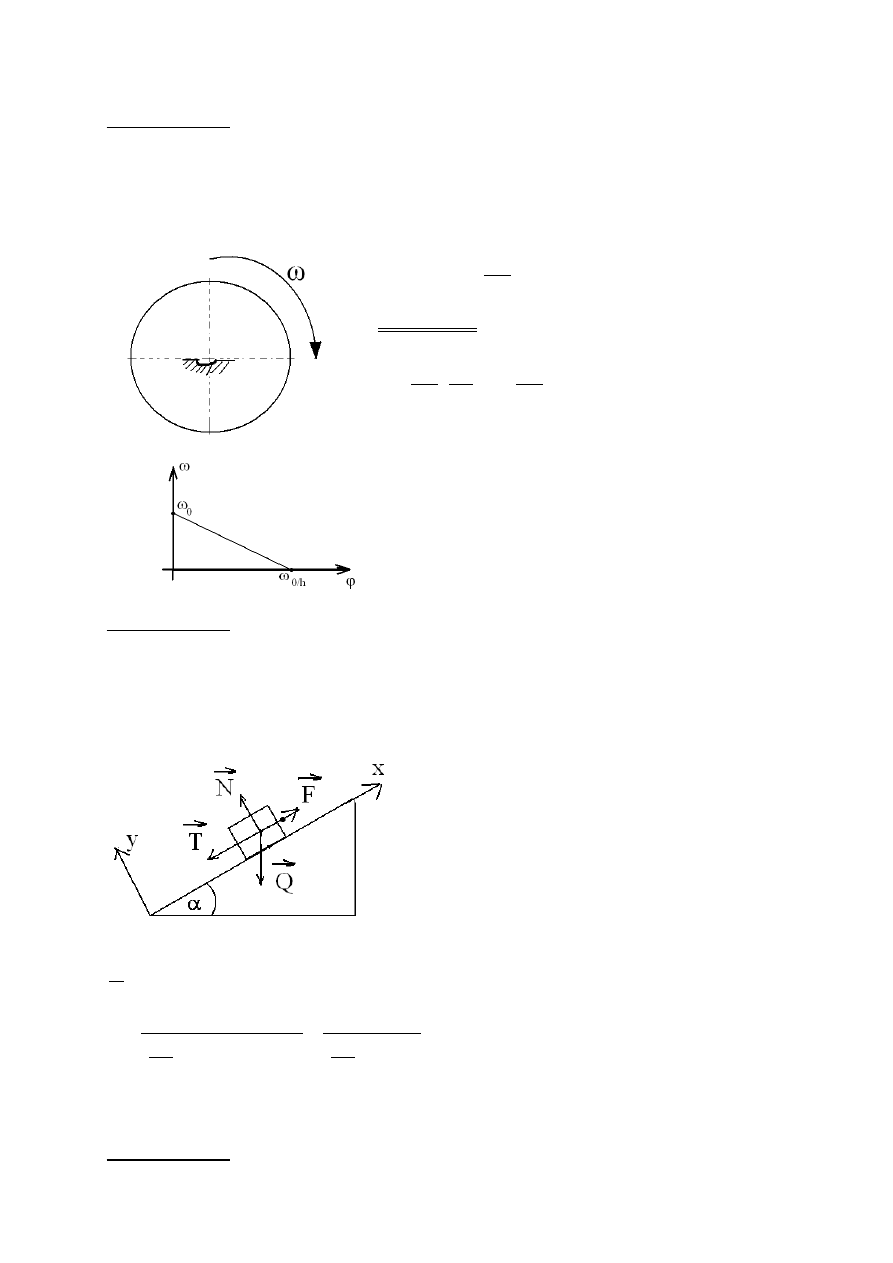
ZADANIE 15
Tarcza koła pasowego obraca się wokół swej nieruchomej osi symetrii tak że jej
opóźnienie kątowe ε jest proporcjonalne do jej prędkości kątowej ω: ε=-hω,
Gdzie h jest stałe. Prędkość początkowa tarczy wynosiła ω
0
[rad/s].
Wyprowadzić równania ω=ω(t) i ω=ω(φ). Oraz narysować wykres ω=ω(φ)
1)
hb
e
t
C
ht
dt
h
d
h
−
•
=
+
−
=
→
−
=
→
−
=
∫
∫
0
1
)
(
ln
ϖ
ϖ
ϖ
ϖ
ϖ
ϖ
ϖ
2)
ϕ
ϖ
ϖ
ϖ
ϖ
ϕ
ϖ
ϖ
ϕ
ϖ
ϖ
ϕ
ϕ
ϖ
ϖ
ϕ
h
C
h
h
d
d
dt
d
d
d
−
=
→
=
+
−
=
→
−
=
→
⋅
=
=
•
0
0
0
2
|
3)
ZADANIE 16
Lokomotywa ciągnie wagon w górę równi o nachyleniu α=0,02[rad]. Między
lokomotywę a wagon wstawiono dynamometr. W ciągu czasu t
1
120 [s]
dynamometr wskazywał średnio siłę F=10 [kN]. W tym czasie pociąg ze stanu
spoczynku nabrał prędkość V
1
=72 [km/h]. Współczynnik tarcia wagon-tor
μ=0,02. Obliczyć ciężar wagonu.
Z zasady zachowania pędu:
]
[
5
,
175
)
(
)
cos
sin
(
)
cos
sin
(
1
1
1
1
1
1
kN
gt
V
F
gt
V
F
Q
t
Q
Q
F
V
g
Q
=
+
+
=
+
+
=
−
−
=
µ
α
α
µ
α
α
µ
α
ZADANIE 17
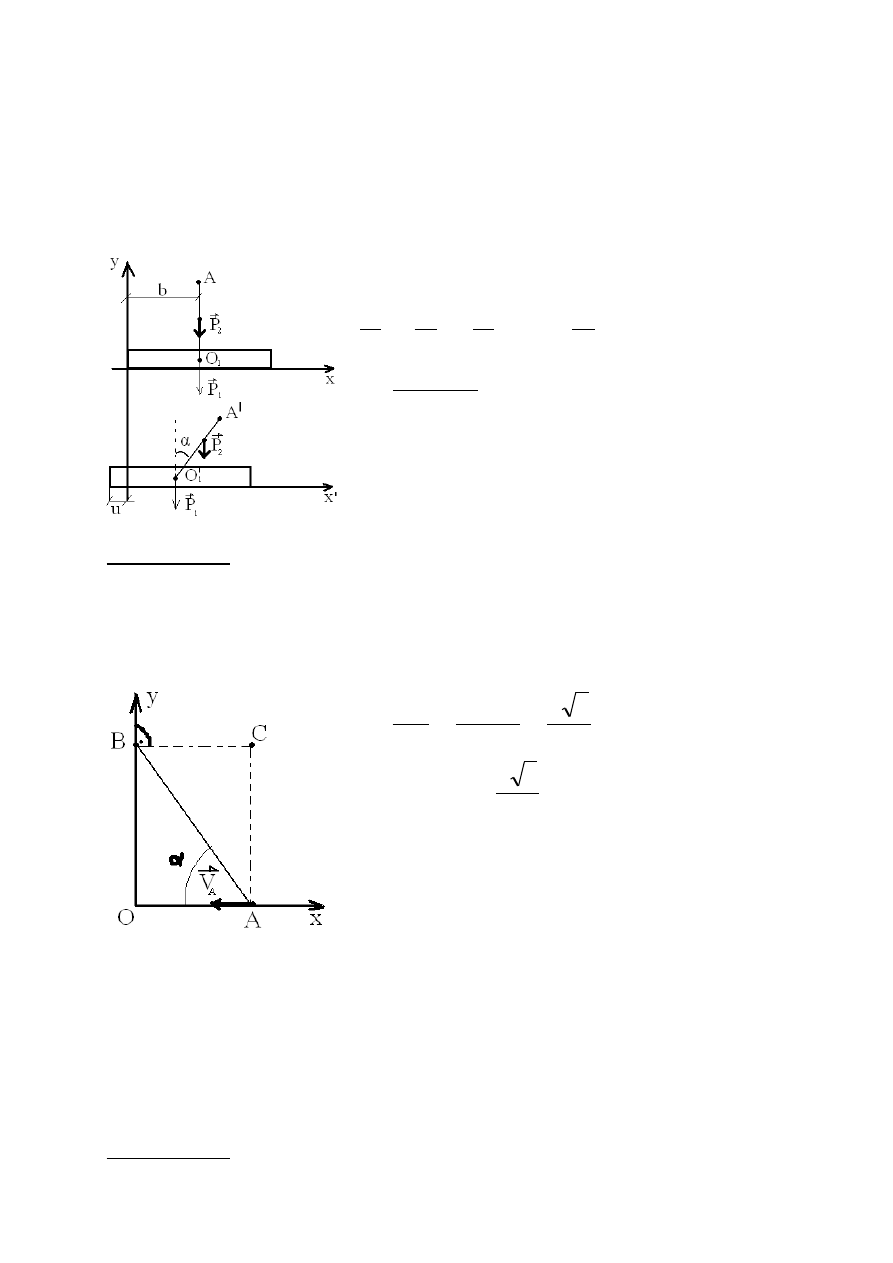
Obliczyć przesunięcie platformy o ciężarze podstawy P
1
=100 [kN],
spoczywającej na stojącej wodzie. Jeśli wysięgnik platformy o ciężarze
p
2
=20[kN] z pozycji pionowej obróci się w prawo o kąt α=30
o
. Wysięgnik
potraktować jako jednorodną prostą belkę. Długość wysięgnikaO
1
A=2l=6[m].
Opory ruchu pomijamy.
Z zasady ruchu środka masy układu:
]
[
25
,
0
)
(
sin
)
sin
(
)
(
2
1
2
2
1
2
1
m
P
P
l
P
u
l
u
b
g
P
u
b
g
P
b
g
P
b
g
P
≈
+
⋅
=
+
−
+
−
=
+
α
α
ZADANIE 18
Pręt prosty AB=b=1[m]ślizga się ruchem płaskim, po osiach układu Oxy. W
chwili gdy tworzy on z osią Ox kąt α=60
o
, prędkość jego końca wynosi
V
A
=2[m/s]. Wyznacz dla tego położenia chwilowy środek obrotu, prędkość
kątową i prędkość pręta.
]
/
[
3
3
2
]
/
[
3
3
4
sin
s
m
ctg
V
V
s
rad
b
V
AC
V
A
B
A
A
=
=
=
=
=
α
α
ϖ
ZADANIE 19
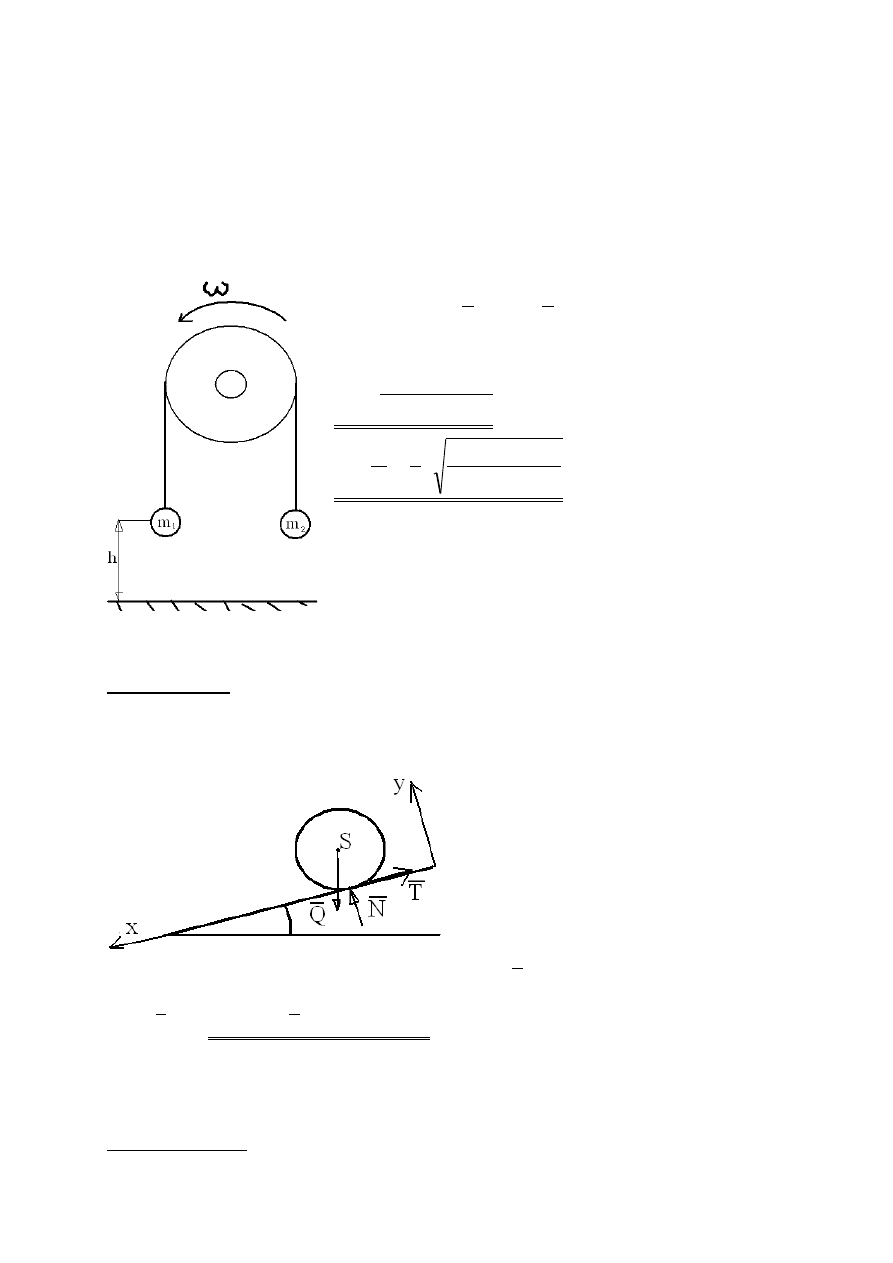
Przez zamocowany obrotowo krążek oo promieniu r, przełożono nierozciągliwą
linkę. Na końcach tej linki zawieszono kuli o masach m
1
i m
2
(m
1>
m
2
) tak, że ich
środki znajdują się na tej samej wysokości i zablokowano ruch. Jaką prędkość
odzyskają kulki po odblokowaniu ruchu, jeżeli kulka o masie m
1
obniży się o
wielkość h? jaka będzie wtedy prędkość kątowa krążka? Zakładamy, żę między
krążkiem a linką brak jest poślizgu a linka krążek są nieważkie.
)
(
)
(
2
1
)
(
)
(
2
)
(
)
(
2
0
2
2
1
2
1
2
1
2
1
2
1
2
1
2
2
2
1
2
1
1
2
2
2
2
1
2
1
m
m
m
m
gh
r
r
V
m
m
m
m
gh
V
V
m
m
m
m
gh
g
m
h
g
m
V
m
V
m
gh
m
gh
m
+
−
⋅
=
=
+
−
=
+
=
−
⋅
+
⋅
+
+
=
+
ϖ
ZADANIE 20
Oblicz jaki kąt α powinna tworzyć z poziomem płaszczyzna na której ma się
toczyć bez poślizgu kula, jeżeli wiadomo, że współczynnik tarcia miedzy kulą a
płaszczyzną wynosi μ=0,2
Q
=mg
T=μr
(1)
ma
x
= mgsinα - μmgcosα
(2)
I
S
ε = μmgrcosα
(3)
a
x
= a
s
= εV
α
µ
cos
2
5
g
a
S
=
do (1):
o
arctg
tg
35
2
7
2
7
≤
≤
→
=
∗
α
µ
α
µ
α
ZADANIE 21
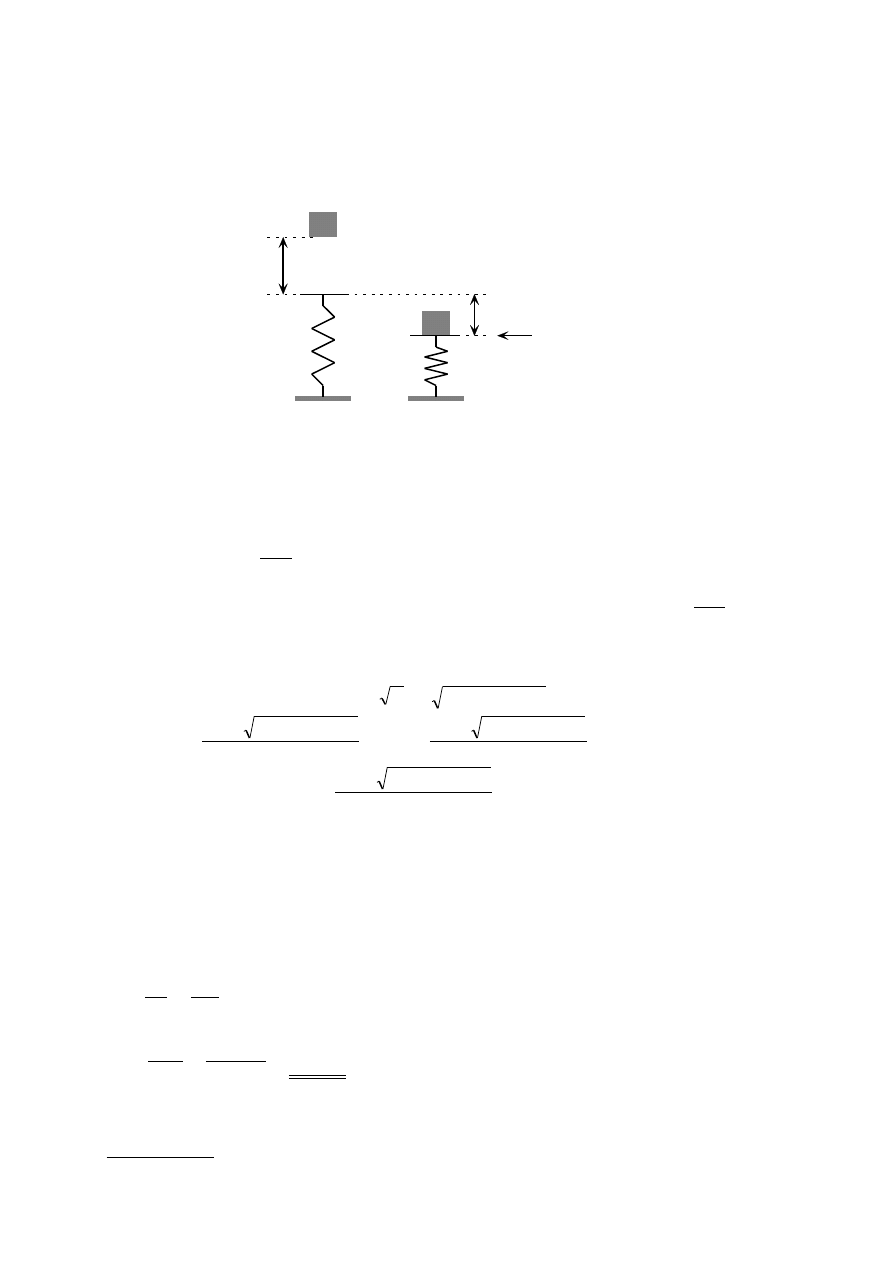
Ciężarek o masie m ze stanu spoczynku spada pionowo z wysokości h na
nieważką sprężynę śrubową o stałej sztywności równej k. Wyznacz ugięcie
λ
tej
sprężyny zakładając, że ciężarek po zetknięciu z górnym końcem sprężyny
przykleił się do niej. Opory ruchu pomijamy.
h
λ
k
poziom
odniesienia
Korzystamy z zasady zachowania energii. Energia kinetyczna ciężarka w chwili
początkowej jak i końcowej jest równa zero. Przyjęto poziom odniesienia dla
energii potencjalnej grawitacji jak pokazano na rysunku. Wobec tego całkowita
energia (E
1
) w położeniu początkowym: E
1
= mg(h +
λ
)
całkowita energia (E
2
) w położeniu końcowym jest energią potencjalną
sprężystości:
2
λ
k
E
2
2
=
Z zasady zachowania energii wynika równanie: E
1
= E
2
→
2
λ
k
λ)
h
mg(
2
=
+
Po przekształceniach otrzymujemy: k
λ
2
−
2mg
λ
−
2mgh = 0
2hk)
4mg(mg
2mgh)
4k(
2mg)
(
Δ
2
+
=
−
−
−
=
2hk)
mg(mg
2
Δ
+
=
k
2hk)
mg(mg
mg
λ
+
+
=
lub
0
k
2hk)
mg(mg
mg
λ
<
+
−
=
−
sprzeczne
czyli odpowiedzią jest:
k
2hk)
mg(mg
mg
λ
+
+
=
[m].
ZADANIE 22
Pociąg poruszający się po torze prostym z prędkością V
0
=72 [km/h] doznaje
przy hamowaniu opóźnienia a=0,4[m/s
2
]. Wyznaczyć po jakim czasie t
1
[s]
pociąg zatrzyma się i jaka będzie droga hamowania s
1
[m]
]
[
500
2
50
4
,
0
2
]
[
50
4
,
0
20
]
/
[
20
]
/
[
72
2
1
1
0
1
m
at
s
s
a
V
t
s
m
h
km
=
⋅
=
=
=
=
=
=
ZDANIE 23
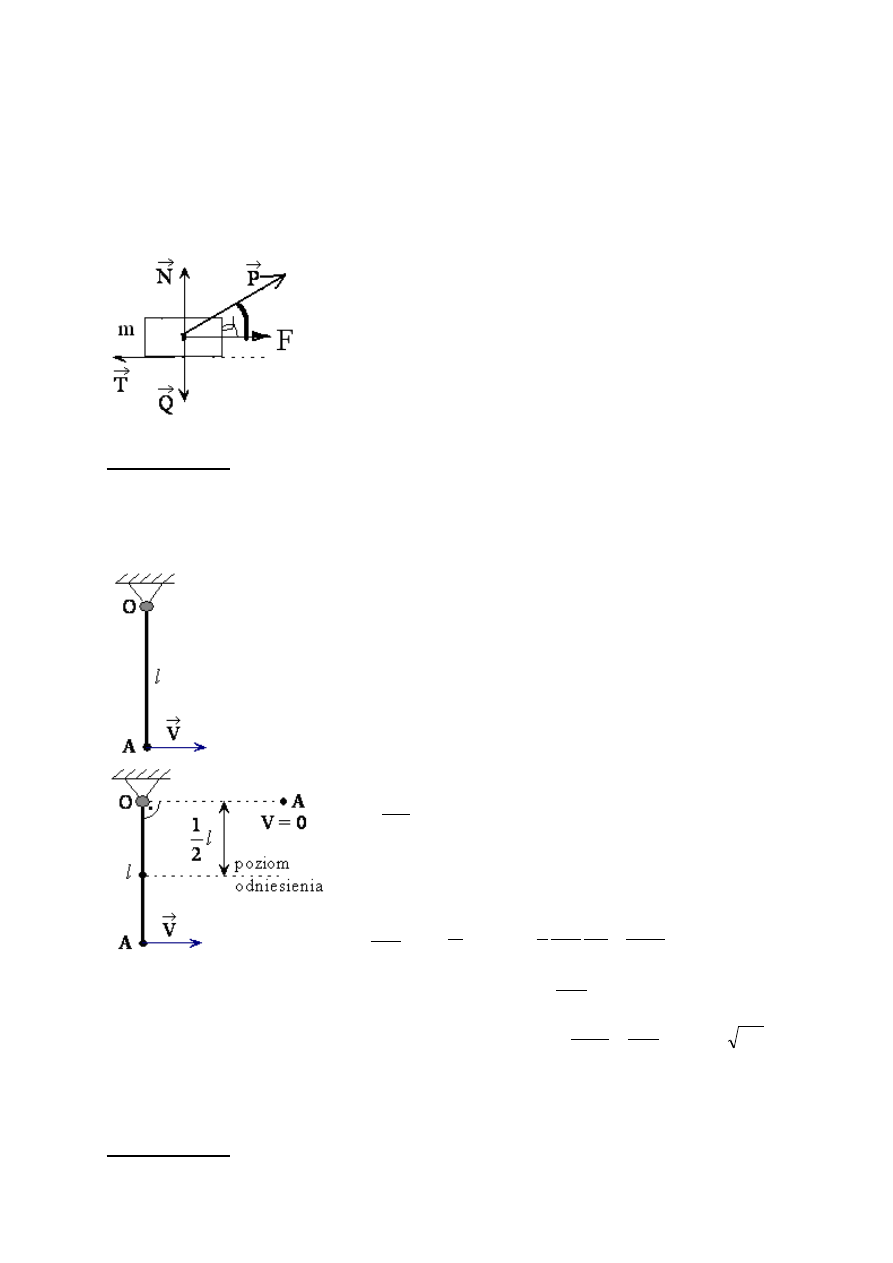
Do ciała o masie m, które może poruszać się prostoliniowym ruchem
postępowym po chropowatej poziomej płaszczyźnie, przyłożona została siła P
tworząca kąt
α
z tą płaszczyzną. Wyznaczyć przyspieszenie, z którym zacznie
poruszać się to ciało. Współczynnik tarcia między ciałem a płaszczyzną jest
równy
µ
.
F=Pcosα
N=Psinα
T=μG; G=Q-N=mg-Psin α
T=μ(mg-Psin α)
P
w
=F-T = Pcosα- μ/(mg-Psin α)
P
w
=P(cos α + μsin α)-μmg
A=P
w
/m
ZADANIE 24
Prosty jednorodny pręt o długości l = 3,27 [m] osadzony jest swoim końcem O
obrotowo na osi i może wykonywać ruchy w płaszczyźnie pionowej,
prostopadłej do tej osi. Jaką prędkość trzeba nadać końcowi A, aby pręt z
położenia równowagi wykonał pół obrotu?
Korzystamy z zasady zachowania energii.
Na poniższym rysunku zaznaczono poziom odniesienia dla energii
potencjalnej (liczona jest względem środka masy)
Całkowita energia (E
1
) w położeniu początkowym:
2
Iω
E
2
1
=
gdzie:
I
−
moment bezwładności pręta
względem własnego końca
ω
−
prędkość kątowa w chwili początkowej
3
m
I
2
l
=
,
l
V
ω
=
→
6
V
m
V
3
m
2
1
E
2
2
2
2
1
=
=
l
l
Całkowita energia (E
2
) w położeniu końcowym:
2
mg
E
2
l
=
Z zasady zachow energii wynika równanie: E
1
= E
2
→
2
mg
6
V
m
2
l
=
→
l
3g
V
=
Podstawiając dane liczbowe otrzymujemy: V = 9,81 [m/s].
ZADANIE 25
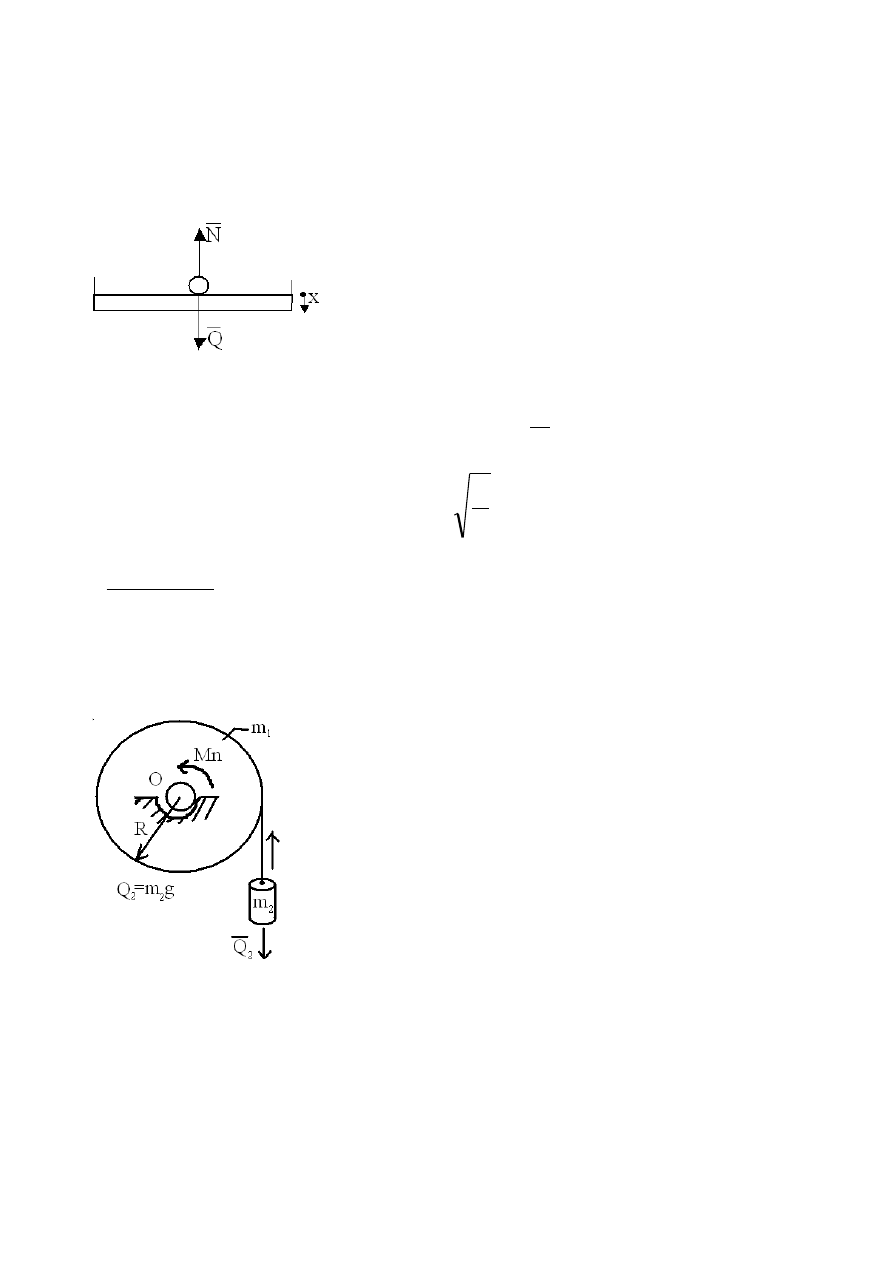
Płytka wykonuje ruch zgodnie z równaniem x=bsin(ωt), gdzie amplituda, t-czas.
Jaka musi być częstość ω, aby kulka spoczywająca na płutce oderwała się od
niej?(odrywanie i podrzucanie do góry)
)
(
min
)
(
max
))
sin(
(
),
sin(
2
2
2
2
ϖ
ϖ
ϖ
ϖ
ϖ
ϖ
b
g
m
N
b
g
m
N
t
b
g
m
N
N
Q
x
m
t
b
x
−
=
+
=
−
=
→
−
=
−
=
•
•
•
•
Moment oderwania się kulki: Nmin=0 ->
b
q
=
2
ϖ
Warunek oderwania i podrzucenia:
b
q
≥
ϖ
ZDANIE 26
Na wał podnośnika o promieniu r i masie m1 nawinięto lekką nierozciągliwą
linkę, na końcu której zamocowano ładunek o masie m2. Na wał działa moment
napędowy M
0
przez co ładunek jest podnoszony do góry. Oblicz przyśpieszenie
kątowe ε wału i naciąg N linki
Równanie zmiany kąta względem osi obrotu
)
(
;
)
2
(
2
)
2
1
(
2
2
2
2
2
2
2
1
2
2
2
2
2
1
)
2
(
R
g
m
N
R
a
g
m
N
a
m
R
m
m
m
M
gR
m
M
R
m
R
m
M
k
n
n
M
O
ε
ε
ε
ε
+
=
=
−
=
+
−
=
−
=
+
→
=
•
ZADANIE 27
Dwie kule, jedna o masie m
1
= 200[g], a druga o masie m
2
= 300[g] poruszają
się do siebie wzdłuż prostej z prędkościami odpowiednio V
1
= 0,5[m/s] i V
2
=
0,4[m/s] W pewnej chwili zderzyły się i następnie zaczęły poruszać się razem.
Znaleźć ich wspólną prędkość oraz kierunek ruchu.
Pęd pierwszej kuli przed zderzeniem: p
1
= m
1
V
1
= 0,1 [kg
⋅
m/s]
Pęd drugiej kuli przed zderzeniem: p
2
= m
2
V
2
= 0,12 [kg
⋅
m/s]
Pęd drugiej kuli jest większy, wobec tego po zderzeniu kule będą poruszać się w
tym kierunku, w którym poruszała się druga kula.
Pęd kul po zderzeniu: p = (m
1
+ m
2
)V
Z zasady zachowania pędu wynika równanie: p
2
−
p
1
= p
→
m
2
V
2
−
m
1
V
1
= (m
1
+ m
2
)V
Stąd:
[m/s]
0,04
m
m
V
m
V
m
V
2
1
1
1
2
2
=
+
−
=
.
ZADNIE 28
Punkt materialny o masie m = 2[kg] porusza się zgodnie z równaniami
x(t) = hcos
ω
t [m],
y(t) = hsin
ω
t [m].
Wyznacz:
a) prędkość w chwili t
1
=
π
/
ω
,
b) przyspieszenie w chwili t
2
= 2
π
/
ω
,
c) siłę działającą na ten punkt w chwili t
2
. Przyjąć do obliczeń: h = 0,05[m],
ω
= 10[rad/s].
a)
2
y
2
x
V
V
V
+
=
,
[m/s]
ωhsinωt
dt
dx
V
x
−
=
=
,
[m/s]
ωhcosωt
dt
dy
V
y
=
=
[m/s]
ωh
ωt
cos
ωt
sin
ωh
t)
hcosω
(ω
ωhsinωt)
(
V
2
2
2
2
=
+
=
+
−
=
[m/s]
0,5
ωh
V
1
t
t
=
=
=
b)
2
y
2
x
a
a
a
+
=
,
t
hcosω
ω
dt
dV
a
2
x
x
−
=
=
[m/s
2
] ,
t
hsinω
ω
dt
dV
a
2
y
y
−
=
=
[m/s
2
]
h
ω
ωt
sin
ωt
cos
h
ω
t)
hsinω
ω
(
t)
hcosω
ω
(
a
2
2
2
2
2
2
2
2
=
+
=
−
+
−
=
[m/s
2
]
5
h
ω
a
2
t
t
2
=
=
=
[m/s
2
]
b)
am
F
=
, F = ω
2
hm [N]
10
hm
ω
F
2
t
t
2
=
=
=
[N].
ZADANIE 29
Punkt A porusza się po krzywej płaskiej zgodnie z równaniem s = b(e
kt
−
1),
gdzie s w [m], b, k są stałymi. Kąt między całkowitym przyspieszeniem, a
prędkością wynosi
α
= 60
o
. Obliczyć prędkość i całkowite przyspieszenie
punktu.
Prędkość punktu wyznaczamy ze wzoru:
kt
bke
dt
ds
V
=
=
[m/s]
Przyspieszenie styczne wynosi:
kt
2
t
e
bk
dt
dV
a
=
=
[m/s
2
]
Całkowite przyspieszenie jest równe:
kt
2
t
e
bk
2
cos60
a
a
=
=
[m/s
2
].
ZADANIE 30
Dla układu dwóch mas M i m połączonych nierozciągliwą i lekką nicią wyznaczyć ich
przyspieszenie oraz naciąg nici. Ciało o masie M spoczywa na chropowatej równi pochyłej o
kącie nachylenia α, współczynnik tarcia o równię wynosi µ. Jaki warunek musi spełniać masa
M, aby jej ruch w dół równi był możliwy?
Rozpatrujemy ruch masy M:
gdzie:
P
−
siła ciężkości, P = Mg, F
1
= Psin
α
=
Mgsin
α
, F
2
= Pcos
α
= Mgcos
α
S
−
siła naciągu linki
N
−
siła nacisku
T
−
siła tarcia
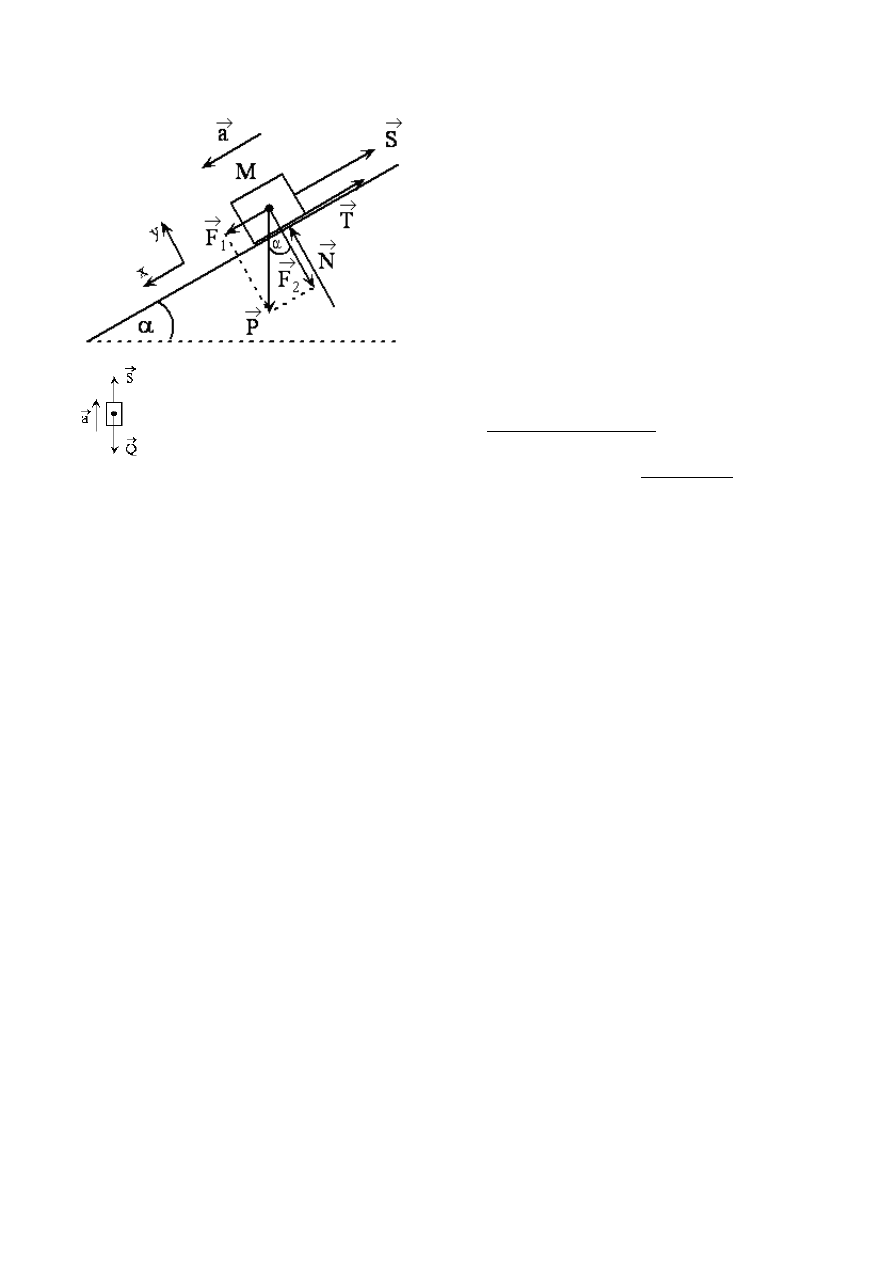
Dynamiczne równania ruchu w kierunku osi x i y
(obranych jak na rysunku)
x: aM = F
1
−
T
−
S
y: 0 = N
−
F
2
Uwzględniając, że: T = Nμ oraz podstawiając
wartości F
1
i F
2
otrzymujemy:
aM = Mgsin
α
−
Nμ
−
S, N = Mgcos
α
→ aM =
Mgsin
α
−
Mgμcos
α
−
S (1)
Rozpatrujemy ruch masy m:
gdzie: Q
−
siła ciężkości, P = mg, S
−
j.w.
Dynamiczne równanie ruchu:
am = S
−
Q → am = S
−
mg (2) (1) + (2)=>
aM + am = Mgsin
α
−
Mg
µ
cos
α
−
mg →
m
M
mg
μcosα)
Mg(sinα
a
+
−
−
=
a > 0, czyli: Mg(sin
α
−
µ
cos
α
)
−
mg > 0 stąd otrzymujemy:
μcosα
sinα
m
M
−
>
.