X L V I I I K O N F E R E N C J A N AU K O W A
KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN
I KOMITETU NAUKI PZITB
Opole – Krynica
2002
Magdalena JAKUBEK
1
Ewa PABISEK
2
Zenon WASZCZYSZYN
3
OSZACOWANIE PARAMETRÓ W CHARAKTERYSTYK
PODATNYCH POŁ Ą CZEŃ STALOWYCH
ZA POMOCĄ SIECI NEURO-ROZMYTEJ
1. Wprowadzenie, cel i zakres pracy
W normie europejskiej EC3 [1] zaproponowano proste modele charakterystyki M –
F
dla
połą czenia ‘rygiel-słup’, gdzie: M – przywę złowy moment zginają cy rygiel,
F
– wzajemny
ką t obrotu stycznych do osi rygla i słupa, schodzą cych się w wę ź le. Parametry modelu
charakterystyki mają być wyznaczone na podstawie wynikó w badań doświadczalnych na
materialnych modelach laboratoryjnych.
Tą drogą poszły pró by zastosowania sztucznych sieci neuronowych do identyfikacji
parametró w modeli proponowanych w EC3, opierają ce się na bankach danych doświad-
czalnych [2-6]. Niestety, wyniki tych prac nie zakończyły się znaczą cym powodzeniem.
Głó wnym powodem były mało reprezentatywne badania, ograniczane do niepowtarzalnych
doświadczeń na mało licznych zbiorach połą czeń. Prowadziło to do wynikó w o niskiej
dokładności predykcji neuronowej.
W naszym referacie podejmujemy pró bę ponownej analizy problemu wyznaczania
parametró w prostej biliniowej charakterystyki ale nie w odniesieniu do wartości ostrych lecz
rozmytych w sensie wartości przedziałowych. W tym celu zbudowano sieć jednokierunkową
o parametrach rozmytych, opierają c się na metodzie zaproponowanej w [7]. Metoda polega
na uczeniu sieci na oddzielnych wzorcach celem wyznaczenia funkcji przynależności dla
parametró w sieci jednokierunkowej.
Tak otrzymaną sieć neuro-rozmytą zastosujemy do wyznaczenia przedziałowych war-
tości parametró w grupy 30 połą czeń analizowanych w [4].
2. Sieć neuro-rozmyta
Ró żnego typu sieci neuro-rozmyte są omawiane w [9]. W naszym referacie zajmujemy się
siecią o parametrach rozmytych, a wię c siecią , któ ra może odwzorowywać rozmyte wartości
1
Mgr inż., Wydział Inżynierii Lą dowej Politechniki Krakowskiej
2
Dr inż., Wydział Inżynierii Lą dowej Politechniki Krakowskiej
3
Prof. dr hab. inż., Wydział Inżynierii Lą dowej Politechniki Krakowskiej
70
wejść w rozmyte wartości wyjść , ale też dla ostrych wejść dawać rozmyte wyjścia. Uczenie
takiej sieci za pomocą operacji na zbiorach rozmytych jest bardzo trudne i ze wzglę du na
efektywność numeryczną wymaga znacznych uproszczeń modelu, np. w odniesieniu do
przyjmowanych funkcji przynależności [9].
Z tych powodó w oparliśmy się na pomyśle algorytmu zaproponowanego w [6]. Polega
on na wstę pnym uczeniu sieci na zbiorze wzorcó w uczą cych:
L = {( x
(p)
, z
(p)
)
|
p = 1,...,L } . (1)
Po nauczeniu sieci zbió r parametró w sieci (wartości wag synaptycznych i wartości
progowych ), oznaczony w skró cie jako {w
i
o
|
i = 1,...,LPS } gdzie LPS jest liczba paramet-
ró w sieci, przyjmujemy jako zbió r parametró w począ tkowych do uczenia sieci dla kolejnych
wzorcó w p = 1,...,L . Obliczone parametry służą do wyznaczania funkcji zależności dla
parametró w sieci i = 1,...,LPS.
Algorytm budowania sieci neuro-rozmytej omó wiono szczegó łowo w [10]. Składa się
on z trzech etapó w. W Etapie I sieć jest uczona na całym zbiorze uczą cym (1). Ten etap jest
poprzedzony etapem wstę pnym projektowania sieci, por. [10]. W Etapie II proces uczenia
jest powtarzany L razy, kolejno dla każdego wzorca uczą cego p. Po obliczeniu zbioru
parametró w {w
i
(p)
½
p=1,...,L; i=1,...,LPA }. W Etapie III obliczamy funkcje przynależności
m
i
=
m
(w
i
) dla wszystkich parametró w sieci i . Dochodzimy w ten sposó b do sieci rozmytej,
któ ra po pozytywnym sprawdzeniu na zbiorze testują cym może być używana w etapie
operacyjnym do predykcji neuronowej dla innych zbioró w niż wcześniej wykorzystane
zbiory uczą cy i testują cy.
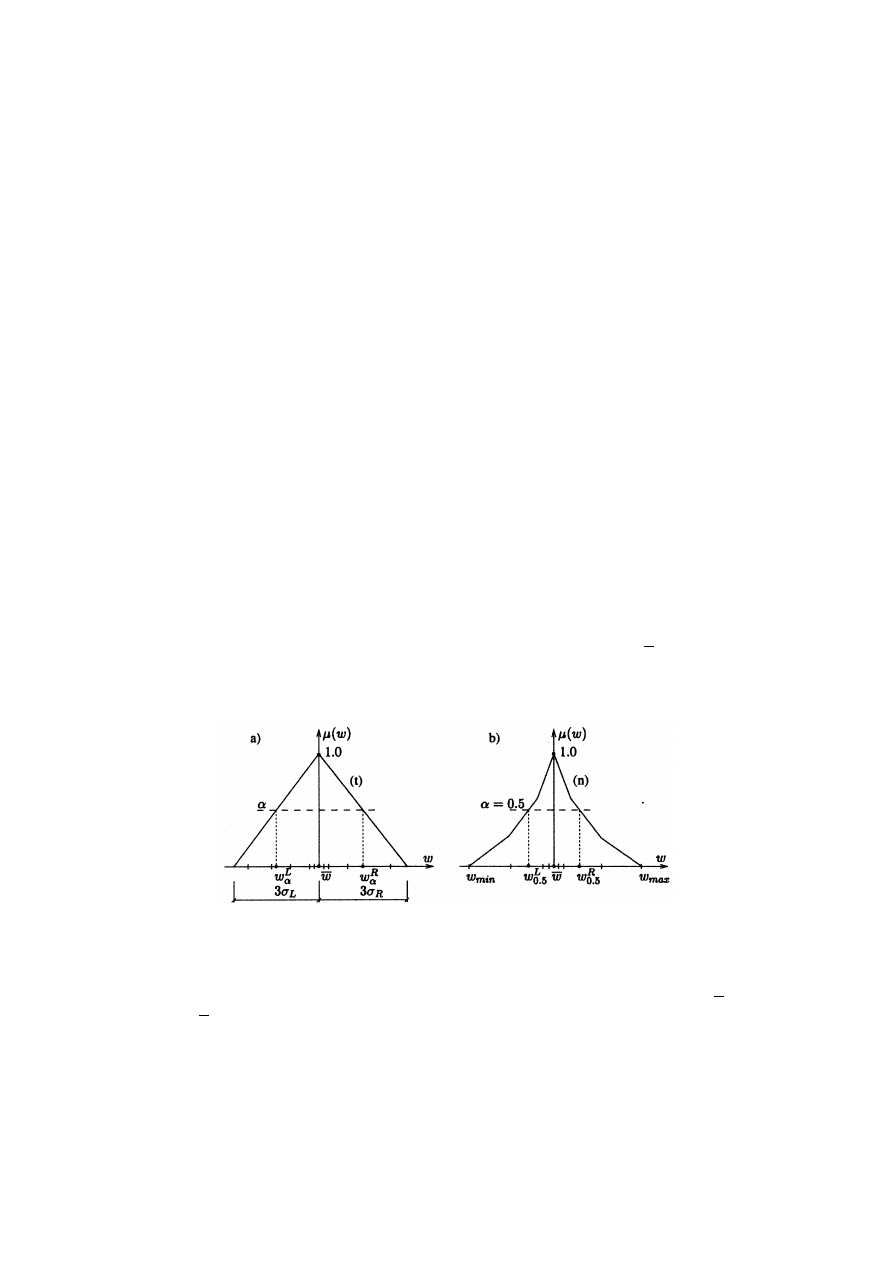
W [11] omó wiono dwie metody obliczania funkcji przynależności. Prostsza metoda,
wzię ta z [6], zakłada funkcje tró jką tne, por. rys. 1a (t), gdzie długości podstawy są obliczone
dla standardowych odchyleń
s
L
i
s
R
odmierzanych od wartości średniej w , gdzie dla
uproszczenia pominię to indeks i parametru sieci. Przekroje
a
odpowiadają wartości przyna-
leżności i wartości przedziałowych [w
L
, w
R
]
a
= [ w
L
a
, w
R
a
] .
Rys. 1. Funkcje przynależności parametru sieci neuro-rozmytej:
a) funkcja tró jką tna (t), b) funkcja nieliniowa (n)
Druga metoda wyznaczania nieliniowej funkcji przynależności parametró w sieci, por.
rys. 1a (n), polega na liczeniu empirycznej dystrubuanty dla parametró w w
min
£
w
(p)
<
w
oraz w
£
w
(p)
£
w
max
. Numery wzorcó w w
L
a
i w
R
a
obliczamy z nieró wności:
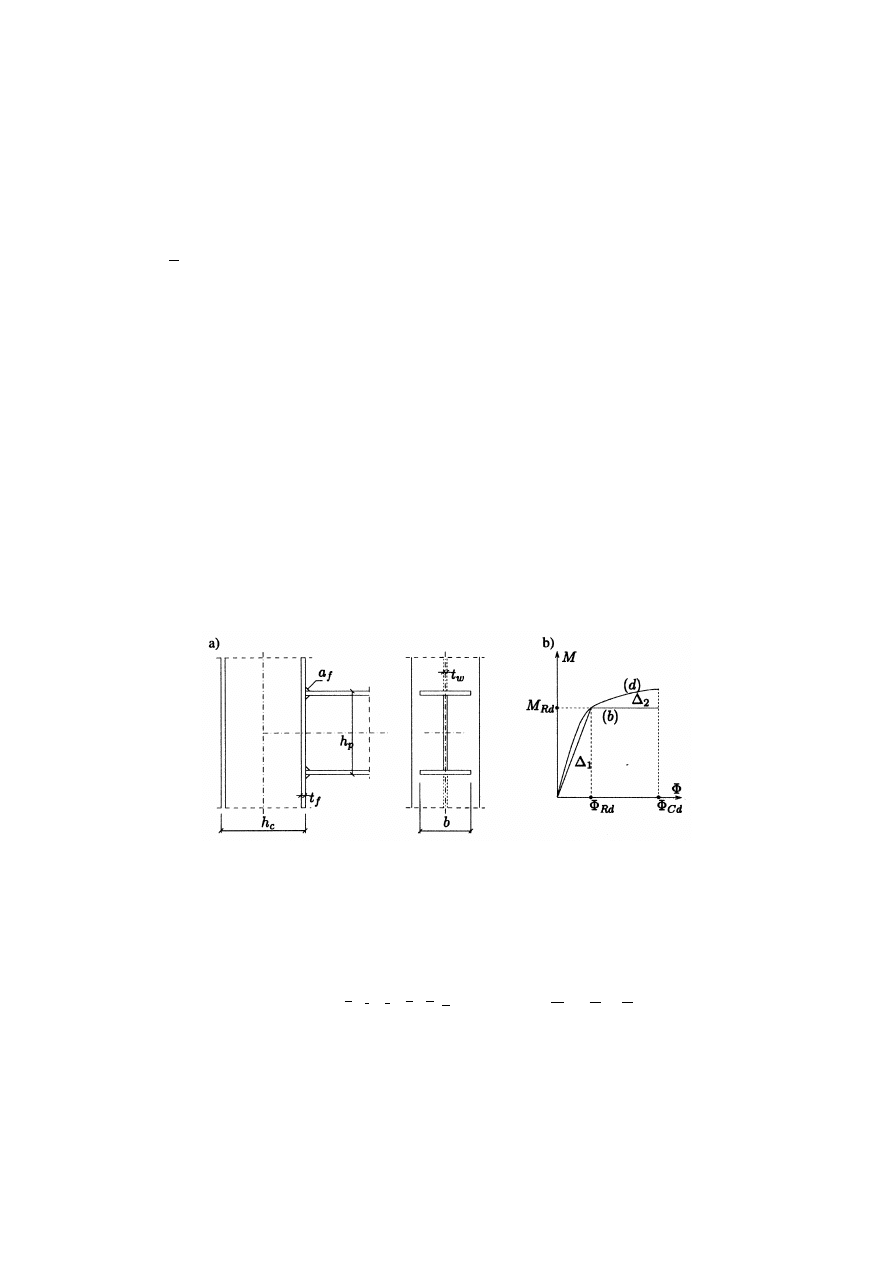
71
(
1
-
2 K/L
)
£
a
<
(
1
-
2 (K
-
1) /L
)
, (2)
gdzie: K = k
L
a
, k
R
a
– numery parametró w liczone na lewo lub na prawo od wartości średniej
w . Jeśli zajdzie przypadek, że
a
Î
(K
-
1 , K ) to wartości w
L
a
, w
R
a
są obliczane z
interpolacji liniowej wartości z przedziału ( w
K-1
, w
K
), por. [11].
Po wyznaczeniu funkcji przynależności dla każdego parametru sieci możemy ją
wykorzystać dla obliczania wartości przedziałowych wyjść [ y
L
, y
R
]
a
dla ustalonej wartości
przekroju
a
. Zmieniają c wartości
a
możemy odtworzyć funkcje przynależności wyjść . Na
skutek rozmycia parametró w sieci, rozmyte wyjścia otrzymamy nie tylko dla rozmytych ale
też ostrych wejść . Po wprowadzeniu wartości przedziałowych składowych wektoró w wejść
[ x
j
L
, x
j
R
] dalej są wykonywane działania na nich zgodnie z rachunkiem przedziałowym [9].
W przypadku ostrych wartości wejść dla wszystkich
a
przyjmujemy x
j
L
, =
x
j
R
.
3. Dane doświadczalne
Z obszernego banku danych Sericon, zgromadzonego w RWTH Aachen [8], przyję to zbió r
30 połą czeń analizowanych w [4]. Na rys. 2a pokazano konstrukcję połą czenia, określonego
6-ma parametrami, któ re przyję to jako składowe wektora wejścia x . Na rys. 2b pokazana
jest krzywa doświadczalna (d) charakterystyki M
-
F
jednego z analizowanych połą czeń.
Aproksymację liniową (b) wykonano w [4] przez obliczenie takich wartości
F
Rd
, M
Rd
i
F
Cd
, któ re dają ró wność powierzchni
D
1
=
D
2
zawartych mię dzy krzywymi (a) i (b). W [4]
przytoczono tablicę z 6-ciu danymi i obliczonymi 3-ma parametrami aproksymacji
biliniowej dla wszystkich wartości 30-tu połą czeń.
Rys. 2. a) Analizowane połą czenie, b) Charakterystyki M
-
F
połą czenia:
(d) krzywa doświadczalna, (b) aproksymacja biliniowa
4. Aproksymacja neuronowa
Tak samo jak w [4] przyję to wektory wejścia i wyjścia o nastę pują cych składowych, por.
rys. 2a:
x
(6x1)
=
{
}
f
b
w
f
c
a
b
h
t
t
h
,
,
,
,
,
, y
(3x1)
=
{
}
Cd
Rd
Rd
Φ
Φ
M
,
,
, (3)
72
gdzie wszystkie składowe (
·
) przeskalowano do przedziału (0, 0.9).
W dalszym cią gu zajmujemy się tylko jednym przypadkiem, oznaczonym [4] jako
przypadek II/3, w któ rym zbió r testują cy składał się z połą czeń o numerach 9, 17, 29, a
pozostałe 27 połą czeń tworzą zbió r uczą cy. Do uczenia zbioru wstę pnych parametró w sieci
{w
i
o
} oraz zbioru parametró w dla indywidualnych wzorcó w {w
i
(p)
}, t.zn. do realizacji Eta-
pó w I i II algorytmu omowionego wyżej w p. 1, zastosowano sieć 6-7-3 o sigmoidalnych
neuronach w warstwie ukrytej i wyjściowej. Posługują c się symulatorem [12] zastosowano
do uczenia sieci metoda Levenberga-Marquardta (LM). Błą d aproksymacji mierzono miarą :
1
V 3
RMS (V ) =
¾
(
å
å
(
z
j
(p
-
y
j
(p)
)
2
)
1/2
, (4)
V
p=1 j=1
gdzie: z
j
(p)
, y
j
(p)
– przeskalowane znane i obliczone siecią wartości wyjść j dla wzorca p,
V = L, T, P – liczba elementó w w zbiorach uczą cym i testują cym oraz pełnym zbiorze P =
L+T .
Uczenie w Etapie I wymagało mniej niż 100 epok aby osią gną ć dokładność rzę du
RMS(L)
»
1
×
10
-3
. Uczenie w Etapie II wymagało ok. 20 epok aby osią gną ć dokładność
RMS(p)
»
1
×
10
-6
. W Tabl. 1 zestawiono błę dy Etapu I i Etapu II dla przekroju
a
= 1.0 ,
określane wzorami:
avr epV
j
=
å
=
V
p
j
ep
V
1
1
, max epV
j
= max {ep
j
½
p=1,...,V } , (5)
dla ep
j
=
½
1
-
y
j
(p)
/ z
j
(p)
½
· 100% .
W tablicy przytoczono też wartości wspó łczynnika korelacji r
P
obliczonego dla wszystkich
par ( y
j
(p)
, z
j
(p)
) całego zbioru P = 30 połą czeń.
Tablica 1. Błę dy neuronowej predykcji
Błę dy sieci
RMS(V)
´
10
2
Błę dy wzglę dne [%]
dla V = P:
M - Rd
Phi - Rd
Phi - Cd
Wspó łczynnik
korelacji r
P
dla
:
Sieć
6-7-3
V = L
V = T
avr
max
avr
max
avr
max
M-Rd
Phi-Rd Phi-Cd
Etap I 3.09 18.87 5.22 27.33 6.42 33.20 5.41 40.13 0.988 0.997 0.977
a
=1.0 8.96 17.28 10.89 23.29 8.64 24.04 15.68 34.46 0.987 0.988 0.989
W tablicy podano błę dy dla wstę pnego uczenia sieci na wszystkich wzorcach (Etap I).
W nastę pnym wierszu zestawiono błę dy dla sieci rozmytej i przekroju
a
= 1.0 . Widać , że
średnie błę dy wzglę dne są wyższe dla sieci rozmytej ale obniżają się błę dy maksymalne.
Dokładność obliczania momentu M
Rd
i obrotu
F
Rd
jest wię ksza niż granicznego obrotu
F
Cd
Na rys. 3 pokazano funkcje przynależne funkcji wyjściowych dla y
j
(p)
=
M
Rd
,
F
Rd ,
F
Rd
dla wzorcó w testują cych p = 9, 17, 29. Funkcje przynależności pokazano przy założeniu
funkcji przynależności wag parametró w sieci o kształtach tró jką tnych (t) i nieliniowych (n),
por. rys. 1. Na rysunkach zaznaczono przez
◊
punkty odpowiadają ce wartościom przedzia-
łowym dla przekrojó w
a
= 0.0, 0.25, 0.75, 0.9, 1.0. Przez
Ú
zaznaczono położenie znanych
wartości wyjściowych z
j
(p)
. Wyniki dla funkcji przynależności (t) są bliskie wynikó w otrzy-
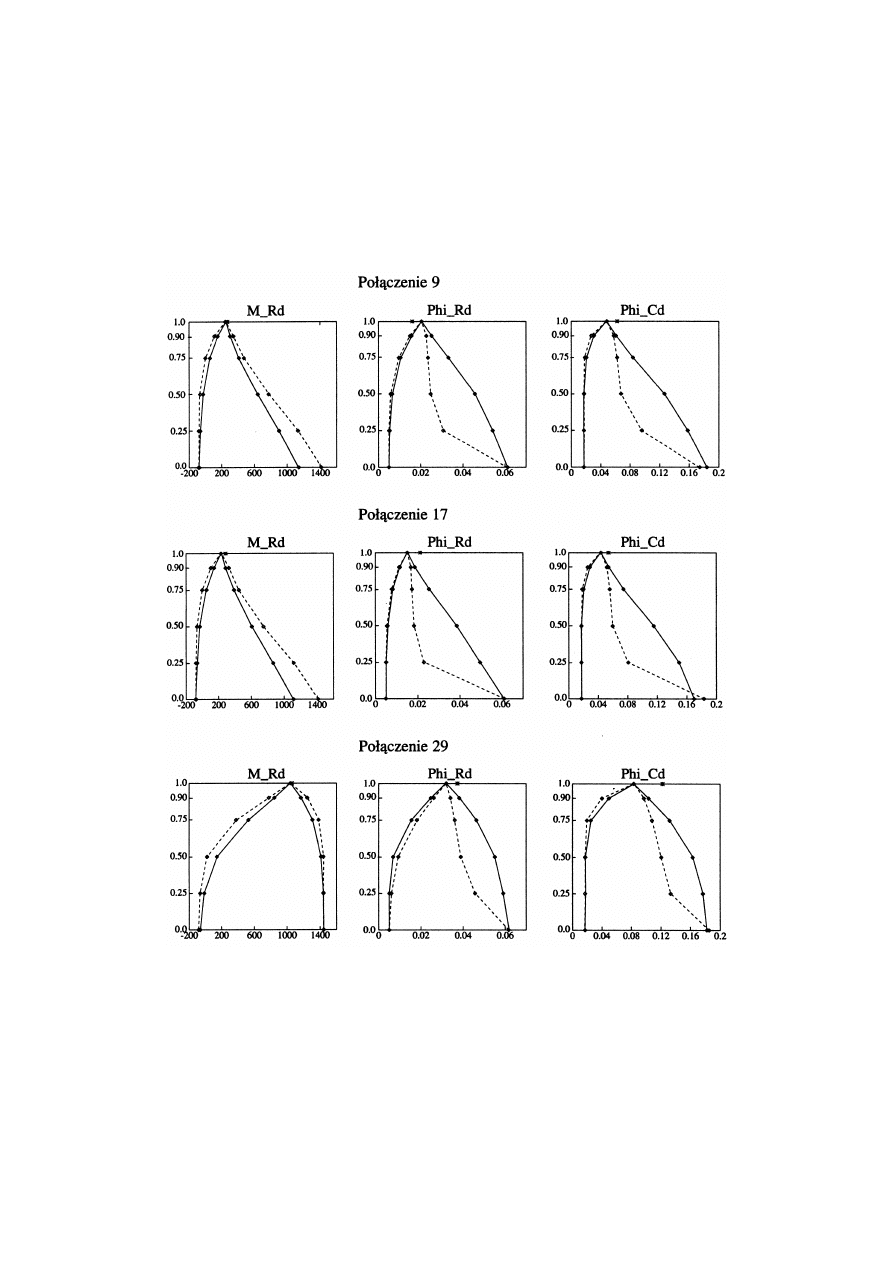
73
manych za pomocą funkcji (n) dla przekroju
a
= 0.9. Dlatego dalszy rysunek jest wyko-
nany dla funkcji (t) i przekrojó w
a
= 1.0 i 0.9 .
Rys. 3. Funkcje przynależności dla wielkości wyjściowych M
Rd
,
F
Rd
i
F
Cd
dla połą czeń 9, 17, 29 przy posługiwaniu się funkcjami przynależności parametró w
sieci oznaczonymi przez: (t)
¾
◊
¾
◊
¾
,
(n)
--◊--◊-- ; Ú
-
wartość doświadczalna
74
W poró wnaniu z pracą [4], w któ rej identyfikacja parametró w charakterystyki
biliniowej była mało dokładna zwłaszcza dla połą czenia testują cego 17, zastosowanie sieci
neuro-rozmytej daje oszacowanie przedziałowe, któ re dla
a
= 0.9 nie obejmuje tylko doś-
wiadczalnej wartości
F
Rd
.
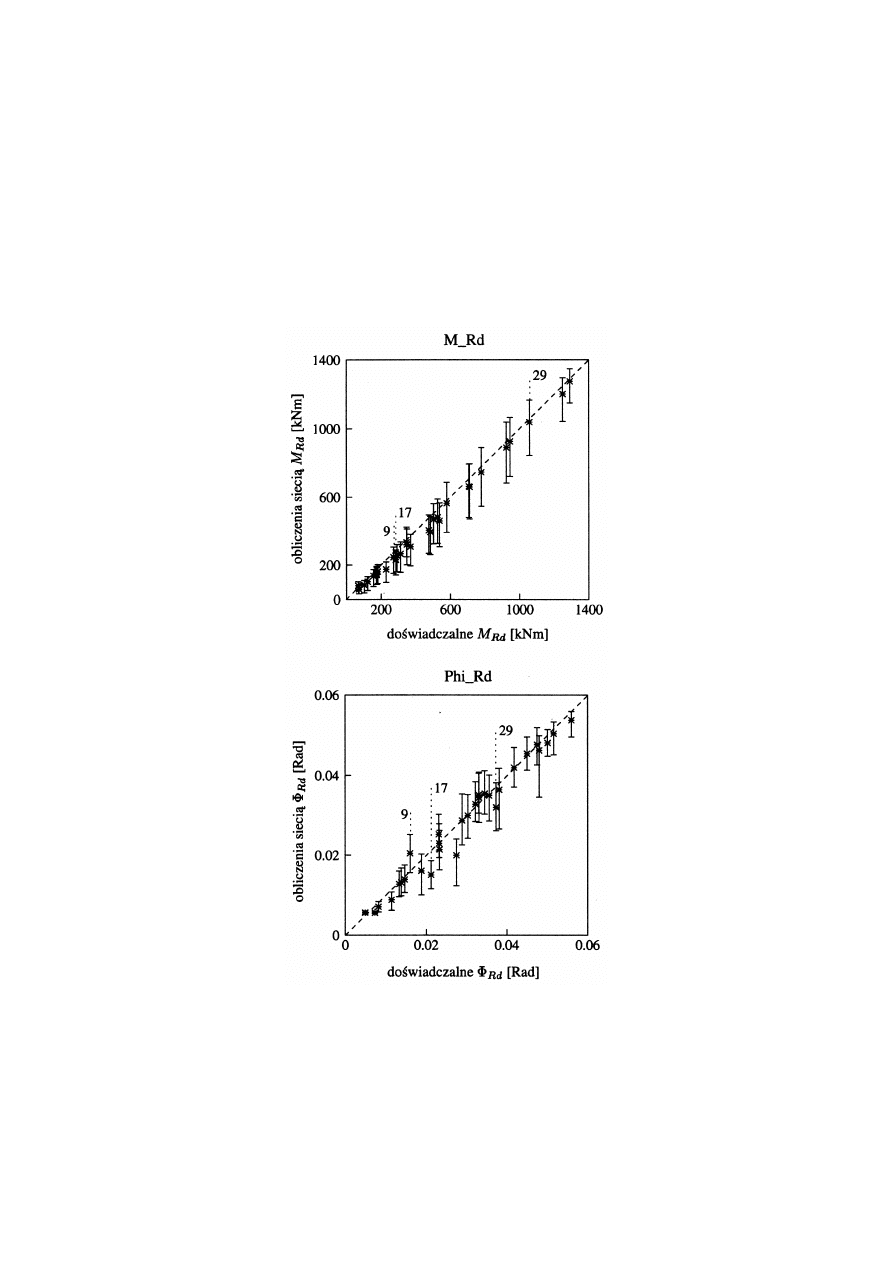
Na rys. 4 poró wnano wartości parametró w charakterystyki biliniowej M-
F
, obliczo-
nych na podstawie wynikó w doświadczeń, z wartościami obliczonymi siecią neuro-rozmytą .
Rys. 4 a,b. Poró wnanie wartości doświadczalnie wyznaczonych parametró w M
Rd
i
F
Rd
charakterystyki biliniowej (na rysunku oznaczone przez
Ú
)
z wartościami
przedziałowymi dla przekroju
a
= 0.9 dla całego zbioru połączeń
75
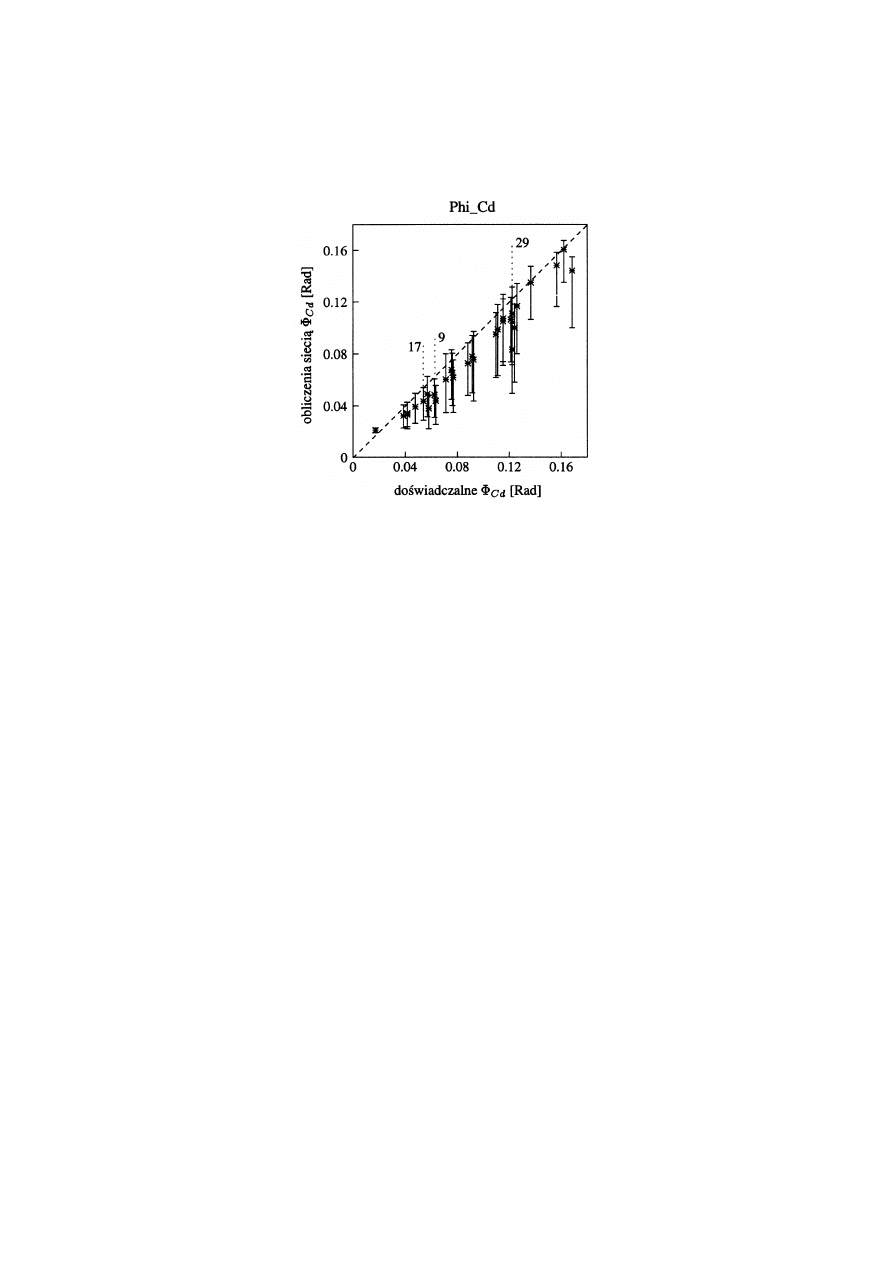
Rys. 4 c. Poró wnanie wartości doświadczalnie wyznaczonych parametró w
F
Cd
charakterystyki biliniowej (na rysunku oznaczone przez
Ú
)
z wartościami
przedziałowymi dla przekroju
a
= 0.9 dla całego zbioru połączeń
Pokazano wartości przedziałowe dla przekroju
a
= 0.9 . Dla zdecydowanej wię kszości
połą czeń obliczone wartości przedziałowe [ y
j
L
, y
j
R
]
a
= 0.9
obejmują doświadczalne wartości
zaznaczone na Rys.4 przez
Ú
.
Wielkość przedziałó w odpowiada dokładności neuronowej
identyfikacji jak też wrażliwości pomiaró w w odniesieniu do wartości identyfikowanych
zmiennych wyjściowych. Zgodnie z oszacowaniem błę dó w podanych w tab. 1 ta uwaga
odnosi się przede wszystkim do granicznego obrotu
F
Cd
, gdyż relatywna długość
przedziałó w jest najwię ksza dla tej wartości wyjściowej.
5. Uwagi koń cowe
1. Kró tko omó wiono nową sieć rozmytą o tró jką tnych (t) lub nieliniowych (n)
funkcjach przynależności parametró w sieci.
2. Sieć rozmytą zastosowano do identyfikacji parametró w biliniowej charakterystyki
dla grupy 30 połą czeń, analizowaną w [4].
3. Praca jest pierwsza pró bą zastosowania sieci rozmytych do identyfikacji parametró w
charakterystyk połą czeń podatnych. Zbliża ona wyniki analizy do specyfiki problemu przez
założenie, że bliższe rzeczywistości są wartości przedziałowe identyfikowanych parametró w
niż wartości ostre.
4. Szereg zgromadzonych wnioskó w na temat perspektyw stosowania pro-
ponowanej sieci rozmytej do analizy problemó w doświadczalnych teorii kon-
strukcji wymaga jeszcze dalszych uzasadnień na tle wię kszej liczby przykładó w
zastosowań.
Literatura
[1] Eurocode 3: Design of Steel Structures, ENV 1993-1-1, 6.9. Beam-to-column
connections.
76
[2] STAVROULAKIS G.E., AVDELAS A.V., ABDALLA K.M., PANAGIOTOPOULOS
P.D., A back-propagation based neural network approach for connections, Steel Struc-
tures - Eurosteel’95, Balkema, Rotterdam 1995, 263-270.
[3] ANDERSON D., HINES E.L., ARTHURS J., EIAP E.L., Application of artificial neural
networks to the prediction of minor axis steel connections, Computers & Structures, 63
(1997), 685-692.
[4] WASZCZYSZYN Z., PETIT J., Zastosowanie sztucznych sieci neuronowych do
identyfikacji charakterystyk stalowych połą czeń podatnych, XLIII Konferencja Naukowa
KILiW PAN i KN PZITB, Materiały T.2, Poznań-Krynica 1997, 149-156.
[5] MILLER B., PIĄ TKOWSKI G., ZIEMIAŃ SKI L., Determination of parameters of
a semi-rigid beam-to-column connections, Proc. 4th Conf. on Neural Networks and their
Appllications, Czę stochowa-Zakopane 1999, 357-362.
[6] URBAŃ SKA A., KALISZUK J., WASZCZYSZYN Z., Neuronowa analiza połą czeń
rurowych w ramach stalowych, X Międzynarodowa Konf. Naukowo-Techn. Konstrukcje
Metalowe - Gdański 2001, T.2, 325-334.
[7] NI S.H., LU P.C, JUANG C.H., A fuzzy neural network approach to evaluation of slope
failure potential, Microcomputers in Civil Engineering, 11 (1996), 59-66.
[8] WEYNAND K., Sericon – data bank on joints in building frames, COST1 First State-of-
the-Art Workshop, ANSAIS, Polytechnicum L. Pasteur, Strasbourg 1992.
[9] RAJASEKARAN S., FEBIN M.F., RAMASAMY J.V., Artificial fuzzy neural networks
in civil engineering, Computers & Structures, 61 (1996), 291-302.
[10] WASZCZYSZYN Z. (Ed.), Neural Networks in the Analysis and Design of Structures,
CISM Courses and Lectures No.404, Wien - New York, Sp[ringer, 1999.
[11] PABISEK E., Jakubek M., Waszczyszyn Z., A Fuzzy neural network for the analysis of
experimental mechanics problems, Proc. 6th Conf .on Neural Networks and Soft
Computing, Zakopane (2002), (w druku).
[12] DEMUTH H., BEALE M., Neural Network Toolbox for Use with MATLAB, User's
Guide, Version 3, Natick, The Math Works Inc., 1998.
ESTIMATION OF PARAMETERS OF SEMI-RIGID STEEL
CONNECTIONS BY A FUZZY NEURAL NETWORK
Summary
A new fuzzy network, developed on the base of approach in [7] is discussed. The
membership functions of the network parameters are formulated on the base of network
training by individual patterns. The network is applied to a group of 30 beam-to-column
connections analyzed in [4]. Intervals of parameters to the bilinear approximation of M
-F
characteristics were computed as a closer approach to the experimental reality.
Praca została wykonana w ramach projektu badawczego KBN Nr 8 T07E 002 20 pt.
"Zastosowanie sztucznych sieci neuronowych do analizy konstrukcji stalowych".