1
9. Metoda różnic skończonych (MRS)
Idea metody różnic skończonych została zaproponowana już przez Carla
Fridricha Gaussa, lecz dopiero w erze komputerowej znalazła ona szersze
zastosowanie. Jest to ogólna metoda rozwiązywania równań różniczkowych.
Polega ona na zastąpieniu równania różniczkowego układem równań różnicowych
i sprowadzeniu problemu do rozwiązywania układu równań algebraicznych.
9.1. Ilorazy różnicowe jako przybliżenia pochodnych
9.1.1. Ilorazy dla pierwszej pochodnej
Pochodna funkcji f(x) w punkcie x
0
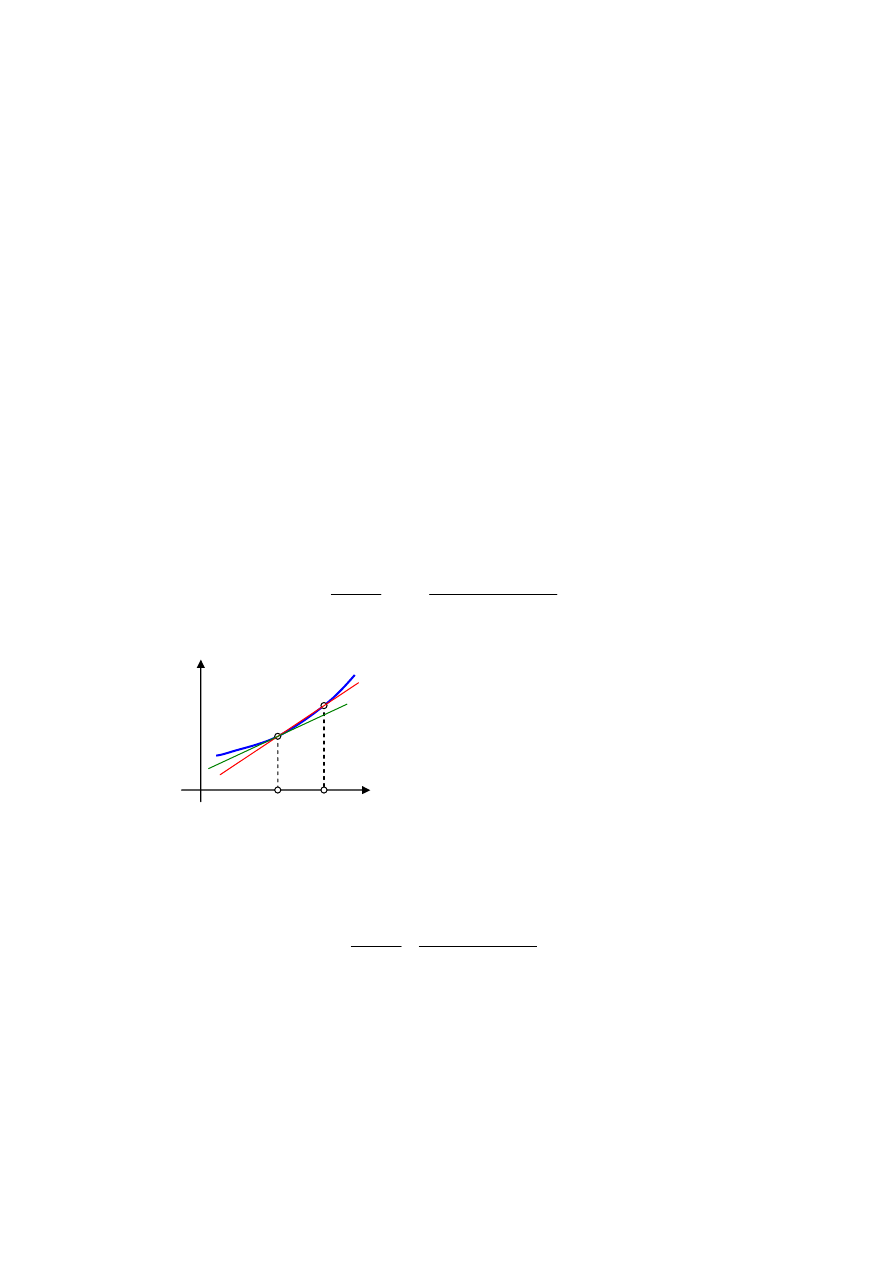
jest zdefiniowana jako (rys. 9.1):
x
∆
x
f
x
∆
x
f
x
x
f
x
∆
)
(
)
(
lim
d
)
(
d
0
0
0
0
−
+
=
→
.
(9.1)
x
f(x)
x
0
x
0
+ ∆x
f(x
0
+ ∆x)
f(x
0
)
sieczna
styczna
Rys. 9.1. Geometryczna interpretacja pochodnej: dla ∆x → 0 sieczna (czerwona linia) dąży do
stycznej (zielona linia)
Geometrycznie, jest to tangens kąta nachylenia stycznej do krzywej y = f(x)
w punkcie x
0
. Stąd dla „małych” h mamy w przybliżeniu
h
x
f
h
x
f
x
x
f
)
(
)
(
d
)
(
d
0
0
0
−
+
≈
,
(9.2)
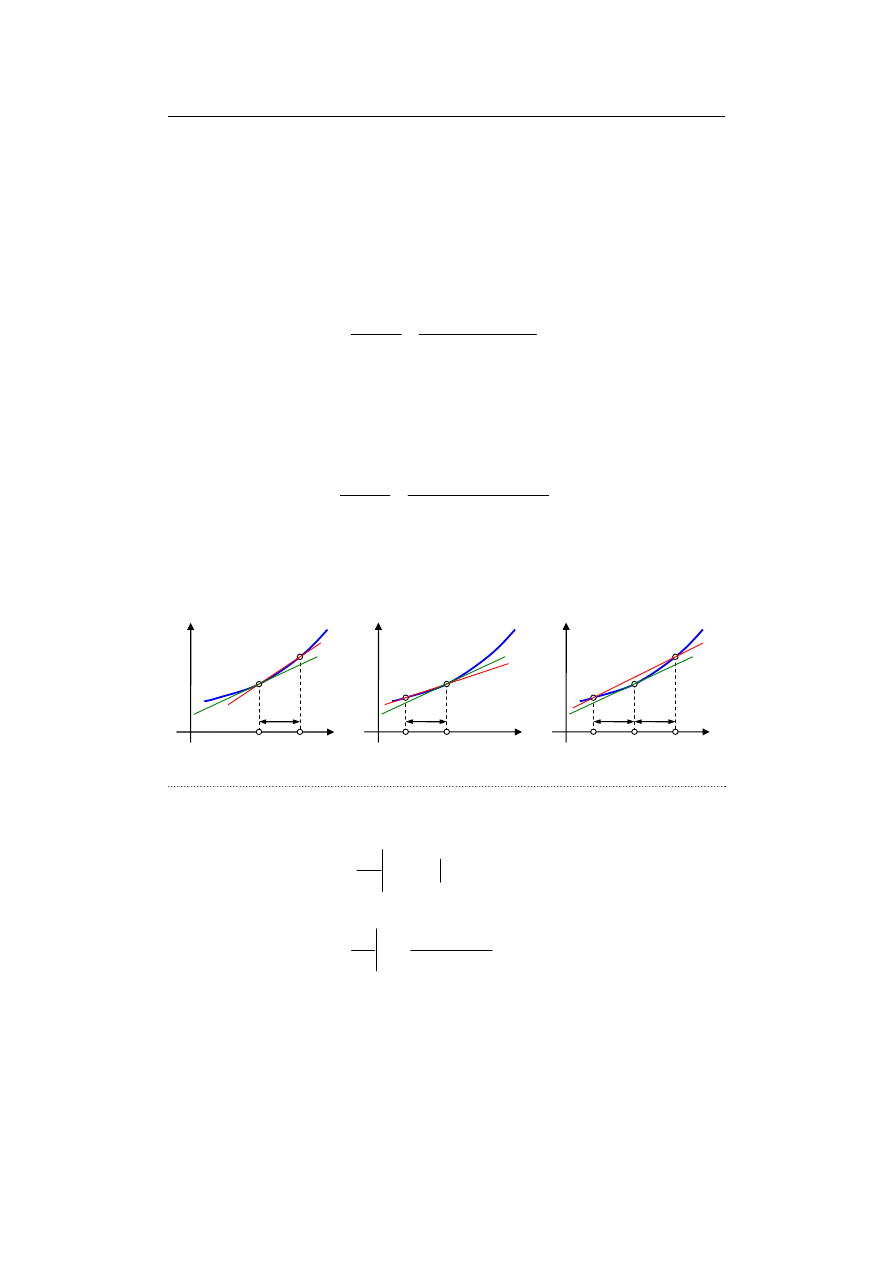
9. Metoda różnic skończonych (MRS)
2
tzn. postępujemy następująco (rys. 9.2a):
•
obliczamy wartość funkcji w punkcie x
0
,
•
obieramy pewien bliski punkt x
0
+ h i obliczamy w nim wartość funkcji,
•
odejmujemy od niej wartość funkcji w punkcie x
0
,
•
dzielimy przez przyrost h zmiennej x.
Tak obliczona wartość jest tym bliższa dokładnej wartości pochodnej, im mniejsza
wartość h, gdyż wtedy sieczna jest „bliższa” stycznej. Wzór (9.2) nazywamy
ilorazem różnicowym dla pochodnej. Dla h > 0 jest to iloraz różnicowy wprzód.
Istnieje też wersja zwana ilorazem różnicowym wstecz (rys. 9.2b):
h
h
x
f
x
f
x
x
f
)
(
)
(
d
)
(
d
0
0
0
−
−
≈
,
(9.3)
Powyższe ilorazy biorą się z założenia o liniowej zmienności funkcji f(x)
w pobliżu punktu x
0
i dlatego są obarczone dość dużym błędem, rzędu O(h
2
).
Dokładniejsze wyrażenia na postać różnicową pochodnej można uzyskać,
rozpatrując interpolację kwadratową, która prowadzi do tzw.
symetrycznego
ilorazu różnicowego dla pierwszej pochodnej (rys. 9.2c):
h
h
x
f
h
x
f
x
x
f
2
)
(
)
(
d
)
(
d
0
0
0
−
−
+
≈
,
(9.4)
który jest obarczony mniejszym błędem, rzędu O(h
3
). Jest to widoczne na rysunku
9.2 – sieczna dla ilorazu różnicowego symetrycznego ma kąt nachylenia znacznie
bliższy kątowi nachylenia stycznej niż dla ilorazów różnicowych wprzód i wstecz.
a)
b)
c)
x
f(x)
x
0
x
0
+ h
f(x
0
+ h)
f(x
0
)
h
x
f(x)
x
0
x
0
– h
f(x
0
– h)
f(x
0
)
h
x
f(x)
x
0
x
0
– h
x
0
+ h
f(x
0
– h)
f(x
0
+ h)
f(x
0
)
h
h
Rys. 9.2. Różnice: a) różnica wprzód b) różnica wstecz, c) różnica symetryczna
Przykład 9.1. Obliczyć przybliżoną wartość pochodnej funkcji f(x) = x
3
w punkcie x
0
= 2,
przyjmując h = 0,1.
Dokładna wartość pochodnej wynosi
12
2
3
3
d
d
2
2
2
2
3
=
⋅
=
=
=
=
x
x
x
x
x
.
Wartość obliczona ilorazem różnicowym wprzód:
61
,
12
1
,
0
2
)
1
,
0
2
(
d
d
3
3
2
3
=
−
+
≈
=
x
x
x
.
9.1. Ilorazy różnicowe jako przybliżenia pochodnych
3
Iloraz różnicowy wstecz daje
41
,
11
1
,
0
)
1
,
0
2
(
2
d
d
3
3
2
3
=
−
−
≈
=
x
x
x
,
natomiast iloraz symetryczny prowadzi do wyniku
01
,
12
1
,
0
2
)
1
,
0
2
(
)
1
,
0
2
(
d
d
3
3
2
3
=
⋅
−
−
+
≈
=
x
x
x
.
9.1.2. Iloraz różnicowy dla drugiej pochodnej
W przypadku drugiej pochodnej najwygodniej jest rozpocząć od rozwinięcia
funkcji f(x) w szereg Taylora w otoczeniu punktu x = x
0
:
...
)
)(
(
!
2
1
)
)(
(
'
!
1
1
)
(
)
(
2
0
0
0
0
0
+
−
′′
+
−
+
=
x
x
x
f
x
x
x
f
x
f
x
f
(9.5)
Przyjmując w nim x = x
0
+ h, gdzie h > 0, dostajemy
)
(
)
(
!
3
1
)
(
!
2
1
)
(
'
!
1
1
)
(
)
(
4
3
0
)
3
(
2
0
0
0
0
h
O
h
x
f
h
x
f
h
x
f
x
f
h
x
f
+
+
′′
+
+
=
+
,
a dla x = x
0
– h mamy
)
(
)
(
!
3
1
)
(
!
2
1
)
(
'
!
1
1
)
(
)
(
4
3
0
)
3
(
2
0
0
0
0
h
O
h
x
f
h
x
f
h
x
f
x
f
h
x
f
+
−
′′
+
−
=
−
.
Po dodaniu stronami powyższych równań i przekształceniu dostajemy
2
0
0
0
2
2
0
)
(
)
(
2
)
(
d
)
(
d
)
(
0
h
h
x
f
x
f
h
x
f
x
x
f
x
f
x
x
+
+
−
−
≈
=
′′
=
.
(9.6)
Dokładność tego wyrażenia jest rzędu O(h
4
), a więc dość dobra.
Przykład 9.2. Obliczyć przybliżoną wartość drugiej pochodnej funkcji f(x) = x
3
w punkcie
x
0
= 2 przyjmując
h = 0,1.
Dokładna wartość drugiej pochodnej wynosi
12
2
6
6
d
d
2
2
2
3
2
=
⋅
=
=
=
=
x
x
x
x
x
,
natomiast wzór różnicowy daje
12
1
,
0
)
1
,
0
2
(
2
2
)
1
,
0
2
(
d
d
2
3
3
3
2
2
3
2
=
+
+
⋅
−
−
≈
=
x
x
x
.
Wynik jest dokładny, gdyż czwarta i wyższe pochodne
f(x) równe są zeru.
9. Metoda różnic skończonych (MRS)
4
9.2. Ogólna idea metody różnic skończonych
Rozwiązywanie równania różniczkowego metodą różnic skończonych można
podzielić na cztery etapy:
1.
Zapisanie równania różniczkowego w postaci różnicowej, tj. na zastąpienie
pochodnych odpowiednimi ilorazami różnicowymi.
2.
Nałożenie na obszar działania siatki węzłów, w których poszukiwane będą
wartości funkcji pola.
3.
Ułożenie równania różnicowego dla każdego węzła, z uwzględnieniem
warunków brzegowych.
4.
Rozwiązanie powstałego układu liniowych równań algebraicznych ze względu
na nieznane wartości węzłowe funkcji pola.
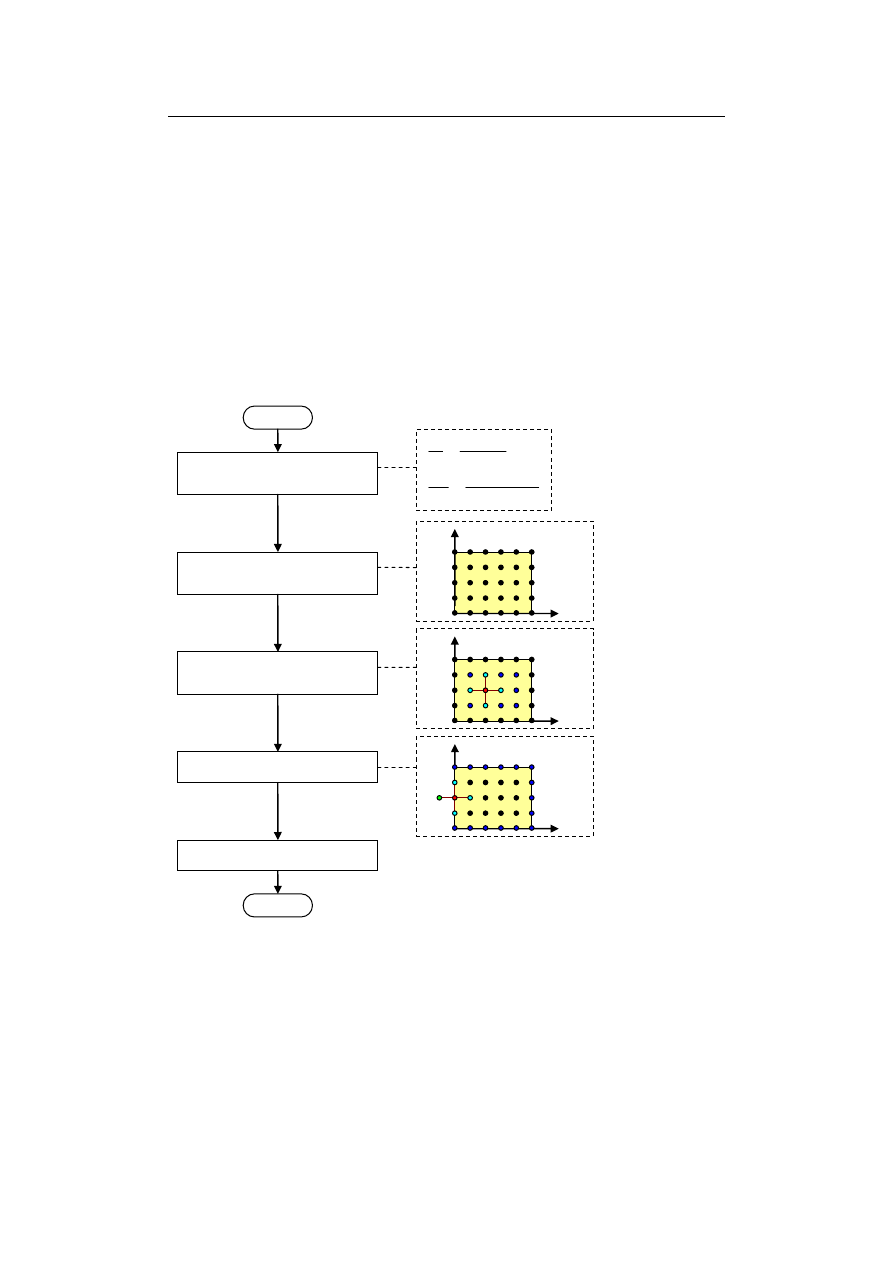
Postępowanie to zobrazowano na rys. 9.3.
Znajdź postać różnicową
rozwiązywanego równania
Nałóż na obszar działania siatkę
węzłów
Ułóż równanie różnicowe dla
każdego węzła
Wprowadź warunki brzegowe
Rozwiąż powstały układ równań
START
STOP
2
1
1
2
2
1
1
2
d
d
2
d
d
h
u
u
u
x
u
h
u
u
x
u
i
i
i
i
i
−
+
−
+
+
−
→
−
→
Rys. 9.3. Schemat rozwiązywania zagadnienia polowego za pomocą MRS
9.3. Zagadnienia jednowymiarowe
5
9.3. Zagadnienia jednowymiarowe
9.3.1. Równanie różnicowe
W przypadku zagadnień jednowymiarowych ograniczymy się do równania
różniczkowego o postaci
)
(
)
(
d
)
(
d
)
(
d
)
(
d
2
2
2
x
f
x
Φ
κ
x
x
Φ
x
g
x
x
Φ
−
=
−
+
,
(9.7)
gdzie Φ(
x) jest poszukiwaną funkcją, κ – stałą, g(x) i f(x) – znanymi funkcjami
zmiennej
x. Wykorzystując wzory (9.6) oraz
(9.4)
, możemy zapisać postać
różnicową równania
)
(
)
(
2
)
(
)
(
)
(
)
(
)
(
2
)
(
2
2
x
f
x
Φ
κ
h
h
x
Φ
h
x
Φ
x
g
h
h
x
Φ
x
Φ
h
x
Φ
−
=
−
−
−
+
+
−
+
−
+
,
co po przekształceniu daje
2
2
1
2
2
2
1
)
(
)
(
]
)
(
1
[
)
(
)
2
(
)
(
]
)
(
1
[
h
x
f
h
x
Φ
h
x
g
x
Φ
h
κ
h
x
Φ
h
x
g
−
=
+
+
+
+
−
−
−
.
(9.8)
Powyższe równanie jest spełnione w przybliżeniu dla każdego x i „niezbyt dużego”
kroku h.
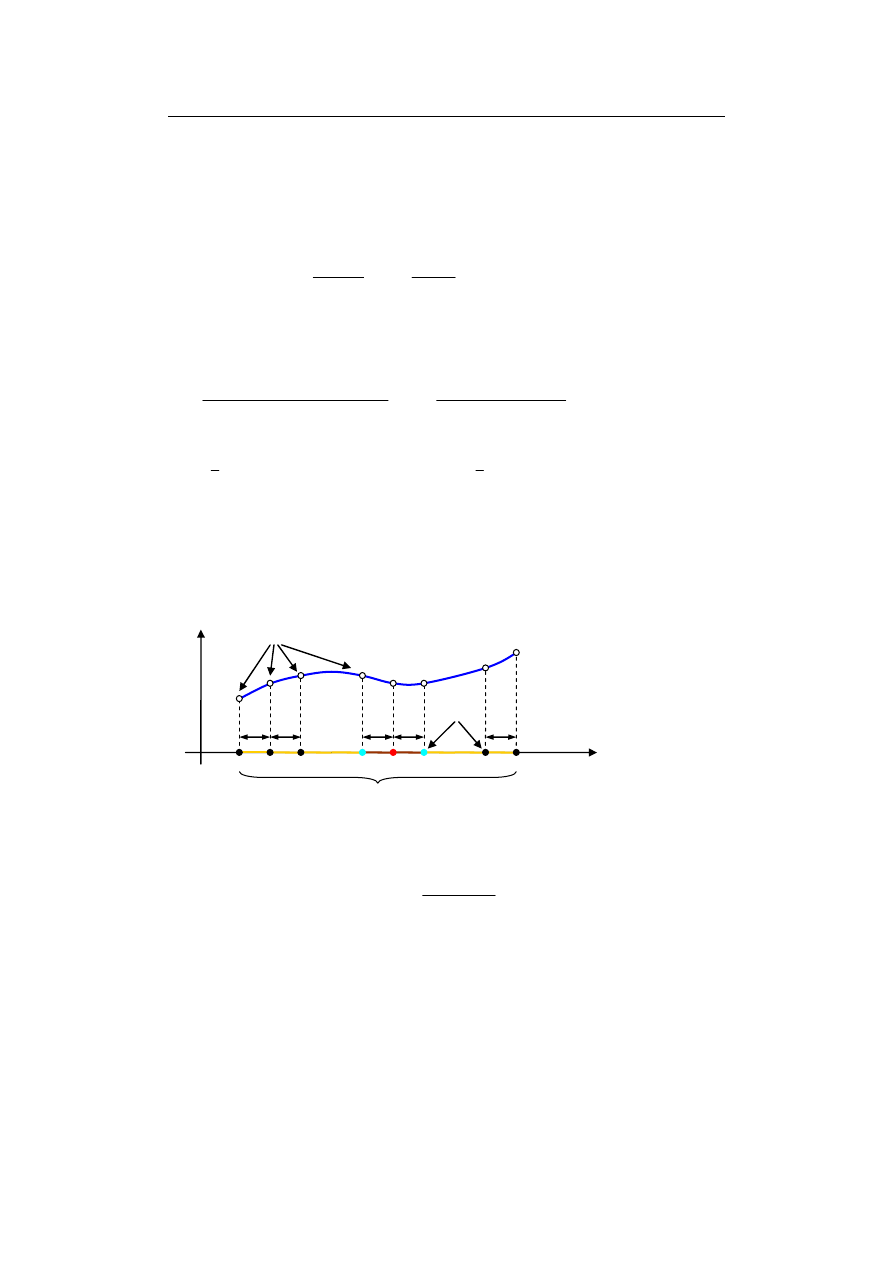
W dalszym ciągu załóżmy, że rozpatrywane równanie (9.7) określone jest na
odcinku (obszarze działania pola) x
min
≤
x
≤
x
max
. Podzielmy ten odcinek na N
części i wprowadźmy na nim N + 1 węzłów (dla uproszczenia równomiernie
rozłożonych) – rys. 9.4.
x
0
= x
min
x
1
x
2
x
i–1
x
i+1
x
i
x
N–1
x
N
= x
max
x
Φ
i
Φ
i–1
Φ
i+1
Φ(x)
h
h
h
h
h
Obszar działania pola
Węzły
Wartości węzłowe
Rys. 9.4. Węzły nałożone na obszar działania pola
Mamy zatem krok siatki węzłów
N
x
x
h
min
max
−
=
(9.9a)
oraz
.
...
,
2
,
1
,
0
,
min
N
i
ih
x
x
i
=
+
=
(9.9b)
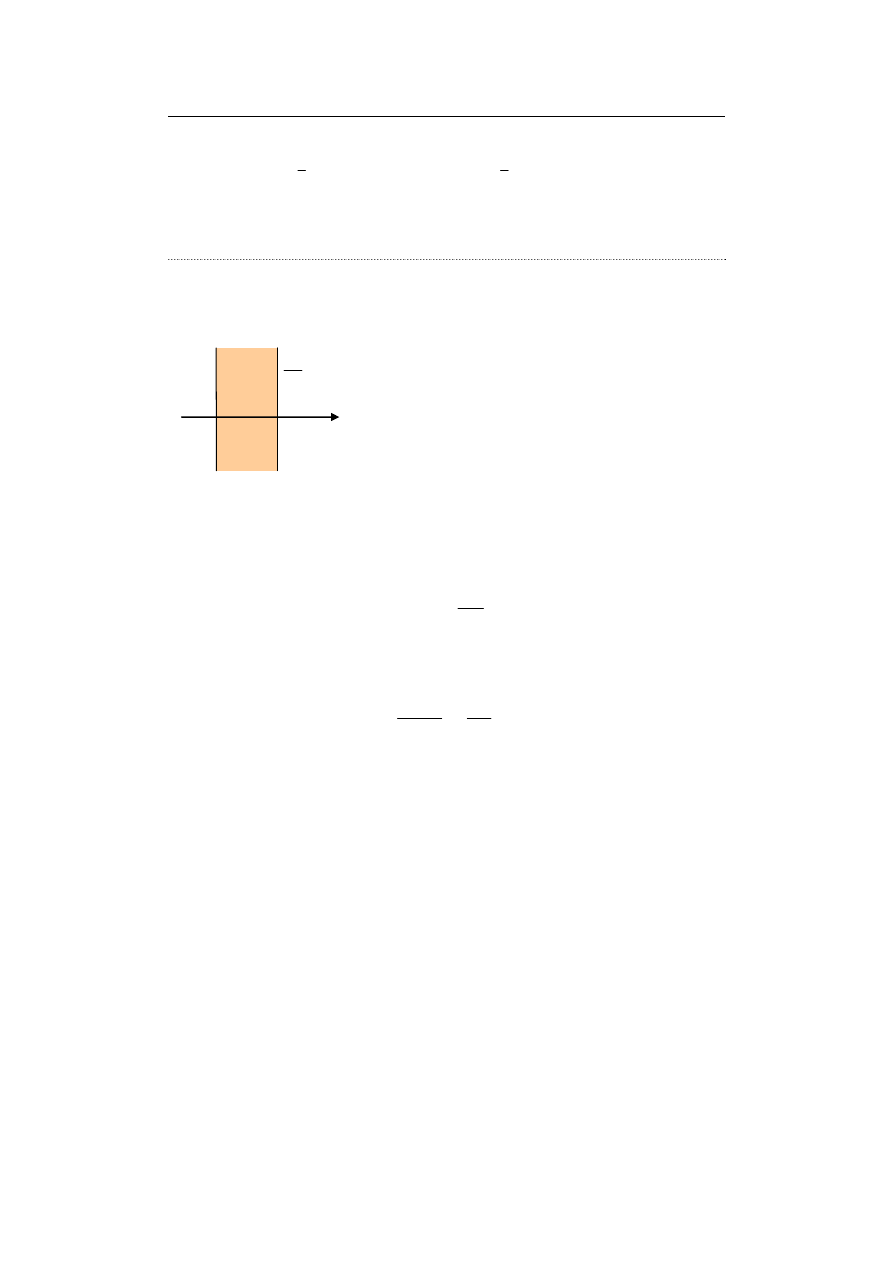
9. Metoda różnic skończonych (MRS)
6
Równanie różnicowe (9.8) zapisane dla dowolnego węzła x = x
i
przyjmuje postać
2
1
2
1
2
2
1
2
1
)
1
(
)
2
(
)
1
(
h
f
Φ
h
g
Φ
h
κ
Φ
h
g
i
i
i
i
i
i
−
=
+
+
+
−
−
+
−
,
(9.9c)
gdzie wprowadzono oznaczenia Φ
i
= Φ(x
i
), f
i
= f(x
i
), g
i
= g(x
i
). Takie równania
układa się dla wszystkich węzłów, przy czym dla węzłów brzegowych (x
0
oraz x
N
)
należy uwzględnić dodatkowo warunki brzegowe.
Przykład 9.3. Znaleźć rozkład potencjału elektrycznego w rozległej płycie dielektrycznej
o grubości a = 1 cm i przenikalności względnej ε
r
= 5 (rys. 9.5), naładowanej ładunkiem
elektrycznym o gęstości objętościowej ρ = ρ
0
(przyjąć ρ
0
/ε
0
= 100 V·cm
–2
). Jedna
powierzchnia płyty ma potencjał 1 V, na drugiej zadano zerowy warunek Neumanna.
0
d
d
=
x
V
x
a
0
V = 1
V(x) = ?
ρ, ε
r
Rys. 9.5. Naładowana płyta (przekrój)
Z równań elektrostatyki
V
ε
ε
ρ
−∇
=
=
=
⋅
∇
E
E
D
D
,
,
0
r
(a)
wynika dla potencjału elektrycznego V równanie Poissona
0
r
2
ε
ε
ρ
V
−
=
∇
.
(b)
W rozpatrywanym przypadku przyjmujemy układ współrzędnych z osią Ox prostopadłą do
powierzchni płyty. Z dala od krawędzi płyty pole zależy tylko od x, a stąd otrzymujemy
równanie
0
r
0
2
2
d
)
(
d
ε
ε
ρ
x
x
V
−
=
.
(c)
Równanie to rozwiążemy za pomocą MRS z N + 1 węzłami rozlokowanymi równomiernie
na odcinku x = <0, 1>. Na podstawie wzoru (9.9c) mamy postać różnicową powyższego
równania (κ = 0, g(x) = 0):
i
i
i
i
f
h
V
V
V
2
1
1
2
−
=
+
−
+
−
,
(d)
gdzie oznaczono f
i
= ρ(x
i
)/(ε
0
ε
r
) oraz h = a/N. W rozpatrywanym przypadku f
i
= 20 V·cm
–2
niezależnie od i oraz h = 1/N cm. Równania takie układamy dla wszystkich wewnętrznych
węzłów, tj. dla i = 1, 2, 3, …, N – 1. Dla węzła i = 0 postępujemy inaczej, gdyż jest to
węzeł brzegowy. Ponieważ zadano w nim warunek Dirichleta V = 1 V, mamy równanie
1
0
=
V
.
(e)
Jeszcze inaczej postępujemy dla węzła i = N, w którym zadano zerowy warunek brzegowy
Neumanna, tzn.

9.3. Zagadnienia jednowymiarowe
7
0
d
d
1
=
=
x
x
V
.
(f)
Zapisujemy chwilowo równanie (d) dla tego węzła
N
N
N
N
f
h
V
V
V
2
1
1
2
−
=
+
−
+
−
,
(g)
przy czym węzeł
N + 1 jest węzłem fikcyjnym (brak go w podziale obszaru działania pola).
Należy więc wyeliminować go z tego równania. W tym celu zapisujemy warunek
Neumanna (f) w postaci różnicowej
0
2
1
1
=
−
−
+
h
V
V
N
N
,
(h)
z której wynika, że V
N+1
= V
N–1
. Uwzględniając to we wzorze (g), dostajemy
N
N
N
f
h
V
V
2
1
2
2
−
=
−
−
.
(i)
Równania (d), (e) oraz (i) dają w sumie N + 1 równań na N + 1 nieznanych wartości V
i
:
−
=
−
−
=
+
−
−
=
+
−
−
=
+
−
=
−
−
−
−
+
−
.
2
2
,
2
,
2
,
2
,
1
2
1
1
2
1
2
2
1
1
1
2
2
1
0
0
N
N
N
N
N
N
N
i
i
i
i
f
h
V
V
f
h
V
V
V
f
h
V
V
V
f
h
V
V
V
V
M
M
(j)
Powstały układ równań można rozwiązać używając komputera. Jeżeli przyjrzymy się
postaci macierzowej tego układu równań,
−
−
−
−
−
=
−
−
−
−
−
−
−
−
−
N
N
N
N
N
N
f
h
f
h
f
h
f
h
f
h
V
V
V
V
V
V
2
1
2
2
2
2
2
1
2
1
2
2
1
0
1
2
2
0
0
0
0
1
2
1
0
0
0
0
1
2
0
0
0
0
0
0
2
1
0
0
0
0
1
2
1
0
0
0
0
0
1
M
M
L
L
L
M
M
M
O
M
M
M
L
L
L
.
(k)
to zauważymy, że macierz główna jest rzadka (w jednym wierszu występują prawie same
zera), pasmowa (wszystkie niezerowe elementy znajdują się w paśmie biegnącym wzdłuż
przekątnej) oraz symetryczna (prawie – odchyłki pojawiają się w równaniach dla węzłów
brzegowych). Są to ogólne cechy macierzy głównych układów równań generowanych przez
MRS.
Przyjmując dalej N = 5, dostajemy następujące wyniki:
V
0
= 1, V
1
= 4,6, V
2
= 7,4, V
3
= 9,4, V
4
= 10,6, V
5
= 11,
(l)
które zobrazowano na rys. 9.6. Rozpatrywane zagadnienie ma rozwiązanie dokładne
V
d
(x) = –10x
2
+ 20x + 1. Można sprawdzić, że jego wartości węzłowe są dokładnie równe
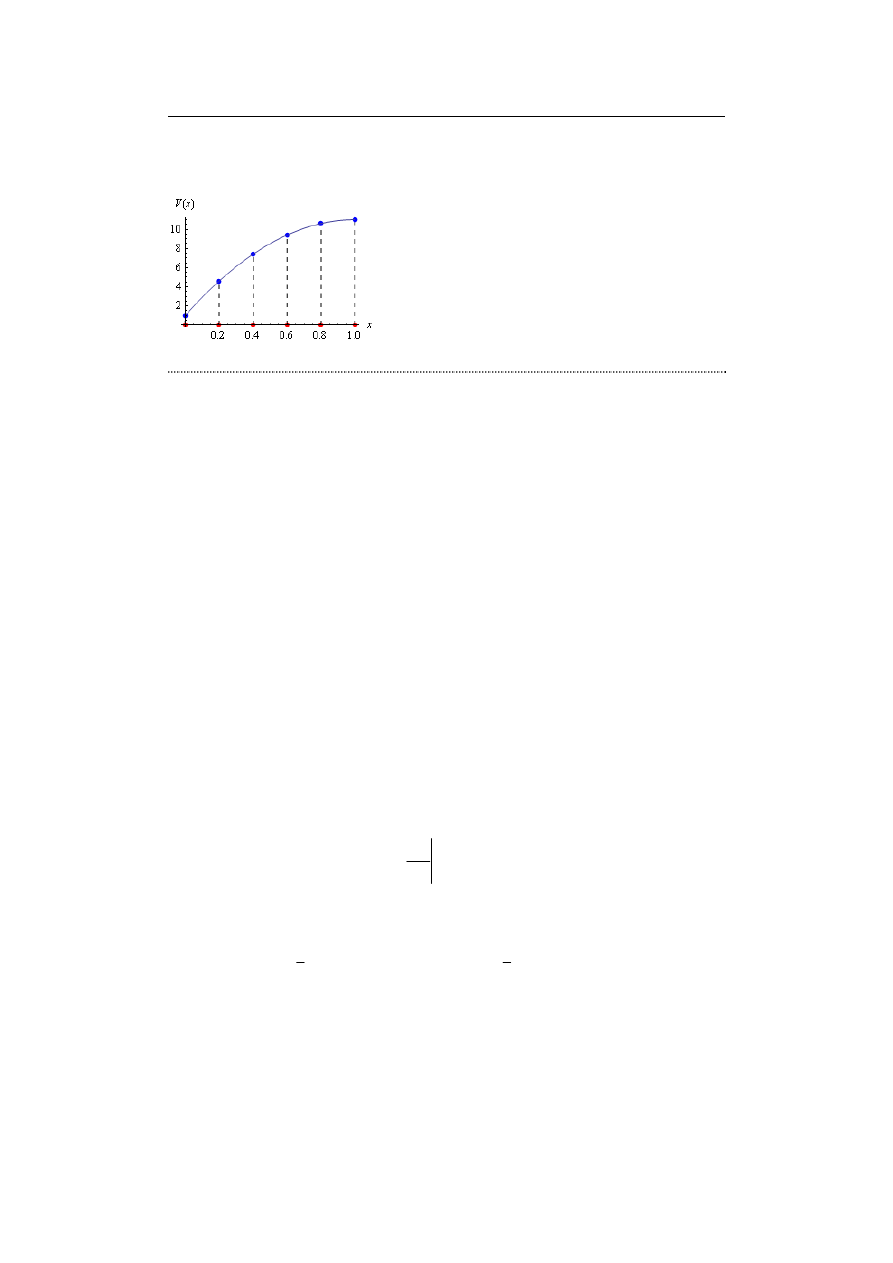
9. Metoda różnic skończonych (MRS)
8
podanym wyżej. Oznacza to, że w tym przypadku MRS generuje dokładne wartości
węzłowe, ale nie należy sądzić, że jest tak zawsze. Raczej przeciwnie – na ogół wartości
węzłowe są tylko zbliżone do wartości dokładnych.
Rys. 9.6. Rozwiązanie zagadnienia: MRS (punkty), rozwiązanie dokładne (linia ciągła)
9.3.2. Wprowadzanie warunków brzegowych
Z przykładu 9.3 wynika sposób wprowadzania warunków brzegowych do
równań MRS.
Warunek brzegowy Dirichleta
W przypadku warunków brzegowych typu Dirichleta jest to wyjątkowo
nieskomplikowane. Istotnie, dla warunku brzegowego Dirichleta w k-tym węźle
(zwykle k = 0 lub N + 1) o postaci
A
x
Φ
k
=
)
(
,
(9.10)
gdzie A znaną funkcją (tutaj stałą), zamiast równania różnicowego układa się
równanie o postaci
A
Φ
k
=
,
(9.11)
W realizacji macierzowej odpowiada to wyzerowaniu k-tego wiersza macierzy
głównej układu równań, wpisaniu na przekątną 1 oraz wpisaniu na k-tą pozycję
wektora wyrazów wolnych wartości A.
Warunek brzegowy Neumanna
W przypadku warunku brzegowego Neumanna o postaci
B
n
Φ
x
x
=
=
0
d
d
(9.12)
sytuacja jest również nieskomplikowana. Najpierw układamy równanie różnicowe
dla danego węzła brzegowego. Dla węzła 0 będzie ono miało postać (9.9c) z i = 0:
2
0
1
0
2
1
0
2
2
1
0
2
1
)
1
(
)
2
(
)
1
(
h
f
Φ
h
g
Φ
h
κ
Φ
h
g
−
=
+
+
+
−
−
−
.
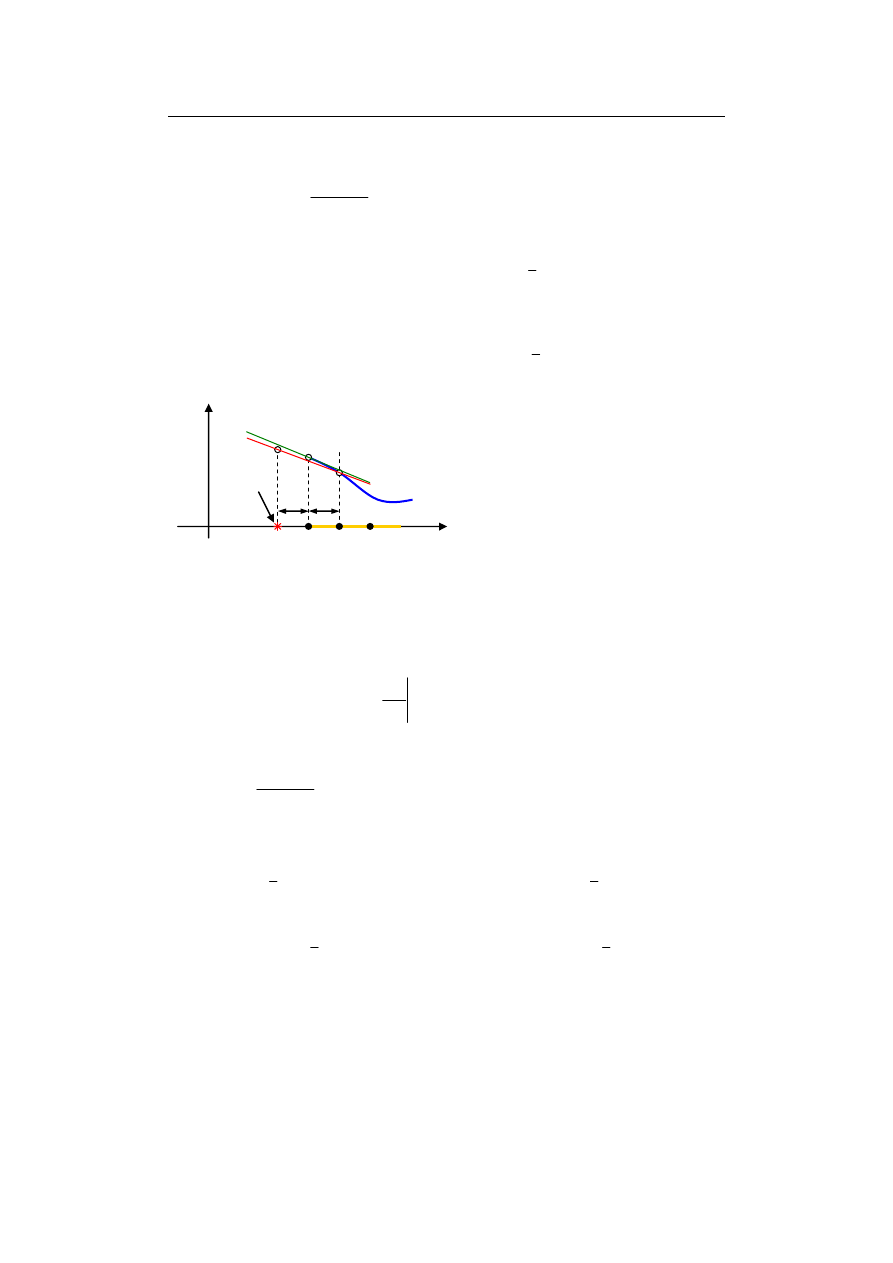
9.3. Zagadnienia jednowymiarowe
9
Występuje w nim fikcyjny węzeł –1, który wyeliminujemy za pomocą warunku
Neumanna. Warunek ten w postaci różnicowej przyjmuje postać (rys. 9.7)
hB
Φ
Φ
B
h
Φ
Φ
2
2
1
1
1
1
+
=
⇒
=
−
−
−
.
Uwzględniając to w poprzednim równaniu, dostajemy
hB
h
g
h
f
Φ
Φ
h
κ
2
)
1
(
2
)
2
(
0
2
1
2
0
1
0
2
2
−
−
−
=
+
+
−
.
(9.13a)
W równaniu tym nie występuje już fikcyjny węzeł
i = –1. Analogicznie, dla
warunku Neumanna na brzegu
x = x
N
dostaniemy
hB
h
g
h
f
Φ
h
κ
Φ
N
N
N
N
2
)
1
(
)
2
(
2
2
1
2
2
2
1
+
−
−
=
+
−
−
.
(9.13b)
x
0
= x
min
x
1
x
Φ(x)
h
h
Węzeł
fikcyjny
x
–1
Φ
1
Φ
0
Φ
–1
Φ
Rys. 9.7. Wprowadzanie warunku Neumanna lub Hankela
Warunek brzegowy Hankela
Również wprowadzenie warunku brzegowego
)
(
d
d
0
β
Φ
α
n
Φ
x
x
−
=
=
(9.14)
nie nastręcza trudności. Zapisany w postaci różnicowej
)
(
2
)
(
2
0
1
1
0
1
1
β
Φ
α
h
Φ
Φ
β
Φ
α
h
Φ
Φ
−
+
=
⇒
−
=
−
−
−
,
pozwala na wyeliminowanie z równania różnicowego (9.9c) fikcyjnego węzła –1.
Ostatecznie otrzymuje się
)
1
(
2
2
)]
2
(
)
1
(
2
[
0
2
1
2
0
1
0
2
2
0
2
1
h
g
αβ
h
h
f
Φ
Φ
h
κ
h
g
α
h
−
+
−
=
+
+
−
−
.
(9.15a)
Podobnie, dla węzła na brzegu x = x
N
dostaniemy
)
1
(
2
)]
2
(
)
1
(
2
[
2
2
1
2
2
2
2
1
1
h
g
αβ
h
h
f
Φ
h
κ
h
g
α
h
Φ
N
N
N
N
N
+
+
−
=
+
−
+
+
−
.
(9.15b)
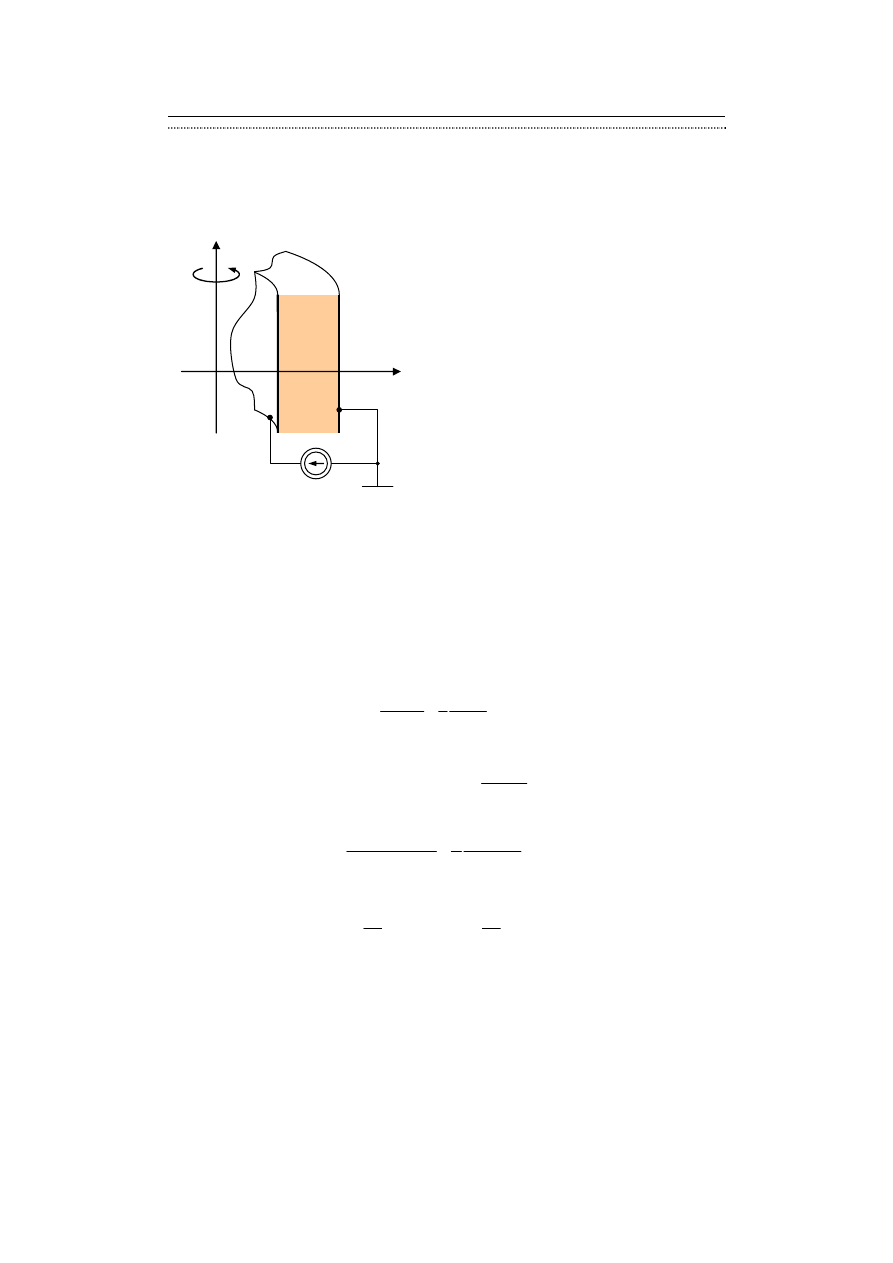
9. Metoda różnic skończonych (MRS)
10
Przykład 9.4. Wyznaczyć rozkład potencjału w obszarze rezystora cylindrycznego
o wysokości H = 1 cm i promieniach R
1
= 0,2 mm i R
2
= 2 mm, wypełnionego materiałem
o konduktywności γ = 1 S/m, jeżeli przez wewnętrzną okładkę wpływa prąd I = 1 A
(założyć równomierną gęstość), a zewnętrzna okładka ma potencjał równy zeru – rys. 9.8.
Rozwiązanie MRS porównać z dokładnym.
r
R
2
R
1
σ = σ
0
V(r) = ?
ρ, ε
r
V = 0
z
I
Rys. 9.8. Rezystor cylindryczny
Wychodząc z równań pola przepływowego
,
,
,
0
V
γ
−∇
=
=
=
⋅
∇
E
E
J
J
(a)
dostajemy dla potencjału elektrycznego V równanie Laplace’a:
,
0
2
=
∇
V
(b)
które w rozpatrywanych warunkach zależności V jedynie od odległości r od osi rezystora
redukuje się do postaci
.
0
d
)
(
d
1
d
)
(
d
2
2
=
+
r
r
V
r
r
r
V
(c)
Wprowadzamy siatkę N węzłów rozłożonych równomiernie wzdłuż odcinka r = [R
1
, R
2
]:
.
,
1
2
1
N
R
R
h
ih
R
r
i
−
=
+
=
(d)
Równanie (c) zapisujemy w postaci różnicowej
,
0
2
1
2
1
1
2
1
1
=
−
+
+
−
−
+
+
−
h
V
V
r
h
V
V
V
i
i
i
i
i
i
(e)
a przemnożeniu przez h
2
dostajemy
.
0
2
1
2
2
1
1
1
=
+
+
−
−
+
−
i
i
i
i
i
V
r
h
V
V
r
h
(f)
9.4. Zagadnienia dwuwymiarowe w układzie kartezjańskim
11
Równania takie układamy dla węzłów i = 1, 2, …, N – 1. W węźle i = 0 (tj. r = R
1
) musimy
uwzględnić warunek brzegowy
.
2
,
d
d
2
d
d
1
1
1
1
HR
πγ
I
B
B
n
V
H
R
π
I
n
V
γ
R
r
R
r
=
=
⇒
=
=
=
(g)
Jest to warunek Neumanna; na podstawie wzoru (9.13a) otrzymujemy zatem
.
2
1
2
2
2
1
1
0
−
−
=
+
−
R
h
Bh
V
V
(h)
Z kolei w węźle i = N (tj. r = R
2
) mamy warunek Dirichleta V = 0, a stąd równanie
przyjmuje postać
.
0
=
N
V
(i)
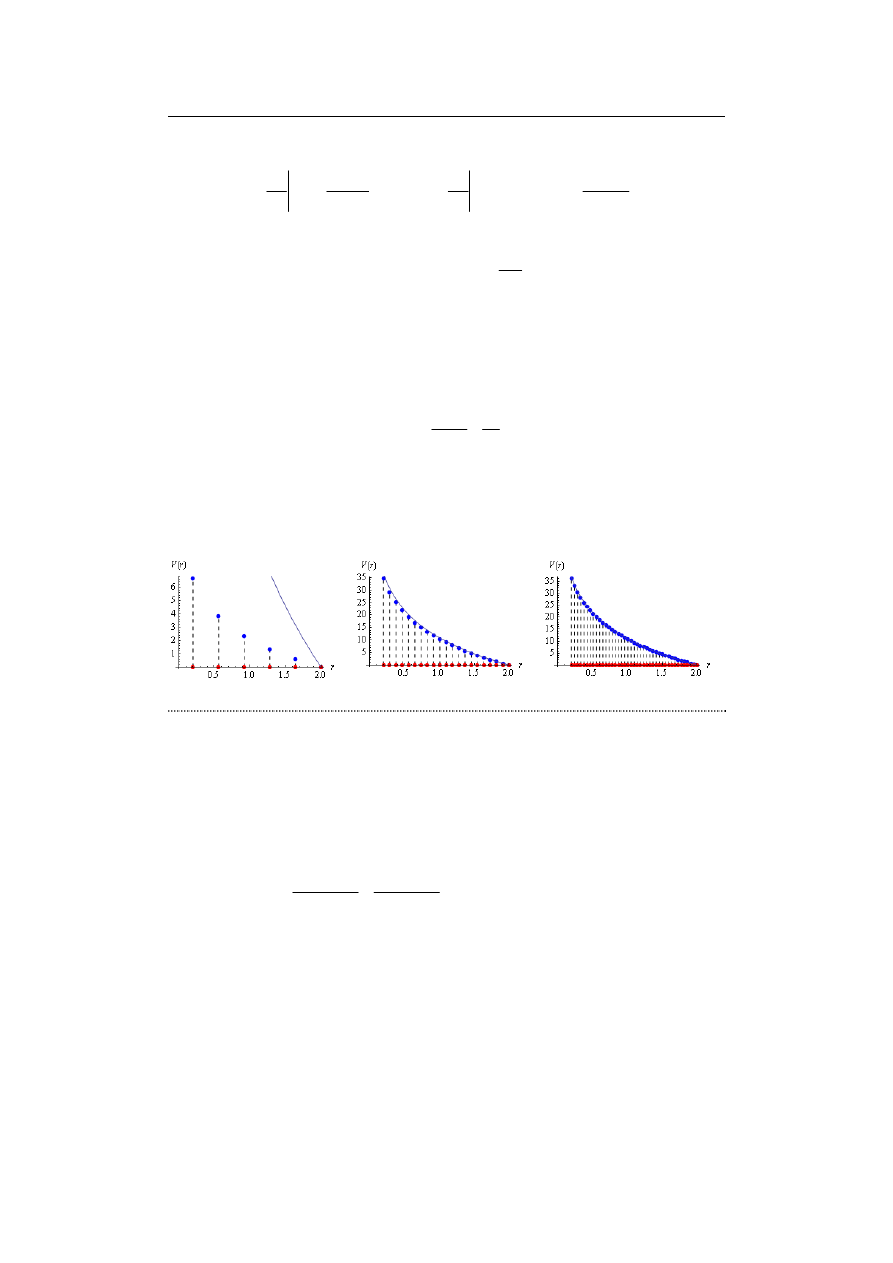
Rozwiązanie uzyskane za pomocą MRS dla różnej liczby węzłów przedstawiono na rys.
9.9. Naniesiono na nim również rozwiązanie dokładne, równe
.
ln
2
)
(
2
r
R
H
πγ
I
r
V
=
(j)
Jak wynika z otrzymanych wyników, w tym przypadku dla zbyt małej liczby węzłów
otrzymuje się wyniki bardzo odległe od rozwiązania dokładnego. Można to co prawda
nieco poprawić, stosując pewne modyfikacje, ale pokazuje to, że dokładność metod
numerycznych, w szczególności – MRS, może pozostawiać wiele do życzenia.
a)
b)
c)
Rys. 9.9. Wyniki obliczeń: a) N = 5, b) N = 20, c) N = 40.
9.4. Zagadnienia dwuwymiarowe w układzie kartezjańskim
9.4.1. Schemat pięciopunktowy
Rozważmy dwuwymiarowe niejednorodne równanie Helmholtza w układzie
współrzędnych kartezjańskich:
)
,
(
)
,
(
)
,
(
)
,
(
2
2
2
2
2
y
x
f
y
x
Φ
Γ
y
y
x
Φ
x
y
x
Φ
−
=
−
∂
∂
+
∂
∂
.
(9.16)
gdzie Γ oraz
f są znanymi stałymi lub funkcjami. Rozpatrywany przypadek
obejmuje także równanie Poissona (gdy Γ
2
= 0) oraz Laplace’a (gdy Γ
2
= 0 i
f = 0).
9. Metoda różnic skończonych (MRS)
12
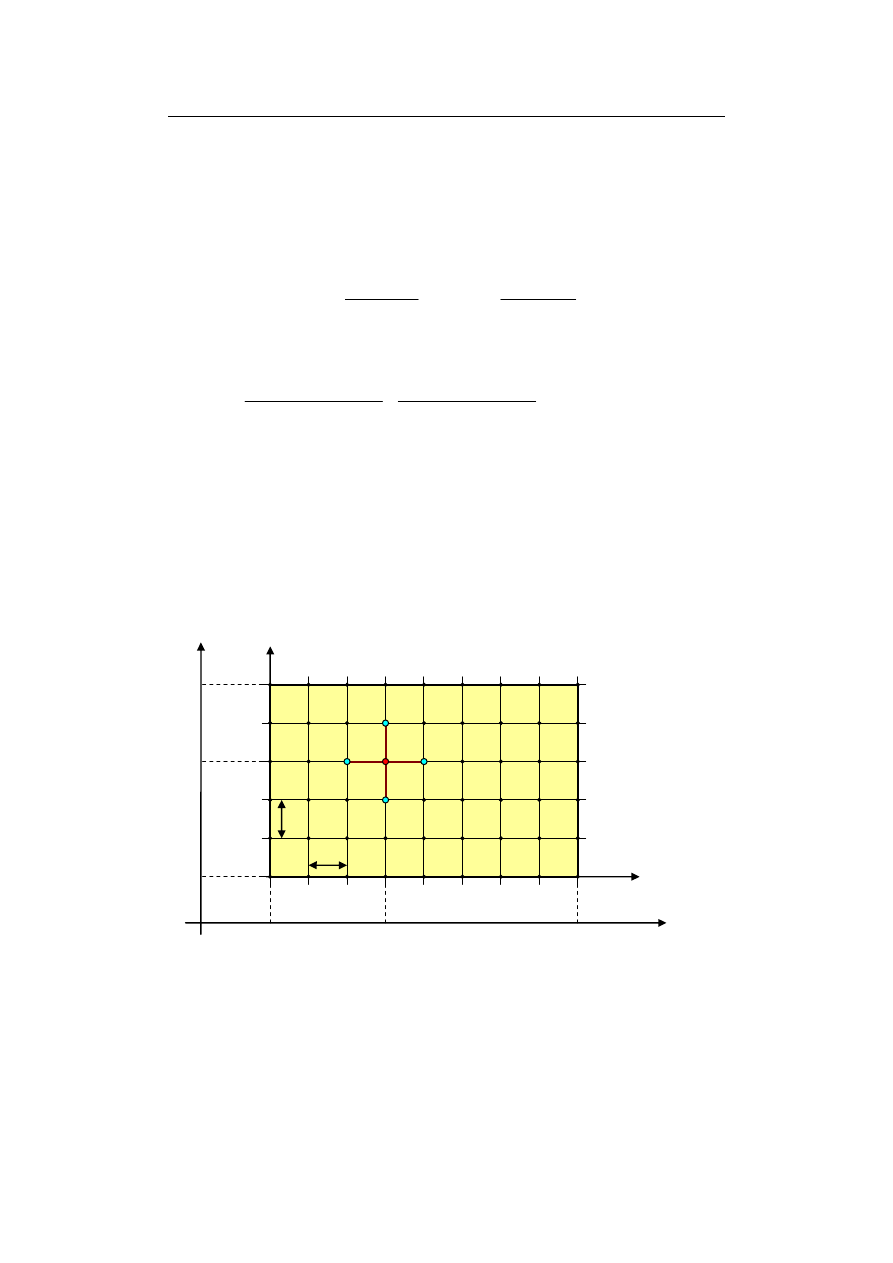
Wprowadźmy prostokątną siatkę węzłów jak na rys. 9.10. Węzły znajdują się na
przecięciu wierszy i kolumn, przy czym mamy I + 1 kolumn numerowanych
indeksem i = 0, 1, …, I oraz J + 1 wierszy numerowanych indeksem j = 0, 1, …, J.
Węzeł o współrzędnych dyskretnych (i, j) ma współrzędne kartezjańskie (x
i
, y
j
),
przy czym
y
j
x
i
jh
y
y
ih
x
x
+
=
+
=
min
min
,
,
(9.17a)
.
,
min
max
min
max
J
y
y
h
I
x
x
h
y
x
−
=
−
=
(9.17b)
Postać różnicową równania (9.16) dla węzła znajdującego się na przecięciu i-tej
kolumny i j-tego wiersza zapiszemy jako
j
i
j
i
y
j
i
j
i
j
i
x
j
i
j
i
j
i
f
Φ
Γ
h
Φ
Φ
Φ
h
Φ
Φ
Φ
,
,
2
2
1
,
,
1
,
2
,
1
,
,
1
2
2
−
=
−
+
−
+
+
−
+
−
+
−
,
(9.17a)
gdzie Φ
i,j
= Φ(x
i
, y
j
), f
i,j
= f(x
i
, y
j
). Jest to równanie różnicowe ułożone wg. tzw.
schematu pięciopunktowego. Oznaczając ζ = h
x
/h
y
, można je zapisać jako
j
i
x
j
i
x
j
i
j
i
j
i
j
i
f
h
Φ
h
Γ
ζ
Φ
ζ
Φ
ζ
Φ
Φ
,
2
,
2
2
2
1
,
2
1
,
2
,
1
,
1
)
2
2
(
−
=
+
+
−
+
+
+
+
−
+
−
. (9.18b)
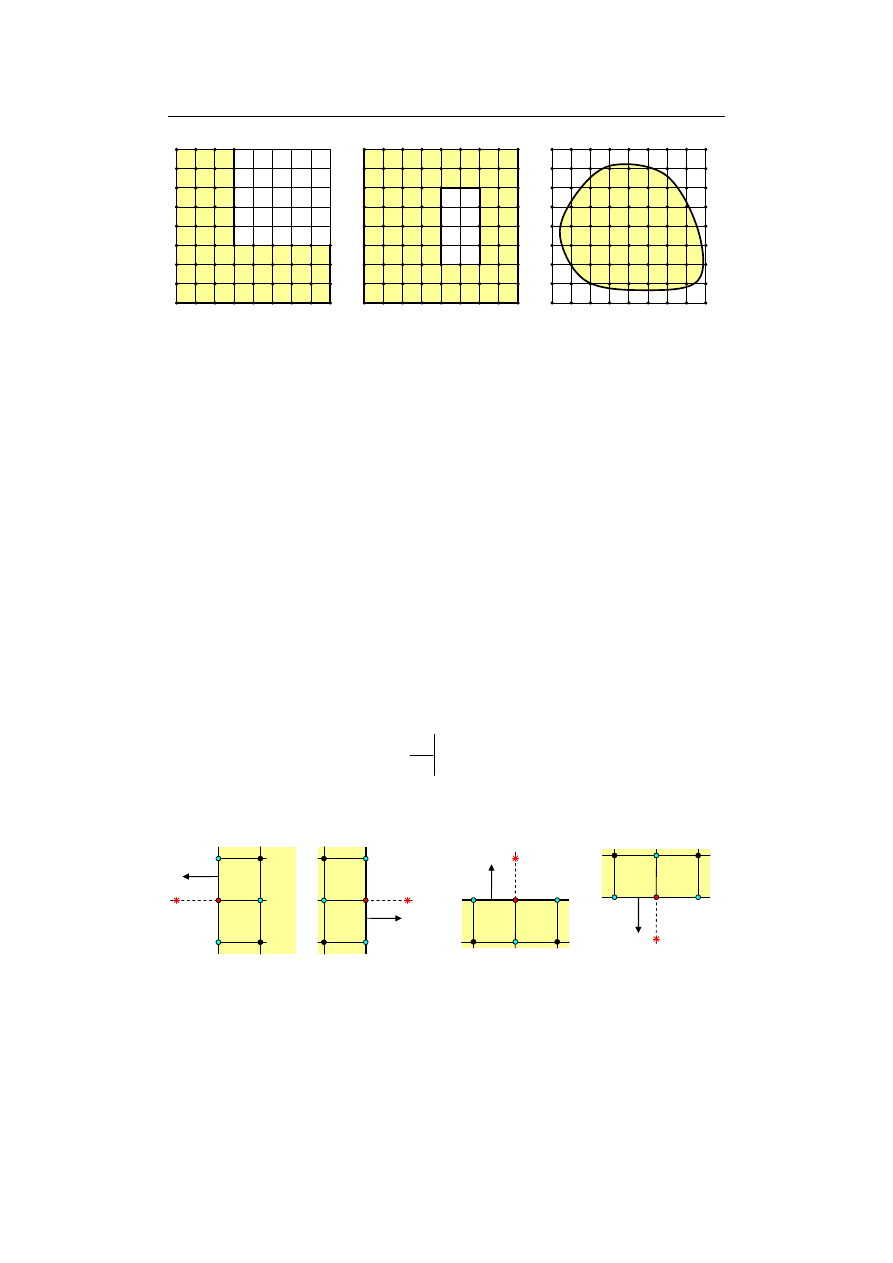
Schemat taki można stosować w obszarach płaskich o różnych kształtach, jednak
najlepsze efekty daje dla prostokąta lub obszaru dającego się rozłożyć na sumę
prostokątów (np. kątownik, prostokąt z prostokątnym otworem – rys. 9.11). Chodzi
o to, aby węzły siatki wypadły na brzegu obszaru. Jeśli tak nie jest, pojawiają się
kłopoty z uwzględnieniem geometrii brzegu oraz warunków brzegowych.
y
x
x
min
x
max
y
min
y
max
y
j
x
i
h
y
h
x
j = 0
j = J
i = I
i = 0
j
i
i
j
(i, j)
Rys. 9.10. Siatka dwuwymiarowa w układzie kartezjańskim nałożona na prostokąt
9.4. Zagadnienia dwuwymiarowe w układzie kartezjańskim
13
a)
b)
c)
Rys. 9.11. Obszary dwuwymiarowe z nałożoną siatką węzłów: a) kątownik, b) prostokąt z otworem
prostokątnym, c) kształt nieregularny – trudny do uwzględnienia w MRS
9.4.2. Wprowadzanie warunków brzegowych
W przypadku obszarów o brzegach wypadających na liniach węzłów warunki
brzegowe do równań MRS wprowadza się zasadniczo tak samo jak to omówiono w
punkcie 9.3.2. Jeżeli obszar ma nieregularny kształt, wprowadzanie warunków jest
kłopotliwe i nie jest tutaj omawiane.
Warunek Dirichleta
Jeżeli w węźle (i, j) znana jest wartość funkcji pola
A
Φ
=
,
(9.19)
to zamiast równania (9.18b) należy zapisać równanie
A
Φ
j
i
=
,
.
(9.20)
Jest to więc dokładnie tak, jak w przypadku jednowymiarowym.
Warunek Neumanna
Jeżeli w węźle brzegowym (i, j) zadany jest warunek Neumanna
B
n
Φ
j
i
=
∂
∂
,
,
(9.21)
to mogą zajść przypadki pokazane na rys. 9.12.
a)
b)
c)
d)
h
x
h
x
(i, j)
(i+1, j)
(i, j+1)
(i, j–1)
(i–1, j)
n
h
y
h
x
h
x
(i, j)
(i+1, j)
(i, j+1)
(i, j–1)
(i–1, j)
n
h
y
h
x
(i, j)
(i+1, j)
(i, j+1)
(i, j–1)
(i–1, j)
n
h
y
h
y
h
x
(i, j)
(i+1, j)
(i, j+1)
(i, j–1)
(i–1, j)
n
h
y
h
y
Rys. 9.12. Możliwe przypadki przy wprowadzaniu warunku Neumanna lub Hankela w siatce XY
9. Metoda różnic skończonych (MRS)
14
Wszystkie one są łatwe do uwzględnienia, dlatego tylko pierwszy zostanie
omówiony. Postać różnicowa warunku (9.21) to wtedy
B
h
Φ
Φ
B
h
Φ
Φ
x
j
i
j
i
x
j
i
j
i
2
2
,
1
,
1
,
1
,
1
+
=
⇒
=
−
+
−
+
−
.
(9.22)
Uzyskana zależność pozwala na wyeliminowanie fikcyjnego węzła (
i–1, j)
z równania różnicowego (9.18b), co prowadzi do zależności
B
h
f
h
Φ
h
Γ
Φ
ζ
Φ
ζ
Φ
ζ
Φ
x
j
i
x
j
i
x
j
i
j
i
j
i
j
i
2
)
2
2
(
2
,
2
,
2
2
,
2
1
,
2
1
,
2
,
1
−
−
=
+
+
−
+
+
+
−
+
. (9.23)
Warunek Hankela
Jeżeli w węźle brzegowym (i, j) zadany jest warunek Hankela
)
(
,
β
Φ
α
n
Φ
j
i
−
=
∂
∂
,
(9.24)
to mogą zajść przypadki pokazane na rys. 9.12. Wszystkie je uwzględnia się
analogicznie, dlatego dalej rozpatrujemy tylko pierwszy z nich. Z postaci
różnicowej warunku brzegowego mamy
)
(
2
)
(
2
,
,
1
,
1
,
,
1
,
1
β
Φ
α
h
Φ
Φ
β
Φ
α
h
Φ
Φ
j
i
x
j
i
j
i
j
i
x
j
i
j
i
−
+
=
⇒
−
=
−
+
−
+
−
, (9.25)
co pozwala wyeliminować z równania (9.18b) fikcyjny węzeł (i–1, j) i daje
x
j
i
x
j
i
x
x
j
i
j
i
j
i
h
αβ
f
h
Φ
h
α
h
Γ
ζ
Φ
ζ
Φ
ζ
Φ
2
)
2
2
2
(
2
,
2
,
2
2
2
1
,
2
1
,
2
,
1
+
−
=
−
+
+
−
+
+
+
−
+
. (9.26)
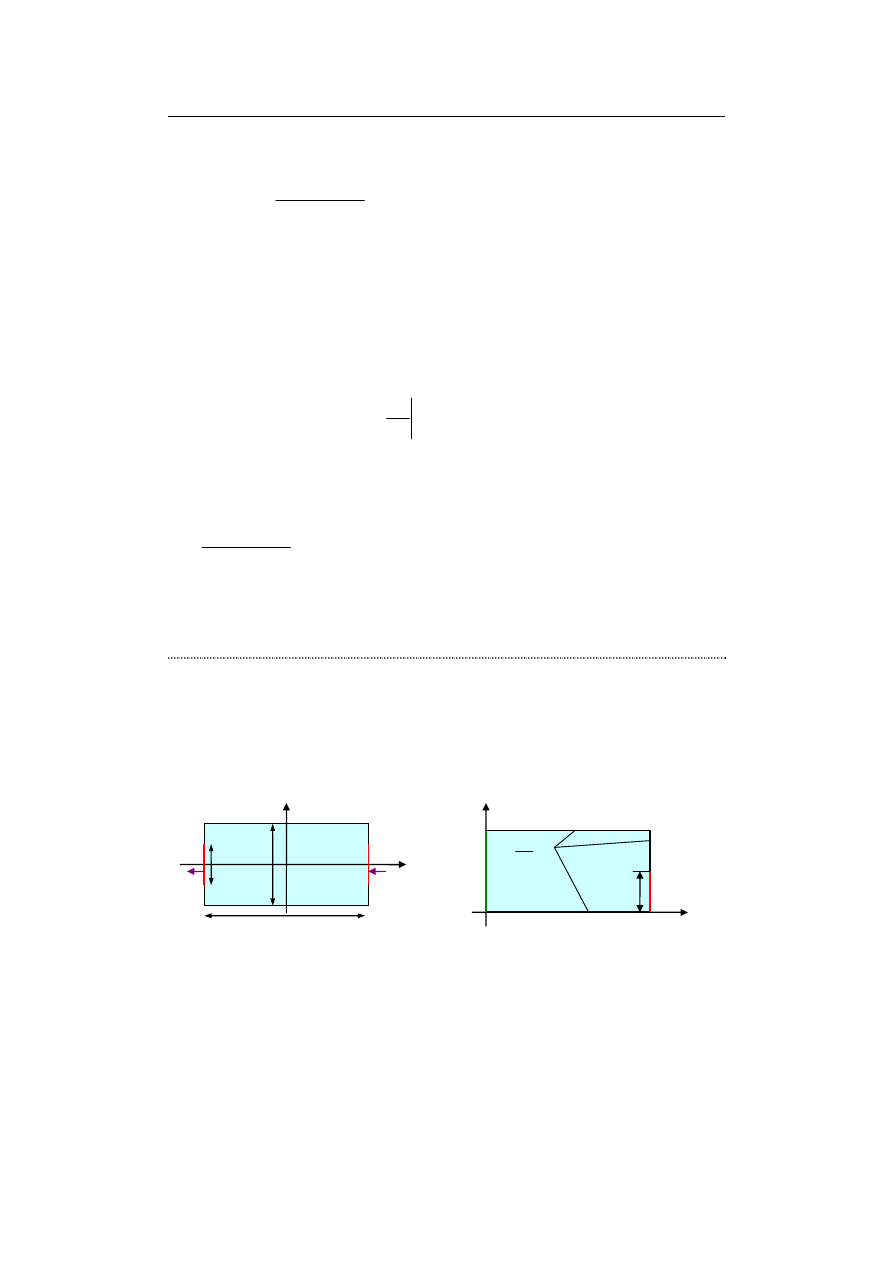
Przykład 9.5. W środowisku nieprzewodzącym umieszczono prostokątną płytkę
o przewodności γ, grubości h, długości 2a i szerokości 2b. Do przeciwległych boków płytki
przyłożono napięcie 2U, przy czym elektrody umieszczone są centralnie i mają długość 2d
(rys. 9.13a). Wyznaczyć rozkład potencjału, przepływający prąd, straty mocy oraz
rezystancję płytki. W obliczeniach numerycznych przyjąć γ = 1000 S/m, h = 1 mm,
a = 1 cm, b = 1 cm, d = 0,5 cm, U = 100 V.
a)
b)
x
y
2a
U
2d
–U
2b
γ
I
I
x
y
a
V = U
d
b
V = 0
0
=
∂
∂
n
V
∇
2
V = 0
Rys. 9.13. Prostokątna płytka z prądem: a) obszar oryginalny, b) obszar przyjęty do analizy ze
względu na symetrię

9.4. Zagadnienia dwuwymiarowe w układzie kartezjańskim
15
Ze względu na symetrię obszaru działania pola i warunków brzegowych analizę
można ograniczyć do ćwiartki obszaru (rys. 9.13b). Z równań pola przepływowego
V
γ
−∇
=
=
=
⋅
∇
E
E
J
J
,
,
0
(a)
wynika dla potencjału
V równanie Laplace’a
.
0
2
2
2
2
=
∂
∂
+
∂
∂
y
V
x
V
(b)
Warunki brzegowe:
-
elektroda: warunek Dirichleta V = U,
-
ścianki płytki (y = b, x = a oprócz elektrody): zerowy warunek Neumanna ∂V/∂n = 0
wynikający z braku możliwości przepływania prądu przez te ścianki,
-
linia x = 0: zerowy warunek Dirichleta V = 0 wynikający z symetrii przyłożenia elektrod
względem osi Oy,
-
linia y = 0: zerowy warunek Neumanna ∂V/∂n wynikający z symetrii przyłożenia
elektrod względem osi Ox.
Na rozpatrywany obszar nakładamy siatkę węzłów wg rys. 9.10. Równanie różnicowe
odpowiadające równaniu (b) ma postać (9.18b) z Γ = f = 0. Po prostym przekształceniu
zapiszemy je jako
.
2
2
2
1
,
2
1
,
2
,
1
,
1
,
ζ
V
ζ
V
ζ
V
V
V
j
i
j
i
j
i
j
i
j
i
+
+
+
+
=
+
−
+
−
(c)
Jest ono poprawne w każdym węźle, z tym, że należy uwzględnić warunki brzegowe.
Ostatecznie mamy:
-
w węzłach wewnętrznych (i, j), tj. dla i = 1, 2, …, I – 1 oraz j = 1, 2, …, J – 1 spełnione
jest równanie (c),
-
na linii x = 0, tj. w węzłach (0, j), dla j = 0, 1, …, J zamiast równania (c) mamy
,
0
,
0
=
j
V
(d)
-
na linii y = 0 oprócz naroży, tj. w węzłach (i, 0) dla i = 1, 2, …, I – 1 należy uwzględnić
zerowy warunek Neumanna, w związku z czym równanie (c) przyjmuje postać
,
2
2
2
2
1
,
2
0
,
1
0
,
1
0
,
ζ
V
ζ
V
V
V
i
i
i
i
+
+
+
=
+
−
(e)
-
na linii y = b oprócz naroży, tj. w węzłach (i, J) dla i = 1, 2, …, I – 1 należy uwzględnić
zerowy warunek Neumanna, w związku z czym równanie (c) przyjmuje postać
,
2
2
2
2
1
,
2
,
1
,
1
,
ζ
V
ζ
V
V
V
J
i
J
i
J
i
J
i
+
+
+
=
−
+
−
(f)
-
na elektrodzie V = U, tj. w węzłach (I, j) dla j = 0, 1, …, J', gdzie J' = [d/b] jest numerem
wiersza węzłów do którego sięga elektroda, mamy warunek Dirichleta
,
,
U
V
j
I
=
(g)
-
na pozostałej części linii x = a (poza elektrodą) oprócz naroża, tj. w węzłach (I, j) dla
j = J' + 1, J' + 2, …, J – 1 mamy zerowy warunek Neumanna, stąd równanie (c)
przyjmuje postać
9. Metoda różnic skończonych (MRS)
16
,
2
2
2
2
1
,
2
1
,
2
,
1
,
ζ
V
ζ
V
ζ
V
V
j
I
j
I
j
I
j
I
+
+
+
=
+
−
−
(h)
-
w narożu (
a, b), tj. w węźle (I, J), który należy zarówno do brzegu x = a, jak i y = b,
należy uwzględnić zerowe warunki Neumanna w obydwu kierunkach; równanie (c) daje
,
2
2
2
2
2
1
,
2
,
1
,
ζ
V
ζ
V
V
J
I
J
I
J
I
+
+
=
−
−
(i)
przy czym jeżeli
J' = J, to pierwszeństwo ma równanie (g).
W ten sposób ułożyliśmy dla każdego węzła równanie. Wszystkich równań jest
(
I + 1)(J + 1). Ze względu na to, że macierz główna jest rzadka i ma normę mniejszą od
jedności można zastosować iteracyjną metodę rozwiązywania takiego układu równań.
Polega to na przyjęciu dowolnych wartości potencjału w poszczególnych węzłach
i wyznaczeniu nowych wartości ze wzorów (c)÷(i). Proces ten należy powtarzać dopóki
nowe wartości węzłowe nie będą dostatecznie bliskie poprzednim.
W celu przyspieszenia zbieżności można zastosować metodę relaksacji (zob. punkt
3.2.5), która polega na tym, że nowe wartości węzłowe obliczane są jako
,
,
(stare)
,
(nowe)
,
j
i
j
i
j
i
V
∆
V
V
+
=
(j)
gdzie
],
(i))
-
(c)
wzór
[(
(stare)
,
,
j
i
j
i
V
ω
V
∆
−
=
(k)
przy czym ω jest parametrem relaksacji z zakresu (0, 2). Dla ω = 1 uzyskuje się zwyczajną
metodę iteracji, która jest dość wolno zbieżna (około 300 iteracji dla δ
max
= 10
–6
przy siatce
10×10, tzn. 11×11 = 121 węzłów). W rozpatrywanym przypadku wartość ω równa około
1,6 zapewnia znacznie szybszą zbieżność (80 iteracji przy tej samej dokładności).
Jako kryterium zakończenia obliczeń można przyjąć warunek
,
)
(
0
0
2
(nowe)
,
max
0
0
2
,
∑∑
∑∑
=
=
=
=
≤
I
i
J
j
j
i
I
i
J
j
j
i
V
δ
V
∆
(l)
gdzie δ
max
jest maksymalnym błędem względnym (np. 10
–5
). Powyższy warunek oznacza,
że poprawki są bardzo małe w porównaniu z wartościami węzłowymi, więc proces
rozwiązywania układu równań można uznać za zakończony.
Wyznaczanie prądu. Z dwóch ostatnich równań (a) wynika, że składowa normalna
gęstości prądu na brzegu płytki wynosi
.
n
V
γ
E
γ
J
n
n
∂
∂
−
=
=
(m)
W węźle (0, j) na brzegu x = 0 postać różnicowa powyższego wyrażenia to
.
,
1
,
0
,
0
x
j
j
j
n
h
V
V
γ
J
−
−
=
(n)
Całkując po powierzchni brzegowej, dostaniemy całkowity prąd
∫
∫
=
⋅
=
=
b
n
x
y
h
J
I
0
0
wy
d
d S
J
.
(o)
9.4. Zagadnienia dwuwymiarowe w układzie kartezjańskim
17
Całkowanie należy wykonać numerycznie, np. metodą trapezów:
.
2
1
1
wy
∑
=
−
+
=
J
j
y
j
n
j
n
h
J
J
h
I
(p)
Jest to prąd płynący w górnej połowie płytki. Całkowity prąd jest równy
I = 2I
wy
.
Rezystancja płytki wynosi R = (2U)/I = U/I
wy
, a
straty mocy P = RI
2
. Przykładowe
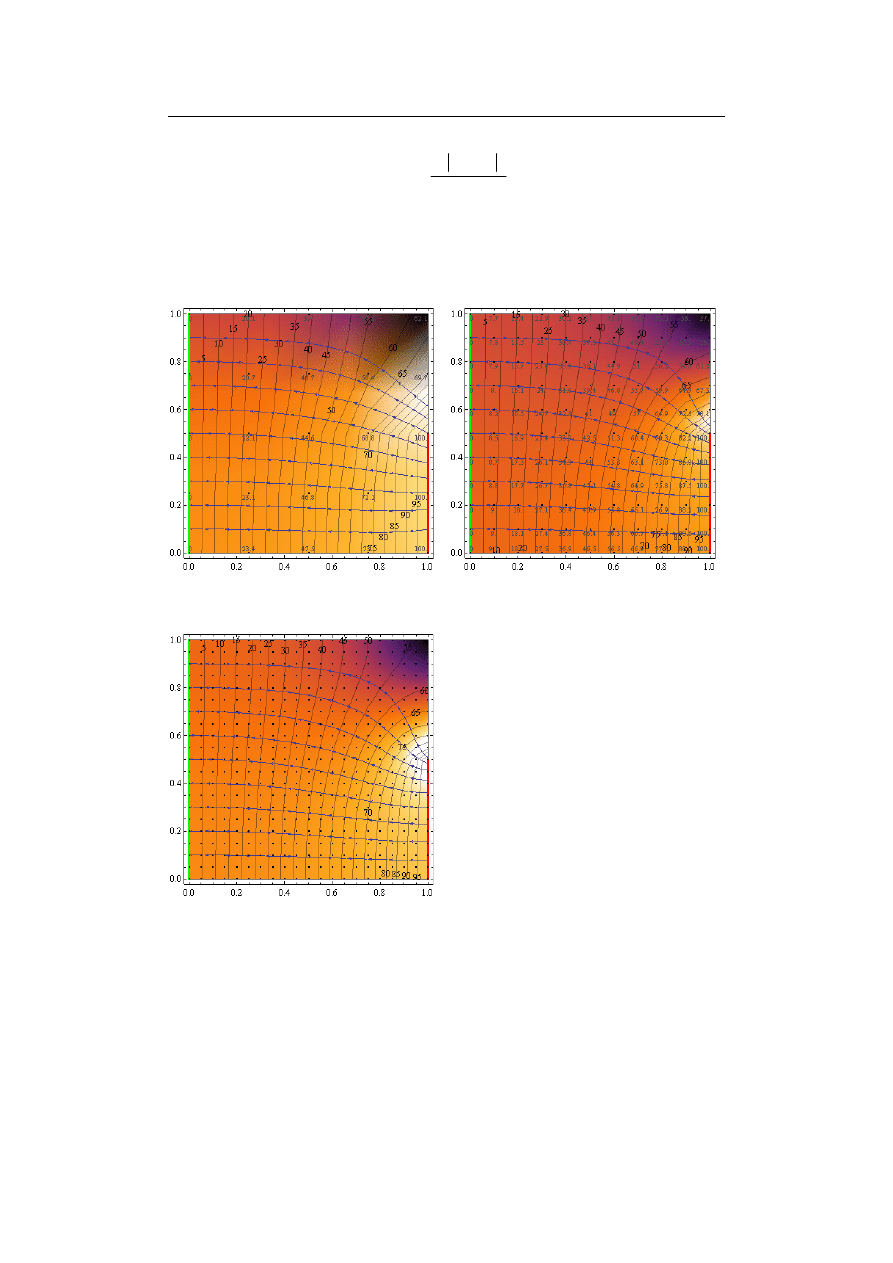
wyniki obliczeń zaprezentowano na rys. 9.14.
a)
b)
5×5 węzłów, I
wy
= 87,7 A, R = 87,7 Ω
11×11 węzłów, I
wy
= 84,3 A, R = 84,3 Ω
c)
21×21 węzłów, I
wy
= 83,1 A, R = 83,1 Ω
Rys. 9.14. Obraz pola w płytce kwadratowej
z elektrodą zajmującą połowę ścianki
(czerwona linia); rysunki przedsta-
wiają ćwiartkę obszaru; zaznaczono
węzły (kropki), wartości węzłowe
potencjału (drobna czcionka), linie
ekwipotencjalne (od 0 do 100 V co
5 V), linie prądu (niebieskie strzałki);
kolor
wypełnienia
wskazuje
na
gęstość wydzielanej mocy: jasne
obszary – duża moc, ciemne – mała:
a) dyskretyzacja zgrubna, ewidentnie
niedokładna, b) dyskretyzacja śred-
nia, widoczne załamania linii ekwi-
potencjalnych wskazują na zbyt małą
dokładność, c) dyskretyzacja drobna,
wydaje się dość dokładna
9. Metoda różnic skończonych (MRS)
18
9.5. Inne typowe siatki węzłów
9.5.1. Schemat pięciopunktowy w układzie biegunowym
Dla obszarów działania pola w kształcie koła, pierścienia, sektora koła lub
wycinka pierścienia wygodniejszy od kartezjańskiego jest układ współrzędnych
biegunowych, w którym laplasjan ma nieco inną postać:
2
2
2
2
2
2
)
,
(
1
)
,
(
1
)
,
(
φ
φ
r
Φ
r
r
φ
r
Φ
r
r
φ
r
Φ
Φ
∂
∂
+
∂
∂
+
∂
∂
=
∇
.
(9.27)
Na obszar działania pola nakładamy siatkę biegunową („pajęczynę”) zbudowaną z
I + 1 łuków okręgów numerowanych indeksem i = 0, 1, …, I oraz z pęku J + 1
półprostych wychodzących ze środka układu współrzędnych i numerowanych
indeksem
j = 0, 1, …, J – rys. 9.15. Dzięki temu węzły wypadają na granicy
obszaru. Dla ustalenia uwagi przypuśćmy, że obszarem działania jest pola jest
wycinek pierścienia o promieniach wewnętrznym
r
min
i zewnętrznym
r
max
i rozpiętości kątowej od φ
min
do φ
max
. Wtedy skoki siatki wynoszą odpowiednio
J
φ
φ
h
I
r
r
h
φ
r
min
max
min
max
,
−
=
−
=
,
(9.28a)
zaś węzeł o współrzędnych dyskretnych (i, j) ma współrzędne biegunowe
φ
j
r
i
jh
φ
φ
ih
r
r
+
=
+
=
min
min
,
.
(9.28b)
Wtedy postać różnicowa laplasjanu dla węzła (i, j) to
2
2
1
,
,
1
,
,
1
,
1
2
,
1
,
,
1
,
2
2
2
2
φ
i
j
i
j
i
j
i
i
r
j
i
j
i
r
j
i
j
i
j
i
j
i
h
r
Φ
Φ
Φ
r
h
Φ
Φ
h
Φ
Φ
Φ
Φ
+
−
−
+
+
−
+
−
+
−
+
+
−
≈
∇
.
(9.29)
x
y
r
min
r
max
φ
min
φ
max
φ
j
r
i
(i, j)
h
φ
h
r
i
j
j = J
i = I
i = 0
j = 0
j
i
Rys. 9.15. Siatka dwuwymiarowa w układzie biegunowym nałożona na wycinek pierścienia
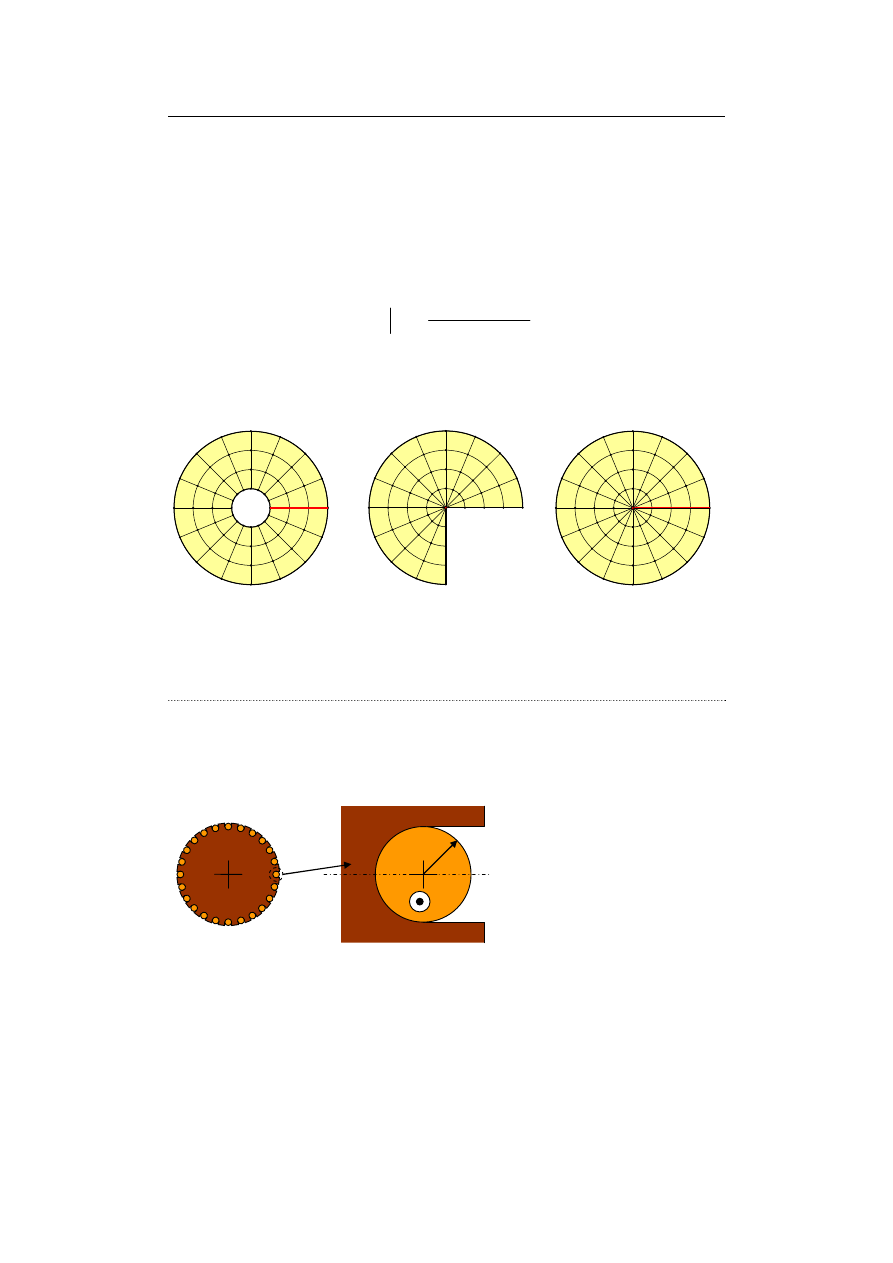
9.5. Inne typowe siatki węzłów
19
Jeżeli mamy do czynienia z pełnym zakresem zmienności kąta φ, tzn. φ
min
= 0
i φ
max
= 2π, to linie j = 0 i j = J należy utożsamić. Jeżeli z kolei r
min
= 0, to okrąg
i = 0 degeneruje się do punktu. Degeneracja ta uniemożliwia skorzystanie ze
pięciopunktowego schematu różnicowego, gdyż węzeł środkowy sąsiaduje wtedy
nie z czterema innymi węzłami w kierunkach zmian r i φ, lecz z wieloma węzłami
położonymi na okręgu i = 1. To wymusza szczególne traktowanie węzła
środkowego. W przypadku koła można pokazać, że
2
0
1
0
,
1
0
0
2
r
i
J
j
j
i
r
h
Φ
J
Φ
Φ
=
−
=
=
=
−
≈
∇
∑
,
(9.30)
natomiast dla sektora sytuacja zależy od rodzaju warunku brzegowego zadanego
w tym węźle i kąta rozwarcia, lecz nie będziemy tego szczegółowo rozpatrywać.
a)
b)
c)
j = 0
j = J
j = 1
j = J–1
i = 0
Rys. 9.16. Przypadku siatki biegunowej wymagające szczególnego traktowania: a) pierścień – pełny
zakres kąta powoduje utożsamienie linii j = 0 i j = J, b) sektor koła – zerowy promień
wewnętrzny r
min
= 0 – degeneracja łuku okręgu i = 0, w węźle środkowym konieczne jest
specyficzne postępowanie zależne od warunków brzegowych, c) pełne koło – następuje
zarówno degeneracja środkowego okręgu do punktu oraz nałożenie linii j = 0 i j = J,
w punkcie środkowym można stosować wzór (9.30)
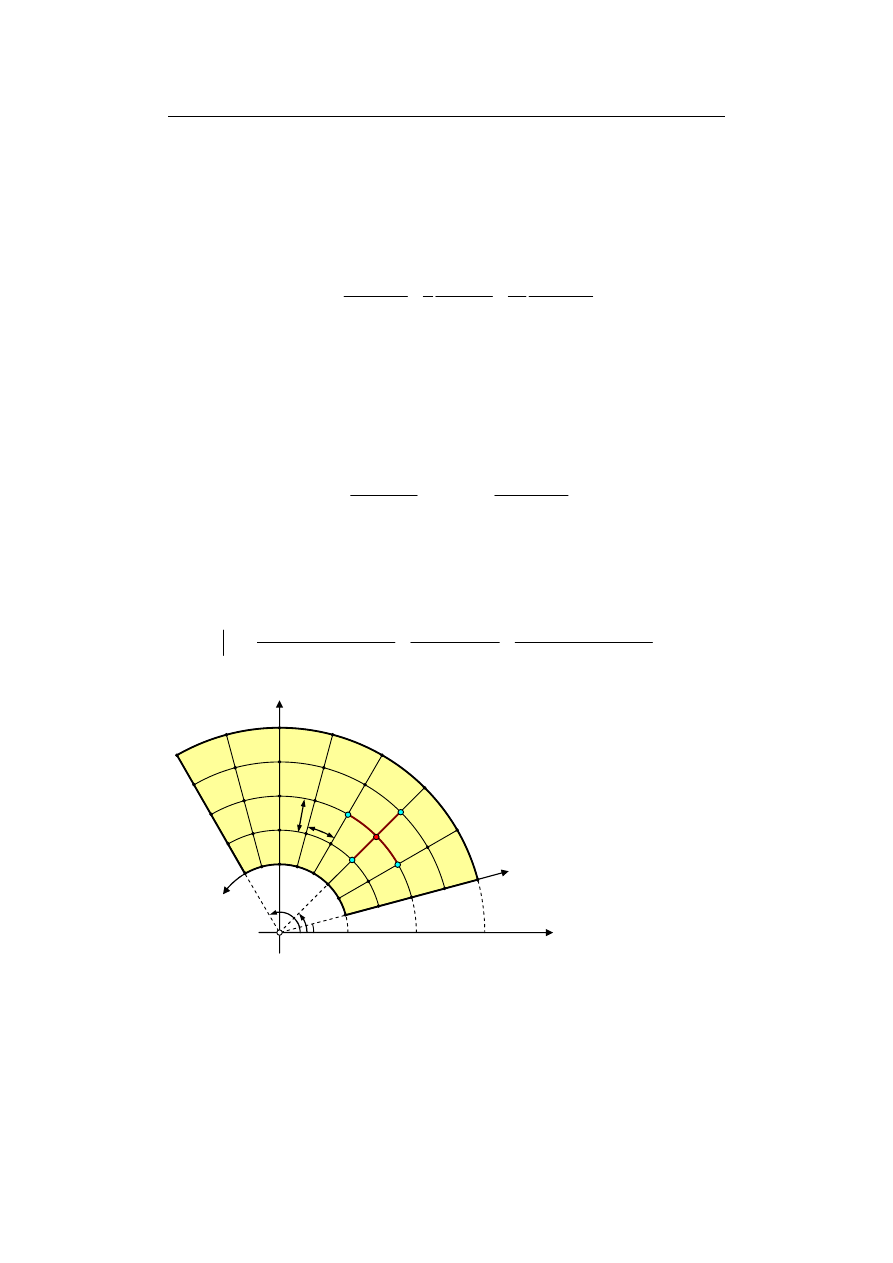
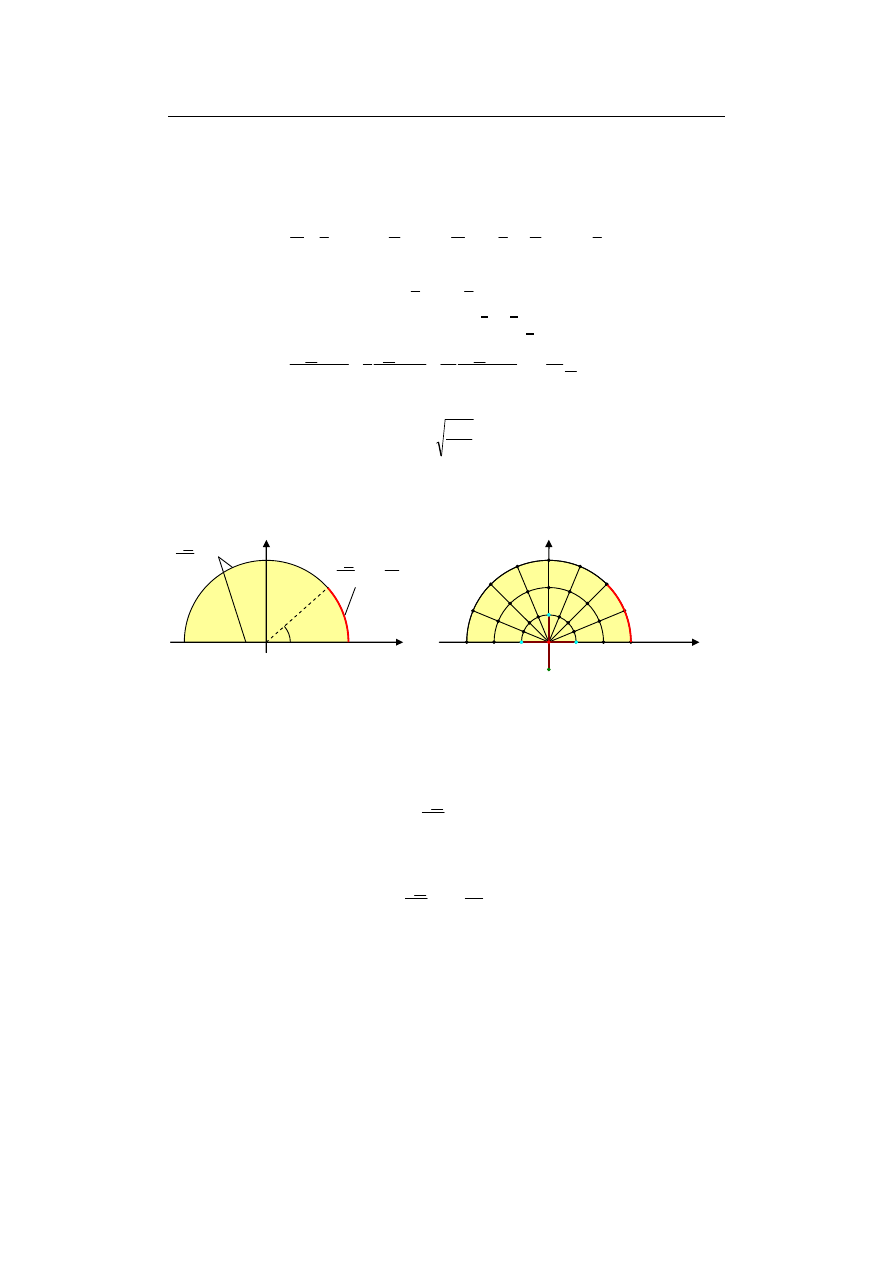
Przykład 9.6. Obliczyć rozkład gęstości prądu w przewodzie maszyny elektrycznej
ułożonym żłobku wyciętym w magnetycznym rdzeniu (rys. 9.17). Parametry pręta:
konduktywność γ, przenikalność magnetyczna µ, promień przekroju poprzecznego a.
Parametry wymuszenia: prąd sinusoidalny o wartości skutecznej natężenia I i pulsacji ω.
Obliczyć rezystancję pręta. W obliczeniach numerycznych przyjąć ωµγa
2
/2 = 1.
a
Cu
γ, µ
Fe
(µ
r
>> 1)
I, ω
Rys. 9.17. Przewody w ułożone w rdzeniu; po prawej powiększenie otoczenia jednego przewodu
9. Metoda różnic skończonych (MRS)
20
Z uwagi na sinusoidalną zależność od czasu można stosować zapis zespolony.
Z powodu geometrii stosujemy biegunowy układ współrzędnych ze środkiem
pokrywającym się ze środkiem przekroju poprzecznego przewodu. Ponieważ długość
przewodu jest znacznie większa w porównaniu z jego wymiarami poprzecznymi, wektor
gęstości prądu ma tylko składową wzdłużną (z-ową). Z równań pola
0
,
,
j
,
=
⋅
∇
=
−
=
×
∇
=
×
∇
J
E
J
H
E
J
H
γ
ωµ
(a)
otrzymuje się równanie dla zespolonego wektora gęstości prądu
.
0
j
2
=
−
∇
J
J
ωµγ
(b)
Wprowadzając względną zespoloną gęstość prądu
J' = J/J
0
, gdzie
J
0
=
I/(πa
2
) jest średnią
gęstością prądu, dostajemy równanie dla składowej
z-owej J':
,
0
2
j
)
,
(
1
)
,
(
1
)
,
(
2
2
2
2
2
2
2
=
′
−
∂
′
∂
+
∂
′
∂
+
∂
′
∂
J
a
κ
φ
φ
r
J
r
r
φ
r
J
r
r
φ
r
J
(c)
gdzie
a
ωµγ
κ
2
=
(d)
jest tzw. względnym współczynnikiem wypierania. Symetria obszaru działania pola
pozwala na rozpatrywanie tylko górnej połowy przekroju pręta (rys. 9.18a).
a)
b)
x
y
0
=
∂
′
∂
n
J
a
α
π
κ
n
J
2
j
=
∂
′
∂
α
x
y
i = 0
i = M
j = N
j = 0
j = N
1
Rys. 9.18. Obszar przyjęty do analizy (a) oraz jego siatka biegunowa (b), w której pokazano
dodatkowo sposób traktowania węzła i = 0
Warunki brzegowe:
-
na styku miedź-żelazo zadany jest zerowy warunek Neumanna, wynikający z ciągłości
składowej stycznej natężenia pola magnetycznego
,
0
=
∂
′
∂
n
J
(e)
-
na styku miedź-powietrze dokładnego warunku brzegowego nie znamy, lecz przyjmuje
się, że jest to stały warunek Neumanna; wtedy z prawa przepływu wyznaczamy
,
j
2
a
α
π
κ
n
J
=
∂
′
∂
(f)
gdzie 2α jest kątem rozwarcia na powietrze (w rozpatrywanym przypadku α = π/2).
-
na linii symetrii (y = 0) mamy zerowy warunek Neumanna (e), który wynika z tego, że
obraz pola w dolnej połowie jest symetrycznym odbiciem obrazu w górnej połowie.
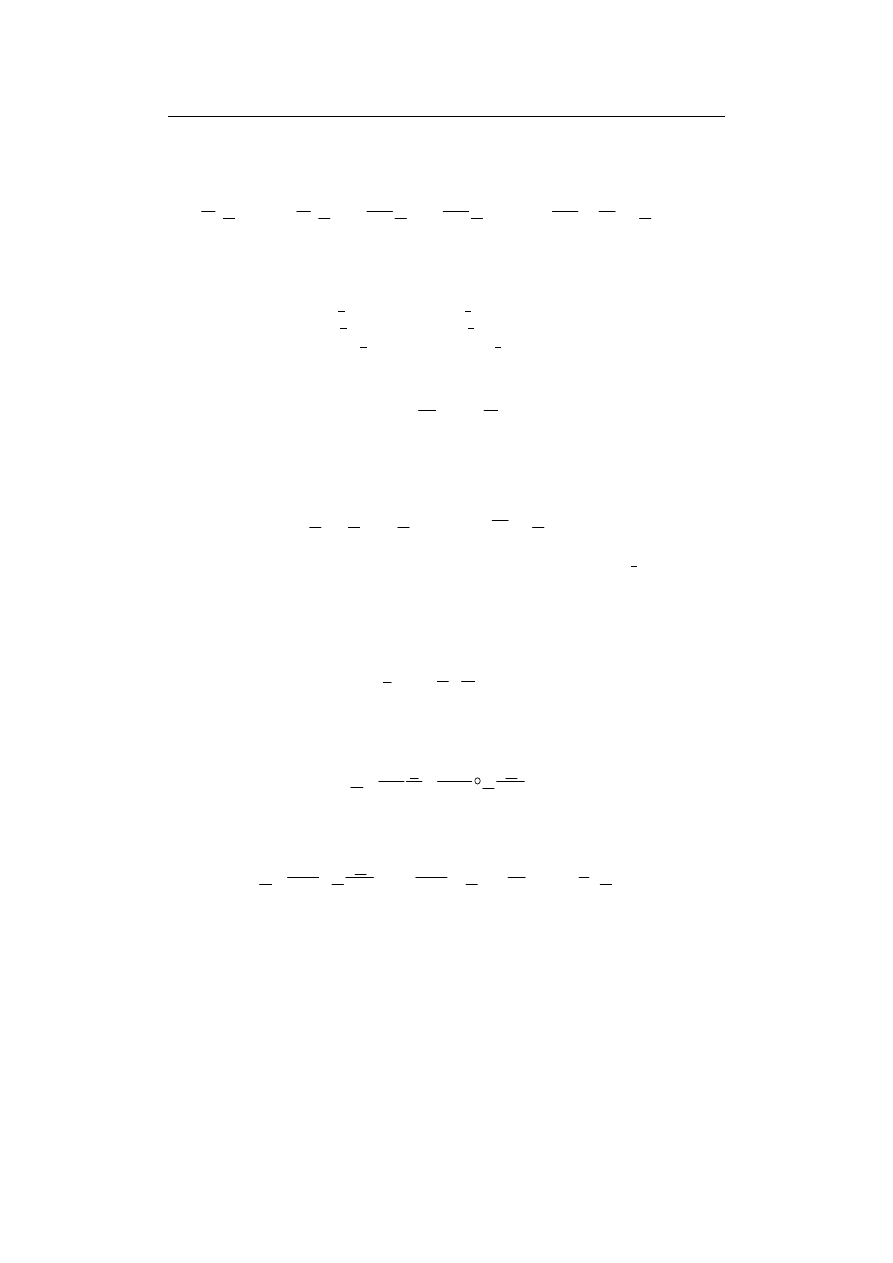
9.5. Inne typowe siatki węzłów
21
Na analizowany obszar nakładamy siatkę biegunową (rys. 9.18b). Postać różnicową
równania (c) dla węzła (i, j) uzyskamy poprzez zależność (9.29). Po prostych
przekształceniach otrzymujemy
.
0
j
1
1
2
1
1
2
1
1
2
1
1
,
2
2
2
2
2
1
,
2
2
1
,
2
2
,
1
,
1
=
′
+
+
−
′
+
′
+
′
+
+
′
−
+
−
+
−
j
i
r
φ
j
i
φ
j
i
φ
j
i
j
i
J
κ
a
h
h
i
J
h
i
J
h
i
J
i
J
i
(g)
Równanie takie jest układane dla każdego węzła (i, j) siatki obszaru, i = 1, 2, …M, j = 0, 1,
…, M, przy czym w węzłach brzegowych należy uwzględnić warunki brzegowe. Wszystkie
one są typu Neumanna, co powoduje, że:
-
jeżeli j = 0, to w miejsce J'
i,j–1
należy wstawić J'
i,1
,
-
jeżeli j = N, to w miejsce J'
i,j+1
należy wstawić J'
i,N–1
,
-
jeżeli i = M, to w miejsce J'
i+1,j
należy wstawić J'
M–1,j
; jeżeli dodatkowo j
≤
N
1
(rys.
9.18b), to należy uwzględnić niezerowy warunek Neumanna (f), co powoduje, że po
prawej stronie równania (g) w miejsce zera należy wstawić
.
2
1
1
2
j
2
+
−
i
h
a
α
π
κ
r
(h)
Punkt i = 0 wymaga szczególnego traktowania (nie można użyć równania (g)). Zauważmy,
że możemy w nim zastosować schemat pięciopunktowy o postaci (9.18b) – rys. 9.18b.
Uwzględniając dodatkowo zerwy warunek Neumanna, dostajemy równanie
.
0
j
2
2
2
,
0
2
2
2
2
/
,
1
,
1
0
,
1
=
′
+
−
′
+
′
+
′
j
r
N
N
J
κ
a
h
J
J
J
(i)
Tak powstały układ równań rozwiązujemy ze względu na wartości węzłowe J'
i,j
.
Obliczanie rezystancji. Rezystancję można obliczyć jako R = P/I
2
, gdzie P jest mocą
czynną wydzielaną w obszarze pręta. Moc tę można obliczyć na dwa sposoby: albo
sumując elementarne moce wydzielane w obszarze przewodu, albo obliczając moc
wnikającą do przewodu przez jego brzeg. Ten drugi sposób jest łatwiejszy
w implementacji. Moc pozorna wnikająca do przewodu wyraża się wzorem
.
d
boczna
pow.
∫∫
⋅
×
−
=
∗
S
H
E
S
(j)
Po przekształceniach dochodzi się do zależności na impedancję wewnętrzną przewodu
o przekroju kołowym odniesioną do rezystancji dla prądu stałego:
,
d
j
1
2
DC
∫
∂
′
∂
′
=
=
′
∗
C
l
n
J
J
S
ωµγ
I
S
R
Z
(k)
która jest poprawna dla dowolnego przewodu o przekroju ograniczonym krzywą C i polu
tego przekroju równym S. W rozpatrywanym przypadku dostaniemy
,
d
1
d
j
2
2
j
d
2
j
0
0
2
2
2
∫
∫
∫
′
=
′
=
∂
′
∂
′
=
′
∗
−
∗
α
α
α
α
φ
J
α
φ
a
a
α
π
κ
J
π
κ
φ
a
n
J
J
π
κ
Z
(l)
gdzie skorzystano z warunku Neumanna (f). Okazuje się więc, że impedancja jest średnią
wartością zespolonej względnej gęstości prądu na powierzchni przewodu stykającą się
z powietrzem. Całkowanie wykonujemy metodą trapezów, dostając zależność
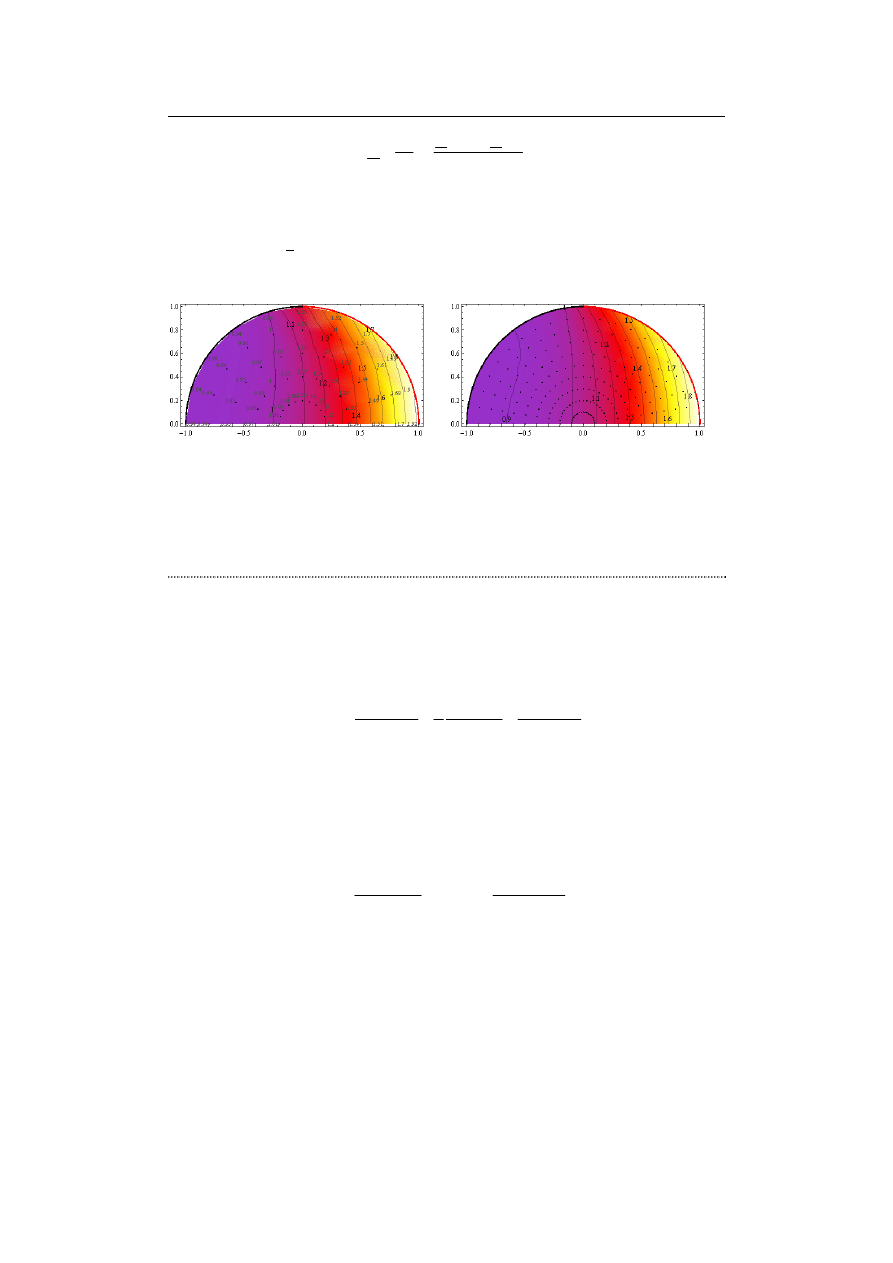
9. Metoda różnic skończonych (MRS)
22
.
2
1
1
1
,
1
,
1
∑
=
−
′
+
′
≈
′
N
j
j
M
j
M
J
J
N
Z
(m)
Wyniki obliczeń dla κ = 1 i różnych dyskretyzacji pokazano na rys. 9.19. Widoczny jest
efekt wypierania prądu w kierunku powietrza (zjawisko naskórkowości). Nierównomierna
gęstość prądu zwiększa straty mocy, a przez to i rezystancję. Istotnie, względna wartość
rezystancji
R' = ReZ' > 1, co oznacza, że rezystancja dla prądu zmiennego jest większa niż
rezystancja tego samego przewodu dla prądu stałego.
a)
b)
5 półokręgów × 10 sektorów, R' = 1,43
10 półokręgów × 20 sektorów, R' = 1,38
Rys. 9.19. Obraz pola w połowie przekroju poprzecznego przewodu dla κ = 1 dla zgrubnej (a) oraz
drobnej (b) dyskretyzacji; zaznaczono linie jednakowej względnej gęstości prądu (jego
modułu), położenie węzłów (w przypadku (a) – także wartości modułu względnej gęstości
prądu); kolor symbolizuje gęstość mocy czynnej (jasne kolory – duże wartości, ciemne
kolory – małe wartości); dla zgrubnej dyskretyzacji widoczne załamania i braki
w wypełnieniu kolorem
9.5.2. Schemat pięciopunktowy w przypadku osiowosymetrycznym
W przypadku zagadnień o symetrii osiowej stosuje się układ cylindryczny,
a laplasjan przyjmuje postać
2
2
2
2
2
)
,
(
)
,
(
1
)
,
(
z
z
r
Φ
r
z
r
Φ
r
r
z
r
Φ
Φ
∂
∂
+
∂
∂
+
∂
∂
=
∇
,
(9.31)
przy czym z założenia funkcja Φ nie zależy od współrzędnej kątowej φ. Obszar
działania pola jest wtedy torusopodobnym kształtem o stałym przekroju, a analizę
pola można ograniczyć właśnie do tego przekroju. Najlepsze wyniki uzyskuje się
dla przekroju prostokątnego lub dającego się rozłożyć na sumę prostokątów. Na
przekrój nakładamy siatkę węzłów analogiczną do rozpatrywanej w punkcie 9.4.1,
przy czym rolę
x przejmuje współrzędna r, a rolę y – współrzędna z (rys. 9.20):
J
z
z
h
I
r
r
h
z
r
min
max
min
max
,
−
=
−
=
,
(9.32a)
z
j
r
i
jh
z
z
ih
r
r
+
=
+
=
min
min
,
.
(9.32b)
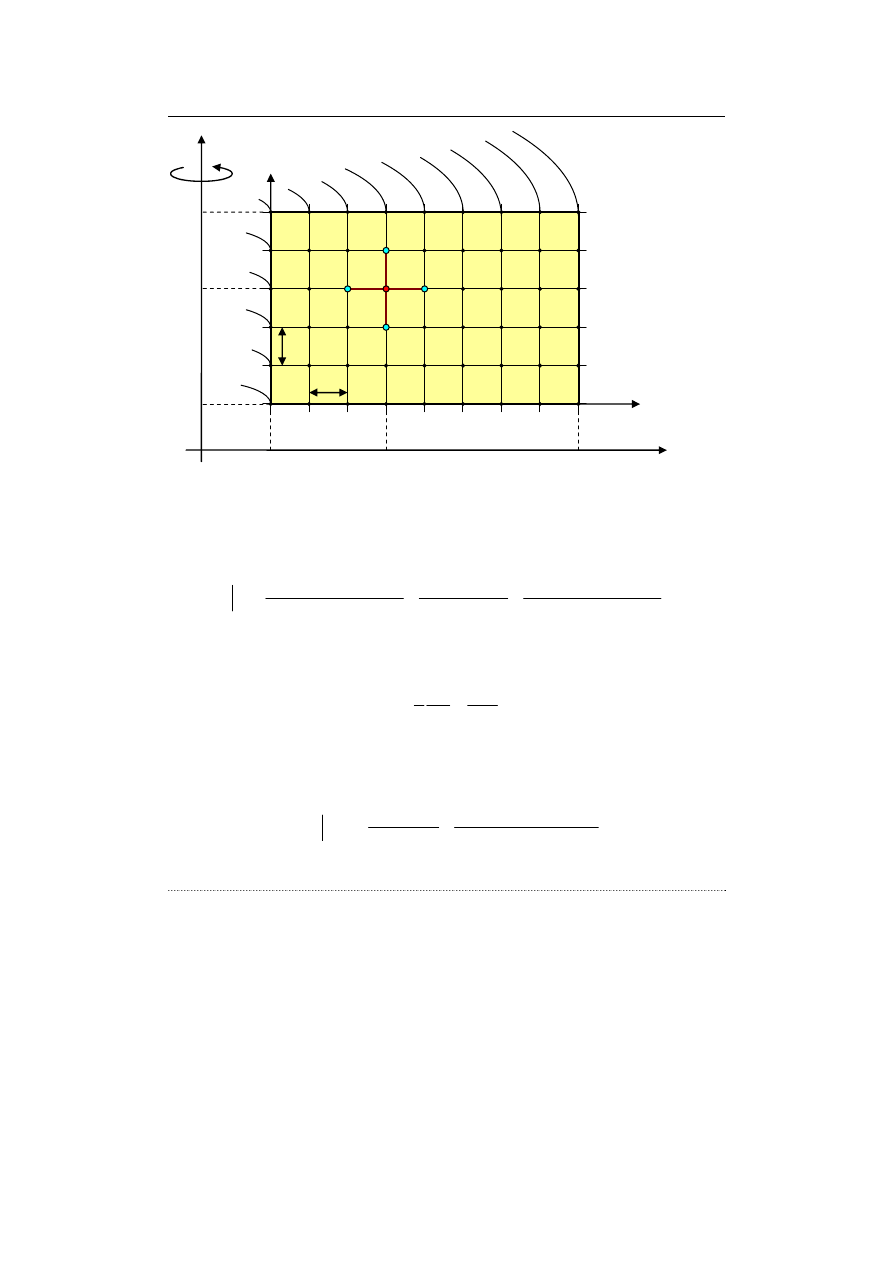
9.5. Inne typowe siatki węzłów
23
z
r
r
min
r
max
z
min
z
max
z
j
r
i
h
z
h
r
j = 0
j = J
i = I
i = 0
j
i
i
j
(i, j)
Rys. 9.20. Siatka dwuwymiarowa w układzie osiowosymetrycznym nałożona na przekrój
Wtedy dla węzła (i, j) laplasjan przyjmuje postać
2
1
,
,
1
,
,
1
,
1
2
,
1
,
,
1
,
2
2
2
2
z
j
i
j
i
j
i
i
r
j
i
j
i
r
j
i
j
i
j
i
j
i
h
Φ
Φ
Φ
r
h
Φ
Φ
h
Φ
Φ
Φ
Φ
+
−
−
+
+
−
+
−
+
−
+
+
−
≈
∇
. (9.33)
Jeżeli r
min
= 0, to wyrażenie r
–1
∂Φ/∂r zawiera dzielenie przez 0. Jego granica przy
r→ 0 wynosi
2
2
0
1
lim
r
Φ
r
Φ
r
r
∂
∂
=
∂
∂
→
.
(9.34)
Co więcej, uwzględnienie symetrii obrotowej prowadzi do wniosku, że wartości
funkcji pola na linii i = –1 są takie jak na linii i = 1. Tak więc w przypadku r
min
= 0
laplasjan dla i = 0 przyjmuje postać
2
1
,
0
,
0
1
,
0
2
,
0
,
1
,
0
2
2
4
z
j
j
j
r
j
j
j
h
Φ
Φ
Φ
h
Φ
Φ
Φ
+
−
+
−
+
−
≈
∇
.
(9.35)
Przykład 9.7. Walec dielektryczny o promieniu a i wysokości 2h oraz przenikalności
elektrycznej ε naładowano ładunkiem o stałej gęstości objętościowej ρ = ρ
0
(rys. 9.21a).
Zakładając, że potencjał powierzchni walca wynosi 0, obliczyć rozkład potencjału
wewnątrz walca. W obliczeniach przyjąć: ρ
0
/ε = 100 V/cm
2
, a = 1 cm, h = 1 cm.
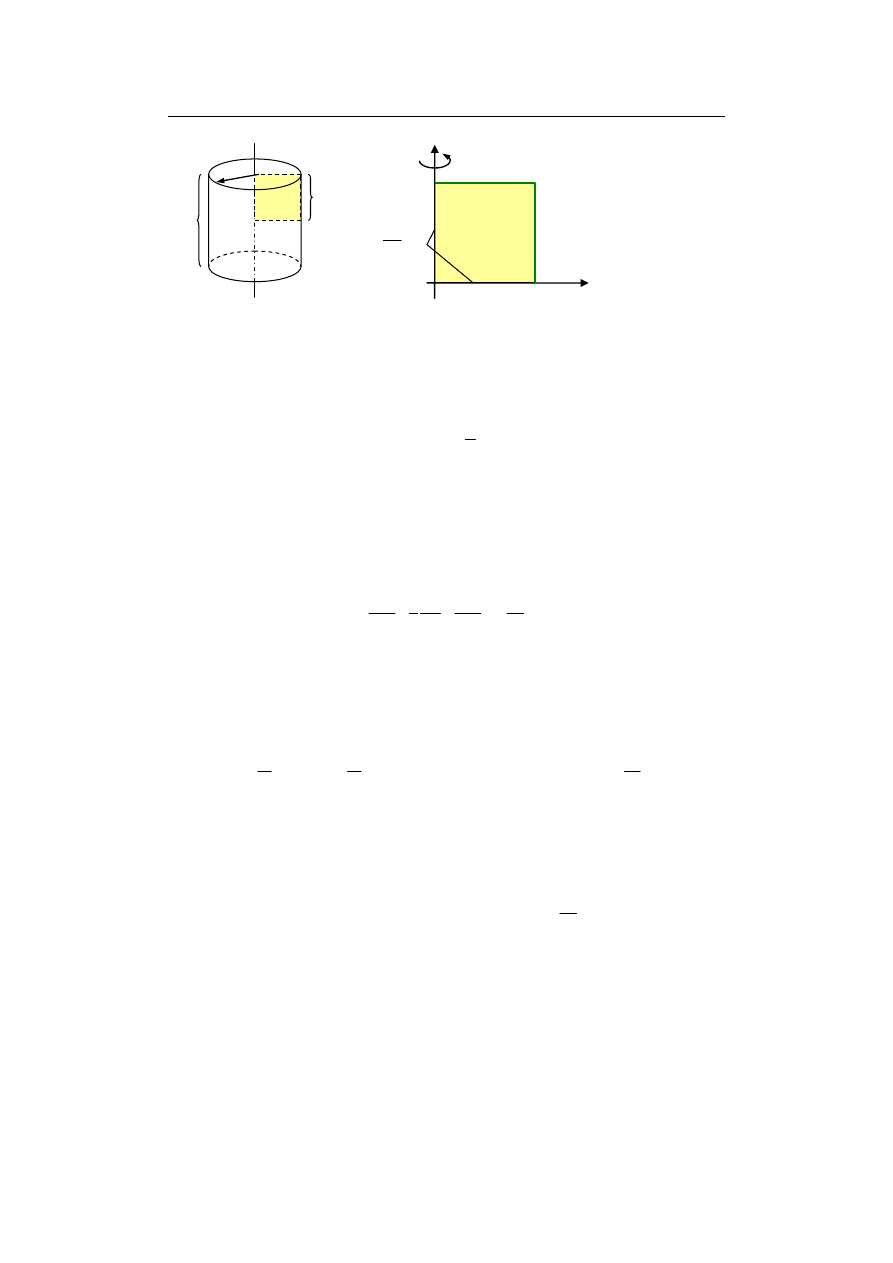
9. Metoda różnic skończonych (MRS)
24
a)
b)
2h
h
a
ρ
0
ε
z
r
a
h
V = 0
V = 0
∇
2
V = 0
0
0
=
∂
∂
n
V
Rys. 9.21. Naładowany walec: a) szkic sytuacyjny, b) obszar poddany analizie
Z równań pola elektrostatycznego
V
,
ε
,
ρ
−∇
=
=
=
⋅
∇
E
E
D
D
(a)
dostajemy równanie Laplace’a dla potencjału elektrycznego:
.
2
ε
ρ
V
−
=
∇
(b)
Z uwagi na geometrię przyjmujemy układ współrzędnych cylindrycznych z osią
Oz
pokrywająca się z osią symetrii walca. Symetria obszaru i warunków brzegowych wskazuje
też, że potencjał
V nie zależy od współrzędnej kątowej φ, więc analizę można ograniczyć
do przekroju osiowego φ = const. Ponadto dolna połowa walca jest odbiciem lustrzanym
górnej, więc ostatecznie analizowany obszar można ograniczyć do górnej połowy przekroju
osiowego walca (rys. 9.21b).
W rozpatrywanej sytuacji równanie Poissona (b) upraszcza się do postaci
ε
ρ
z
V
r
V
r
r
V
0
2
2
2
2
1
−
=
∂
∂
+
∂
∂
+
∂
∂
(c)
z następującymi warunkami brzegowymi:
-
V = 0 na powierzchni bocznej walca (r = a) oraz na górnej podstawie (z = h),
-
∂V/∂n = 0 na osi walca (r = 0) oraz w płaszczyźnie symetrii z = 0.
Na analizowany obszar nakładamy siatkę węzłów rozmieszczonych w I + 1
kolumnach oraz J + 1 wierszach. Na podstawie (9.33) równanie (c) w wersji różnicowej dla
węzła (i, j) przyjmuje postać:
,
)
2
2
(
2
1
1
2
1
1
2
0
,
2
1
,
2
1
,
2
,
1
,
1
r
j
i
j
i
j
i
j
i
j
i
h
ε
ρ
V
ζ
V
ζ
V
ζ
V
i
V
i
−
=
+
−
+
+
+
+
−
+
−
+
−
(d)
gdzie ζ = h
r
/h
z
. Dla węzłów brzegowych należy je zmodyfikować:
-
jeżeli i = I (czyli r = a) lub j = J (czyli z = h), wprowadzamy zerowy warunek Dirichleta:
,
0
,
=
j
i
V
(e)
-
jeżeli i = 0 (czyli r = 0), należy skorzystać z równania wynikającego z (9.35)
,
)
2
4
(
4
2
0
,
0
2
1
,
0
2
1
,
0
2
,
1
r
j
j
j
j
h
ε
ρ
V
ζ
V
ζ
V
ζ
V
−
=
+
−
+
+
+
−
(f)
-
jeżeli j = 0 (czyli z = 0), zamiast V
i,j–1
należy wziąć V
i,1
(dotyczy równań (d) jak i (f)).
Wyniki obliczeń dla wybranych dyskretyzacji przedstawiono na rys. 9.22.
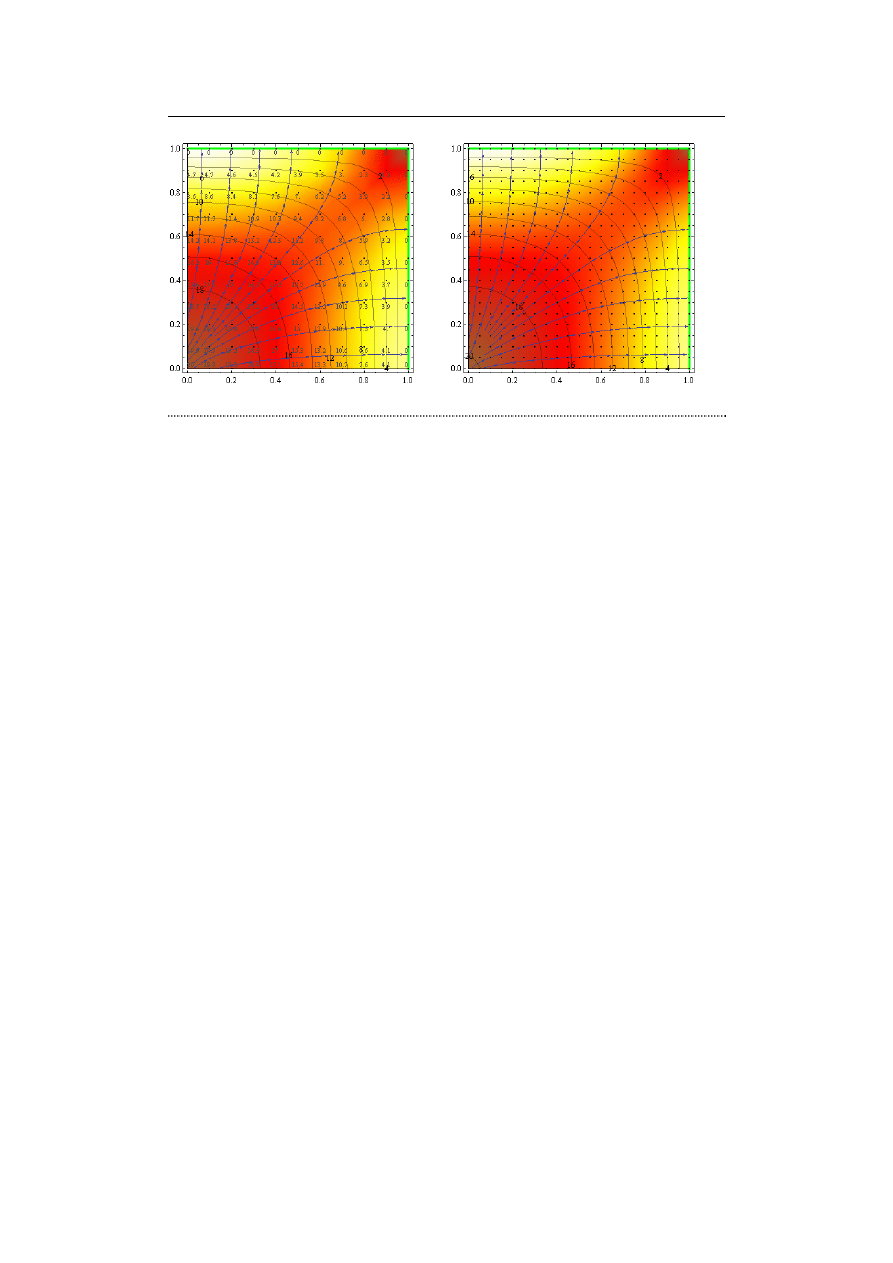
9.6. Podsumowanie
25
a)
b)
Rys. 9.22. Wyniki obliczeń: a) podział 10×10 (121 węzłów), b) podział 21×21 (441 węzłów)
9.6. Podsumowanie
9.6.1. Ogólna idea metody różnic skończonych
Metoda różnic skończonych rozwiązywania równań różniczkowych
zwyczajnych i cząstkowych polega na sprowadzeniu tego równania do postaci
różnicowej. W tym celu wszystkie pochodne zastępuje się odpowiednimi ilorazami
różnicowymi. Następnie na obszar działania pola nakłada się siatkę węzłów,
w których poszukuje się wartości funkcji pola. Występuje zatem tyle
niewiadomych, ile jest węzłów. Dla każdego węzła układa się równanie różnicowe
wynikające z oryginalnego równania. Dla węzłów brzegowych uwzględnia się
ponadto warunki brzegowe. W efekcie powstaje układ liniowych równań
algebraicznych, w którym niewiadomymi są wartości funkcji pola w węzłach
siatki. Po rozwiązaniu układu równań dostajemy przybliżone rozwiązanie. Należy
podkreślić, że macierz układu równań jest symetryczna, pasmowa, a przede
wszystkim rzadka, co pozwala na stosowanie specyficznych, szybkich metod
rozwiązywania takich układów równań, w szczególności metody iteracyjnej.
9.6.2. Zalety i wady metody
Najważniejsze zalety metody różnic skończonych to:
•
teoretycznie nadaje się do rozwiązania dowolnego rodzaju równania
różniczkowego (zwyczajnego, cząstkowego, liniowego, nieliniowego),
•
pozwala na uwzględnianie niejednorodności materiałowych,
•
jest łatwa pojęciowo i nieskomplikowana do zaimplementowania na
komputerze,
•
generuje układ równań o rzadkiej macierzy głównej, co umożliwia stosowanie
szybkich iteracyjnych metod rozwiązywania takiego układu.
9. Metoda różnic skończonych (MRS)
26
Podstawowymi wadami są:
•
trudności w uwzględnieniu geometrii w przypadku nieregularnych kształtów,
•
dla zbyt grubej siatki może prowadzić do dużych błędów (zob. przykład 9.4),
a zbyt drobna siatka prowadzi do ogromnej liczby węzłów i niewiadomych,
•
istnieje co prawda możliwość lokalnego zagęszczenia siatki węzłów, ale
komplikuje to znacznie układanie samych równań,
•
raczej nie nadaje się do rozwiązywania równań pola w obszarach
nieograniczonych, gdyż wymaga nałożenia na obszar siatki skończonej liczby
węzłów,
•
jako metoda numeryczna, nie pozwala na uzyskanie zależności ogólnych.
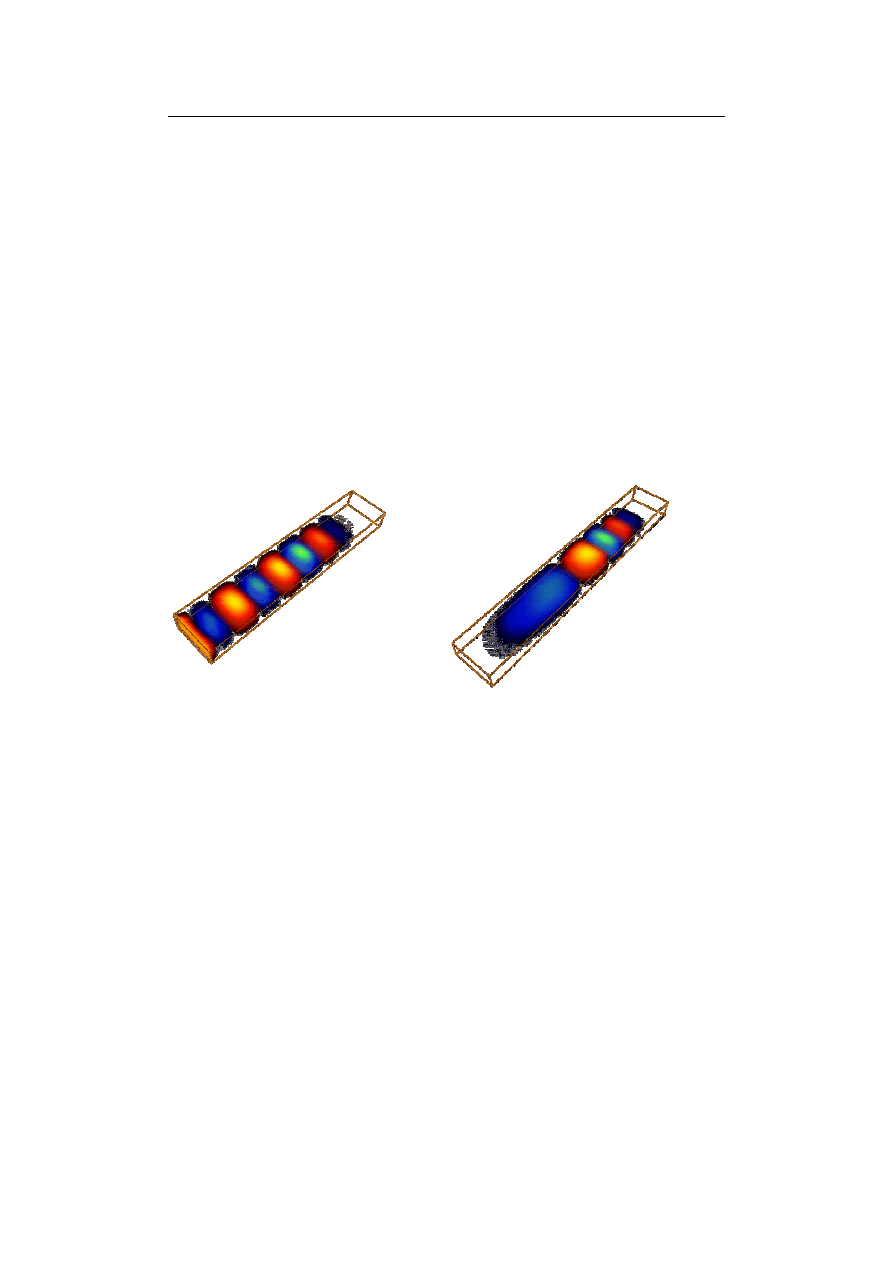
Zakres zastosowań jest dość spory: zagadnienia pola elektromagnetycznego,
pola temperatury, mechaniki, hydromechaniki. Jej odmiana FDTD (Finite-
-Difference-Time-Domain – MRS w dziedzinie czasu) stosowana jest do m.in.
rozwiązywania równań falowych, a w szczególności rozchodzenia się fal
elektromagnetycznych, np. generowanych przez telefony komórkowe lub
propagujących w falowodach (rys. 9.23).
a)
b)
Rys. 9.23. Obrazy fali TE10 elektromagnetycznej (a) oraz impulsu elektromagnetycznego (b) rozchodzącego się
w falowodzie (za http://www.cemtach.com/reference/software/toyFDTD/ToyFDTD1)
Wyszukiwarka
Podobne podstrony:
Metoda Różnic Skończonych MRS przykład
MES el prętowego, A T e o r i a S p r ę ż y s t o ś c i, T E M A T Y B L O K O W E, Metoda elemen
Zagadnienia z MES (1), UCZELNIE, Mechanika i Budowa Maszyn UWM OLSZTYN [MECHANICY], Semestr 4, Metod
Metoda różnic skończonych
SPRAWOZDANIE 6 Metoda elementów skończonych
Metoda Różnic Skończonych
ćw 18 Metoda Różnic Skończonych
Metoda różnic skończonych
Metoda elementow skonczonych(2)
Metoda elementów skończonych sprawko
Wyznaczenie ugięcia?lki i momentów metodą różnic skończonych
Metoda różnic skończonych
Konderla Metoda elementów skończonych Teoria i zastosowania
Metoda różnic skończonych
Zbiór zadań z mechaniki budowli Metoda przemieszczeń i metoda elementów skończonych Tadeusz Chmiel
Metoda róŜnic skończonych
więcej podobnych podstron