9. Optyka

9.3. Interferencja w cienkich warstwach.

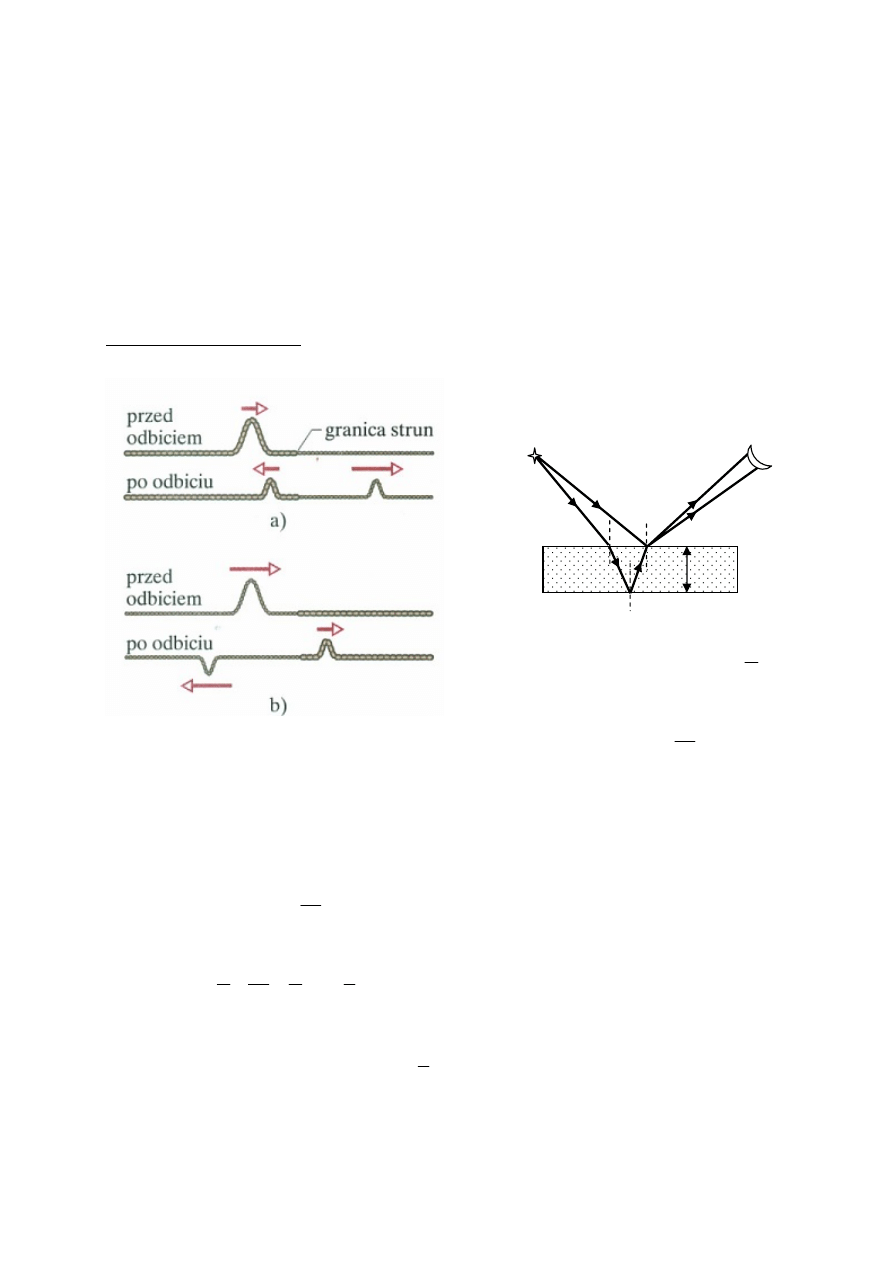
Światło odbijając się od ośrodka optycznie gęstszego ( o większym n) zmienia fazę.

Natomiast gdy odbicie zachodzi od powierzchni ośrodka optycznie rzadszego, fala odbija się

bez zmiany fazy.

Wyobrażenie mechaniczne

n

d

P

S

Długość fali w warstwie

n

n

λ

λ

=

2

2

n

m

d

n

λ

λ

+

=

Różnica dróg optycznych promieni: załamanego i

odbitego

d

2

=

Δ

Dla zmiany fazy

2

n

λ

π

ϕ

⇒

=

⎟

⎠

⎞

⎜

⎝

⎛ +

=

+

=

2

1

2

2

m

n

n

n

m

d

λ

λ

λ

Czyli

⎟

⎠

⎞

⎜

⎝

⎛ +

=

2

1

2

m

dn

λ

Maksimum interferencyjne:

Minimum interferencyjne: 2dn = m

λ

gdzie

m = 0, 1, 2, … - rząd widma

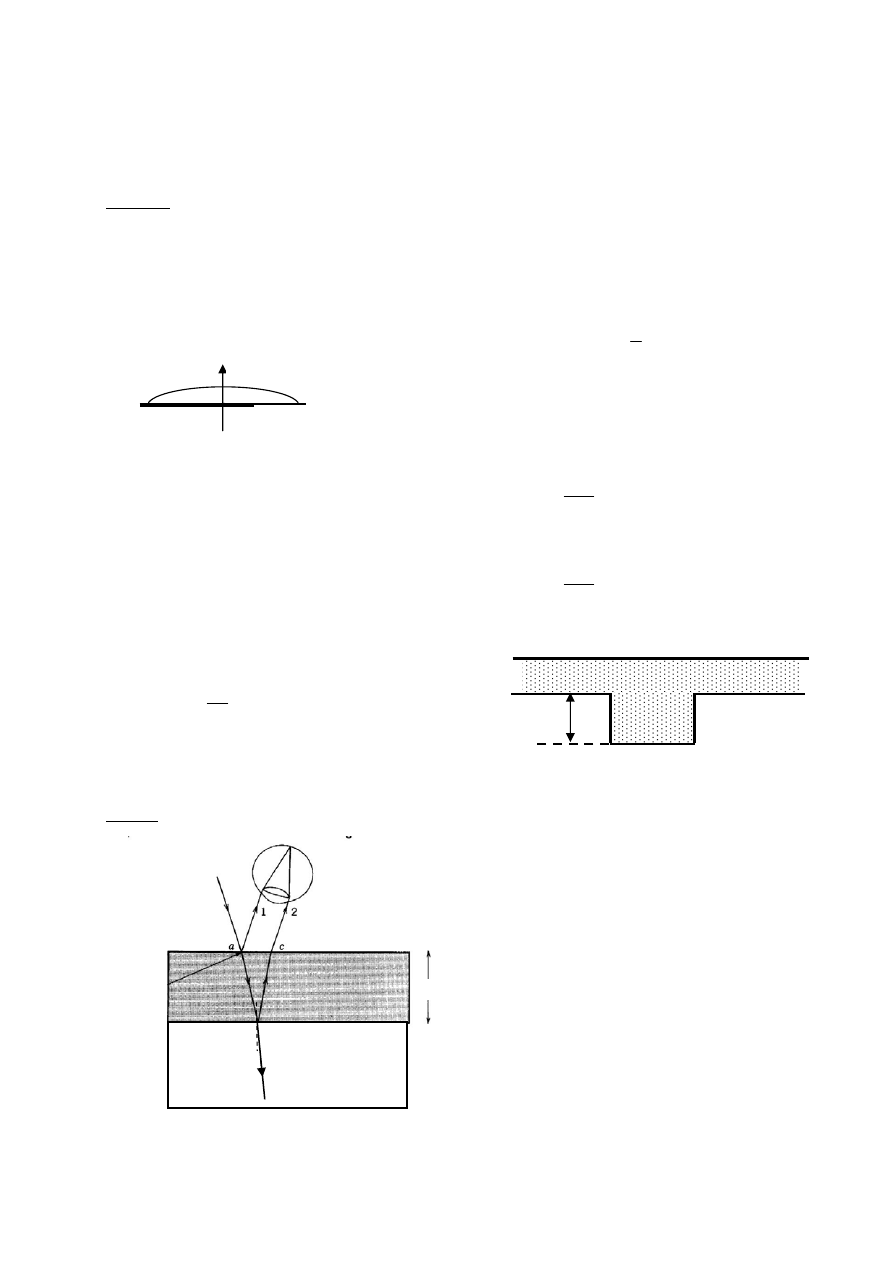
Ponieważ z punktu S wychodzą fale spójne, to dla oka maksimum/minimum interferencyjne

jest obrazem punktu P.

Przykład:

1. Obliczyć długość fali (kolor) plamy oleju (lub bańki mydlanej), o grubości 350 nm

j światłem białym padającym prostopadle do jej powierzchni.

λ

światła białego

≈

400

÷

oświetlone

700 nm. n = 1,33

2dn = m

λ

⎟

⎠

⎞

⎛

1

⎜

⎝

+

=

2

2

m

dn

λ

max.

λ

= 4 dn

⇒

λ

= 1862 nm

m = 0

Kolor czerwony

Plama oleju

m

=

1

min.

m

=

1

max.

λ

=2dn

⇒

λ

= 931 nm

nm

621

3

=

⇒

=

λ

λ

(cz

dn

4

erwony)

m

m

=

2

max.

=

2

min.

λ

= dn

⇒

λ

= 465 nm

nm

372

5

=

⇒

=

λ

λ

(po

dn

4

za

zakresem widzialnym)

2. Jaka jest głębokość rowka w płycie CD ?

n

d

m

4

0

λ

=

⇒

=

max

d

n = 1,33

λ

≈

70

⇒ d = 132 nm = 0,13 μm

0 nm

Filtry

Promień 1 odbija się od

powierzchni filtra ze zmianą fazy,

2.

jało

interferując z promieniem

Jaka ma być grubość filtra, aby

szkło pokryte filtrem nie odbi

światła ?

n

1

= 1

filtr

zmiana fazy

n

2

= 1,4

szkło

powietrze

d

= 98,2nm

n

3

= 1,5

Minimum interferencyjne dla promienia odbitego od dolnej powierzchni filtra:

d = (nieparzysta liczba)

λ/2:

2

⎟

⎠

⎞

⎜

⎝

⎛ +

λ

2

1

m

=

⇒

=

2

0

dn

m

nm

n

d

2

,

98

4

,

1

4

550

4

=

⋅

=

=

λ

Inne zastosowania:

- pomiary grubości cienkich warstw i powłok,

tyzujące.

.4. Dyfrakcja na 1 szczelinie i na 2 szczelinach.

Dyfrakcja Fresnela

- filtry monochroma

9

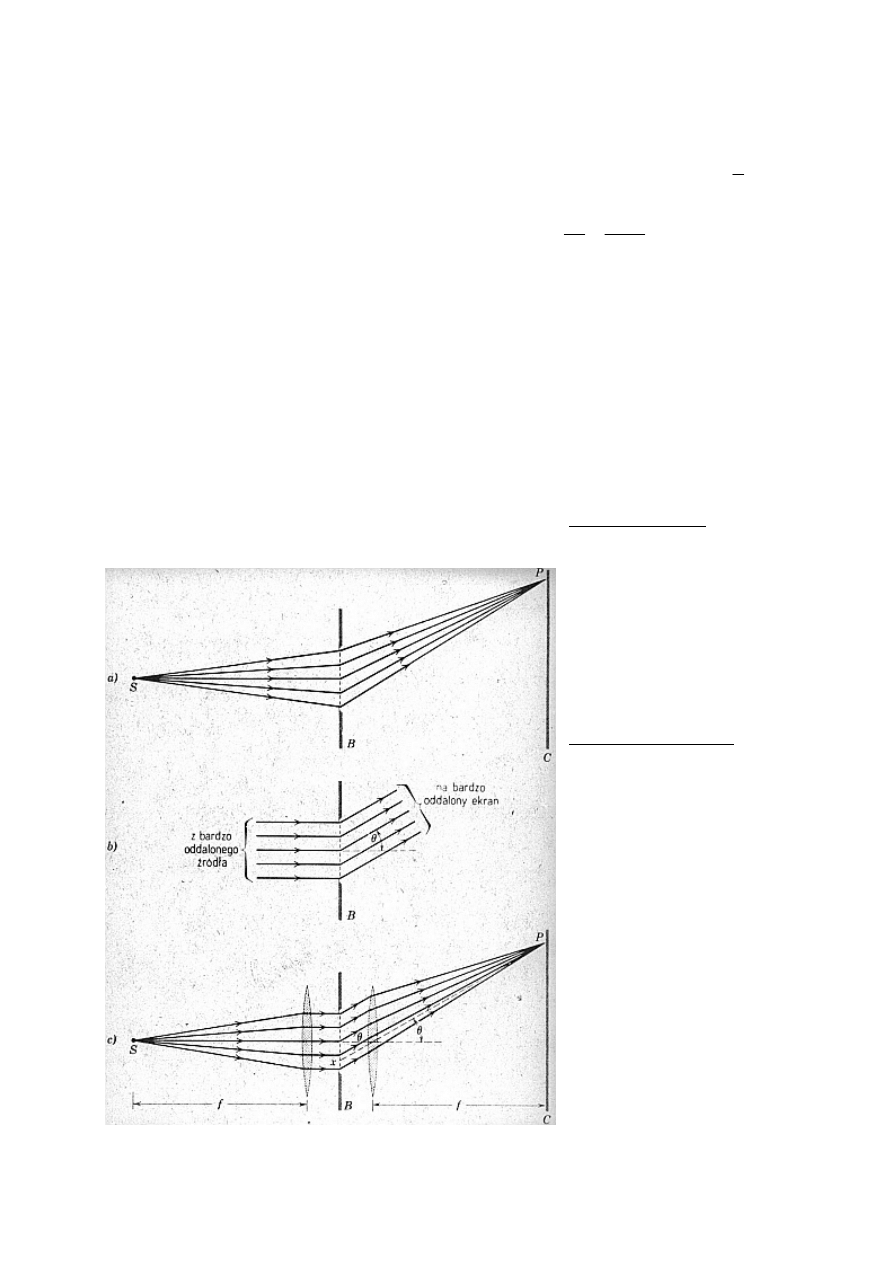
Ekran jest w skończonej

, czoła

łe.

odległości od otworu

fal padających na otwór i

ugiętych nie są płaskie,

promienie nie są równoleg

Dyfrakcja Farunhofera

Ekran w dużej odległości od

aunchofera przy

y

łe.

szczeliny, czoła fal

padających i ugiętych są

płaskie, a promienie

równoległe.

Praktyczna realizacja

dyfrakcji Fr

pomocy soczewek, prz

niewielkiej odległości ekranu

od szczeliny uginającej.

Promienie padające i ugięte

na szczelinie są równoleg

akcji Fresnela.

Dyfrakcja Fraunchofera jest granicznym przypadkiem dyfr

2

sin

1

λ

2

θ

=

⋅

a

λ

θ

=

⋅sin

a

Dla a =

λ

⇒

θ

= 90

0

1-sze minimum

la

pojedyn

szczeliny:

⋅

sin

θ

…

D

czej

warunek

na

minimum

a

= m

λ

m = 1, 2,

warunek na maksimum

(

)

2

1

2

sin

λ

θ

+

=

⋅

m

a

m = 1, 2, …

Dzielimy szczelinę na N jednakowych stref, z których każd

nej fali o

amplitudzie

Δ

E

θ

. Dodając poszczególne wskazy otrzymamy amplitudę fali wypadkowej E .

Natężenie światła

-

dodawanie zaburzeń falowych o stałej amplitudzie.

kierunki kolejnych wskazów tworzą

ze sobą kąt

ΔΦ

, amplituda

w

lituda

E

θ

jest równa zero. Różnica faz

między pierwszym i ostatnim

a

a jest źródłem elementar

θ

- dla centralnego maksimum,

różnica faz między sąsiednimi

falami jest równa zero.

- dla punktu leżącego blisko osi,

wypadkowa E

θ

jest mniejsza, niż

poprzednim przypadku.

- pierwsze minimum, amp

wskazem wynosi

Φ

= 2

π

.

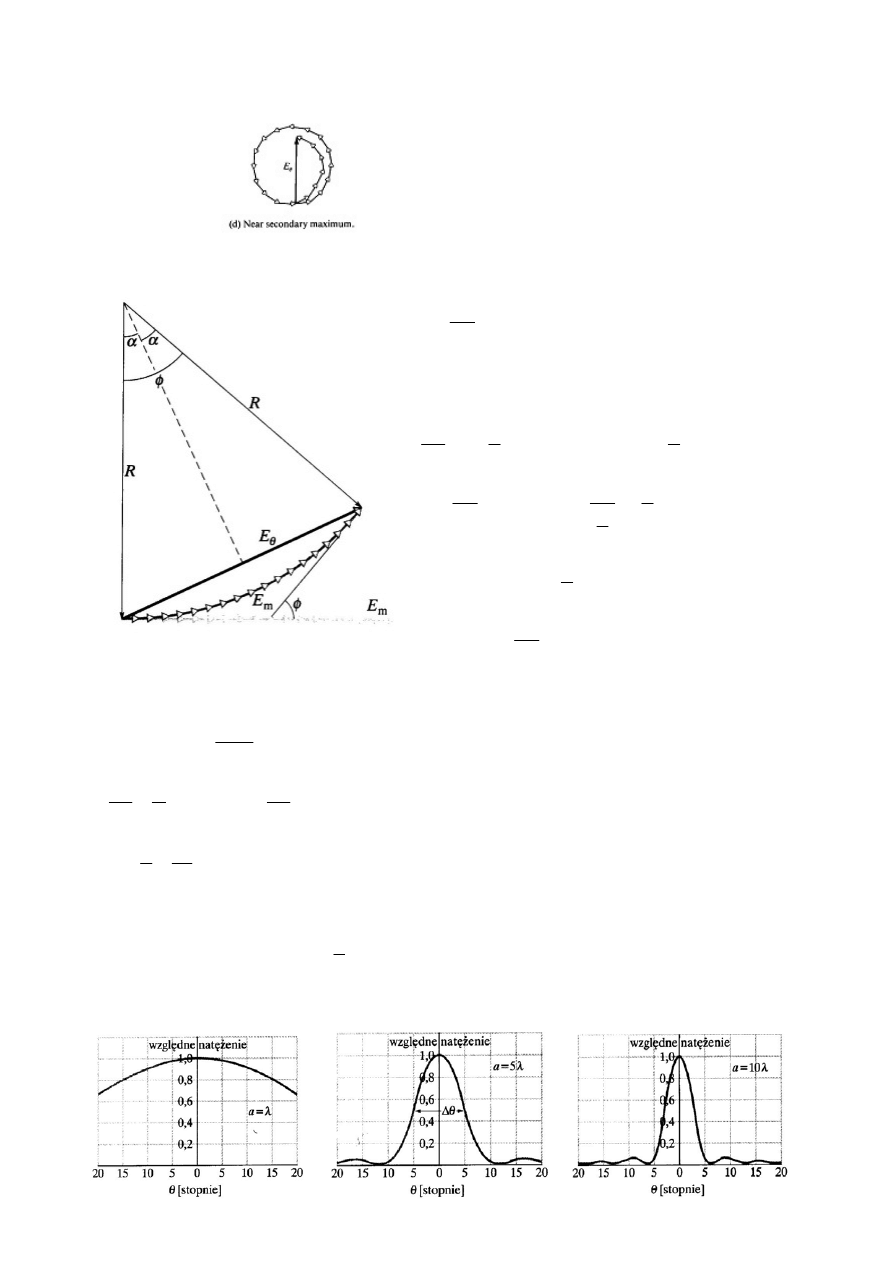
zwiększaniu kąta

θ

, kąt

ΔΦ

ększa i krz

- przy dalszym

również się zwi

ywa diagramu się

Geom

e

zwija, zmniejszając E

θ

.

nia światła.

etryczna konstrukcja obliczania natęż

R

E

m

=

φ

- różnica fazy między skrajnymi

ami biegnącymi z góry i dołu szczeliny.

wskazami łuku, czyli różnica fazy między

promieni

2

sin

2

2

n

θ

⋅

=

⇒

R

E

si

2

φ

φ

φ

=

R

E

2

sin

φ

φ

φ

θ

m

m

E

E

E

R

=

⇒

=

2

Podstawiając

2

φ

α

=

otrzym emy

uj

α

α

θ

sin

m

E

E

=

Natężenie I

θ

∼

2

θ

E

2

sin

⎟

⎠

⎞

⎜

⎝

⎛

=

α

α

θ

m

I

I

więc

3

2

1

Δ

⋅

=

⇒

=

Δ

θ

λ

π

φ

λ

π

φ

sin

2

a

2

θ

λ

π

φ

α

2

=

sin

a

=

I

θ

→

minimum dla

α

= m

⋅π

gdzie m = 1, 2, 3, …

I

θ

→

maksimum dla

π

α

⎟

⎠

⎞

⎜

⎝

⎛ +

=

2

1

m

Względne natężenie w obrazie dyfrakcyjnym dla różnych szerokości szczeliny.

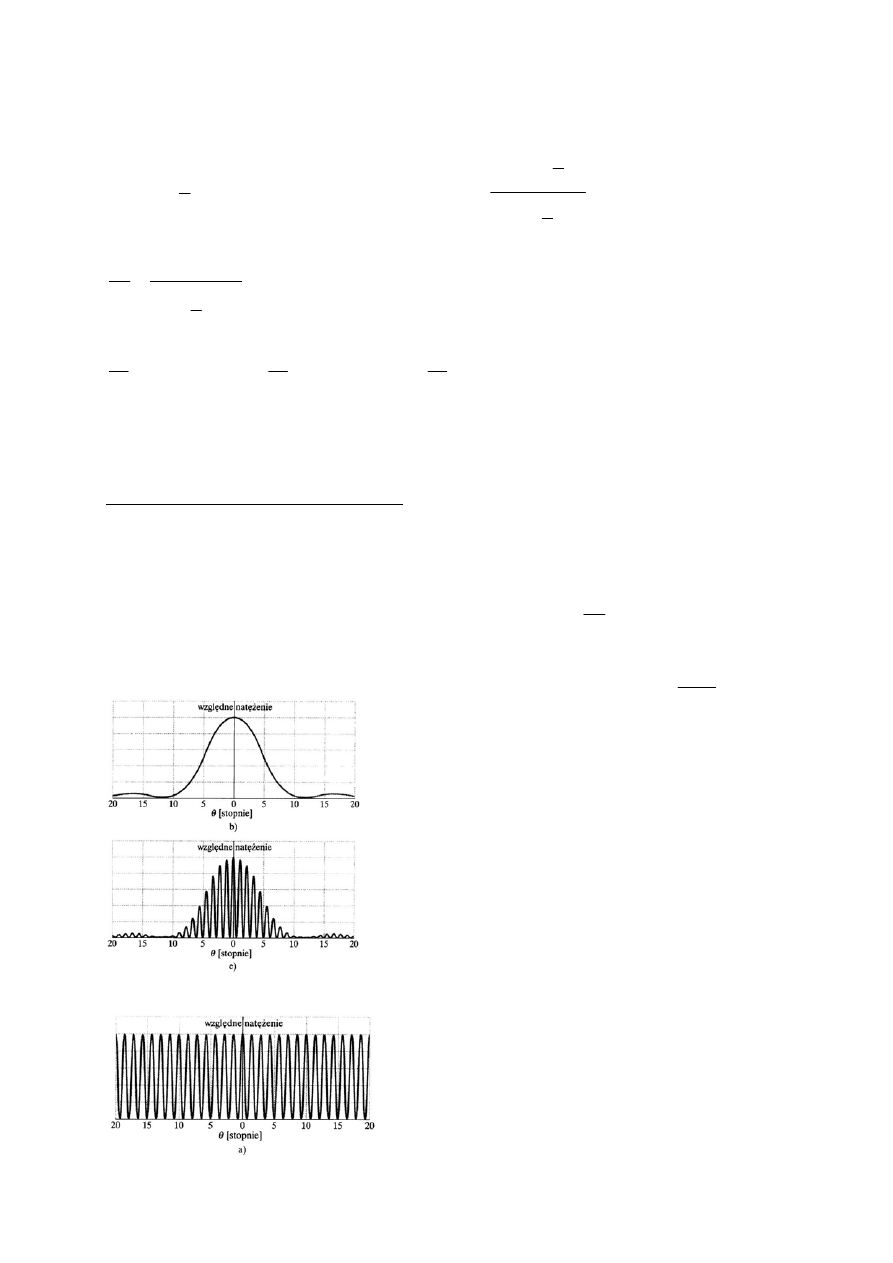
Obliczyć natężenia trzech kolejnych maksimów dla dyfrakcji Fraunhofera.

π

α

⎟

⎠

⎞

⎜

⎝

⎛ +

=

2

1

m

m = 1, 2, 3.

2

2

1

2

1

sin

⎥

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛ +

⎟

⎠

⎞

⎜

⎝

⎛ +

=

π

π

θ

m

m

I

I

m

2

2

2 ⎠

⎝

1

1

π

θ

⎟

⎞

⎜

⎛ +

=

m

I

I

m

045

,

0

1

=

I

I

θ

;

016

,

0

2

=

I

I

θ

;

083

,

0

3

=

I

I

θ

9.4. Dyfrakcja na 1 szc

Interferencja i dyfrakcja na 2 szczelinach

zelinie i na 2 szczelinach.

.

ąskie szczeliny) w wyniku dyfrakcji otrzymuje się

ści szczelin:

gdzie

Przy założeniu

λ

>> a (nieskończenie w

prążki o jednakowym natężeniu.

β

θ

2

cos

m

I

I

=

θ

λ

π

β

sin

d

=

Rzeczywiste szeroko

(

)

2

2

sin

cos

⎟

⎠

⎞

⎜

⎝

⎛

=

α

α

β

θ

m

I

I

Wypadkowy efekt:

Wykres natężenia dla dyfrakcji na pojedynczej
szczelinie o szerokości a.

Rozkład natężeń w obrazie interferencyjnym dwóch

j szerokości a.

Poprzedni wykres jest obwiednią wykresu dla 2

ykres natężeń w obrazie dwóch szczelin o

ieskończenie małej szerokości a <<

λ

.

szczelin o skończone

szczelin.

W
n

9.5. Siatka dyfrakcyjna.

Układ N równoległych szczelin o szerokości a <<

λ

λ

θ

m

d

=

⋅sin

interferencyjne

gdzie m = 0, 1, 2,… - maksima

Wykres natężenia w funkcji kąta

θ

dla:

a) dwóch szczelin – szerokie prążki,

b) sześciu szczelin – węższe prążki.

• Nie zmienia się odległość między głównymi

mi;

ównych nie zależą od N;

N

maksima

wtórne.

Kątowa szerokość połówkowa:

maksima

• Położenia maksimów gł
• Ze wzrostem liczby szczelin zwężają się maksima główne i powstają

λ

m

m

Nd

θ

θ

cos

=

Δ

dla m = 0

Nd

λ

θ

Δ

la

go maksimum głównego.

Zdolność rozdzielcza siatki d

=

0

• Różnica faz między falami wychodzącymi z sąsiednich szczelin równa jest zeru d

środkowe

yfrakcyjnej

λ

λ

Δ

=

R

gdzie:

λ

jest średnią długością fali 2 linii widmowych ledwie rozróżnialnych,

Δλ

jest różnicą długości tych fal.

Dyspersja kątowa

λ

θ

d

d

D

=

jest to odległość kątowa 2 linii widmowych

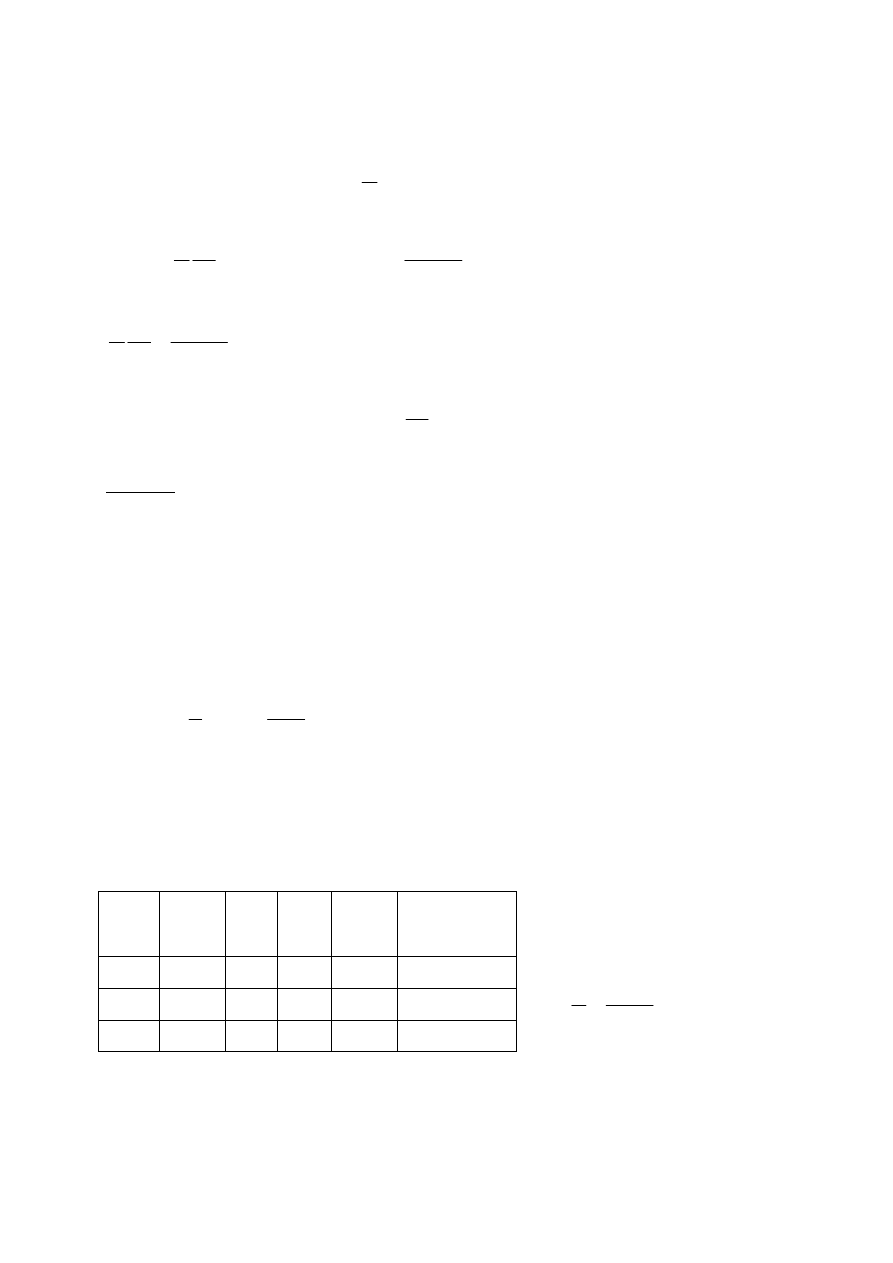
Skoro

λ

θ

m

d

=

⋅sin

S

niczkując:

tąd róż

λ

θ

θ

d

m

d

=

cos

d

λ
θ

θ

d

d

m

=

cos

oraz

d

m

λ

Nd

m

m

θ

θ

Δ

=

cos

więc stąd otrzymujemy:

Nd

d

d

d

⋅

d

m

=

θ

λ

θ

λ

A więc zdolność rozdzielcza

m

N

d

R

⋅

=

=

λ

λ

Przykład:

1. Siatka dyfrakcyjna o N = 8000 szczelin na 2,54 cm długości siatki (stąd stała siatki d =

3170 nm), jest oświetlana światłem białym.

θ = 0

0

wszystkie d

ści fal są nałożone na siebie

m = 1

λ

= 400 nm

d

⋅

sin

θ

= m

λ

dla m = 0

⇒

ługo

0

3

,

7

3170

400

arcsin

=

=

d

1

arcsin

=

λ

θ

dla

λ

= 700 nm

θ

1

= 12,8

0

2. Trzy różne siatki dyfrakcyjne oświetlono światłem o długości

λ

= 589 nm. Dla m = 1

jest:

20000

589

=

=

Δ

R

λ

λ

można rozróżnić

fale o

Δλ

= 0,0289 nm

Siatka N

d

θ

R

D

[

⋅10

-3

deg/nm]

[nm] [deg]

A 10

000

2540 13,4

0

10 000

0,232

B 20

000

2540 13,4

0

20 000

0,232

C 10

00

1370 25,5

0

10 000

0,464

0

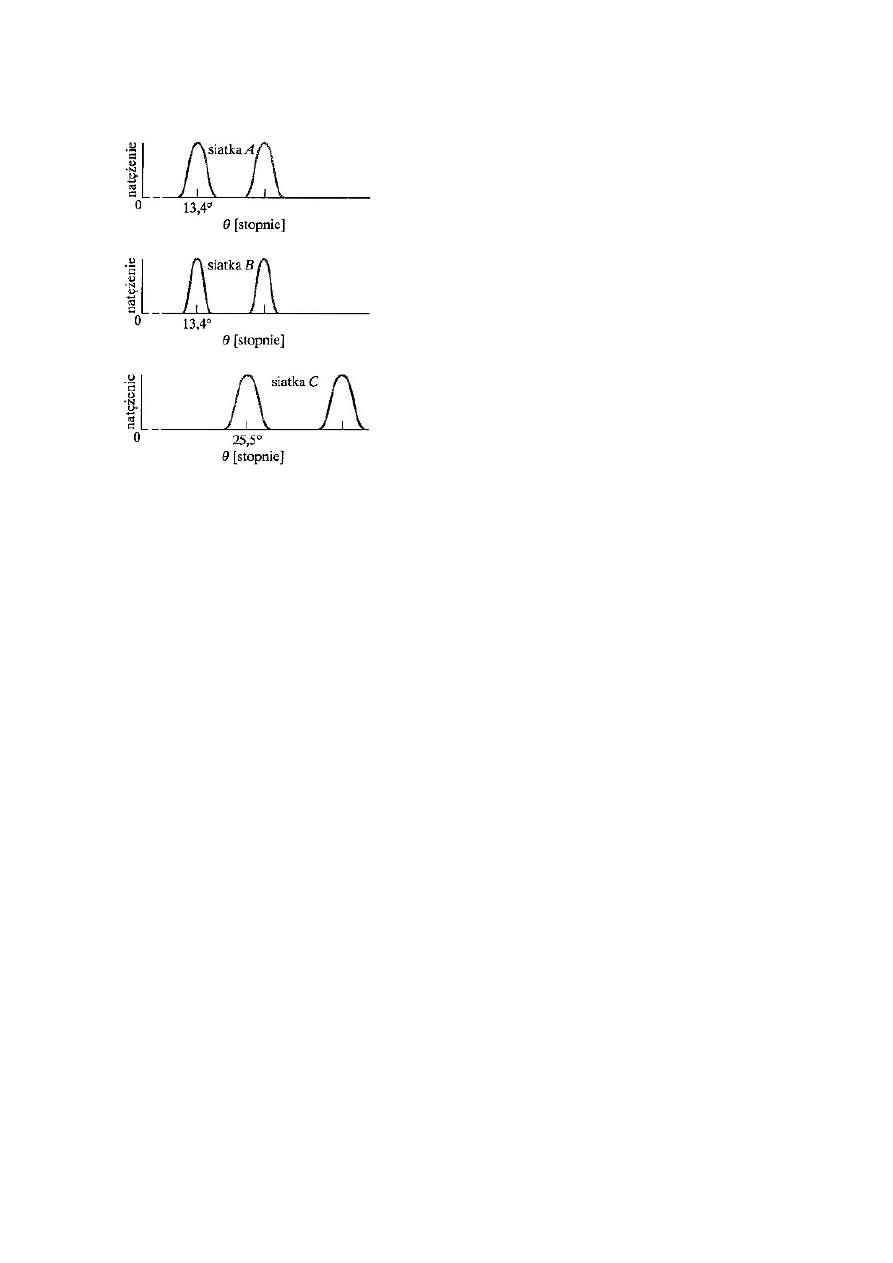
K

a la światła o dwóch długościach

fali

λ

1

pobli u linii o długości

λ

= 589 nm,

przec

go przez siatki opisane w tabeli.

Siatka B ma największą zdolność rozdzielczą, ma
węższe linie i przy jej pomocy można rozróżnić linie,
których długości fal są bardziej zbliżone do siebie,
natomiast

atka C ma największą dyspersję – daje większą

rzywe natężeni d

ż

i

λ

2

w

hodzące

si
odległość kątową między liniami.