ROZDZIAŁ III: Stany nieustalone 

 

 

Temat 8 : Stan ustalony i nieustalony w obwodach  

  elektrycznych.

 

 
 
 

Dotychczas  rozpatrywane  obwody  elektryczne  pr du  stałego  i  zmiennego 

rozpatrywane były w tzw. stanie ustalonym. Charakterystyczne dla tego stanu jest to, 

e  przy  okre lonych  warto ciach  napi   i  pr dów  ródłowych  odpowied   obwodu 

(pr dy  i  napi cia  na  elementach)  ma  „taki  sam  charakter”  jak  wymuszenie.  Je eli 

przykładowo  działały  w  obwodzie  wymuszenia  stałe,  to  przyjmowali my,  e  pr dy  i 

napi cia  we  wszystkich  gał ziach  i  napi cia  na  elementach  s   równie   stałe  i  nie 

zmieniaj  si  w czasie. 

Nale y  sobie  zdawa   spraw ,  e  obwód  elektryczny  zawieraj cy  cewki  i 

kondensatory,  tzn.  elementy  zdolne  do  gromadzenia  energii  elektrycznej,  po 

doł czeniu  do  ródła  energii  nie  mo e  natychmiast  znale   si   w  stanie  ustalonym. 

Elementy  te  przed  doł czeniem  do  ródła  mogły  znajdowa   si   w  stanie 

bezenergetycznym lub z elementami tymi mogła by  zwi zana pewna energia. 

Z przytoczonych rozwa a  wynika,  e zarówno w obwodzie, który zostaje 

doł czony  do  ródła  energii,  jak  i  w  obwodzie,  w  którym  nast puje  zmiana 

struktury, powstaje 

stan nieustalony

. 

Poj cie  stanu  ustalonego  i  stanu  nieustalonego  odnosz   si   nie  tylko  do 

obwodów, w których działaj  napi cia i pr dy  ródłowe stałe w czasie. Bezpo rednio 

po  doł czeniu  ródeł  stałych  lub  zmiennych  w  czasie  lub  po  dokonaniu  zmiany 

struktury  obwodu,  w  obwodzie  powstaje  stan  nieustalony  i  w  miar   upływu  czasu 

nast puje ustalanie si  przebiegów napi  i pr dów. 

Poniewa   w  stanach  nieustalonych  mog   pojawi   si   przepi cia  jak  i 

przet enia,  znajomo   zmienno ci  pr dów  i  napi   w  funkcji  czasu  ma  istotne 

znaczenie.  Z  reguły  napi cia  i  pr dy  w  stanie  nieustalonym  charakteryzuj   si   inn  

zmienno ci  w czasie ni  w stanie ustalonym. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

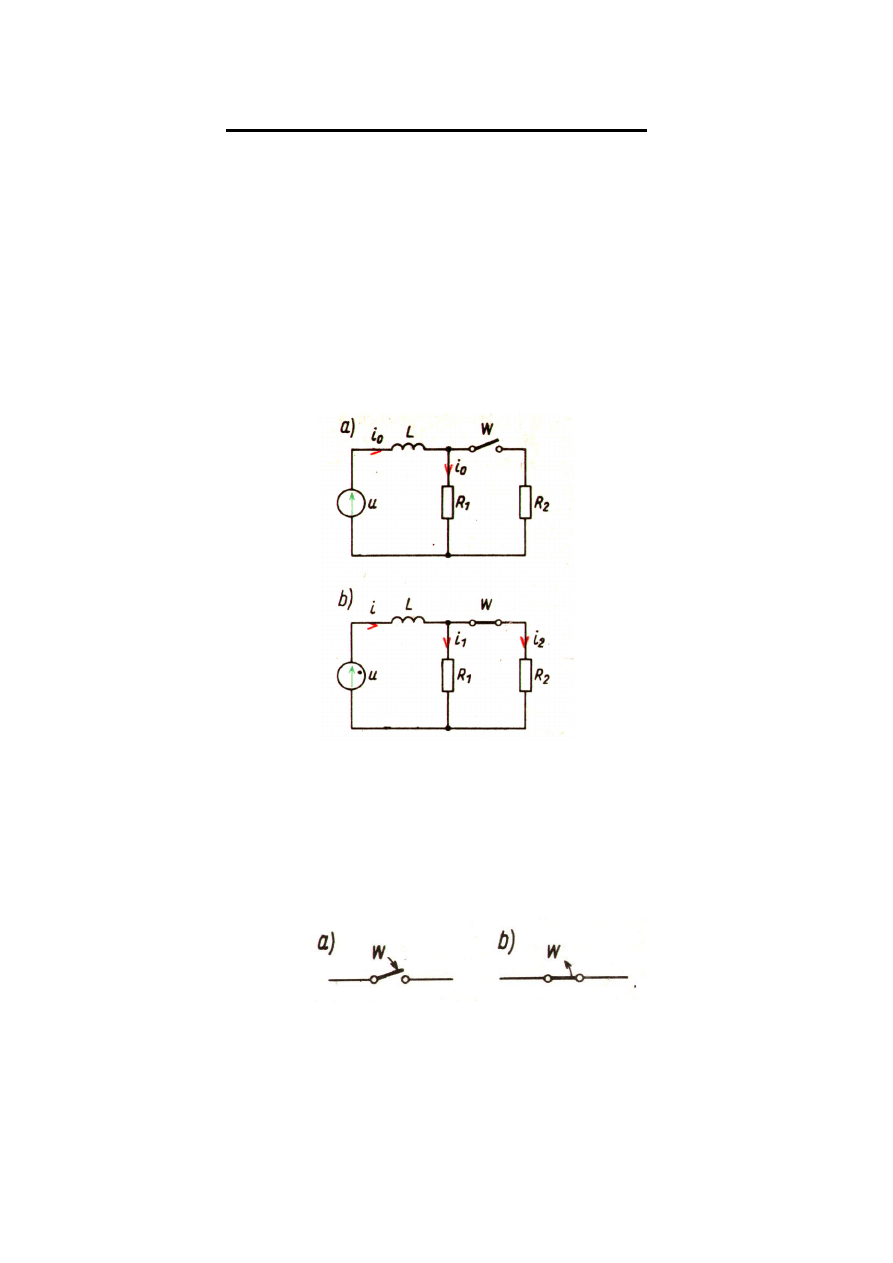
Temat 9 : Warunki pocz tkowe. Prawa komutacji.

 

 

Stanem pocz tkowym 

obwodu nazywamy stan obwodu w chwili, w 

której  rozpoczynamy  badanie  zjawisk  w  tym  obwodzie.  W  wi kszo ci 

przypadków przyjmuje si  jako stan pocz tkowy stan w chwili  t = 0. Stan 

pocz tkowy jest przewa nie stanem ustalonym, poprzedzaj cym czynno ci 

ł czeniowe  prowadz ce  do  powstania  stanu  nieustalonego.  Mo e  to  by  

stan,  w  którym  wszystkie  napi cia  i  pr dy    w  obwodzie  s   równe  zeru.  

Mówimy  wtedy,  e 

stan  pocz tkowy

 

jest

 

zerowy

,  albo,  e 

warunki 

pocz tkowe s  zerowe

. Je eli w chwili t = 0 na jakimkolwiek elemencie 

obwodu  wyst puje  napi cie  lub  płynie  pr d,  to 

warunki  pocz tkowe  s  

niezerowe

.  

 

Rys. 9.1. Powstawanie stanu nieustalonego: a) obwód tu  przed komutacj ; 

b) obwód tu  po komutacji. 

 

Zmiany  stanu  zachodz ce  w  obwodzie  w  pewnej  okre lonej  chwili 

nazywamy 

komutacj

.  Komutacja  mo e  by   wywołana  zarówno 

zamykaniem wył cznika, jak i jego otwieraniem.  

 

 

Rys.9.2. Oznaczanie czynno ci: a) zamykanie wył cznika w;  

b) otwieranie wył cznika w. 

 

Z  zamykaniem  i  otwieraniem  wył cznika  w  obwodzie  z 

indukcyjno ci   i  w  obwodzie  z  pojemno ci   zwi zane  s   dwa  prawa 

fizyczne zwane 

prawami komutacji

. 

Pierwsze prawo komutacji: 

Pr d  w  obwodzie  z  indukcyjno ci   nie  mo e  zmieni   si  

„skokiem” i w chwili tu  przed komutacj  ma tak  sam  warto  jak 

w chwili tu  po komutacji. 

Pierwsze prawo komutacji nazywane jest te  zasad  ci gło ci pr du i 

strumienia  magnetycznego  w  cewce.  Poniewa   strumie   magnetyczny 

skojarzony  z  cewk   wynosi  =L·i,  zatem  zasada  niezmienno ci  pr du  w 

chwili  komutacji  jest  równowa na  zasadzie  niezmienno ci  strumienia 

magnetycznego skojarzonego z cewk . 

 

Drugie prawo komutacji: 

Napi cie  na  kondensatorze  nie  mo e  si   zmieni   „skokiem”  i  w 

chwili tu  przed komutacj  ma tak  sam  warto  jak w chwili tu  po 

komutacji. 

Drugie prawo komutacji nazywane jest te  zasad  ci gło ci ładunku 

na  pojemno ci.  Poniewa   ładunek  zgromadzony  na  okładzinach 

kondensatora  wynosi  q=C·u,  zatem  zasada  niezmienno ci  napi cia  na 

kondensatorze  w  chwili  komutacji  jest  równowa na  zasadzie 

niezmienno ci ładunku zwi zanego z kondensatorem. 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 
 
 
 
 
 

 
 
 

Temat 10 : Stan nieustalony w układzie szeregowym R,L

 

 
 

Załó my,  e do gał zi, w której s  poł czone szeregowo elementy 

R, 

L doprowadzono w chwili t = 0 napi cie stałe. Odpowiada to zamkni ciu 

wył cznika 

W  w  chwili  t  =  0  w  obwodzie  jak  na  rys.  10.1.  Stan 

pocz tkowy  obwodu  jest  zerowy,  tzn.  w  chwili 

t  =  0  z  elementem 

indukcyjnym 

L nie jest zwi zana  adna energia. 

 

 

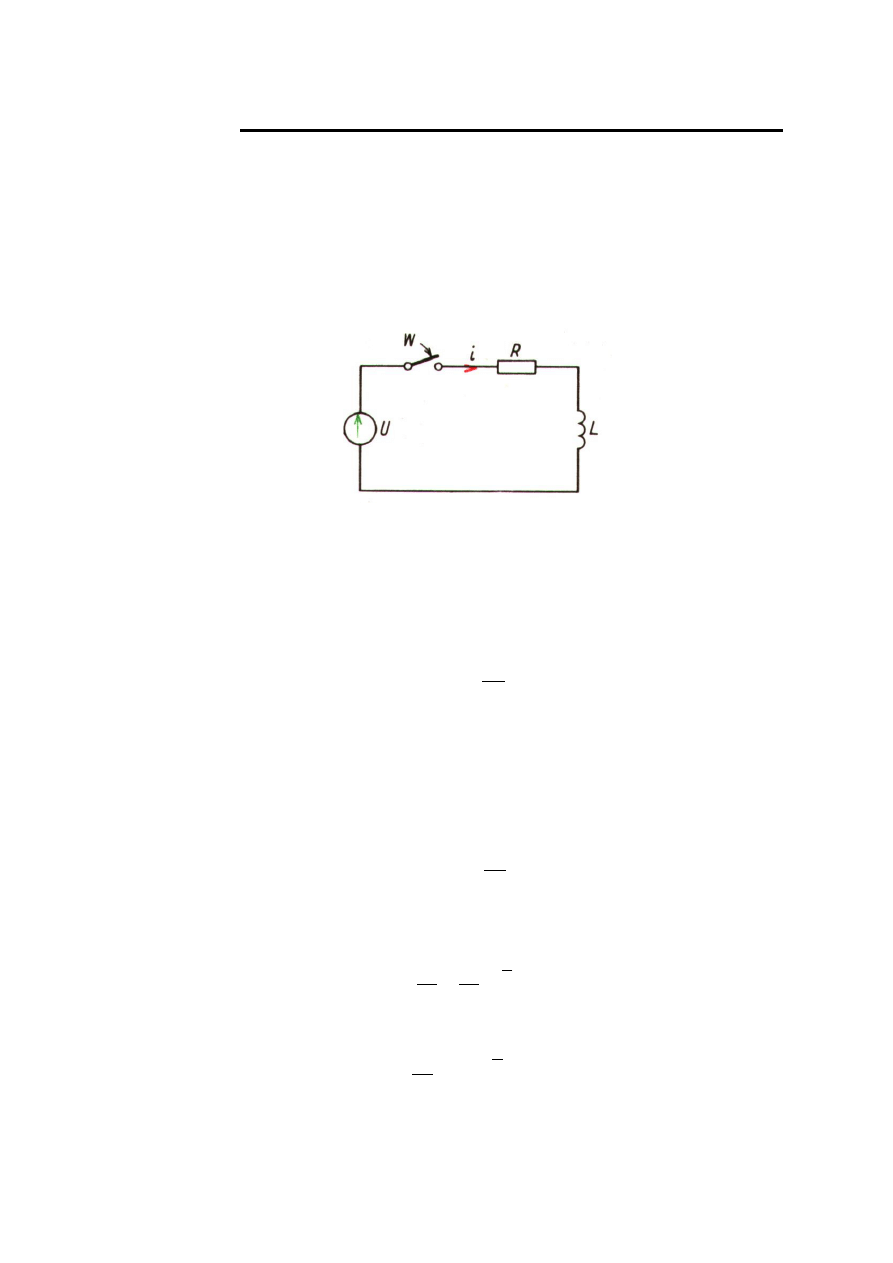
Rys. 10.1. Dwójnik szeregowy R,L wł czony na napi cie stałe. 

 

 

Po zamkni ciu wył cznika 

W w obwodzie powstaje stan nieustalony. 

Wyznaczony  przebieg  pr du 

i  w  funkcji  czasu  zmienia  si   od  zera  do 

warto ci ustalonej 

R

U

i

u

=

 

 

gdy  w obwodzie pr du stałego w stanie ustalonym napi cie na elemencie 

indukcyjnym jest równe zeru. 

Zgodnie z drugim prawem Kirchhoffa w obwodzie z powy szego rysunku 

bilans napi  ma posta : 

dt

di

L

Ri

U

+

=

 

Po przekształceniach (rachunek całkowy), ostatecznie otrzymujemy,  e dla 

dowolnej chwili t > 0 otrzymujemy: 

                                             

t

L

R

e

R

U

R

U

i

−

−

=

                                       

(1)

 

lub 

                                             

−

=

− t

L

R

e

R

U

i

1

                                       

(2)

 

Pierwsza  składowa  prawej  strony  równania  (1)  jest  nazywana 

składow  

ustalon

 pr du, a druga jest nazywana 

składow

 

przej ciow  

pr du. 

 

Składowa  przej ciowa  pr du  ma  w  chwili  t  =  0  warto  

R

U

−

  i  w  miar  

upływu czasu asymptotycznie d y do zera. 

Na rysunku 10.2a przedstawiony został przebieg funkcji czasu składowej 

ustalonej 

i

u

, składowej przej ciowej 

i

p

 oraz pr du wypadkowego 

 

i = i

u

+i

p 

 

Pr d wypadkowy d y

 

asymptotycznie do pr du ustalonego i ma charakter 

krzywej wykładniczej. 

 

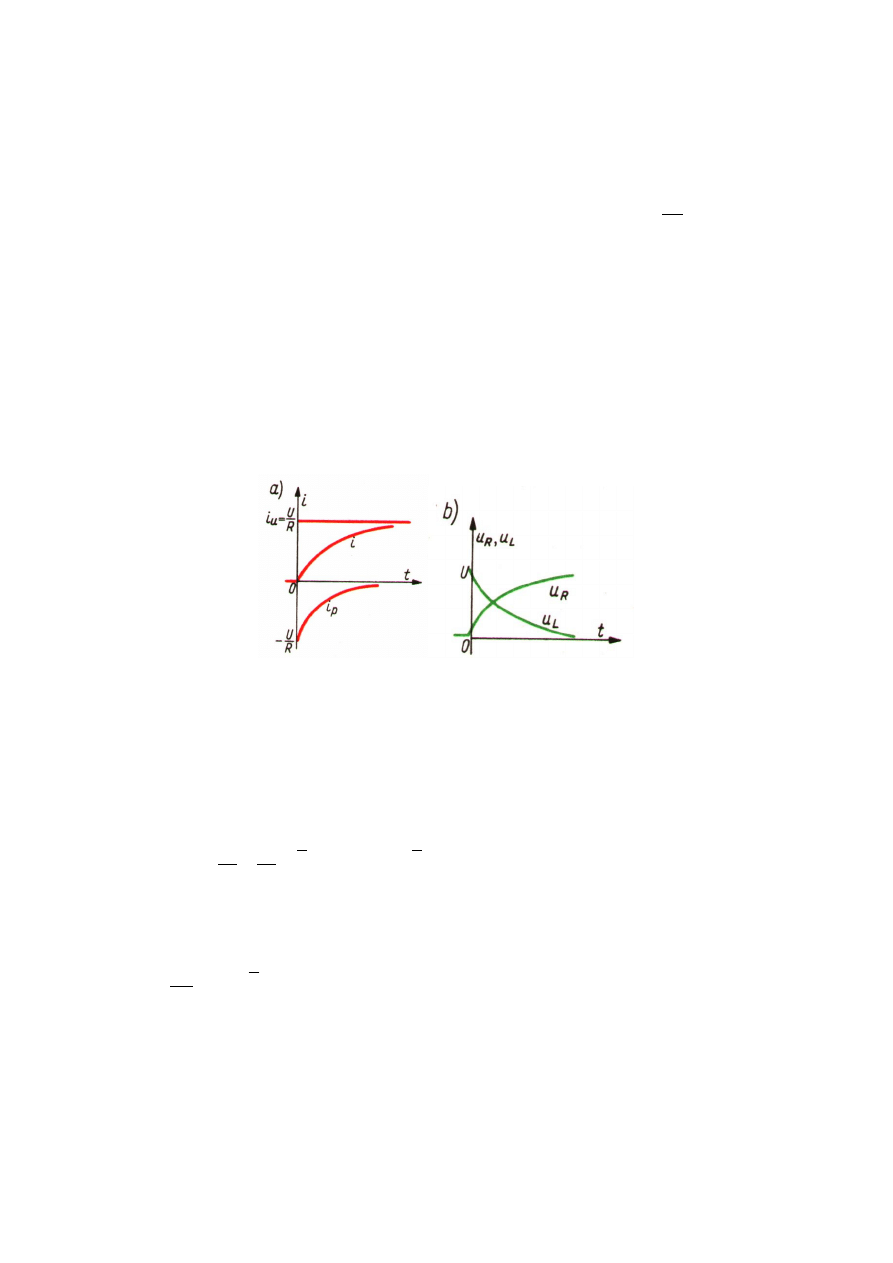
Rys.10.2 Przebiegi czasowe pr du i napi  w dwójniku szeregowym 

R,L wł czonym 

na napi cie stałe: a) przebieg pr du; b) przebiegi napi  

u

R

 i 

u

L

 

 

Je eli mamy wyznaczony pr d w stanie nieustalonym, to mo emy równie  

wyznaczy  napi cie na rezystancji 

u

R

 i napi cie na indukcyjno ci 

u

L

. 

 

Napi cie na rezystancji: 

t

L

R

t

L

R

R

Ue

U

e

R

U

R

U

R

Ri

u

−

−

−

=

−

=

=

 

 

Napi cie na indukcyjno ci: 

t

L

R

L

Ue

dt

di

L

u

−

=

=

 

 
 
 
 
 
 
 

Temat 11 : Stan nieustalony w układzie szeregowym R,C

 

 

Załó my,  e do gał zi, w której s  poł czone szeregowo elementy 

R, 

C doprowadzono w chwili t = 0 napi cie stałe. Odpowiada to zamkni ciu 

wył cznika 

W  w  chwili  t  =  0  w  obwodzie  jak  na  rys.  11.1.  Stan 

pocz tkowy  obwodu  jest  zerowy,  tzn.  w  chwili 

t  =  0  napi cie  na 

pojemno ci  u

C

  =  0,  a  zatem  z  elementem  pojemno ciowym   

C  nie  jest 

zwi zana  adna energia. 

 

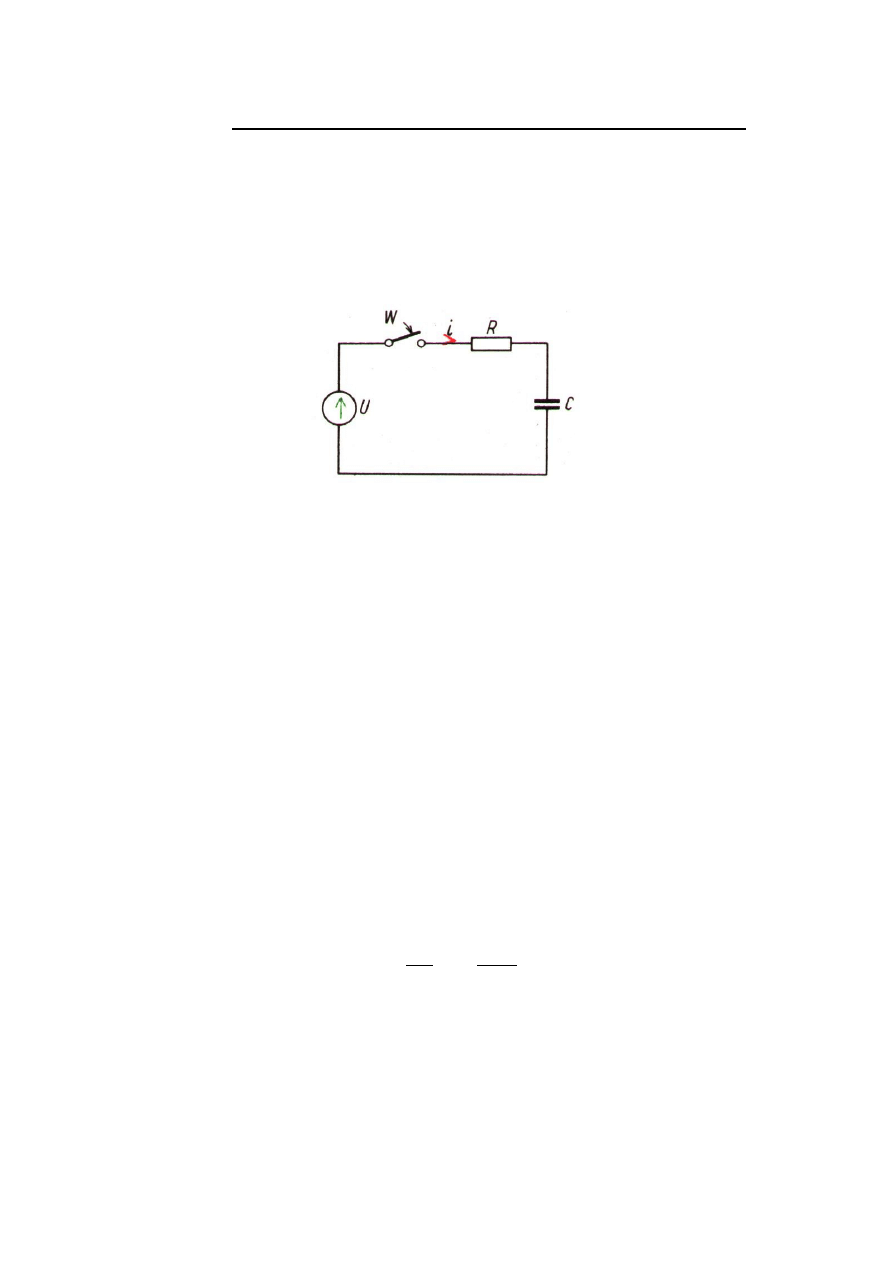
Rys.11.1 Dwójnik szeregowy R,C wł czony na napi cie stałe. 

 
 

Po  zamkni ciu  wył cznika 

W  w  obwodzie  powstaje  stan  nieustalony. 

Wyznaczony przebieg napi cia u

C

 w funkcji czasu b dzie zmieniał si  od 

zera do warto ci ustalonej wynosz cej  

 

U

u

Cu

=

 

 

Oznacza to,  e z biegiem czasu napi cie na kondensatorze osi gnie warto  

napi cia  ródła.  Proces  zachodz cy  w  rozpatrywanym  obwodzie 

nazywamy  procesem  ładowania  kondensatora  przez  rezystor  ze  ródła 

napi cia stałego. 

Zgodnie z drugim prawem Kirchhoffa w obwodzie z powy szego rysunku 

bilans napi  ma posta :

 

                                          

C

u

Ri

U

+

=

  

 

 

    

(1) 

Pr d ładowania kondensatora: 

dt

du

C

dt

dq

i

C

=

=

 

 

gdy   dq  =  Cdu

C

  (q  = Cu

C

). Ładunek elementarny jest proporcjonalny do 

napi cia elementarnego. 

 

 

 

Podstawiaj c powy sze do wzoru (1) otrzymamy: 

 

C

C

u

dt

du

RC

U

+

=

 

 

Po przekształceniach (rachunek całkowy), ostatecznie otrzymujemy,  e dla 

dowolnej chwili t > 0 otrzymujemy: 

t

RC

C

Ue

U

u

1

−

−

=

 

albo 

−

=

−

t

RC

C

e

U

u

1

1

 

 

Przez  analogi   do  obwodu  z  indukcyjno ci   wprowadzamy  poj cie stałej 

czasowej  obwodu  z  pojemno ci ,  przy  czym  dla  obwodu  z  pojemno ci  

stała czasowa 

 = RC 

 

Po wprowadzeniu stałej czasowej powy sze równania mo emy zapisa  w 

postaci: 

                                             

t

C

Ue

U

u

τ

1

−

−

=

                                          

(2) 

albo 

−

=

− t

C

e

U

u

τ

1

1

 

 

Pierwsza  składowa  prawej  strony  równania  (2)  jest 

składow   ustalon

 

napi cia na kondensatorze, a druga – 

składow  przej ciow

 napi cia. 

Składowa  przej ciowa  ma  w  chwili 

t  =  0  warto   –U  i  w  miar   upływu 

czasu asymptotycznie d y do zera. 

Na rysunku 11.2a przedstawiony został przebieg funkcji czasu składowej 

ustalonej 

u

Cu

, składowej przej ciowej 

u

Cp

 oraz napi cia wypadkowego na 

kondensatorze. 

u

C

 = u

Cu

+u

Cp

 

 

Napi cie  ładowania  kondensatora  asymptotycznie  d y  do  warto ci 

napi cia ustalonego 

U i ma charakter krzywej wykładniczej. 

 

 

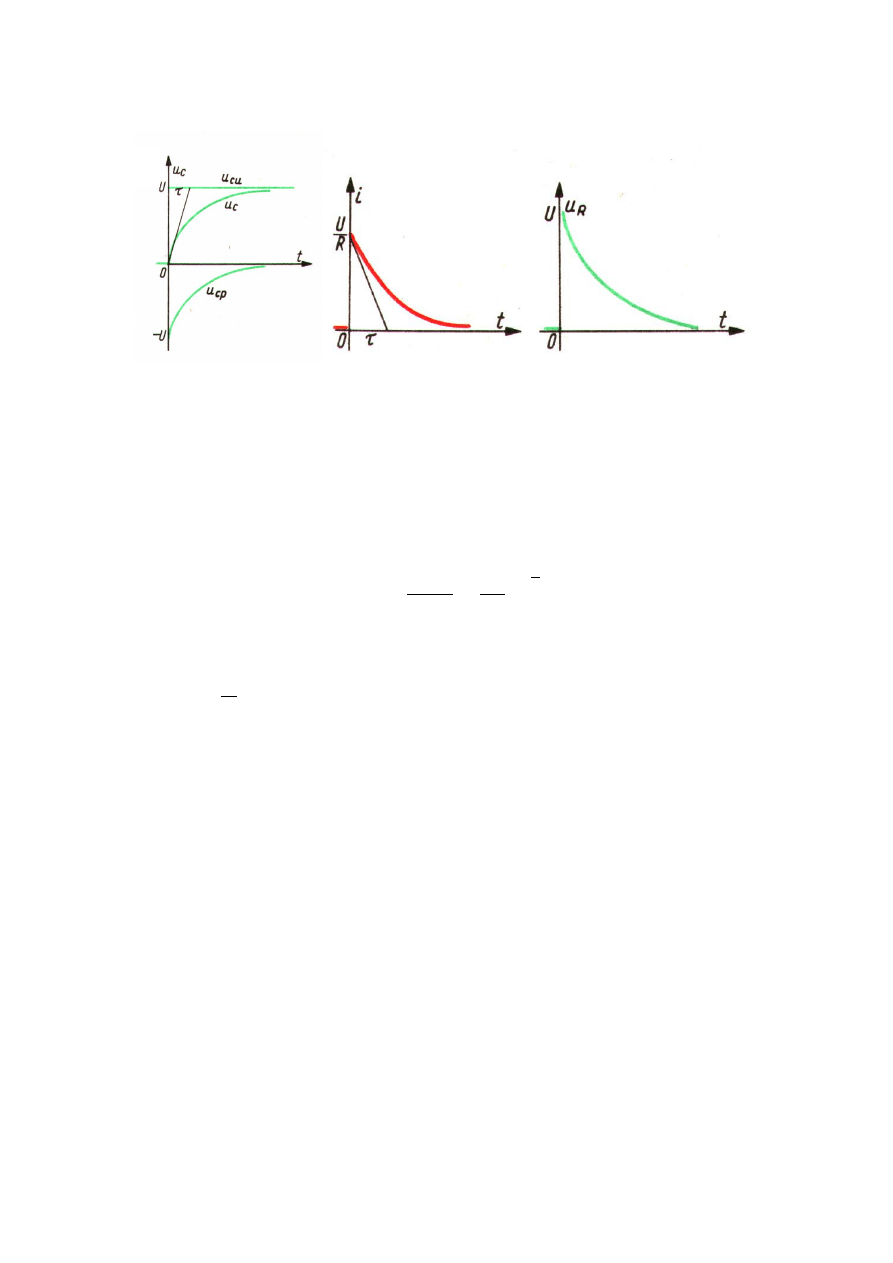
Rys. 11.2. Przebiegi czasowe napi  i pr du ładowania kondensatora przez rezystancj  ze 

ródła napi cia stałego: a) przebieg napi cia na pojemno ci; b) przebieg pr du ładowania;  

c) przebieg napi cia na rezystancji. 

 

 

W celu wyznaczenia przebiegu pr du ładowania kondensatora korzystamy 

ze wzoru: 

 

τ

1

−

=

=

e

R

U

dt

du

C

i

C

 

 

Pr d  ładowania  kondensatora  ma  najwi ksz   warto   w  chwili 

t  =  0, 

wynosz cej 

R

U

. Rezystor o rezystancji R ogranicza wi c pr d w pierwszej 

chwili.   

Im wi ksza jest rezystancja R w obwodzie ładowania i im wi ksza jest 

pojemno  C ładowanego kondensatora, tym wolniej przebiega proces 

ładowania

. 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

a) 

b) 

c) 

Temat 12 : Stała czasowa. Wpływ stałej czasowej na kształt napi  

i pr dów. 

 

Z równania 

t

L

R

e

R

U

R

U

i

−

−

=

 

 

 

 

 

(1)

 

 

wynika,  e  w  zale no ci  od  warto ci  rezystancji  R  i  indukcyjno ci  L 

zanikanie  składowej  przej ciowej  w  funkcji  czasu  mo e  by   szybsze  lub 

wolniejsze.  W  celu  zbadania  tego  zagadnienia  wprowadza  si   wielko  

fizyczn  zwan  

stał  czasow

, okre lon  wzorem: 

R

L

=

τ

 

Stała czasowa jest mierzona w sekundach. Po uwzgl dnieniu powy szego 

wzoru i wstawieniu do równania (1) otrzymujemy: 

τ

t

e

R

U

R

U

i

−

−

=

 

oraz 

−

=

−

τ

t

e

R

U

i

1

 

Jak  wida , 

stała  czasowa    jest

 

to  czas,  po  upływie  którego  warto  

bezwzgl dna składowej przej ciowej maleje e razy

. 

W  chwili t = 0 składowa przej ciowa pr du ma warto  

R

U

i

p

−

=

. W celu 

wyznaczenia  warto ci  składowej  przej ciowej  pr du  po  upływie  czasu 

równego jednej stałej czasowej podstawimy t=  , a wi c otrzymamy  

Re

1

U

e

R

U

i

p

−

=

−

=

−

 

W ten sposób otrzymali my potwierdzenie powy szej definicji. W ten sam 

sposób  mo na  wyznaczy   warto   składowej  przej ciowej  pr du  po 

upływie czasu t = 2 , t=3  itd. 

Czas t 

0 

 

2  

3  

4  

5  

6  

7  

%

100

u

p

i

i

  100  36,78  13,53  4,98  1,83  0,674  0,248  0,091 

 

Z  przytoczonych  danych  wynika,  e  po  czasie  5   składowa  przej ciowa 

pr du  stanowi  mniej  ni   1%  składowej  ustalonej.  W  praktyce  przyjmuje 

si ,  e po 4 ....5  obwód znajduje si  w stanie ustalonym. 

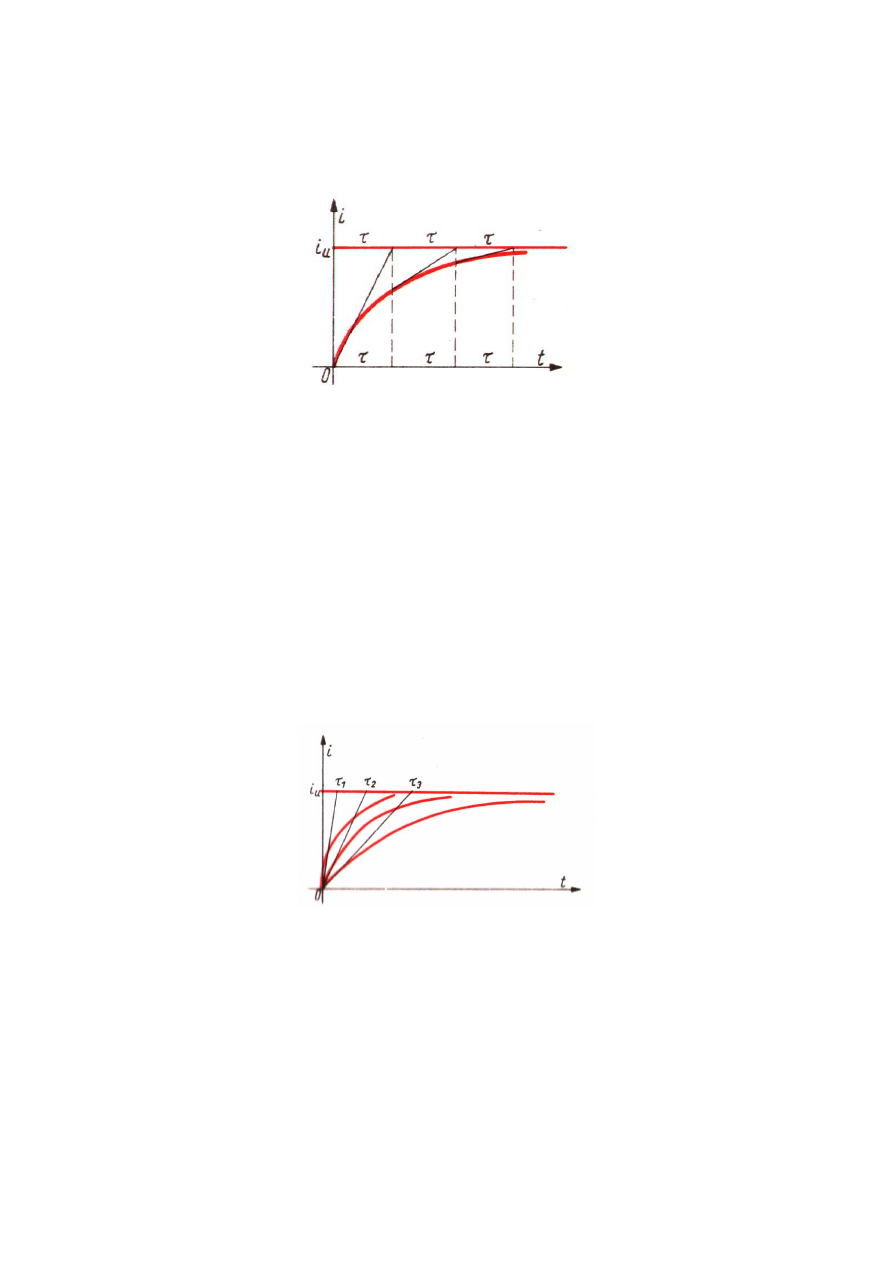
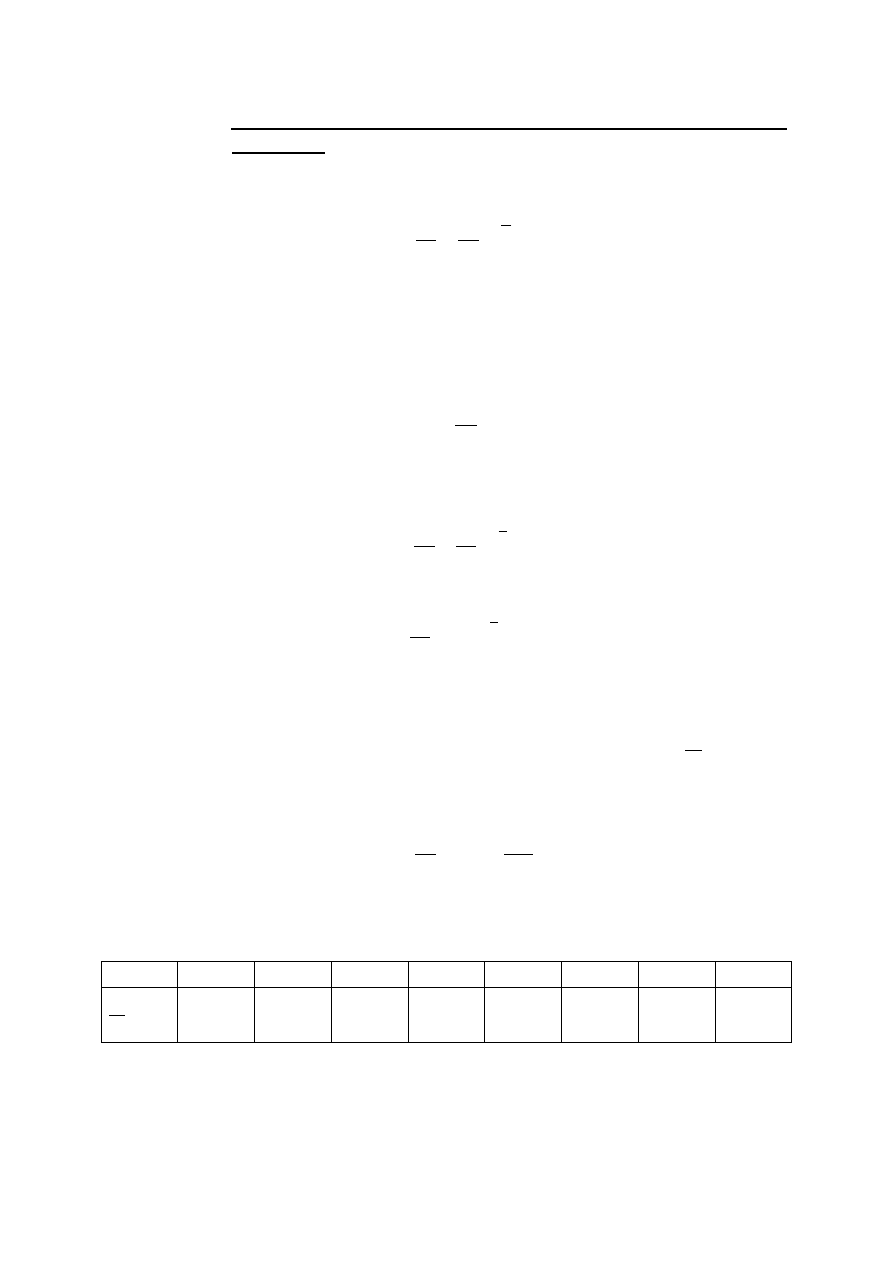
Stał   czasow   mo na  zdefiniowa   równie   w  inny  sposób.  Mo na 

udowodni ,  e je li poprowadzimy styczn  do krzywej pr du w chwili  

t = 0, to przetnie ona asymptot  pr du po czasie  .  

 

Rys.12.1. Wyznaczanie graficzne stałej czasowej. 

 

Z  rys.12.1.  wida ,  e  twierdzenie  jest  słuszne  dla  stycznej  do  krzywej  w 

dowolnym punkcie. 

Stała  czasowa    jest  to  czas,  po  upływie  którego  pr d  nieustalony 

osi gn łby  warto   ustalon ,  gdyby  jego  narastanie  miało  charakter 

liniowy,  czyli  pr dko   zwi kszania  si   pr du  była  stała  i  równa 

pr dko ci zwi kszania si  w chwili pocz tkowej. 

Od  warto ci  stałej  czasowej,  a  wi c  od  warto ci  parametrów  obwodu 

zale y  czas  trwania  stanu  nieustalonego.  Im  bowiem  wi ksza  jest  stała 

czasowa,  tym  łagodniej  narasta  pr d.  Na  rys.12.2.  przedstawione  s   trzy 

krzywe pr du dla ró nych warto ci  , a wi c dla ró nych stosunków L do 

R

. 

 

Rys.12.2. Wpływ warto ci stałej czasowej na przebieg pr du w stanie ustalonym. 

 

Je eli zało ymy,  e rezystancja obwodu jest stała, a indukcyjno  mo e si  

zmienia ,  to  w  miar   zwi kszania  L  wzrasta  stała  czasowa  i  narastanie 

pr du jest wolniejsze. St d wniosek: 

obwody o du ej indukcyjno ci wolno 

osi gaj  warto ci ustalone

.