1

Częśd III

1. Mostki cieplne

Do tej pory zakładaliśmy że struktura przegrody jest jednorodna. Mostki cieplne to miejsca gdzie
występuje lokalne zwiększenie współczynnika przewodzenia ciepła na skutek niejednorodności
cieplnej w konstrukcji.

Mostki cieplne mogą byd punktowe lub liniowe. Mostki punktowe to przede wszystkim elementy
różnego rodzaju zamocowao metalowych (kotwy). Z mostkami liniowymi mamy do czynienia na
obrzeżach stolarki okiennej ościeżnic itp.

Ogólnie można powiedzied że mostki w ścianie przewodzą ciepło równolegle do materiału ściany. Dla
oporów cieplnych połączonych równolegle opór wypadkowy jest równy

2

1

1

1

1

R

R

R

W przypadku oporów cieplnych odwrotnością oporu przenikania ciepła jest współczynniki
przenikania ciepła U. Czyli mamy

M

S

U

U

U

Gdzie U

S

to opór cieplny warstw ściany a U

M

opór cieplny mostków. Wzór na opór cieplny mostków

będzie analogicznie jak dla ściany.

m

m

MO

A

U

Współczynnik odniesiony do powierzchni ściany

m

s

m

M

A

A

U

A

m

– pole powierzchni mostków równe iloczynowi liczby mostków i powierzchni jednego

λ

m

- współczynnik przewodzenia ciepła mostka

δ – długośd mostka

1.1 Mostki cieplne punktowe

Na podstawie tego co napisano wyżej wpływ mostka uwzględniamy przez obliczenie poprawki do
współczynnika przenikania ciepła ściany.

U

U

U

Gdzie

2

t

t

i

A

n

U

s

A

1

Współczynnik to jakby odwrotnośd długości mostka. Przyjmuje się =5 dla płyt izolacyjnych lub
dachu =6 dla kotew między warstwami muru. Norma PN-EN 6946 poleca wyznaczanie
współczynnika przy czym danymi są długośd kotwy i opory warstwy izolacyjnej przez którą
przechodzi kotwa oraz całej ściany bez mostków.

λ - współczynnik przewodzenia ciepła łącznika

n – liczba łączników na m

2

A – pole przekroju jednego łącznika [m

2

]

Zad. Ściana w technologii monolitycznej składa się z dwóch warstw betonu i środkowej warstwy

styropianu połączonych kotwami. Współczynnik przewodzenia ciepła kotew λ

stal

=58

K

m

W

2

Styropian λ

ster

=0,035

K

m

W

2

, beton λ

bet

=0,5

K

m

W

2

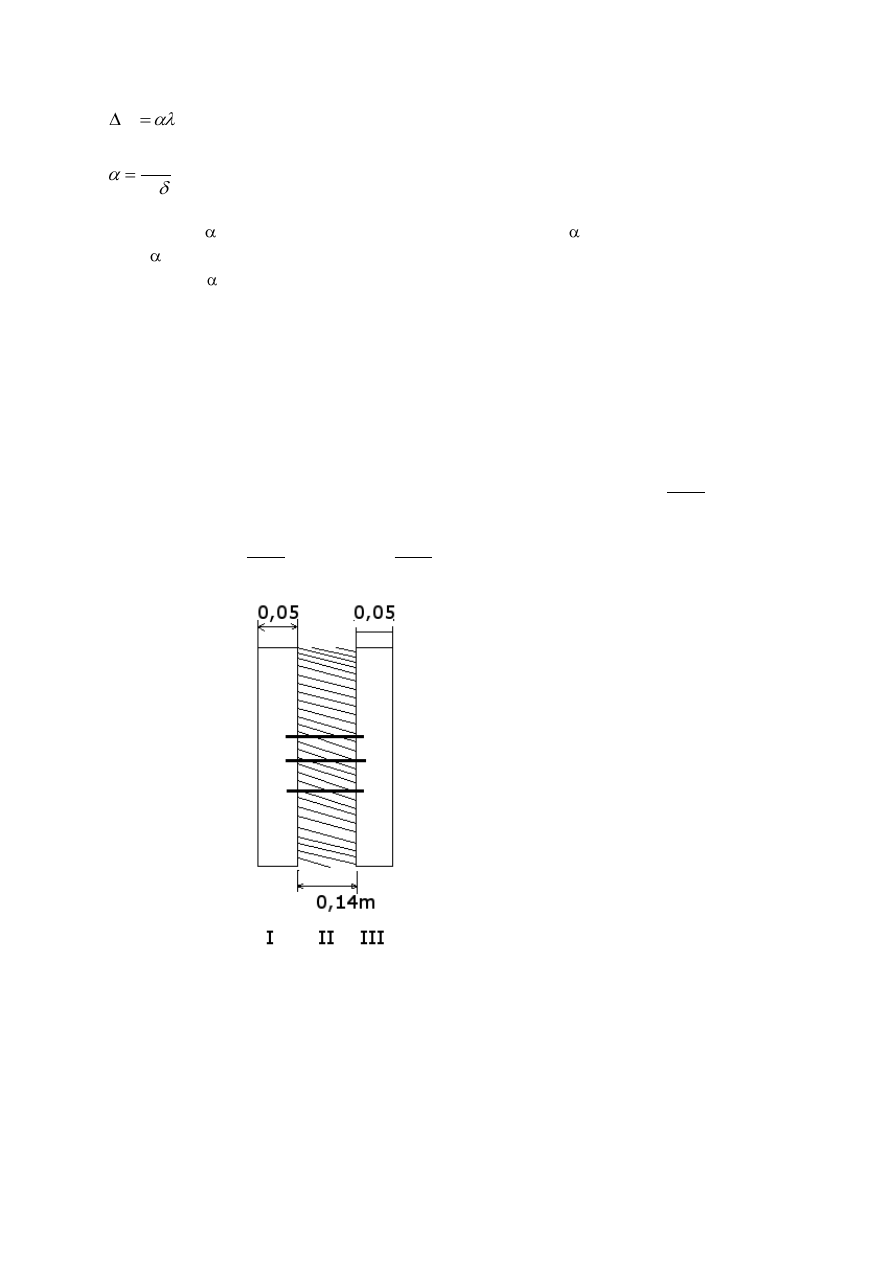
. Wymiary ściany jak na rysunku 1

Rys 1. Ściana połączona kotwami

Ściana zawiera 20 kotew na m

2

o średnicy 0,003 m

Opór cieplny bez kotew

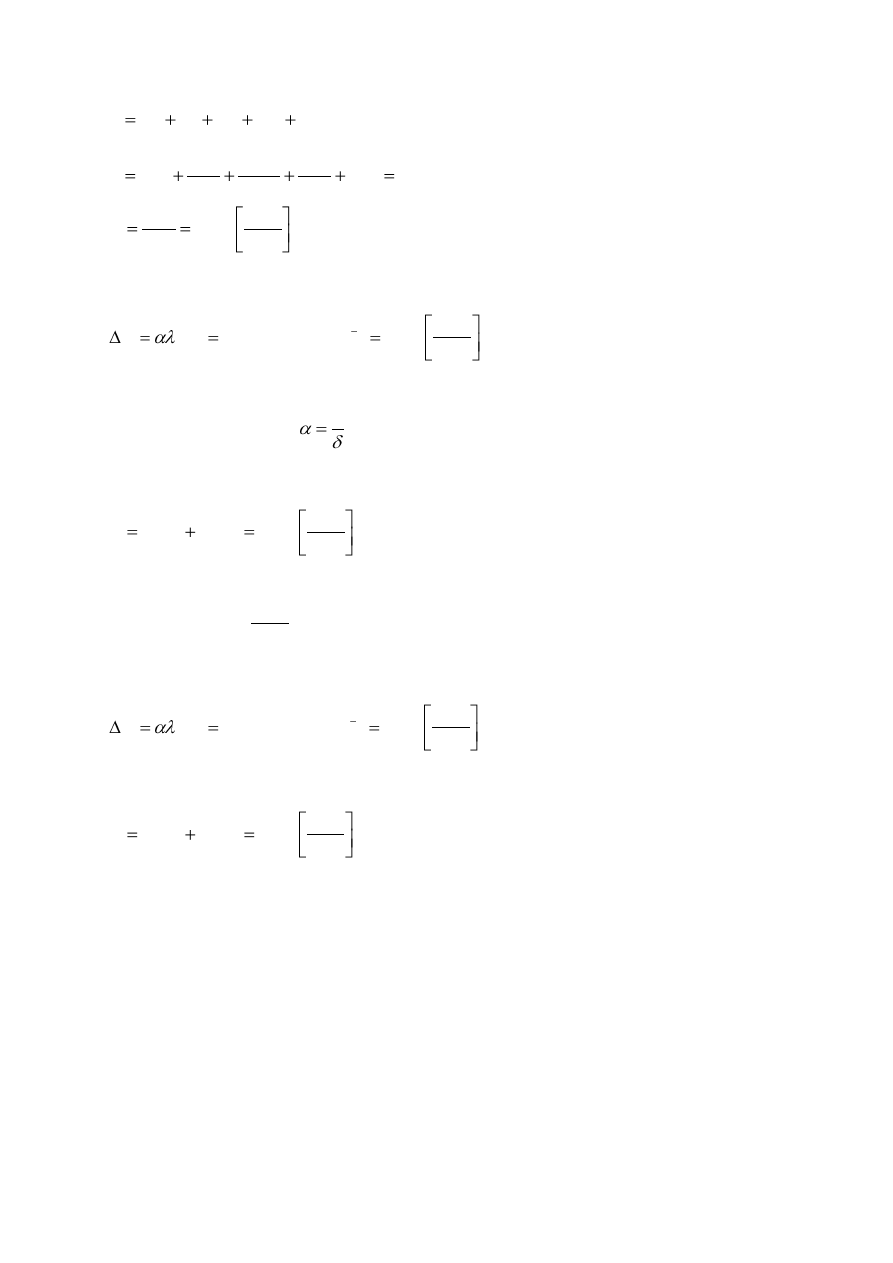
3

ce

III

II

I

ci

R

R

R

R

R

R

K

m

W

U

R

2

229

0

37

4

1

37

4

03

0

5

0

05

0

035

0

14

0

5

0

05

0

14

0

,

,

,

,

,

,

,

,

,

,

,

Poprawka na kotwie

K

m

W

e

nA

U

f

2

6

049

0

07

7

20

58

6

,

,

*

*

*

Ponieważ mamy tu liczbę kotew na m

2

ściany nie musimy już dzielid wyniku przez powierzchnie

ściany, czyli w tym wypadku

1

.

Współczynnik całkowity

K

m

W

U

2

278

0

049

0

229

0

,

,

,

Zad Ściane z poprzedniego przykładu przeprojektowano zamieniając materiał kotew na stal

nierdzewną o λ

stal

=17

K

m

W

2

Jak zmieni się wsp przenikania ciepła?

Obliczamy tylko poprawkę na kotwie

K

m

W

e

nA

U

f

2

6

014

0

07

7

20

17

6

,

,

*

*

*

I całkowity współczynnik

K

m

W

U

2

243

0

014

0

229

0

,

,

,

1.2 Mostki liniowe

Mostki liniowe występują na różnego rodzaj nieciągłościach liniowych. Na przykład stolarka okienna
lub dzwi

4

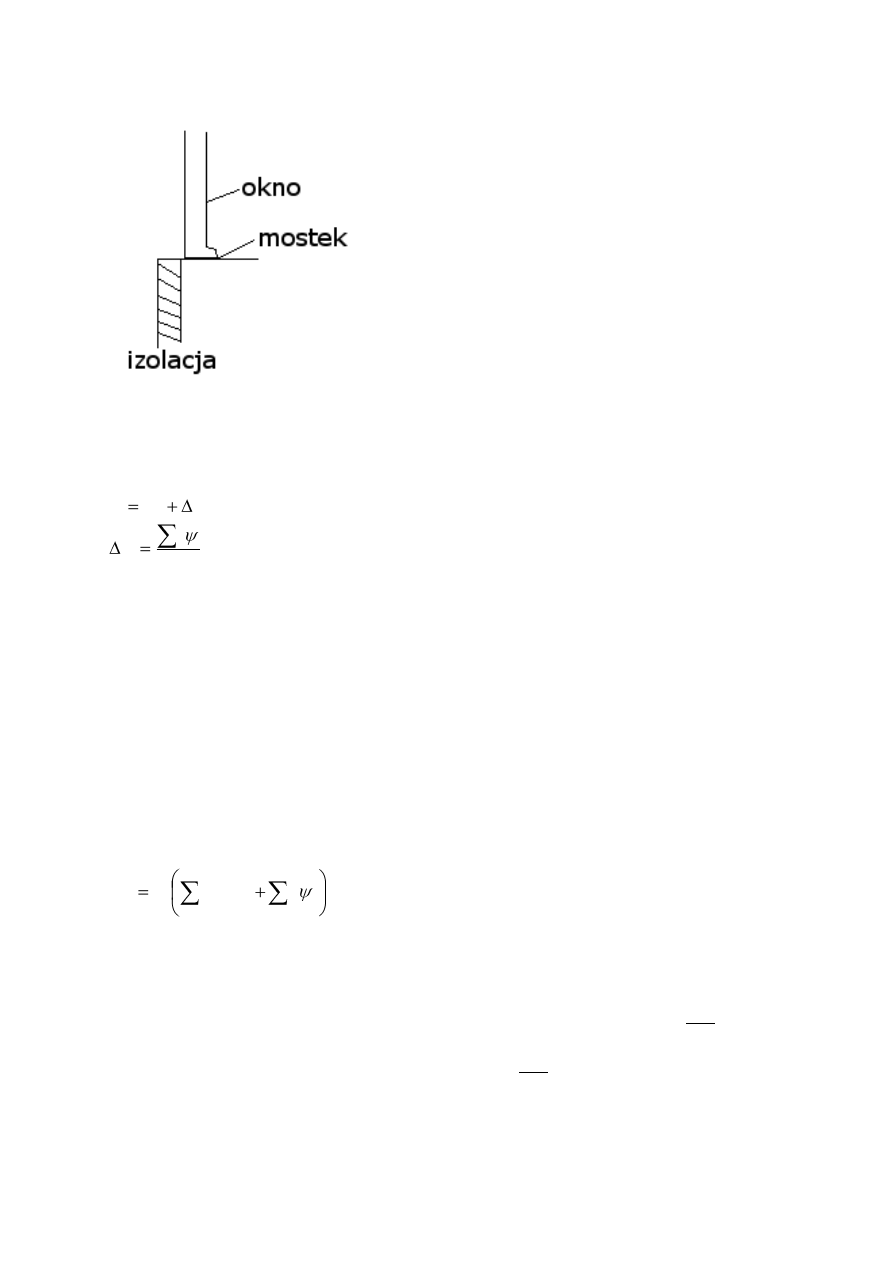
Rys 2. Mostek cieplny pod ościeżnicą

Dawniej współczynnik przenikania ciepła był obliczany też w postaci poprawki do współczynnika bez
mostków

A

l

U

U

U

U

o

l* Ψ to współczynnik na całą powierzchnie ściany dlatego trzeba odnieśd do metra kwadratowego
ściany.

l –długośd mostków

Ψ – wsp przenikania ciepła mostka

A – powierzchnia przegrody bez otworów okiennych liczonych w świetle otworów w ścianie

Współczynnik Ψ określa się z obliczeo numerycznych.

Zgodnie z ostatnimi normami współczynnik ten oblicza się jako poprawkę do całkowitego
współczynnika strat ciepła z budynku.

i

i

i

i

wi

wi

w

w

l

U

A

b

H

Można oczywiście tym sposobem również obliczyd współczynnik strat ciepła tylko dla jednej ściany.

Zad. Obliczyd współczynnik przenikania ciepła przez ściane A=10m

2

z oknem o wymiarach 1,6x1,6 m i

polem powierzchni 2,56 m

2

. Ściana składa się z warstwy betonu o δ

bet

= 0,20 m λ

bet

=0,5

mK

W

. Ściana w

technologii monolitycznej i warstwy izolacji δ

iz

=0,1m λ

iz

=0,04

mK

W

. Okno jest umieszczone w licu

zewnętrznym muru a izolacja cieplna nie zachodzi na ościeżnicę.

5

U

U

U

o

Opory bez mostków

K

m

W

R

U

R

R

R

o

o

ce

iz

iz

bet

bet

ci

o

2

326

0

1

07

3

04

0

04

0

1

0

5

0

2

0

13

0

,

,

,

,

,

,

,

,

Współczynnik przejmowania ciepła mostków określamy z tablic w tym przypadku otrzymanych
programem EUROKOBRA , jak w tabeli 1.

Tabela 1. Wartości liniowego współczynnika przenikania ciepła obliczone przy użyciu
programu EUROKOBRA

Nr

Charakterystyka rozwiązania

ψ (W/(mK]

Detalu

detalu izolacji

1

Ościeże okienne; okno w licu zewnętrznym
Muru, izolacja muru nie zachodzi na ościeżnicę

0,19

2

Ościeże okienne; okno w licu zewnętrznym mu-
ru, izolacja muru zachodzi 3 cm na ościeżnicę

0,05

3

Ościeże okienne; okno w licu wewnętrznym
Muru, ościeże bez izolacji

0,39

4

Nadproże okienne; okno w licu zewnętrznym
Ściany, izolacja muru nie zachodzi na ościeżnicę

0,29

5

Nadproże okienne; okno w licu zewnętrznym
Muru, izolacja muru zachodzi 3 cm na ościeżnicę

0,06

6

Nadproże okienne; okno w licu wewnętrznym
Muru, nadproże bez izolacji od spodu

0,60

7

Nadproże okienne; okno w licu wewnętrznym
Muru, izolacja nadproża od spodu

0,20

8

Podokiennik; okno w licu zewnętrznym muru,
kamienny podokiennik wewnętrzny oddzielony
od kamiennego podokiennika zewnętrznego 1
cm
Przekładką ze styropianu

0,39

9

Podokiennik; okno w licu wewnętrznym muru,
Wierzch muru nieprzykryty izolacją

0,57

10

Podokiennik; okno w licu wewnętrznym muru,
Wierzch muru przykryty izolacją grubości 3 cm

0,22

11

Podokiennik; okno w licu zewnętrznym muru,
kamienny podokiennik wewnętrzny, izolacja
cieplna zachodzi 3 cm na ościeżnicę.

0,07

12

Płyta balkonowa wspornikowa w przekroju poza
Drzwiami balkonowymi

0,65

6

13

Płyta balkonowa o własnej konstrukcji w
przekroju poza drzwiami balkonowymi; beton
płyty oddzielony od betonu stropu przekładką
izolacji o grubości jak na murze

0,07

14

Płyta balkonowa wspornikowa w przekroju przez
drzwi balkonowe

0,91

15

Płyta balkonowa o własnej konstrukcji w prze-
kroju przez drzwi balkonowe; beton płyty oddzie-
lony od betonu stropu przekładką izolacji o gru-
bości jak na murze; na zewnątrz przechodzi
kamienna płytka podłogowa

0,57

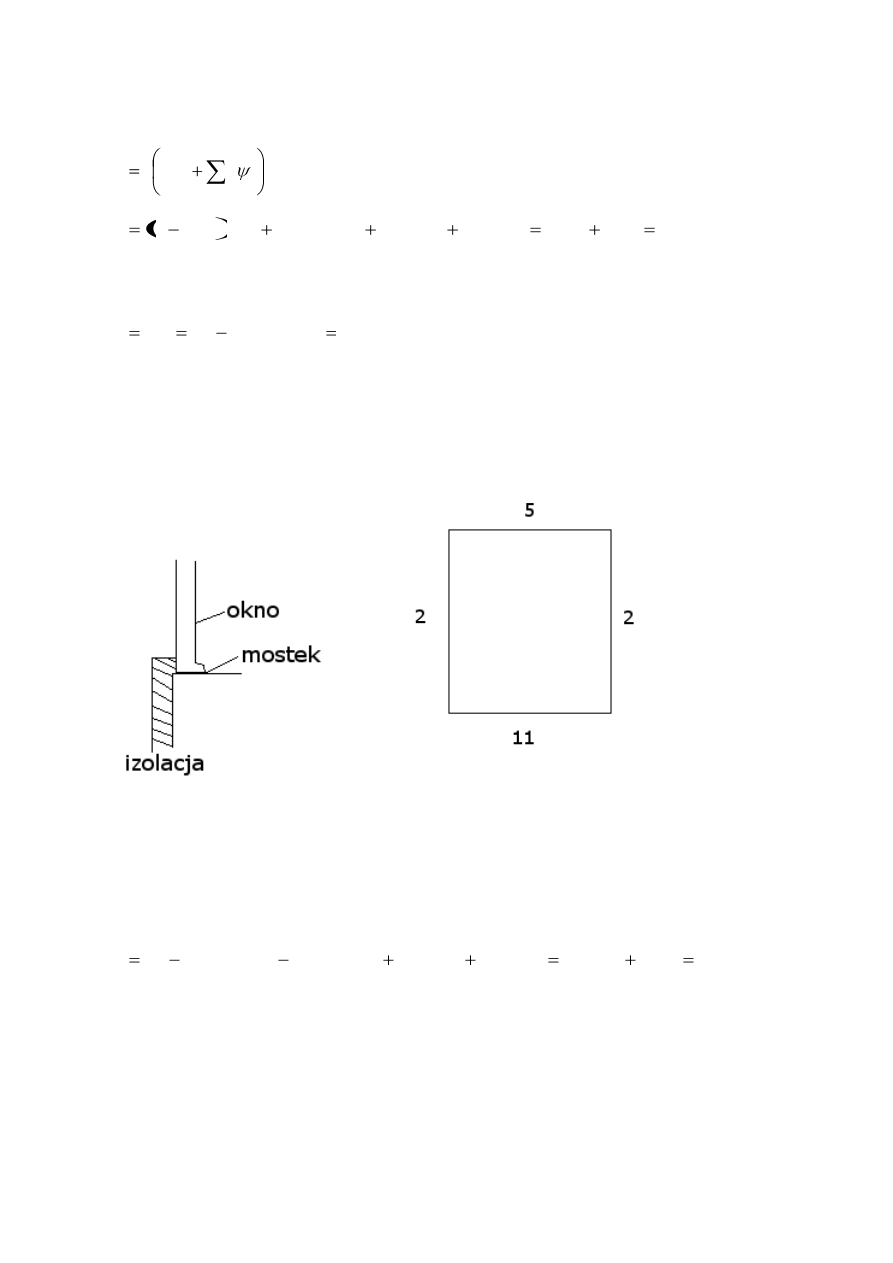
Z tabeli 1 dla ościeżnicy bierzemy detale jak na rysunku 3

Rys 3. Numery mostków z tabeli dla zadania

Ψ

1

=0,19

Ψ

4

=0,29

Ψ

8

=0,39

228

0

56

2

10

39

0

6

1

29

0

6

1

19

0

6

1

2

,

,

,

*

,

,

*

,

,

*

,

*

U

Całkowity współczynnik

K

m

W

U

2

554

0

228

0

326

0

,

,

,

Zad. Obliczmy to samo nowym sposobem

Współczynnik U dla ściany bez mostków obliczmy identycznie jak poprzednio. Następnie

7

Dla jednej ściany mamy

i

i

i

l

AU

b

H

136

4

696

1

440

2

39

0

6

1

29

0

6

1

19

0

6

1

2

328

0

56

2

10

,

,

,

,

*

,

,

*

,

,

*

,

*

,

,

H

Dla porównania współczynnik strat ciepła obliczony na podstawie współczynnika U z poprzedniego
zadania wynosi.

121

4

545

0

56

2

10

,

,

*

)

,

(

AU

H

A więc mamy zgodnośd obu sposobów.

Zad. To samo okno zaprojektowano do montażu w licu zewnętrznym muru ale z izolacją zachodzącą
na ościeżnice 3 cm. Obliczyd współczynnik przenikania ciepła.

Rys 4. Izolacja zachodzi na ościeżnice. Schemat i numery detali z tabeli 1.

Współczynnik U bez mostków pozostaje taki sam jak poprzednio. Obliczmy współczynnik start ciepła.

Współczynniki Ψ

Ψ

2

=0,05, Ψ

5

=0,06, Ψ

11

=0,07

80832

2

368

0

44032

2

07

0

6

1

06

0

6

1

05

0

6

1

2

326

0

56

2

10

,

,

,

,

*

,

,

*

,

,

*

,

*

,

*

)

,

(

H

Odpowiednio wykonana izolacja zmniejsza straty ciepła.