Akademia Górniczo-Hutnicza

w Krakowie

Wydział Energetyki i Paliw

Modelowanie komputerowe

w energetyce

Projekt

Karolina Wszoła

IV rok Energetyka

1. Temat projektu

W belce więźby dachowej zalęgły się korniki. Belka ma wymiary 10x25x350 [cm].

Szkodniki trzeba unicestw

ić poprzez zamrażanie belki w temperaturze -20

o

C przez

10 godzin. Należy to zrobić bez przemieszczania belki. Żeby możliwe było tak długie

utrzymanie belki w niskiej temperaturze, trzeba

ją szczelnie odizolować folią

termoizolacyjną. Przez otwór w izolacji wtłaczamy gaz (powietrze) o temperaturze -

40

o

C. Zaatakowana przez szkodniki belka jest wykonana z wysuszonego drewna

bukowego.

2. Model matematyczny

Równanie transportu ciepła:

(

) (

)

gdzie:

ρ - gęstość w temperaturze T [kg/m

3

]

c

p

-

ciepło właściwe przy stałym ciśnieniu [J/(kg*K)]

T - temperatura [K]
x, y, z - kierunki [m]
t - czas [s]
V

x

, V

y

, V

z

-

prędkości w kierunkach x,y,z [m/s]

- współczynnik przewodzenia [J/(m*s*K)]
S -

źródło

Po uproszczeniu otrzymujemy:

(

) (

)

Warunki brzegowe:

Temperatura wszystkich

ścianek belki: -40

o

C

Warunki początkowe:

Temperatura w środku belki dla t = 0s => T

ini

= 0

o

C

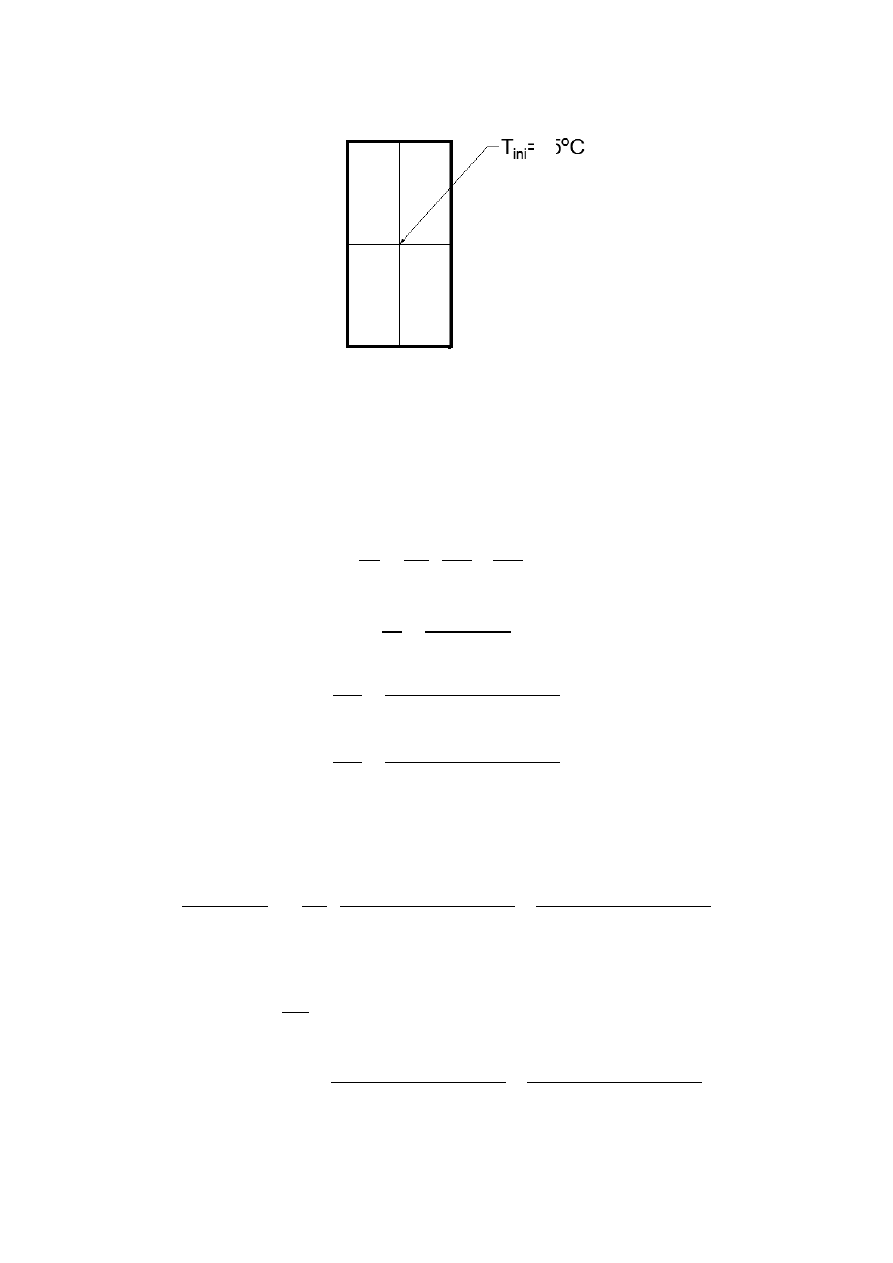
3. Model numeryczny

Model obliczony metodą niejawną

( )

(

)

( )

( )

Po podstawieniu do uproszczonego równania transportu ciepła otrzymano:

(

)

(

( )

( )

)

(

( )

( )

)

0

-40

o

C

-40

o

C

-40

o

C

-40

o

C

(

( )

(

) ( )

(

)

( )

( )

)

( )

( )

[( )

(

) ( )

(

)]

( )

( )

[( )

(

) ( )

(

) ( )

(

)

( )

(

)]

[( )

(

) ( )

(

)]

[( )

( )

]

[( )

( )

] [( )

(

) ( )

(

)]

[ (( )

( )

)] [( )

(

) ( )

(

)]

Ostatecznie otrzymano równanie:

[( )

(

) ( )

(

)]

[( )

( )

]

4.

Rozwiązanie

Zakładamy wartości parametrów (środek belki):

dt = 20 [s]
dx = 0,05 [m]
dy = 0,125 [m]
r = 0,0701

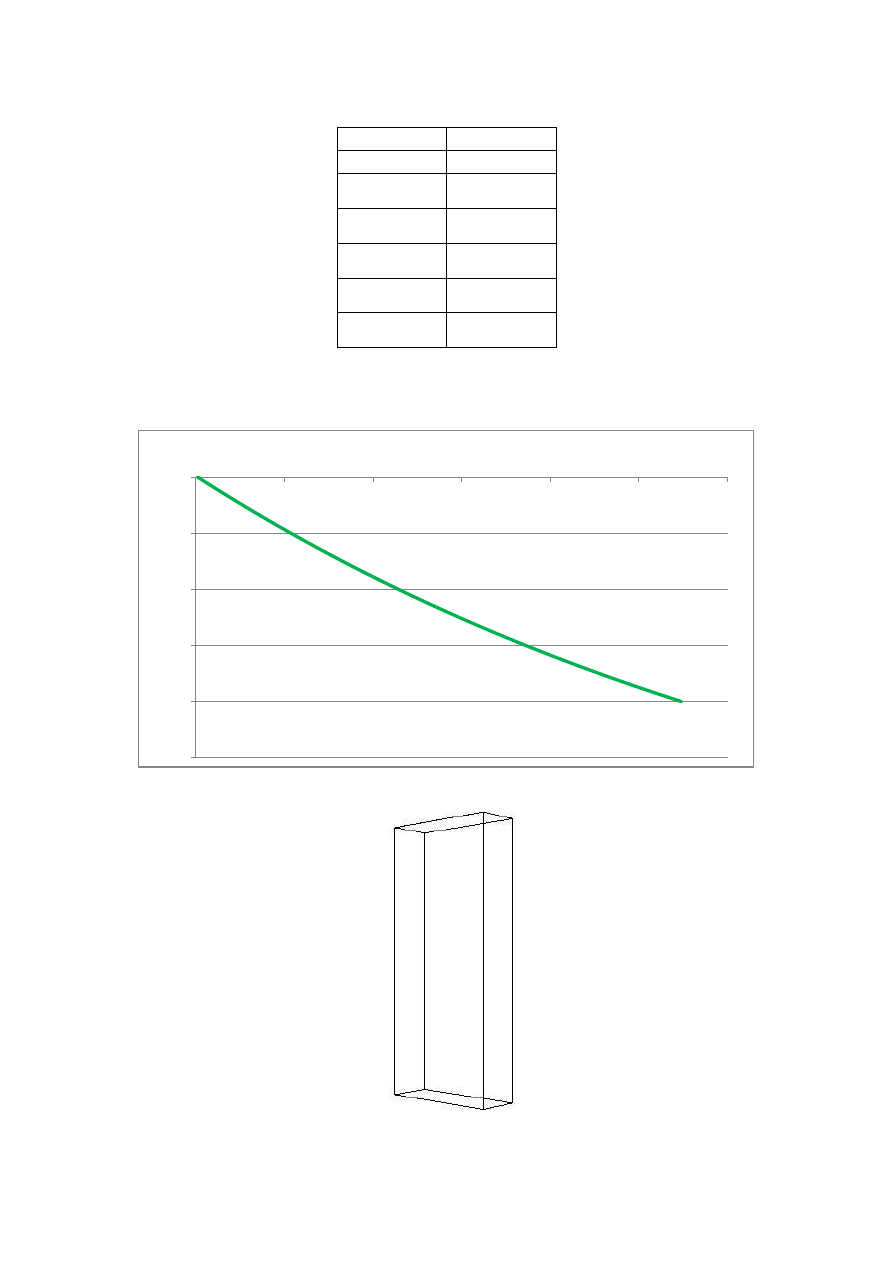
Otrzymujemy rozwiązanie:

Temp [˚C]

Czas [s]

…

…

-19,7971

5380

-19,8484

5400

-19,8995

5420

-19,9505

5440

-20,0013

5460

Otrzymany czas

oziębiania się belki (-20

o

C w

ewnątrz), dla podanych parametrów,

wynosi 91 minut.

-25

-20

-15

-10

-5

0

0

1000

2000

3000

4000

5000

6000

te

m

p

T

[

o

C]

czas t [s]

Zależność temperatury w funkcji czasu T(t)

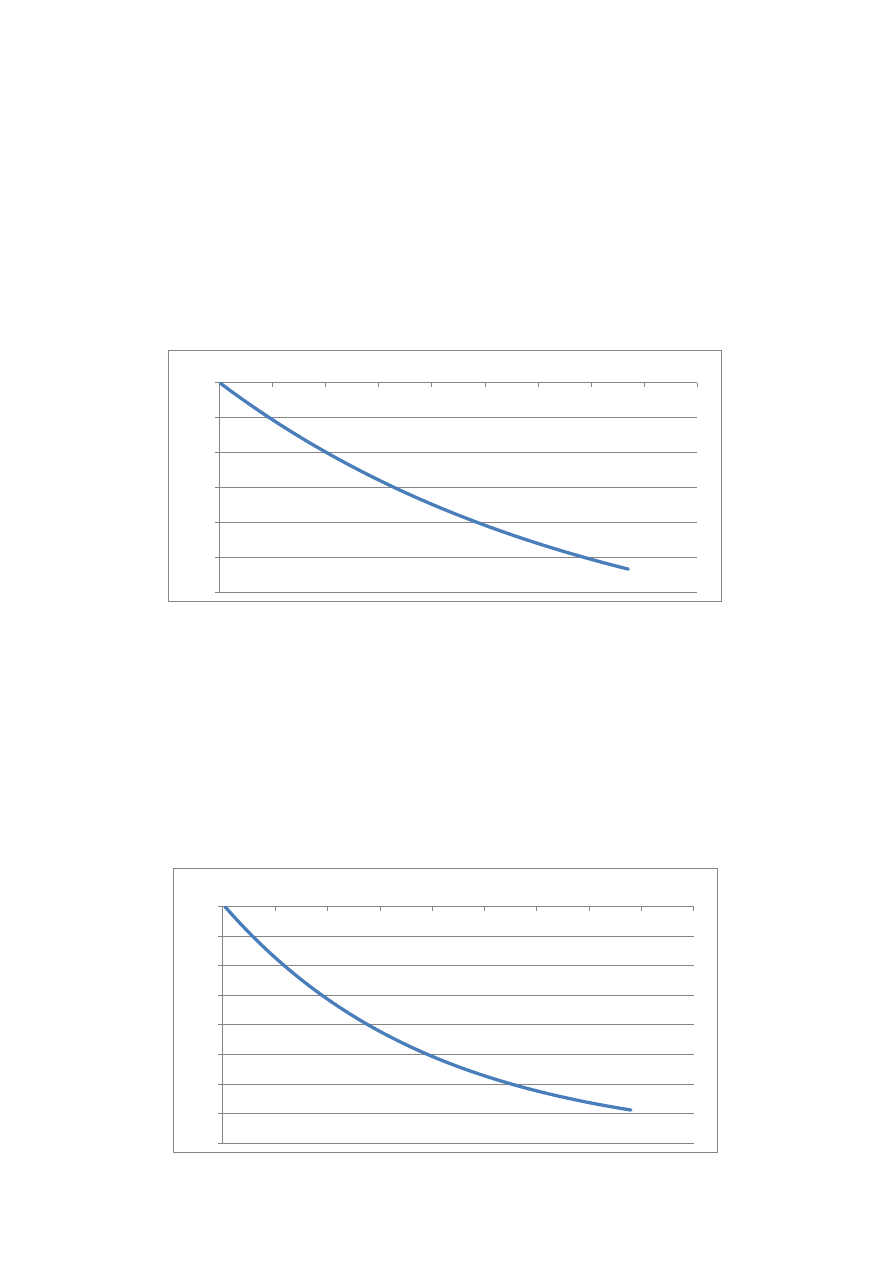
Rozważamy również inny przypadek, w punkcie 1.:

dt = 20 [s]
dx = 0,025 [m]
dy = 0,125 [m]
r = 0,2805

Otrzymany czas

oziębiania się belki (-20

o

C

w odległości ¼ węższej krawędzi od

zewnętrznej ścianki), dla innych parametrów bez zmian, wynosi 25 minut
i 40 sekund.

Oziębianie w punkcie 2.:

dt = 20 [s]
dx = 0,05 [m]
dy = 0,0625 [m]
r = 0,2805

Otrzymany czas

oziębiania się belki (-20

o

C

w odległości ¼ szerszej krawędzi od

zewnętrznej ścianki), dla innych parametrów bez zmian, wynosi 64 minut
i 40 sekund.

-30

-25

-20

-15

-10

-5

0

0

200

400

600

800

1000

1200

1400

1600

1800

te

m

p

T

[

o

C]

czas t [s]

Zależność temperatury w funkcji czasu T(t)

-40

-35

-30

-25

-20

-15

-10

-5

0

0

500

1000

1500

2000

2500

3000

3500

4000

4500

te

m

p

T

[

o

C]

czas t [s]

Zależność temperatury w funkcji czasu T(t)

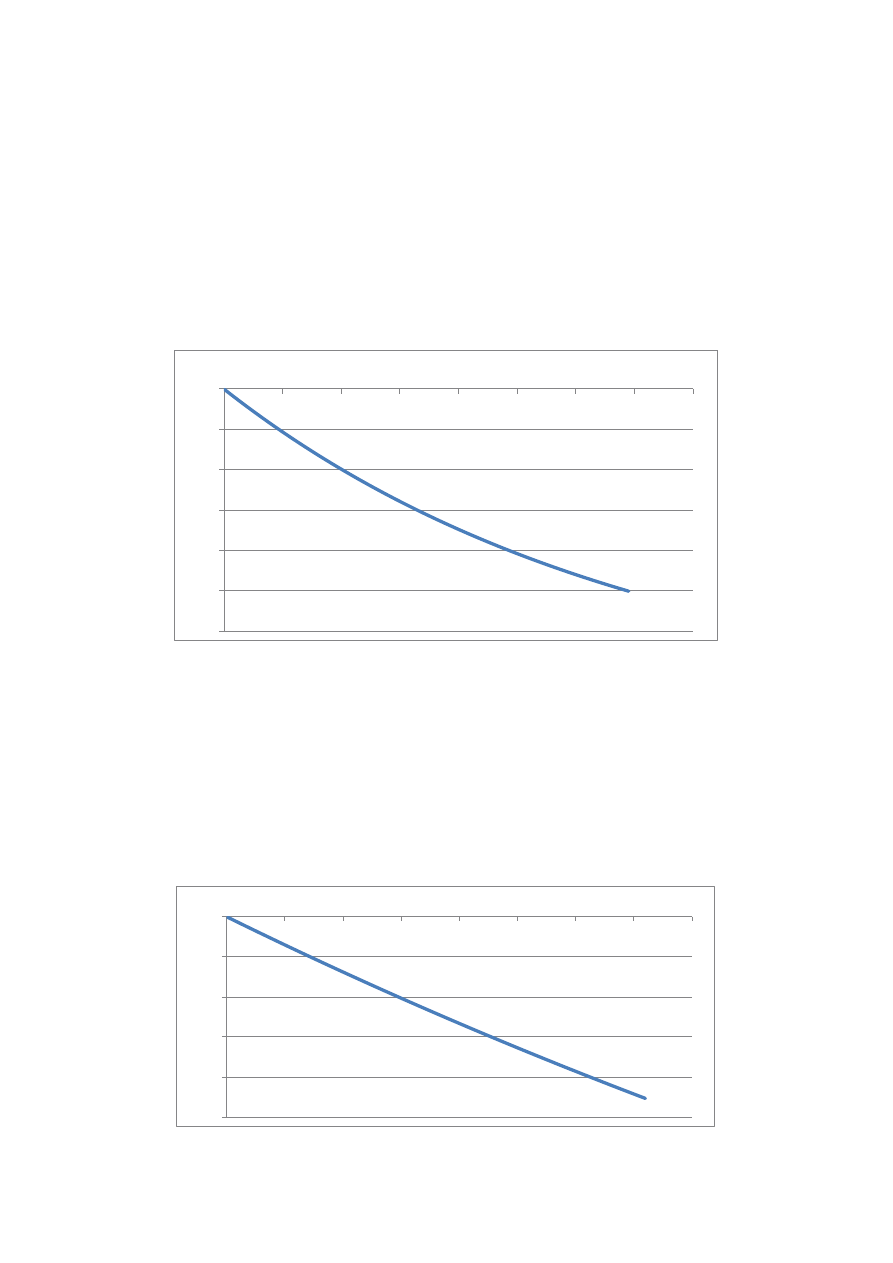
Oziębianie w punkcie 3.:

dt = 20 [s]
dx = 0,05 [m]
dy = 0,0625 [m]
r = 1,122

Otrzymany czas

oziębiania się belki (-20

o

C

w odległości ¼ szerszej i ¼ węższej

krawędzi od zewnętrznej ścianki), dla innych parametrów bez zmian, wynosi
23 minuty.

Oziębianie w punkcie 4.:

dt = 20 [s]
dx = 0,0125 [m]
dy = 0,03125 [m]
r = 17,96

Otrzymany czas

oziębiania się belki w punkcie 4, dla innych parametrów bez zmian,

wynosi 5 minut i 50 sekund.

-30

-25

-20

-15

-10

-5

0

0

200

400

600

800

1000

1200

1400

1600

te

m

p

T

[

o

C]

czas t [s]

Zależność temperatury w funkcji czasu T(t)

-10

-8

-6

-4

-2

0

0

50

100

150

200

250

300

350

400

te

m

p

T

[

o

C]

czas t [s]

Zależność temperatury w funkcji czasu T(t)

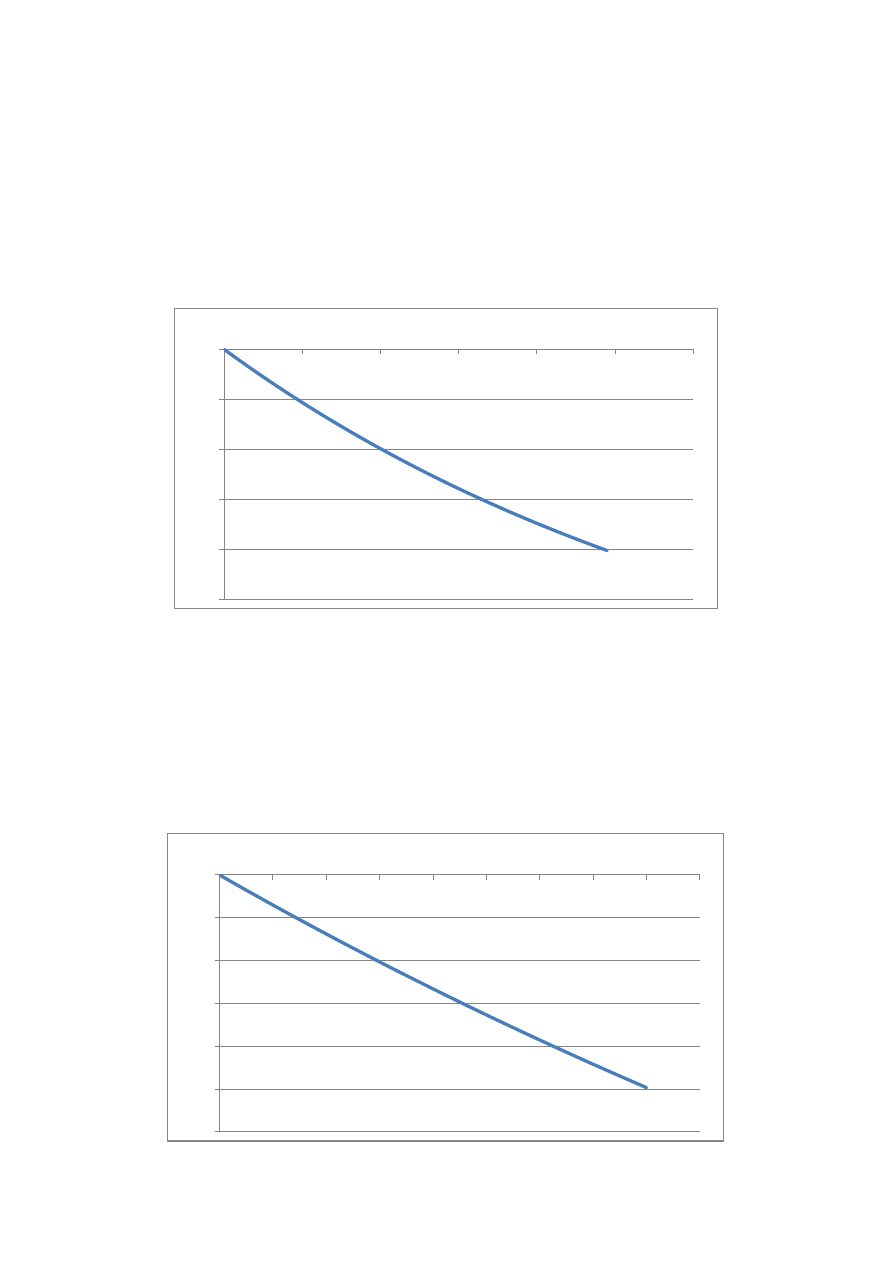
Oziębianie w punkcie 5.:

dt = 20 [s]
dx = 0,025 [m]
dy = 0,03125 [m]
r = 4,489

Otrzymany czas

oziębiania się belki w punkcie 5, dla innych parametrów bez zmian,

wynosi 16 minut i 20 sekund.

Oziębianie w punkcie 6.:

dt = 20 [s]
dx = 0,0125 [m]
dy = 0,0625 [m]
r = 4,489

Otrzymany czas

oziębiania się belki w punkcie 5, dla innych parametrów bez zmian,

wynosi 6 minut i 40 sekund.

-25

-20

-15

-10

-5

0

0

200

400

600

800

1000

1200

te

m

p

T

[

o

C]

czas t [s]

Zależność temperatury w funkcji czasu T(t)

-12

-10

-8

-6

-4

-2

0

0

50

100

150

200

250

300

350

400

450

te

m

p

T

[

o

C]

czas t [s]

Zależność temperatury w funkcji czasu T(t)

5. Weryfikacja otrz

ymanych wyników

Aby zweryfikować otrzymane wyniki ponownie przeprowadzamy obliczenia
w punkcie 0, dla innych

stałych czasowych Δt:

o

dla Δt = 5s (r=0,0175) czas nagrzania się belki to 90 minut i 55 sekund;

o

dla Δt = 15s (r=0,0526) czas nagrzania się belki to 91 minut;

o dla

Δt = 35s (r=0,1227) czas nagrzania się belki to 91 minut i 35 sekund;

o

dla Δt = 55s (r=0,1929) czas nagrzania się belki to 91 minut i 40 sekund

Po

przeprowadzonej weryfikacji wyników, można wnioskować, że rozwiązanie jest

prawidłowe. Dla różnych stałych czasowych wyniki są niemal jednakowe.